A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model for Predicting Shale Gas Production
Abstract
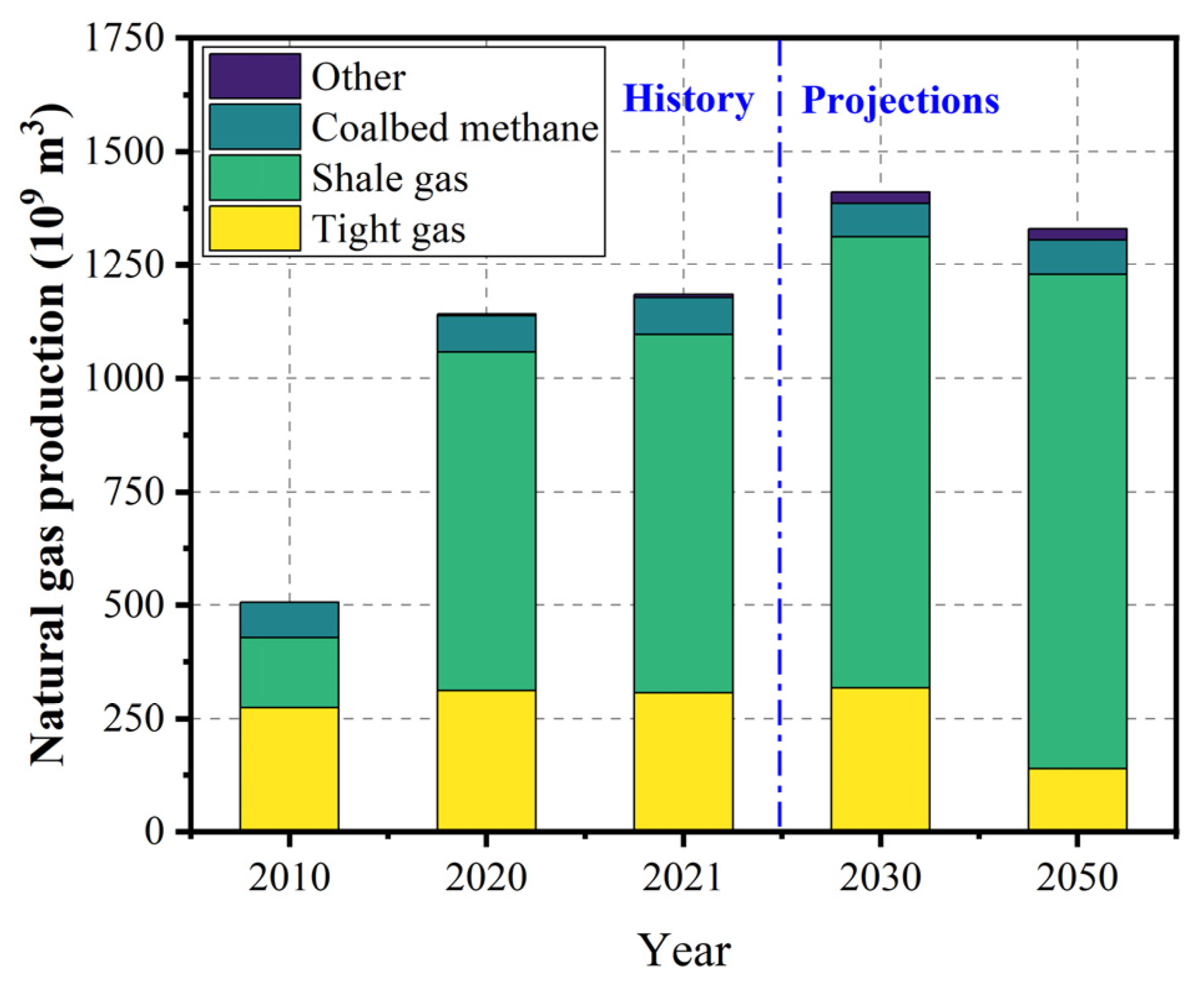
1. Introduction
2. Methodology
2.1. Embedded Discrete Fracture Model
2.2. GRU-MLP Combined Neural Network
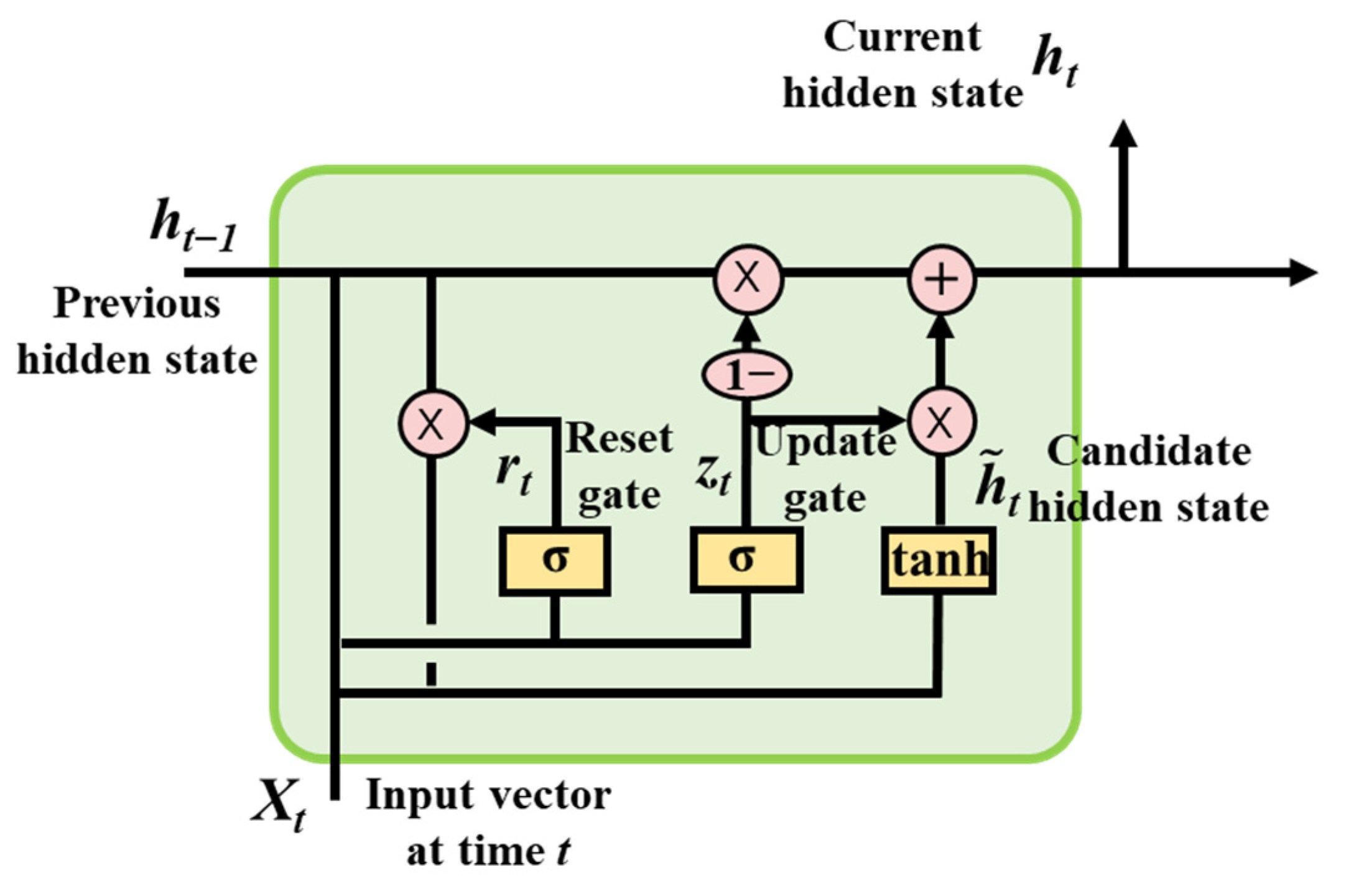
2.2.1. Gated Recurrent Unit (GRU)
2.2.2. Multilayer Perceptron (MLP)
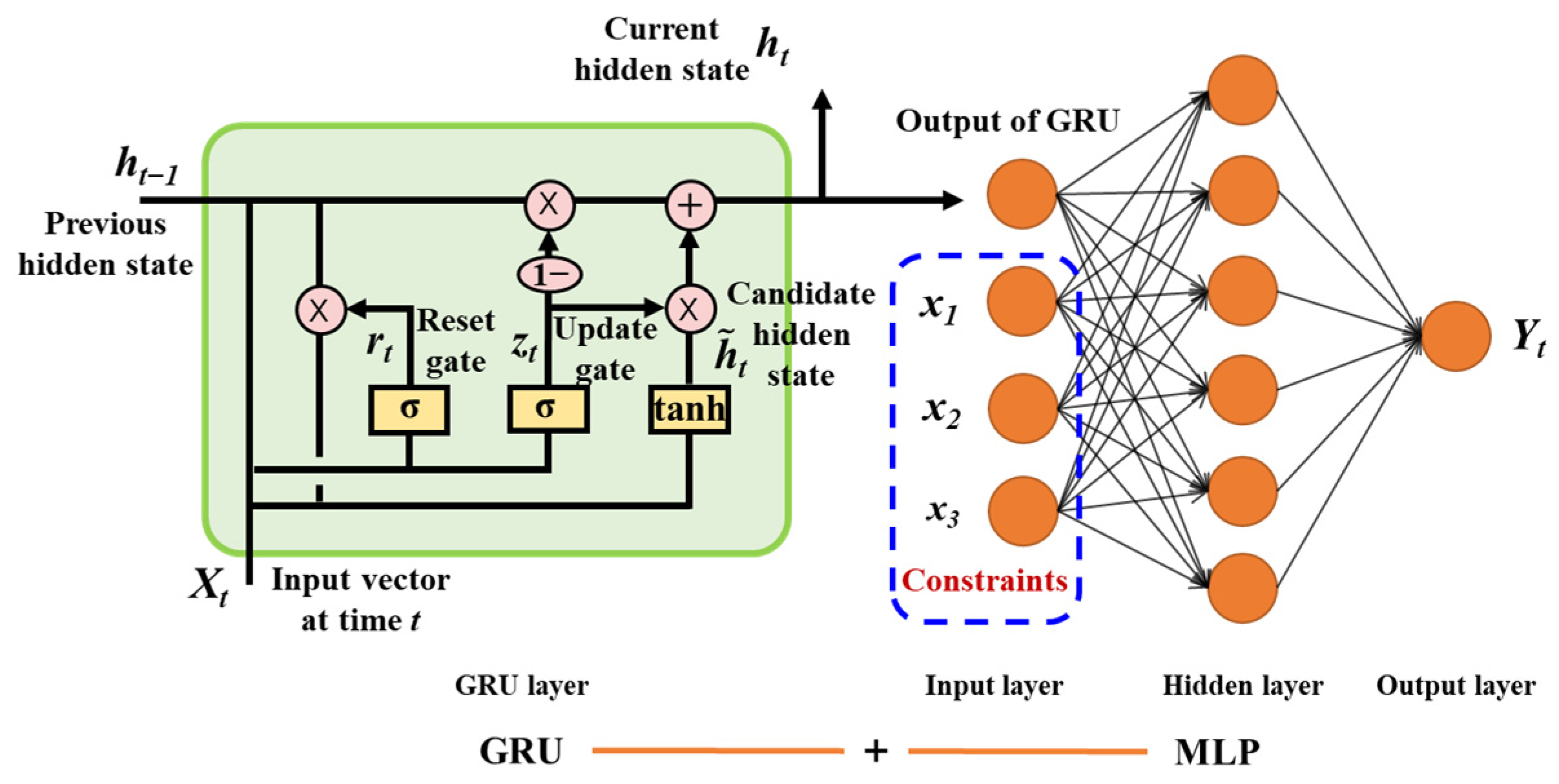
2.2.3. GRU-MLP Combined Neural Network
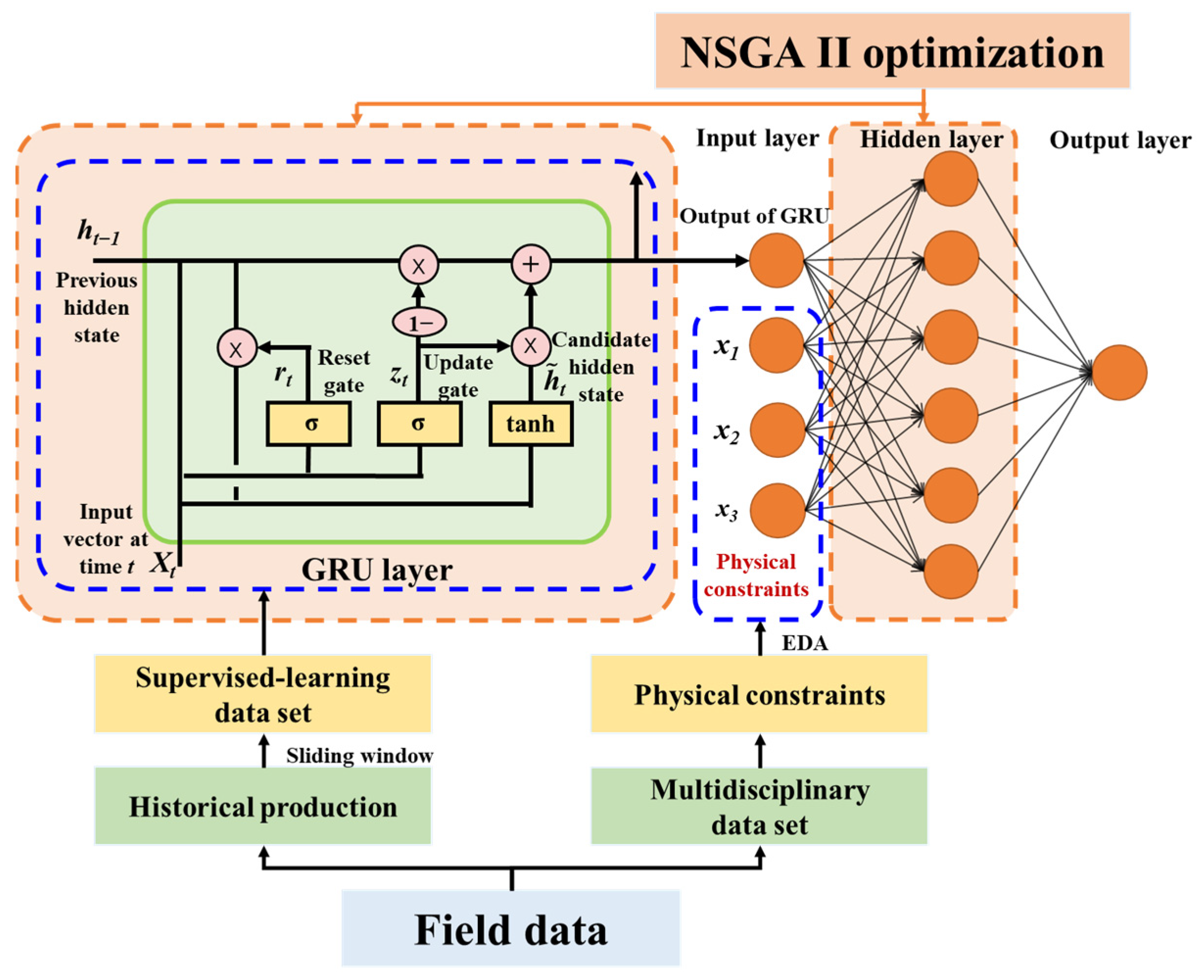
2.2.4. Workflow Based on the GRU-MLP Model
3. Field Application
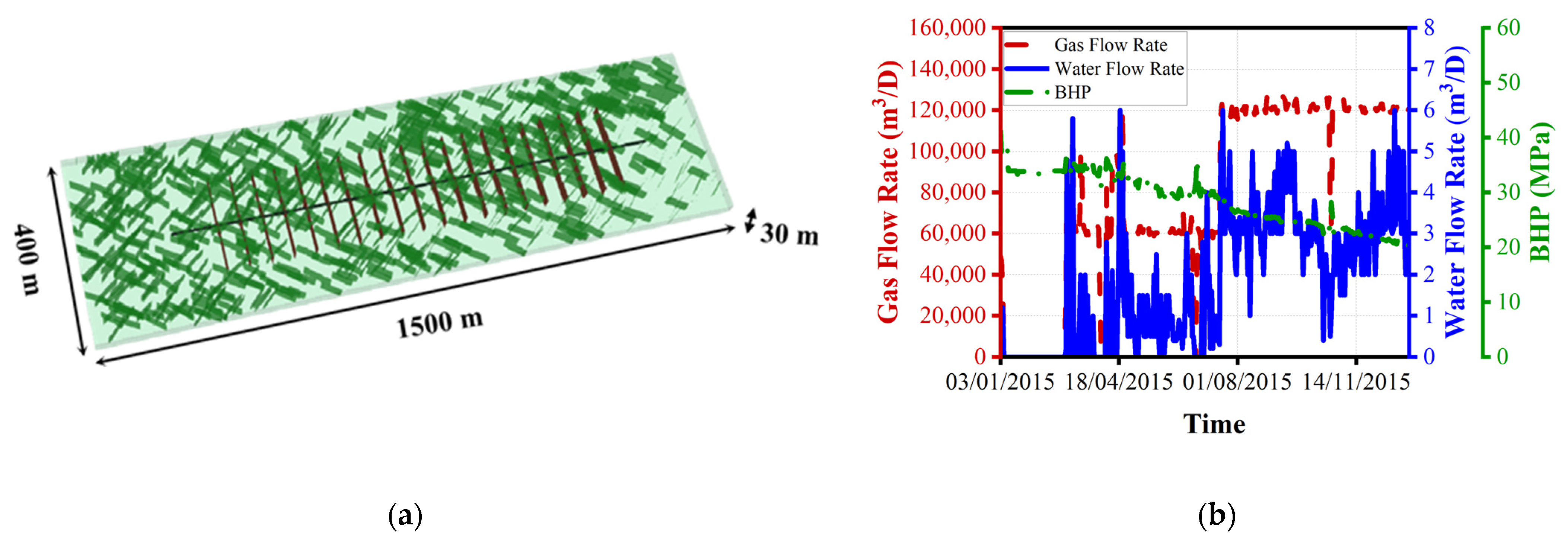
3.1. Reservoir Simulation Model
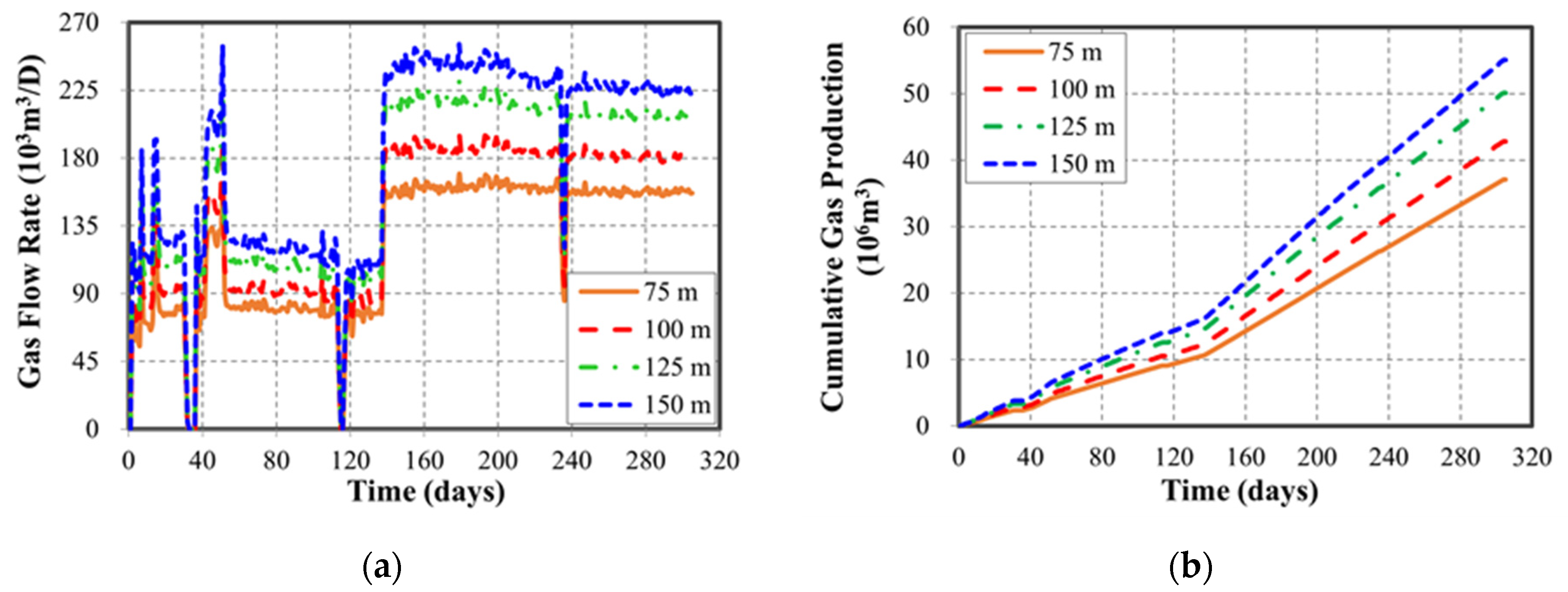
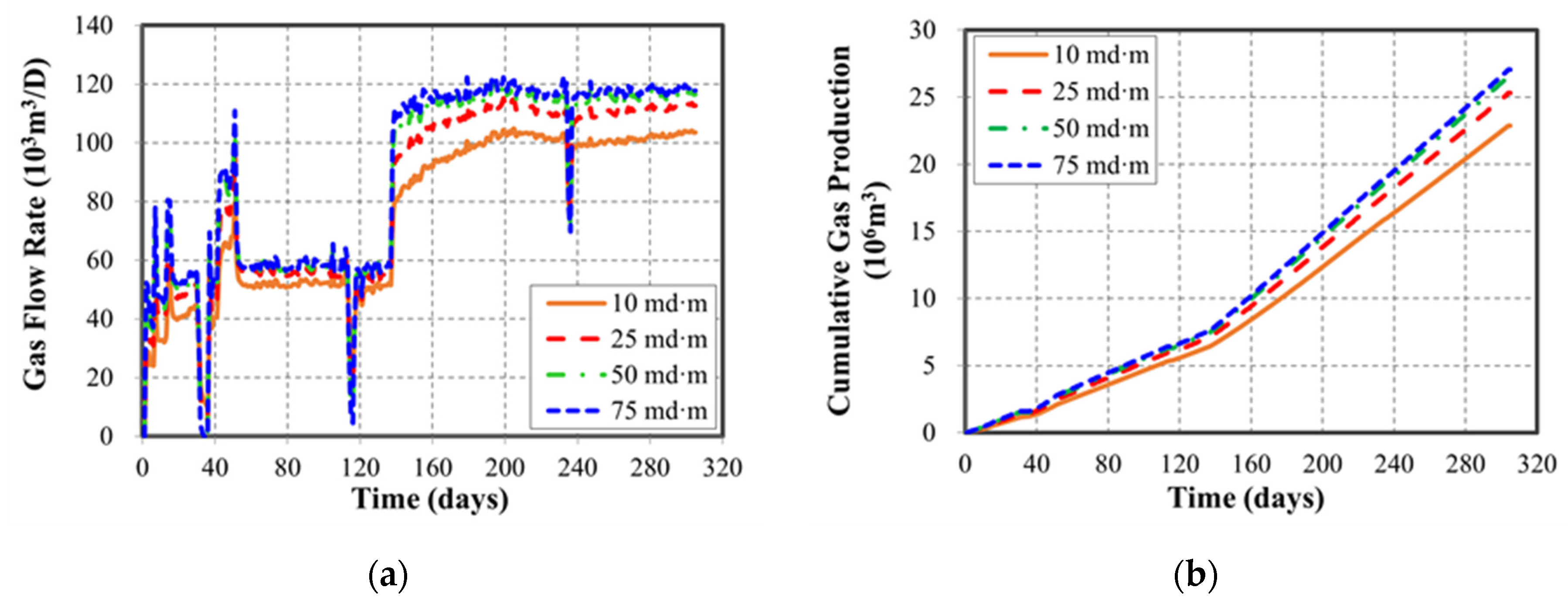
3.1.1. Effect of Hydraulic Fracture
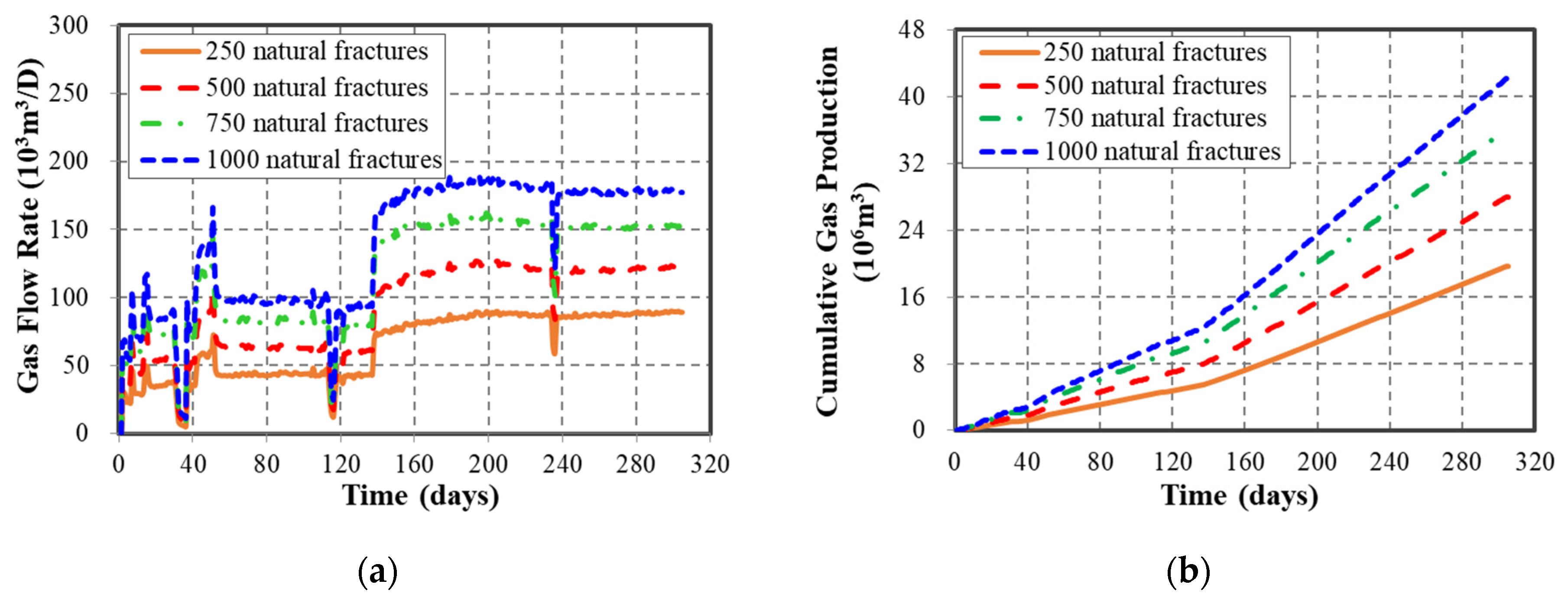
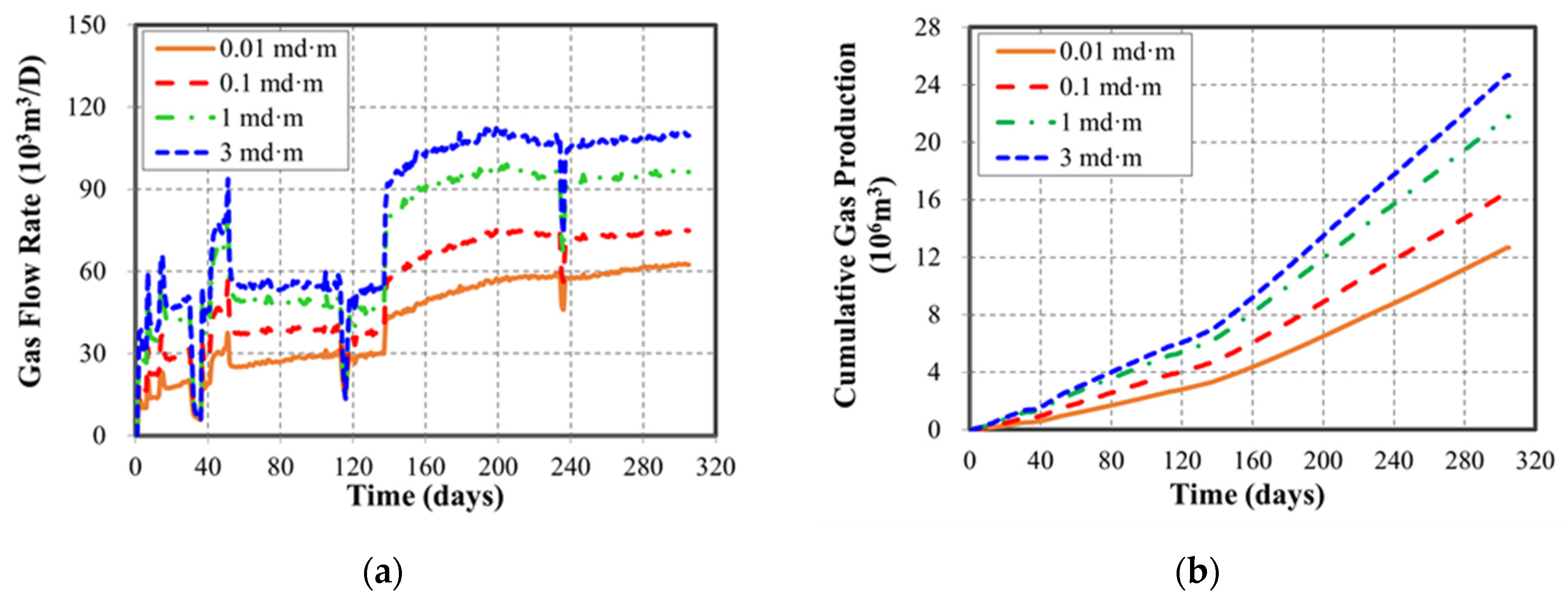
3.1.2. Effect of Natural Fracture
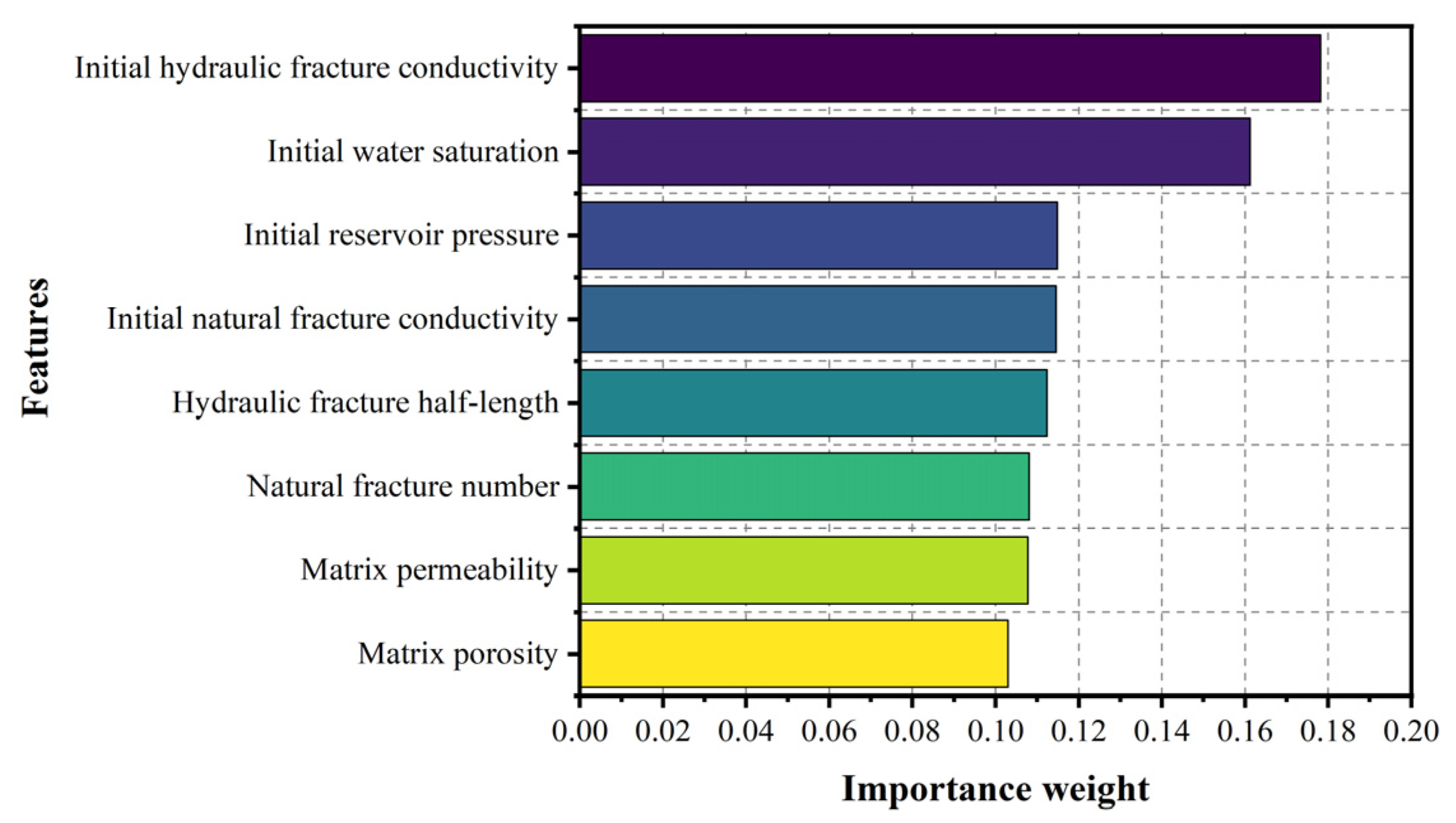
3.1.3. Sensitivity Analysis Results
3.1.4. Data Generating
3.2. GRU-MLP Model
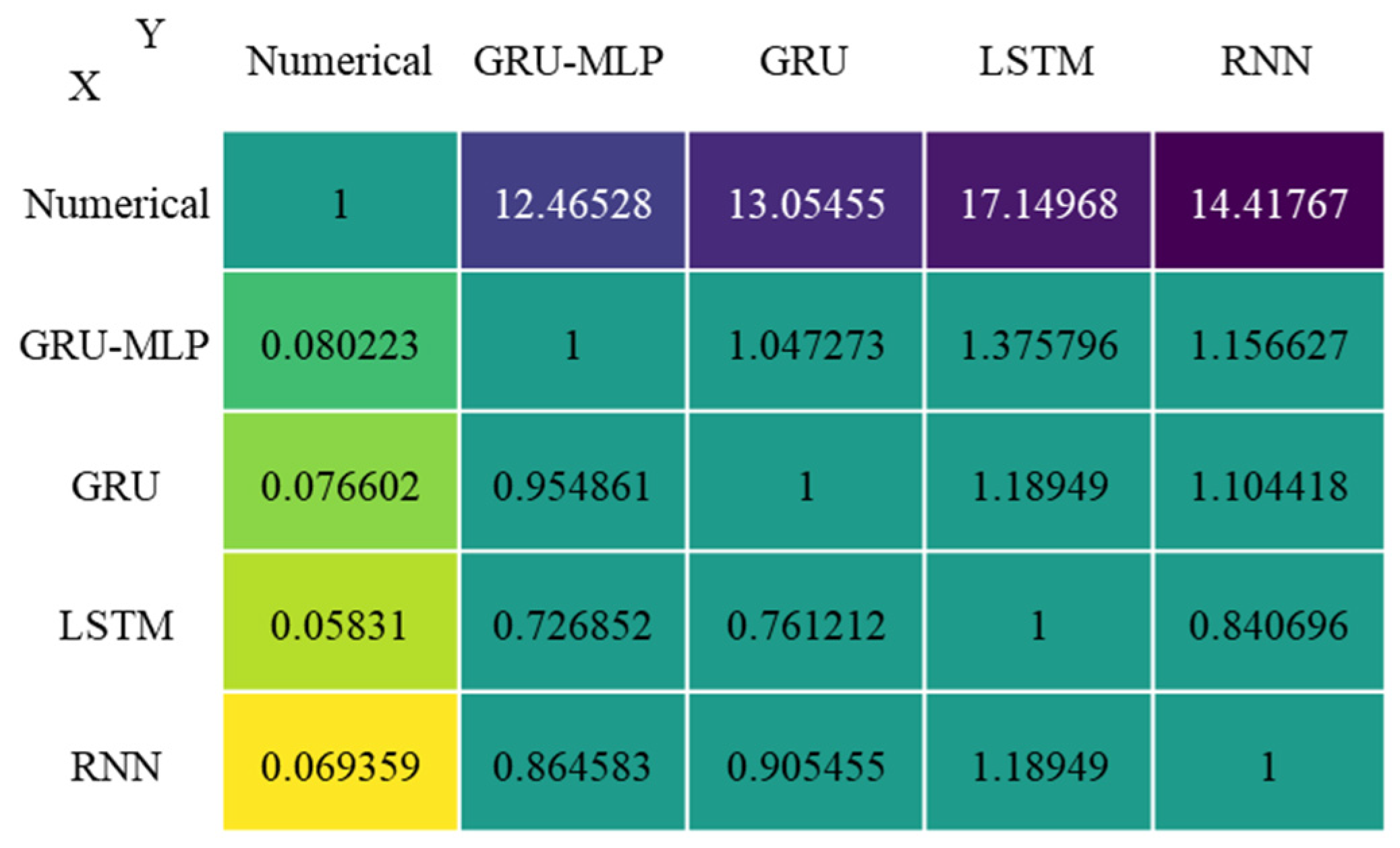
3.2.1. Error Comparisons
3.2.2. CPU-Time Comparison
Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Xiong, B.; Xue, H.; Zheng, D.; Ge, Z.; Wang, Y.; Jiang, L.; Pan, S.; Wu, S. The role of new energy in carbon neutral. Petrol. Explor. Dev. 2021, 48, 480–491. [Google Scholar] [CrossRef]
- Yang, R.; Liu, X.; Yu, R.; Hu, Z.; Duan, X. Long short-term memory suggests a model for predicting shale gas production. Appl. Energ. 2022, 322, 119415. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- Amorin, R.; Mensah, A. An Oil and Gas Retrofitted Carbon Capture Utilisation and Storage Value Chain: A Green Industry. J. Pet. Eng. Technol. 2022, 12, 10–18. [Google Scholar]
- Jukić, L.; Vulin, D.; Lukić, M.; Karasalihović Sedlar, D. Enhanced gas recovery and storability in a high CO2 content gas reservoir. Int. J. Greenh. Gas Con. 2022, 117, 103662. [Google Scholar] [CrossRef]
- Suriamin, F.; Ko, L.T. Chapter 2—Geological Characterization of Unconventional Shale-Gas Reservoirs. In Unconventional Shale Gas Development; Moghanloo, R.G., Ed.; Gulf Professional Publishing: Houston, TX, USA, 2022; pp. 33–70. [Google Scholar]
- Zhang, C.; Liu, S.; Ma, Z.; Ranjith, P. Combined micro-proppant and supercritical carbon dioxide (SC-CO2) fracturing in shale gas reservoirs: A review. Fuel 2021, 305, 121431. [Google Scholar] [CrossRef]
- Khormali, A.; Koochi, M.R.; Varfolomeev, M.A.; Ahmadi, S.J.J. Experimental study of the low salinity water injection process in the presence of scale inhibitor and various nanoparticles. Petrol. Explor. Dev. 2022, 13, 903–916. [Google Scholar] [CrossRef]
- Temizel, C.; Canbaz, C.; Aydin, H.; Wijaya, Z. A Deep Investigation of EOR/EGR and Stimulation Enhancement Methods in Unconventional Reservoirs. IOR 2021, 2021, 1–27. [Google Scholar]
- Wang, H.; Chen, L.; Qu, Z.; Yin, Y.; Kang, Q.; Yu, B.; Tao, W.-Q. Modeling of multi-scale transport phenomena in shale gas production—A critical review. Appl. Energ. 2020, 262, 114575. [Google Scholar] [CrossRef]
- Syed, F.I.; Muther, T.; Dahaghi, A.K.; Negahban, S. AI/ML assisted shale gas production performance evaluation. J. Pet. Explor. Prod. Technol. 2021, 11, 3509–3519. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, W.; Zhu, H.; Yin, Y.; Qu, Z. Review of Shale Gas Transport Prediction: Basic Theory, Numerical Simulation, Application of AI Methods, and Perspectives. Energy Fuels 2023, 37, 2520–2538. [Google Scholar] [CrossRef]
- Zhu, Q.; Lin, B.; Yang, G.; Wang, L.; Chen, M. Intelligent production optimization method for a low pressure and low productivity shale gas well. Petrol. Explor. Dev. 2022, 49, 886–894. [Google Scholar] [CrossRef]
- Koroteev, D.; Tekic, Z. Artificial intelligence in oil and gas upstream: Trends, challenges, and scenarios for the future. Energy AI 2021, 3, 100041. [Google Scholar] [CrossRef]
- Yang, R.Y.; Qin, X.Z.; Liu, W.; Huang, Z.W.; Shi, Y.; Pang, Z.Y.; Zhang, Y.Q.; Li, J.B.; Wang, T.Y. A Physics-Constrained Data-Driven Workflow for Predicting Coalbed Methane Well Production Using Artificial Neural Network. SPE J. 2022, 27, 1531–1552. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Lee, K.-K. Application of machine learning to predict CO2 trapping performance in deep saline aquifers. Energy 2022, 239, 122457. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Zamanyad, A.; Safaei-Farouji, M.; Ashraf, U.; Hemeng, Z. Application of hybrid artificial intelligent models to predict deliverability of underground natural gas storage sites. Renew Energy 2022, 200, 169–184. [Google Scholar] [CrossRef]
- Costa, L.A.N.; Maschio, C.; José Schiozer, D. Application of artificial neural networks in a history matching process. J. Petrol. Sci. Eng. 2014, 123, 30–45. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, F. Integrating linear and nonlinear forecasting techniques based on grey theory and artificial intelligence to forecast shale gas monthly production in Pennsylvania and Texas of the United States. Energy 2019, 178, 781–803. [Google Scholar] [CrossRef]
- Syed, F.I.; Alnaqbi, S.; Muther, T.; Dahaghi, A.K.; Negahban, S. Smart shale gas production performance analysis using machine learning applications. Pet. Res. 2022, 7, 21–31. [Google Scholar] [CrossRef]
- Nguyen-Le, V.; Shin, H. Artificial neural network prediction models for Montney shale gas production profile based on reservoir and fracture network parameters. Energy 2022, 244, 123150. [Google Scholar] [CrossRef]
- Niu, W.; Lu, J.; Sun, Y. Development of shale gas production prediction models based on machine learning using early data. Energy Rep. 2022, 8, 1229–1237. [Google Scholar] [CrossRef]
- Lee, K.; Lim, J.; Yoon, D.; Jung, H. Prediction of Shale-Gas Production at Duvernay Formation Using Deep-Learning Algorithm. SPE J. 2019, 24, 2423–2437. [Google Scholar] [CrossRef]
- Li, Y.; Sun, R.; Horne, R. Deep Learning for Well Data History Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September 2019. [Google Scholar]
- He, Q.; Chen, J.-S. A physics-constrained data-driven approach based on locally convex reconstruction for noisy database. Comput. Methods Appl. Mech. Eng. 2020, 363, 112791. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Xiao, F.; Xiao, C.; Wang, F.; Zhang, S. A physics-constrained long-term production prediction method for multiple fractured wells using deep learning. J. Petrol. Sci. Eng. 2022, 217, 110844. [Google Scholar] [CrossRef]
- Salehi, A.; Arslan, I.; Deng, L.; Darabi, H.; Smith, J.; Suicmez, S.; Castiñeira, D.; Gringarten, E. A Data-Driven Workflow for Identifying Optimum Horizontal Subsurface Targets. In Proceedings of the SPE Annual Technical Conference and Exhibition, 21–23 Paper presented at the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 21–23 September 2021. [Google Scholar]
- Park, J.; Datta-Gupta, A.; Singh, A.; Sankaran, S. Hybrid physics and data-driven modeling for unconventional field development and its application to US onshore basin. J. Petrol. Sci. Eng. 2021, 206, 109008. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient Field-Scale Simulation of Black Oil in a Naturally Fractured Reservoir Through Discrete Fracture Networks and Homogenized Media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Panfili, P.; Cominelli, A. Simulation of Miscible Gas Injection in a Fractured Carbonate Reservoir using an Embedded Discrete Fracture Model. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 10–13 November 2014. [Google Scholar]
- Shakiba, M.; Sepehrnoori, K. Using Embedded Discrete Fracture Model (EDFM) and Microseismic Monitoring Data to Characterize the Complex Hydraulic Fracture Networks. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Shakiba, M.; de Araujo Cavalcante Filho, J.S.; Sepehrnoori, K. Using Embedded Discrete Fracture Model (EDFM) in numerical simulation of complex hydraulic fracture networks calibrated by microseismic monitoring data. J. Nat. Gas Sci. Eng. 2018, 55, 495–507. [Google Scholar] [CrossRef]
- Zeng, Q.-D.; Yao, J.; Shao, J. Study of hydraulic fracturing in an anisotropic poroelastic medium via a hybrid EDFM-XFEM approach. Comput. Geotech. 2019, 105, 51–68. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.; Yu, W.; Sepehrnoori, K. Discrete-Fracture Modeling of Complex Hydraulic-Fracture Geometries in Reservoir Simulators. SPE Reserv. Eval. Eng. 2017, 20, 403–422. [Google Scholar] [CrossRef]
- Sun, J.; Ma, X.; Kazi, M. Comparison of Decline Curve Analysis DCA with Recursive Neural Networks RNN for Production Forecast of Multiple Wells. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 22–27 April 2018. [Google Scholar]
- Li, X.; Ma, X.; Xiao, F.; Xiao, C.; Wang, F.; Zhang, S. Intelligence-Driven Prediction of Shear Wave Velocity Based on Gated Recurrent Unit Network. In Proceedings of the 56th U.S. Rock Mechanics/Geomechanics Symposium, Santa Fe, NM, USA, 26–29 June 2022. [Google Scholar]
- Olah, C. Understanding Lstm Networks. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 27 August 2015).
- Siréta, F.-X.; Zhang, D. Smart Mooring Monitoring System for Line Break Detection from Motion Sensors. In Proceedings of the Thirteenth ISOPE Pacific/Asia Offshore Mechanics Symposium, Jeju, Republic of Korea, 14–17 October 2018. [Google Scholar]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Shi, Y.; Song, X.; Song, G. Productivity prediction of a multilateral-well geothermal system based on a long short-term memory and multi-layer perceptron combinational neural network. Appl. Energ. 2021, 282, 116046. [Google Scholar] [CrossRef]
- Yang, R.; Liu, W.; Qin, X.; Huang, Z.; Shi, Y.; Pang, Z.; Zhang, Y.; Li, J.; Wang, T. A physics-constrained data-driven workflow for predicting coalbed methane well production using a combined gated recurrent unit and multi-layer perception neural network model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirate, 21–23 September 2021. [Google Scholar]
- Nie, H.; Chen, Q.; Zhang, G.; Sun, C.; Wang, P.; Lu, Z. An overview of the characteristic of typical Wufeng–Longmaxi shale gas fields in the Sichuan Basin, China. NGIB 2021, 8, 217–230. [Google Scholar] [CrossRef]
- Yang, R.-Y.; Li, G.-S.; Qin, X.-Z.; Huang, Z.-W.; Li, J.-B.; Sheng, M.; Wang, B. Productivity enhancement in multilayered coalbed methane reservoirs by radial borehole fracturing. Pet. Sci. 2022, 19, 2844–2866. [Google Scholar] [CrossRef]
- Wang, T.; Tian, S.; Zhang, W.; Ren, W.; Li, G. Production model of a fractured horizontal well in shale gas reservoirs. Energ. Fuel 2020, 35, 493–500. [Google Scholar] [CrossRef]
- Ahmadi, S.; Khormali, A.; Khoutoriansky, F.M. Optimization of the demulsification of water-in-heavy crude oil emulsions using response surface methodology. Fuel 2022, 323, 124270. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Hydraulic fracture properties | ||
| Hydraulic fracture half-length | 75, 100, 125, 150 | m |
| Initial hydraulic fracture conductivity | 10, 25, 50, 75 | mD·m |
| Natural fractures properties | ||
| Natural fracture number | 250, 500, 750, 1000 | - |
| Initial natural fracture conductivity | 0.01, 0.1, 1 3 | mD·m |
| Parameter | Value | Unit |
|---|---|---|
| Reservoir properties | ||
| Model dimensions [L × W × H] | 1500 × 400 × 30 | m |
| Reservoir temperature | 80 | °C |
| Reservoir depth | 3000 | m |
| Initial reservoir pressure | 35 | MPa |
| Matrix permeability | 0.0009 | mD |
| Matrix porosity | 0.08 | % |
| Reservoir thickness | 30 | m |
| Initial water saturation | 35 | % |
| Hydraulic fracture properties | ||
| Hydraulic fracture number | 20 | - |
| Hydraulic fracture spacing | 50 | m |
| Hydraulic fracture half-length | 100 | m |
| Hydraulic fracture width | 0.025 | m |
| Initial hydraulic fracture conductivity | 10 | mD·m |
| Natural fracture properties | ||
| Natural fracture number | 800 | - |
| Natural fracture width | 0.001 | m |
| Initial natural fracture conductivity | 3.5 | mD·m |
| Well parameters | ||
| Wellbore diameter | 0.057 | m |
| Horizontal length | 600 | m |
| Numerical Model(s) | GRU-MLP(s) | GRU(s) | LSTM(s) | RNN(s) | |
|---|---|---|---|---|---|
| Gas | 107.7 | 8.64 | 8.25 | 6.28 | 7.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Hu, X.; Liu, H.; Shi, W.; Cui, J. A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model for Predicting Shale Gas Production. Processes 2023, 11, 806. https://doi.org/10.3390/pr11030806
Qin X, Hu X, Liu H, Shi W, Cui J. A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model for Predicting Shale Gas Production. Processes. 2023; 11(3):806. https://doi.org/10.3390/pr11030806
Chicago/Turabian StyleQin, Xiaozhou, Xiaohu Hu, Hua Liu, Weiyi Shi, and Jiashuo Cui. 2023. "A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model for Predicting Shale Gas Production" Processes 11, no. 3: 806. https://doi.org/10.3390/pr11030806
APA StyleQin, X., Hu, X., Liu, H., Shi, W., & Cui, J. (2023). A Combined Gated Recurrent Unit and Multi-Layer Perception Neural Network Model for Predicting Shale Gas Production. Processes, 11(3), 806. https://doi.org/10.3390/pr11030806





