Research on an Adaptive Compound Control Strategy of a Hybrid Compensation System

Abstract

This paper investigates the parallel harmonic resonance problem for hybrid compensation systems, consisting of active power filters and thyristor-switched capacitors, and proposes an adaptive composite control strategy for solving the parallel harmonic resonance problem that may arise in practical applications of hybrid compensation systems. In practice, a hybrid compensation system can effectively solve harmonic and reactive power problems, but the equivalent reactance of the thyristor-switched capacitor and the supply line may form a parallel resonant circuit, which may generate parallel harmonic resonance when excited by a harmonic source at the non-linear load side, affecting the quality and stable operation of the system. The adaptive composite control strategy employs a second-order generalized integrator-frequency-locked loop (SOGI-FLL) to extract the harmonic voltage at the point of common coupling (PCC) and generate an adaptive damping current command using an adaptive algorithm, which adaptively adjusts the parameters of the resonance suppression controller through harmonic content limitation. Matlab/Simulink simulations show that the method effectively achieves harmonic resonance suppression of the power supply system under complex operating conditions, thus ensuring the stable operation and power quality of the power supply system. Therefore, the proposed control strategy is feasible and effective.

1. Introduction

The rapid development of power electronics has led to their increasing popularity and usage in distribution grids, resulting in a significant rise in non-linear loads [1,2,3,4]. These loads generate notable harmonic currents and reactive power losses that have adverse impacts on both power quality and economic operation [5,6,7,8,9]. To address this issue, a hybrid compensation system that combines an Active Power Filter (APF) and a Thyristor Switching Capacitor (TSC) has been utilized [10,11,12]. The TSC enables graded reactive power compensation [13], while the APF compensates for harmonics and provides step-less continuous compensation of reactive power between TSC stages [14]. This system achieves simultaneous reactive power compensation and harmonic current suppression, resulting in excellent compensation effects and better economy [15,16]. As a result, this hybrid system has been widely adopted. However, in weak grids, the TSC capacitive impedance and the grid-side inductive impedance can form a parallel resonant network for this system [17,18]. Under these circumstances, harmonic currents in the load current near the resonant frequency can excite parallel resonance in the system [19,20], resulting in increased harmonic content and additional distortion of the voltage waveform, negatively impacting power quality and seriously affecting power consumption of other loads [21,22,23].

In order to solve the resonance problem in the operation of hybrid compensation systems, researchers have mostly adopted active damping control methods in APF. Dahono, P.A. [24] first proposed an active resistance control algorithm to replace the actual damping resistor, which generates a negative resonant peak to cancel out the positive resonant peak produced by the original system transfer characteristic, thereby suppressing system resonance. Gao et al. [25] and Xu et al. [26] proposed a control method utilizing capacitor current feedback to obtain virtual damping for suppressing harmonic resonance in the system. However, this method increases the additional equipment costs of the power system due to the need for extra capacitor voltage sensors. Du et al. [27] presented an adaptive resonance damping strategy based on the least mean squares algorithm. This method compensates for the phase lag caused by control delay by predicting the current waveform, avoiding negative impedance characteristics of the filter, and eliminating resonance risks. However, the calculation process is complex. Huang et al. [28] designed a double-loop control system, in which the inner loop of the grid-connected inverter system based on virtual impedance uses the second-order differential term of the grid current to suppress the inherent resonance frequency of the LCL filter; the outer loop directly controls the grid current as the controlled object, forming a double-loop control system. However, due to the reduction in the feedback state variables, the system is prone to oscillate when the grid voltage contains harmonic components, which reduces the anti-interference ability of the inverter system.

The use of harmonic compensation or resonance damping methods alone often fails to meet the requirements of practical applications. Therefore, a composite control strategy has emerged, combining the functions of harmonic compensation and resonance damping to achieve better harmonic control effects. Wu et al. [29] added an additional damping control algorithm based on PCC voltage feedback to the harmonic compensation control in APFs to form a harmonic compensation and resonance damping composite control algorithm. This composite control method uses the sensing of harmonic resonance information via PCC voltage to achieve harmonic compensation and resonant suppression in APF devices. However, the paper only conducted theoretical analysis, without specific application cases. Chen et al. [30] studied a harmonic compensation and resonance damping composite control strategy based on hybrid compensation systems that achieve the basic functions of reactive power and harmonic compensation while also possessing the capability for harmonic resonance suppression. However, the harmonic resonance suppression of this strategy is designed based on specific system conditions, and its effectiveness will quickly deteriorate with changes in those conditions, resulting in poor adaptability. To solve this adaptability problem, Yu et al. [31] proposed a resonance suppression method based on harmonic current frequency compensation, which designs different compensation commands based on the comparison of the harmonic current frequency to be compensated and the resonant frequency, thereby adapting to changes in grid parameters to achieve certain adaptability. However, the entire control process of this method requires continuous frequency comparison, data acquisition, and calculation, which is labor-intensive and has a high engineering implementation difficulty. Cheng et al. [32] proposed a composite control strategy that uses the discrete Fourier algorithm to extract resonant voltage at the PCC point and revise the control parameters based on this voltage value. However, this control algorithm requires prior knowledge of the resonance frequency of the system and can only perform resonance damping under specific grid parameters.

In summary, if the grid is weak, the inductive impedance on the grid side and the capacitive impedance of the TSC in a hybrid compensation system will create a parallel resonant grid [33]. This can cause harmonic resonance to occur at the load side, which can damage the quality of the power supply. Researchers have proposed a composite control strategy for harmonic compensation and resonance damping based on APF harmonic compensation control in hybrid compensation systems [34]. However, the traditional hybrid compensation system’s additional damping control technology mostly relies on the system’s inherent parameters. Existing adaptive design solutions still have issues with suitability and flexibility for engineering implementation, which cannot adapt to the current complex and changing power supply system. To address these problems, this paper proposes a new adaptive additional damping composite control strategy based on the composite control strategy for hybrid compensation systems. The control strategy uses a second-order generalized integrator-frequency-locked loop (SOGI-FLL) to obtain the harmonic voltage content at the common coupling point, which indirectly reflects changes in the system’s operating conditions. It then adaptively adjusts the parameters of the resonance suppression controller by limiting the harmonic content at the common coupling point. This is carried out to design and achieve harmonic resonance suppression of the system under complex transformation operating conditions.

2. Hybrid Compensation Systems and Composite Control Strategies

This section provides a brief introduction to the components and operating principles of hybrid compensation systems, establishes the equivalent circuit model and mathematical model of the hybrid compensation system, and analyzes and discusses the root causes of harmonic resonances generated by the hybrid compensation system. The traditional harmonic compensation and resonance suppression composite control strategy is then introduced and explained, providing the basis for further research.

2.1. Hybrid Compensation Systems and Harmonic Resonance Issues

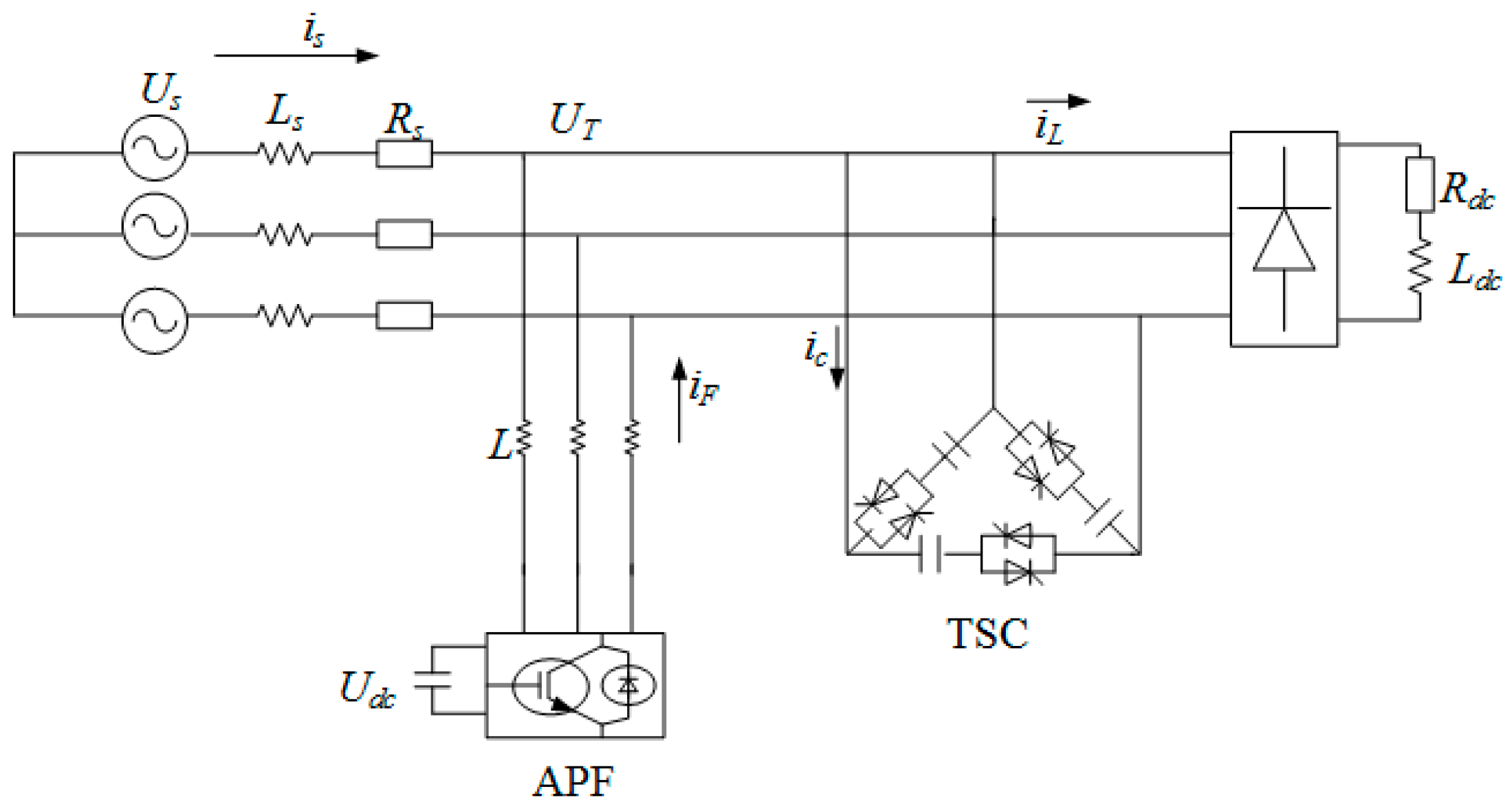
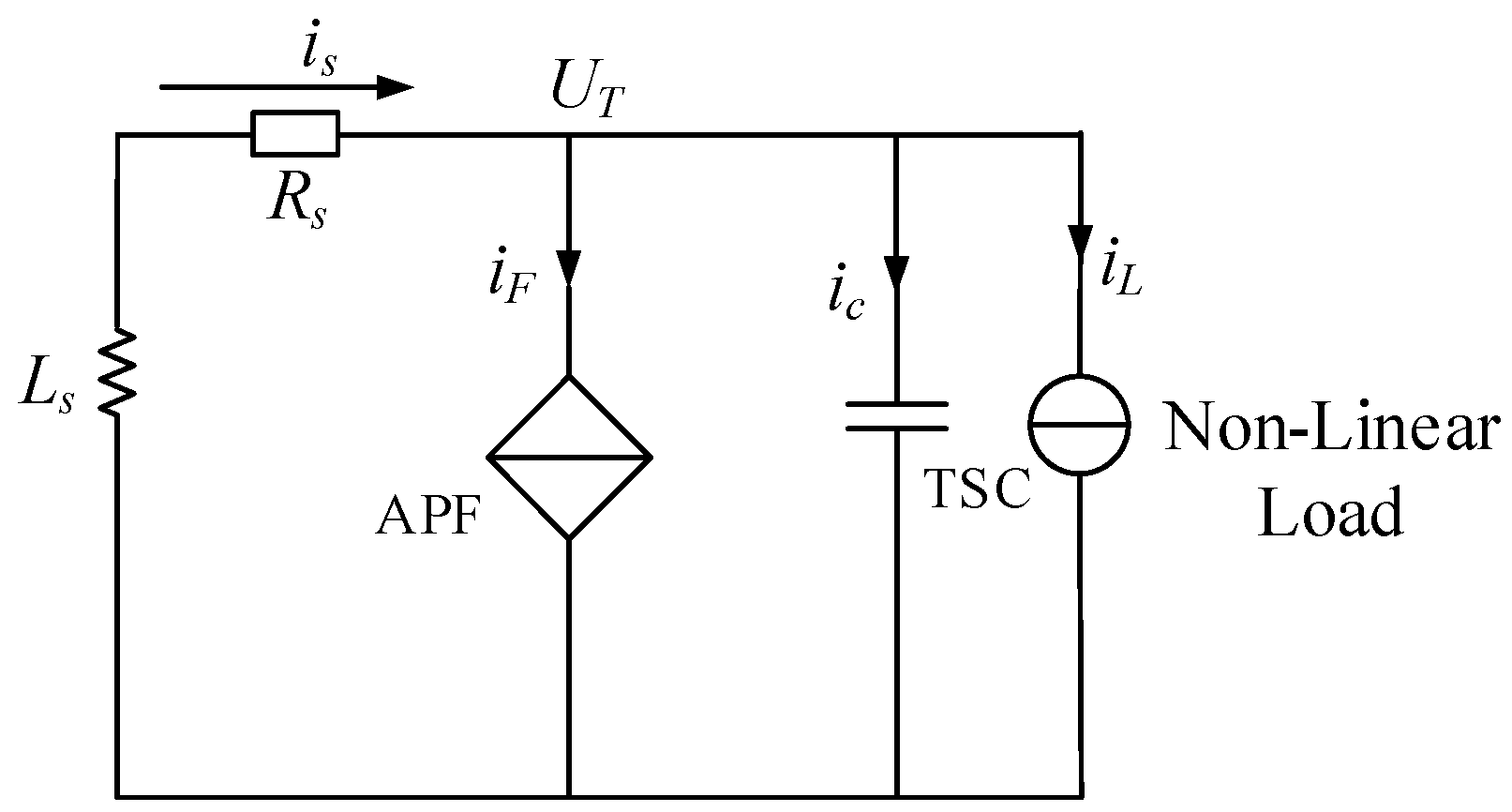
2.1.1. How Hybrid Compensation Systems Work

The system schematic of the hybrid compensation system is shown in Figure 1. The main circuit consists of a three-phase voltage source, APF, multiple sets of TSC, and a three-phase uncontrollable rectifying inductive load. The APF and TSC are connected in parallel to the grid to form a hybrid compensation system. The APF is composed of a voltage-source inverter and an L-type filter, which realizes harmonic compensation actively. The TSC is composed of multiple sets of TSC connected in a triangle and controlled by anti-parallel thyristors to realize passive reactive power compensation. In the figure, $U_s$, $i_s$ are the grid-side supply voltage and current, respectively. $U_T$ is the voltage at the PCC point where the hybrid compensation system is connected, $L_s$ and $R_s$ are the equivalent inductance and resistance of the grid-side line, $i_c$ is the reactive power compensation current of the TSC, $i_F$ is the harmonic compensation current of the APF, and $i_L$ is the load current. The uncontrollable rectifier bridge, resistor $R_{dc}$, and inductor $L_{dc}$ are used to simulate the nonlinear load and harmonic source under actual operating conditions.

The hybrid compensation system initially adjusts the TSC capacitor throw in response to changes in grid load, enabling graded compensation of larger capacity reactive power through the TSC. It then achieves precise reactive power compensation between layers using the APF, while also suppressing harmonics. This combination of TSC’s economy and reliability with APF’s accuracy and flexibility has made it widely used in power supply systems [16]. However, in practical applications, it has been observed that under specific operating conditions, harmonic currents at the load side may affect the distribution system, resulting in more severe harmonic resonance phenomena that seriously impact power quality and normal system operation.

2.1.2. Parallel Resonance and the Effects of Hybrid Compensation Systems

Based on the hybrid compensation system depicted in Figure 1, the parallel resonant circuit formed by the TSC and the equivalent impedance of the grid and the equivalent circuit of the harmonic excitation source is shown in Figure 2. To simplify the analysis, the three-phase circuit is reduced to a single-phase circuit in the case of three-phase symmetry. This paper considers only the resonant component in the analysis, so the resonant circuit equivalence process treats the frequency voltage source as a short circuit, the APF as a controlled current source, and the non-linear load as an excitation harmonic current source. In the figure, $i_L$ is the load current and $i_F$, $i_c$ are the currents flowing into the APF and TSC, respectively, while $U_T$ is the voltage of the hybrid compensation system at the PCC point.

As shown in Figure 2, the TSC and the equivalent impedance of the grid form a parallel resonant grid, which may be excited by the non-linear harmonic source and result in a parallel resonance phenomenon. Simultaneously, owing to the small equivalent resistance $R_s$ of the parallel resonant circuit, a large harmonic voltage is generated, which in turn generates a large harmonic resonant current in the parallel resonant circuit. This can severely affect the voltage at the PCC node and degrade the power quality of the system, thereby affecting the normal power consumption of customers [35].

2.2. Composite Control Strategies and Issues

As indicated by the analysis in Section 2.1.2, the hybrid compensation system encounters issues such as harmonic resonance caused by parallel resonance. To address this problem, the industry typically utilizes the Active Power Filter (APF) in the hybrid compensation system, which is based on traditional harmonic compensation control technology, and incorporates additional damping control technology to form a composite control strategy. This strategy aims to achieve harmonic compensation while suppressing resonance, thereby ensuring the safe operation of the hybrid compensation system. In the composite control strategy, the harmonic compensation command employs a recursive discrete Fourier algorithm to extract the harmonic components of the current, and its control still employs traditional control methods, which will not be reiterated in this paper.

The equivalent control principle based on the traditional composite control strategy is shown in Figure 3. In contrast to Figure 2, the APF output current (i.e., composite control current) $i_F$ contains an additional harmonic resonance suppression current component, in addition to the harmonic compensation current. This harmonic resonance suppression current is generated using the measured PCC node voltage, and it is equivalent to creating a virtual resistor in the resonant circuit in order to suppress harmonic resonance. The diagram shows the composite control strategy controller consisting of $K_v$, $K_h$, and $G_c$, and $K_v$ is the resonance damping gain, $K_h$ is the harmonic suppression gain, and $G_c$ is the closed loop transfer gain of the current tracking link. $i_r^{\ast }$, $i_h^{\ast }$, and $i_F^{\ast }$, respectively, represent the expected compensation values for the harmonic compensation current, the resonant damping current, and the composite control current.

According to Kirchhoff’s Voltage Law, Figure 3 can be used to obtain the PCC voltage, as shown in Equation (1):

$$U_T=\left(i_L-i_c\right)\frac{L_{S}s+R_s}{L_{s}C{s}^2+R_{s}Cs+1}$$

(1)

$i_r^{\ast }$ and the PCC node voltages $U_T$, $i_h^{\ast }$ and the load currents $i_L$ are related as in Equations (2) and (3), respectively:

$$i_r^{\ast }=K_v{U}_T$$

(2)

$$i_h^{\ast }=K_h{i}_L$$

(3)

The compound control current $i_F$ is shown in Equation (4):

$$i_F=G_c{i}_F^{\ast }=G_c\left(i_h^{\ast }+i_r^{\ast }\right)=G_c\left(K_h{i}_L+K_v{U}_T\right)$$

(4)

Thus, we can deduce the transfer functions of the PCC node voltage and load current, as well as the net measurement current and load current, based on the schematic diagram in Figure 3, as shown in Equation (5):

$$\left\{\begin{array}{c}\frac{U_T}{i_L}=\frac{\left(1-G_c{K}_h\right)\left(L_{s}s+R_s\right)}{L_{s}C{s}^2+\left(R_{s}C+G_c{K}_v{L}_s\right)s+1+G_c{K}_v{R}_s}\\ \frac{i_s}{i_L}=\frac{1-G_c{K}_h}{L_{s}C{s}^2+\left(R_{s}C+G_c{K}_v{L}_s\right)s+1+G_c{K}_v{R}_s}\end{array}\right.$$

(5)

Equation (5) illustrates the impact of load current on both the PCC voltage and grid-side current, with the ratio indicating the composite control strategy’s ability to compensate for harmonic voltage at the PCC point and grid harmonic current.

From Equation (5), the characteristic equation can be obtained as shown in Equation (6):

$$L_{s}C{s}^2+\left(R_{s}C+G_c{K}_v{L}_s\right)s+1+G_c{K}_v{R}_s=0$$

(6)

As the net-side equivalent resistance is very small and negligible, when the cut-off frequency of the current closed-loop controller is high enough with good current tracking accuracy, $G_c$ can be approximated as 1. Using this approximation, a simplified expression for the damping ratio ζ can be derived from the characteristic equation as follows:

$$\zeta =\frac{K_v}{2}\sqrt{\frac{L_s}{C}}$$

(7)

As shown in Equation (7), increasing $K_v$ results in a further increase in the damping ratio ζ. According to classical control theory, the resonance peaks of the closed-loop transfer function amplitude-frequency characteristics can be effectively suppressed when ζ $\ge$ $\sqrt{2}$/2.

Equation (8) can be derived from the analysis above:

$$\zeta =\frac{K_v}{2}\sqrt{\frac{L_s}{C}}\ge \frac{\sqrt{2}}{2}$$

(8)

As a result, the expression for $K_v$ can be obtained as Equation (9):

$$K_v\ge \sqrt{\frac{2C}{L_s}}$$

(9)

In this case, the value of $K_v$ can be determined by taking into account the system circuit parameters and the necessary damping requirements. The value $K_h$ in the hybrid control strategy of harmonic suppression and harmonic resonance damping is a fixed value. To further analyze the impact of different system conditions on control quality under specific compound control parameters, this paper provides the Bode plots of the transfer functions of the PCC node voltage to load current ratio ($U_T$/$i_L$) and the grid-side current to load current ratio ($i_s$/$i_L$). These plots are based on typical system parameters for two different operating conditions. The circuit parameters for operating condition one are L_s = 340 μH and C = 250 μF, while the circuit parameters for operating condition two are L_s = 340 μH and C = 610 μF. Figure 4 shows the Bode plots for these two conditions.

As can be seen from the amplitude-frequency characteristic curves in Figure 4a,b, based on the set compound control parameters, that the amplitude–frequency characteristics of $U_T$/$i_L$ and $i_s$/$i_L$ are smoother under operating condition one, and there are no resonance peaks in the entire frequency range. However, under operating condition two, resonance peaks appear in specific frequency bands in both $U_T$/$i_L$ and $i_s$/$i_L$ amplitude–frequency characteristics, indicating the possibility of harmonic resonance under specific operating conditions.

Through the above discussion and analysis, it can be seen that the existing hybrid compensation system with fixed compound control parameters can operate stably under specific operating conditions, effectively suppressing harmonic resonance while achieving hybrid compensation function. However, when the system operating conditions change, resonance peaks may still exist, which may cause parallel resonance in specific frequency bands.

3. Adaptive Hybrid Control Strategy

In order to adapt to the complex and variable power system operating conditions and ensure the operating capability and quality of the hybrid compensation system during complex operating conditions, this paper proposes a new adaptive composite control strategy based on the existing hybrid compensation system composite control strategy for harmonic resonance suppression in composite control. The strategy uses the detected PCC node voltages to generate adaptive damping current commands through an adaptive algorithm, whose control parameters can vary with the operating conditions and can achieve harmonic resonance suppression of the power supply system under complex operating conditions. The diagram of the hybrid compensation system based on adaptive composite control is shown in Figure 5.

As shown in Figure 5, the working principle of the adaptive hybrid control is as follows: the harmonic voltage is obtained by extracting the harmonic resonance voltage from the PCC node voltage $U_T$, and then the adaptive algorithm is used to obtain the resonance damping gain $K_v$ and the resonance damping current $i_r^{\ast }$. The harmonic compensation command current $i_h^{\ast }$ can be obtained by sampling and filtering the load current $i_L$, and the composite control command current $i_F^{\ast }$ of the APF can be obtained by adding the resonance damping command current and the harmonic compensation command current. The command current $i_F^{\ast }$ is then controlled by a proportional-integral (PI) parallel repetitive control current tracking control strategy to achieve the control of the composite command current, ultimately achieving adaptive hybrid control of harmonic compensation and resonance damping.

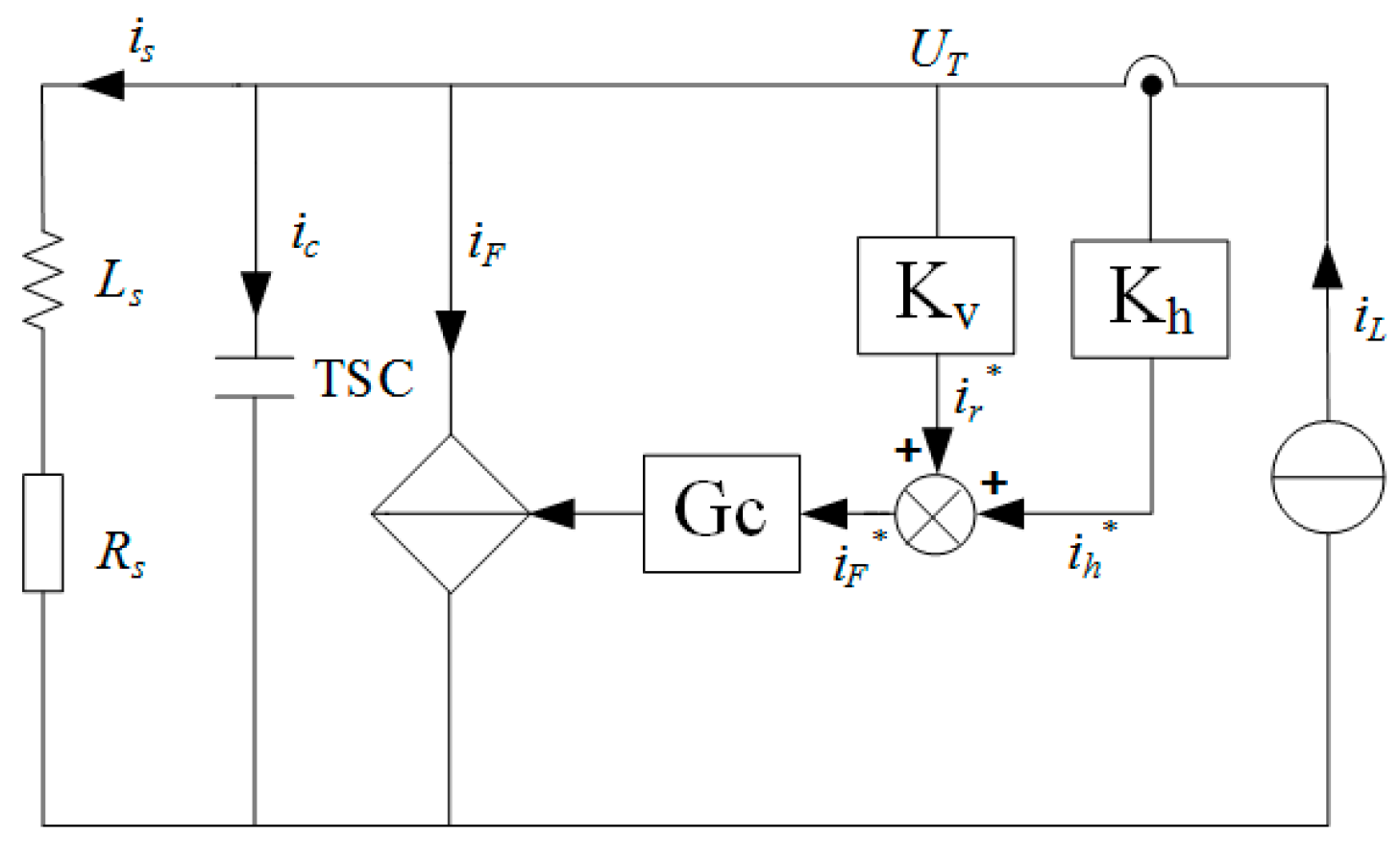
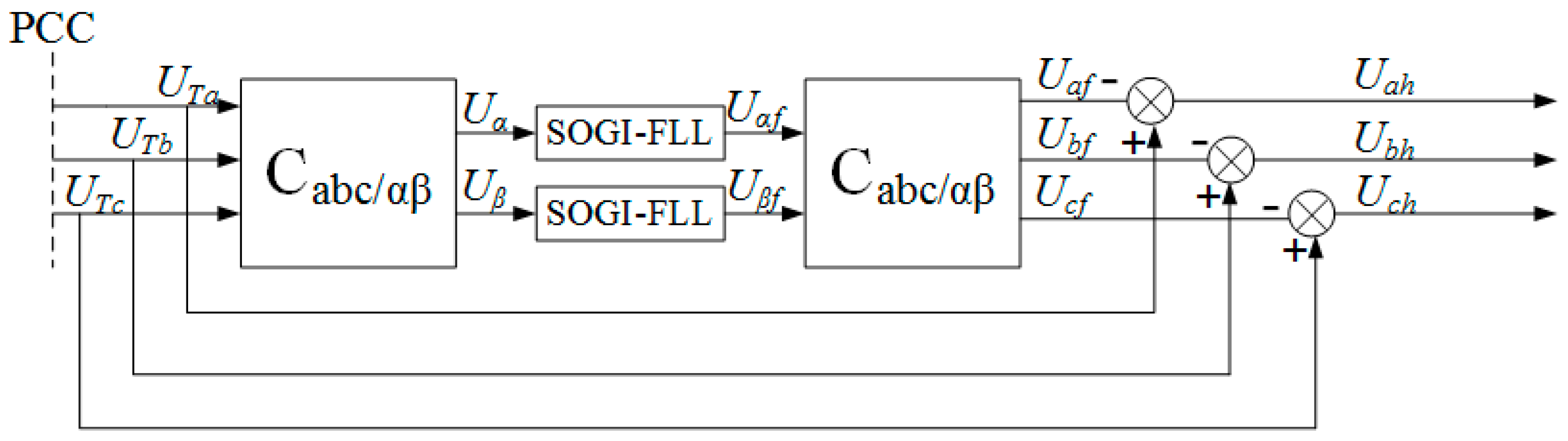
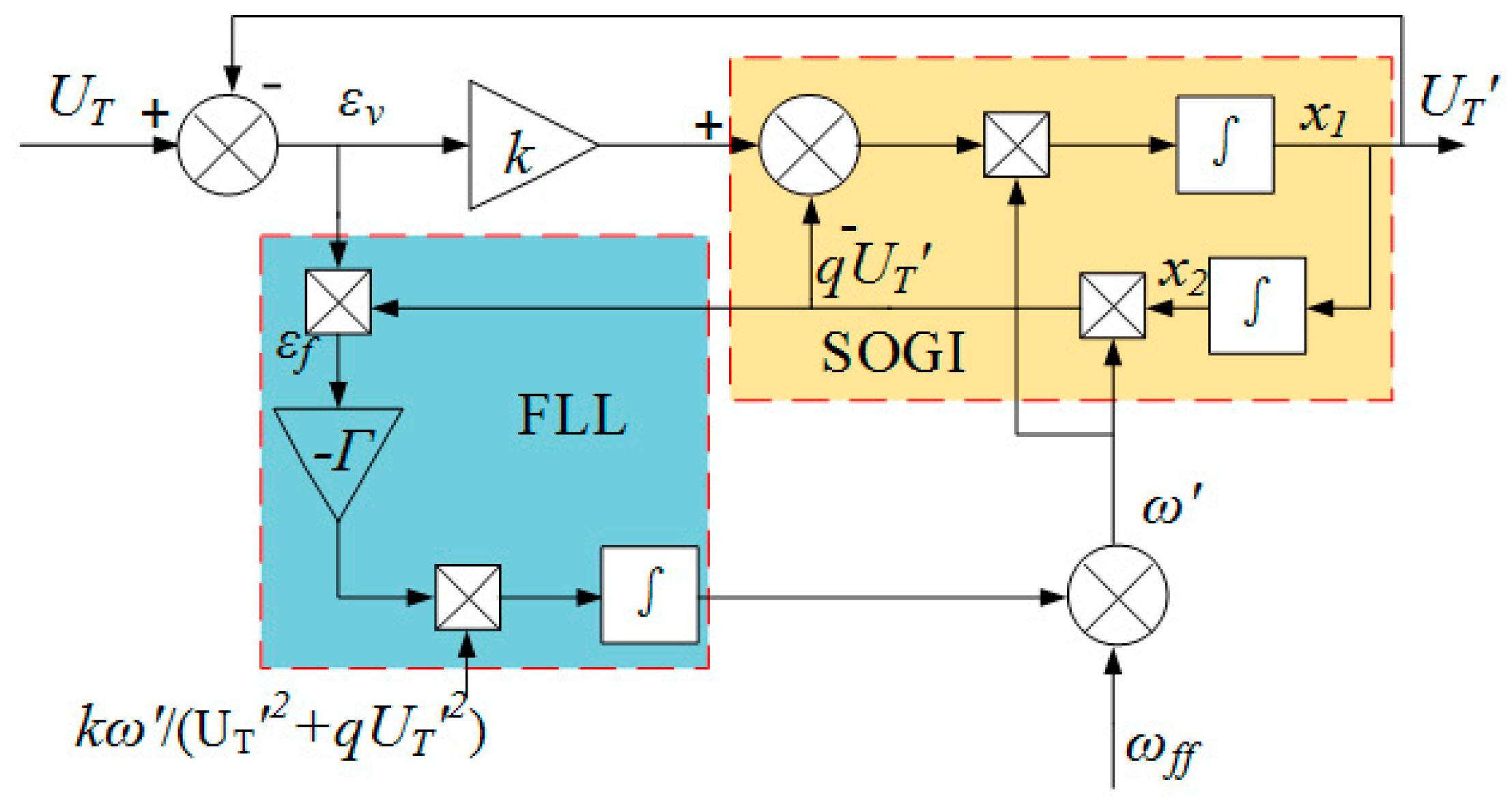
3.1. Principle of Harmonic Resonance Voltage Detection Based on PCC Node Voltage

According to the previously mentioned harmonic resonance suppression technology, the key to achieving adaptive damping of harmonic resonance is to accurately perceive the harmonic voltage at the PCC node during harmonic resonance. The second-order generalized integrator-frequency-locked loop (SOGI-FLL) method has good anti-interference ability and can effectively track and detect the fundamental component in the input signal. It also has good response speed under stable input signal conditions. In this paper, the indirect extraction method based on SOGI-FLL [36] is used to extract the harmonic resonance voltage.

The harmonic signal detection method based on SOGI-FLL is shown in Figure 6. Firstly, the three-phase voltage at the system’s common coupling point is transformed into two-phase voltage on the α-β coordinate system through the Clarke transformation, and then the fundamental voltage in the two-phase voltage on the α-axis and β-axis is extracted via the SOGI-FLL method. Finally, the two-phase fundamental voltage is transformed into the three-phase fundamental voltage of the power grid through the Clarke inverse transformation. The three-phase harmonic voltage signals $U_{Tah}$, $U_{Tbh}$, and $U_{Tch}$ can be separated by subtracting the three-phase voltage $U_{Ta}$, $U_{Tb}$, and $U_{Tc}$ at the common coupling point with the fundamental components of the extracted three-phase voltage $U_{Taf}$, $U_{Tbf}$, and $U_{Tcf}$. The obtained fundamental and harmonic components of the three-phase voltage can be used as inputs for the subsequent adaptive harmonic resonance damping device.

Using SOGI-FLL for PCC point resonance detection can not only quickly and effectively track and detect the fundamental component in the input signal under stable input signal conditions, but also has good anti-interference ability. SOGI acts as a filtering element, which can allow the signal to pass through without attenuation at the input frequency, while attenuating the signal to varying degrees outside the input frequency range. After passing through the SOGI element, two output signals can be obtained, with the same amplitude but a phase difference of 90 degrees. The FLL element is also an important component of SOGI-FLL, which can dynamically detect the frequency of the input signal in real time, thus achieving the goal of tracking the given frequency without static error.

The control block diagram of the SOGI-FLL algorithm principle is shown in Figure 7. U_T is the input signal of the system, ${\omega }_{ff}$ is the input frequency, $U_T^{\prime }$ is the output signal value of the SOGI-FLL, ${qU}_T^{\prime }$ is the orthogonal value of the output signal of the SOGI-FLL, ${\mathsf{\epsilon }}_v$ is the error value, k is the gain coefficient, Γ is the time constant, and ω^′ is the frequency of the input signal obtained via the SOGI-FLL method.

According to the block diagram of the SOGI-FLL algorithm, it can be seen that the frequency ${\omega }_{ff}$ of the signal to be tracked is fed into the system, specifying the frequency of the extracted signal required by the system. At the same time, the difference ${\mathsf{\epsilon }}_v$ between the input signal U_T and the output signal $U_T^{\prime }$ is made to multiply with the quadrature output signal ${qU}_T^{\prime }$, whose product ${\mathsf{\epsilon }}_f$ is then multiplied by the coefficient −Γ. Then, after the integration link, the tracking of the frequency is achieved and the output value at the input frequency is finally obtained.

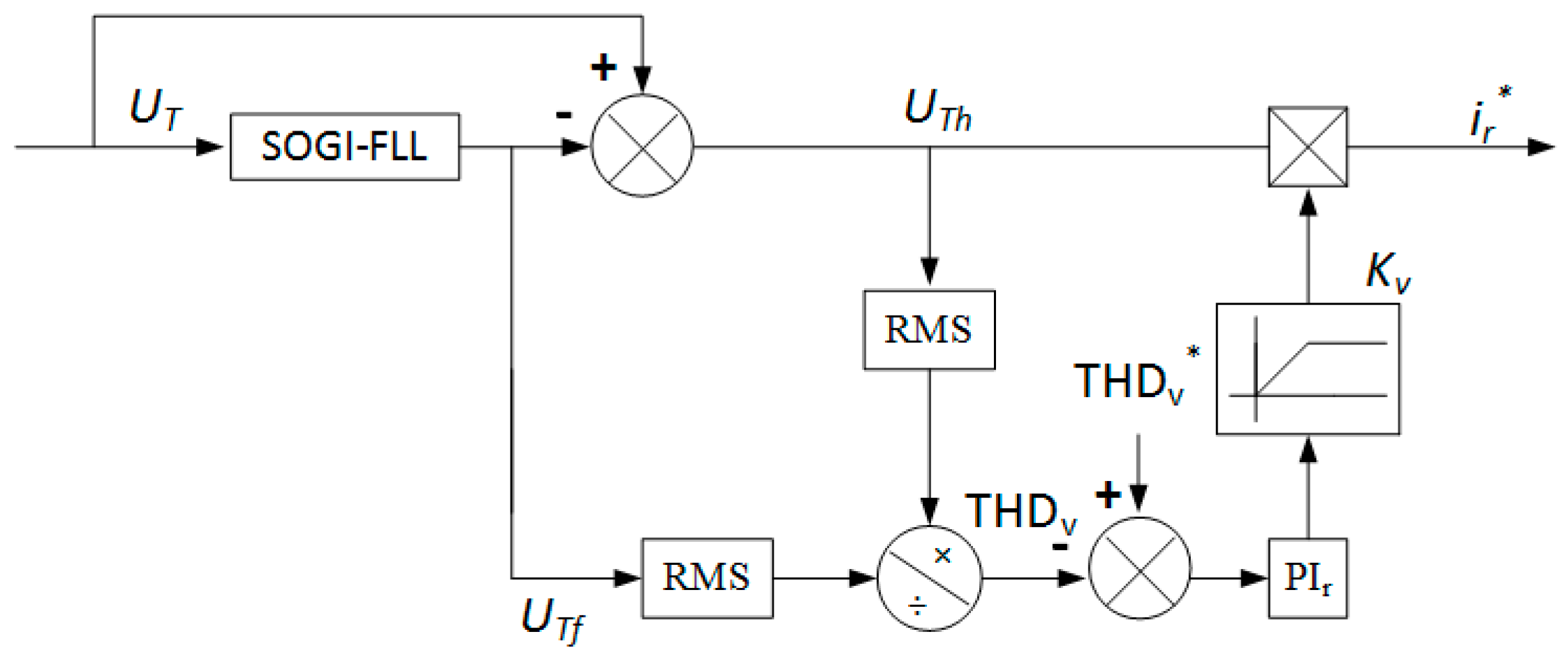
3.2. Design of Adaptive Harmonic Resonance Damping Controller

Section 3.1 provided the detection and extraction method of harmonic resonance voltage. This section mainly focuses on the adaptive design of the harmonic resonance damping current generation process. When the grid-side inductance and the capacitance of the TSC in the hybrid compensation system cause harmonic resonance under specific operating conditions, it usually leads to a sharp increase in the content of harmonic voltage at the PCC. At this time, the resonant frequency voltage occupies a large proportion in the harmonic voltage at the PCC, and its magnitude fully reflects the intensity of harmonic resonance. Therefore, it is feasible and effective to perceive the harmonic voltage and use appropriate algorithms to achieve adaptive damping of harmonic resonance.

In this paper, the extracted harmonic voltage is used to adaptively adjust the resonance damping by limiting the content of the harmonic voltage. If the value of the harmonic voltage $U_{Th}$ is large and increases rapidly, it is considered that the virtual resistance value is not sufficient to suppress the resonance generated by the system, and the virtual resistance value needs to be changed until the content of the harmonic voltage $U_{Th}$ at the PCC node is reduced to a reasonable range, and vice versa.

The control block diagram of the adaptive damping current instruction is shown in Figure 8. U_T is the voltage at the PCC point, and $U_{Tf}$ and $U_{Th}$ are the fundamental voltage and harmonic voltage detected by the adaptive SOGI-FLL at the PCC point, respectively. ${THD}_v$ is the actual harmonic voltage content in the system, and ${THD}_v^{\ast }$ is the allowable limit of harmonic voltage required by the relevant standards of the power system. $K_v$ is the resonance damping gain value obtained after adaptive control, and $i_r^{\ast }$ is the generated resonance damping current value.

In the design of PI control parameters in the adaptive resonance damping section, the proportional coefficient is related to dynamic performance. However, an excessive $K_{pr}$ can cause oscillation or overshoot of the virtual resistance value during the dynamic process, leading to the port voltage reference exceeding the bus voltage and causing overmodulation. The integral coefficient $K_{ir}$ is related to the steady-state error. Increasing the integral coefficient can reduce or eliminate the steady-state error, but it will degrade the system’s dynamic performance and stability. The proportional relationship between $K_{pr}$ and $K_{ir}$ determines the crossover frequency of the PI regulator. The goal of the virtual resistance regulator is to keep the harmonic voltage content at the PCC point within a defined range under steady-state conditions, ensure that the virtual resistance does not oscillate, and maintain good dynamic response. The design of PI control parameters is already quite mature and is not the focus of this paper. Therefore, based on relevant references, this paper selects specific PI control parameters, namely, $K_{pr}$ = 1.2 and $K_{ir}$ = 600.

The adaptive resonance damping control first extracts the harmonic voltage signal $U_{Th}$ and the fundamental voltage signal $U_{Tf}$ at the system common coupling point through the SOGI-FLL module, and the root-mean-square value of the extracted voltage values is obtained through the RMS calculation module, and the ratio between them is the harmonic voltage content ${THD}_v$ at the PCC point. Then, with the ${THD}_v^{\ast }$ limit value of the harmonic voltage content as the control target, a PI controller is constructed, and the control deviation value is input to the PI controller, and the adaptive resonance damping gain $K_v$ is set according to its output. Finally, the resonance current reference value $i_r^{\ast }$ is calculated using the harmonic voltage $U_{Th}$ and the resonance damping gain $K_v$ to achieve the expected harmonic voltage content setting. Because the power used for harmonic resonance in the system is limited, the value of $i_r^{\ast }$ should not be too large, so a limiting module is added in the adaptive damping module.

According to Figure 8, the expression for the resonance damping gain $K_v$ is as follows:

$$K_v=\left(TH{D}_v^{\ast }-TH{D}_v\right)\left(K_{pr}+K_{ir}/s\right)$$

(10)

In general, when the rated voltage of the system grid-side is below 1 KV, the total harmonic voltage distortion limit at the PCC, that is, ${THD}_v^{\ast }$, should not exceed 5% [37]. In this paper, ${THD}_v^{\ast }$ is set to 5%.

The expression for the resonance damping current is Formula (11):

$$i_r^{\ast }=K_v{U}_{Th}$$

(11)

The adaptive harmonic resonance suppression controller aims to control the content of resonance voltage at the PCC within the allowable range, and adaptively adjusts the size of the resonance damping control gain to meet the combined requirements of harmonic compensation and harmonic resonance damping under different operating conditions. The main idea of resonance damping control is to generate an adaptive damping current based on the harmonic content of the voltage at the PCC, which is equivalent to constructing an “active resistor” for damping of resonance. Only when the appropriate resonance damping gain $K_v$ is obtained through control can the harmonic resonance of the system be effectively damped.

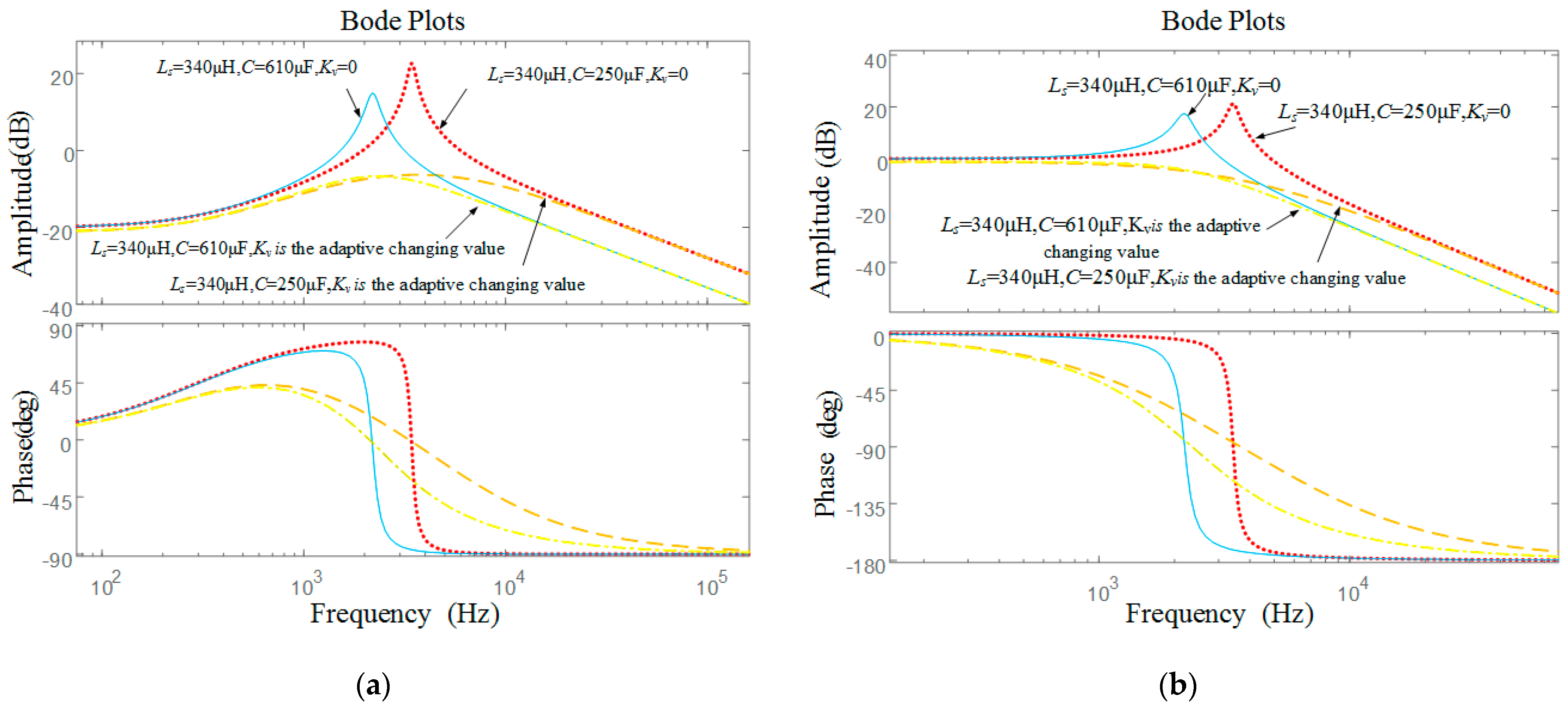
3.3. Effectiveness Analysis of Adaptive Composite Control Strategy

The adaptive composite control strategy can adjust the resonance damping gain $K_v$ in real-time according to the power system operating conditions, achieving effective suppression of harmonic resonance in the system. To further analyze its design effectiveness, this paper presents the $U_T$/$i_L$ and $i_s$/$i_L$ Bode plots under different resonance damping gain conditions based on Formula (5), as shown in Figure 9a,b, respectively. $K_v$ is set to 0 and the adaptive changing value under different operating conditions, as described in Section 2.2.

From the amplitude–frequency response curve, it can be observed that the resonance peaks are evident in the amplitude–frequency response curves under two different operating conditions when the system does not have a harmonic resonance suppression circuit ($K_v$ = 0), indicating that the system may experience resonance in a specific frequency range. However, when the system is equipped with a harmonic resonance suppression circuit and the adaptive composite control strategy is used to automatically adjust the damping gain $K_v$, the amplitude–frequency responses under different operating conditions are smoother and the resonance peaks disappear.

According to the Bode plot analysis above, it can be concluded that without additional damping control measures, the system may experience harmonic resonance in a specific frequency range under two different operating conditions. However, with the adaptive composite control strategy proposed in this paper, the resonance peaks under the two operating conditions are smoothed out due to the adaptive adjustment of the resonance damping gain value.

4. Simulation Analysis

To verify the effectiveness and feasibility of the proposed adaptive composite control strategy in this paper, a simulation model of the hybrid compensation system and the proposed adaptive composite control algorithm, as shown in Figure 1, is constructed using the Matlab/Simulink simulation platform. Based on the specific operating conditions described in Section 3.3, simulations are conducted to compare and verify the functional effectiveness of the composite control under two specific conditions and changing operating conditions. At the same time, the simulation is used to verify the robustness of the system when there is a voltage sag or frequency variation in the system. The system simulation parameters are found in

Table 1. Simulation parameters.

Parameters		Numerical Values
AC grid	Voltage Us/V	220
	Frequency fs/Hz	50
	Reactance Ls1/μH	340
	Reactance Ls2/μH	340
	Resistance Rs/Ω	0.01
APF	Filter inductance Lf/μH	450
	Switching frequency fw/kHz	9.6
	DC side voltage Udc/V	700
	Rated current if*/A	100
TSC	Thyristor capacitance per phase C1/μF	250
	Thyristor capacitance per phase C2/μF	610
Non-linear loads	Load-side reactance L/μH	100
	Load-side resistance R/Ω	12.5
Voltage outer-loop PIv parameters	Kpv	3.2
	Kiv	520
PIr parameters	Kpr	1.2
	Kir	600

.

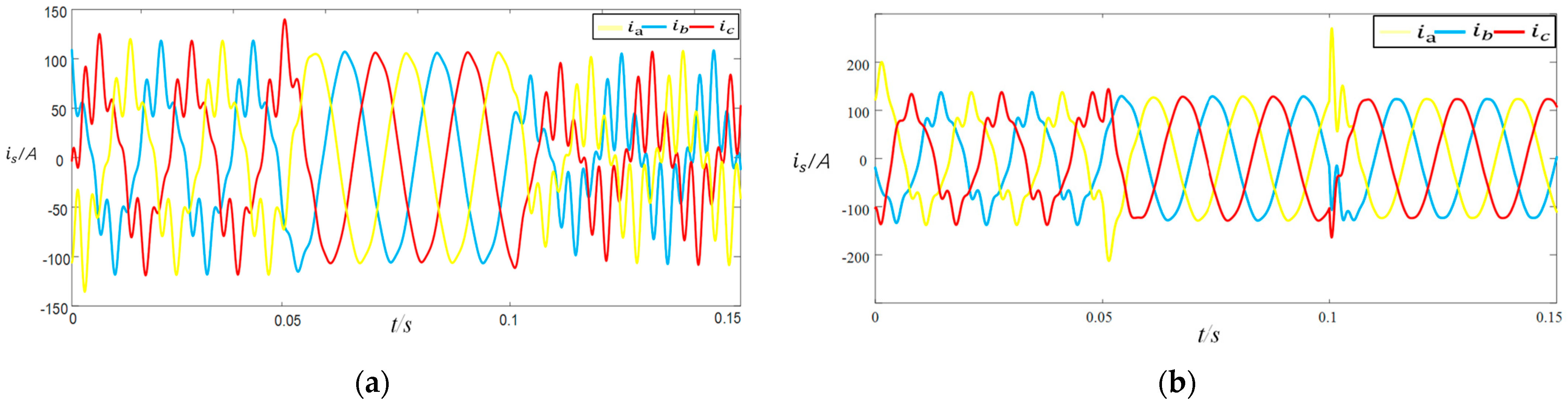
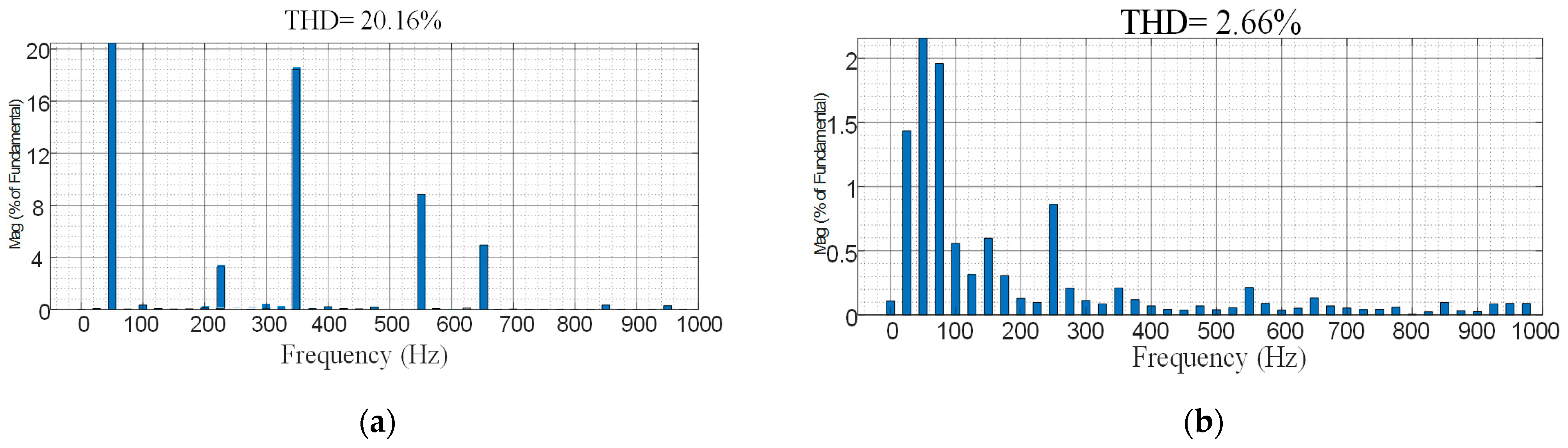
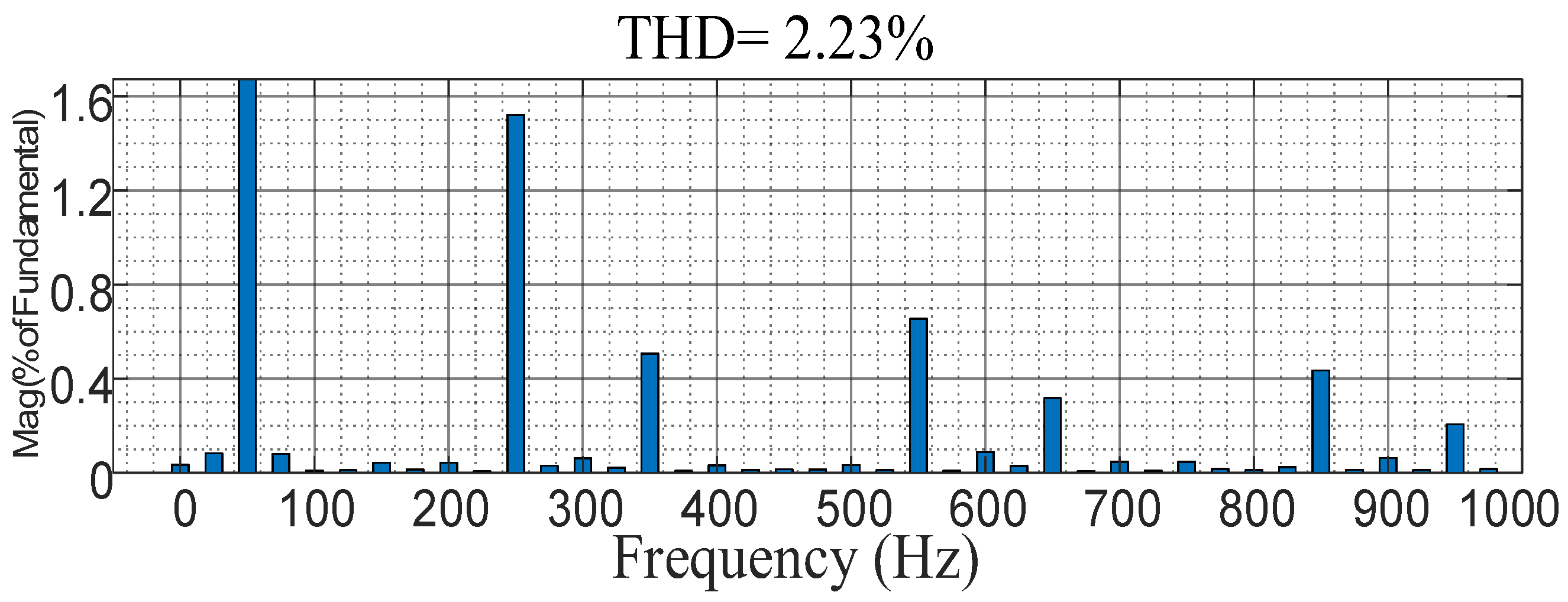
4.1. Experimental Verification of the Harmonic Resonance Suppression Function of the Adaptive Composite Control Strategy

Assuming that at t = 0 s, the system line impedance $L_s$ is 340 $\mathsf{\mu }\mathrm{H}$ and the operation is stable, the capacitance value of the TSC input compensation capacitor is 250 $\mathsf{\mu }\mathrm{F}$, and the harmonic resonance suppression control parameter is set to $K_v$ = 0.0, the harmonic resonance suppression function is effectively disabled. At t = 0.05 s, the control parameter is changed to a fixed value of $K_v$ = 1.3, enabling the harmonic resonance suppression function in the conventional composite control strategy. At t = 0.1 s, the adaptive composite control strategy is implemented at the PCC node. Additionally, at t = 0.1 s, the compensation capacitance of the TSC is adjusted to 610 $\mathsf{\mu }\mathrm{F}$ due to a change in the inductive load in the system. The simulation results, including the PCC node voltage, network side current, and the corresponding Total Harmonic Distortion (THD) spectra for both the conventional and adaptive composite control strategies, are presented in Figure 10, Figure 11, Figure 12 and Figure 13, respectively.

Based on the simulation results shown in Figure 10 and Figure 11, it is observed that between 0 to 0.05 s, there is a certain degree of distortion in the PCC node voltage and grid-side current due to the removal of the harmonic resonance suppression function, indicating the presence of harmonic resonance in the system during this time. Between 0.05 to 0.1 s, in the traditional composite control strategy, the addition of the harmonic resonance suppression function results in smoother PCC node voltage and grid-side current, effectively suppressing harmonic resonance. In the adaptive composite control strategy, the adaptive control also results in smoother PCC node voltage and grid-side current. After 0.1 s, due to changes in system conditions, the value of the TSC compensation capacitor increases significantly, leading to significant changes in PCC node voltage and grid-side current in the traditional composite control strategy, with severe distortion in the grid-side current and THD values of 20.16% and 26.14% for PCC node voltage and grid-side current, respectively, exceeding the THD limit in the power system. In contrast, the adaptive composite control strategy results in only slight fluctuations in the PCC node voltage and grid-side current waveforms for a short period of time, with the waveforms quickly and smoothly recovering after a brief period of fluctuation. The THD values of voltage and grid-side current at the PCC point are 2.66% and 2.78%, respectively, which are within the standard values of the power system.

The comparison of the above simulation results shows that in traditional composite control, the harmonic resonance suppression parameter damping gain $K_v$ is a fixed parameter designed based on the actual operating conditions of the power supply system. When the system operating conditions do not change significantly, it can effectively suppress harmonic resonance. However, when the system operating conditions change significantly, its harmonic resonance performance is difficult to guarantee, which may make the harmonic resonance suppression effect worse, and in severe cases, it may affect the quality of electrical energy and the stable operation of the system. On the other hand, the adaptive composite control strategy can adjust the resonance damping gain value in real time to adapt to system changes, effectively suppress harmonic resonance, and make the system harmonic resonance content comply with the relevant standards of the power system, ensuring the safe and stable operation of the system. Moreover, the control method proposed in this paper effectively suppresses harmonic resonance by introducing suitable control links in the system to achieve virtual damping. This approach does not incur additional hardware costs and simplifies the design of the control process. Consequently, the method presented in this paper offers notable advantages over conventional control methods.

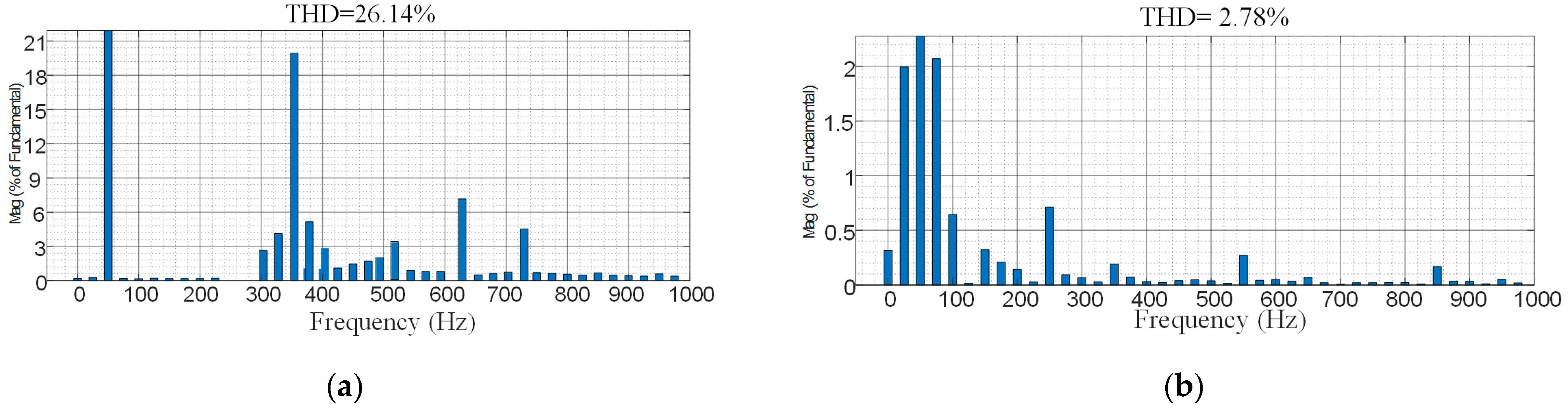
4.2. Experimental Verification of Robustness of Adaptive Composite Control Strategy

Sometimes, there may be temporary voltage drops and frequency changes in the power grid. This section verifies the robustness of the adaptive composite control strategy when these two situations occur. This section simulates two common problems in the power grid and verifies the effectiveness and robustness of the adaptive composite control strategy through the voltage at the PCC and the waveform of the grid-side current.

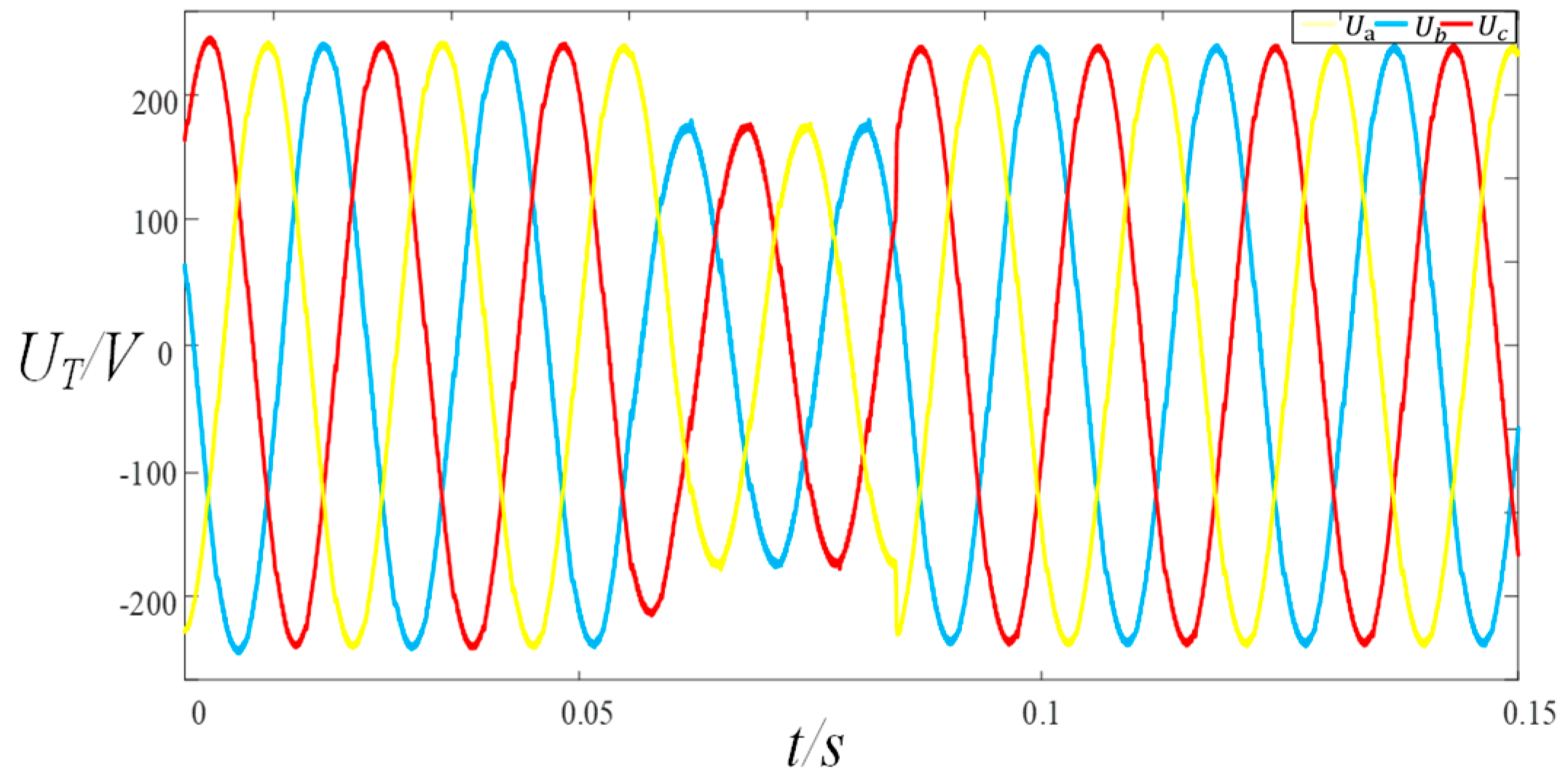
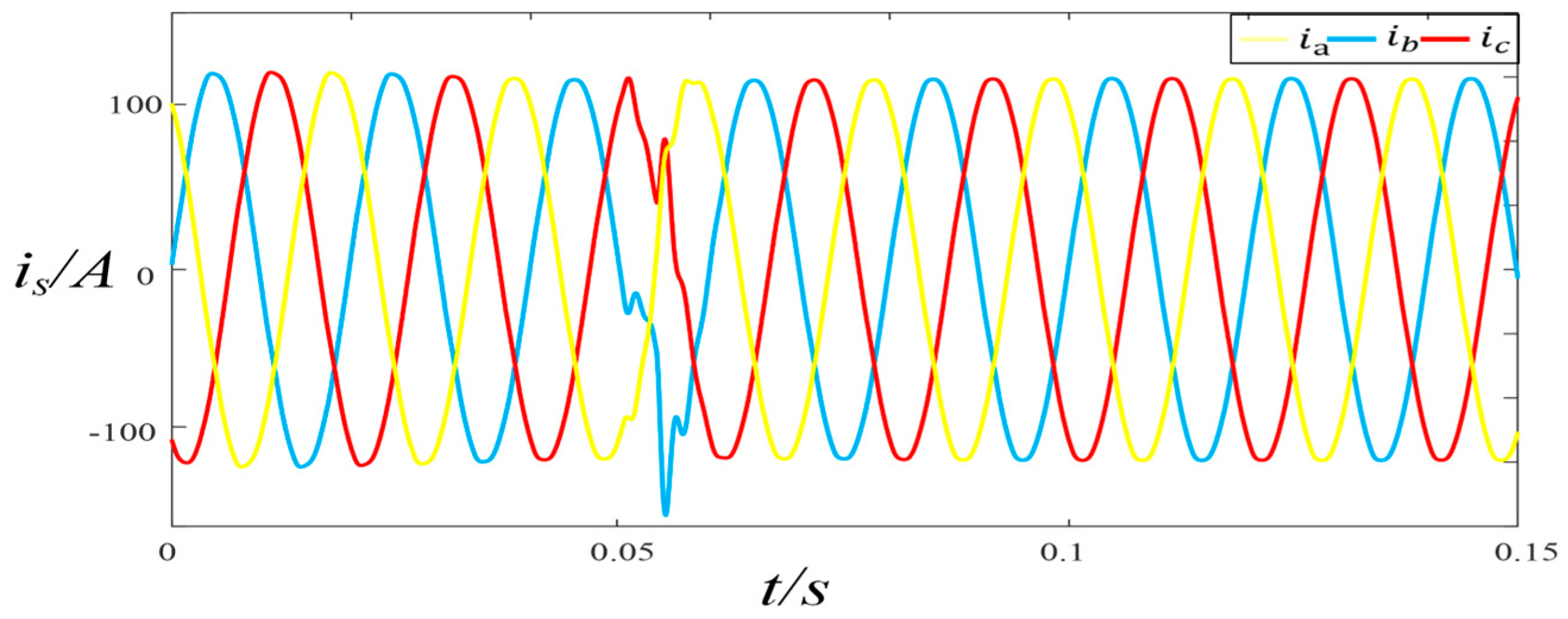
4.2.1. Experimental Verification of Voltage Transients in the Power Grid with Adaptive Composite Control Strategy

A voltage drop is used to simulate an actual temporary decrease in grid voltage. At 0 s, the system grid impedance Ls is 340$\mathsf{\mu }\mathrm{H}$, and the TSC-inputted compensation capacitor has a capacitance of 610 μF. The voltage in the system is stable at 220 v, operating steadily. At 0.05 s, the grid voltage abruptly decreases by 30v, and then increases back to 220 v at 0.08 s. The simulation results of the voltage at the PCC and the corresponding THD spectrum are shown in Figure 14 and Figure 15, respectively.

As shown in the simulation results in Figure 14, from 0 to 0.05 s, the voltage waveform at the PCC point is smooth due to the effect of the adaptive composite control strategy. At 0.05 s, due to the temporary voltage drop in the grid, the voltage waveform at the PCC point shows a certain degree of decrease. At 0.08 s, the grid voltage recovers, the voltage waveform at the PCC point rises, and the waveform returns to its original form. At this time, the THD value of the voltage at the PCC point is 2.57%, which is within the standard value in the power system. This shows that the adaptive composite control strategy can ensure the stability of the system during a voltage drop.

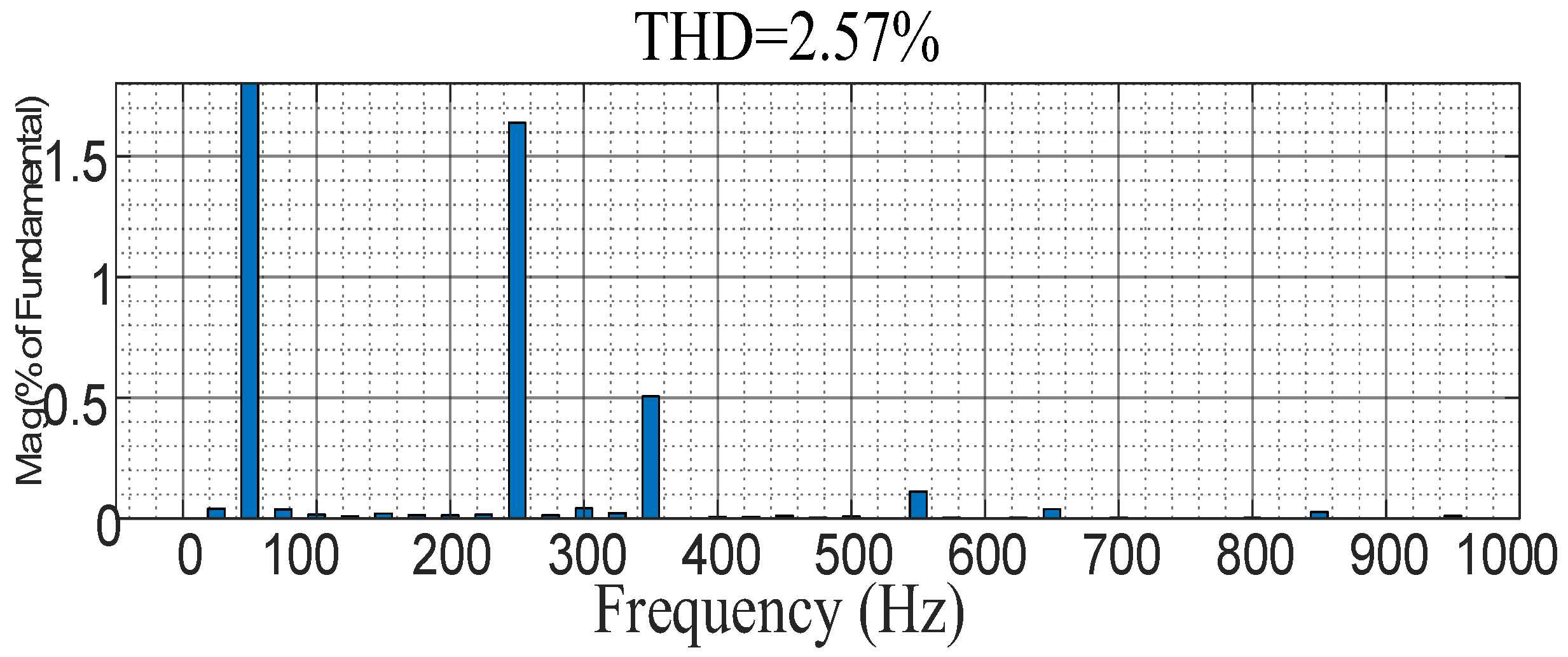
4.2.2. Experimental Verification of Frequency Fluctuations with Adaptive Composite Control Strategy

Under the same initial operating conditions as described in Section 4.2.1, the system integrates with the adaptive compound control strategy proposed in this paper at 0 s. At 0.05 s, the system frequency experiences a brief fluctuation due to changes in the system load. At 0.054 s, the system frequency stabilizes. The simulation results for the grid-side current are shown in Figure 16, and the corresponding spectral diagram is shown in Figure 17.

As depicted in Figure 16, during the period from 0 to 0.05 s, the grid-side current waveform is smooth, demonstrating that the system effectively suppresses harmonic resonance under the adaptive composite control strategy. At 0.05 s, due to fluctuations in the system frequency, the grid-side current waveform experiences noticeable distortion. However, by 0.054 s, when the frequency stabilizes, the waveform smooths out again. At this point, the THD value of the grid-side current is 2.23%, which is within the standard values defined for power systems. This indicates that the adaptive composite control strategy can maintain system stability even during frequency fluctuations.

The simulations from Section 4.2 demonstrate that the adaptive composite control strategy is a feasible and effective solution in situations where there are transient grid voltage or system frequency changes in the power system. The harmonic resonance content in the system adheres to the relevant power system standards, thereby ensuring safe and stable system operation.

Through theoretical analysis and multi-condition simulations, the effectiveness of the adaptive composite control strategy designed in this paper for suppressing harmonic resonance has been verified. It improves the problems of poor control performance under changing conditions commonly encountered with traditional composite control strategies, thereby enhancing the performance of the hybrid compensation system under complex and changing conditions.

5. Conclusions

This paper focuses on the hybrid compensation system composed of TSC and APF, and investigates the harmonic resonance problem caused by the parallel resonance circuit in the hybrid compensation system and corresponding suppression measures. Based on the analysis of the problems in traditional compound control strategies, an improved adaptive compound control technique is proposed. Theoretical analysis and simulation results led to the following conclusions:

(1)

The parallel resonance circuit composed of the grid-side inductance and the switching capacitor in the thyristor-controlled reactor (TCR) may cause harmonic resonance problems when the system is excited by nonlinear load harmonic sources, which could have a significant impact on the power quality and safe operation of the power supply system.

(2)

In the hybrid compensation system, adding harmonic resonance suppression control on the basis of harmonic compensation to form a compound control strategy can effectively suppress harmonic resonance. However, the traditional compound control strategy using fixed control parameters may be severely affected by changes in the system operating conditions.

(3)

In response to the weakened ability of traditional hybrid compensation system composite control strategies to suppress harmonic resonance when system operating conditions change, the mechanism causing the weakening of the control effects of traditional composite control strategies has been analyzed and clarified. A new adaptive composite control strategy has been proposed and designed. By using the resonance voltage at the PCC point to indirectly reflect changes in system operating conditions, the adaptive adjustment of active damping control parameters in composite control was designed and implemented. Theoretical analysis and simulation validation demonstrate that this technical solution can sense changes in system operating conditions and adaptively adjust damping control parameters, effectively suppressing harmonic compensation and harmonic resonance under complex operating conditions, and enhancing the operating quality and adaptability of the hybrid compensation system.

(4)

The strategy proposed in this paper presents an effective solution for a hybrid compensation system composed of TSC and APF. It holds great potential to improve the power quality and stability of power systems, providing a new approach to solving the problem of harmonic resonance in hybrid compensation systems. However, the composition of the hybrid compensation system is complex. In addition to the inherent oscillation loops present in the power supply side and compensation capacitor that this paper focuses on, the inductance and impedance of the LCL-type Active Power Filter itself can also form a resonance network with the distributed capacitance in the system. This naturally leads to the existence of resonance loops and resonance-induced power quality and stable operation issues. These can be attempted to be suppressed by adding virtual impedance to the resonance network.