Prediction of Single-Well Production Rate after Hydraulic Fracturing in Unconventional Gas Reservoirs Based on Ensemble Learning Model
Abstract
1. Introduction
2. Process for Predicting the Gas Rate in Unconventional Gas Reservoirs
- (1)
- Data collection and cleaning. Gather relevant data on the geology, reservoirs, and engineering, perform quality checks on the data, handle abnormal values and missing values, and normalize or standardize the data.
- (2)
- Feature engineering and dimensionality reduction. Based on the characteristics of the dataset, select appropriate methods to extract the features specific to tight gas and shale gas rates, transforming high-dimensional raw data into low-dimensional feature vectors to reduce the redundant information and noise interference.
- (3)
- Model construction and training. Choose multiple machine learning models according to the prediction objectives and problem types, utilize the historical data of known production as the training set, optimize and fit the model parameters, and evaluate the generalization ability of the models using metrics such as Mean Absolute Error (MAE) and Mean Squared Error (MSE).
- (4)
- Production rate prediction and result analysis. Utilize the trained model to predict the production rate of the testing set and compare it with the actually observed values. Adjust or improve the above models based on the accuracy and stability of the prediction results.
- (5)
- Ensemble of machine learning models. To further enhance the accuracy of the production rate predictions, ensemble learning can be used to integrate the prediction results of multiple base models, improving the generalization ability and accuracy of the machine learning models.
3. Production Rate Prediction in Tight Gas Field A
3.1. Overview
3.2. Data Processing and Preparation
3.3. Model Selection
4. Production Rate Prediction in Shale Gas Field B
4.1. Overview
4.2. Production Forecast
5. Conclusions and Future Work
- (1)
- This article proposes a reasonable production prediction model and method for single-well tight gas and shale gas rate based on artificial intelligence analysis. The method combines the predictions of multiple base models, such as random forest (RF), extremely randomized trees (ET), light gradient boosting machine (LightGBM), and gradient boosting regressor (GBR), and further improves the accuracy and generalization ability of the model predictions through ensemble learning.
- (2)
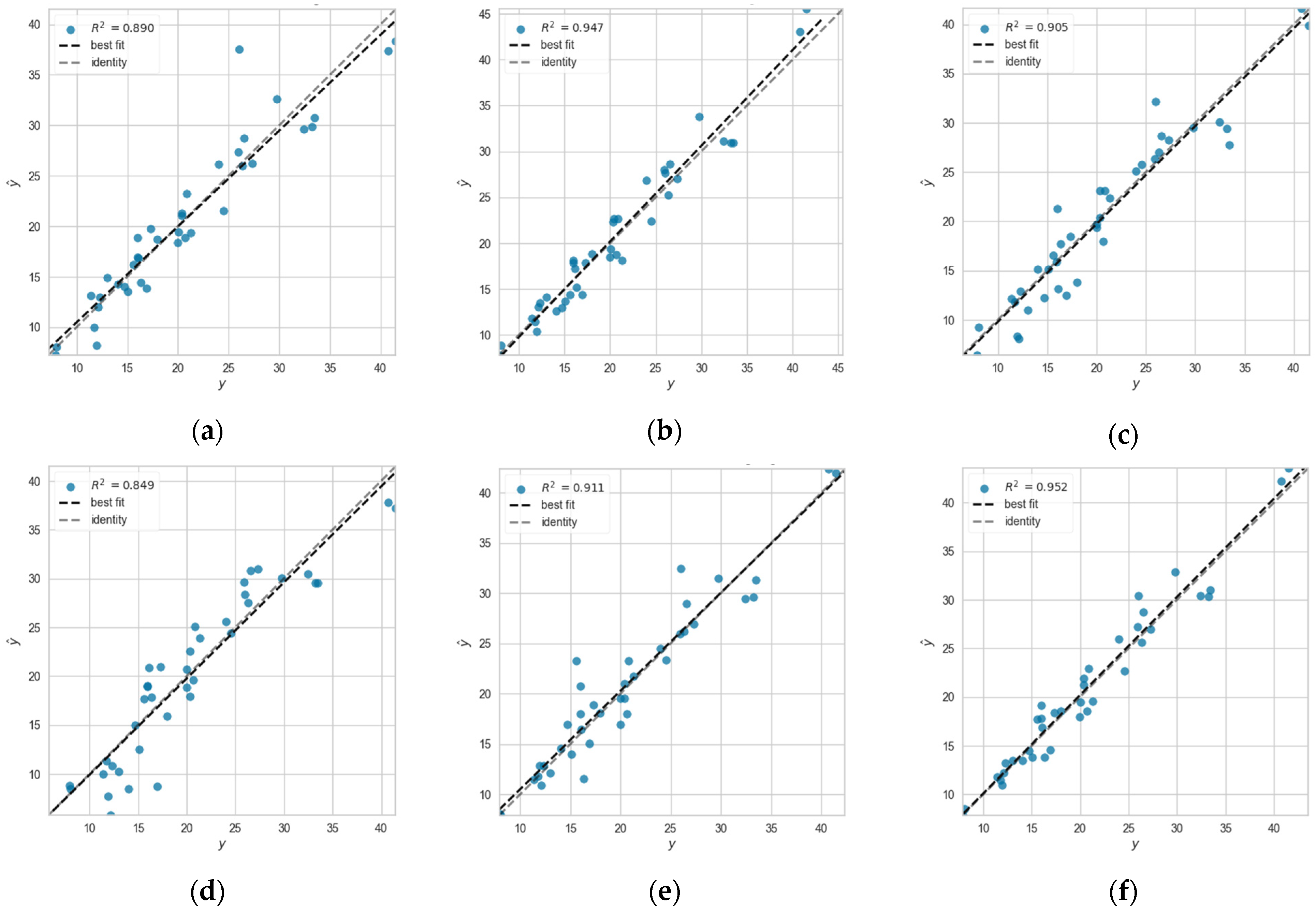
- The blending-based ensemble learning model has higher accuracy and reliability for predicting the single-well gas rate of unconventional reservoirs. The blending ensemble model, utilizing the advantages of multiple basic models, predicts the production of the tight gas rate, with an accuracy rate improved to 0.8812. The blending ensemble model also improves the accuracy rate for predicting the shale gas production rate to 0.9524.
- (3)
- Considering the characteristics of the multiple influencing factors and a limited number of effective samples in the gas production prediction rate, further research is planned to be conducted on the production prediction driven by data and knowledge graph integration. The temporal and spatial relationships of oil well production are represented using knowledge graphs, with graph embedding techniques employed to represent the vector feature graphs. The vector features of the knowledge graph and the features extracted via deep learning are organically fused using embedding layers to achieve an integrated prediction of the gas well production rate through the fusion of data and knowledge.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development status and prospect of tight sandstone gas in China. Nat. Gas Ind. 2022, 42, 83–92. [Google Scholar] [CrossRef]
- Li, L.G. Development of natural gas industry in China: Review and prospect. Nat. Gas Ind. 2022, 9, 187–196. [Google Scholar] [CrossRef]
- Pan, J.P. New Progress and Outlook of China’s Oil and Gas Exploration and Development. Pet. Sci. Technol. Forum 2023, 42, 23–31. [Google Scholar]
- Guo, J.; Lu, Q.; Liu, Z.; Zeng, F.; Guo, T.; Liu, Y.; Liu, L.; Qiu, L. Concept and key technology of “multi-scale high-density” fracturing technology: A case study of tight sandstone gas reservoirs in the western Sichuan Basin. Nat. Gas Ind. 2023, 43, 67–76. [Google Scholar] [CrossRef]
- Zhang, N. Optimization of horizontal well pattern in southeast area of Su 53 block. Unconv. Oil Gas 2021, 8, 77–83. [Google Scholar]
- Chen, G.S.; Wu, J.F.; Liu, Y.; Huang, H.Y.; Zhao, S.J.; Chang, C.; Zhong, C.X. Geology-engineering integration key technologies for ten billion cubic meters of shale gas productivity construction in the southern Sichuan basin. Nat. Gas Ind. 2021, 41, 72–81. [Google Scholar]
- Gong, Y.; Gao, H.Q.; Li, X.Y. Study on the distribution characteristics of occurrence modes of shale gas in the Sichuan Basin and its periphery. Unconv. Oil Gas 2023, 10, 49–56. [Google Scholar]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Micheal, M.; Xu, W.; Jin, J.; Yu, H.; Liu, J.; Jiang, W.; Liu, H.; Wu, H. A multi-scale quadruple-continuum model for production evaluation of shale gas reservoirs considering complex gas transfer mechanisms and geomechanics. J. Pet. Sci. Eng. 2022, 213, 110419. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Dong, W.; Li, Q.; Wang, F.; Bai, H.; Zhang, R.; Owusu, A.B. Effect of different factors on the yield of epoxy-terminated polydimethylsiloxane and evaluation of CO2 thickening. RSC Adv. 2018, 8, 39787–39796. [Google Scholar] [CrossRef]
- Duong, A.N. An unconventional rate decline approach for tight and fracture-dominated gas wells. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar]
- Zhang, N. A new method of productivity evaluation for fractured horizontal well in tight gas reservoir. Sci. Technol. Eng. 2014, 14, 76–80. [Google Scholar]
- Ye, J.W. EUR Evaluation Method for Intensive Cutting Fracturing Horizontal Wells in Tight Sandstone Reservoirs. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2021. [Google Scholar]
- Zhang, N. Classification evaluation of production dynamic for horizontal well in Su 53 block. Unconv. Oil Gas 2021, 8, 88–94. [Google Scholar]
- Song, H.; Su, Y.; Xiong, X.; Liu, Y.; Zhong, S.C.; Wang, J.J. EUR evaluation workflow and influence factors for shale gas well. Nat. Gas Geosci. 2019, 30, 1531–1537. [Google Scholar]
- Zhao, Y.L.; Liang, H.B.; Jing, C.; Shang, S.F.; Li, C.Y. A new method for quick EUR evaluation of shale gas wells. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2019, 41, 124–131. [Google Scholar]
- Ma, W.D. Productivity Regularity Research of Fractured Well in Tight Gas Reservoir. Master’s Thesis, China University of Petroleum, Beijing, China, 2015. [Google Scholar]
- Tian, Y.P.; Ju, B.S. A model for predicting shale gas production decline based on the BP neural network improved by the genetic algorithm. China Sci. Pap. 2016, 11, 1710–1715. [Google Scholar]
- Zhu, H.; Kong, D.Q.; Qian, X. Shale gas production prediction method based on adaptive threshold denoising BP neural network. Sci. Technol. Eng. 2017, 17, 128–132. [Google Scholar]
- Lu, Z.Y. Research on Production Forecast Method of Gas Well in Tight Gas Reservoir Based on Big Data Analysis. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2019. [Google Scholar]
- Ma, W.L.; Li, Z.P.; Sun, Y.P.; Zhang, J.P.; Deng, S.Z. Non-deterministic shale gas productivity forecast based on machine learning. Spec. Oil Gas Reserv. 2019, 26, 101–105. [Google Scholar]
- Fan, Y.; Huang, H.Y.; Wang, X.H.; Chen, J.; Deng, Y.C. Study on the production prediction technology for shale gas horizontal well by applying data mining. In Proceedings of the 31st National Natural Gas Academic Annual Conference, Hefei, China, 31 October–1 November 2019. [Google Scholar]
- Li, Y.Z.; Bai, Y.H.; Xu, B.X. Application of NARX model in production performance prediction of tight gas wells. In Proceedings of the International Field Exploration and Development Conference, Chengdu, China, 23–25 September 2020. [Google Scholar]
- Chen, J.; Huang, H.Y.; Liu, J.C.; Zeng, B.; Yang, X.R. Production predicting technology of shale gas fracturing Horizontal well in changning area based on the GA-BP neural network mode. Sci. Technol. Eng. 2020, 20, 1851–1858. [Google Scholar]
- Zhao, Q.Y.; Liu, Y.; Liu, L.P.; Chen, H.; Ning, M.; Liu, J.; Gao, W.B.; Miao, R.J. Application of machine learning in the production prediction of horizontal wells in tight gas reservoirs. In Proceedings of the 17th Ningxia Young Scientists Forum Petroleum and Petrochemical Special Forum, Yinchuan, China, 15 September 2021. [Google Scholar]
- Yan, Z.M.; Wang, T.; Liu, Z.L.; Zhuang, Z. Machine-learning-based prediction methods on shale gas recovery. Chin. J. Solid Mech. 2021, 42, 221–232. [Google Scholar]
- He, Y.W.; He, Z.Y.; Tang, Y.; Qin, J.Z.; Song, J.J.; Wang, Y. Shale gas well production evaluation and prediction based on machine learning. Oil Drill. Prod. Technol. 2021, 43, 518–524. [Google Scholar]
- Otchere, D.A.; Ganat, O.T.; Gholami, R.; Lawal, M. A Novel Custom Ensemble Learning Model for an Improved Reservoir Permeability and Water Saturation Prediction. J. Nat. Gas Sci. Eng. 2021, 91, 103962. [Google Scholar] [CrossRef]
- Niu, W.; Lu, J.; Sun, Y. Development of shale gas production prediction models based on machine learning using early data. Energy Rep. 2022, 8, 1229–1237. [Google Scholar] [CrossRef]
- Wang, H.; Qiao, L.; Lu, S.; Chen, F.; Fang, Z.; He, X.; Zhang, J.; He, T. A novel shale gas production prediction model based on machine learning and its application in optimization of multistage fractured horizontal wells. Front. Earth Sci. 2021, 9, 726537. [Google Scholar] [CrossRef]
- Syed, F.I.; Alnaqbi, S.; Muther, T.; Dahaghi, A.K.; Negahban, S. Smart shale gas production performance analysis using machine learning applications. Pet. Explor. Dev. 2022, 49, 21–31. [Google Scholar] [CrossRef]
- Liao, L.; Li, G.; Zhang, H.; Feng, J.; Zeng, Y.; Ke, K.; Wang, Z. Well completion optimization in Canada tight gas fields using ensemble machine learning. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2020. [Google Scholar]




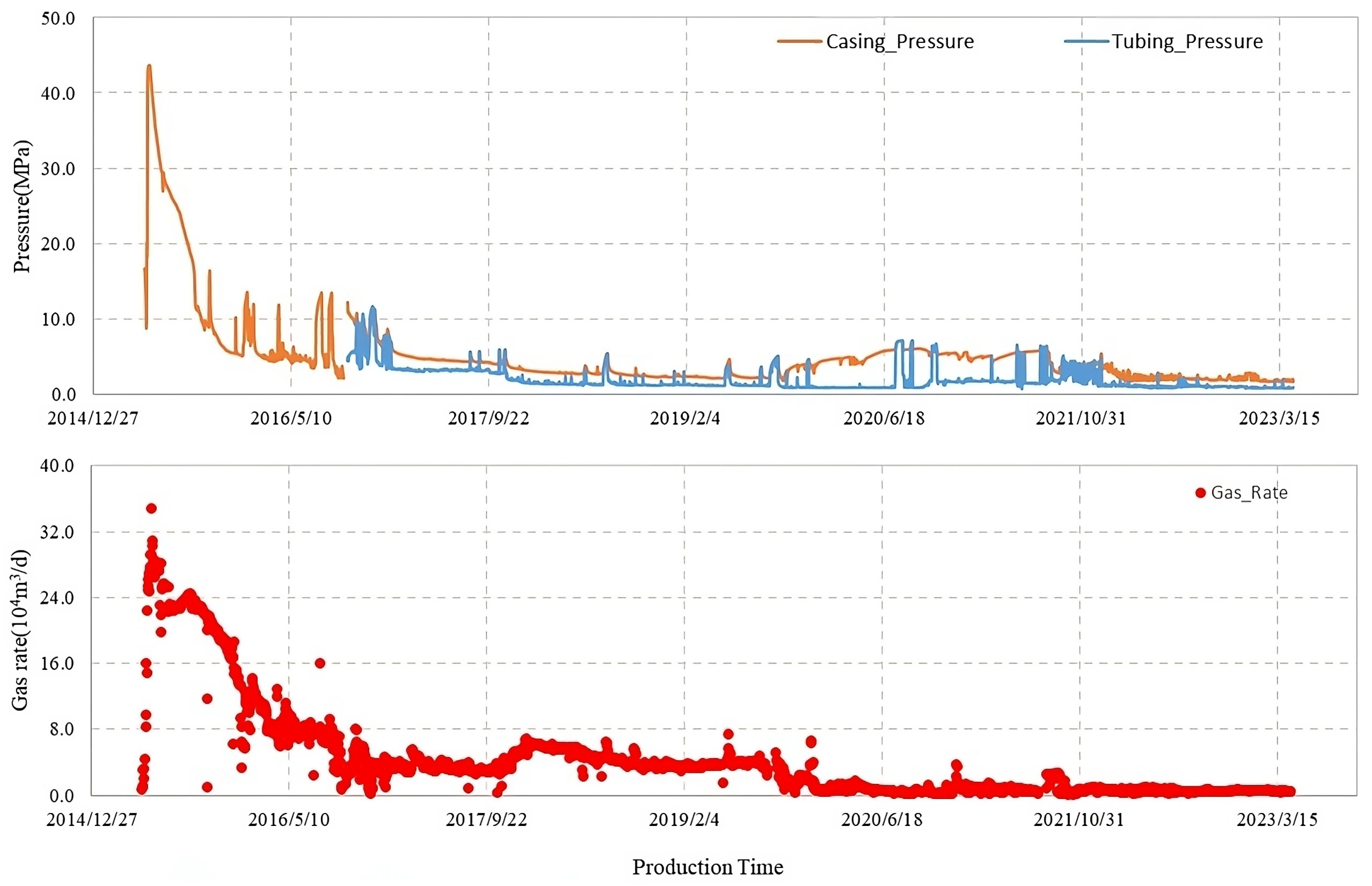

| Para. Name | Reservoir Type | Netpay(ft) | Porosity(%) | Ave. Sg (%) | Controlled Reserves/Well (mmcf) | Horizontal Length (ft) | Rate of Sand Body (%) | |
|---|---|---|---|---|---|---|---|---|
| Indicator | ||||||||
| Min. | 1.0 | 16.4 | 6.0 | 28.1 | 1448 | 1981.6 | 16.3 | |
| Max. | 3.0 | 73.8 | 11.2 | 73.1 | 10,877 | 7217.8 | 100.0 | |
| Mean | 1.9 | 44.0 | 8.5 | 55.6 | 4944 | 3568.6 | 85.3 | |
| Std. Dev. | 0.7 | 12.1 | 0.9 | 9.4 | 1766 | 614.8 | 15.8 | |
| Para. Name | Effective Rate of Sand Body (%) | Total Liquid Volume (mcf) | Total Sand Volume (mcf) | Flowback Volume (mcf) | Rate of Flowback (%) | Number of Fracturing Sections | ||
| Indicator | ||||||||
| Min. | 8.3 | 29.1 | 3.0 | 3.6 | 2.6 | 5.0 | ||
| Max. | 100.0 | 256.6 | 28.0 | 45.3 | 75.1 | 14.0 | ||
| Mean | 61.1 | 120.8 | 13.7 | 18.1 | 17.8 | 7.1 | ||
| Std. Dev. | 21.1 | 39.1 | 4.2 | 5.5 | 9.3 | 1.4 | ||
| Model Name | MAE | MSE | R2 |
|---|---|---|---|
| RF | 0.9525 | 1.3319 | 0.8553 |
| ET | 0.9022 | 1.2497 | 0.8642 |
| LightGBM | 1.0335 | 1.7214 | 0.8129 |
| GBR | 1.0638 | 1.8242 | 0.8017 |
| LR | 0.9582 | 1.6091 | 0.8251 |
| Model Name | MAE | MSE | R2 |
|---|---|---|---|
| Blending | 0.8419 | 1.0930 | 0.8812 |
| Model Name | MAE | MSE | R2 |
|---|---|---|---|
| RF | 1.9597 | 7.3169 | 0.8898 |
| ET | 1.6428 | 3.5326 | 0.9468 |
| LightGBM | 1.9183 | 6.3411 | 0.9045 |
| GBR | 1.6678 | 5.9207 | 0.9109 |
| LR | 2.6313 | 10.0568 | 0.8486 |
| Model Name | MAE | MSE | R2 |
|---|---|---|---|
| Blending model | 1.4841 | 3.1629 | 0.9524 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Li, X.; Zhang, N.; Xu, F. Prediction of Single-Well Production Rate after Hydraulic Fracturing in Unconventional Gas Reservoirs Based on Ensemble Learning Model. Processes 2024, 12, 1194. https://doi.org/10.3390/pr12061194
Ye F, Li X, Zhang N, Xu F. Prediction of Single-Well Production Rate after Hydraulic Fracturing in Unconventional Gas Reservoirs Based on Ensemble Learning Model. Processes. 2024; 12(6):1194. https://doi.org/10.3390/pr12061194
Chicago/Turabian StyleYe, Fan, Xiaobo Li, Nan Zhang, and Feng Xu. 2024. "Prediction of Single-Well Production Rate after Hydraulic Fracturing in Unconventional Gas Reservoirs Based on Ensemble Learning Model" Processes 12, no. 6: 1194. https://doi.org/10.3390/pr12061194
APA StyleYe, F., Li, X., Zhang, N., & Xu, F. (2024). Prediction of Single-Well Production Rate after Hydraulic Fracturing in Unconventional Gas Reservoirs Based on Ensemble Learning Model. Processes, 12(6), 1194. https://doi.org/10.3390/pr12061194





