Dynamic Coupling Model of the Magnetic Separation Process Based on FEM, CFD, and DEM
Abstract
1. Introduction
2. Dynamic Coupling Model Establishment
2.1. Model of the Particle Phase
2.2. CFD Model of the Fluid
2.3. FEM of the Magnetic Field
3. Model of Magnetic Agglomeration Force
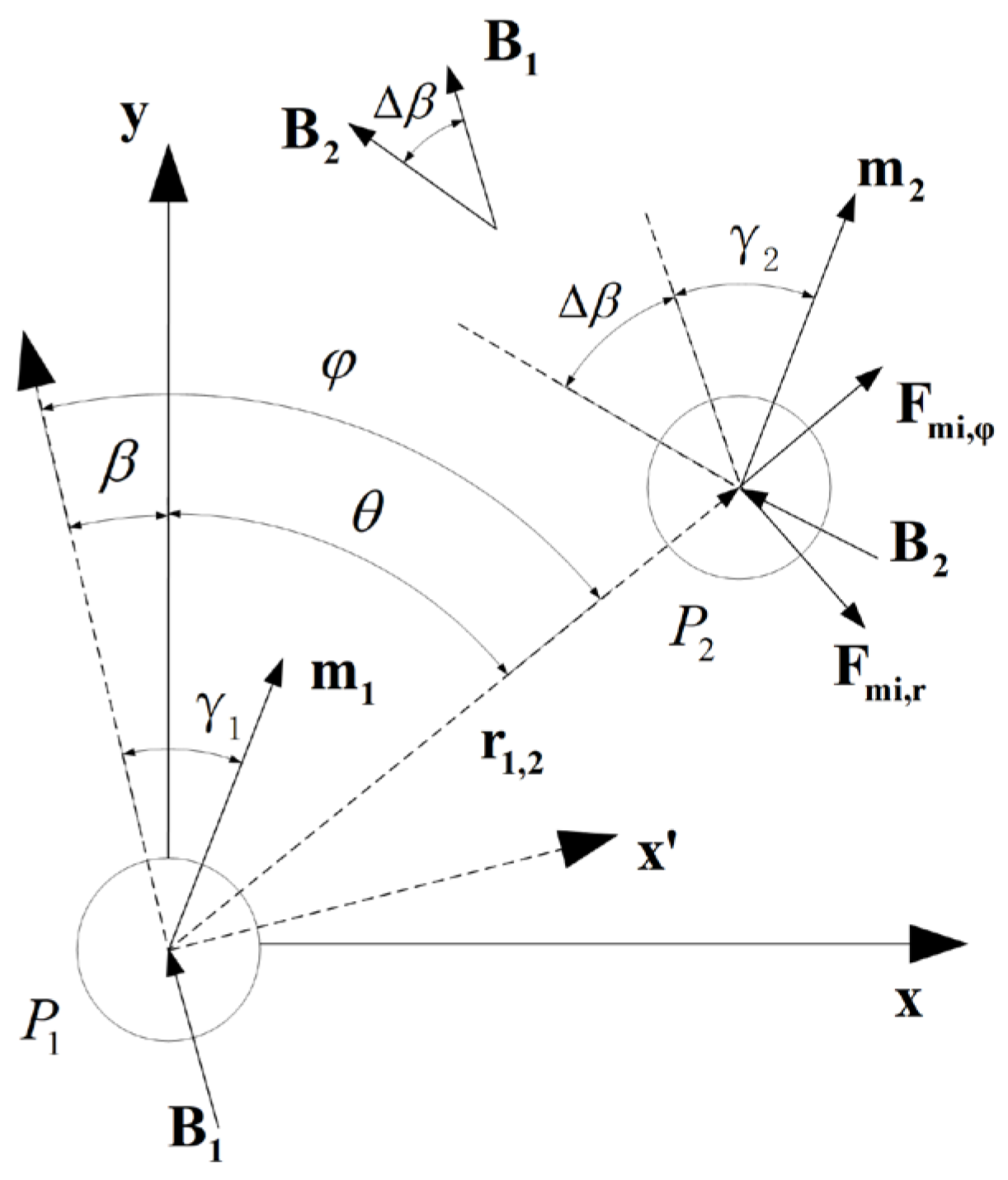
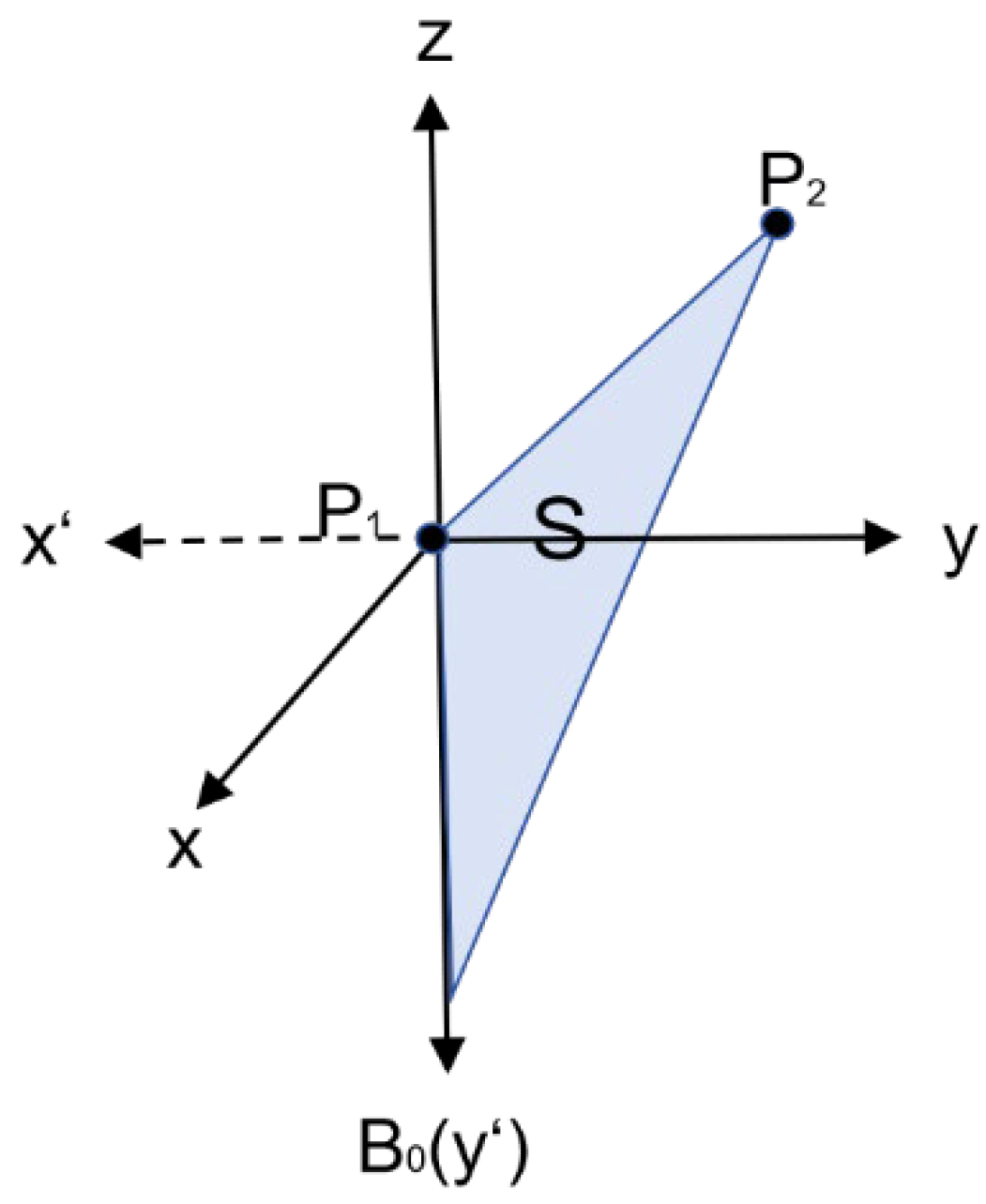
3.1. Dynamic Multi-Dipole Magnetic Moment Algorithm
3.2. Calculation of Magnetic Agglomeration Force
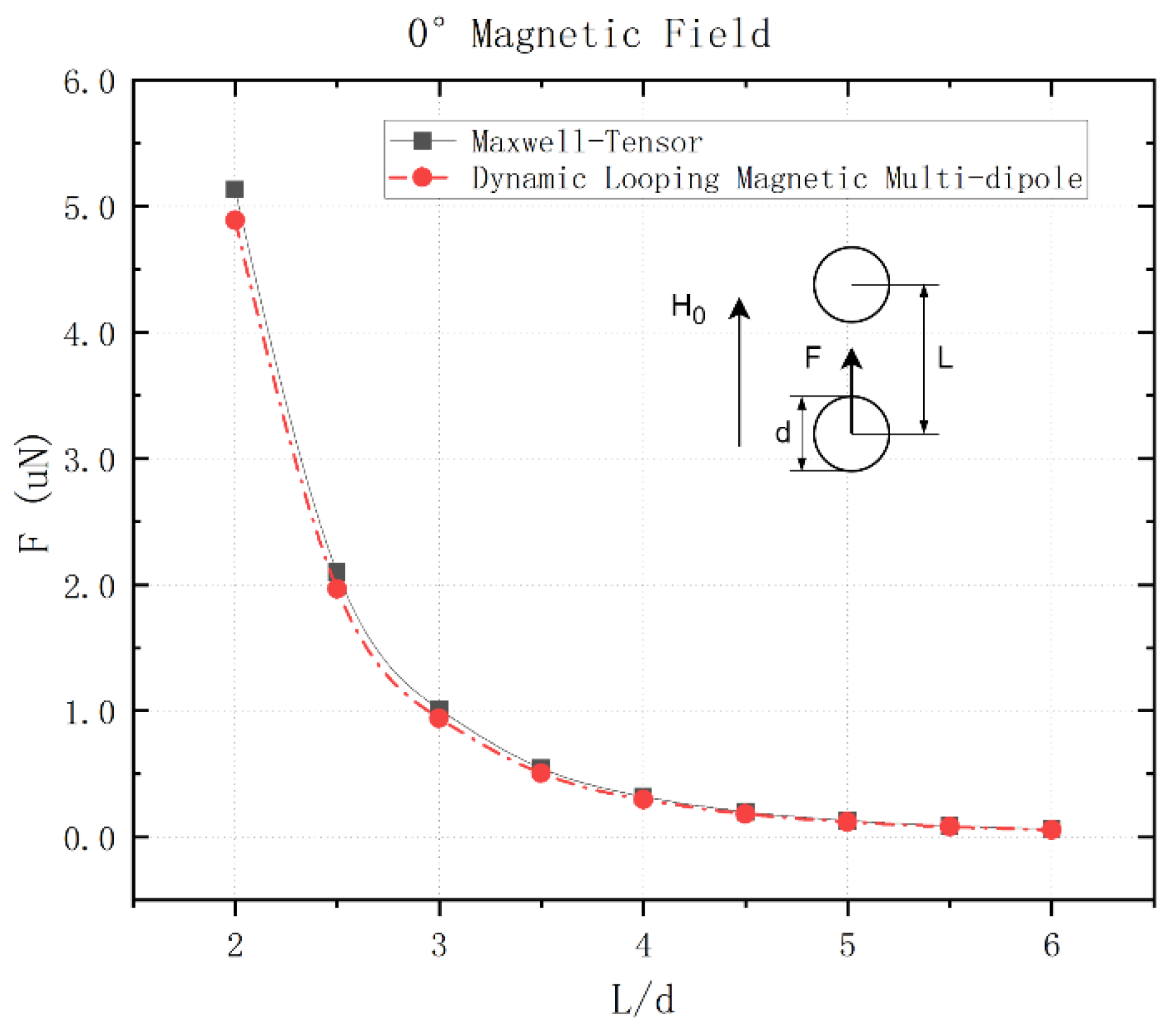
3.3. Results and Comparison of the Model Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, Z. Magnetoelectric Separation; Metallurgical Industry Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Xie, P.; Wang, F.; Tang, D.; Zhao, M.; Dai, H. Research Progress in the Application of Numerical Simulation in Magnetic Separation. Nonferrous Met. (Miner. Process. Sect.) 2023, 6, 9–18. (In Chinese) [Google Scholar]
- Murariu, V. Simulating a Low Intensity Magnetic Separator Model (LIMS) using DEM, CFD and FEM Magnetic Design Software. In Proceedings of the 4th International Computational Modelling Symposium, Singapore, 20–22 June 2025; Minerals Engineering International: Cornwall, UK, 2013; pp. 301–314. [Google Scholar]
- Lindner, J.; Menzel, K.; Nirschl, H. Simulation of magnetic suspensions for HGMS using CFD, FEM and DEM modeling. Comput. Chem. Eng. 2013, 54, 111–121. [Google Scholar] [CrossRef]
- Hu, Y. Analysis on simulation of magnetic separation process using dynamic coupled FEM, CFD and DEM model. Nonferrous Met. (Miner. Process. Sect.) 2016, 68–72, 82. (In Chinese) [Google Scholar]
- Wu, J.; Yue, X.; Guo, X.; Dai, S.; Zhang, M.; Ren, J. Simulation of Three Product Magnetic Separation Column Process Simulation Based on FEM, CFD and DEM Coupling. Met. Mine 2024, 2, 225–231. (In Chinese) [Google Scholar]
- Pinto-Espinoza, J. Dynamic Behavior of Ferromagnetic Particles in a Liquid-Solid Magnetically Assisted Fluidized Bed (MAFB): Theory, Experiment, and CFD-DPM Simulation. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2003. [Google Scholar]
- Chen, J.; An, R.; Shu, J.; Li, D.; Liu, X.; Mao, Y.; Chen, J.; Gao, H.; Lyu, W.; Meng, F. Study on motion of multi-component ferromagnetic particles with modified magnetization model. Chin. J. Theor. Appl. Mech. 2024, 56, 740–750. (In Chinese) [Google Scholar]
- Zhang, L.A.; Diao, Y.F.; Zhuang, J.W.; Zhou, F.S.; Shen, H.G. Performance of single fiber collection PM 2.5 under different magnetic field forms in the iron and steel industry. Chin. J. Eng. 2020, 42, 154–162. [Google Scholar]
- Rosensweig, R.E. Fluidization: Hydrodynamic stabilization with a magnetic field. Science 1979, 204, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Lampropoulos, N.K.; Karvelas, E.G.; Papadimitriou, D.I.; Sarris, I.E. Computational study of the optimum gradient magnetic field for the navigation of spherical particles into targeted areas. J. Phys. Conf. 2015, 637, 012038. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Lampropoulos, N.K.; Sarris, I.E. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM. Comput. Methods Programs Biomed. 2017, 142, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Watson, J.H.P.; Li, Z. A study on mechanical entrapment in HGMS and vibration HGMS. Miner. Eng. 1991, 4, 815–823. [Google Scholar] [CrossRef]





| Content | Parameter | Definition |
|---|---|---|
| Particle properties | Material type | Wolframite |
| Magnetic susceptibility | 3400 × 10−6 (SI) | |
| Density | 6.63 g/cm3 | |
| Particle diameter | 10 μm | |
| Wire medium properties | Material | Nickel |
| Magnetic susceptibility | 600 | |
| Diameter | 10 μm | |
| Parameter | Reynolds number Re | 6 |
| Background magnetic field strength | 1 T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Shen, Z.; Hu, Y.; Liang, G. Dynamic Coupling Model of the Magnetic Separation Process Based on FEM, CFD, and DEM. Processes 2025, 13, 1303. https://doi.org/10.3390/pr13051303
Wang X, Shen Z, Hu Y, Liang G. Dynamic Coupling Model of the Magnetic Separation Process Based on FEM, CFD, and DEM. Processes. 2025; 13(5):1303. https://doi.org/10.3390/pr13051303
Chicago/Turabian StyleWang, Xiaoming, Zhengchang Shen, Yonghui Hu, and Guodong Liang. 2025. "Dynamic Coupling Model of the Magnetic Separation Process Based on FEM, CFD, and DEM" Processes 13, no. 5: 1303. https://doi.org/10.3390/pr13051303
APA StyleWang, X., Shen, Z., Hu, Y., & Liang, G. (2025). Dynamic Coupling Model of the Magnetic Separation Process Based on FEM, CFD, and DEM. Processes, 13(5), 1303. https://doi.org/10.3390/pr13051303






