Stacked Auto-Encoder Based CNC Tool Diagnosis Using Discrete Wavelet Transform Feature Extraction
Abstract
:1. Introduction
2. Related Works
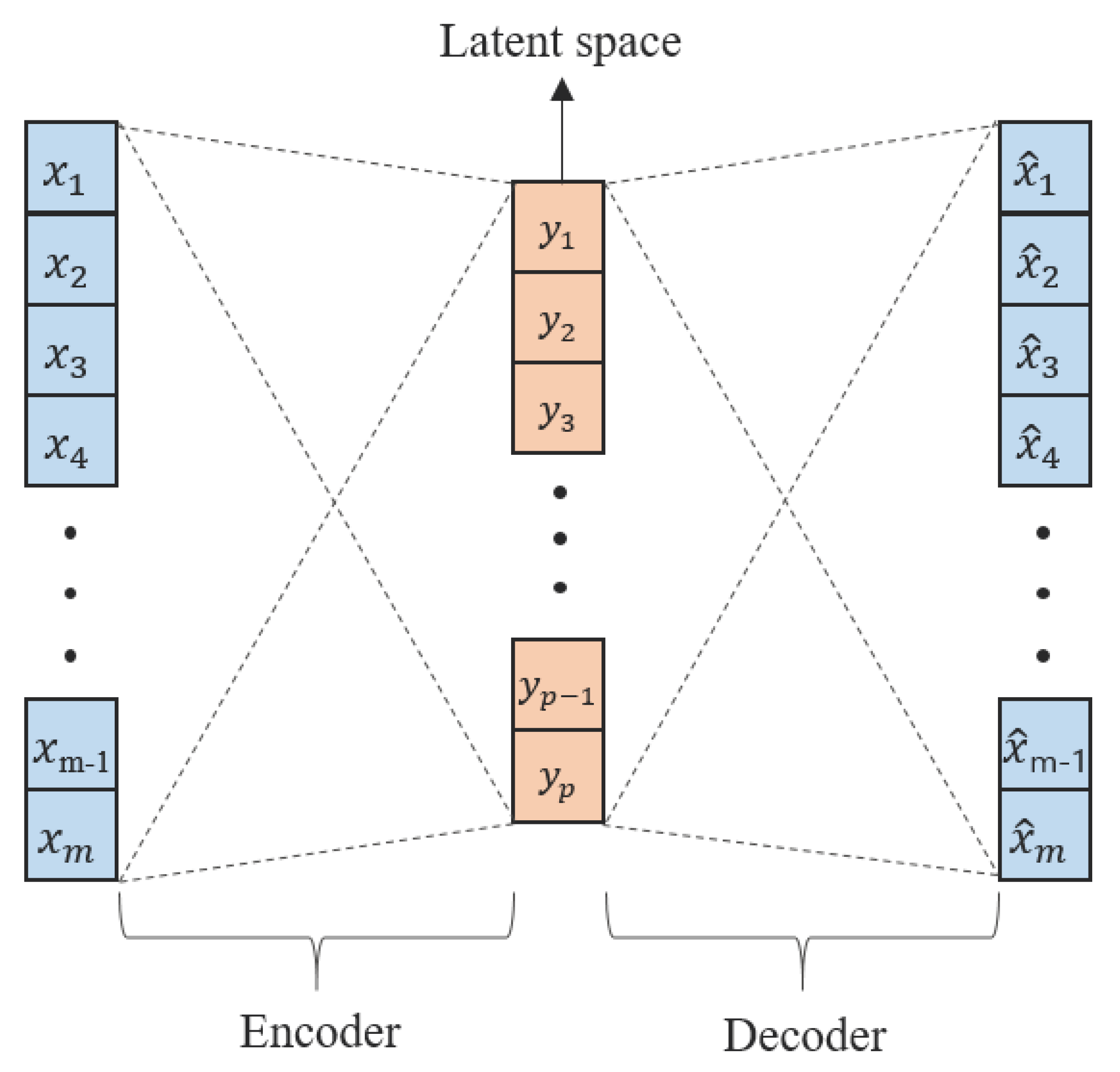
2.1. Auto-Encoder
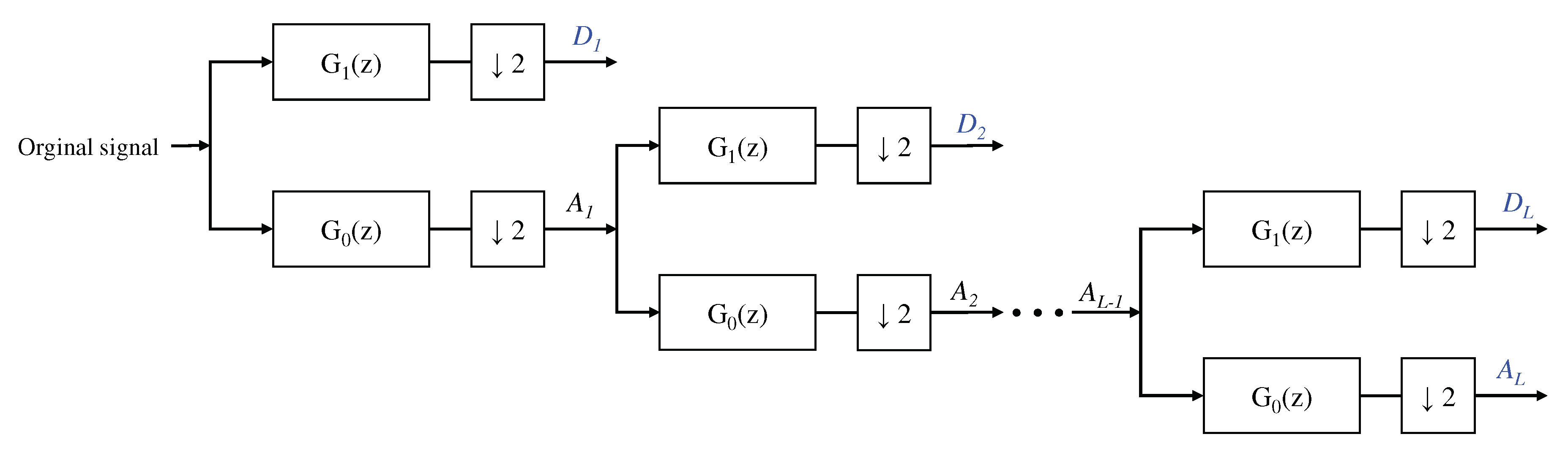
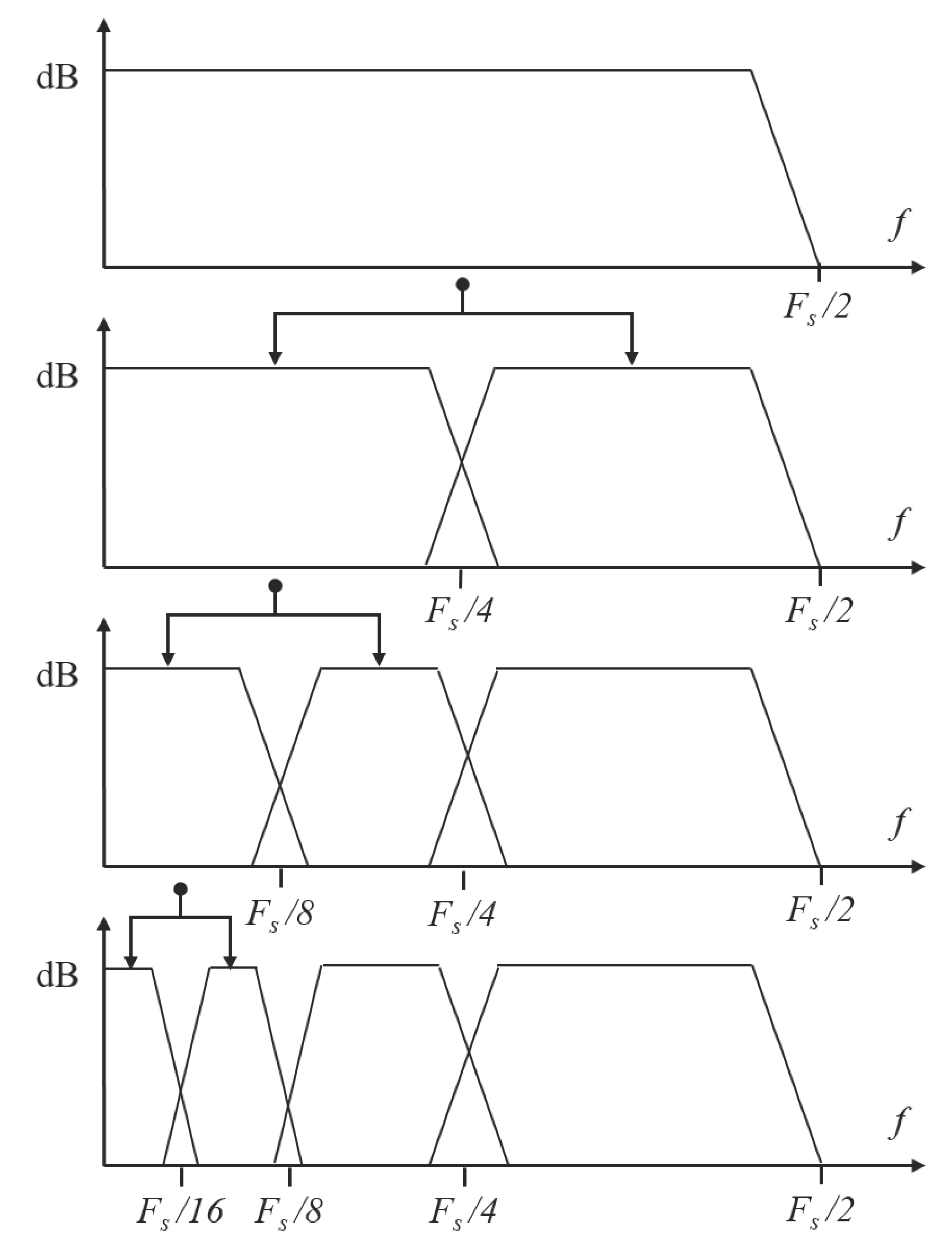
2.2. Wavelet Transform
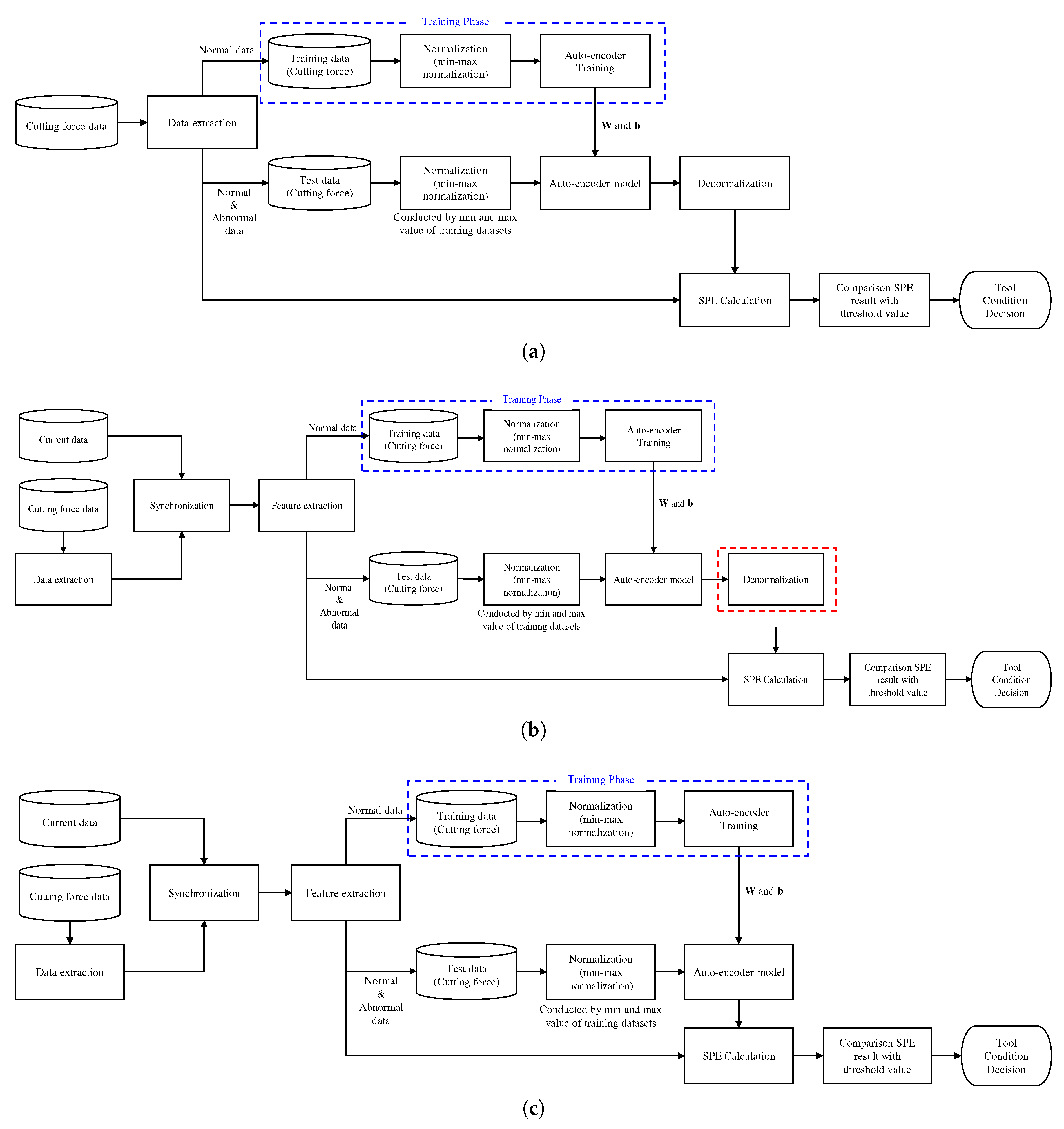
3. Data Description and Detection Index
3.1. Data Description
3.2. Feature Extraction
3.3. Detection Index
4. Experiment and Discussion
4.1. Data Preparation
4.2. Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lauro, C.; Brandão, L.; Baldo, D.; Reis, R.; Davim, J. Monitoring and processing signal applied in machining processes—A review. Measurement 2014, 58, 73–86. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.; Medjaher, K.; Zerhouni, N. CNC machine tool’s wear diagnostic and prognostic by using dynamic Bayesian networks. Mech. Syst. Signal Process. 2012, 28, 167–182. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, A.; Goyal, D.; Shimi, S.L.; Akula, A. Condition monitoring and fault diagnosis of induction motors: A review. Arch. Comput. Methods Eng. 2019, 26, 1221–1238. [Google Scholar] [CrossRef]
- Bassiuny, A.; Li, X. Flute breakage detection during end milling using Hilbert–Huang transform and smoothed nonlinear energy operator. Int. J. Mach. Tools Manuf. 2007, 47, 1011–1020. [Google Scholar] [CrossRef]
- Reñones, A.; de Miguel, L.J.; Perán, J.R. Experimental analysis of change detection algorithms for multitooth machine tool fault detection. Mech. Syst. Signal Process. 2009, 23, 2320–2335. [Google Scholar] [CrossRef]
- Ghosh, N.; Ravi, Y.; Patra, A.; Mukhopadhyay, S.; Paul, S.; Mohanty, A.; Chattopadhyay, A. Estimation of tool wear during CNC milling using neural network-based sensor fusion. Mech. Syst. Signal Process. 2007, 21, 466–479. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Liu, C.; Xie, Q.; Xu, Y. A new tool wear monitoring method based on multi-scale PCA. J. Intell. Manuf. 2019, 30, 113–122. [Google Scholar] [CrossRef]
- Luo, B.; Wang, H.; Liu, H.; Li, B.; Peng, F. Early fault detection of machine tools based on deep learning and dynamic identification. IEEE Trans. Ind. Electron. 2018, 66, 509–518. [Google Scholar] [CrossRef]
- Glowacz, A. Fault detection of electric impact drills and coffee grinders using acoustic signals. Sensors 2019, 19, 269. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh-Alisaraei, A.; Mahdavian, A. Fault detection of injectors in diesel engines using vibration time-frequency analysis. Appl. Acoust. 2019, 143, 48–58. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.; Wong, Y.; De Silva, C.; Goh, H.; Tan, W. Tool wear detection and fault diagnosis based on cutting force monitoring. Int. J. Mach. Tools Manuf. 2007, 47, 444–451. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A data-driven fault diagnosis methodology in three-phase inverters for PMSM drive systems. IEEE Trans. Power Electron. 2016, 32, 5590–5600. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, H.; Guo, Y.; Wang, J.; Li, G.; Shen, L. Sensor fault detection and diagnosis for a water source heat pump air-conditioning system based on PCA and preprocessed by combined clustering. Appl. Therm. Eng. 2019, 160, 114098. [Google Scholar] [CrossRef]
- Saari, J.; Strömbergsson, D.; Lundberg, J.; Thomson, A. Detection and identification of windmill bearing faults using a one-class support vector machine (SVM). Measurement 2019, 137, 287–301. [Google Scholar] [CrossRef]
- Wang, X.; Ma, L.; Wang, T. An optimized nearest prototype classifier for power plant fault diagnosis using hybrid particle swarm optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 58, 257–265. [Google Scholar] [CrossRef]
- Yu, J.; Jang, J.; Yoo, J.; Park, J.H.; Kim, S. A Clustering-Based Fault Detection Method for Steam Boiler Tube in Thermal Power Plant. J. Electr. Eng. Technol. 2016, 11, 848–859. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Wang, H.; Liu, P.; Huang, S.; Fan, P. A sparse stacked denoising autoencoder with optimized transfer learning applied to the fault diagnosis of rolling bearings. Measurement 2019, 146, 305–314. [Google Scholar] [CrossRef]
- Yu, H.; Wang, K.; Li, Y.; Zhao, W. Representation Learning With Class Level Autoencoder for Intelligent Fault Diagnosis. IEEE Signal Process. Lett. 2019, 26, 1476–1480. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, S.; Wang, J.; Xiong, N.N. Anomaly Detection Based on Convolutional Recurrent Autoencoder for IoT Time Series. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Hung, C.W.; Li, W.T.; Mao, W.L.; Lee, P.C. Design of a Chamfering Tool Diagnosis System Using Autoencoder Learning Method. Energies 2019, 12, 3708. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.; He, H.; Xie, P.; Tang, Y. Stacked multilevel-denoising autoencoders: A new representation learning approach for wind turbine gearbox fault diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 2391–2402. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Bao, H.; Han, B. A stacked autoencoder-based deep neural network for achieving gearbox fault diagnosis. Math. Probl. Eng. 2018, 2018, 5105709. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, Y.; Wang, K. Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network. J. Intell. Manuf. 2013, 24, 1213–1227. [Google Scholar] [CrossRef]
- Rai, V.; Mohanty, A. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Mark, S.; Sahu, R.; Kantarovich, K.; Podshyvalov, A.; Guterman, H.; Goldstein, J.; Jagannathan, R.; Mordechai, S. Fourier transform infrared microspectroscopy as a quantitative diagnostic tool for assignment of premalignancy grading in cervical neoplasia. J. Biomed. Opt. 2004, 9, 558–568. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zuo, M. Gearbox fault diagnosis using adaptive wavelet filter. Mech. Syst. Signal Process. 2003, 17, 1259–1269. [Google Scholar] [CrossRef]
- Singh, G.; Ahmed, S.A.K.S. Vibration signal analysis using wavelet transform for isolation and identification of electrical faults in induction machine. Electr. Power Syst. Res. 2004, 68, 119–136. [Google Scholar] [CrossRef]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 2007, 452, 155–176. [Google Scholar] [CrossRef] [Green Version]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: New York, NY, USA, 2000; Volume 4. [Google Scholar]
- Sharma, M.; Achuth, P.V.; Deb, D.; Puthankattil, S.D.; Acharaya, U.R. An automated diagnosis of depression using three-channel bandwidth-duration localized wavelet filter bank with EEG signals. Cog. Syst. Res. 2018, 52, 508–520. [Google Scholar] [CrossRef]
- Shah, S.; Sharma, M.; Deb, D.; Pachori, R.B. An automated alcoholism detection using orthogonal wavelet filter bank. In Machine Intelligence and Signal Analysis; Springer: Singapore, 2019; pp. 473–483. [Google Scholar]
- Kia, S.H.; Henao, H.; Capolino, G.A. Diagnosis of broken-bar fault in induction machines using discrete wavelet transform without slip estimation. IEEE Trans. Ind. Appl. 2009, 45, 1395–1404. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Morgan Kaufmann: Waltham, MA, USA, 2011. [Google Scholar]






| Notation | Description | Unit | Notation | Description | Unit |
|---|---|---|---|---|---|
| Average of cutting force | N | RMS value of (v-phase) | - | ||
| Maximum value of cutting force | N | RMS value of (v-phase) | - | ||
| Minimum value of cutting force | N | RMS value of (v-phase) | - | ||
| Median of cutting force | N | RMS value of (v-phase) | - | ||
| STD of cutting force | N | RMS value of (u-phase) | - | ||
| RMS value of u-phase | A | RMS value of (u-phase) | - | ||
| Maximum value of u-phase | A | RMS value of (u-phase) | - | ||
| STD of u-phase | A | RMS value of (u-phase) | - | ||
| RMS value of v-phase | A | RMS value of (u-phase) | - | ||
| Maximum value of v-phase | A | RMS value of (u-phase) | - | ||
| STD of v-phase | A | RMS value of (u-phase) | - | ||
| RMS value of w-phase | A | RMS value of (w-phase) | - | ||
| Maximum value of w-phase | A | RMS value of (w-phase) | - | ||
| STD of w-phase | A | RMS value of (w-phase) | - | ||
| RMS value 3-phase | A | RMS value of (w-phase) | - | ||
| RMS value of (v-phase) | - | RMS value of (w-phase) | - | ||
| RMS value of (v-phase) | - | RMS value of (w-phase) | - | ||
| RMS value of (v-phase) | - | RMS value of (w-phase) | - |
| Model | Code Size | Number of Layers | Whole Structure | Learning Epoch |
|---|---|---|---|---|
| CFSAE | 20 | 7 | 350 | |
| FSAE | 10 | 7 | 200 | |
| FSAENR | 10 | 7 | 200 |
| Model | FNR (%) | FPR (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| New | Used | New | Used | New | Used | |||||
| CFSAE | 8 | 56 | 12 | 156 | 0 | 6 | 60.00 | 0.00 | 25.69 | 97.25 |
| FSAE | 14 | 0 | 6 | 1 | 0 | 217 | 30.00 | 0.00 | 0.00 | 0.46 |
| FSAENR | 16 | 0 | 4 | 1 | 0 | 217 | 20.00 | 0.00 | 0.00 | 0.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lee, H.; Jeon, J.W.; Kim, J.M.; Lee, H.U.; Kim, S. Stacked Auto-Encoder Based CNC Tool Diagnosis Using Discrete Wavelet Transform Feature Extraction. Processes 2020, 8, 456. https://doi.org/10.3390/pr8040456
Kim J, Lee H, Jeon JW, Kim JM, Lee HU, Kim S. Stacked Auto-Encoder Based CNC Tool Diagnosis Using Discrete Wavelet Transform Feature Extraction. Processes. 2020; 8(4):456. https://doi.org/10.3390/pr8040456
Chicago/Turabian StyleKim, Jonggeun, Hansoo Lee, Jeong Woo Jeon, Jong Moon Kim, Hyeon Uk Lee, and Sungshin Kim. 2020. "Stacked Auto-Encoder Based CNC Tool Diagnosis Using Discrete Wavelet Transform Feature Extraction" Processes 8, no. 4: 456. https://doi.org/10.3390/pr8040456
APA StyleKim, J., Lee, H., Jeon, J. W., Kim, J. M., Lee, H. U., & Kim, S. (2020). Stacked Auto-Encoder Based CNC Tool Diagnosis Using Discrete Wavelet Transform Feature Extraction. Processes, 8(4), 456. https://doi.org/10.3390/pr8040456






