Model-Based Monitoring of Biotechnological Processes—A Review
Abstract
:1. Topicality of the Monitoring of Biotechnological Processes
2. Issues with Biotechnological Process Monitoring
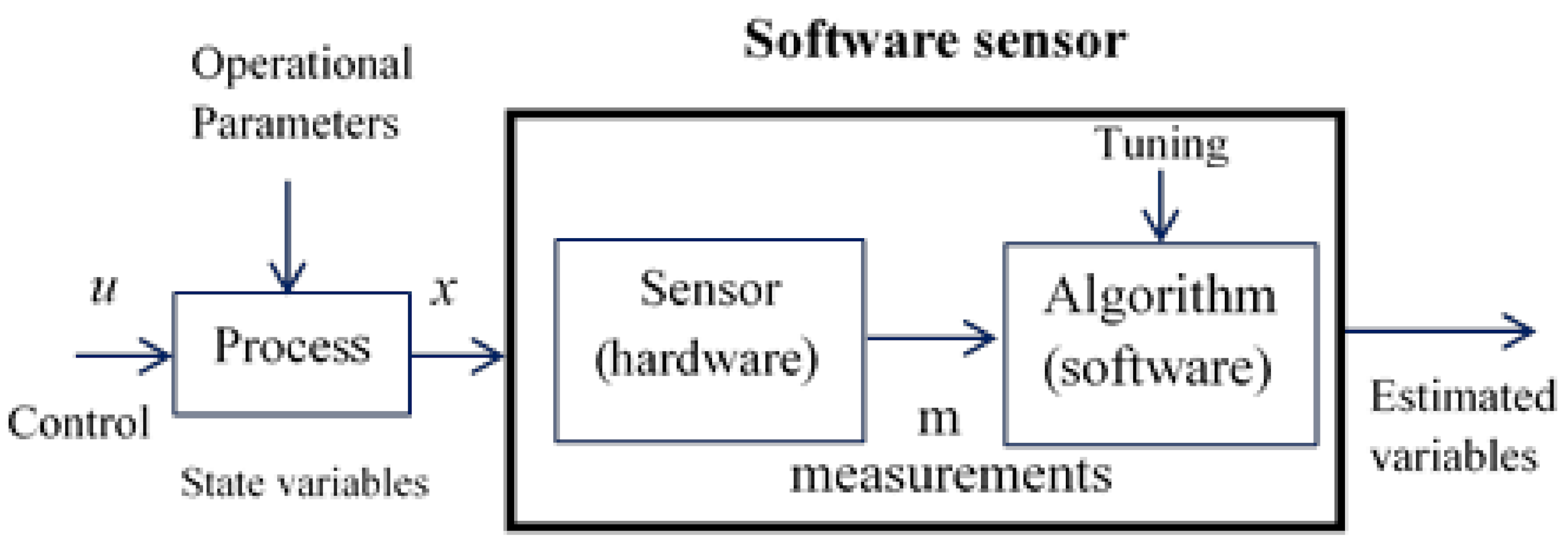
3. Software Sensor Concept and Software Sensor Types
4. Model-Based Software Sensors
4.1. Linear Observers
4.2. Extension of Linear Observers
4.3. Observers for Linear Time Varying Systems
4.4. Nonlinear Observers
5. Model-Based BTP Software Sensors
6. General Dynamical Model Approach and its Further Development for SS Synthesis
- ξ—vector of concentrations of components dissolved in the nutrient medium;
- K—a matrix of yield coefficients;
- φ—a reaction rate vector;
- D—dilution rate;
- F—a vector of feed rates;
- Q—flow rates of gaseous components from the reactor.
7. Discussion
- Complexity of the specific process;
- Full/partial knowledge of the model structure;
- Available process information (quality and quantity of available offline and online measurements), the types of noises and uncertainties, etc.
- A process database creation module.
- Module containing programs that solve the differential equations of SS and/or model used.
- Module containing programs for tuning of SS parameters and/or model identification.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pohlscheidt, М.; Charaniya, S.; Bork, C.; Jenzsch, M.; Noetzel, T.; Luebbert, A. Bioprocess and Fermentation Monitoring. Encycl. Ind. Biotechnol. 2013, 1469–1491. [Google Scholar] [CrossRef]
- Tamburini, E.; Marchetti, M.; Pedrini, P. Monitoring Key Parameters in Bioprocesses Using Near-Infrared Technology. Sensors 2014, 14, 18941–18959. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitford, W.; Julien, C. Bioreactors: Analytical Technology and PAT. Bioprocess Int. 2007, 5, 32–42. [Google Scholar]
- Vojinovi, V.; Cabral, J.; Fonseca, L. Real-time bioprocess monitoring. Part I: In situ sensors. Sens. Actuators B Chem. 2006, 114, 1083–1091. [Google Scholar] [CrossRef]
- Soons, Z.I.T.A.; Voogt, J.A.; van Straten, G.; van Boxtela, A.J.B. Constant specific growth rate in fedbatch cultivation of Bordetella pertussis using adaptive control. J. Biotechnol. 2006, 125, 252–268. [Google Scholar] [CrossRef]
- Dochain, D. Bioprocesses Control; ISTE Publishing and Wiley & Sons: Hoboken, NJ, USA, 2008; p. 217. [Google Scholar]
- Silveira, B.M.; Barcelos, M.C.; Vespermann, K.A.; Pelissari, F.M.; Molina, G. An Overview of Biotechnological Processes in the Food Industry. Bioprocess. Biomol. Prod. 2019, 1–19. [Google Scholar] [CrossRef]
- Tang, L.; Huimin, Z. Industrial biotechnology: Tools and applications. Biotechnol. J. Healthc. Nutr. Technol. 2009, 4, 1725–1739. [Google Scholar] [CrossRef]
- Chen, G.Q. New challenges and opportunities for industrial biotechnology. Microb. Cell Factories 2012, 11, 111. [Google Scholar] [CrossRef] [Green Version]
- Dochain, D.; Perrier, M. Dynamical modelling, analysis, monitoring and control design for nonlinear bioprocesses. In Biotreatment, Downstream Processing and Modelling; Springer: Berlin/Heidelberg, Germany, 1997; pp. 147–197. [Google Scholar]
- Zhang, H. Software Sensors and Their Applications in Bioprocess. In Computational Intelligence Techniques for Bioprocess Modelling, Supervision and Control, Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 25–56. [Google Scholar]
- Veloso, A.; Rocha, I.; Ferreira, E.C. Monitoring of fed-batch E. coli fermentations with software sensors. Bioprocess Biosyst. Eng. 2009, 32, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Thibault, J.; Van Breusegem, V.; Chéruy, A. On-line prediction of fermentation variables using neural networks. Biotechnol. Bioeng. 1990, 36, 1041–1048. [Google Scholar] [CrossRef]
- Mears, L.; Stocks, S.M.; Albaek, M.O.; Sin, G.; Gernaey, K.V. Mechanistic Fermentation Models for Process Design, Monitoring, and Control. Trends Biotechnol. 2017, 35, 914–924. [Google Scholar] [CrossRef]
- Misawa, E.; Hedrick, J.K. Nonlinear observers—a state-of-the-art survey. J. Dyn. Syst. Meas. Control 1989, 111, 344–352. [Google Scholar] [CrossRef]
- Reif, K.; Unbehauen, R. The extended Kalman filter as an exponential observer for nonlinear systems. IEEE Trans. Signal Process. 1999, 47, 2324–2328. [Google Scholar] [CrossRef]
- Bastin, G.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier Science: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Zeitz, M. The extended Luenberger observer for nonlinear systems. Syst. Control Lett. 1987, 9, 149–156. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 887–892. [Google Scholar]
- Jin, X.-B.; Jeremiah, R.J.R.; Su, T.-L.; Bai, Y.-T.; Kong, J.-L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors 2021, 21, 2085. [Google Scholar] [CrossRef]
- Mareels, I.M.Y.; Gevers, M. Persistency of excitation criteria for linear, multivariable, time-varying systems. Math. Cont. Signals Syst. 1988, 1, 203–226. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Stable Adaptive Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Sun, X.; Jin, L.; Xiong, M. Extended Kalman Filter for Estimation of Parameters in Nonlinear State-Space Models of Biochemical Networks. PLoS ONE 2008, 3, 3758. [Google Scholar] [CrossRef]
- Kravaris, C.; Hahn, J.; Chu, Y. Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 2013, 51, 111–166. [Google Scholar] [CrossRef]
- Guay, M. Observer linearization by output-dependent time scale transformations. IEEE Trans. Autom. Control 2002, 47, 1730–1735. [Google Scholar] [CrossRef]
- Gauthier, J.; Kupka, I. Observability and observers for nonlinear systems. SIAM J. Control Optim. 1994, 32, 975–994. [Google Scholar] [CrossRef]
- Deza, F.; Busvelle, E.; Gauthier, J.; Rakotopara, D. High gain estimation for nonlinear systems. Syst. Control Lett. 1992, 18, 292–299. [Google Scholar] [CrossRef]
- Elsheikh, M.; Hille, R.; Tatulea-Codrean, A.; Krämer, S. A Comparative Review of Multi-Rate Moving Horizon Estimation Schemes for Bioprocess Applications. Comput. Chem. Eng. 2021, 146, 107219. [Google Scholar] [CrossRef]
- Fazlyab, M.; Robey, A.; Hassani, H.; Morari, M.; Pappas, G.J. Efficient and accurate estimation of lipschitz constants for deep neural networks. arXiv 2019, arXiv:1906.04893. [Google Scholar]
- Wood, G.R.; Zhang, B.P. Estimation of the Lipschitz constant of a function. J. Glob. Optim. 1996, 8, 91–103. [Google Scholar] [CrossRef]
- Calliess, J.P. Lipschitz optimisation for Lipschitz interpolation. In Proceedings of the IEEE 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 3141–3146. [Google Scholar]
- Paulavičius, R.; Žilinskas, J. Simplicial Lipschitz optimization without Lipschitz constant. In Simplicial Global Optimization; Springer: New York, NY, USA, 2014; pp. 61–86. [Google Scholar]
- Zhu, F.; Han, Z. A note on observers for Lipschitz nonlinear systems. IEEE Trans. Autom. Control 2002, 47, 1751–1754. [Google Scholar]
- Moreno, J. Nonlinear observer design: A dissipative approach. In Technical Report; Universidad Nacional Autonoma de Mexico: Mexico City, Mexico, 2009. [Google Scholar]
- Hou, M.; Muller, P. Design of obsevers for linear systems with unknown inputs. IEEE Trans. Autom. Control 1991, 37, 871–875. [Google Scholar] [CrossRef]
- Rouche, N.; Habets, P.; Laloy, M. Stability Theory by Liapunov’s Direct Method. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1977. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1978. [Google Scholar]
- Willems, J.L. Stability Theory of Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1970. [Google Scholar]
- Vaitkus, V.; Brazauskas, K.; Repšytė, J. Soft-sensors based on Black-box Models for Bioreactors Monitoring and State Estimation. In Proceedings of the 2020 12th International Conference on Bioinformatics and Biomedical Technology, Xi’an, China, 22–24 May 2020; pp. 43–47. [Google Scholar]
- Zhu, X.; Rehman, K.U.; Wang, B.; Shahzad, M. Modern soft-sensing modeling methods for fermentation processes. Sensors 2020, 20, 1771. [Google Scholar] [CrossRef] [Green Version]
- Cheruy, A. Software sensors in bioprocess engineering. J. Biotechnol. 1997, 52, 193–199. [Google Scholar] [CrossRef]
- Kalchev, B.; Popova, S.; Simeonov, I. Comparative study of two Kalman-based estimators for a simple anaerobic digestion model. Int. Conf. Autom. Inform. 2009, I, 181–186. [Google Scholar]
- Luttmann, R.; Bracewell, D.G.; Cornelissen, G.; Gernaey, K.V.; Glassey, J.; Hass, V.C.; Kaiser, C.; Preusse, C.; Striedner, G.; Mandenius, C.-F. Soft sensors in bioprocessing: A status report and recommendations. Biotechnol. J. 2012, 7, 1040–1048. [Google Scholar] [CrossRef]
- Selişteanu, D.; Petre, E.; Răsvan, V. Sliding mode and adaptive sliding–mode control of a class of nonlinear bioprocesses. Int. J. Adapt. Control Signal Process. 2007, 21, 795–822. [Google Scholar] [CrossRef]
- García-Mañas, F.; Guzmán, J.L.; Berenguel, M.; Acién, F.G. Biomass estimation of an industrial raceway photobioreactor using an extended Kalman filter and a dynamic model for microalgae production. Algal Res. 2019, 37, 103–114. [Google Scholar] [CrossRef]
- Jianlin, W.; Xuying, F.; Liqiang, Z.; Tao, Y.U. Unscented transformation based robust Kalman filter and its applications in fermentation process. Chin. J. Chem. Eng. 2010, 18, 412–418. [Google Scholar]
- Neeleman, R.; Van Boxtel, A.J.B. Estimation of specific growth rate from cell density measurements. Bioprocess Biosyst. Eng. 2001, 24, 179–185. [Google Scholar]
- Patarinska, T.; Trenev, V.; Popova, S. Software Sensors Design for a Class of Aerobic Fermentation Processes. Int. J. Bioautomation 2010, 14, 99–118. [Google Scholar]
- Popova, S.; Ignatova, M.; Lyubenova, V. State and parameters estimation by Extended Kalman Filter for studying inhomogeneous dynamics in industrial bioreactors. In Proceedings of the 3rd European Conference of Control (ECC’12), Paris, France, 2–4 December 2012; pp. 43–47.
- Simutis, R.; Galvanauskas, V.; Levisauskas, D.; Repsyte, J.; Grincas, V. State Estimation of a Biotechnological Process Using Extended Kalman Filter and Particle Filter. Vet. Agric. Eng. 2014, 8, 933–937. [Google Scholar]
- Stelzer, I.V.; Kager, J.; Herwig, C. Comparison of particle filter and extended Kalman filter algorithms for monitoring of bioprocesses. Comput. Aided Chem. Eng. 2017, 40, 1483–1488. [Google Scholar]
- Popova, S.; Kostov, G.; Ignatova, M.; Lubenova, V.; Naydenova, V.; Pircheva, D.; Angelov, M. State and kinetic parameters estimation of bio-ethanol production with immobilized cells. In WSEAS International Conference on Applied and Computational Mathematics Athens, Proceedings of the 2nd International Conference on Applied and Computational Mathematics (ICACM ’13), Vouliagmeni, Athens, Greece, 14–16 May 2013; WSEAS: Athens, Greece, 2013; pp. 51–57. [Google Scholar]
- Soons, Z.I.T.A.; Shi, J.; Van Der Pol, L.A.; Van Straten, G.; Van Boxtel, A.J. Biomass growth and kLa estimation using online and offline measurements. IFAC Proc. Vol. 2007, 40, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Zorzetto, L.F.M.; Wilson, J.A. Monitoring bioprocesses using hybrid models and an extended kalman filter. Comput. Chem. Eng. 1996, 20, 689–694. [Google Scholar] [CrossRef]
- Chachuat, B.; Bernard, O. Probabilistic observers for a class of uncertain biological processes. Int. J. Robust Nonlinear Control 2006, 16, 157–171. [Google Scholar] [CrossRef] [Green Version]
- Feyo de Azevedo, S.; Pimenta, P.; Oliveira, R.; Ferreira, E.; Oliveira, F. Studies on On-line State and Parameter Estimation through a real-time Process Simulator. IFAC Proc. Vol. 1992, 25, 453–458. [Google Scholar] [CrossRef] [Green Version]
- Ignatova, M.; Lubenova, V.; Georgieva, P. MIMO adaptive linearizing control of fed-batch amino acids simultaneous production. Bioprocess Eng. 2000, 22, 79–84. [Google Scholar] [CrossRef]
- Ochoa, S. Process from Starch to Ethanol. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2008; Volume 25, pp. 489–494. [Google Scholar]
- Oliveira, R.; Simutis, R.; Feyo de Azevedo, S. Design of a stable adaptive controller for driving aerobic fermentation processes near maximum oxygen transfer capacity. J. Process Control 2004, 14, 617–626. [Google Scholar] [CrossRef]
- Pomerleau, Y.; Perrier, M. Non-Linear Estimation of Specific Growth Rates in Baker’s Yeast Fed-Batch Fermentation; Annual AIChE Meeting: Washington, DC, USA, 1988; p. 132B. [Google Scholar]
- Rocha, I.; Veloso, A.; Ferreira, E.C. Design of estimators for specific growth rate control in a fed-batch E. coli fermentation. In Proceedings of the 5th MATHMOD Vienna–5th Vienna Symposium on Mathematical Modelling, Vienna, Austria, 8–10 February 2006. [Google Scholar]
- Oliveira, R.; Ferreira, E.C.; Feyo de Azevedo, S. Stability, dynamics of convergence and tuning of observer-based kinetics estimators. J. Process Control 2002, 12, 311–323. [Google Scholar] [CrossRef] [Green Version]
- Perrier, M.; Feyo de Azevedo, S.; Ferreira, E.C.; Dochain, D. Tuning of observer-based estimators: Theory and application to the on-line estimation of kinetic parameters. Control Eng. Pract. 2000, 8, 377–388. [Google Scholar] [CrossRef] [Green Version]
- Čelikovský, S.; Torres-Munoz, J.A.; Dominguez-Bocanegra, A.R. Adaptive high gain observer extension and its application to bioprocess monitoring. Kybernetika 2018, 54, 155–174. [Google Scholar] [CrossRef] [Green Version]
- Farza, M.; M’Saad, M.; Maatoug, T.; Kamounb, M. Adaptive observers for nonlinearly parameterized class of nonlinear systems. Automatica 2009, 45, 2292–2299. [Google Scholar] [CrossRef] [Green Version]
- Farza, M.; Othman, S.; Hammouri, H.; Biston, J. A nonlinear approach for the on-line estimation of the kinetic rates in bioreactors. Application to a lactic acid production process. Bioprocess Eng. 1997, 17, 143–150. [Google Scholar] [CrossRef]
- Roman, M.; Selişteanu, S. Nonlinear on-line estimation and adaptive control of a wastewater treatment bioprocess. Elektronika ir Elektrotechnika 2012, 117, 23–28. [Google Scholar] [CrossRef] [Green Version]
- Selisteanu, D.; Petre, E.; Roman, M.; Popescu, D.; Bobasu, E. On-line estimation of unknown kinetics for the enzymatic synthesis of ampicillin. In Proceedings of the 12th International Carpathian Control Conference (ICCC), Velke Karlovice, Czech Republic, 25–28 May 2011; pp. 331–336. [Google Scholar]
- Selisteanu, D.; Petre, E.; Marin, C.; Şendrescu, D. High-gain observers for estimation of kinetics in a nonlinear bioprocess. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 5236–5241. [Google Scholar]
- Selisteanu, D.; Petre, E.; Şendrescu, D.; Roman, M. High-gain observers for estimation of kinetics in biological sequencing batch reactors. In Proceedings of the ICAL ’09, IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009; pp. 1623–1628. [Google Scholar]
- Tréangle, C.; Farza, M.; M’saad, M. On-line estimation of the reaction rates in bioreactors from multirate sampled outputs with multiple delays. IFAC-PapersOnLine 2019, 52, 703–708. [Google Scholar] [CrossRef]
- Farza, M.; Hammouri, H.; Jallut, C.; Lieto, J. State observation of a nonlinear system: Application to (bio)chemical processes. AIChE J. 1999, 45, 93–106. [Google Scholar] [CrossRef]
- De Battista, H.; Picó, J.; Garelli, F.; Navarro, J.L. Reaction rate reconstruction from biomass concentration measurement in bioreactors using modified second-order sliding mode algorithms. Bioprocess Biosyst. Eng. 2012, 35, 1615–1625. [Google Scholar] [CrossRef]
- Jamilis, M.; Garelli, F.; Mozumder, M.S.I.; Castañeda, T.; Battista, H.D. Modeling and estimation of production rate for the production phase of non-growth-associated high cell density processes. Bioprocess Biosyst. Eng. 2015, 38, 1903–1914. [Google Scholar] [CrossRef]
- Lara-Cisneros, G.; Dochain, D. Software Sensor for Online Estimation of the VFA’s Concentration in Anaerobic Digestion Processes via a High-Order Sliding Mode Observer. Ind. Eng. Chem. Res. 2018, 57, 14173–14181. [Google Scholar] [CrossRef]
- Nuñez, S.; Garelli, F.; De Battista, H. Second-order sliding mode observer for biomass concentration and growth rate estimation in batch photo-bioreactors. Int. J. Hydrogen Energy 2014, 39, 8772–8779. [Google Scholar] [CrossRef]
- Picó, J.; De Battista, H.; Garelli, F. Smooth sliding-mode observers for specific growth rate and substrate from biomass measurement. J. Process Control 2009, 19, 1314–1323. [Google Scholar] [CrossRef]
- Narayanan, H.; Behle, L.; Luna, M.F.; Sokolov, M.; Guillén-Gosálbez, G.; Morbidelli, M.; Butté, A. Hybrid-EKF: Hybrid model coupled with extended Kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnol. Bioeng. 2020, 117, 2703–2714. [Google Scholar] [CrossRef]
- Bogaerts, P.; Coutinho, D. Robust nonlinear state estimation of bioreactors based on H∞ hybrid observers. Comput. Chem. Eng. 2014, 60, 315–328. [Google Scholar] [CrossRef]
- Hulhoven, X.; Wouwer, A.V.; Bogaerts, P. Hybrid Extended Luenberger-Asymptotic Observer for Bioprocess State Estimation. Chem. Eng. Sci. 2006, 61, 7151–7160. [Google Scholar] [CrossRef]
- Campani, G.; Ribeiro, M.P.; Zangirolami, T.C.; Lima, F.V. A hierarchical state estimation and control framework for monitoring and dissolved oxygen regulation in bioprocesses. Bioprocess Biosyst. Eng. 2019, 42, 1467–1481. [Google Scholar] [CrossRef]
- Oubabas, H.; Djennoune, S.; Bettayeb, M. Interval sliding mode observer design for linear and nonlinear systems. J. Process Control 2018, 61, 12–22. [Google Scholar] [CrossRef]
- Golabgir, A.; Hoch, T.; Zhariy, M.; Herwig, C. Observability analysis of biochemical process models as a valuable tool for the development of mechanistic soft sensors. Biotechnol. Prog. 2015, 31, 1703–1715. [Google Scholar] [CrossRef] [PubMed]
- Bezzaoucha, S.; Marx, B.; Maquin, D.; Ragot, J. Nonlinear joint state and parameter estimation: Application to a wastewater treatment plant. Control Eng. Pract. 2013, 21, 377–1385. [Google Scholar] [CrossRef] [Green Version]
- Cazzador, L.; Lubenova, V. Nonlinear estimation of specific growth rate for aerobic fermentation processes. Biotechnol. Bioeng. 1995, 47, 626–632. [Google Scholar] [CrossRef]
- Georgieva, P.; Feyo de Azevedo, S. Novel Computational Methods for Modeling and Control in Chemical and Biochemical Process Systems. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; Volume 218, pp. 99–125. [Google Scholar]
- Keesman, K. State and parameter estimation in biotechnical batch reactors. Control Eng. Pract. 2002, 10, 219–225. [Google Scholar] [CrossRef]
- Morel, E.; Tartakovsky, B.; Guiot, S.R.; Perrier, M. Design of a multi-model observer-based estimator for anaerobic reactor monitoring. Comput. Chem. Eng. 2006, 31, 78–85. [Google Scholar] [CrossRef]
- Moshksar, E.; Guay, M. A geometric approach for adaptive estimation of unknowm growth kinetics in bioreactor. J. Process Control 2014, 24, 1496–1503. [Google Scholar] [CrossRef]
- Selisteanu, D.; Tebbani, S.; Roman, M.; Petre, E.; Georgeanu, V. Microbial production of enzimes: Nonlinear state and kinetic reaction rates estimation. Biochem. Eng. J. 2014, 91, 23–36. [Google Scholar] [CrossRef]
- Wang, F.S.; Lee, W.C.; Chang, L.L. On-line state estimation of biomass based on acid production in Zymomonas mobilis cultures. Bioprocess Eng. 1998, 18, 329–333. [Google Scholar] [CrossRef]
- San, K.Y.; Stephanopoulos, G. Studies on on-line bioreactor identification IV. Utilization of pH measurements for product estimation. Biotechnol. Bioeng. 1984, 26, 1209–1218. [Google Scholar] [CrossRef]
- Lubenova, V.; Ignatova, M. An approach for parameter estimation of biotechnological processes. Bioprocess Eng. 1994, 11, 107–113. [Google Scholar] [CrossRef]
- Lubenova, V. On-line Estimation of Biomass Concentration and Non Stationary Parameters for Aerobic Bioprocesses. J. Biotehnol. 1996, 46, 197–207. [Google Scholar] [CrossRef]
- Lubenova, V.; Rocha, I.; Ferreira, E.C. Estimation of Multiple Biomass Growth Rates and Biomass Concentration in a Class of Bioprocesses. Bioprocess Biosyst. Eng. 2003, 25, 395–406. [Google Scholar] [CrossRef] [Green Version]
- Lyubenova, V.; Ignatova, M.; Roeva, O.; Junne, S.; Neubauer, P. Adaptive Monitoring of Biotechnological Processes Kinetics. Processes 2020, 8, 1307. [Google Scholar] [CrossRef]
- Simeonov, I.; Lubenova, V.; Queinnec, I. Parameter and State Estimation of the Anaerobic Digestion of Organic Wastes with Addition of Stimulating Substances. Int. J. Bioautomation 2009, 12, 88–106. [Google Scholar]
- Zlatkova, A.; Lyubenova, V. Dynamics Monitoring of Fed-batch E. coli Fermentation. Int. J. Bioautomation 2017, 21, 121–132. [Google Scholar]
- Zlatkova, А.; Lyubenova, V. Monitoring the Dynamics of Bioprocesses Using Intermediate Metabolite Proceed. Int. Conf. Autom. Inform. 2017, 231–234. [Google Scholar]
- García, M.R.; Vilas, C.; Banga, J.R.; Lyubenova, V.N.; Ignatova, M.N.; Alonso, A.A. State Reconstruction in Spatially Distributed BioProcess Systems using Reduced Order Models: Application to the Gluconic Acid Production. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 6256–6261. [Google Scholar]
- Dochain, D. State observers for tubular reactors with unknown kinetics. J. Process Control 2000, 10, 259–268. [Google Scholar] [CrossRef]
- Delvigne, F.; Zacchetti, B.; Fickers, P.; Fifani, B.; Roulling, F.; Lefebvre, C.; Neubauer, P.; Junne, S. Improving controllability of microbial cell factories: From single cell to large-scale bioproduction. FEMS Microbiol. Lett. 2018, 365, 236–247. [Google Scholar]
- Junne, S.; Klingner, A.; Kabisch, J.; Schweder, T.; Neubauer, P. A two-compartment bioreactor system made of commercial parts for bioprocess scale-down studies: Impact of oscillations on Bacillus subtilis fed-batch cultivations. Biotechnol. J. 2011, 6, 1009–1017. [Google Scholar] [CrossRef]
- Ignatova, M.N.; Lyubenova, V.N.; García, M.R.; Vilas, C.; Alonso, A.A. Indirect adaptive linearizing control of a class of bioprocesses–Estimator tuning procedure. J. Process Control 2008, 18, 27–35. [Google Scholar] [CrossRef]
- Ignatova, M.; Lyubenova, V.; Eerikäinen, T.; Salonen, K. Software sensor of substrate kinetics and its application for control of α-amylase production by Bacillus subtilis. Comptes Rendus L’Academie Bulg. Sci. 2008, 61, 1449–1458. [Google Scholar]
- Lyubenova, V.; Kostov, G.; Ignatova, M. Discrete Adaptive Control of Continuous Fermentation with Immobilized Yeasts Saccharomyces Cerevisiae 46 EVD. In Proceed. ECC’12; WSEAS: Paris, France, 2012; pp. 25–29. [Google Scholar]
- Ignatova, M.; Lyubenova, V. Dynamics monitoring of laboratory model microorganisms in fed-batch cultivation. In XXIII International Conference, Automation of Discrete Production; Technical University of Sofia: Sozopol, Bulgaria, 2014; pp. 463–467. [Google Scholar]
- Lyubenova, V.; Ignatova, M. Cascade software sensors for monitoring of activated sludge waste water treatment processes. Comptes Rendus L’Academie Bulg. Sci. 2011, 64, 395–404. [Google Scholar]
- Lyubenova, V.; Junne, S.; Ignatova, M.; Neubauer, P. Software sensors for investigation of inhomogeneous dynamics in industrial bioreactors. Biotechnol. Bioeng. 2013, 110, 1945–1955. [Google Scholar] [CrossRef]
- Gomez-Acata, R.V.; Neria-Gonzalez, M.I.; Aguilar-López, R. Robust Software Sensor Design for the State Estimation in A Sulfate-Reducing Bioreactor. Теoретические Оснoвы Химическoй Технoлoгии 2016, 50, 71. [Google Scholar] [CrossRef]
| Model-Based SS (White Box Type) | Data-Based SS (Black Box Type) | Hybrid SS (Grey Box Type) |
|---|---|---|
| Nonlinear observers, Kalman and Luenberger filters, Adaptive observers, etc. | Principal component analysis Least squares approach Neural networks, Neural fuzzy logics, etc. | Combinations between data-based and model-based methods: hybrid model with EKF EKF with Neural Networks, etc. |
| No | Observer | Number of Tuning Parameters | Stability |
|---|---|---|---|
| 1 | Extended Kalman Filter | Two (R,Q) | Local |
| 2 | Extended Luenberger Observer | Number of the poles (ordered by the system) | Local |
| 3 | Linearization of the error | Depends on the linear method | Global |
| 4 | Accurate linearization | Depends on the linear method | Local or global |
| 5 | High gain observer | Number of the poles | Local or global |
| 6 | Moving horizon observer | One | Asymptotic |
| 7 | Linear matrix inequality | Two | Global |
| 8 | Based on inertia | Number of states | Global |
| 9 | Asymptotic Observer | Depends on experimental conditions of the process | Asymptotic |
| Method | A Priori Information | Advantages | Disadvantages |
|---|---|---|---|
| Balance equations | Input–output connections | Simple calculations based on approximate models | There are no reliable estimates in the presence of uncertainty |
| Extended Kalman Filter | Mathematical Model (MM) | Good results in stochastic disturbances and measurement noise | Accurate process models; problems at inaccurate initial estimates and covariance matrices. |
| Hybrid observers (EO+AO) | MM | Exact estimates for deterministic nonlinear processes | Exact model of the exponential observer; limited AO convergence rate. |
| Observer-based estimator | MM; On-line measurements related to the estimated rate | Simple linear structure; robustness; possibility for optimal tuning | A large number of tuning parameters; estimates depend on changes in rates, constant yield coefficients |
| High gain SS | MM; On-line measurements related to the estimated rate | One tuning parameter; effective work with nonlinear processes; robustness | The estimates depend on changes in rates; constant yield coefficients; the exponential stability depends on the Lipschitz condition. |
| Sliding mode SS | MM; On-line measurements related to the estimated rate | Smooth estimates for second-order systems, without errors at limited changes in estimated variables | First-order methods-effect of rapid change of estimates until entering the sliding plane; constant yield coefficients. |
| A Priori Information | ||
|---|---|---|
| Software sensors | Matrix K | |
| Exponential and asymptotic observers Limitation: Nonlinear models | Known | Known |
| Asymptotic observers with auxiliary variables Advantages: Simple structure in comparison with EKF and ELO and independence from ; Limitations: Limited rate of convergence; conditions for matrix inversion. | Unknown | Known |
| Adaptive observers Extended Observers of Kalman and Luenberger Limitations: Nonlinear structure Asymptotic observers Constraints: Structural identifiability | Unknown | Unknown |
| K | |
|---|---|
| Observer-based estimator of Limitations: The disturbance vector includes quite a few members resulting from considering the kinetics a product of three members | Estimation of with known К |
| Conditions: (1) Need for z transformation, in which the dynamics is independent of economic coefficients; (2) Reformulation of kinetics , so that be independent of yield coefficients | Estimation of independently from К |
| Case 1: Complete measurements of state variables Reformulation of kinetics The estimation of and f to be invertible, i.e., Case 2: Incomplete measurements of state variables Constraints: Condition for invertibility of matrix and constantly stimulating at unknown yield coefficients | Simultaneous estimation of and K |
| Limitations: Structural identifiability of yield coefficients from function f i.e., | Estimation of K independently from |
| Process Kinetics Formalization | |
|---|---|
| ϕ(t) fully unknown time-varying parameter | ϕm(t) = Y(t)φ(t) ϕm(t)—vector of known kinetics; φ(t)—key kinetic parameter, which describes the dynamics of the main state variables; Y(t)—vector of yield coefficients comprising remaining parts of the state variables’ kinetics. |
| General SS | |
|---|---|
| General SS of ϕ(t) The asymptotic upper limit of the estimation error is derived, which is the basis of the proposed optimal tuning. The advantage of the new software sensor is that it provides reliable kinetic information when the kinetics models are unknown or inexact ones. Disadvantage: The effect of measuring noise cannot be completely ruled out. Applications: [58,104,105,106]. | General SS of Y(t) and φ(t) A linear structure of a generalized software sensor of 4th/5th order is derived. The input is the measurable kinetics and a simultaneous estimation of both parameters at the output is achieved. An analysis of the stability of the obtained structures is performed and original tuning procedures for processes taking place in an inhomogeneous/homogeneous environment are proposed. Advantage: The tuning is reduced to selecting two parameters for processes that are realized in an inhomogeneous environment, while for the same processes in a homogeneous environment only one parameter is needed. Disadvantage: Only local asymptotic stability can be proven. Applications: [107,108,109]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyubenova, V.; Kostov, G.; Denkova-Kostova, R. Model-Based Monitoring of Biotechnological Processes—A Review. Processes 2021, 9, 908. https://doi.org/10.3390/pr9060908
Lyubenova V, Kostov G, Denkova-Kostova R. Model-Based Monitoring of Biotechnological Processes—A Review. Processes. 2021; 9(6):908. https://doi.org/10.3390/pr9060908
Chicago/Turabian StyleLyubenova, Velislava, Georgi Kostov, and Rositsa Denkova-Kostova. 2021. "Model-Based Monitoring of Biotechnological Processes—A Review" Processes 9, no. 6: 908. https://doi.org/10.3390/pr9060908
APA StyleLyubenova, V., Kostov, G., & Denkova-Kostova, R. (2021). Model-Based Monitoring of Biotechnological Processes—A Review. Processes, 9(6), 908. https://doi.org/10.3390/pr9060908







