A Numerical Method Based on Operator Splitting Collocation Scheme for Nonlinear Schrödinger Equation

Abstract

In this paper, a second-order operator splitting method combined with the barycentric Lagrange interpolation collocation method is proposed for the nonlinear Schrödinger equation. The equation is split into linear and nonlinear parts: the linear part is solved by the barycentric Lagrange interpolation collocation method in space combined with the Crank–Nicolson scheme in time; the nonlinear part is solved analytically due to the availability of a closed-form solution, which avoids solving the nonlinear algebraic equation. Moreover, the consistency of the fully discretized scheme for the linear subproblem and error estimates of the operator splitting scheme are provided. The proposed numerical scheme is of spectral accuracy in space and of second-order accuracy in time, which greatly improves the computational efficiency. Numerical experiments are presented to confirm the accuracy, mass and energy conservation of the proposed method.

1. Introduction

In 1926, the famous Schrödinger equation was proposed by the Austrian physicist Schrödinger [1]. It’s a fundamental equation in the field of quantum mechanics. In recent years, the Schrödinger equation has been studied in different fields of research, such as atomic, molecular, nuclear physics and solid state physics, etc.

In this paper, we consider the following nonlinear Schrödinger (NLS) equation

$$\left\{\begin{array}{c}i{u}_t+\rho \Delta u+v\left(\mathbf{x}\right)u+\beta {\left|u\right|}^{2}u=0,(\mathbf{x},\mathrm{t})\in \mathsf{\Omega }\times (0,\mathrm{T}]\hfill \\ u(\mathbf{x},0)=u_0\left(\mathbf{x}\right),\mathbf{x}\in \mathsf{\Omega }\hfill \\ u(\mathbf{x},t)=0,\mathbf{x}\in \partial \mathsf{\Omega },\mathrm{t}\in (0,\mathrm{T}]\hfill \end{array},\right.$$

(1)

where i is the imaginary unit, $\rho ,\beta$ are real-valued constants, $\mathsf{\Omega }\subset R^d(d=1,2)$ is a bounded area and $\Delta$ is the Laplace operator. The function $u_0\left(\mathbf{x}\right)$ is a given sufficiently smooth function and $v\left(\mathbf{x}\right)$ is a real-valued potential function. This model reflects the quantum mechanical effects and microscopic system properties and can well describe the state of microscopic particles over time.

In fact, the NLS Equation (1) also conserves both mass and energy with the following mass and energy functions:

$$M\left(t\right)={\int }_{\mathsf{\Omega }}|u(\mathbf{x},t){|}^{2}d\mathbf{x}=M\left(0\right)$$

(2)

and

$$E\left(t\right)={\int }_{\mathsf{\Omega }}(\rho |\nabla u(\mathbf{x},t){|}^2-v\left(\mathbf{x}\right)|u(\mathbf{x},t){|}^2-\frac{\beta }{2}|u(\mathbf{x},t){|}^4)d\mathbf{x}=E\left(0\right).$$

(3)

Recently, many numerical methods have been developed for solving the NLS equation. Gong et al. [2] presented a conservative Fourier pseudo-spectral method for the nonlinear Schrödinger equation. Cui et al. [3] developed mass- and energy-preserving exponential Runge–Kutta methods for the nonlinear Schrödinger equation. Feng et al. [4] developed the high-order mass- and energy-conserving SAV-Gauss collocation finite element methods for the NLS equation. Wang et al. [5] used the two-grid finite element method for the NLS equation and the given superconvergence analysis of the scheme. Wang et al. [6] studied leapfrog finite element methods for a class of nonlinear Schrödinger equations with damped terms. Hu et al. [7] presented the Newton iterative Crank–Nicolson finite element method for the NLS equation. Chen et al. [8] applied the two-grid finite volume element method for the time-dependent Schrödinger equation. Deng et al. [9] considered a second-order SAV scheme for the nonlinear Schrödinger equation in the whole space with typical generalized nonlinearities and carried out a rigorous error analysis. Su et al. [10] considered the numerical solution of the nonlinear Schrödinger equation with a highly oscillatory potential (NLSE-OP) and rigorously analyzed the error bounds of the splitting schemes for solving the NLSE-OP to a fixed time. Wang et al. [11] proposed finite difference methods for the coupled Gross–Pitaevskii equations in high dimensions and the given error estimates.

There are some advantages, such as no dividing elements, simple formulas, no integrals and easy programming, of the collocation method, which is called the barycentric Lagrange interpolation collocation (BLIC) method. The method has captured the attention of many scholars because of its high accuracy. The numerical stability of the barycentric Lagrange interpolation collocation method with Chebyshev points is very good, and it can also effectively overcome the "Runge" phenomenon. The method has been extended to solve various partial differential equations, such as the sine-Gordon equation [12], the Burgers equation [13], the viscoelastic wave equation [14], the Allen–Cahn equation [15,16], nonlinear convection-diffusion optimal control problems [17] and the fractional telegraph equation [18], among others.

To the best of our knowledge, there are few studies regarding using the barycentric interpolation collocation method combined with the operator splitting method [19,20,21] for the nonlinear Schrödinger equation. Based on the above work, we focus on the convergence analysis of the proposed scheme. We analyze the fully discretized consistency of the linear subproblem. Moreover, the error estimates of the operator splitting scheme are derived.

The remaining parts of the paper are structured as follows. In Section 2, we present the barycentric Lagrange interpolation collocation method. In Section 3, we present a second-order operator splitting collocation scheme for the NLS equation. The convergence analyses of the proposed method are presented in Section 4. Numerical experiments are conducted in Section 5 to evaluate the accuracy and efficiency of the proposed method, while Section 6 presents some conclusions derived from these experiments.

2. Preliminary

Suppose that $m+1$ distinct interpolation nodes, $x_j$$(j=0,1,\dots ,m)$, and their corresponding function values, $u_j$, are provided. Therefore, there exists a unique interpolation polynomial whose degree is not exceeding m, satisfying $q\left(x_j\right)=u_j$$(j=0,1,\dots ,m)$. As we know, $q\left(x\right)$ has the Lagrange form as follows,

$$q\left(x\right)=\sum _{j=0}^m{G}_j\left(x\right)u_j,$$

(4)

where $G_j\left(x\right)$ represents the Lagrange interpolation basis function and

$$G_j\left(x\right)={\displaystyle \frac{{\displaystyle \prod _{i=0,i\ne j}^m}\left(x-x_i\right)}{{\displaystyle \prod _{i=0,i\ne j}^m}\left(x_j-x_i\right)}},j=0,1,\cdots ,m.$$

(5)

Suppose that

$$g\left(x\right)=(x-x_0)(x-x_1)\dots (x-x_m),$$

(6)

and the barycentric weights are defined as follows:

$$w_j={\displaystyle \frac{1}{{\displaystyle \prod _{i=0,i\ne j}^m}\left(x_j-x_i\right)}},j=0,1,\cdots ,m.$$

(7)

Then, from Equations (5)–(7), we can obtain

$$G_j\left(x\right)=g\left(x\right)\frac{w_j}{x-x_j},j=0,1,\cdots ,m.$$

(8)

By Equations (8) and (4), we have

$$q\left(x\right)=g\left(x\right)\sum _{j=0}^m\frac{w_j}{x-x_j}{u}_j.$$

(9)

If $u=1$, it has the following form:

$$1=g\left(x\right)\sum _{j=0}^m\frac{w_j}{x-x_j}.$$

(10)

By Equations (10) and (9), the barycentric interpolation formula of $q\left(x\right)$ can be derived:

$$q\left(x\right)={\displaystyle \frac{{\displaystyle \sum _{j=0}^m}{\displaystyle \frac{w_j}{x-x_j}}{u}_j}{{\displaystyle \sum _{j=0}^m}{\displaystyle \frac{w_j}{x-x_j}}}}=\sum _{j=0}^m{\displaystyle \frac{{\displaystyle \frac{w_j}{x-x_j}}}{{\displaystyle \sum _{j=0}^m}{\displaystyle \frac{w_j}{x-x_j}}}}{u}_j:=\sum _{j=0}^m{\tilde{G}}_j\left(x\right)u_j.$$

(11)

To ensure the numerical stability of the barycentric Lagrange interpolation, we adopt Chebyshev points:

$$x_j=cos\left(\frac{j}{m}\pi \right),j=0,1,\cdots ,m.$$

(12)

The v-order derivative of $q\left(x\right)$ defined as Equation (11) with respect to x is

$$q^{\left(v\right)}\left(x_i\right)=\frac{d^{v}q\left(x_i\right)}{d{x}^v}={\displaystyle \sum _{j=0}^m}{\tilde{G}}_j^{\left(v\right)}\left(x_i\right)u_j=\sum _{j=0}^m{P}_{ij}^{\left(v\right)}{u}_j,v=1,2,\cdots ,m,$$

(13)

where $P_{ij}^{\left(v\right)}$ denotes the element of the v-order differentiation matrix $P^{\left(v\right)}$.

From Equations (11) and (13), we can obtain [22]

$$\left\{\begin{array}{c}{P}_{ij}^{\left(1\right)}={\tilde{G}}_j^{\prime }\left(x_i\right)={\displaystyle \frac{w_j/w_i}{x_i-x_j}},j\ne i,\hfill \\ P_{ii}^{\left(1\right)}=-{\displaystyle \sum _{j=0,j\ne i}^m}{P}_{ij}^{\left(1\right)},\hfill \end{array}\right.$$

(14)

$$\left\{\begin{array}{c}{P}_{ij}^{\left(2\right)}={\tilde{G}}_j^{″}\left(x_i\right)=-2{\displaystyle \frac{w_j/w_i}{x_i-x_j}}\left({\displaystyle \sum _{k\ne i}}{\displaystyle \frac{w_k/w_i}{x_i-x_k}}+{\displaystyle \frac{1}{x_i-x_j}}\right),j\ne i,\hfill \\ P_{ii}^{\left(2\right)}=-{\displaystyle \sum _{j=0,j\ne i}^m}{P}_{ij}^{\left(2\right)}.\hfill \end{array}\right.$$

(15)

Next, we will derive the approximation format for a given function, $u(x,y)$, and its derivative using the barycentric Lagrange interpolation formula.

For $m+1$ distinct nodes, $(x_0,y),(x_1,y),\dots ,(x_m,y)$, the unknown function $u(x,y)$, evaluated at node $(x_i,y)$, can be expressed as follows:

$$u(x_i,y),i=0,1,\dots ,m.$$

(16)

From Equations (16) and (11), we can obtain the approximation function of $u(x,y)$:

$$u(x,y)=\sum _{i=0}^m{\alpha }_i\left(x\right)u(x_i,y),i=0,1,\dots ,m.$$

(17)

Similarly, the expression of $u(x_i,y)$ is as follows:

$$u(x_i,y)=\sum _{j=0}^n{\beta }_j\left(y\right)u(x_i,y_j),j=0,1,\dots ,n.$$

(18)

From Equations (17) and (18), we can obtain

$$u(x,y)=\sum _{i=0}^m\sum _{j=0}^n{\alpha }_i\left(x\right){\beta }_j\left(y\right)u(x_i,y_j),$$

(19)

and its second-order partial derivative has the following form:

$$u_{xx}(x,y)=\sum _{i=0}^m\sum _{j=0}^n{\alpha }_i^{″}\left(x\right){\beta }_j\left(y\right)u(x_i,y_j),$$

(20)

$$u_{yy}(x,y)=\sum _{i=0}^m\sum _{j=0}^n{\alpha }_i\left(x\right){\beta }_j^{″}\left(y\right)u(x_i,y_j).$$

(21)

3. Operator Splitting Collocation Method

In this section, we propose an operator splitting collocation scheme for the NLS equation, which is based on the Strang splitting procedure. Our approach combines the barycentric Lagrange interpolation collocation method for spatial approximation and a second-order Crank–Nicolson scheme for temporal approximation.

First, rewrite Equation (1) as follows,

$$i{u}_t=L\left(u\right)+N\left(u\right),$$

(22)

where $L\left(u\right)=-\rho \Delta u$ and $N\left(u\right)=-v\left(\mathbf{x}\right)u-\beta |u{|}^{2}u$.

Then, Equation (1) is split into the linear part,

$$i{u}_t=L\left(u\right)=-\rho \Delta u,$$

(23)

and the nonlinear part,

$$i{u}_t=N\left(u\right)=-v\left(\mathbf{x}\right)u-\beta |u{|}^{2}u.$$

(24)

Next, for a given time step, $\tau$, the solution of Equation (1) evolves from t to $t+\tau$ via the Strang splitting method [23], which consists of three substeps:

$$u(x,y,t+\tau )=S^B\left(\frac{\tau }{2}\right)S^A\left(\tau \right)S^B\left(\frac{\tau }{2}\right)u(x,y,t)+O\left({\tau }^3\right),$$

(25)

where $S^A$ and $S^B$ are the exact solution operators of Equation (23) and Equation (24), respectively.

Then, we will provide numerical approximations $S_h^A$ and $S_h^B$ for the exact solution operators $S^A$ and $S^B$, respectively. Suppose $\mathsf{\Omega }=[a,b]\times [c,d]$ and ${\mathsf{\Omega }}_h=\{(x_i,y_j),i=0<1<\dots <m,j=0<1<\dots <n\}$. Here, $x_i$ and $y_j$ are Chebyshev mesh points.

To solve Equation (23), the barycentric Lagrange interpolation collocation method is applied to discretize the spatial derivative. The semi-discretized scheme in space is obtained based on the barycentric Lagrange interpolation collocation method, as introduced in Section 2.

$$i{u}_t(x_i,y_j,t)=-\rho \sum _{i=0}^m\sum _{j=0}^n\left({\alpha }_i^{″}\left(x\right){\beta }_j\left(y\right)+{\alpha }_i\left(x\right){\beta }_j^{″}\left(y\right)\right)u(x_i,y_j,t).$$

(26)

The matrix form of (26) can be expressed as

$$i{\left(u_h\left(t\right)\right)}_t=-\rho \left(P^{\left(2\right)}\otimes I_n+I_m\otimes Q^{\left(2\right)}\right)u_h\left(t\right),$$

(27)

where $u_h\left(t\right)=[u_{00}\left(t\right),\cdots ,u_{0n}\left(t\right),u_{10}\left(t\right),\cdots ,u_{1n}\left(t\right),\cdots ,u_{m0}\left(t\right),\cdots ,u_{mn}\left(t\right)]$, $u_{ij}\left(t\right)=u(x_i,y_j,t)$; $P^{\left(2\right)}$ and $Q^{\left(2\right)}$ are second-order differentiation matrices on nodes $x_0,x_1,\dots ,x_m$ and $y_0,y_1,\dots ,y_n$, respectively; ⊗ represents the Kronecker product of the matrix; $I_m$ and $I_n$ are the identity matrices of $m+1$ and $n+1$ order, respectively. Then, setting $u_h^k=u_h\left(t_k\right)$, we can obtain the following fully discretized scheme:

$$i{\displaystyle \frac{u_h^{k+1}-u_h^k}{\tau }}=-\rho ({\displaystyle \frac{1}{2}}(P^{\left(2\right)}\otimes I_n+I_m\otimes Q^{\left(2\right)})u_h^{k+1}+{\displaystyle \frac{1}{2}}(P^{\left(2\right)}\otimes I_n+I_m\otimes Q^{\left(2\right)})u_h^k).$$

(28)

Therefore, we obtain

$$S_h^A:u_h^{k+1}={(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}(iI-{\displaystyle \frac{\rho \tau }{2}}W)u_h^k,$$

(29)

where I is the identity matrix of order $(m+1)(n+1)$, $W=P^{\left(2\right)}\otimes I_n+I_m\otimes Q^{\left(2\right)}$.

Then, Equation (24) can be solved analytically by

$$S_h^B:u_h^{k+1}=e^{i\frac{\tau }{2}(v(x,y)+\beta |u_h^k{|}^2)}{u}_h^k.$$

(30)

The second-order operator splitting scheme can be derived as follows:

$$\begin{array}{c}\hfill \mathbf{MI}:\left\{\begin{array}{cc}& u_h^{\left(1\right)}=e^{i\frac{\tau }{2}(v(x,y)+\beta |u_h^k{|}^2)}{u}_h^k\hfill \\ & u_h^{\left(2\right)}={(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}(iI-{\displaystyle \frac{\rho \tau }{2}}W)u_h^{\left(1\right)}\hfill \\ & u_h^{k+1}=e^{i\frac{\tau }{2}(v(x,y)+\beta |u_h^{\left(2\right)}{|}^2)}{u}_h^{\left(2\right)}\hfill \end{array}\right..\end{array}$$

(31)

4. Convergence Analysis

Firstly, in this section we analyze the consistency of the semi-discretized scheme (26). Suppose that $q(x,y)$ is the Lagrange interpolation function of $u(x,y)$, satisfying $q(x_i,y_j)=u\left(x_i,y_j\right),i=0<1<\dots <m,j=0<1<\dots <n$.

By defining

$$r(x,y)=u(x,y)-q(x,y),$$

(32)

we can obtain the following estimates [18],

Lemma 1. 

Suppose $u(x,y)\in C^{(\tilde{m}+1)}([a,b]\times [c,d])$, where $\tilde{m}=\max \{m,n\}$, we have

$$\begin{array}{c}\left\{\begin{array}{cc}\hfill & \Vert r(x,y){\Vert }_{\infty }\le C_1\Vert u^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2m}\right)}^m+C_2{\Vert u^{(m+1)}\Vert }_{\infty }{\left(\frac{e{h}_y}{2n}\right)}^n\hfill \\ \hfill & \Vert r_{xx}(x,y){\Vert }_{\infty }\le C_1^{**}\Vert u_{}^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+C_2\Vert u_{}^{(n+1)}{\Vert }_{\infty }{\left(\frac{e{h}_y}{2n}\right)}^n\hfill \\ \hfill & \Vert r_{yy}(x,y){\Vert }_{\infty }\le C_1\Vert u_{}^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2m}\right)}^m+C_2^{**}\Vert u_{}^{(n+1)}{\Vert }_{\infty }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}\hfill \end{array}\right.\hfill \end{array},$$

where $h_x=\frac{b-a}{2}$, $h_y=\frac{d-c}{2}$, and e is the natural constant.

Let $u(x,y,t)$ be the solution of Equation (1) and $u(x_i,y_j,t)$ is the numerical solution of $u(x,y,t)$ discretized by barycentric Lagrange interpolation collocation method; we then have

$$\mathcal{T}u(x_i,y_j,t)=0$$

(33)

and

$$\underset{i,j\to \infty }{\lim }\mathcal{T}u(x_i,y_j,t)=0,$$

(34)

where $\mathcal{T}=i{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}$.

Based on the above results, we obtain the following theorem.

Theorem 1. 

Let $u(x_i,y_j,t):\mathcal{T}u(x_i,y_j,t)=0$, we have

$$\Vert u(x,y,t)-u(x_i,y_j,t){\Vert }_{\infty }\le C_1^{**}\Vert u^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+C_2^{**}\Vert u^{(n+1)}{\Vert }_{\infty }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}.$$

Proof. 

As

$$\begin{array}{c}\mathcal{T}u(x,y,t)-\mathcal{T}u(x_i,y_j,t)\hfill \\ =i{u}_t(x,y,t)+u_{xx}(x,y,t)+u_{yy}(x,y,t)-\left(i{u}_t(x_i,y_j,t)+u_{xx}(x_i,y_j,t)+u_{yy}(x_i,y_j,t)\right)\hfill \\ =i{u}_t(x,y,t)-i{u}_t(x_i,y_j,t)+u_{xx}(x,y,t)-u_{xx}(x_i,y_j,t)+u_{yy}(x,y,t)-u_{yy}(x_i,y_j,t)\hfill \\ :=A_1+A_2+A_3,\hfill \end{array}$$

(35)

where $A_1$, $A_2$ and $A_3$ represent

$$\begin{array}{cc}\hfill & A_1=i{u}_t(x,y,t)-i{u}_t(x_i,y_j,t),\hfill \\ \hfill & A_2=u_{xx}(x,y,t)-u_{xx}(x_i,y_j,t),\hfill \\ \hfill & A_3=u_{yy}(x,y,t)-u_{yy}(x_i,y_j,t).\hfill \end{array}$$

(36)

For $A_1$, we obtain

$$\begin{array}{c}{A}_1=i(u_t(x,y,t)-u_t(x_i,y_j,t))\hfill \\ =i(u_t(x,y,t)-u_t(x_i,y,t)+u_t(x_i,y,t)-u_t(x_i,y_j,t))\hfill \\ =i(r_t(x_i,y,t)+r_t(x_i,y_j,t)).\hfill \end{array}$$

(37)

From Lemma 1, we can derive

$$\begin{array}{c}\Vert A_1{\Vert }_{\infty }=\Vert i\left(r_t(x_i,y,t)+r_t(x_i,y_j,t)\right){\Vert }_{\infty }\hfill \\ \le \Vert r_t(x_i,y,t){\Vert }_{\infty }+\Vert r_t(x_i,y_j,t){\Vert }_{\infty }\hfill \\ \le C_1\Vert u^{(m+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_x}{2m}}\right)}^m+C_2\Vert u^{(n+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_y}{2n}}\right)}^n.\hfill \end{array}$$

(38)

Similar estimates can be derived as follow:

$$\begin{array}{c}\Vert A_2{\Vert }_{\infty }=\Vert r_{xx}(x_i,y,t)+r_{xx}(x_i,y_j,t){\Vert }_{\infty }\hfill \\ \le C_1^{**}\Vert u^{(m+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_x}{2(m-2)}}\right)}^{m-2}+C_2\Vert u^{(n+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_y}{2n}}\right)}^n,\hfill \end{array}$$

(39)

$$\begin{array}{c}\Vert A_3{\Vert }_{\infty }=\Vert r_{yy}(x_i,y,t)+r_{yy}(x_i,y_j,t){\Vert }_{\infty }\hfill \\ \le C_1\Vert u^{(m+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_x}{2m}}\right)}^m+C_2^{**}\Vert u^{(n+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_y}{2(n-2)}}\right)}^{n-2}.\hfill \end{array}$$

(40)

From (38)–(40) and (35), the proof is completed. □

Next, we consider consistency analysis of the full-discretized scheme (28).

Theorem 2. 

Suppose $u(x,y,t)\in C^{(\tilde{m}+1)}\left(\mathsf{\Omega }\right)\times C^2\left(0,T\right],\mathsf{\Omega }=[a,b]\times [c,d],$ where $\tilde{m}=\max \{m,n\}$ and $u(x_i,y_j,t_{k+1})$ is the corresponding numerical solution of $u(x,y,t)$, we have

$$\Vert u(x,y,t)-u(x_i,y_j,t_{k+1}){\Vert }_{\infty }\le C_3\left({\tau }^3+\Vert u^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+\Vert u^{(n+1)}{\Vert }_{\infty }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}\right),$$

where $C_3$ is a positive constant.

Proof. 

Let $u(x,y,t_{k+1})$ be the corresponding numerical solution using the Crank–Nicolson scheme for temporal approximation of $u(x,y,t)$; we can obtain

$$i\delta u_t(x,y,t_{k+\frac{1}{2}})=-\rho \Delta u(x,y,t_{k+\frac{1}{2}})+R^k,$$

(41)

where $\delta u_t(x,y,t_{k+\frac{1}{2}})=u(x,y,t_{k+1})-u(x,y,t_k)$, and $R^k=u_t(x,y,t_{k+\frac{1}{2}})-\delta u_t(x,y,t_{k+\frac{1}{2}})$ is the truncation error in time. Based on the principle of Taylor expansion, we can obtain

$$\left|R^k\right|\le C_4{\tau }^3.$$

(42)

Equation (41) is discretized by the BLIC scheme, and supposing that $u(x_i,y_j,t_{k+1})$ is the numerical solution of $u(x,y,t_{k+1})$ based on the BLIC method, it holds that

$$i\delta u_t(x_i,y_j,t_{k+\frac{1}{2}})=-\rho \Delta u^h(x_i,y{}_j,t_{k+\frac{1}{2}})+R^k+{\gamma }^{i,j},$$

(43)

where ${\gamma }^{i,j}$ represents the truncation error in space.

Combining Equations (41) and (43), we have

$$i\delta u_t(x,y,t_{k+\frac{1}{2}})-i\delta u_t(x_i,y_j,t_{k+\frac{1}{2}})=-\rho \Delta u(x,y,t_{k+\frac{1}{2}})+\rho \Delta u^h(x_i,y{}_j,t_{k+\frac{1}{2}})-{\gamma }^{i,j}.$$

(44)

If we use a similar technique in Theorem 1, we can derive

$$\left|{\gamma }^{i,j}\right|\le C_1^{**}\Vert u^{(m+1)}{\Vert }_{\infty }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+C_2^{**}\Vert u^{(n+1)}{\Vert }_{\infty }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}.$$

(45)

Combining (42) and (45), the proof is completed. □

We will now analyze the error results of the operator splitting scheme.

Define a grid function space on ${\mathsf{\Omega }}_h$,

$${\mathcal{W}}^h=\left\{U\right|U=\left\{U_{ij}\right|0\le i\le m,0\le j\le n\}\},$$

and a mapping $I^h:\tilde{H}\left(\mathsf{\Omega }\right)⟶{\mathcal{W}}_h$ by

$$I^h\left(u\right)=U,$$

where $\tilde{H}\left(\mathsf{\Omega }\right)=\{u\in H^2\left(\mathsf{\Omega }\right)|u(\mathbf{x},t)=0\}$.

Lemma 2. 

Supposing that $U\in {\mathcal{W}}^h$, $\Vert W{\Vert }_{\infty }$ is bounded and τ is small enough, we have

$$\Vert S_h^A{\left(\tau \right)U\Vert }_{\infty }\le (1+\kappa \tau ){\Vert U\Vert }_{\infty }.$$

Proof. 

By Taylor expansion, the approximation of ${(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}$ at the zero matrix is

$${(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}=-iI+{\displaystyle \frac{\rho \tau }{2}}W+i{\displaystyle \frac{{\left(\rho \tau \right)}^2}{4}}{W}^2-{\displaystyle \frac{{\left(\rho \tau \right)}^3}{8}}{W}^3+\mathcal{O}\left({\tau }^4\right).$$

(46)

Then, combining with the above formula, we can obtain

$$\Vert {(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}(iI-{\displaystyle \frac{\rho \tau }{2}}W){\Vert }_{\infty }=\Vert I+i\rho \tau W-{\displaystyle \frac{{\left(\rho \tau \right)}^2}{2}}{W}^2-{\displaystyle \frac{{\left(\rho \tau \right)}^4}{16}}{W}^4{\Vert }_{\infty }\le 1+\kappa \tau .$$

(47)

Therefore,

$$\begin{array}{c}\Vert S_h^A\left(\tau \right)U{\Vert }_{\infty }=\Vert {(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}(iI+{\displaystyle \frac{\rho \tau }{2}}W)U{\Vert }_{\infty }\hfill \\ \le \Vert {(iI+{\displaystyle \frac{\rho \tau }{2}}W)}^{-1}(I+{\displaystyle \frac{\rho \tau }{2}}W){\Vert }_{\infty }\Vert U{\Vert }_{\infty }\hfill \\ \le (1+\kappa \tau )\Vert U{\Vert }_{\infty }\hfill \end{array},$$

(48)

where $\kappa$ is a positive constant independent of $\tau$. □

Lemma 3. 

Supposing that $U\in {\mathcal{W}}^h$, we have

$$\Vert S_h^B\left({\displaystyle \frac{\tau }{2}}\right){U\Vert }_{\infty }={\Vert U\Vert }_{\infty }.$$

Proof. 

$$\left|S_h^B\left({\displaystyle \frac{\tau }{2}}\right)u_{ij}\right|=\left|e^{i\frac{\tau }{2}(v(x,y)+\beta |u_{ij}{|}^2)}\right|\left|u_{ij}\right|=\left|u_{ij}\right|.$$

(49)

□

By Theorem 2, we can obtain the following result.

Lemma 4. 

Supposing that $u_0\in \tilde{H}\left(\mathsf{\Omega }\right)$, we have

$$\Vert I^h{S}^A{u}_0-S_h^A{I}^h{u}_0{\Vert }_{\infty }\le C_1^{**}\Vert u^{(m+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_x}{2(m-2)}}\right)}^{m-2}+C_2^{**}\Vert u^{(n+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_y}{2(n-2)}}\right)}^{n-2}+C_4{\tau }^3.$$

For convenience, suppose

$$\eta =C_5\left(\Vert u^{(m+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_x}{2(m-2)}}\right)}^{m-2}+\Vert u^{(n+1)}{\Vert }_{\infty }{\left({\displaystyle \frac{e{h}_y}{2(n-2)}}\right)}^{n-2}+{\tau }^3\right),$$

where $C_5=\max \left\{C_1^{**},C_2^{**},C_4\right\}$.

Theorem 3. 

Let $u^{k+1}\in \tilde{H}\left(\mathsf{\Omega }\right)$ be the exact solution of Equation (1) and $\tilde{u}(x,y,t)$ and $U^{k+1}$ be the exact solution of Equation (25) and the numerical solution at $t_{k+1}$ of Equation (31), respectively. According to Theorem 1 and Lemma 2, we have

$$\Vert I^h{u}^{k+1}-U^{k+1}{\Vert }_{\infty }\le C\left(\frac{\Vert u^{(m+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+\frac{\Vert u^{(n+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}+{\tau }^2\right),$$

where C is a positive constant independent of $\tau$.

Proof. 

For $k\ge 0$, we obtain

$$\Vert I^h{u}^{k+1}-U^{k+1}{\Vert }_{\infty }\le \Vert I^h{u}^{k+1}-I^h{\tilde{u}}^{k+1}{\Vert }_{\infty }+{\Vert I^h{\tilde{u}}^{k+1}-U^{k+1}\Vert }_{\infty }.$$

(50)

From [23], we obtain

$$\Vert I^h{\tilde{u}}^{k+1}-I^h{u}^{k+1}{\Vert }_{\infty }\le C_6{\tau }^2.$$

(51)

By Lemma 3, we obtain

$$\begin{array}{cc}\hfill \Vert & I^h{\tilde{u}}^{k+1}-U^{k+1}{\Vert }_{\infty }\hfill \\ \hfill & =\Vert I^h{S}^B{S}^A{S}^B{\tilde{u}}^k-S_h^B{S}_h^A{S}_h^B{U}^k{\Vert }_{\infty }\hfill \\ \hfill & \le \Vert I^h{S}^B{S}^A{S}^B{\tilde{u}}^k-S_h^B{I}^h{S}^A{S}^B{\tilde{u}}^k{\Vert }_{\infty }+{\Vert S_h^B{I}^h{S}^A{S}^B{\tilde{u}}^k-S_h^B{S}_h^A{S}_h^B{U}^k\Vert }_{\infty }\hfill \\ \hfill & \le \Vert I^h{S}^A{S}^B{\tilde{u}}^k-S_h^A{S}_h^B{U}^k{\Vert }_{\infty }\hfill \end{array}.$$

(52)

From Lemmas 2 and 4, we obtain

$$\begin{array}{cc}\hfill \Vert & I^h{S}^A{S}^B{\tilde{u}}^k-S_h^A{S}_h^B{U}^k{\Vert }_{\infty }\hfill \\ \hfill & \le \Vert I^h{S}^A{S}^B{\tilde{u}}^k-S_h^A{I}^h{S}^B{\tilde{u}}^k{\Vert }_{\infty }+{\Vert S_h^A{I}^h{S}^B{\tilde{u}}^k-S_h^A{S}_h^B{U}^k\Vert }_{\infty }\hfill \\ \hfill & \le \eta +(1+\kappa \tau )\Vert I^h{S}^B{\tilde{u}}^k-S_h^B{U}^k{\Vert }_{\infty }\hfill \end{array}.$$

(53)

From Lemma 3, we derive

$$\begin{array}{cc}\hfill \Vert & I^h{S}^B{\tilde{u}}^k-S_h^B{U}^k{\Vert }_{\infty }\hfill \\ \hfill & \le \Vert I^h{S}^B{\tilde{u}}^k-S_h^B{I}^h{\tilde{u}}^k{\Vert }_{\infty }+{\Vert S_h^B{I}^h{\tilde{u}}^k-S_h^B{U}^k\Vert }_{\infty }\hfill \\ \hfill & \le \Vert I^h{\tilde{u}}^k-U^k{\Vert }_{\infty }\hfill \end{array}.$$

(54)

Due to $\Vert I^h{\tilde{u}}^0-U^0{\Vert }_{\infty }=0$, and by the Gronwall inequality, we can obtain

$$\begin{array}{cc}\hfill \Vert & I^h{\tilde{u}}^{k+1}-U^{k+1}{\Vert }_{\infty }\hfill \\ \hfill \le & \eta +(1+\kappa \tau )\Vert I^h{\tilde{u}}^k-U^k{\Vert }_{\infty }\hfill \\ \hfill \le & \sum _{j=0}^k{(1+\kappa \tau )}^j\eta +{(1+\kappa \tau )}^{k+1}{\Vert I^h{\tilde{u}}^0-U^0\Vert }_{\infty }\hfill \\ \hfill \le & {\displaystyle \frac{{(1+\kappa \tau )}^{k+1}-1}{1+\kappa \tau -1}}\eta \hfill \\ \hfill \le & \frac{e^{\kappa \tau }}{\kappa \tau }\eta \hfill \end{array}.$$

(55)

By the above estimates and the expression of $\eta$, we have

$$\begin{array}{cc}\hfill \Vert & I^h{u}^{k+1}-U^{k+1}{\Vert }_{\infty }\hfill \\ \hfill \le & {\displaystyle \frac{e^{\kappa \tau }}{\kappa }}\left(C_5\left(\frac{\Vert u^{(m+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+\frac{\Vert u^{(n+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}+{\tau }^2\right)\right)\hfill \\ \hfill \le & C\left(\frac{\Vert u^{(m+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_x}{2(m-2)}\right)}^{m-2}+\frac{\Vert u^{(n+1)}{\Vert }_{\infty }}{\tau }{\left(\frac{e{h}_y}{2(n-2)}\right)}^{n-2}+{\tau }^2\right)\hfill \end{array},$$

(56)

where $C=\max \left\{C_5{\displaystyle \frac{e^{\kappa \tau }}{\kappa }},C_5{\displaystyle \frac{e^{\kappa \tau }}{\kappa }}+C_6\right\}$. The proof is completed. □

5. Numerical Experiments

In this section, we will provide some numerical results for the NLS Equation (1) to test the high accuracy and efficiency of our scheme. For convenience, the error notations are given as follows,

$${\mathrm{E}}_{\infty }={\Vert u_h-u_e\Vert }_{\infty },$$

(57)

$${\mathrm{E}}_r=\frac{\Vert u_h-u_e{\Vert }_{\infty }}{\Vert u_e{\Vert }_{\infty }},$$

(58)

where $u_h$ and $u_e$ denote the numerical solution and the exact solution, respectively. ${\Vert ·\Vert }_{\infty }$ is the $L^{\infty }$ norm. All computations presented in this work were performed on a standard i5 Intel 1.8GHz laptop in MATLAB R2020b.

5.1. Example 1

This example is used to test the accuracy and convergence of our scheme. Considering the following 2D NLS equation on ${[0,2\pi ]}^2\times (0,T]$,

$$\left\{\begin{array}{c}i{u}_t+\frac{1}{2}\Delta u-(1-{\sin }^{2}x{\sin }^{2}y)u-{\left|u\right|}^{2}u=0\hfill \\ u(x,y,0)=\sin x\sin y\hfill \\ u(0,y,t)=u(2\pi ,y,t)=0\hfill \\ u(x,0,t)=u(x,2\pi ,t)=0\hfill \end{array},\right.$$

where the exact solution is in the following form:

$$u(x,y,t)=e^{-2it}\sin x\sin y.$$

To verify the accuracy and the convergence rate of the operator splitting scheme based on the barycentric Lagrange interpolation collocation method MI, the operator splitting scheme based on the barycentric rational interpolation collocation method [24] MII and the classical second-order finite difference scheme SI, we choose the simulation parameters $n=m$, $\tau =0.001$ and $T=1$.

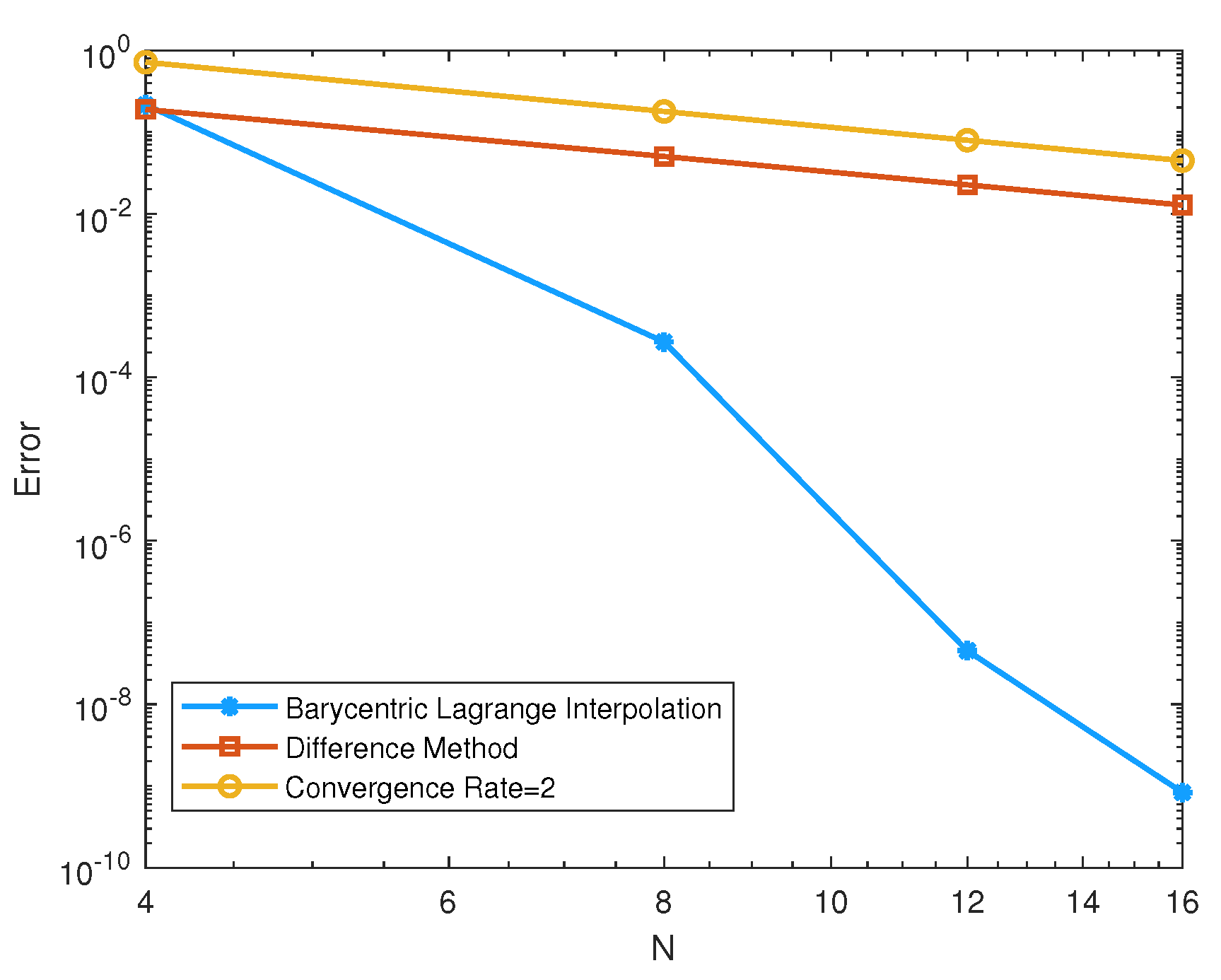
The results are shown in Table 1, Table 2, Table 3 and Table 4 and Figure 1, Figure 2 and Figure 3. Table 1, Table 2 and Table 3 show the spatial errors of the three schemes. By comparing Table 1 and Table 3, it can be seen that the MI scheme, based on the barycentric Lagrange interpolation collocation method in space, can achieve a higher accuracy using only $8\times 8$ mesh points. However, for the same accuracy, the SI scheme, based on a second-order center difference method in space, requires more than $80\times 80$ mesh points. Furthermore, by comparing Table 1 and Table 2, it is easy to see that the MI scheme is slightly more efficient than the MII scheme. The comparison of the three schemes shows that the barycentric Lagrange interpolation collocation scheme can achieve higher accuracy with fewer points in space. In addition, the CPU time of the MI scheme is significantly reduced compared with the SI scheme and is similar to the MII scheme.

Table 1. Error of barycentric Lagrange interpolation collocation scheme for Example 1.

m	${\mathbf{E}}_{\mathit{\infty }}$	${\mathbf{E}}_{\mathit{r}}$	$\mathit{CPU}$
6	8.4010 × 10${}^{-3}$	8.4010 × 10${}^{-3}$	0.152 s
8	2.3542 × 10${}^{-4}$	2.7054 × 10${}^{-4}$	0.288 s
10	1.9318 × 10${}^{-6}$	2.0865 × 10${}^{-6}$	0.694 s
12	5.6755 × 10${}^{-8}$	5.6755 × 10${}^{-8}$	1.039 s
16	8.0816 × 10${}^{-8}$	8.3330 × 10${}^{-8}$	2.914 s

Table 2. Error of barycentric rational interpolation collocation method for Example 1.

m	${\mathbf{E}}_{\mathit{\infty }}$	${\mathbf{E}}_{\mathit{r}}$	$\mathit{CPU}$
6	2.9302 × 10${}^{-3}$	2.9302 × 10${}^{-3}$	0.178 s
8	2.7122 × 10${}^{-3}$	3.1167 × 10${}^{-3}$	0.289 s
10	5.4257 × 10${}^{-6}$	5.8602 × 10${}^{-6}$	0.735 s
12	2.0948 × 10${}^{-6}$	2.0948 × 10${}^{-6}$	1.082 s
16	8.3994 × 10${}^{-8}$	8.6607 × 10${}^{-8}$	3.066 s

Table 3. Error of difference scheme for Example 1.

m	${\mathbf{E}}_{\mathit{\infty }}$	${\mathbf{E}}_{\mathit{r}}$	$\mathit{CPU}$
10	2.9367 × 10${}^{-2}$	3.2467 × 10${}^{-2}$	0.202 s
20	8.1977 × 10${}^{-3}$	8.1977 × 10${}^{-3}$	3.586 s
40	2.0546 × 10${}^{-3}$	2.0546 × 10${}^{-3}$	160.534 s
60	9.1360 × 10${}^{-4}$	9.1360 × 10${}^{-4}$	1665.769 s
80	5.1402 × 10${}^{-4}$	5.1402 × 10${}^{-4}$	8993.522 s

Table 4. Errors and convergence rate in time for Example 1.

$\mathit{\tau }$	${\mathbf{E}}_{\mathit{\infty }}$	$\mathit{Rate}$	${\mathbf{E}}_{\mathit{r}}$	$\mathit{Rate}$
1/8	1.2598 × 10${}^{-3}$	-	1.2990 × 10${}^{-3}$	-
1/16	3.1552 × 10${}^{-4}$	1.9975	3.2533 × 10${}^{-4}$	1.9975
1/32	7.8913 × 10${}^{-5}$	1.9994	8.1368 × 10${}^{-5}$	1.9994
1/64	1.9731 × 10${}^{-5}$	1.9998	2.0344 × 10${}^{-5}$	1.9998

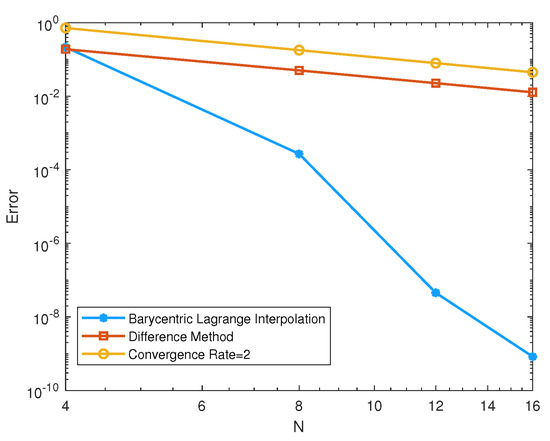
Figure 1. Spatial $L^{\infty }$ errors at t = 1 for NLS equation for Example 1.

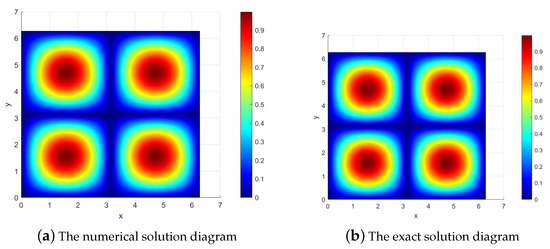
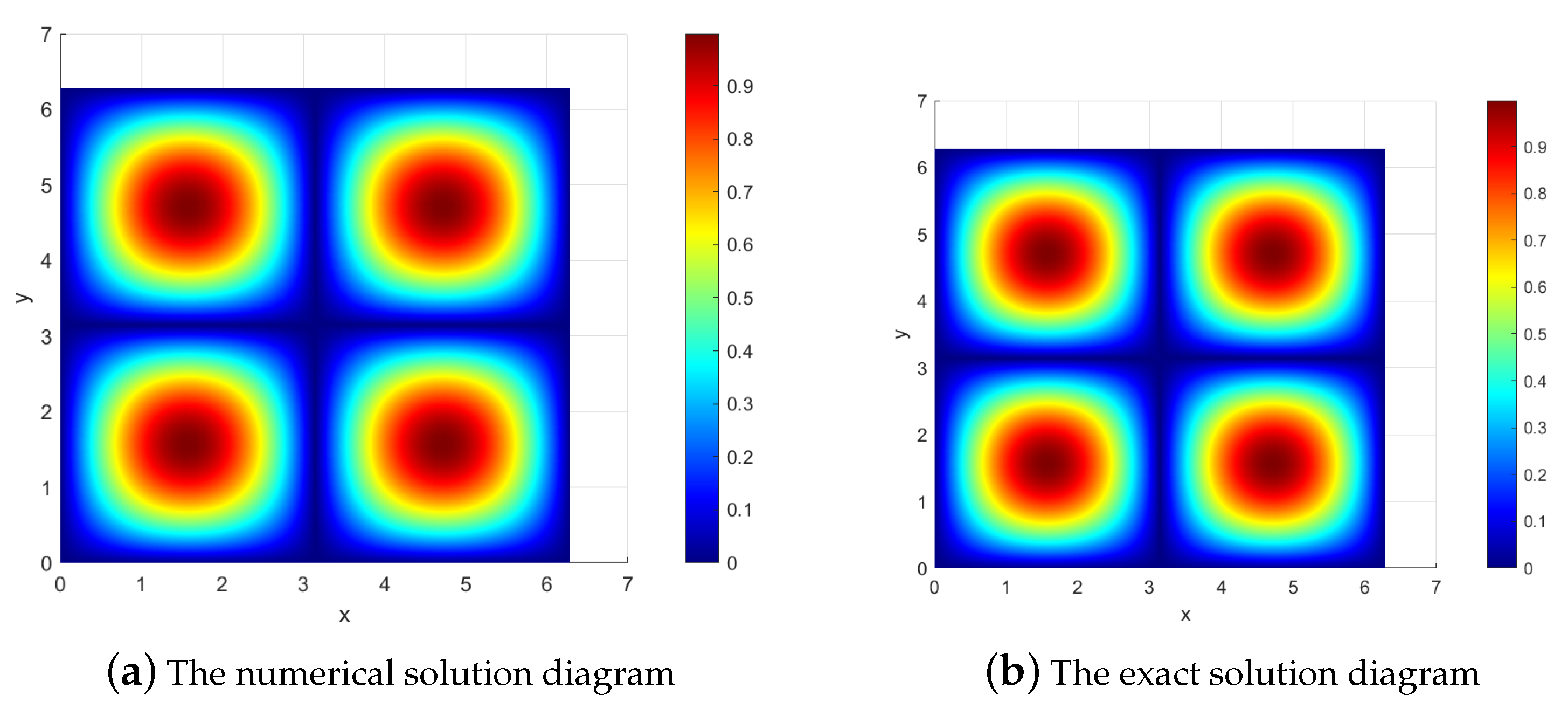
Figure 2. The numerical solution and the exact solution diagrams at T = 1 for Example 1.

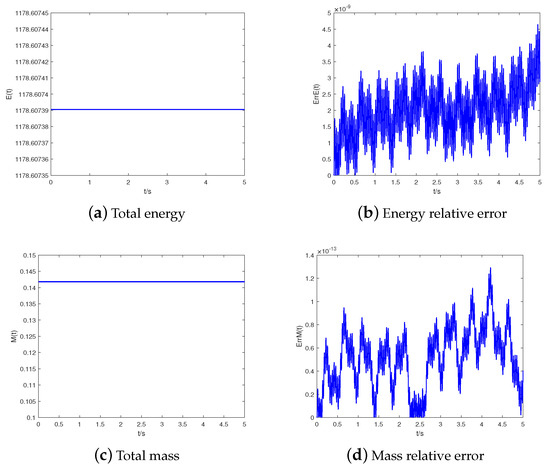
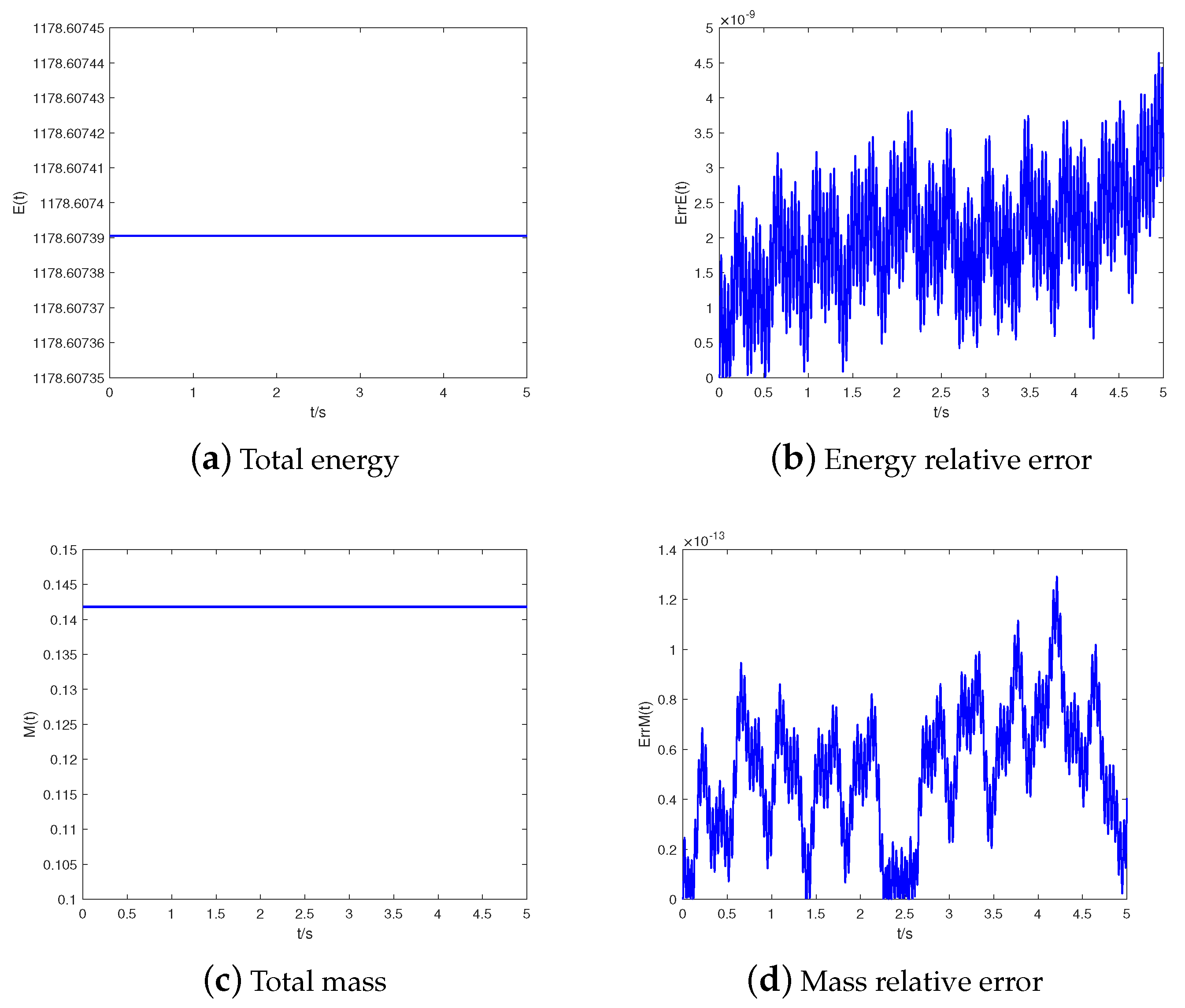
Figure 3. Conservation situation of energy and mass at T = 1 for Example 1.

If we fix $m=n=16$ and vary the temporal step, $\tau$, we can obtain errors and temporal convergence rate, as shown in Table 2. It shows that the MI scheme based on the barycentric interpolation collocation scheme for the NLS equation has second-order accuracy in time. In addition, the spatial convergence rate is also obtained, and the $L^{\infty }$ errors at time T = 1 for NLS equation are shown in Figure 1.

Choose $m=n=20$; the numerical solution and the exact solution of the NLS equation are shown in Figure 2a,b. Moreover, it is necessary to verify the conservation of energy and mass. We plot images of mass and energy varying over time. From Figure 3, it is obvious that mass and energy are conserved.

5.2. Example 2

Consider the following 1D problem on $[-10,40]\times (0,9]$:

$$\left\{\begin{array}{c}i{u}_t+\Delta u+2{\left|u\right|}^{2}u=0,\hfill \\ u(-10,t)=u(40,t)=0,\hfill \\ u_0\left(x\right)=\mathrm{sech}\left(x\right)\exp \left(2ix\right)+\mathrm{sech}(x-30)\exp (-i(x-30)).\hfill \end{array}\right.$$

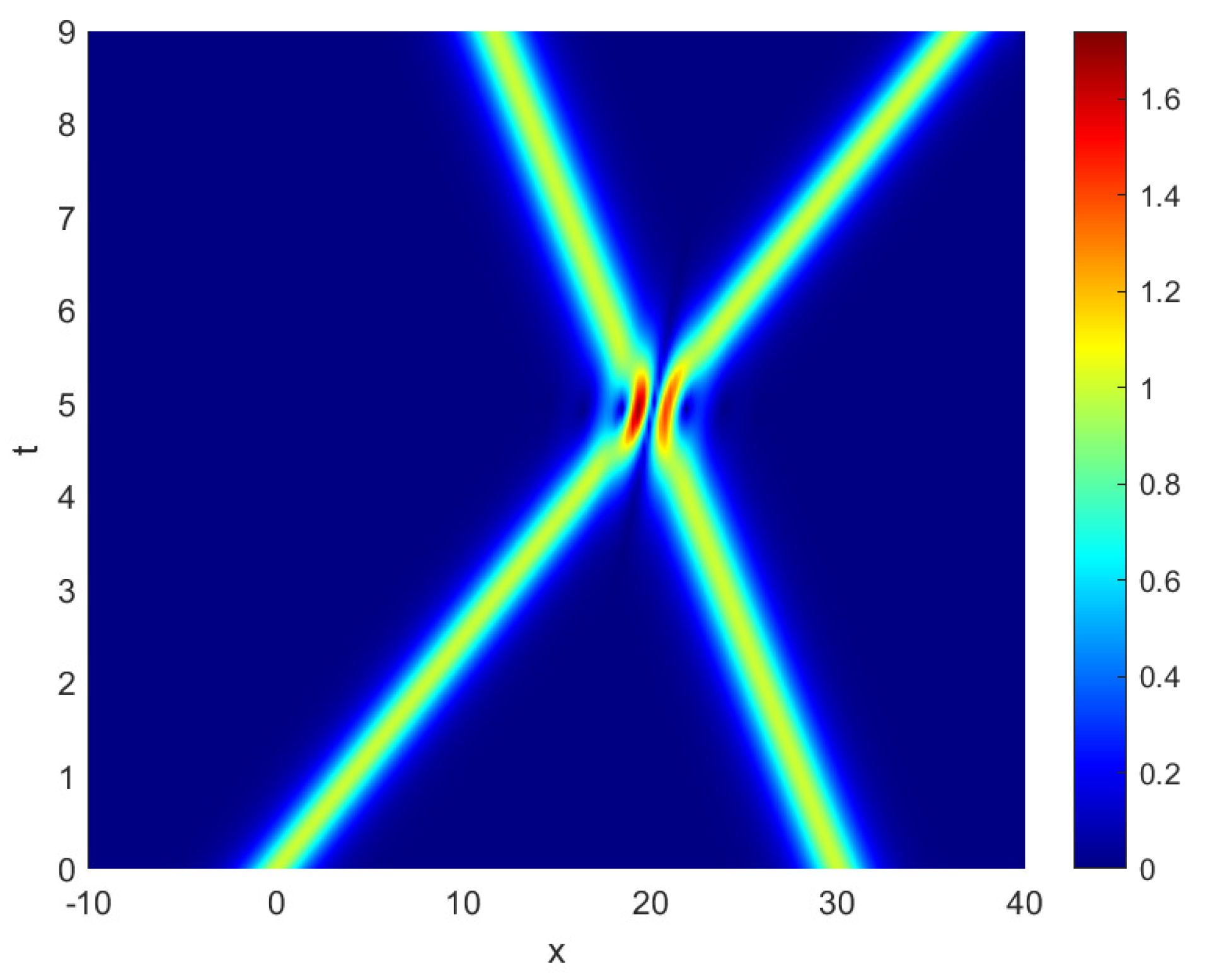
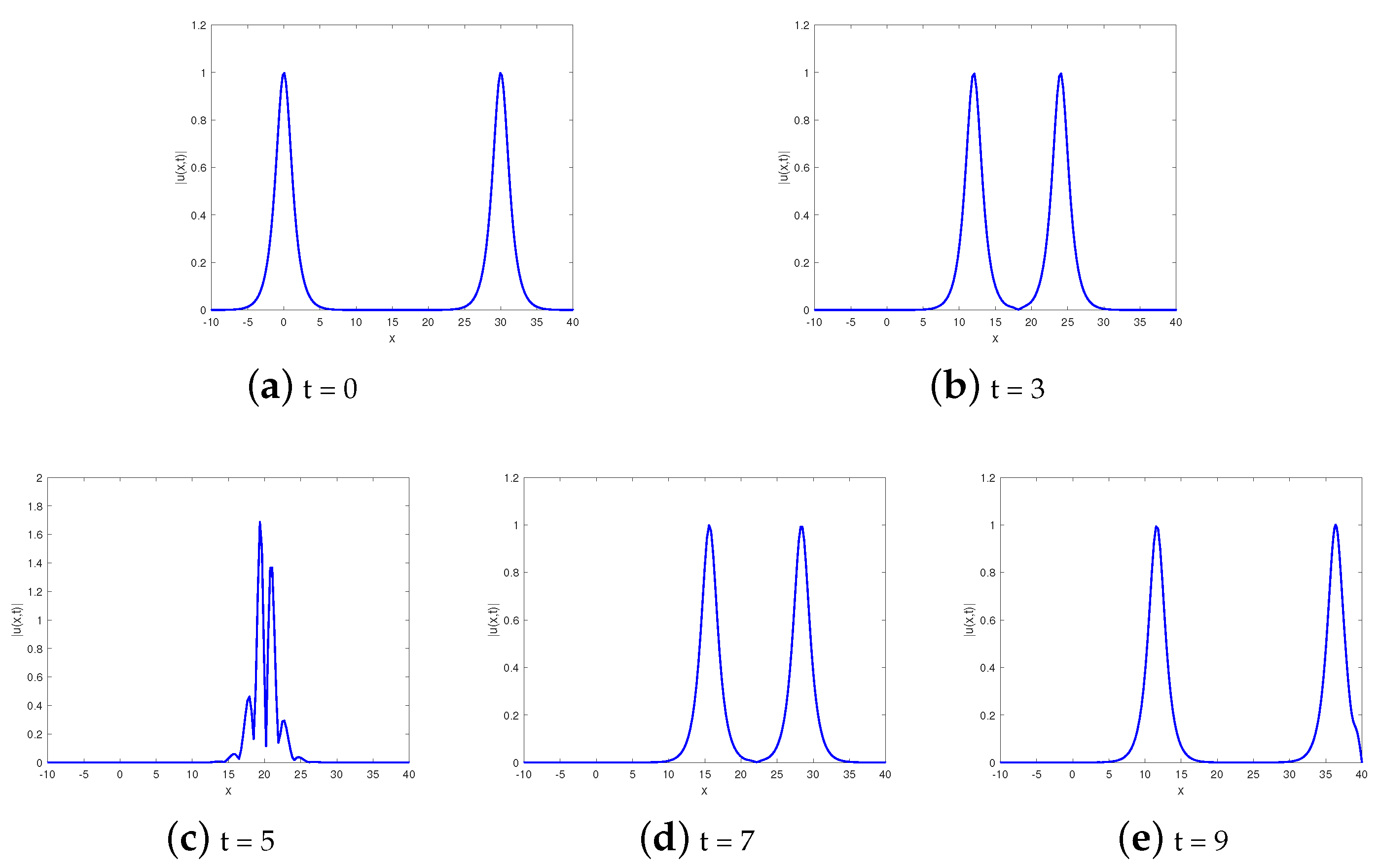
This example shows the collision behavior of two solitary waves. If we provide the initial value condition, a double solitary wave can be generated. When t = 0, two solitary waves are separated. The fast wave will catch up with the slow wave over time, and it will then surpass the slow wave after the collision, and there is only one phase change between them. This is consistent with the theory of waves; see Figure 4 and Figure 5.

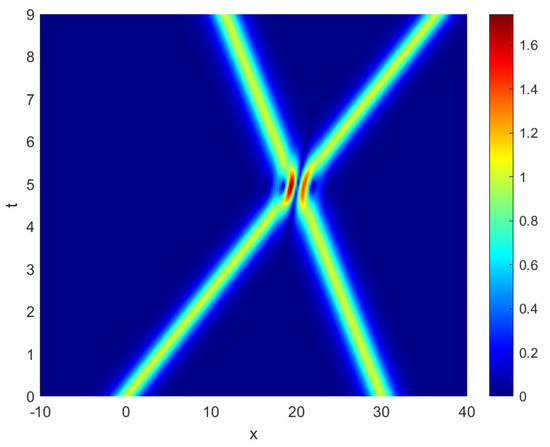
Figure 4. The interaction of two solitary waves without damping at T = 9 for Example 2.

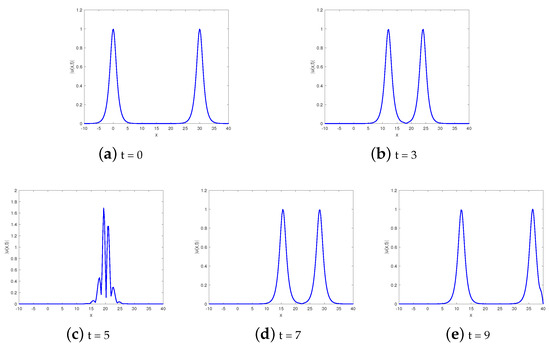
Figure 5. Head-on collisions of two solitary waves without damping for Example 2.

6. Conclusions

In this work, we have proposed an effective operator splitting scheme based on the barycentric Lagrange interpolation collocation method for the nonlinear Schrödinger equation. The convergence analysis is proved theoretically and verified numerically. Numerical examples are presented to show the mass and energy conservation of the proposed scheme. The operator splitting collocation scheme is second-order in time and convergent exponentially in space. The two barycentric interpolation collocation schemes have high accuracy, and the barycentric Lagrange interpolation collocation method is slightly more efficient than the barycentric rational interpolation collocation method. Compared with the finite difference method, the barycentric interpolation collocation method can achieve high accuracy with fewer points. In the future, we plan to extend this method to coupled Schrödinger equations, KdV equations and Klein–Gordon equations, etc.