Design of a Polarization-Insensitive and Wide-Angle Triple-Band Metamaterial Absorber
Abstract
1. Introduction
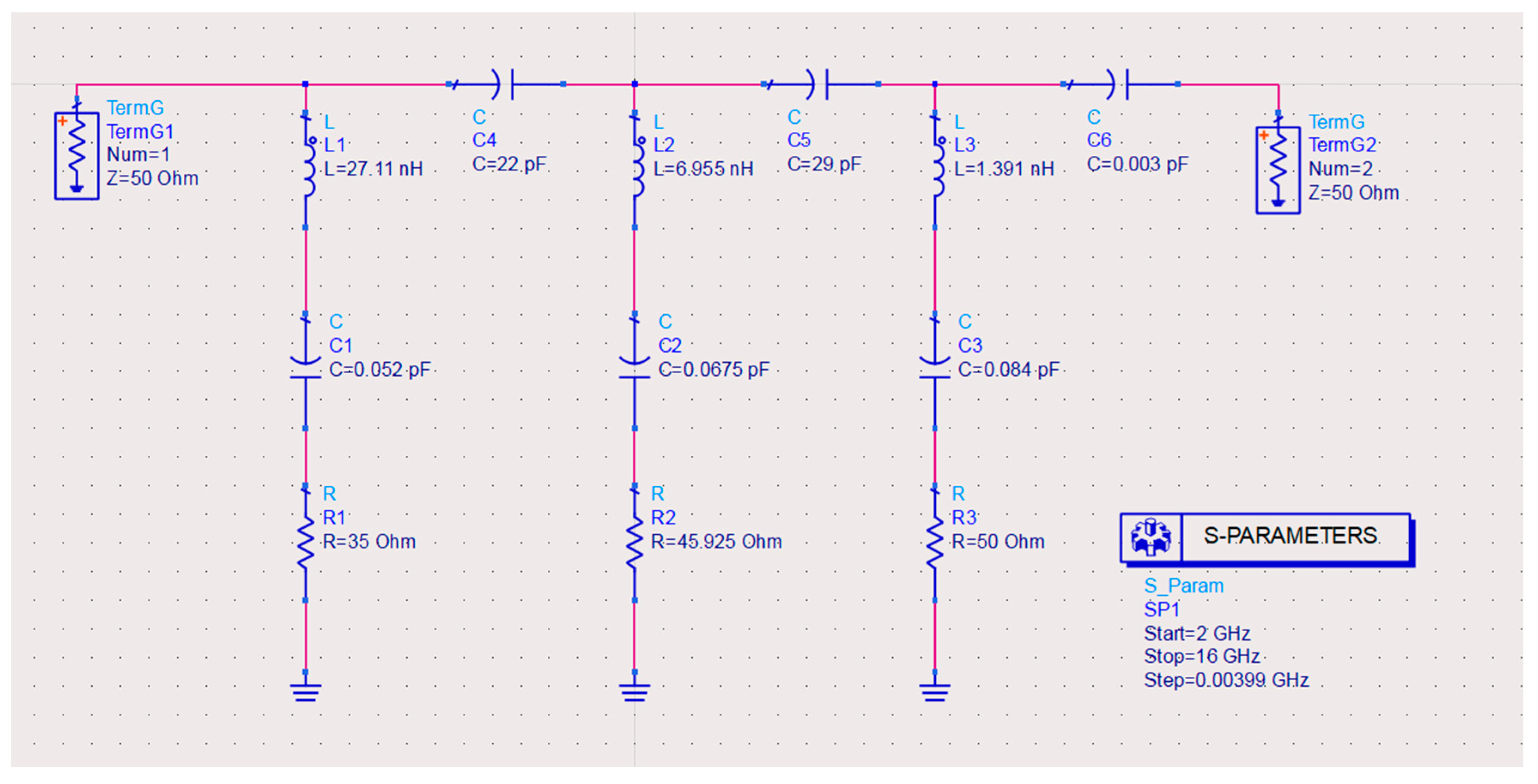
2. Modeling and Theoretical Analysis
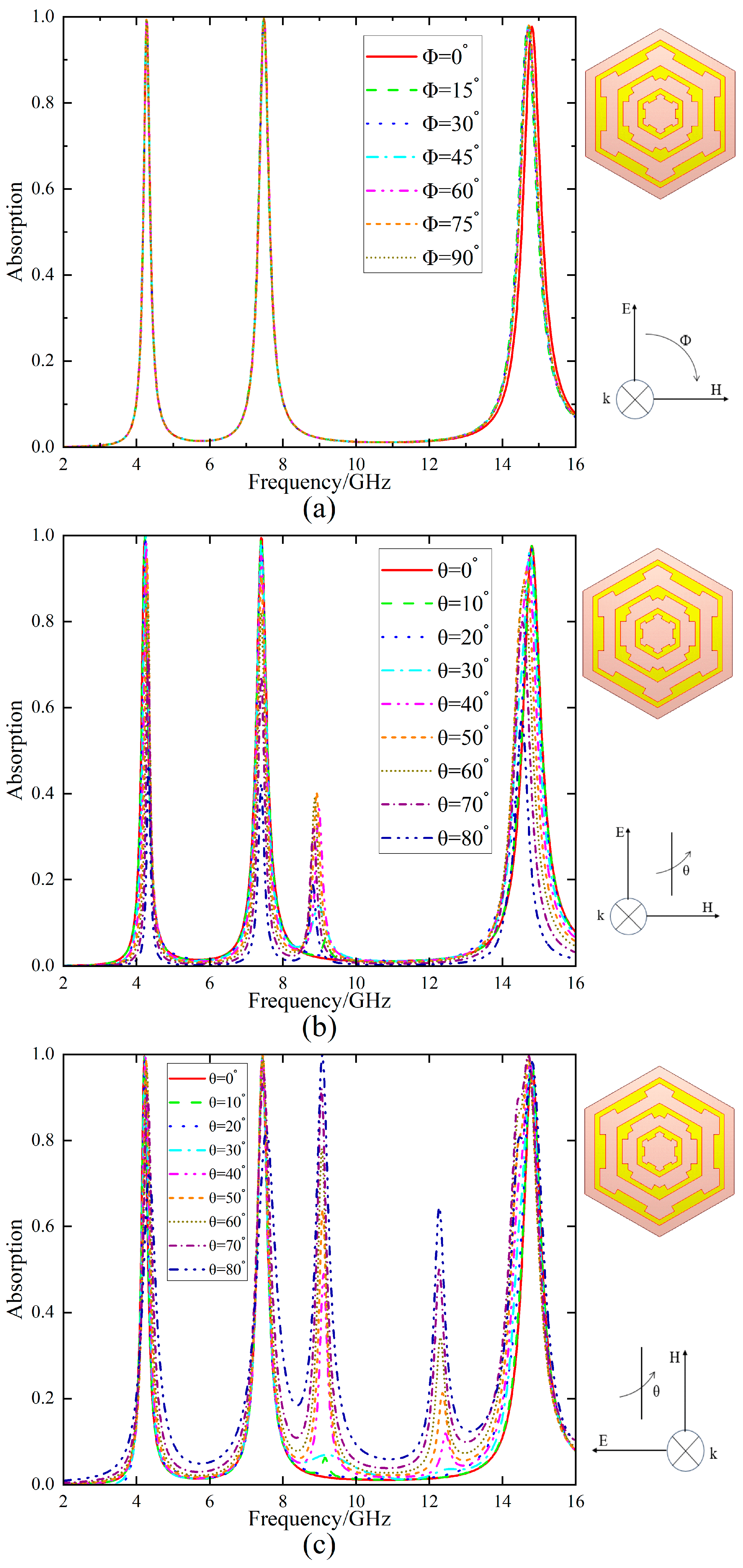
3. Analysis and Discussion
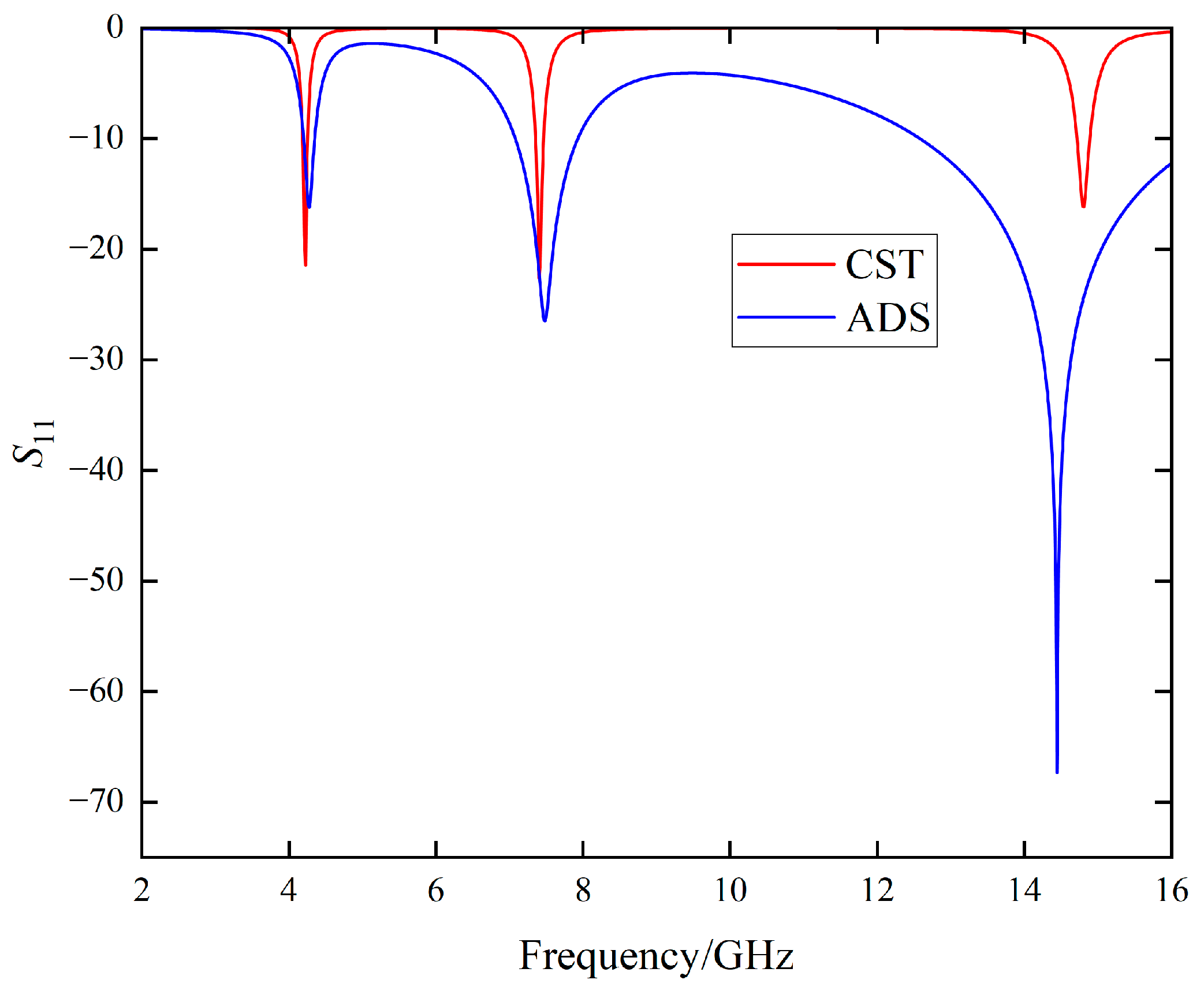
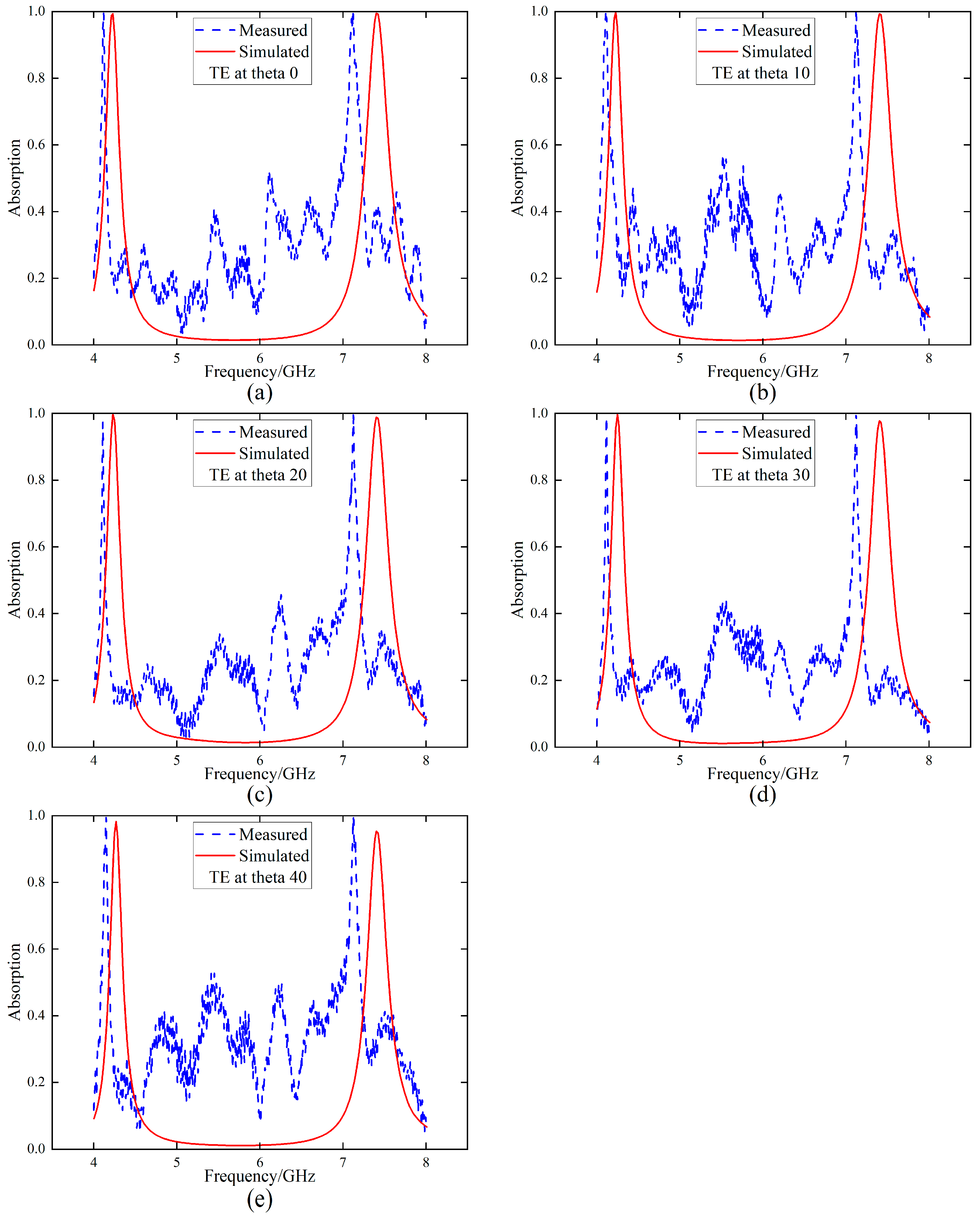
4. Experiment and Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Liu, Z.; Zhou, F.; Yi, Z.; Wang, J. Perfect absorption properties of a near-infrared super-surface perfect absorber based on a multilayer subwavelength array structure. Phys. Lett. A 2025, 540, 130395. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, J.; Zhou, Z.; Gao, Q. L1 model-driven recursive multi-scale denoising network for image super-resolution. Knowl. Based Syst. 2021, 225, 107115. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, C.; Zhou, Z.; Cao, F. Single image super-resolution based on adaptive convolutional sparse coding and convolutional neural networks. J. Vis. Commun. Image Represent. 2019, 58, 651–661. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, N.; Zhou, Z. A temporal sparse collaborative appearance model for visual tracking. Multimed. Tools Appl. 2020, 79, 14103–14125. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, T.; Zhou, Z.; Cao, F. A Compact Recursive Dense Convolutional Network for image classification. Neurocomputing 2020, 372, 8–16. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, Y.; Zhou, Z. Correlation filters based on temporal regularization and background awareness. Comput. Electr. Eng. 2020, 86, 106757. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Zhou, Z.; Cao, F. A novel deep learning algorithm for incomplete face recognition: Low-rank-recovery network. Neural Netw. 2017, 94, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Sun, T.; Cao, F. Image super-resolution via adaptive sparse representation and self-learning. IET Comput. Vis. 2018, 12, 753–761. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, W.; Cao, F. Robust object tracking using a sparse coadjutant observation model. Multimed. Tools Appl. 2018, 77, 30969–30991. [Google Scholar] [CrossRef]
- Zhou, Z.; Xue, B.; Wang, H.; Zhao, J. Bidirectional Multi-scale Deformable Attention for Video Super-Resolution. Multimed. Tools Appl. 2024, 83, 27809–27830. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, W.; Zhao, J. Robust visual tracking using discriminative sparse collaborative map. Int. J. Mach. Learn. Cybern. 2019, 10, 3201–3212. [Google Scholar] [CrossRef]
- Tao, H.; Landy, N.I.; Bingham, C.M.; Zhang, X.; Averitt, R.D.; Padilla, W.J. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt. Express 2008, 16, 7181–7188. [Google Scholar] [CrossRef] [PubMed]
- Taya, S.A. Dispersion properties of lossy, dispersive, and anisotropic left-handed material slab waveguide. Optik 2015, 126, 1319–1323. [Google Scholar] [CrossRef]
- Taya, S.A.; Colak, I.; Suthar, B.; Ramahi, O.M. Cancer cell detector based on a slab waveguide of anisotropic, lossy, and dispersive left-handed material. Appl. Opt. 2021, 60, 8360–8367. [Google Scholar] [CrossRef]
- Chen, Z.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Chen, J.; Zhang, J.; Tang, C. Ultra wideband absorption absorber based on Dirac semimetallic and graphene metamaterials. Phys. Lett. A 2024, 517, 129675. [Google Scholar] [CrossRef]
- Cheng, S.; Li, W.; Zhang, H.; Akhtar, M.N.; Yi, Z.; Zeng, Q.; Ma, C.; Sun, T.; Wu, P.; Ahmad, S. High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals. Opt. Commun. 2024, 569, 130816. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Yi, Z.; Zhang, H.; Song, Q.; Hao, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Ma, C.; Wu, P.; Zeng, Q.; Raza, R. Multi-functional metasurface: Ultra-wideband/multi-band absorption switching by adjusting guided-mode resonance and local surface plasmon resonance effects. Commun. Theor. Phys. 2024, 76, 065701. [Google Scholar] [CrossRef]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active tunable terahertz bandwidth absorber based on single layer graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, S.; Zhang, H.; Yang, W.; Yi, Z.; Yi, Y.; Wang, J.; Ahmad, S.; Raza, R. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, H.; Zhang, H.; Cheng, S.; Yi, Y.; Yi, Z.; Wang, J.; Zhang, J. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Photonics Nanostruct.-Fundam. Appl. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Cheng, Y.; Cao, W.; He, X. Hybrid Plasmonic Waveguides with Tunable ENZ Phenomenon Supported by 3D Dirac Semimetals. Laser Photonics Rev. 2024, 18, 2400167. [Google Scholar] [CrossRef]
- Liu, S.; Cao, W.; Jiang, S.; He, L.; Lin, F.; He, X. 3D Dirac Semimetal Supported Tunable Multi-Frequency Terahertz Metamaterial Absorbers. Adv. Quantum Technol. 2024, 7, 2300386. [Google Scholar] [CrossRef]
- Wang, G.; Cao, W.; He, X. 3D Dirac Semimetal Elliptical Fiber Supported THz Tunable Hybrid Plasmonic Waveguides. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 3284231. [Google Scholar] [CrossRef]
- Corbitt, S.J.; Francoeur, M.; Raeymaekers, B. Implementation of optical dielectric metamaterials: A review. J. Quant. Spectrosc. Radiat. Transf. 2015, 158, 3–16. [Google Scholar] [CrossRef]
- Dewangan, L.; Patinavalasa, M.S.; Acharjee, J.; Solunke, Y.; Ghosh, S.; Mishra, N.K. Broadband metamaterial absorber for stealth applications at K-band. AEU-Int. J. Electron. Commun. 2023, 170, 154828. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Sayed, A.M.; Amr, A.M.; Sayed, M.O.; Hameed, M.F.O.; Obayya, S.S.A. Broadband polarization insensitive metamaterial absorber. Opt. Quantum Electron. 2023, 55, 652. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, H.; Gupta, A. Design and development of high-performance metamaterial absorber for moisture-sensing application. Appl. Phys. A 2023, 129, 377. [Google Scholar] [CrossRef]
- Yoon, Y.; Lim, D.; Tentzeris, M.M.; Lim, S. Low-cost metamaterial absorber using three-dimensional circular truncated cone. Microw. Opt. Technol. Lett. 2018, 60, 1622–1630. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.K.; Pandey, P.C. Cone-shaped resonator-based highly efficient broadband metamaterial absorber. Opt. Quantum Electron. 2023, 55, 579. [Google Scholar] [CrossRef]
- Armghan, A.; Aliqab, K.; Alsharari, M. Polarization and wide-angle incidence MXene-based metamaterial absorber for visible and infrared wavelengths. Opt. Quantum Electron. 2024, 56, 1265. [Google Scholar] [CrossRef]
- Huang, X.; Chen, Y.; Chen, S.; Yang, K.; Liang, J.; Zhou, Z.; Dai, W. Ultrasensitive and tunable multi-narrowband metamaterial absorber. Results Phys. 2023, 47, 106364. [Google Scholar] [CrossRef]
- Abdalla, M.A.; Choudhary, D.K.; Chaudhary, R.K. A compact reconfigurable bandpass/lowpass filter with independent transmission zeros based on generalized NRI metamaterial. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22074. [Google Scholar] [CrossRef]
- Kukreja, J.; Choudhary, D.K.; Chaudhary, R.K. A Metamaterial Inspired ZOR Antenna Using IDC and Spiral Inductor with Partial Ground Plane for WLAN Application. Wirel. Pers. Commun. 2019, 107, 137–147. [Google Scholar] [CrossRef]
- Garg, P.; Jain, P. Novel ultrathin penta-band metamaterial absorber. AEU-Int. J. Electron. Commun. 2020, 116, 153063. [Google Scholar] [CrossRef]
- Hannan, S.; Islam, M.T.; Faruque, M.R.I.; Rmili, H. Polarization-independent perfect metamaterial absorber for C, X and, Ku band applications. J. Mater. Res. Technol. 2021, 15, 3722–3732. [Google Scholar] [CrossRef]
- Al-Khafaji, R.M.; AbdulAmeer, S.A.; Husain, A.; Al Mashhadani, Z.I.; Ali, B.M.; Abdulkadhim, A.H.; Albahash, Z.F. On mechanical behavior and optimization of elliptical-rectangular absorbers made by ABS and PLA in both experimental and numerical methods. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 383. [Google Scholar] [CrossRef]
- Narkis, M.; Shach-Caplan, M.; Haba, Y.; Silverstein, M.S. PVC modification through polymerization of a monomer absorbed in porous suspension-type PVC particles. J. Vinyl Addit. Technol. 2004, 10, 109–120. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.-G.; Kim, T.-T.; Ha, T.; Lee, S.H.; Kim, J.-H.; Lee, Y.H. High-temperature differences in plasmonic broadband absorber on PET and Si substrates. Sci. Rep. 2020, 10, 13279. [Google Scholar] [CrossRef]
- Han, W.; Park, Q.H. Broadband absorber with dispersive metamaterials. Nanophotonics 2023, 12, 2443–2449. [Google Scholar] [CrossRef]
- Laur, V.; Maalouf, A.; Chevalier, A.; Comblet, F. Three-Dimensional Printing of Honeycomb Microwave Absorbers: Feasibility and Innovative Multiscale Topologies. IEEE Trans. Electromagn. Compat. 2021, 63, 390–397. [Google Scholar] [CrossRef]
- Kshirsagar, D.E.; Dubey, H.; Puri, V.; Sharon, M.; Sharon, M. X-band absorber carbon microbeads. Mater. Lett. 2021, 299, 130054. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, J.; Shen, Z. Water-based metamaterial absorber for temperature modulation. Phys. Scr. 2024, 99, 105563. [Google Scholar] [CrossRef]
- AbdelAll, N.; Almokhtar, M.; Khouqeer, G.; Abood, I.; El Soliman, S. Rainbow Trapping with Engineered Topological Corner States and Cavities in Photonic Crystals. Adv. Quantum Technol. 2024, 7, 2400050. [Google Scholar] [CrossRef]
- Istokskaia, V.; Lefebvre, B.; Versaci, R.; Dreghici, D.B.; Doria, D.; Grepl, F.; Olšovcová, V.; Schillaci, F.; Stanček, S.; Tryus, M.; et al. Real-time bremsstrahlung detector as a monitoring tool for laser–plasma proton acceleration. High Power Laser Sci. Eng. 2024, 12, e57. [Google Scholar] [CrossRef]
- Li, S.; Fang, Y.; Wang, J. Control of light–matter interactions in two-dimensional materials with nanoparticle-on-mirror structures. Opto-Electron. Sci. 2024, 3, 240011. [Google Scholar] [CrossRef]
- Liang, M.; Lu, D.; Ma, Y. Vectorial optical fields manipulation via metasurfaces. Opto-Electron. Eng. 2024, 51, 240068. [Google Scholar] [CrossRef]
- Luo, Z.; Ding, Y.; Peng, F.; Wei, G.; Wang, Y.; Wu, S.-T. Ultracompact and high-efficiency liquid-crystal-on-silicon light engines for augmented reality glasses. Opto-Electron. Adv. 2024, 7, 240039. [Google Scholar] [CrossRef]
- Peters, C.; Forbes, A. Controlling the hidden parity in vectorial light with metasurfaces. Adv. Photonics 2024, 6, 040501. [Google Scholar] [CrossRef]
- Rane, S.; Prabhu, S.; Chowdhury, D.R. Physics and applications of terahertz metagratings. Opto-Electron. Sci. 2024, 3, 230049. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Fan, C.; Zeng, Z.; Xiong, C.; Wu, J.; Yan, Z.; Liu, D.; Sun, Q. Adaptive decentralized AI scheme for signal recognition of distributed sensor systems. Opto-Electron. Adv. 2024, 7, 240119. [Google Scholar] [CrossRef]
- Md Sadman Sakib, R.; Aydogan, O. Physics and artificial intelligence: Illuminating the future of optics and photonics. Adv. Photonics 2024, 6, 050500. [Google Scholar] [CrossRef]
- Seo, J.; Jo, J.; Kim, J.; Kang, J.; Kang, C.; Moon, S.-W.; Lee, E.; Hong, J.; Rho, J.; Chung, H. Deep-learning-driven end-to-end metalens imaging. Adv. Photonics 2024, 6, 066002. [Google Scholar] [CrossRef]
- Shi, J.; Yang, C.; Chen, Y.; Wang, T.; Yu, H.; Cao, J.; Geng, Z.; Wang, Z.; Wen, H.; Tan, H.; et al. Precise mode control of mid-infrared high-power laser diodes using on-chip advanced sawtooth waveguide designs. High Power Laser Sci. Eng. 2024, 12, e42. [Google Scholar] [CrossRef]
- Taha, B.A.; Addie, A.J.; Haider, A.J.; Chaudhary, V.; Apsari, R.; Kaushik, A.; Arsad, N. Exploring Trends and Opportunities in Quantum-Enhanced Advanced Photonic Illumination Technologies. Adv. Quantum Technol. 2024, 7, 2300414. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.; Zhu, H.; Dong, H.; Wang, S. Research progress and prospects of metasurface polarization devices. Opto-Electron. Eng. 2024, 51, 240095. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Q.; Shen, B.; Tao, Y.; Zhang, X.; Tao, Z.; Xing, L.; Ge, Z.; Li, T.; Bai, B.; et al. Multifunctional mixed analog/digital signal processor based on integrated photonics. Opto-Electron. Sci. 2024, 3, 240012. [Google Scholar] [CrossRef]
- Yang, H.; He, H.; Hu, Y.; Duan, H. Metasurface-empowered vector light field regulation, detection and application. Opto-Electron. Eng. 2024, 51, 240168. [Google Scholar] [CrossRef]
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic algorithm assisted meta-atom design for high-performance metasurface optics. Opto-Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Zhou, L.; Lou, H.; Deng, Z.; Qin, X.; Pan, J.; Di, Y.; Gu, C.; Luo, D.; Li, W. Compact mid-infrared dual-comb spectrometer over 3–4 μm via intra-pulse difference frequency generation in LiNbO3 waveguides. High Power Laser Sci. Eng. 2024, 12, e23. [Google Scholar] [CrossRef]
- Berhe, A.M.; As’ham, K.; Al-Ani, I.; Hattori, H.T.; Miroshnichenko, A.E. Strong coupling and catenary field enhancement in the hybrid plasmonic metamaterial cavity and TMDC monolayers. Opto-Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Nan, T.; Zhao, H.; Guo, J.; Wang, X.; Tian, H.; Zhang, Y. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces. Opto-Electron. Sci. 2024, 3, 230052. [Google Scholar] [CrossRef]
- Refaeli, Z.; Marcus, G.; Shamir, Y. A simple method for pulse contrast enhancement via self-focusing. High Power Laser Sci. Eng. 2024, 12, e18. [Google Scholar] [CrossRef]
- Shen, C.-Y.; Li, J.; Li, Y.; Gan, T.; Bai, L.; Jarrahi, M.; Ozcan, A. Multiplane quantitative phase imaging using a wavelength-multiplexed diffractive optical processor. Adv. Photonics 2024, 6, 056003. [Google Scholar] [CrossRef]
- Ullah, M.; Mikki, S. Optical Nonreciprocity in a Multimode Cavity Optomechanical System Controlled by Dynamic Casimir Force. Adv. Quantum Technol. 2024, 7, 2400007. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Hu, K.-X.; Zhang, J.; Cao, J.; Zhang, S.; Wang, H.-F. Topological Phase Transition and Edge States with Tunable Localization in the Cyclic Four-Mode Optical System. Adv. Quantum Technol. 2024, 7, 2400165. [Google Scholar] [CrossRef]
- Zhang, J.C.; Chen, M.K.; Fan, Y.; Chen, Q.; Chen, S.; Yao, J.; Liu, X.; Xiao, S.; Tsai, D.P. Miniature tunable Airy beam optical meta-device. Opto-Electron. Adv. 2024, 7, 230171. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, T.; Zhu, Q.; Gu, M. Ultrahigh performance passive radiative cooling by hybrid polar dielectric metasurface thermal emitters. Opto-Electron. Adv. 2024, 7, 230194. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Ye, D.; Wang, Z.; Xu, K.; Li, H.; Huangfu, J.; Wang, Z.; Ran, L. Ultrawideband Dispersion Control of a Metamaterial Surface for Perfectly-Matched-Layer-Like Absorption. Phys. Rev. Lett. 2013, 111, 187402. [Google Scholar] [CrossRef]
- Zhou, F.; Ji, C.; Liu, Z.; Jiang, N. Polarization-desensitization dynamically adjustable quintuple plasmon-induced transparency multi-frequency modulator based on graphene metamaterial. J. Appl. Phys. 2024, 136, 143107. [Google Scholar] [CrossRef]
- Jorwal, S.; Dubey, A.; Gupta, R.; Agarwal, S. Triple-Band Ultrathin Minkowski Fractal-Inspired Polarization-Insensitive Microwave Absorber for Stealth Application. J. Electron. Mater. 2024, 53, 8171–8179. [Google Scholar] [CrossRef]
- Shukoor, M.A.; Kumar, V.; Dey, S. Compact polarisation insensitive wide angular stable triple band absorber for RF energy harvesting, RCS reduction, and sensor applications. Int. J. RF Microw. Comput. Aided Eng. 2021, 31, e22763. [Google Scholar] [CrossRef]
- Genikala, S.; Ghosh, A.; Roy, B. Triple band single layer microwave absorber based on closed loop resonator structures with high stability under oblique incidence. AEU-Int. J. Electron. Commun. 2023, 164, 154629. [Google Scholar] [CrossRef]
- Amugothu, R.; Damera, V. Wide incidence angle triple-band metamaterial EM wave absorber at X and Ku frequency band applications. J. Electromagn. Waves Appl. 2023, 37, 1208–1220. [Google Scholar] [CrossRef]
- Berka, M.; Fellah, B.; Islam, T.; Bendaoudi, A.; Das, S.; Mahdjoub, Z.; Tarricone, L. A triple band square-interlinked-rhombus shaped metamaterial absorber for microwave C and X-band utilizations. Opt. Quantum Electron. 2023, 55, 1223. [Google Scholar] [CrossRef]
- Mishra, N.; Choudhary, D.K.; Chowdhury, R.; Kumari, K.; Chaudhary, R.K. An Investigation on Compact Ultra-Thin Triple Band Polarization Independent Metamaterial Absorber for Microwave Frequency Applications. IEEE Access 2017, 5, 4370–4376. [Google Scholar] [CrossRef]
- Hossain, M.B.; Faruque, M.R.I.; Islam, M.T.; Singh, M.; Jusoh, M. Triple band microwave metamaterial absorber based on double E-shaped symmetric split ring resonators for EMI shielding and stealth applications. J. Mater. Res. Technol. 2022, 18, 1653–1668. [Google Scholar] [CrossRef]
- Cheng, H.; Fang, B.; Huang, W.; Li, R.; Shen, C.; Ke, L.; Jing, X.; Li, C.; Hong, Z. Far-field steering of beams based on dynamic encoding metasurface. Opt. Laser Technol. 2022, 156, 108520. [Google Scholar] [CrossRef]
- Jing, X.; Gui, X.; Zhou, P.; Hong, Z. Physical Explanation of Fabry–Pérot Cavity for Broadband Bilayer Metamaterials Polarization Converter. J. Light. Technol. 2018, 36, 2322–2327. [Google Scholar] [CrossRef]
- Jing, X.; Tang, X.; Tian, Y.; Kong, Z.; Li, C.; Shen, C.; Hong, Z. Enhancement of Diffraction Efficiency Based on the Addition Principle of Coded Digital Gratings. J. Light. Technol. 2022, 40, 136–142. [Google Scholar] [CrossRef]
- Qin, G.; Dong, Y.; Zhang, P.; Liu, J.; Li, C.; Huang, W.; Hong, Z.; Shen, C.; Jing, X. Broadband absorber coupled with anti-reflection inverted pyramid type all-dielectric microstructure. Opt. Lasers Eng. 2023, 160, 107288. [Google Scholar] [CrossRef]
- Wang, Q.; Li, C.; Fang, B.; Ke, L.; Lu, J.; Ma, X.; Hong, Z.; Jing, X. Flexible and Independent Control of Asymmetric Vortex Beams Based on Spin Multiplexing all Dielectric Metasurface. J. Light. Technol. 2023, 41, 7098–7104. [Google Scholar] [CrossRef]
- Xia, R.; Jing, X.; Gui, X.; Tian, Y.; Hong, Z. Broadband terahertz half-wave plate based on anisotropic polarization conversion metamaterials. Opt. Mater. Express 2017, 7, 977–988. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Cheng, H.; Fang, B.; Lu, J.; Ma, X.; Wang, L.; Hong, Z.; Jing, X. Anisotropic programmable metasurface beam splitter based on diode real-time control. Opt. Lasers Eng. 2023, 169, 107723. [Google Scholar] [CrossRef]
- Zhao, J.; Jing, X.; Wang, W.; Tian, Y.; Zhu, D.; Shi, G. Steady method to retrieve effective electromagnetic parameters of bianisotropic metamaterials at one incident direction in the terahertz region. Opt. Laser Technol. 2017, 95, 56–62. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Fan, J.; Qi, C.; Liu, J.; He, Y.; Li, C.; Jing, X.; Gan, H.; et al. Terahertz high and near-zero refractive index metamaterials by double layer metal ring microstructure. Opt. Laser Technol. 2020, 123, 105949. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Li, C.; Fu, J.; Gan, H.; Hong, Z.; Jing, X. Improvement of unidirectional scattering characteristics based on multiple nanospheres array. Microw. Opt. Technol. Lett. 2020, 62, 2405–2414. [Google Scholar] [CrossRef]
- Jing, X.; Xu, Y.; Gan, H.; He, Y.; Hong, Z. High Refractive Index Metamaterials by Using Higher Order Modes Resonances of Hollow Cylindrical Nanostructure in Visible Region. IEEE Access 2019, 7, 144945–144956. [Google Scholar] [CrossRef]
- Wang, W.; Jing, X.; Zhao, J.; Li, Y.; Tian, Y. Improvement of accuracy of simple methods for design and analysis of a blazed phase grating microstructure. Opt. Appl. 2017, 47, 183–198. [Google Scholar] [CrossRef]
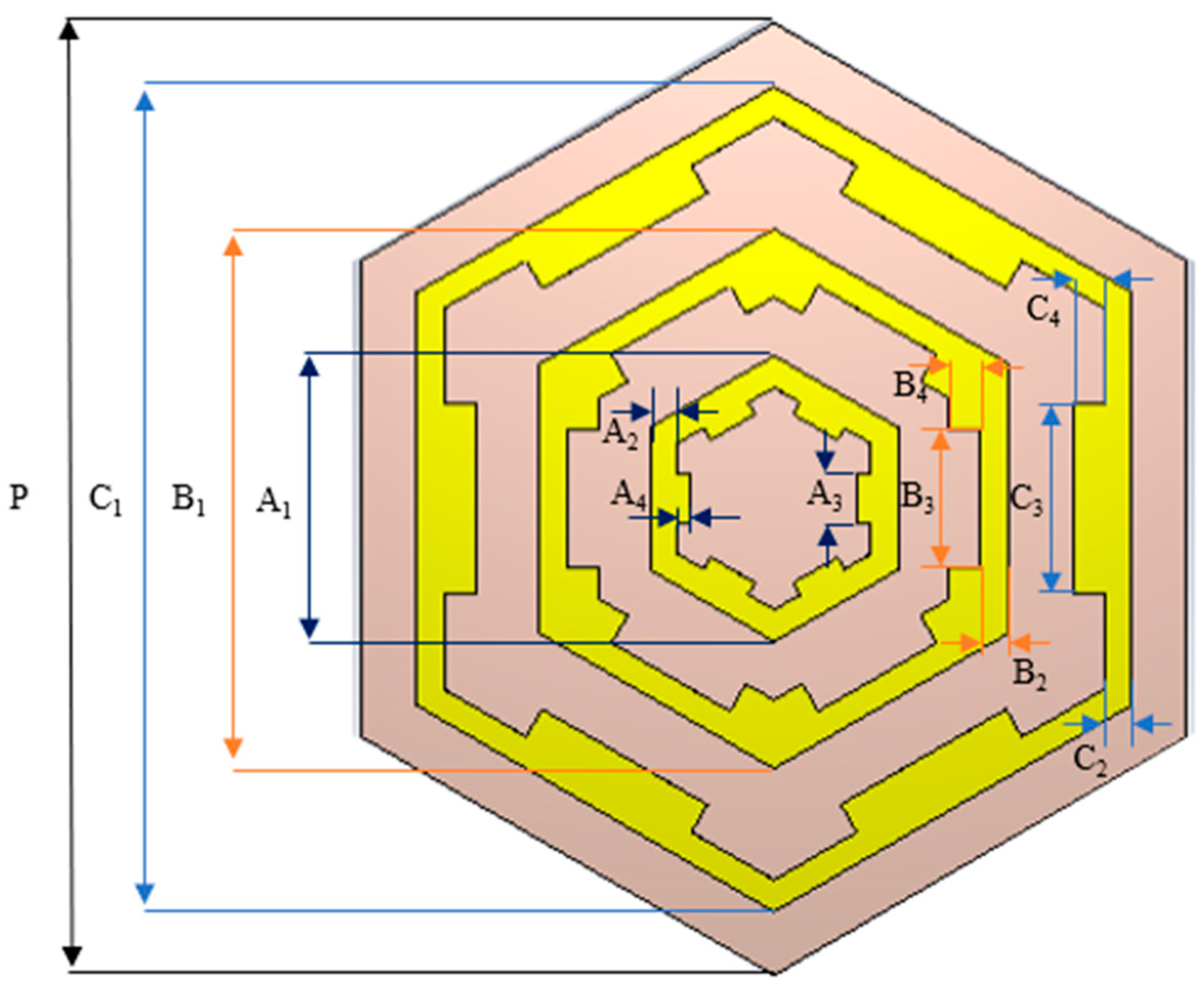

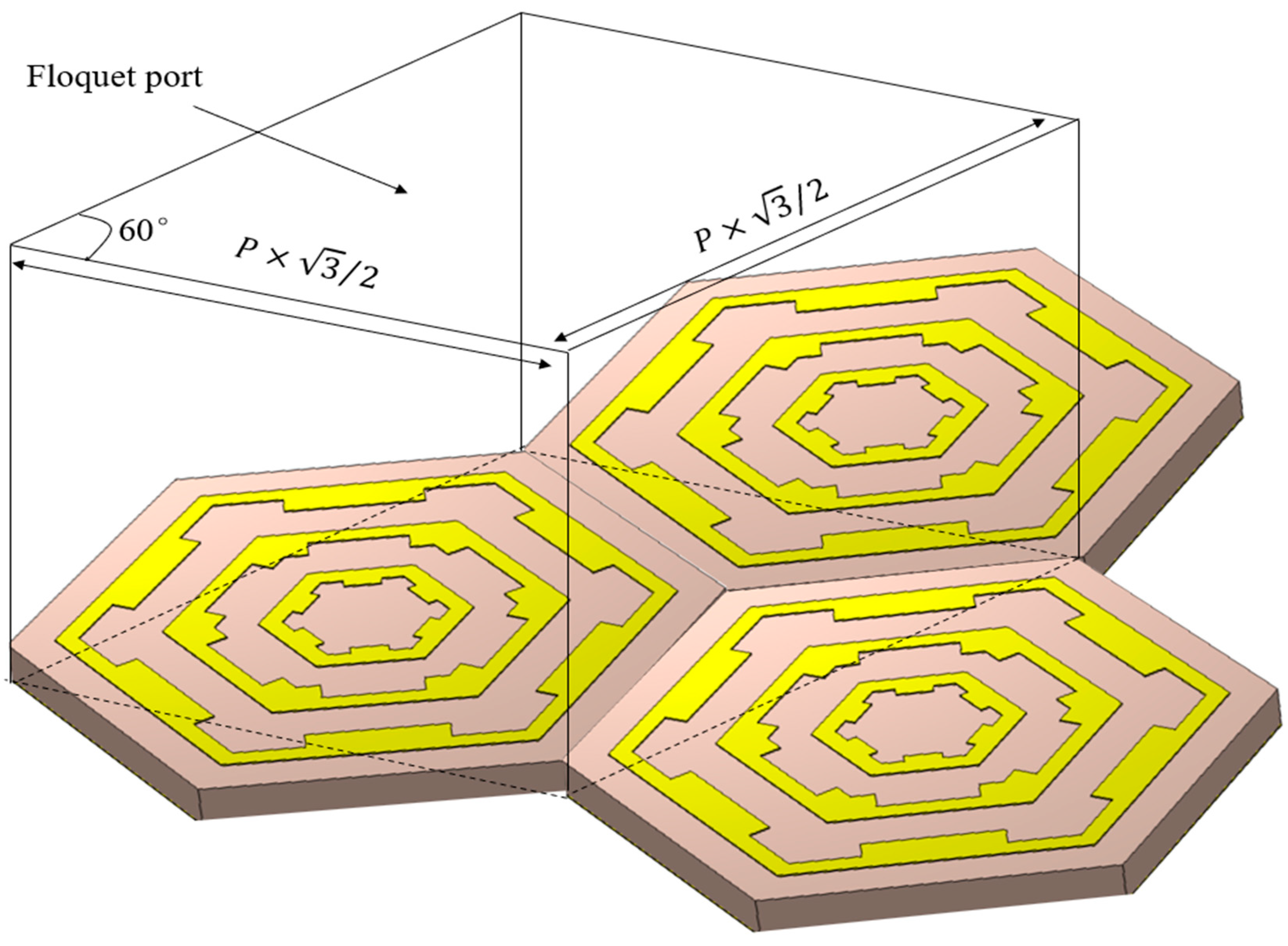

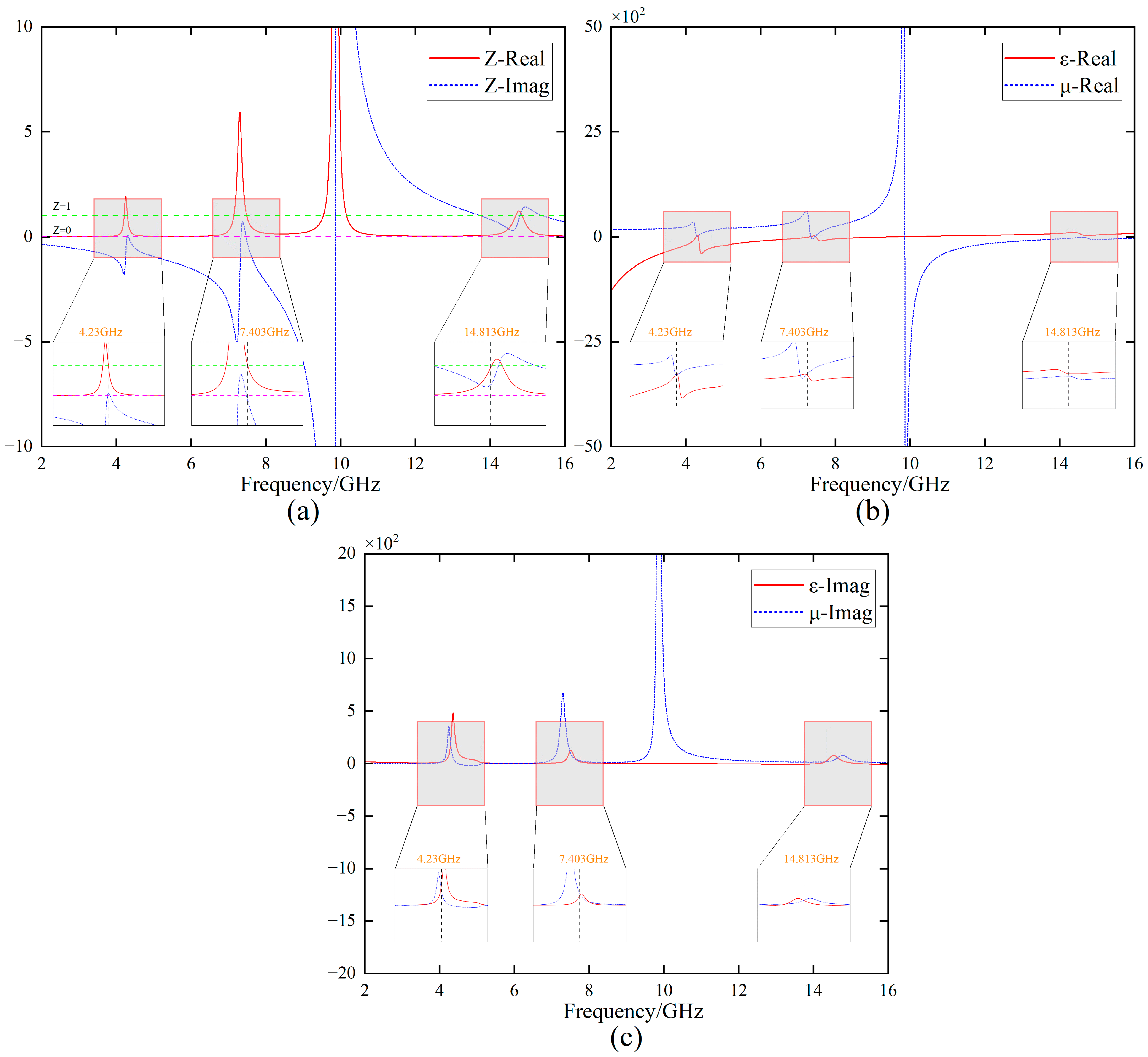
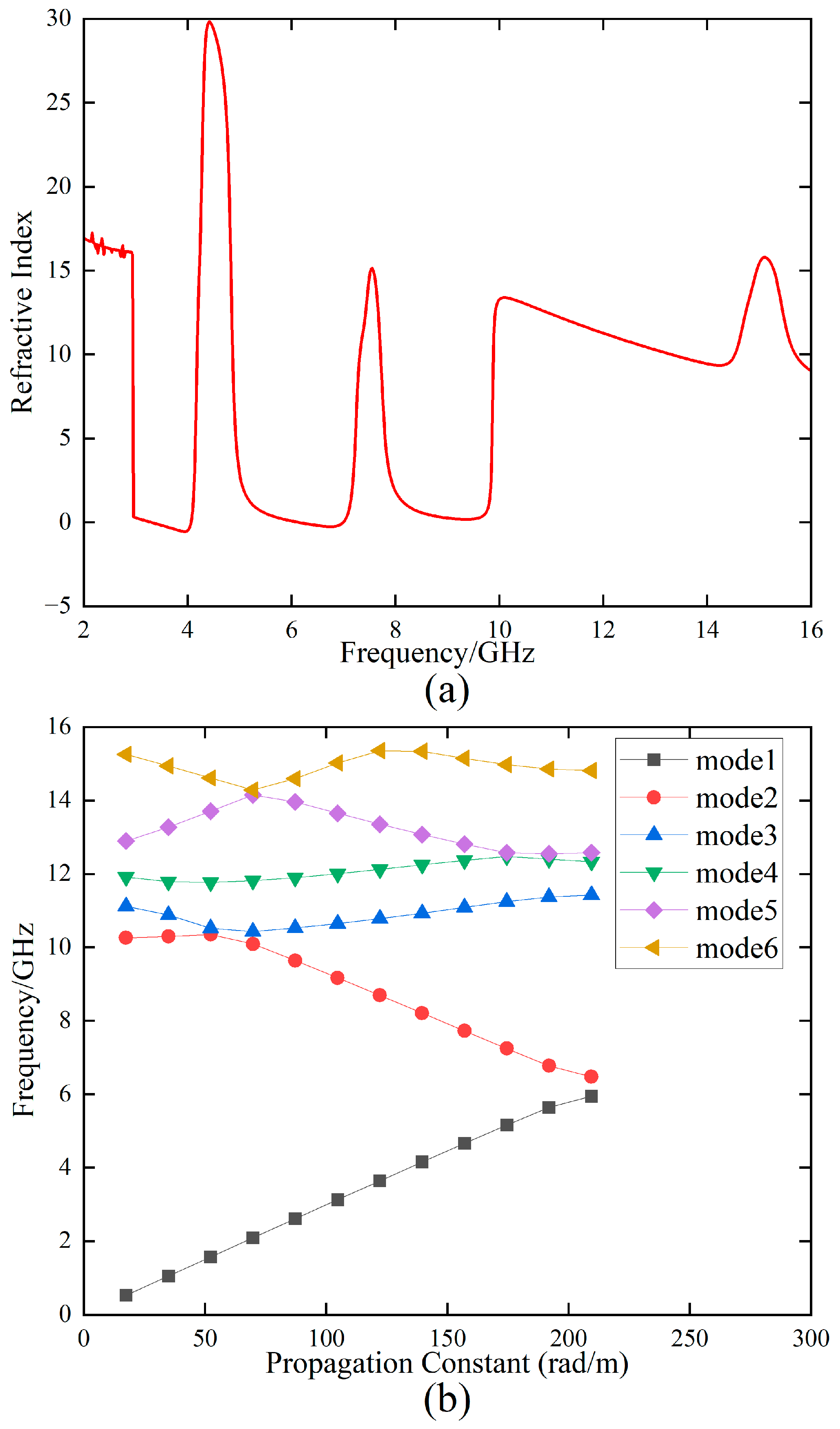
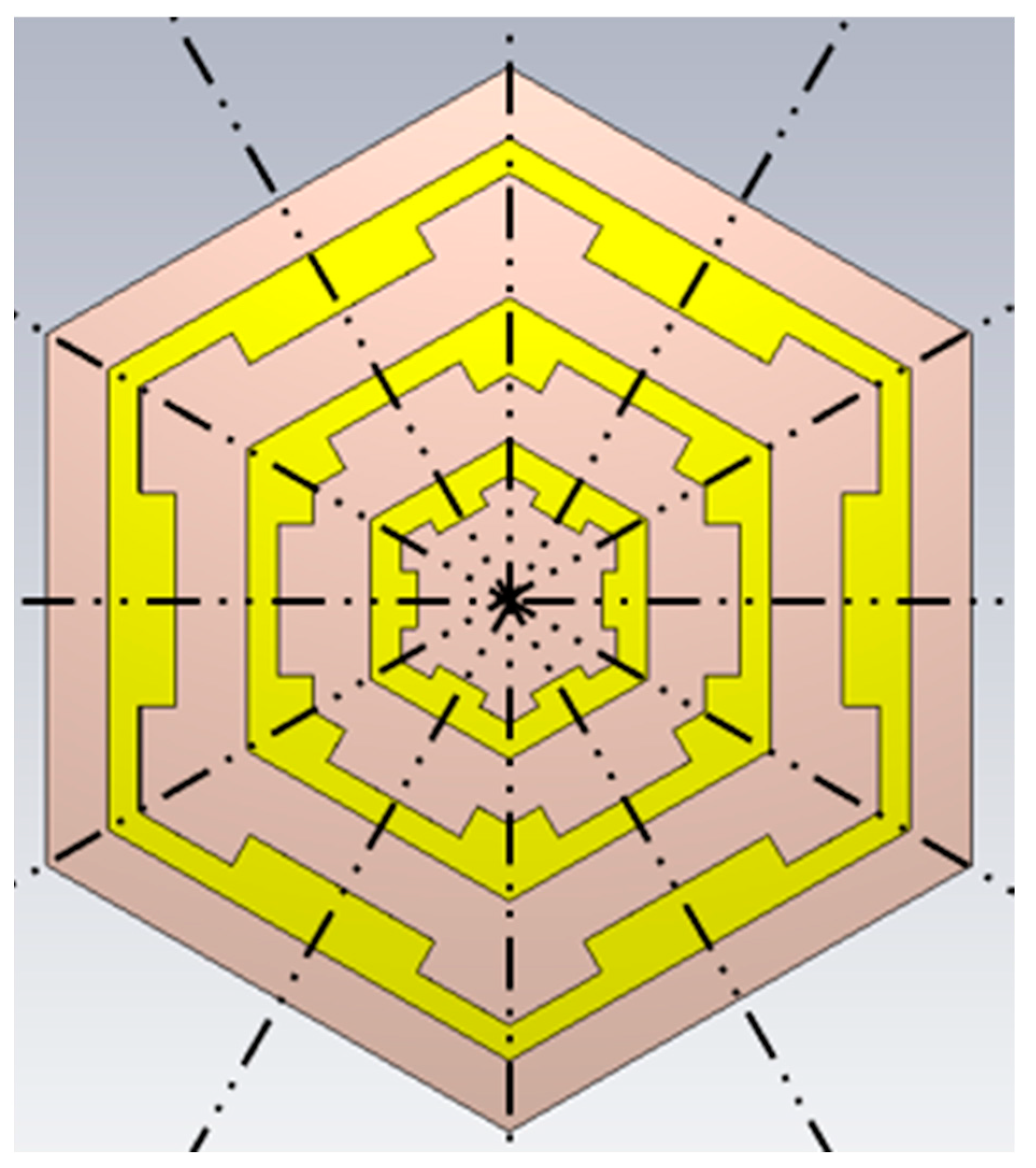

| Parameter | Size/mm | Parameter | Size/mm | Parameter | Size/mm | Parameter | Size/mm |
|---|---|---|---|---|---|---|---|
| A1 | 4.5 | B1 | 8.5 | C1 | 13 | P | 15 |
| A2 | 0.433 | B2 | 0.433 | C2 | 0.433 | H | 1 |
| A3 | 0.8 | B3 | 2.15 | C3 | 3 | H1 | 0.035 |
| A4 | 0.22 | B4 | 0.5 | C4 | 0.5 |
| Degree/° | First Absorption Peak | Second Absorption Peak | Third Absorption Peak | |||
|---|---|---|---|---|---|---|
| Frequency/GHz | Absorption/% | Frequency/GHz | Absorption/% | Frequency/GHz | Absorption/% | |
| 0 | 4.21 | 99.6 | 7.44 | 99.6 | 14.81 | 97.6 |
| 10 | 4.21 | 99.3 | 7.44 | 99.6 | 14.80 | 97.7 |
| 20 | 4.23 | 99.7 | 7.44 | 99.7 | 14.80 | 98.3 |
| 30 | 4.23 | 99.4 | 7.44 | 99.8 | 14.78 | 98.0 |
| 40 | 4.25 | 99.7 | 7.44 | 99.9 | 14.74 | 98.2 |
| 50 | 4.23 | 99.0 | 7.44 | 99.9 | 14.72 | 98.7 |
| 60 | 4.29 | 96.8 | 7.46 | 99.2 | 14.70 | 99.4 |
| 70 | 4.31 | 90.8 | 7.46 | 95.4 | 14.72 | 99.9 |
| 80 | 4.34 | 72.6 | 7.54 | 82.2 | 14.81 | 98.2 |
| Degree/° | First Absorption Peak | Second Absorption Peak | Third Absorption Peak | |||
|---|---|---|---|---|---|---|
| Frequency/GHz | Absorption/% | Frequency/GHz | Absorption/% | Frequency/GHz | Absorption/% | |
| 0 | 4.23 | 99.3 | 7.40 | 99.5 | 14.81 | 97.6 |
| 10 | 4.23 | 99.7 | 7.40 | 99.3 | 14.80 | 97.6 |
| 20 | 4.23 | 99.7 | 7.40 | 98.9 | 14.78 | 97.6 |
| 30 | 4.25 | 99.7 | 7.40 | 97.7 | 14.76 | 96.3 |
| 40 | 4.27 | 98.2 | 7.40 | 95.3 | 14.72 | 94.4 |
| 50 | 4.29 | 94.6 | 7.40 | 90.6 | 14.67 | 91.6 |
| 60 | 4.31 | 86.8 | 7.40 | 82.0 | 14.56 | 88.6 |
| 70 | 4.33 | 71.5 | 7.40 | 67.3 | 14.55 | 79.9 |
| 80 | 4.33 | 46.7 | 7.40 | 72.4 | 14.53 | 57.1 |
| Ref | Absorption Frequency (GHz) | Frequency Band | Absorptivity | Unit Cell Thickness (mm) | Unit Cell Size (mm) | Polarization Insensitivity | Angular Stability |
|---|---|---|---|---|---|---|---|
| [72] | 2.5, 5.2, 9.8, and 11.0 | S, C, and X | 90%, 91%, 97%, and 94% | 1.6 (0.013λ0) | 19 × 19 (0.18λ0 × 0.18λ0) | 60° | 60° for TE and TM |
| [73] | 4.9, 10, and 14.05 | C, X, and Ku | 99.53%, 99.76%, and 98.71% | 0.8 (0.013λ0) | 10 × 10 (0.163λ0 × 0.163λ0) | Yes | 45° for TE and 75 for TM |
| [74] | 2.4, 5.5, and 7.5 | S and C | 99.53%, 99.33%, and 99.90% | 1.6 (0.0128λ0) | 15.1 × 15.1 (0.12λ0 × 0.12λ0) | Yes | 52° for TE and TM |
| [75] | 11.6, 14.04, and 16.56 | X and Ku | 99.88%, 99.72%, and 96.41% | 1.6 (0.0618λ0) | 13 × 13 (0.425λ0 × 0.425λ0) | Yes | 60° for TE and TM |
| [76] | 5.86, 6.57, and 8.94 | C and X | 86.23%, 92.92%, and 82.07% | 1.52 (0.029λ0) | 10 × 10 (0.19λ0 × 0.19λ0) | Yes | 90° for TE and TM |
| [77] | 4.19, 9.34, and 11.48 | C and X | 99.67%, 99.48%, and 99.42% | 0.8 (0.011λ0) | 8 × 8 (0.11λ0 × 0.11λ0) | Yes | 60° for TE and TM |
| [78] | 5.376, 10.72, and 12.25 | C, X, and Ku | 99.9%, 99.9%, and 99.7% | 1.6 (0.028λ0) | 10 × 10 (0.179λ0 × 0.179λ0) | No | 30° for TE and TM |
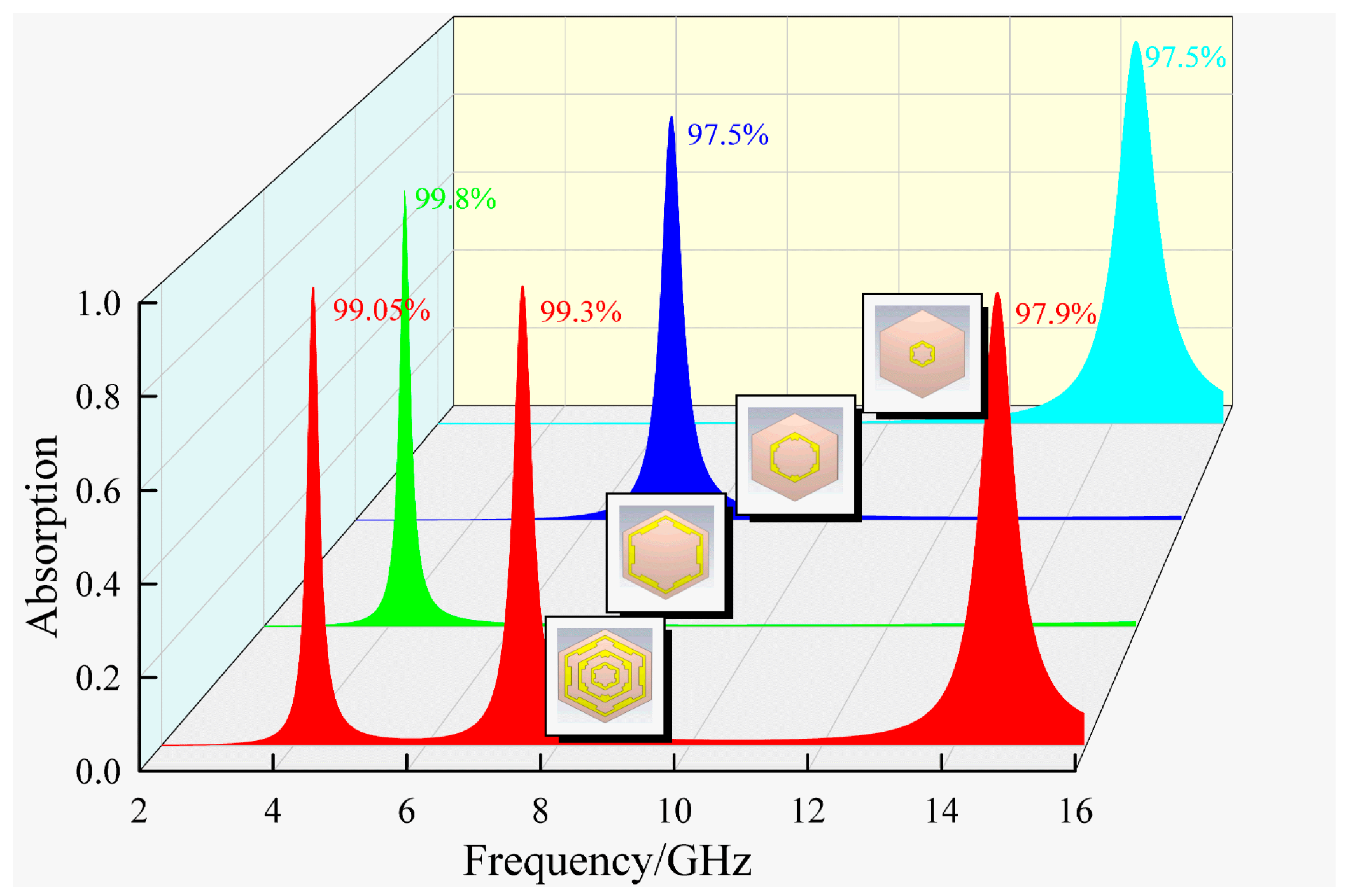
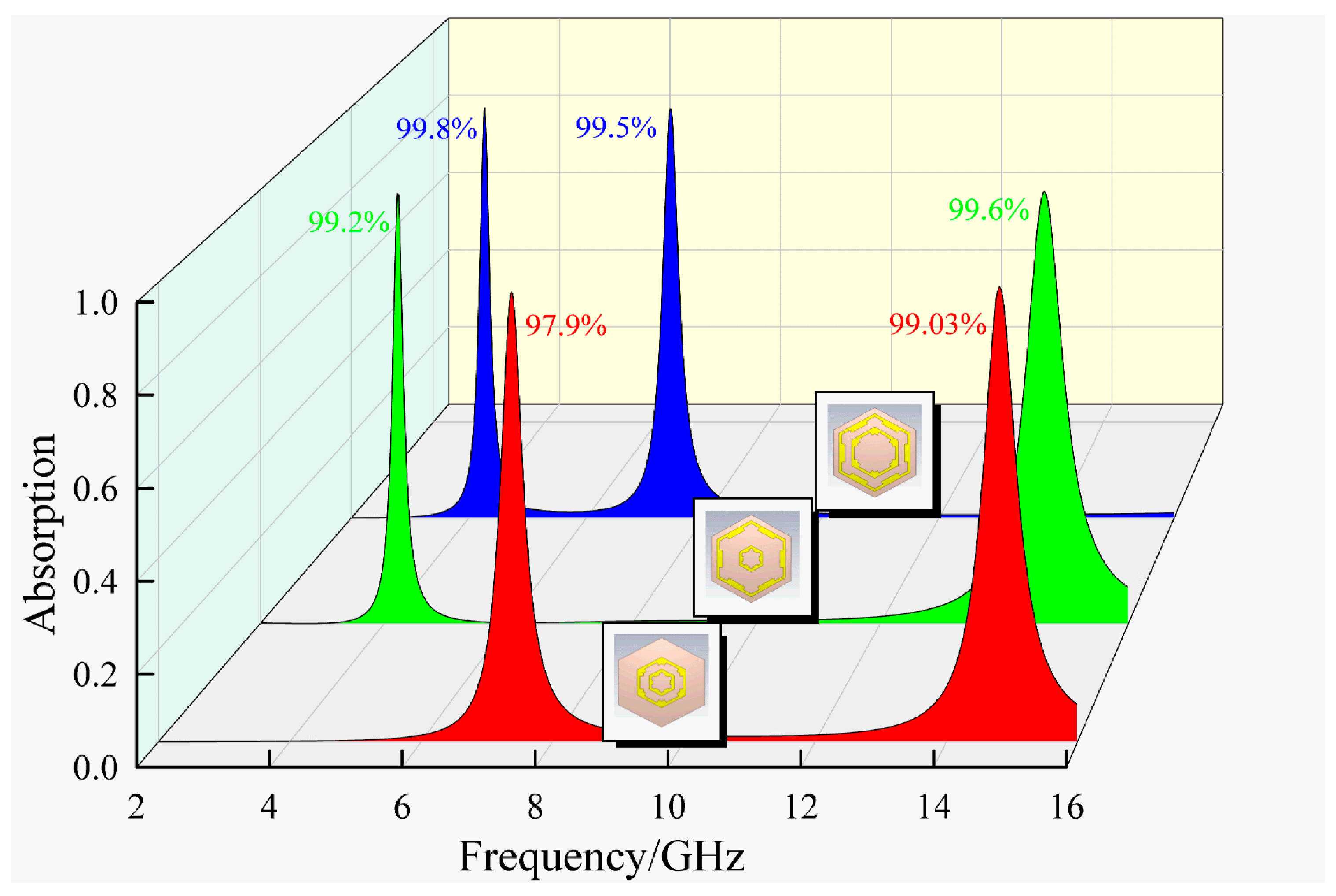
| This work | 4.306, 7.479, and 14.661 | C and Ku | 99.05%, 99.3%, and 97.9% | 1.07 (0.0154λ0) | 6 × 7.5 × 7.5 × ×= 146 mm2 (6 × 0.108λ0 × 0.108λ0 × × ) | Yes | 50° for TE and 70° for TM |
| Simulation | Experiment | |||||
|---|---|---|---|---|---|---|
| Theta = 0 | Theta = 0 | Theta = 0 | Theta = 0 | Theta = 0 | ||
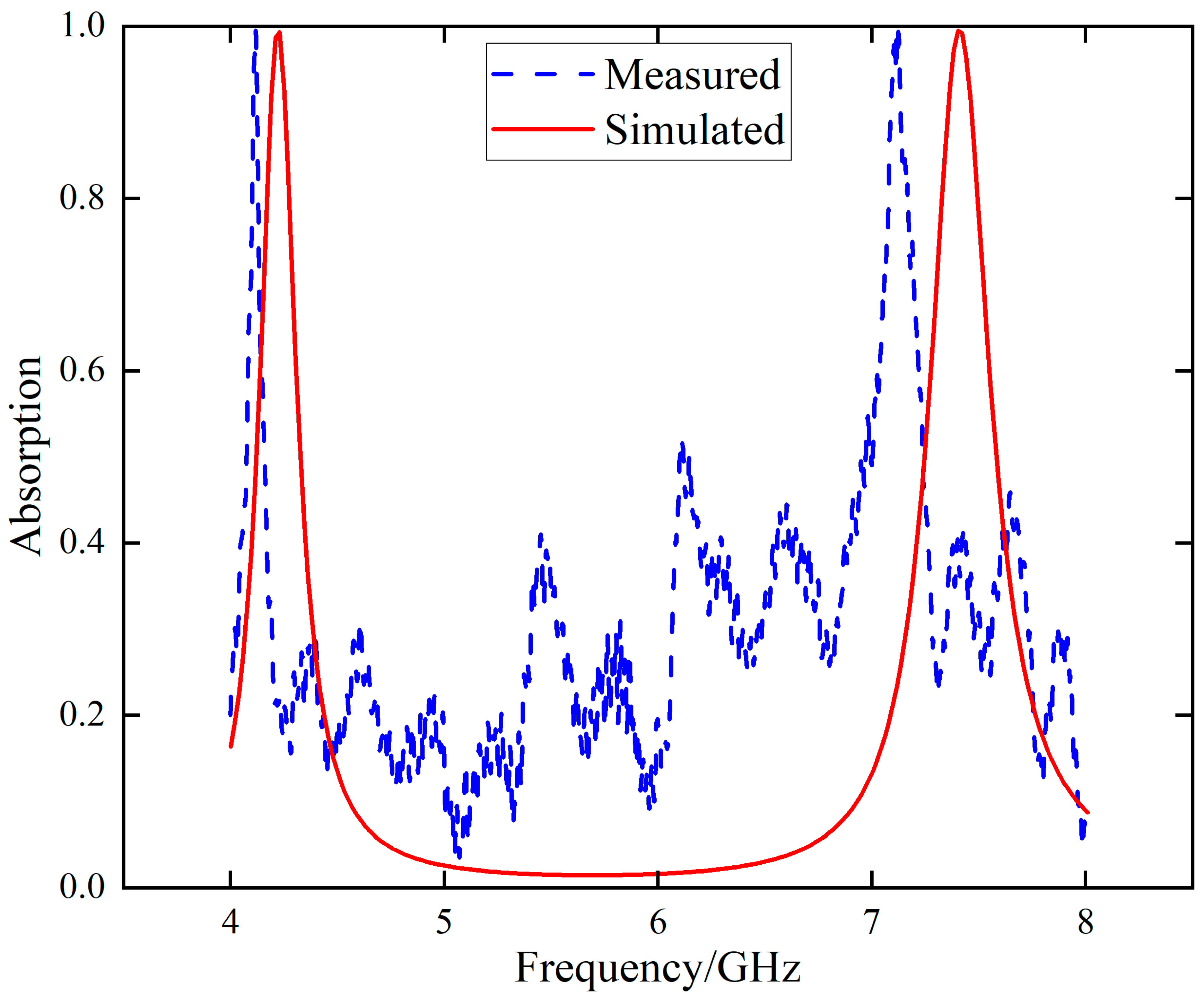
| First Absorption peak/GHz | 4.230 | 4.120 | 4.109 | 4.109 | 4.116 | 4.149 |
| Second Absorption peak/GHz | 7.403 | 7.123 | 7.121 | 7.124 | 7.121 | 7.126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Gu, M.; Feng, G.; Zheng, M.; Zhao, T.; Jing, X. Design of a Polarization-Insensitive and Wide-Angle Triple-Band Metamaterial Absorber. Photonics 2025, 12, 386. https://doi.org/10.3390/photonics12040386
Zheng S, Gu M, Feng G, Zheng M, Zhao T, Jing X. Design of a Polarization-Insensitive and Wide-Angle Triple-Band Metamaterial Absorber. Photonics. 2025; 12(4):386. https://doi.org/10.3390/photonics12040386
Chicago/Turabian StyleZheng, Shaoxin, Manna Gu, Guilan Feng, Mingfeng Zheng, Tianqi Zhao, and Xufeng Jing. 2025. "Design of a Polarization-Insensitive and Wide-Angle Triple-Band Metamaterial Absorber" Photonics 12, no. 4: 386. https://doi.org/10.3390/photonics12040386
APA StyleZheng, S., Gu, M., Feng, G., Zheng, M., Zhao, T., & Jing, X. (2025). Design of a Polarization-Insensitive and Wide-Angle Triple-Band Metamaterial Absorber. Photonics, 12(4), 386. https://doi.org/10.3390/photonics12040386





