Improving the Hydrodynamic Performance of Underwater Tags for Blue Shark Monitoring
Abstract
:1. Introduction
2. Materials and Methods
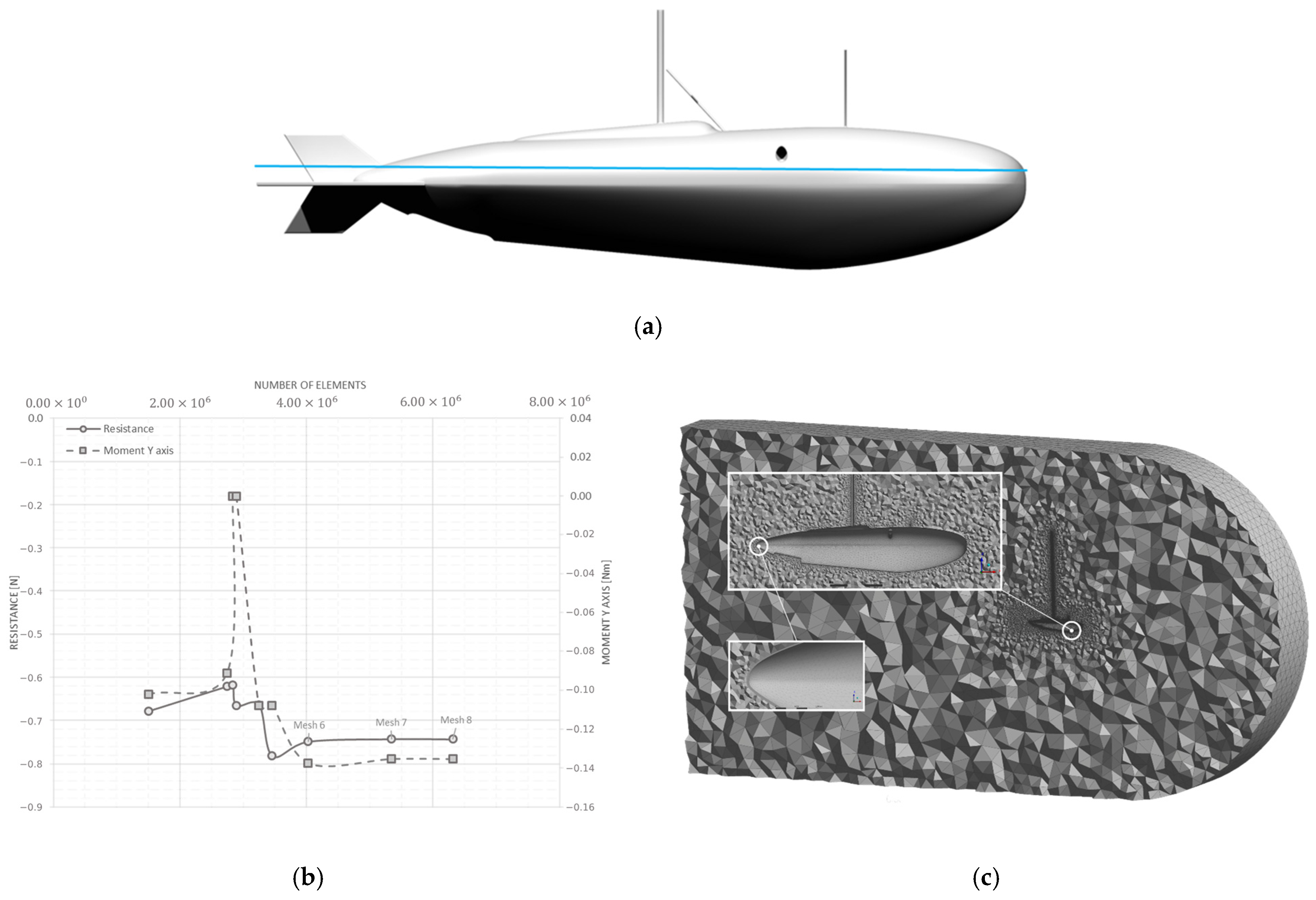
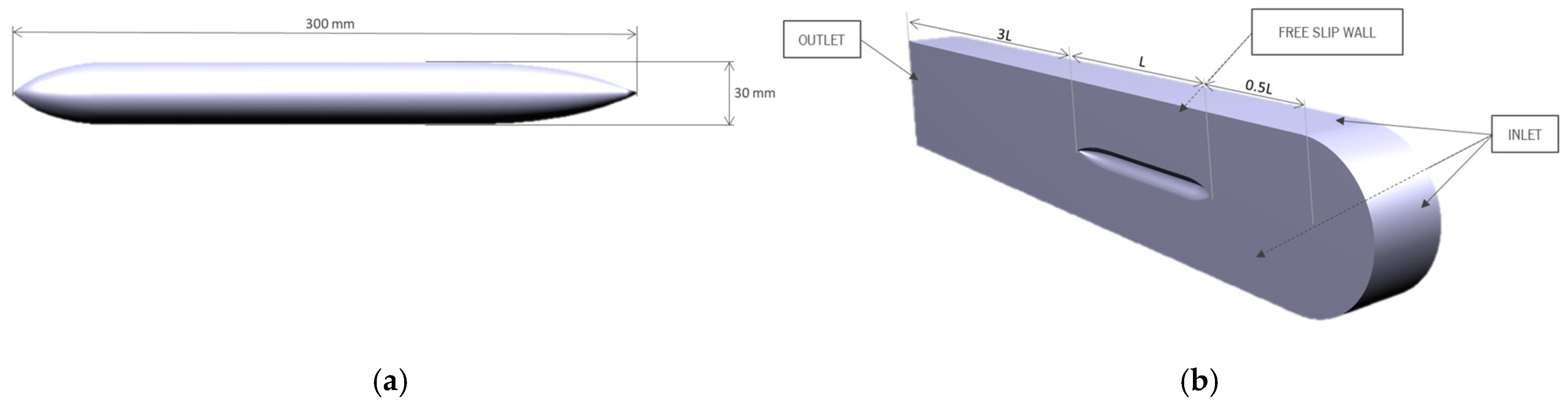
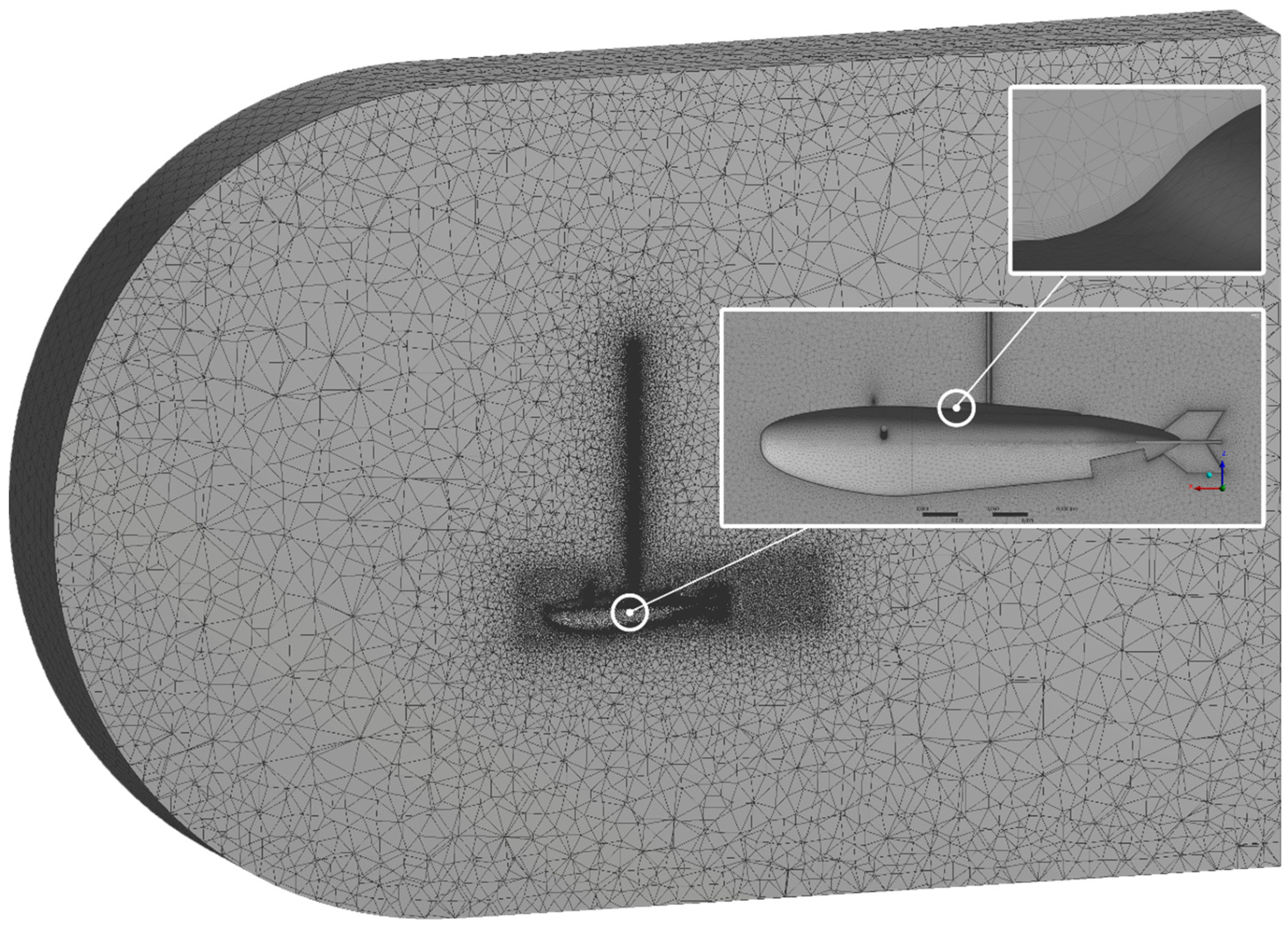
2.1. Geometry and Mesh
2.2. Governing Equations
2.3. Boundary Conditions and Fluid Properties
3. Numerical Model Validation
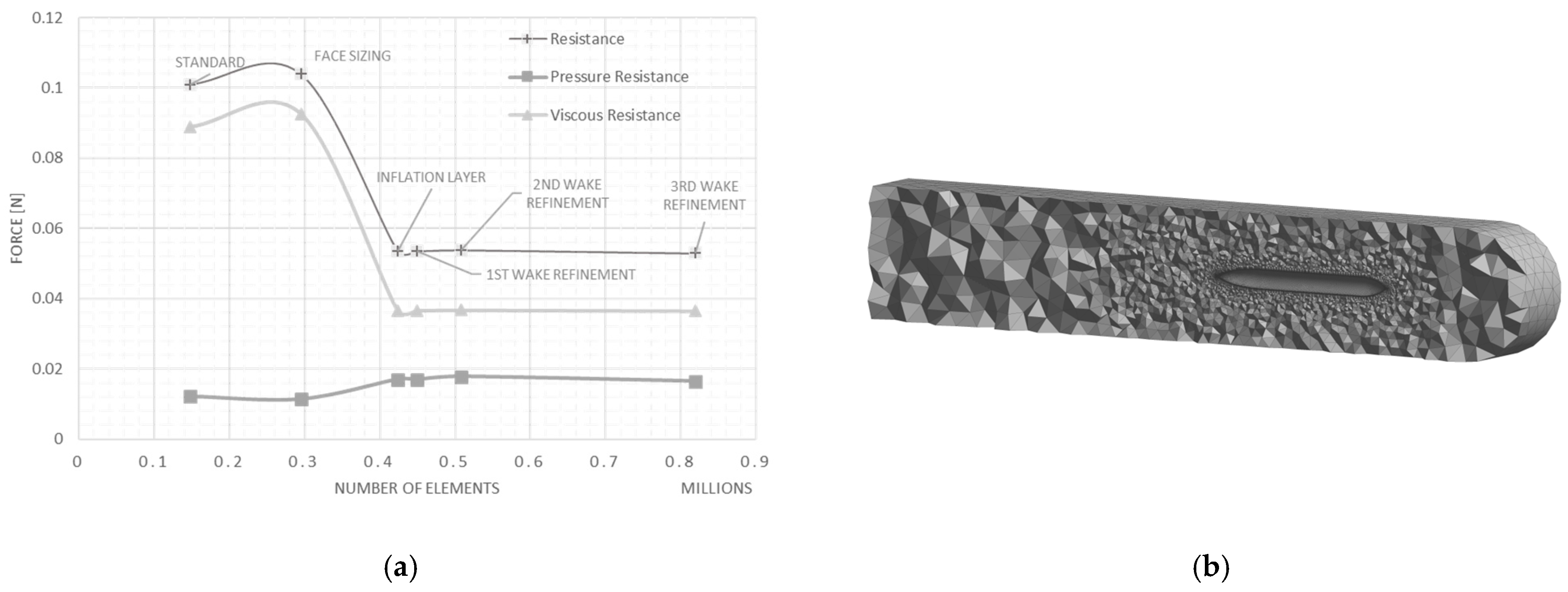
3.1. Geometry and Mesh
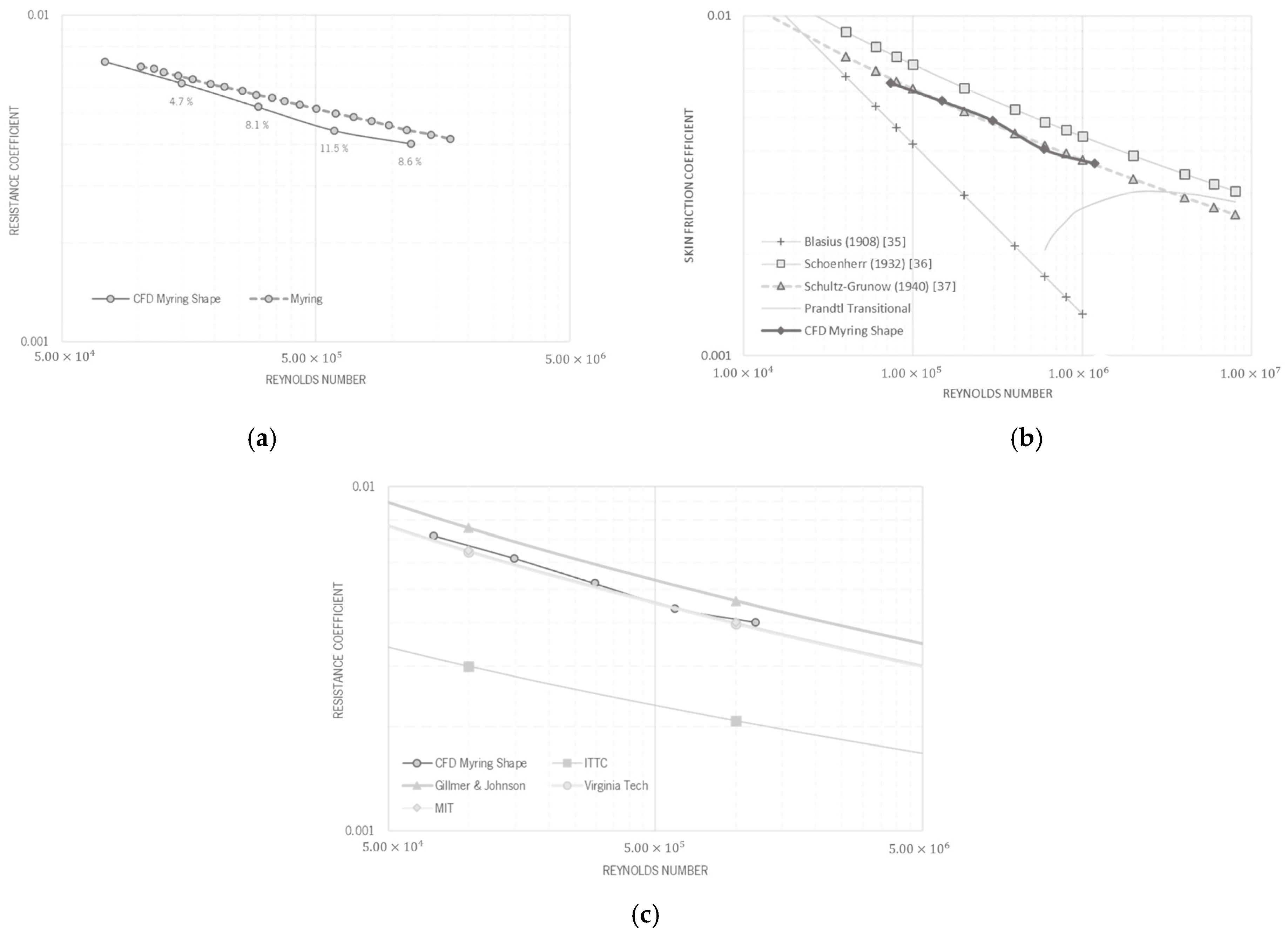
3.2. Validation Results
4. Results and Discussion
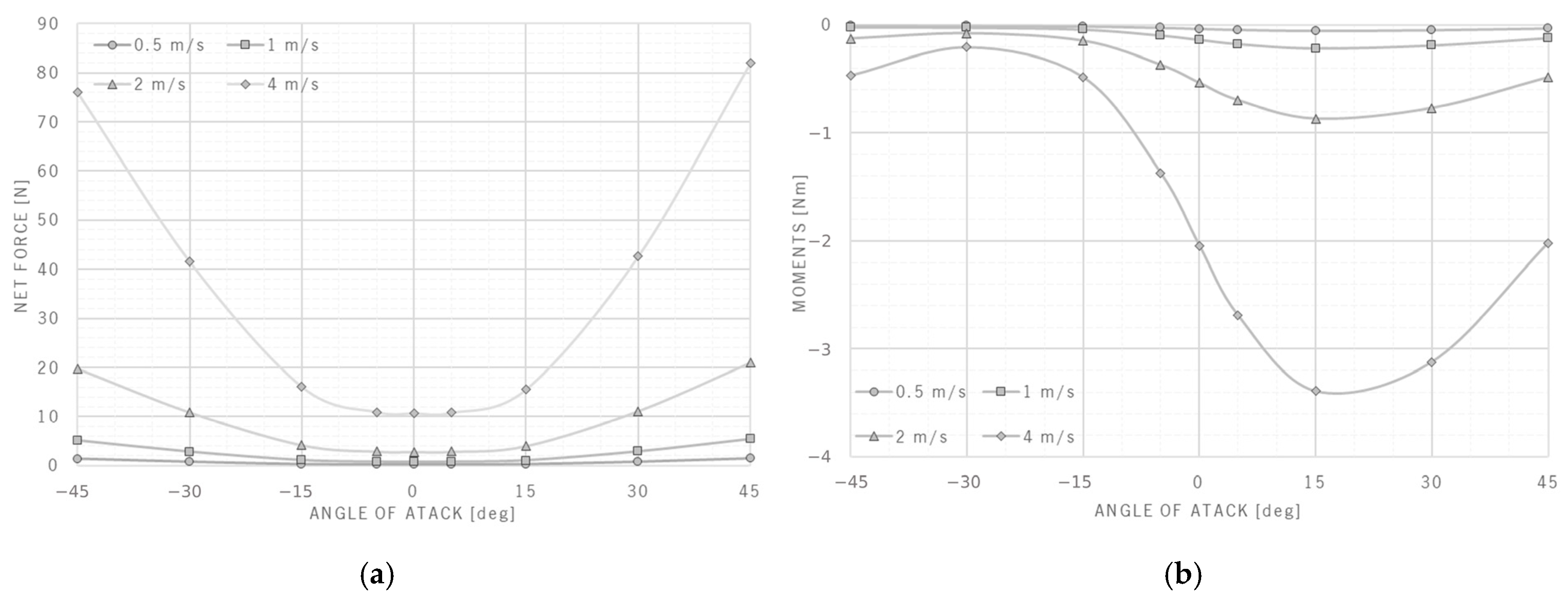
4.1. Motion and Drag
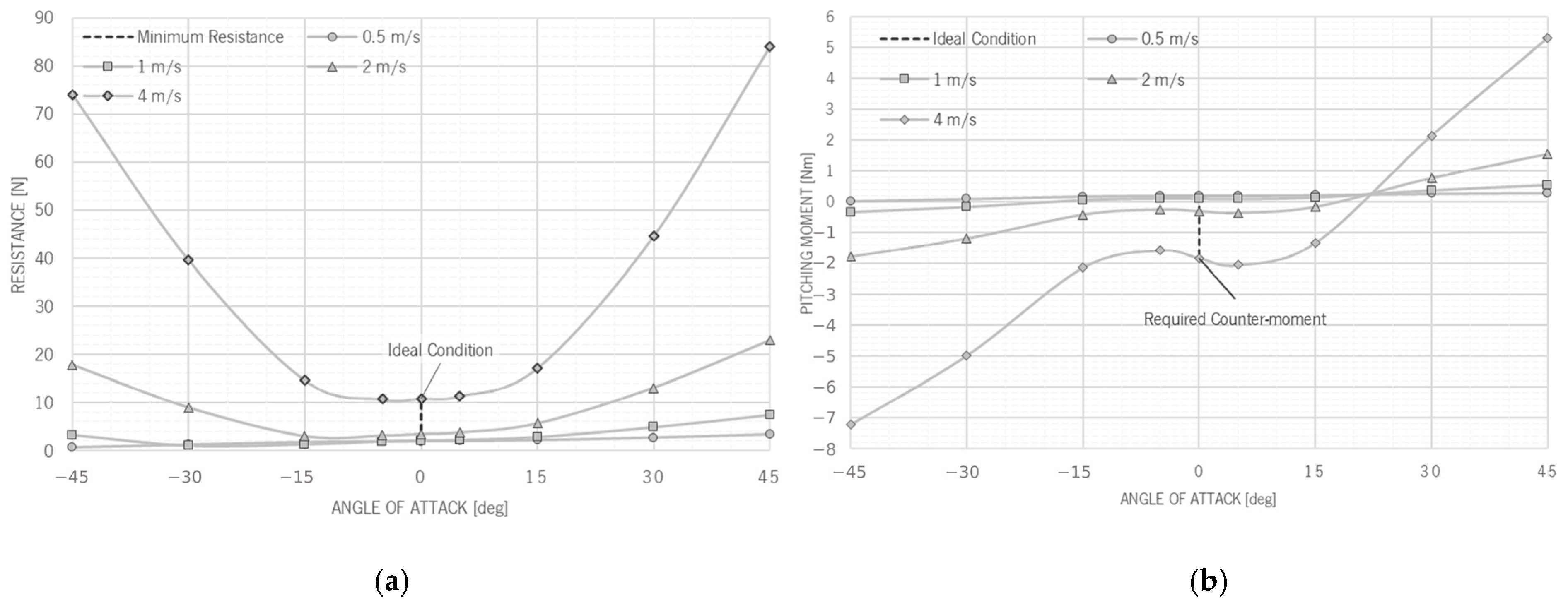
4.2. Assessment of the Operation Attitude
5. Improved Design
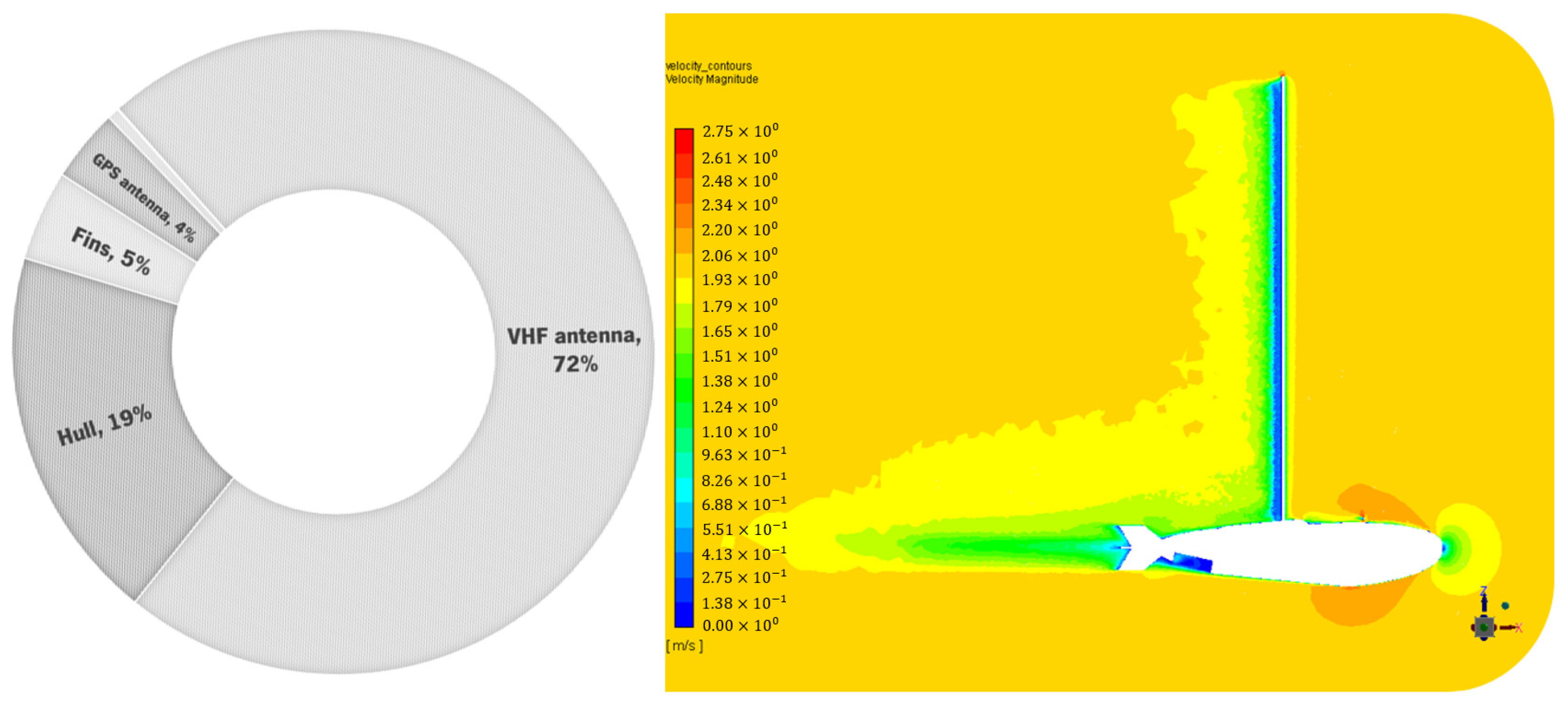
5.1. Design of Stabilizing Elements
5.2. Improved Tag Concept
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hammerschlag, N.; Gallagher, A.J.; Lazarre, D.M. A review of shark satellite tagging studies. J. Exp. Mar. Biol. Ecol. 2011, 398, 1–8. [Google Scholar] [CrossRef]
- Witt, M.J.; Doherty, P.D.; Godley, B.J.; Graham, R.T.; Hawkes, L.A.; Henderson, S.M. Basking Shark Satellite Tagging Project: Insights into Basking Shark (Cetorhinus maximus) Movement, Distribution and Behaviour Using Satellite Telemetry; Final Report; Scottish Natural Heritage: Stirling, Scotland, 2016; 72p.
- Cooke, S.J.; Hinch, S.G.; Wikelski, M.; Andrews, R.D.; Kuchel, L.J.; Wolcott, T.G.; Butler, P.J. Biotelemetry: A mechanistic approach to ecology. Trends Ecol. Evol. 2004, 19, 334–343. [Google Scholar] [CrossRef]
- Cooke, S.J.; Midwood, J.D.; Thiem, J.D.; Klimley, P.; Lucas, M.C.; Thorstad, E.B.; Eiler, J.; Holbrook, C.; Ebner, B.C. Tracking animals in freshwater with electronic tags: Past, present and future. Anim. Biotelem. 2013, 1, 5. [Google Scholar] [CrossRef]
- Pouca, C.P.V. High-Resolution Diving Behaviour of Satellite Tagged Blue Sharks under Different Oceanographic Gradients. Master’s Thesis, Universidade do Porto, Porto, Portugal, 2012. [Google Scholar]
- Queiroz, N.; Humphries, N.E.; Noble, L.R.; Santos, A.M.; Sims, D.W. Spatial dynamics and expanded vertical niche of blue sharks in oceanographic fronts reveal habitat targets for conservation. PLoS ONE 2012, 7, e32374. [Google Scholar] [CrossRef]
- Nielsen, J.L.; Arrizabalaga, H.; Fragoso, N.; Hobday, A.; Lutcavage, M.; Sibert, J. (Eds.) Reviews: Methods and Technologies in Fish Biology and Fisheries; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Ahuekwe, E.F.; Isibor, P.O.; Akinduti, P.A.; Salami, A.O.; Onuselogu, C.C.; Oshamika, O.O.; Oyesola, O.L.; Ichor, T.; Ezekiel, O.M.; Oziegbe, O.; et al. Application of Nanochitosan in Tagging and Nano-Barcoding of Aquatic and Animal Meats; Adetunji, C., Hefft, D., Jeevanandam, J., Danquah, M.B.T.-N.G.N., Eds.; Academic Press: New York, NY, USA, 2023; pp. 483–498. [Google Scholar] [CrossRef]
- Baeyaert, J.; Graça, G.; Sobral, A.; Prieto, R.; Afonso, P.; Fontes, J. EcoDive Azores—Summer Season—Short Report. 2016. Available online: https://www.researchgate.net/publication/318724014_EcoDive_Azores_-_Summer_Season_2016_Short_Report (accessed on 10 April 2024).
- Grusha, D.S.; Patterson, M.R. Quantification of drag and lift imposed by pop-up satellite archival tags and estimation of the metabolic cost to cownose rays (Rhinoptera bonasus). Fish. Bull. 2005, 103, 63–70. [Google Scholar]
- Arai, N.; Okuyama, J. Biologging. In Field Informatics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 21–38. [Google Scholar] [CrossRef]
- Domeier, M.L.; Nasby-Lucas, N. Two-year migration of adult female white sharks (Carcharodon carcharias) reveals widely separated nursery areas and conservation concerns. Anim. Biotelem. 2013, 1, 2. [Google Scholar] [CrossRef]
- Trotter, A.W.; Rathjens, L.; Schmiegel, S.; Mews, S.; Cowley, P.D.; Gennari, E. Short-term effects of standard procedures associated with surgical transmitter implantation on a benthic shark species requiring anaesthesia. Fish. Res. 2024, 270, 106880. [Google Scholar] [CrossRef]
- Gleiss, A.C.; Norman, B.; Liebsch, N.; Francis, C.; Wilson, R.P. A new prospect for tagging large free-swimming sharks with motion-sensitive data-loggers. Fish. Res. 2009, 97, 11–16. [Google Scholar] [CrossRef]
- Hazekamp, A.A.H.H.; Mayer, R.; Osinga, N. Flow simulation along a seal: The impact of an external device. Eur. J. Wildl. Res. 2010, 56, 131–140. [Google Scholar] [CrossRef]
- Zhang, D.Y.; Luo, Y.H.; Li, X.; Chen, H.W. Numerical simulation and experimental study of drag-reducing surface of a real shark skin. J. Hydrodyn. 2011, 23, 204–211. [Google Scholar] [CrossRef]
- Shaari, M.F. Drag Analysis of Contractile Water Jet Locomoted Micro AUV in Laminar Fluid. Appl. Mech. Mater. 2015, 799, 1188–1192. [Google Scholar] [CrossRef]
- Cheng, B.; Qin, D.; Hu, Z. Research on the propulsion motor cooling by the coupled flow field of unmanned underwater vehicles. Appl. Therm. Eng. 2024, 237, 121797. [Google Scholar] [CrossRef]
- Liu, B.; Xu, X.; Pan, D. Resistance reduction optimization of an amphibious transport vehicle. Ocean Eng. 2023, 280, 114854. [Google Scholar] [CrossRef]
- Karim, M.; Rahman, M.; Alim, A. Numerical computation of viscous drag for axisymmetric underwater vehicles. J. Mek. 2018, 26, 9–21. [Google Scholar]
- Pan, Y.; Zhang, H.; Zhou, Q. Numerical prediction of submarine hydrodynamic coefficients using CFD simulation. J. Hydrodyn. Ser. B 2012, 24, 840–847. [Google Scholar] [CrossRef]
- Myring, D.F. A Theoretical Study of Body Drag in Subcritical Axisymmetric Flow. Aeronaut. Q. 1976, 27, 186–194. [Google Scholar] [CrossRef]
- Bartolomeu, T.C. Hydrodynamic Optimization of a Torpedo-Shaped Hull. Ph.D. Thesis, Universidade da Beira Interior, Covilhã, Portugal, 2016. [Google Scholar]
- Wang, J.; Cui, Z. Modeling and experiment validation of a seawater micro hydropower system for marine animal telemetry tag. Renew. Energy 2021, 174, 73–85. [Google Scholar] [CrossRef]
- Wang, G. Machine Learning for Inferring Animal Behavior from Location and Movement Data. Ecol. Inform. 2019, 49, 69–76. [Google Scholar] [CrossRef]
- Thiede, S.; Ghafoorpoor, P.; Sullivan, B.P.; Bienia, S.; Demes, M.; Dröder, K. Potentials and Technical Implications of Tag Based and AI Enabled Optical Real-Time Location Systems (RTLS) for Manufacturing Use Cases. CIRP Ann. 2022, 71, 401–404. [Google Scholar] [CrossRef]
- Szpilman, M. Tubarões no Brasil: Guia Prático de Identificação; Mauad Editora Ltd.a: Rio de Janeiro, Brazil, 2004. [Google Scholar]
- Stevens, J. Prionace glauca, Blue Shark, IUCN Red List Threat. Species 2009, 11. [Google Scholar] [CrossRef]
- Geng, Z.; Wang, Y.; Kindong, R.; Zhu, J.; Dai, X. Demographic and harvest analysis for blue shark (Prionace glauca) in the Indian Ocean. Reg. Stud. Mar. Sci. 2021, 41, 101583. [Google Scholar] [CrossRef]
- Azevedo, J.; Bartolomeu, T.; Teixeira, S.; Teixeira, J.C. Design Concept of a Non-invasive Tagging Device for Blue Sharks José. In International Conference Innovation in Engineering; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Moonesun, M.; Korol, Y.M.; Dalayeli, H. CFD analysis on the bare hull form of submarines for minimizing the resistance. Int. J. Marit. Technol. 2015, 3, 1–16. [Google Scholar]
- ITTC. Recommended Procedures—Fresh water and Seawater Properties. Proc. ITTC—Section 7.5-02-01-03. 2011. Available online: https://www.ittc.info/media/7989/75-02-01-03.pdf (accessed on 10 April 2024).
- Fluent. ANSYS Fluent 12.0 User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2009; Volume 15317, pp. 1–2498. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Pearson Education Limited: Edinburgh, UK, 2007. [Google Scholar] [CrossRef]
- Blasius, H. Grenzschischten in Flussigkeiten mit Kleiner Reibung, 1908; Translated into NACA Technical Memorandum 1256 as the Boundary Layer in Fluids with Little Friction. 1950. Available online: https://ntrs.nasa.gov/citations/20050028493 (accessed on 10 April 2024).
- Schoenherr, K.E. Resistance of Flat Surfaces Moving through a Fluid. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 1932. [Google Scholar]
- Shultz-Grunow, F. New Frictional Resistance Law for Smooth Plates; NACA Technical Memorandum 986; National Advisory Commitee for Aeronautics: Washington, DC, USA, 1941.
- Newman, J.N.; Landweber, L. Marine Hydrodynamics. J. Appl. Mech. 1978, 45, 457. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 8th ed.; Academic Press: New York, NY, USA, 2016. [Google Scholar]



| Velocity | Shark Resistance | −15° Angle of Attack | −5° Angle of Attack | 0° Angle of Attack | 5° Angle of Attack | 15° Angle of Attack | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Resistance | Variation | Resistance | Variation | Resistance | Variation | Resistance | Variation | Resistance | Variation | ||
| m s−1 | N | N | % | N | % | N | % | N | % | N | % |
| 0.5 | 0.8 | 0.3 | 36 | 0.2 | 25 | 0.2 | 25 | 0.2 | 25 | 0.3 | 36 |
| 1.0 | 5.3 | 1.1 | 21 | 0.8 | 14 | 0.7 | 14 | 0.8 | 14 | 1.1 | 20 |
| 2.0 | 23.2 | 4.2 | 18 | 2.9 | 13 | 2.8 | 12 | 2.9 | 12 | 4.0 | 17 |
| 4.0 | 98.4 | 16.1 | 17 | 11.0 | 12 | 10.7 | 11 | 10.8 | 11 | 15.6 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azevedo, J.; Carvalho, V.; Bartolomeu, T.; Arieira, A.; Teixeira, S.F.; Teixeira, J.C. Improving the Hydrodynamic Performance of Underwater Tags for Blue Shark Monitoring. Inventions 2024, 9, 48. https://doi.org/10.3390/inventions9030048
Azevedo J, Carvalho V, Bartolomeu T, Arieira A, Teixeira SF, Teixeira JC. Improving the Hydrodynamic Performance of Underwater Tags for Blue Shark Monitoring. Inventions. 2024; 9(3):48. https://doi.org/10.3390/inventions9030048
Chicago/Turabian StyleAzevedo, José, Violeta Carvalho, Tiago Bartolomeu, Ana Arieira, Senhorinha F. Teixeira, and José C. Teixeira. 2024. "Improving the Hydrodynamic Performance of Underwater Tags for Blue Shark Monitoring" Inventions 9, no. 3: 48. https://doi.org/10.3390/inventions9030048
APA StyleAzevedo, J., Carvalho, V., Bartolomeu, T., Arieira, A., Teixeira, S. F., & Teixeira, J. C. (2024). Improving the Hydrodynamic Performance of Underwater Tags for Blue Shark Monitoring. Inventions, 9(3), 48. https://doi.org/10.3390/inventions9030048











