Adaptive Neural Fault-Tolerant Control for Nonlinear Fractional-Order Systems with Positive Odd Rational Powers
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
- (1)
- All the signals in the FNS with PORP are proven to be bounded.
- (2)
- The tracking error can be able to tend to a small neighborhood near the origin.
3. Design of Controller
- (1)
- All signals of the FNS with PORP are bounded.
- (2)
- The FNS with PORP output signal can track the reference signal.
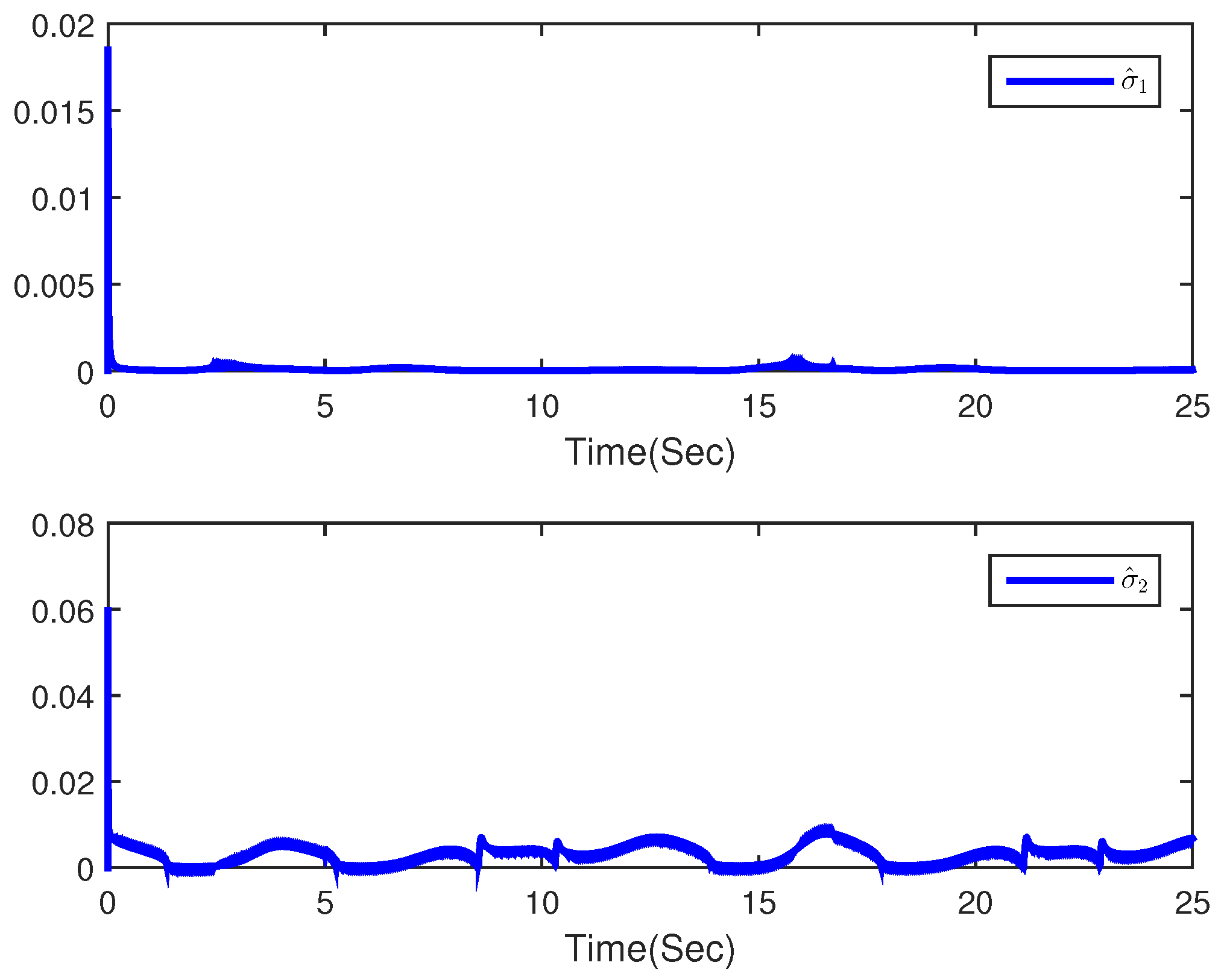
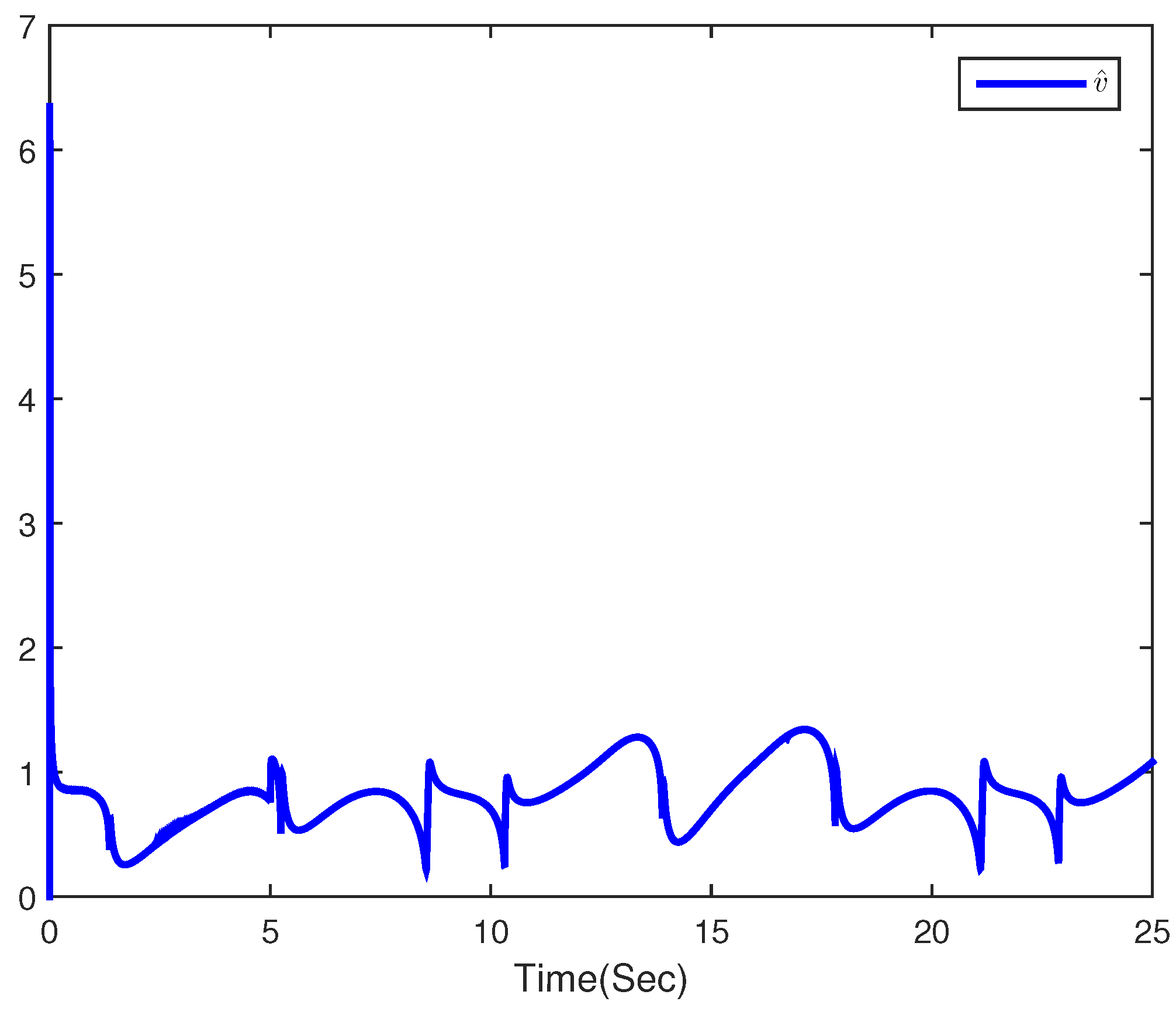
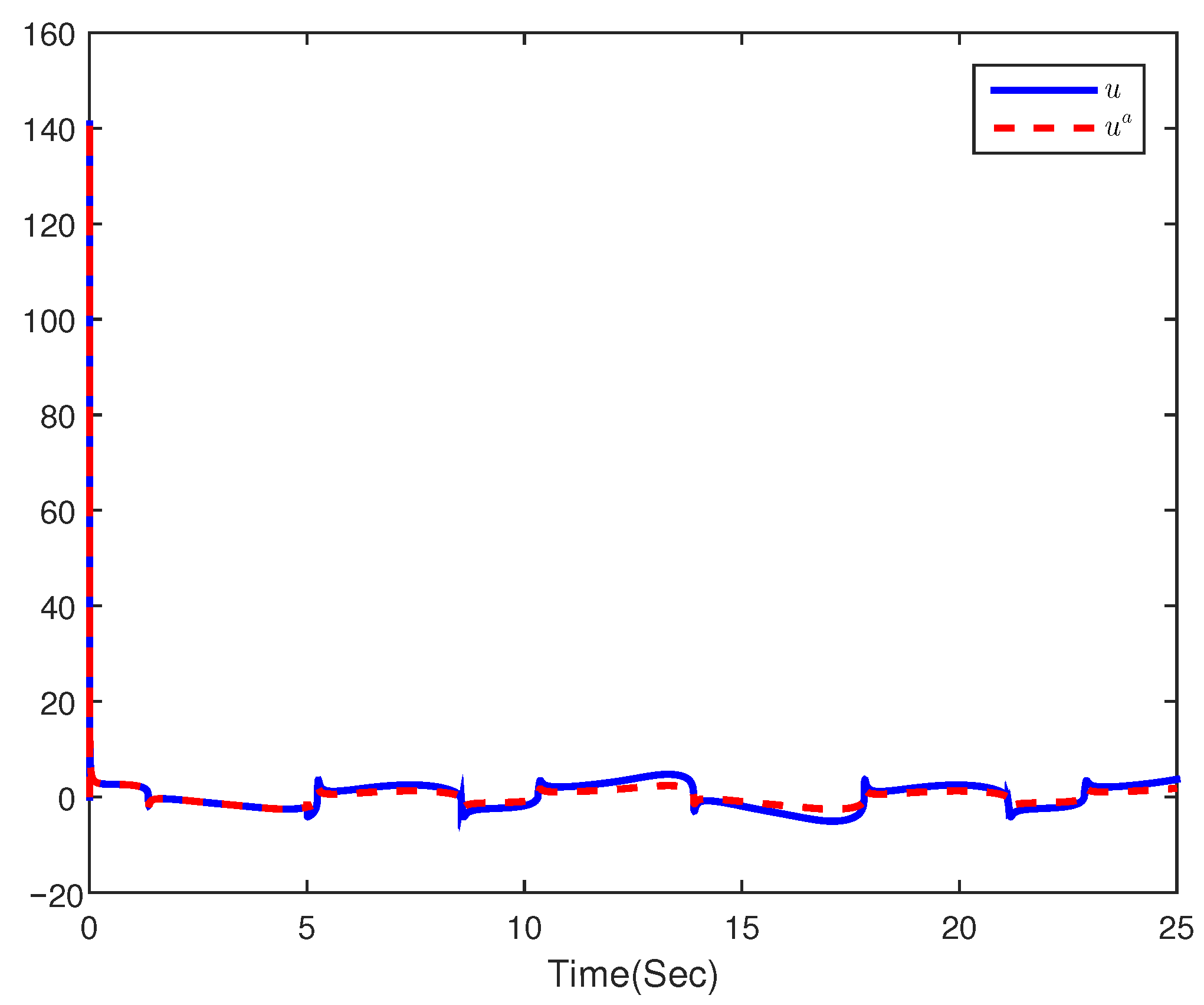
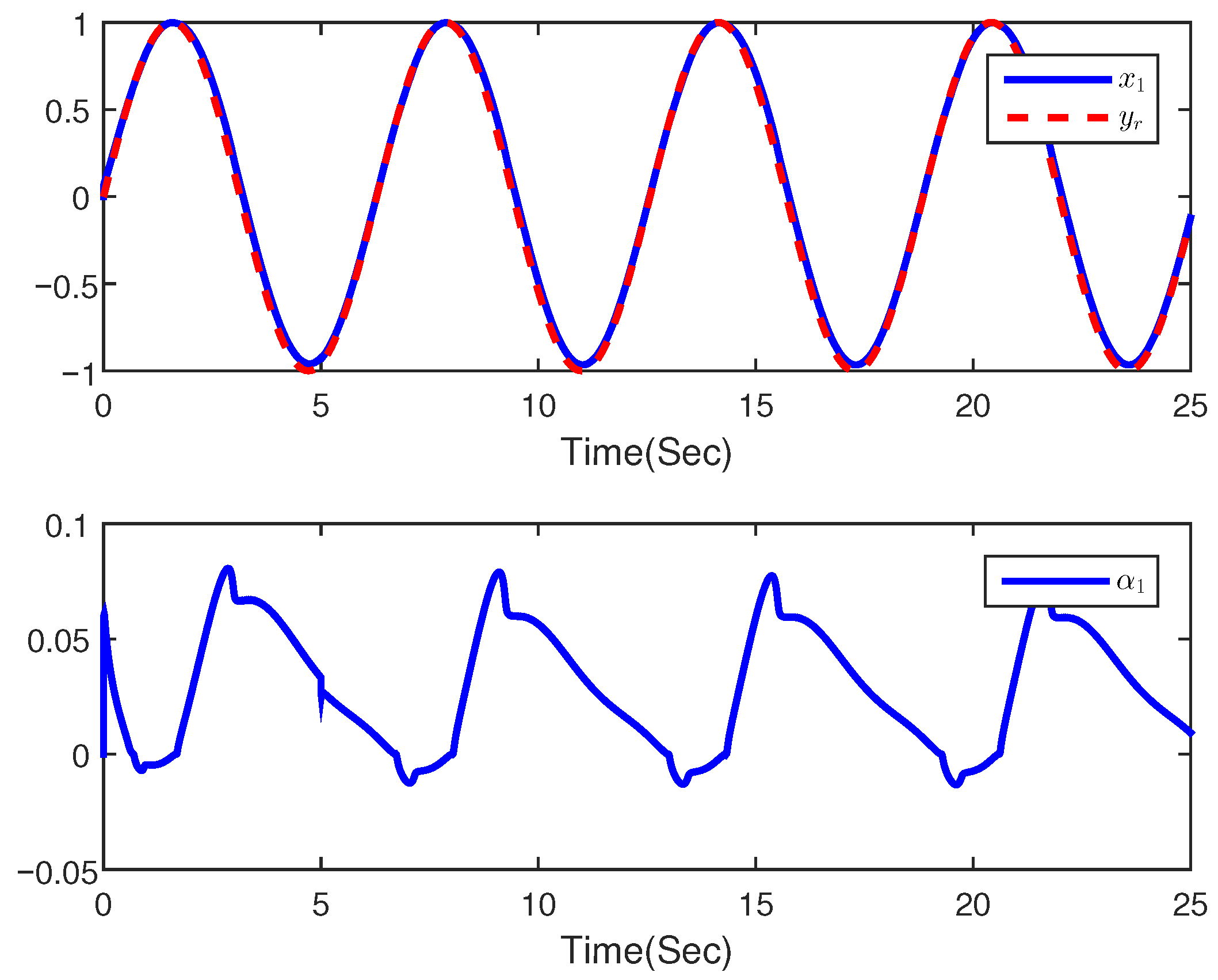
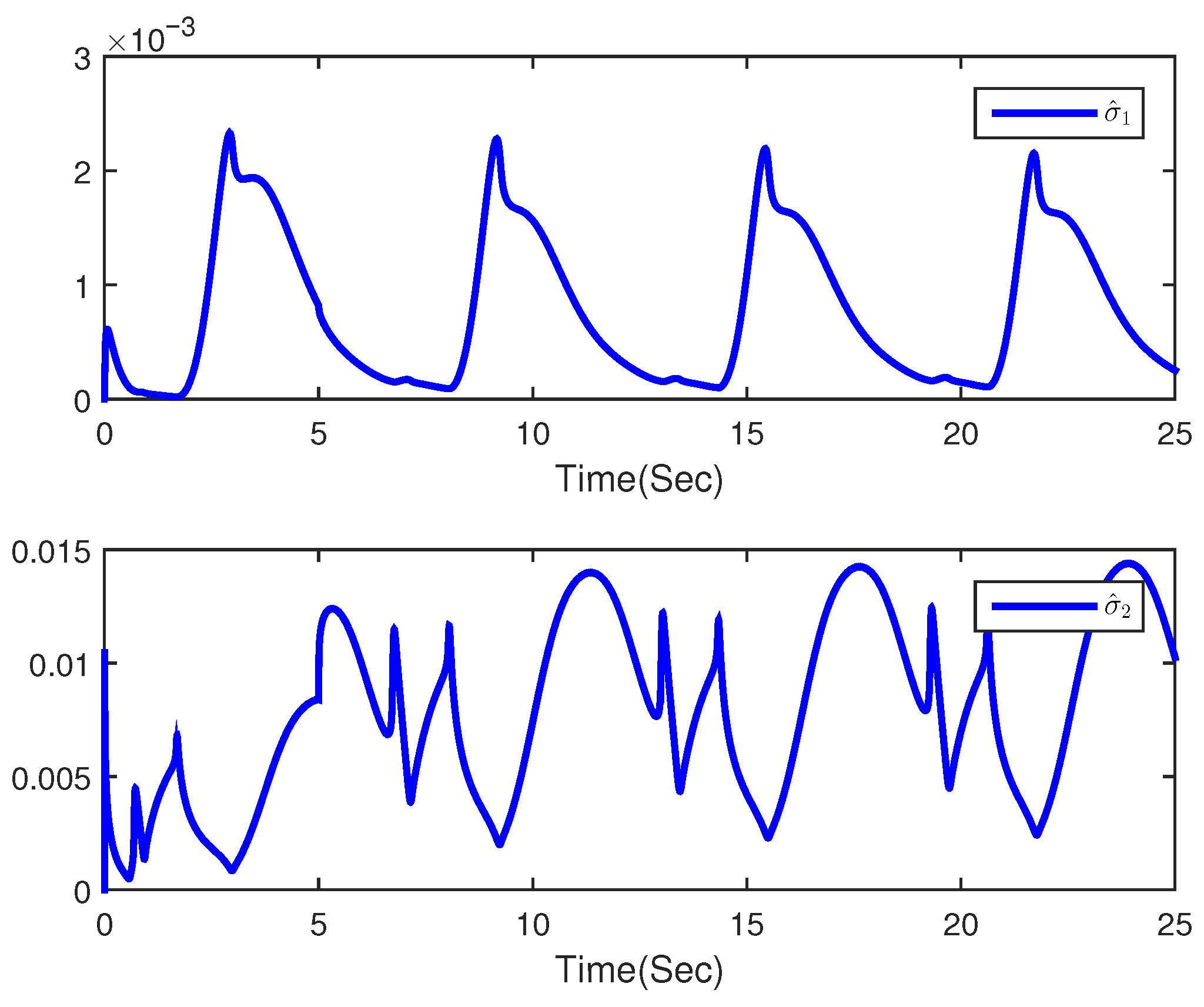
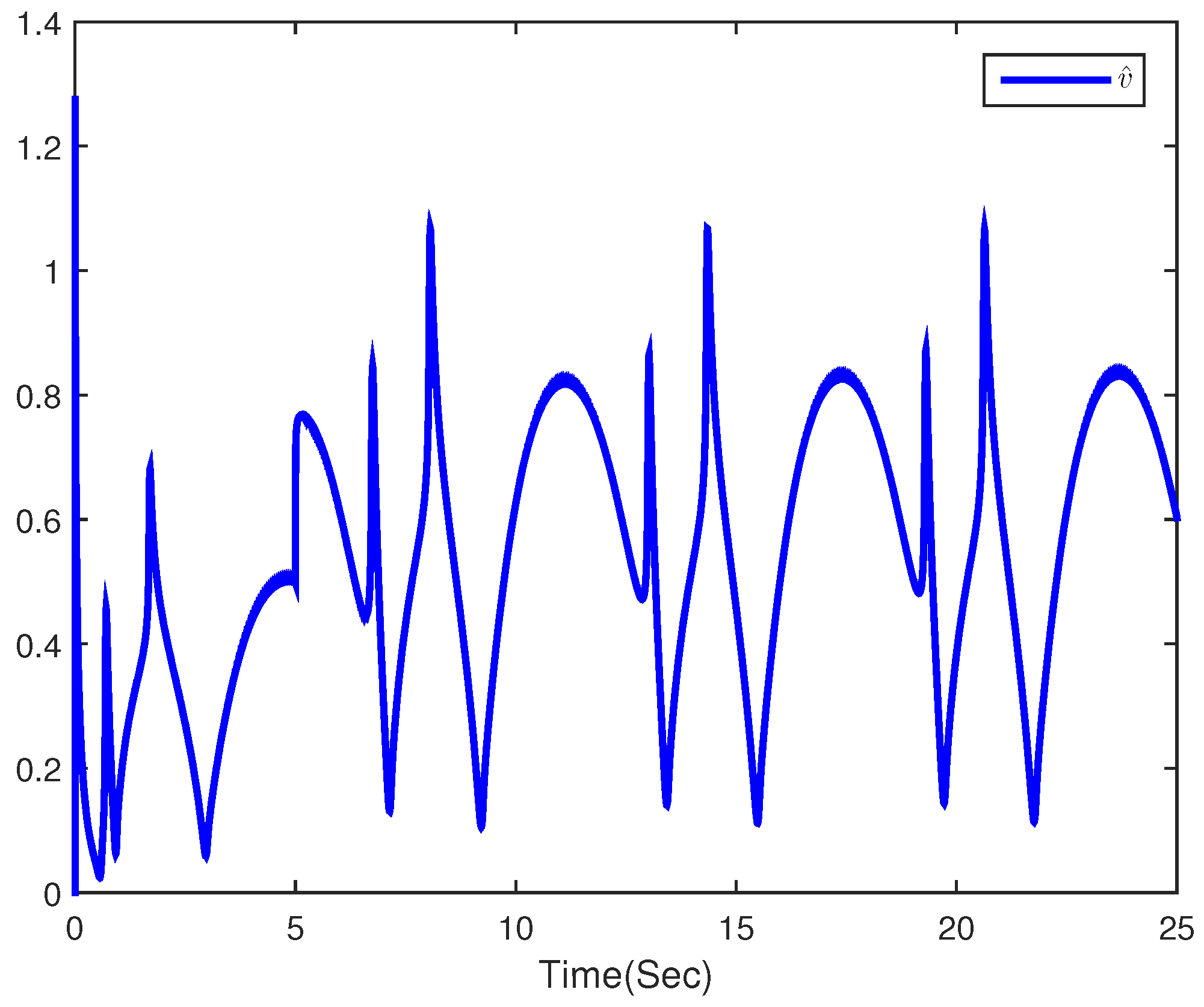
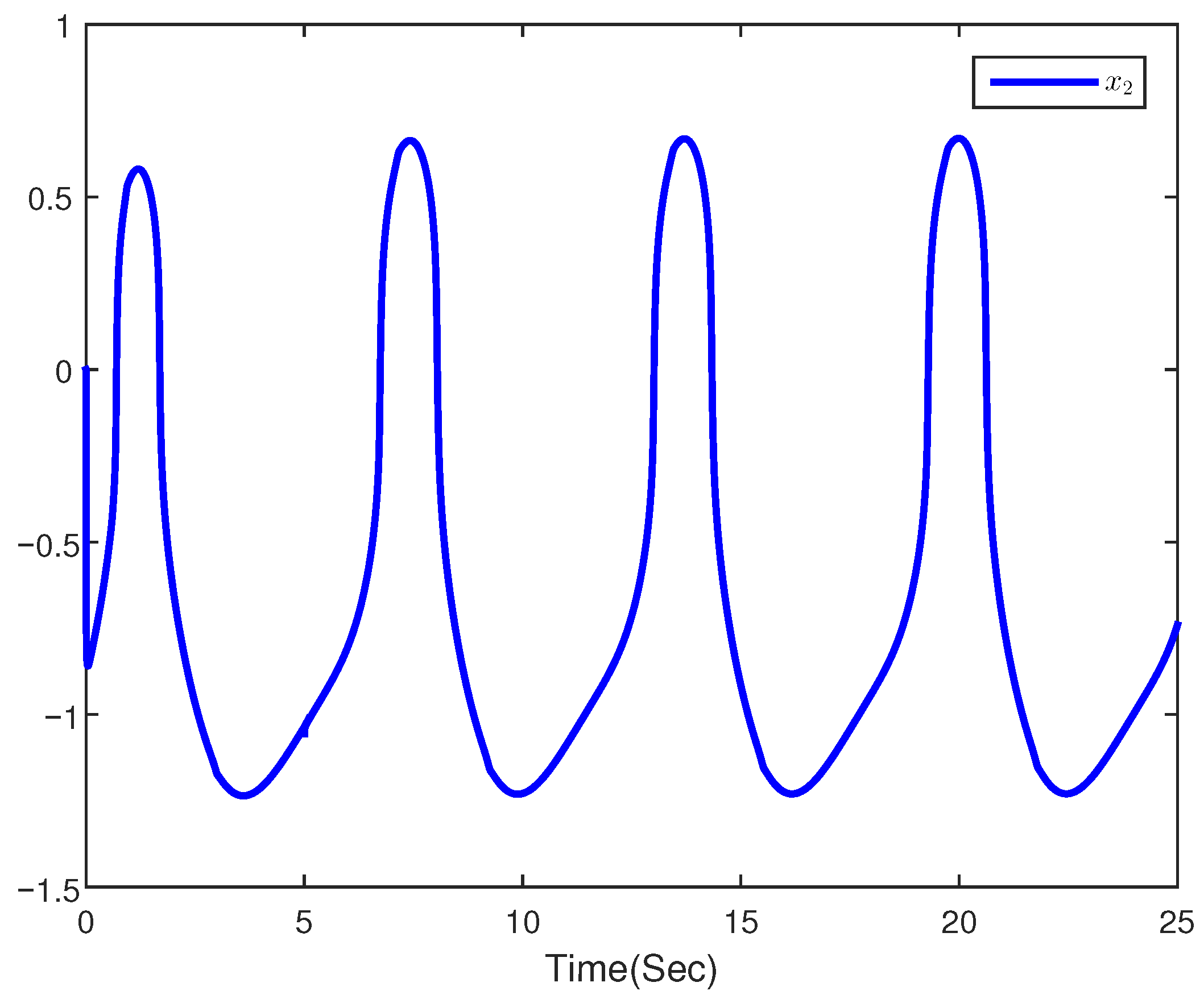
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Differ. Appl. 2001, 5, 230–237. [Google Scholar]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2004, 50, 547–551. [Google Scholar] [CrossRef]
- Shen, J.; Lam, J. Stability and performance analysis for positive fractional-order systems with time-varying delays. IEEE Trans. Autom. Control 2016, 61, 2676–2681. [Google Scholar] [CrossRef]
- Zhao, X.; Yin, Y.; Zheng, X. State-dependent switching control of switched positive fractional-order systems. ISA Trans. 2016, 62, 103–108. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, S.E.; Moura, S.J.; Peng, H. State-of-charge estimation for lithium-ion batteries based on a nonlinear fractional model. IEEE Trans. Control Syst. Technol. 2017, 25, 3–11. [Google Scholar] [CrossRef]
- Zheng, S. Robust stability of fractional order system with general interval uncertainties. Syst. Control Lett. 2017, 99, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. 2014, 19, 2951–2958. [Google Scholar] [CrossRef]
- Aghababa, M.P. Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller. Commun. Nonlinear Sci. Numer. Simul. 2012, 1, 2670–2681. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Y.; Liang, S.; Wang, Y. A novel algorithm on adaptive backstepping control of fractional order systems. Neurocomputing 2015, 1, 395–402. [Google Scholar] [CrossRef]
- Wei, Y.; Peter, T.; Yao, Z.; Wang, Y. Adaptive backstepping output feedback control for a class of nonlinear fractional order systems. Nonlinear Dyn. 2016, 1, 1047–1056. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 1, 437–445. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, S.; Liu, F.; Xie, Y. Adaptive output feedback control for fractional-order multi-agent systems. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.Y.; Zheng, S.Q.; Ahn, C.K.; Liu, F. Adaptive fuzzy control for fractional-order interconnected systems with unknown control directions. IEEE Trans. Fuzzy Syst. 2022, 30, 75–87. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [PubMed]
- Li, R.C.; Zhang, X.F. Adaptive sliding mode observer design for a class of T-S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 2020, 28, 1951–1959. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L. Normalization and stabilization for rectangular singular fractional order T-S fuzzy systems. Fuzzy Sets Syst. 2020, 38, 140–153. [Google Scholar] [CrossRef]
- Zhang, X.F. Relationship between integer order systems and fractional order systems and Its two applications. IEEE-CAA J. Autom. Sin. 2018, 5, 539–643. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0 < α < 2. IEEE Trans. Circuit Syst. II-Express 2020, 67, 3237–3241. [Google Scholar]
- Zhang, X.F.; Huang, W.K. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Xie, R.M.; Guo, C.; Xie, X.J. Asymptotic tracking control of state-constrained nonlinear systems with time-varying powers. IEEE Trans. Cybern. 2022, 52, 4073–4078. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Qian, C. Adding one power integrator: A tool for global stabilization of high-order lower-triangular systems. Syst. Control Lett. 2000, 39, 339–351. [Google Scholar] [CrossRef]
- Wang, H.Q.; Chen, M.; Liu, X.P. Fuzzy adaptive fixed-time quantized feedback control for a class of nonlinear systems. Acta Autom. Sin. 2021, 47, 2823–2830. [Google Scholar]
- Wang, H.Q.; Xu, K.; Liu, X.P.; Qiao, J.F. Adaptive fuzzy fast finite-time dynamic surface tracking control for nonlinear systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4337–4348. [Google Scholar] [CrossRef]
- Wang, H.Q.; Kang, S.J.; Zhao, X.D.; Xu, N.; Li, T.S. Command filter-based adaptive neural control design for nonstrict-feedback nonlinear systems with multiple actuator constraints. IEEE Trans. Cybern. 2021, 68, 1–10. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liu, P.X.P.; Bao, J.L.; Xie, X.J. Adaptive neural output-feedback decentralized control for large-scale nonlinear systems with stochastic disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 972–983. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, Q.G.; Ding, W. Global output-feedback prescribed performance control of nonlinear systems with unknown virtual control coefficients. IEEE Trans. Autom. Control 2021. Early Access. [Google Scholar] [CrossRef]
- Wang, H.Q.; Ling, S.; Liu, P.X.P.; Li, Y.X. Control of high-order nonlinear systems under error-to-actuator based event-triggered framework. Int. J. Control 2022, 95, 2758–2770. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Wen, G.X.; Liu, Y.J.; Liu, Z. Observer-based adaptive backstepping consensus tracking control for high-order nonlinear semi-strict-feedback multiagent systems. IEEE Trans. Cybern. 2015, 46, 1591–1601. [Google Scholar] [CrossRef]
- Jiang, M.M.; Xie, X.J.; Zhang, K. Finite-time stabilization of stochastic high-order nonlinear systems with FT-SISS inverse dynamics. IEEE Trans. Autom. Control 2019, 64, 313–320. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liu, S.W.; Wang, D.; Niu, B.; Chen, M. Adaptive neural tracking control of high-order nonlinear systems with quantized input. Neurocomputing 2021, 456, 156–167. [Google Scholar] [CrossRef]
- Tong, S.; Li, K.; Li, Y. Robust fuzzy adaptive finite-time control for high-order nonlinear systems with unmodeled dynamics. IEEE Trans. Fuzzy Syst. 2021, 29, 1576–1598. [Google Scholar] [CrossRef]
- Chen, M.; Tao, G. Adaptive fault-tolerant control of uncertain nonlinear large-scale systems with unknown dead zone. IEEE Trans. Cybern. 2015, 46, 1851–1862. [Google Scholar] [CrossRef]
- Tang, X.; Tao, G.; Joshi, S.M. Adaptive actuator failure compensation for nonlinear mimo systems with an aircraft control application. Automatica 2007, 43, 1869–1883. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C. Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance. Automatica 2010, 1, 2082–2091. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, B.; Cocquempot, V. Fuzzy logic system-based adaptive fault-tolerant control for near-space vehicle attitude dynamics with actuator faults. IEEE Trans. Fuzzy Syst. 2012, 21, 289–300. [Google Scholar] [CrossRef]
- Sun, K.K.; Liu, L.; Qiu, J.B.; Feng, G. Fuzzy adaptive finite-time fault-tolerant control for strict-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 29, 786–796. [Google Scholar] [CrossRef]
- Yang, H.Y.; Jiang, Y.C.; Shen, Y. Adaptive fuzzy fault-tolerant control for markov jump systems with additive and multiplicative actuator faults. IEEE Trans. Fuzzy Syst. 2021, 29, 772–785. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fault-tolerant output-constrained control of unknown Euler-Lagrange systems with prescribed tracking accuracy. Automatica 2020, 111, 108606. [Google Scholar] [CrossRef]
- Zhang, X.F.; Huang, W.K.; Wang, Q.G. Robust H-infinity adaptive sliding mode fault tolerant control for T-S fuzzy fractional order systems with mismatched disturbances. IEEE Trans. Circuit Syst. I-Regul. Pap. 2021, 68, 1297–1307. [Google Scholar] [CrossRef]
- Martinez-Fuentes, O.; Melendez-Vazquez, F.; Martinez-Guerra, R. Fractional-order nonlinear systems with fault tolerance. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar]
- Li, X.M.; Zhan, Y.L.; Tong, S.C. Adaptive neural network decentralized fault-tolerant control for nonlinear interconnected fractional-order systems. Neurocomputing 2022, 488, 14–22. [Google Scholar] [CrossRef]
- Hu, X.R.; Song, Q.; Ge, M.; Li, R.M. Fractional-order adaptive fault-tolerant control for a class of general nonlinear systems. Nonlinear Dyn. 2020, 101, 379–392. [Google Scholar] [CrossRef]
- Benchaita, H.; Ladaci, S. Fractional adaptive SMC fault tolerant control against actuator failures for wing rock supervision. Aerosp. Sci. Technol. 2021, 114, 106745. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.Y. Adaptive Backstepping Control of Uncertain Systems: Nonsmooth Nonlinearities, Interactions or Time-Variations; Springer: Berlin, Germany, 2008. [Google Scholar]
- Qian, C.; Lin, W. Practical output tracking of nonlinear systems with uncontrollable unstable linearization. IEEE Trans. Autom. Control 2021, 47, 21–36. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Liu, S.W.; Wang, H.Q.; Li, T.S. Adaptive composite dynamic surface neural control for nonlinear fractional-order systems subject to delayed input. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]
- Yang, B.; Lin, W. Homogeneous observers, iterative design, and global stabilization of high-order nonlinear systems by smooth output feedback. IEEE Trans. Autom. Control 2004, 49, 1069–1080. [Google Scholar] [CrossRef]
- Sanner, R.M.; Slotine, J.E. Gaussian networks for direct adaptive control. IEEE Trans. Neural Netw. 1992, 3, 837–863. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Wang, H.; Su, Y.; Liu, C.; Chen, M. Adaptive Neural Fault-Tolerant Control for Nonlinear Fractional-Order Systems with Positive Odd Rational Powers. Fractal Fract. 2022, 6, 622. https://doi.org/10.3390/fractalfract6110622
Ma J, Wang H, Su Y, Liu C, Chen M. Adaptive Neural Fault-Tolerant Control for Nonlinear Fractional-Order Systems with Positive Odd Rational Powers. Fractal and Fractional. 2022; 6(11):622. https://doi.org/10.3390/fractalfract6110622
Chicago/Turabian StyleMa, Jiawei, Huanqing Wang, Yakun Su, Cungen Liu, and Ming Chen. 2022. "Adaptive Neural Fault-Tolerant Control for Nonlinear Fractional-Order Systems with Positive Odd Rational Powers" Fractal and Fractional 6, no. 11: 622. https://doi.org/10.3390/fractalfract6110622
APA StyleMa, J., Wang, H., Su, Y., Liu, C., & Chen, M. (2022). Adaptive Neural Fault-Tolerant Control for Nonlinear Fractional-Order Systems with Positive Odd Rational Powers. Fractal and Fractional, 6(11), 622. https://doi.org/10.3390/fractalfract6110622




