Multiple Terms Identification of Time Fractional Diffusion Equation with Symmetric Potential from Nonlocal Observation
Abstract
:1. Introduction
2. Preliminary and Weak Solution of the Direct Problem
2.1. Preliminary
2.2. The Weak Solution of the Direct Problem
3. Uniqueness of the Inverse Problem
4. Numerical Inversion Method
4.1. Numerical Inversion Algorithm Based on Levenberg–Marquardt Method
4.2. Finite Difference Method for Solving the Direct Problem
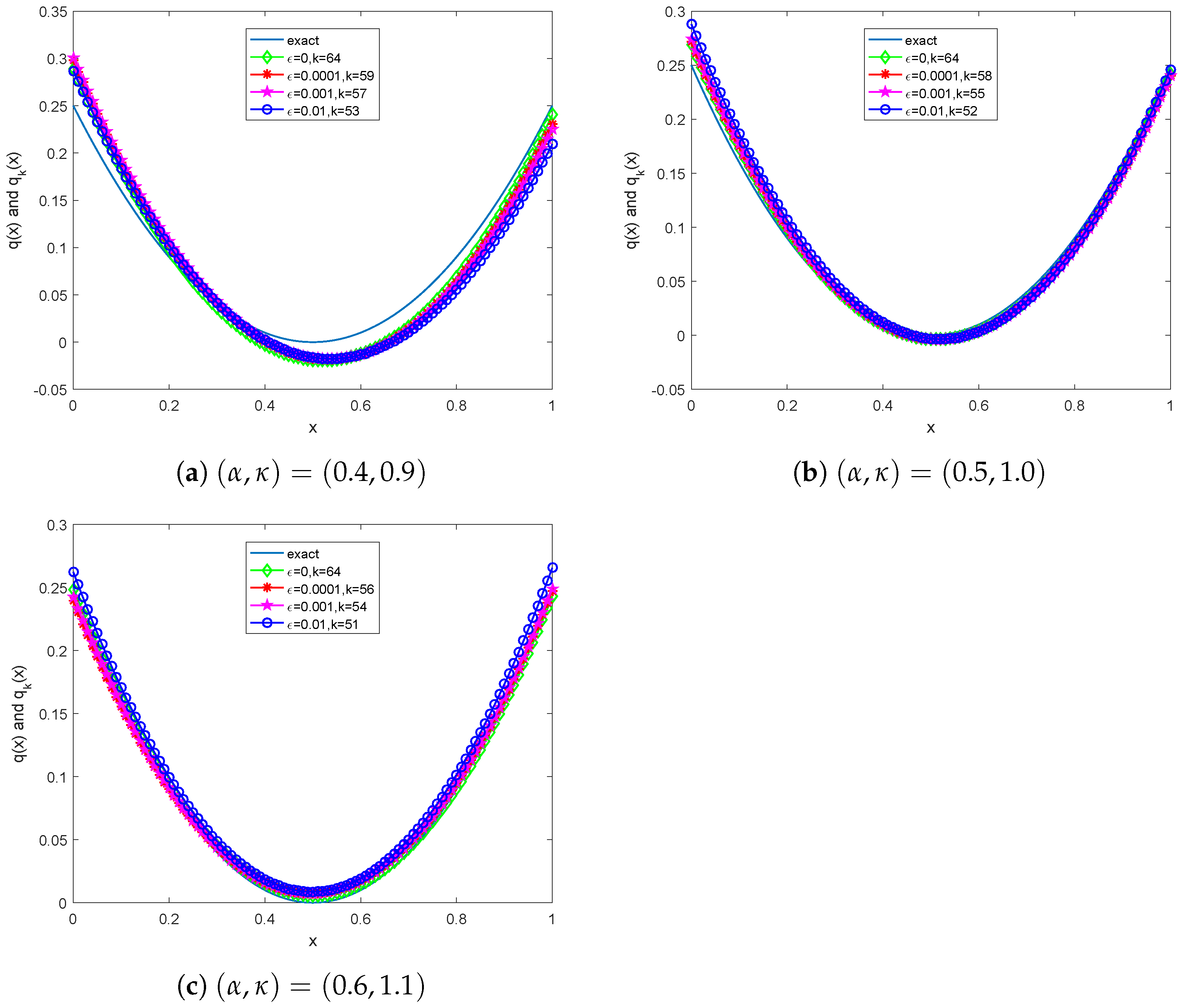
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sakamoto, K.; Yamamoto, M. Inverse source problem with a final overdetermination for a fractional diffusion equation. Math. Control Relat. Fields 2011, 1, 509–518. [Google Scholar] [CrossRef]
- Hendy, A.S.; van Bockstal, K. On a reconstruction of a solely time-dependent source in a time-fractional diffusion equation with non-smooth solutions. J. Sci. Comput. 2022, 90, 41. [Google Scholar] [CrossRef]
- Partohaghighi, M.; Karatas Akgül, E.; Weber, G.W.; Yao, G.; Akgül, A. Recovering source term of the time-fractional diffusion equation. Pramana 2021, 95, 153. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Z. Recovering the potential term in a fractional diffusion equation. IMA J. Appl. Math. 2017, 82, 579–600. [Google Scholar] [CrossRef]
- Wang, J.G.; Ran, Y.H.; Yuan, Z.B. Uniqueness and numerical scheme for the Robin coefficient identification of the time-fractional diffusion equation. Comput. Math. Appl. 2018, 75, 4107–4114. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, Z.Q. Robin coefficient identification for a time-fractional diffusion equation. Inverse Probl. Sci. Eng. 2016, 24, 647–666. [Google Scholar] [CrossRef]
- Wei, T.; Liao, K. Identifying a time-dependent zeroth-order coefficient in a time-fractional diffusion-wave equation by using the measured data at a boundary point. Appl. Anal. 2022, 101, 6522–6547. [Google Scholar] [CrossRef]
- Wei, T.; Yan, X.B. Uniqueness for identifying a space-dependent zeroth-order coefficient in a time-fractional diffusion-wave equation from a single boundary point measurement. Appl. Math. Lett. 2021, 112, 106814. [Google Scholar] [CrossRef]
- Wei, T.; Luo, Y. A generalized quasi-boundary value method for recovering a source in a fractional diffusion-wave equation. Inverse Probl. 2022, 38, 045001. [Google Scholar] [CrossRef]
- Sun, L.; Yan, X.; Liao, K. Simultaneous inversion of a fractional order and a space source term in an anomalous diffusion model. J. Inverse III-Posed Probl. 2022, 30, 791–805. [Google Scholar] [CrossRef]
- Ruan, Z.; Zhang, W.; Wang, Z. Simultaneous inversion of the fractional order and the space-dependent source term for the time-fractional diffusion equation. Appl. Math. Comput. 2018, 328, 365–379. [Google Scholar] [CrossRef]
- Ruan, Z.; Zhang, S. Simultaneous inversion of time-dependent source term and fractional order for a time-fractional diffusion equation. J. Comput. Appl. Math. 2020, 368, 112566. [Google Scholar] [CrossRef]
- Jing, X.; Peng, J. Simultaneous uniqueness for an inverse problem in a time-fractional diffusion equation. Appl. Math. Lett. 2020, 109, 106558. [Google Scholar] [CrossRef]
- Sun, L.L.; Li, Y.S.; Zhang, Y. Simultaneous inversion of the potential term and the fractional orders in a multi-term time-fractional diffusion equation. Inverse Probl. 2021, 37, 055007. [Google Scholar] [CrossRef]
- Sun, L.; Wei, T. Identification of the zeroth-order coefficient in a time fractional diffusion equation. Appl. Numer. Math. 2017, 111, 160–180. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Wei, T. Recovering the time-dependent potential function in a multiterm time-fractional diffusion equation. Appl. Numer. Math. 2019, 135, 228–245. [Google Scholar] [CrossRef]
- Jiang, S.Z.; Wu, Y.J. Recovering a time-dependent potential function in a multi-term time fractional diffusion equation by using a nonlinear condition. J. Inverse III-Posed Probl. 2021, 29, 233–248. [Google Scholar] [CrossRef]
- Jin, B.; Zhou, Z. Recovering the potential and order in one-dimensional time-fractional diffusion with unknown initial condition and source. Inverse Probl. 2021, 37, 105009. [Google Scholar] [CrossRef]
- Yan, X.; Wei, T. Identifying a fractional order and a time-dependent coefficient in a time-fractional diffusion wave equation. J. Comput. Appl. Math. 2023, 424, 114995. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, Z.; Wei, T. Simultaneous inversion of a time-dependent potential coefficient and a time source term in a time fractional diffusion-wave equation. Chaos Solitons Fractals 2022, 157, 111901. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, Y.; Gao, D. Identification of the zeroth-order coefficient and fractional order in a time-fractional reaction-diffusion-wave equation. Math. Methods Appl. Sci. 2023, 46, 142–166. [Google Scholar] [CrossRef]
- Bogachev, V.I.; Ruas, M.A.S. Measure Theory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Freiling, G.; Yurko, V.A. Inverse Sturm-Liouville Problems and Their Applications; NOVA Science Publishers: New York, NY, USA, 2001. [Google Scholar]
- Sakamoto, K.; Yamamoto, M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 2011, 382, 426–447. [Google Scholar] [CrossRef]
- Jin, B. Fractional Differential Equations: An Approach Via Fractional Derivatives; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]

| (1.0, 0.4, 0.9) | (2.0, 0.5, 1.0) | (2.5, 0.6, 1.1) | |
|---|---|---|---|
| 0 | (1.0000, 0.4000, 0.9000) | (2.0000, 0.5000, 1.0000) | (2.5000, 0.6000, 1.1000) |
| 0.0001 | (0.9999, 0.4001, 0.8999) | (2.0000, 0.5000, 0.9999) | (2.5001, 0.6000, 1.0999) |
| 0.001 | (0.9993, 0.4001, 0.8991) | (1.9996, 0.5002, 0.9991) | (2.4998, 0.6002, 1.0993) |
| 0.01 | (0.9913, 0.4017, 0.8895) | (1.9959, 0.5019, 0.9898) | (2.4975, 0.6019, 1.0906) |
| 0 | 0.0001 | 0.001 | 0.01 | |
|---|---|---|---|---|
| (1.0, 0.4, 0.9) | (64) | (30) | (29) | (27) |
| (2.0, 0.5, 1.0) | (64) | (31) | (30) | (28) |
| (2.5, 0.6, 1.1) | (64) | (30) | (29) | (27) |
| (0.4, 0.9) | (0.5, 1.0) | (0.6, 1.1) | |
|---|---|---|---|
| 0 | (0.3998, 0.9002) | (0.5000, 1.0021) | (0.6000, 1.1012) |
| 0.0001 | (0.3998, 0.9021) | (0.5000, 1.0024) | (0.6001, 1.1003) |
| 0.001 | (0.3999, 0.9027) | (0.5000, 1.0029) | (0.6000, 1.1009) |
| 0.01 | (0.3999, 0.8997) | (0.4999, 1.0055) | (0.5999, 1.1048) |
| 0 | 0.0001 | 0.001 | 0.01 | |
|---|---|---|---|---|
| (0.4, 0.9) | (64) | (59) | (57) | (53) |
| (0.5, 1.0) | (64) | (58) | (55) | (52) |
| (0.6, 1.1) | (64) | (56) | (54) | (51) |
| (0.4, 0.9) | (0.5, 1.0) | (0.6, 1.1) | |
|---|---|---|---|
| 0 | (0.3998, 0.9105) | (0.4997, 1.0142) | (0.5996, 1.1156) |
| 0.0001 | (0.3999, 0.9106) | (0.4997, 1.0141) | (0.5996, 1.1169) |
| 0.001 | (0.3999, 0.9110) | (0.4998, 1.0144) | (0.5997, 1.1171) |
| 0.01 | (0.3995, 0.9171) | (0.4998, 1.0185) | (0.5987, 1.1219) |
| 0 | 0.0001 | 0.001 | 0.01 | |
|---|---|---|---|---|
| (0.4, 0.9) | (64) | (55) | (53) | (51) |
| (0.5, 1.0) | (64) | (53) | (51) | (49) |
| (0.6, 1.1) | (64) | (51) | (50) | (47) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Qiu, Z.; Qiu, S.; Ruan, Z. Multiple Terms Identification of Time Fractional Diffusion Equation with Symmetric Potential from Nonlocal Observation. Fractal Fract. 2023, 7, 778. https://doi.org/10.3390/fractalfract7110778
Wang Z, Qiu Z, Qiu S, Ruan Z. Multiple Terms Identification of Time Fractional Diffusion Equation with Symmetric Potential from Nonlocal Observation. Fractal and Fractional. 2023; 7(11):778. https://doi.org/10.3390/fractalfract7110778
Chicago/Turabian StyleWang, Zewen, Zhonglong Qiu, Shufang Qiu, and Zhousheng Ruan. 2023. "Multiple Terms Identification of Time Fractional Diffusion Equation with Symmetric Potential from Nonlocal Observation" Fractal and Fractional 7, no. 11: 778. https://doi.org/10.3390/fractalfract7110778






