Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion
Abstract
:1. Introduction
- (1)
- An fGPm with an adaptive diffusion is proposed to model the uncertainty of the degradation. The statistical requirements for the engineering application are also analyzed.
- (2)
- Only temporal features are reliable for the planetary gearbox degradation. Therefore, multiple temporal features are extracted from the vibration signals. A metric-based feature selection algorithm is proposed in this paper to illustrate the significance of the degradation features.
- (3)
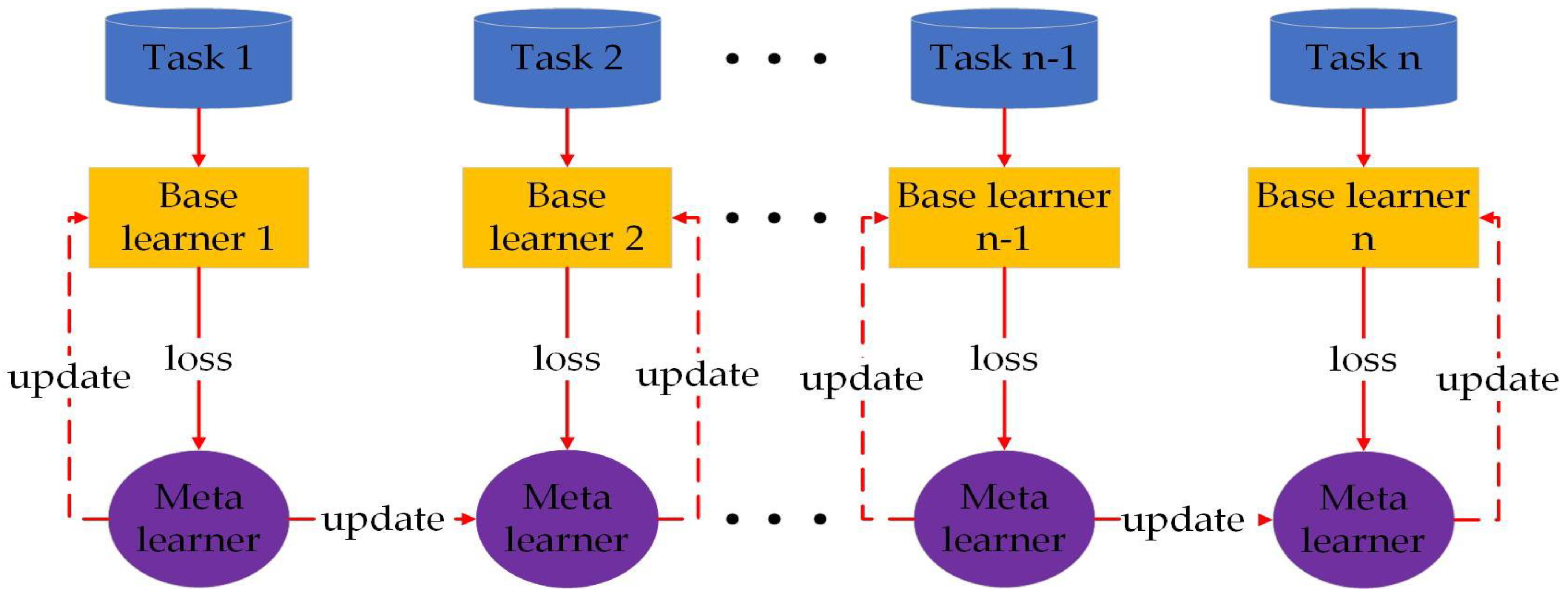
- In this paper, the meta-LSTM model is proposed to learn a general representation of the non-analytical planetary gearbox degradation trend, featuring the unit-to-unit variability.
- (4)
- The measurement error is not negligible for the planetary gearbox degradation due to the time-varying vibration transmission paths. In this work, a white Gaussian noise term is used to represent the measurement error.
2. The Adaptive fGPm for the Modelling of Degradation Uncertainty
2.1. Simulation of the fGPm
2.2. Degradation Uncertainty Modelling with the Adaptive fGPm
2.3. Statistical Requirements of the fGPm with an Adaptive Diffusion
3. Adaptive RUL Prediction Model for the Wind Turbine Planetary Gearboxes
3.1. Multi-Stage Procedures for the Proposed RUL Prediction Model
3.2. Metric-Based Feature Selection Algorithm
3.3. Drift Term Considering the Unit-to-Unit Variability
3.4. Adaptive RUL Prediction Model with a Measurement Error Term
4. Case Study
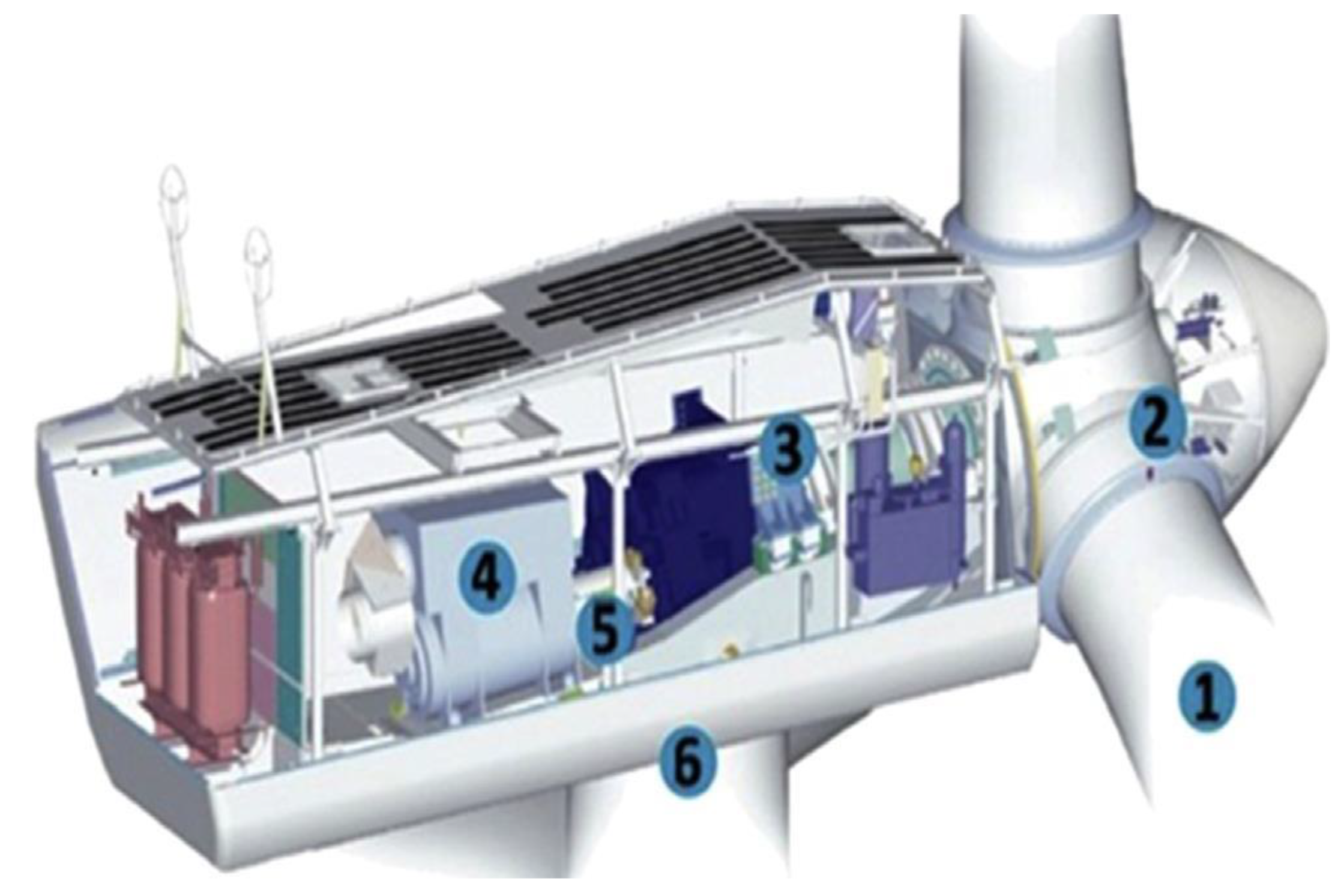
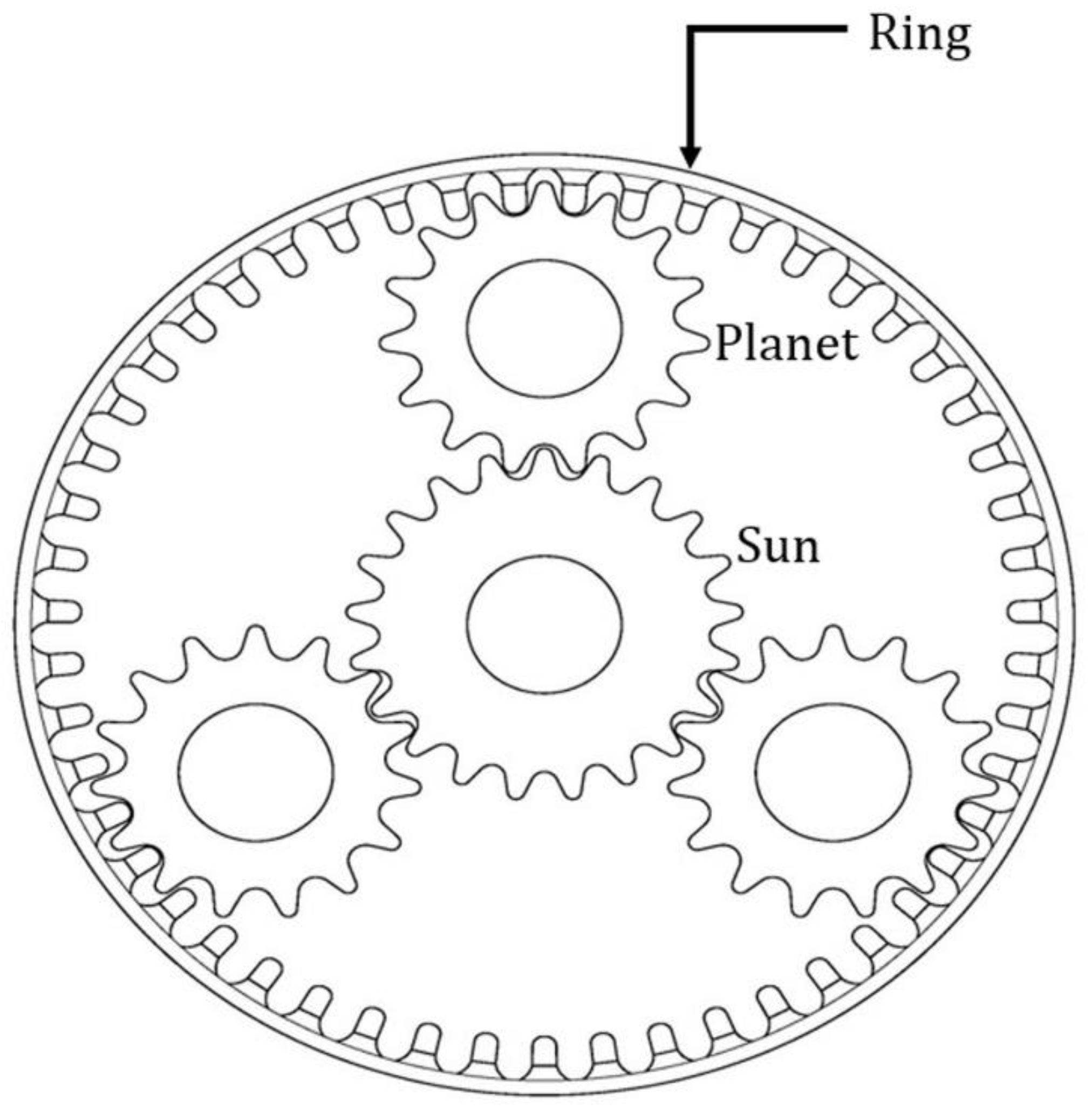
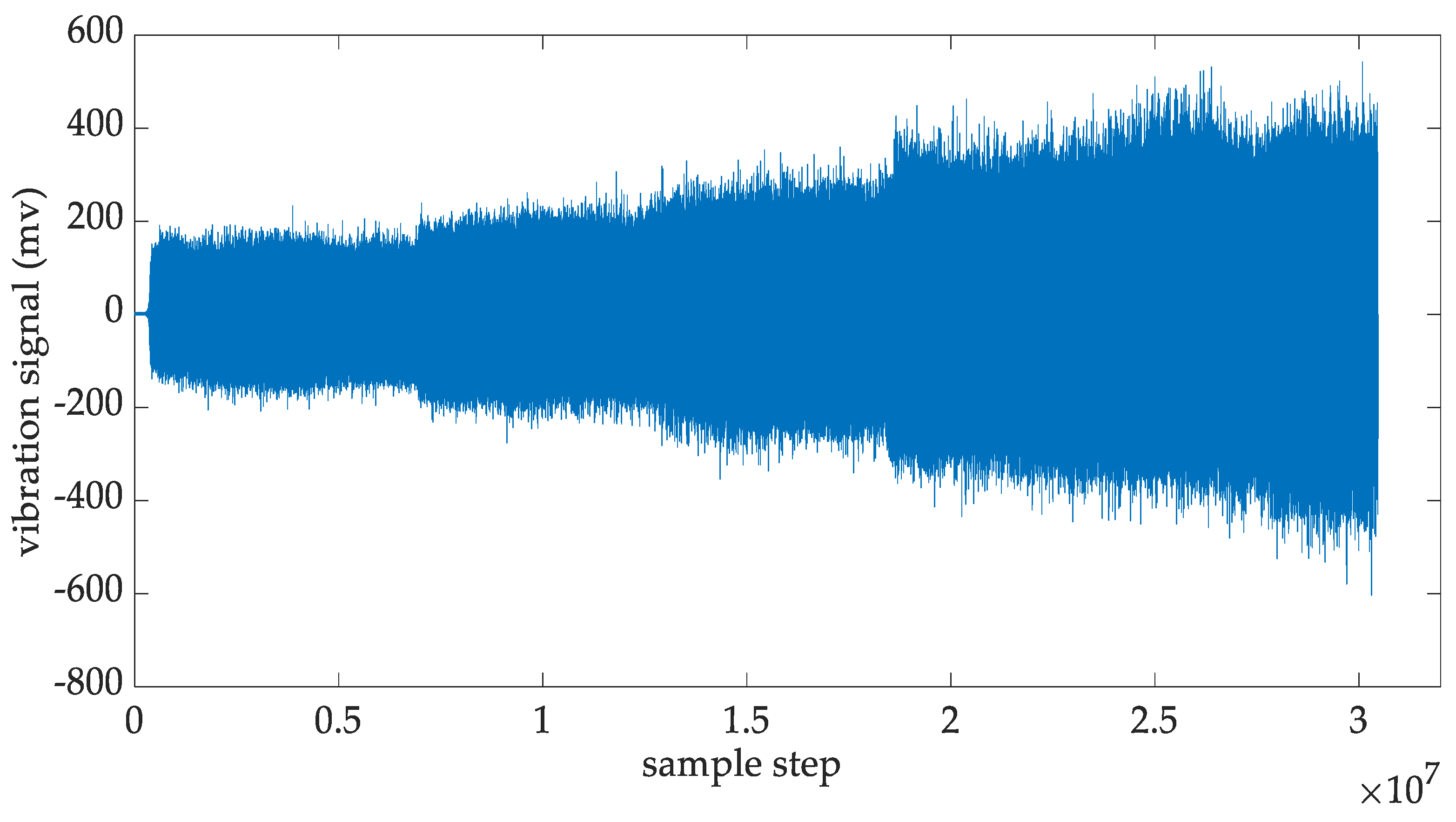
4.1. Planetary Gearbox Degradation Experiments
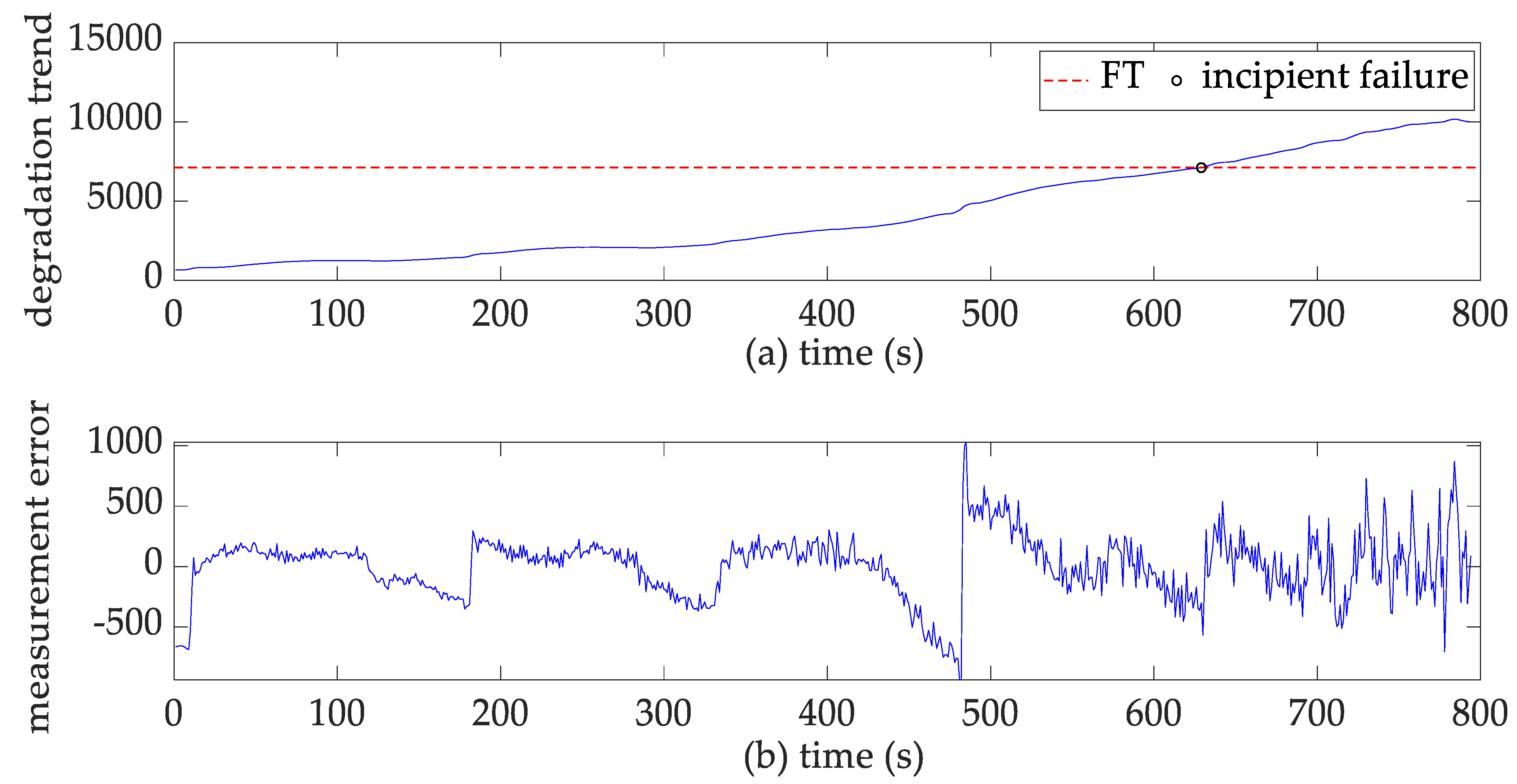
4.2. Feature Selection and Incipient Failure Detection
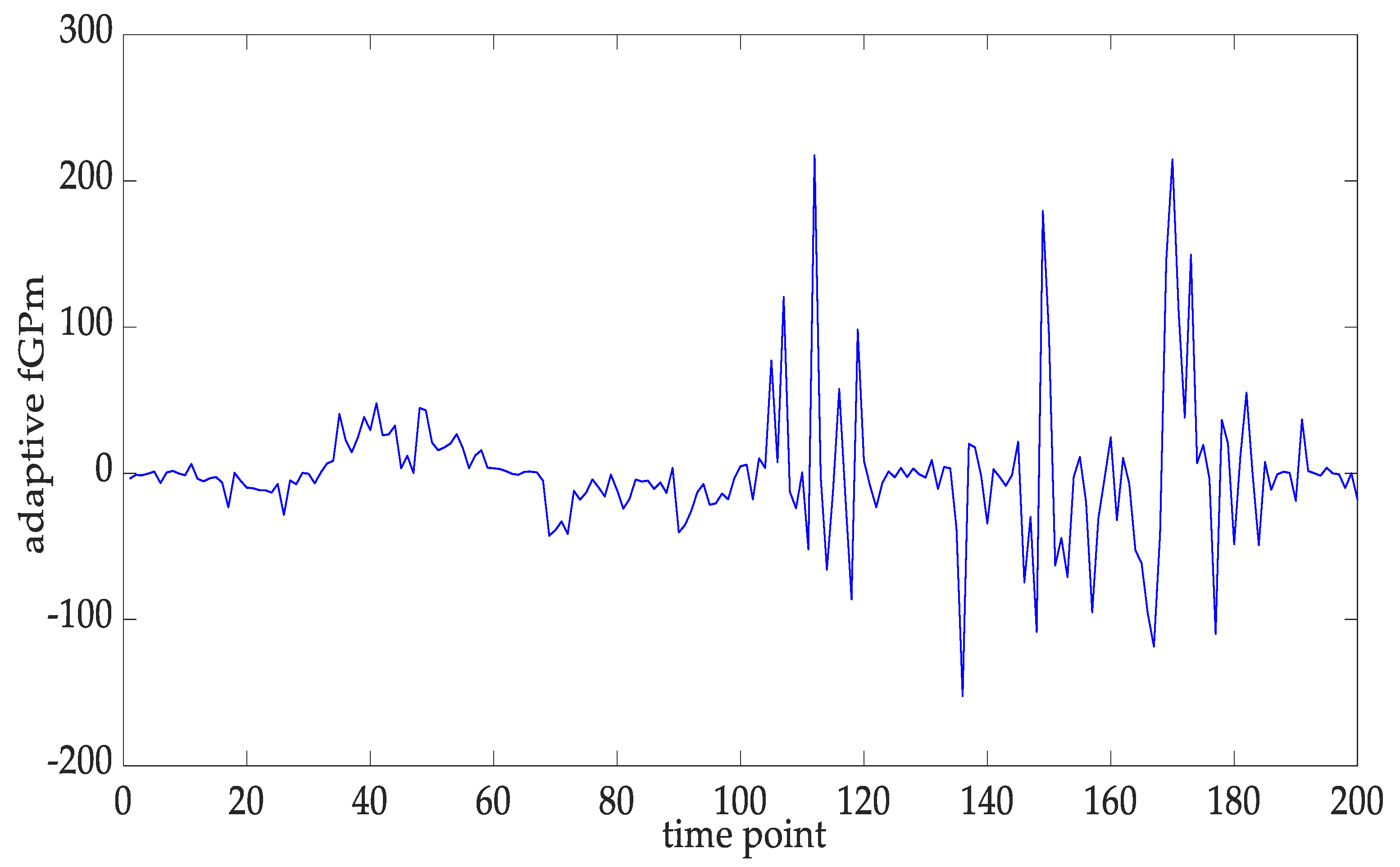
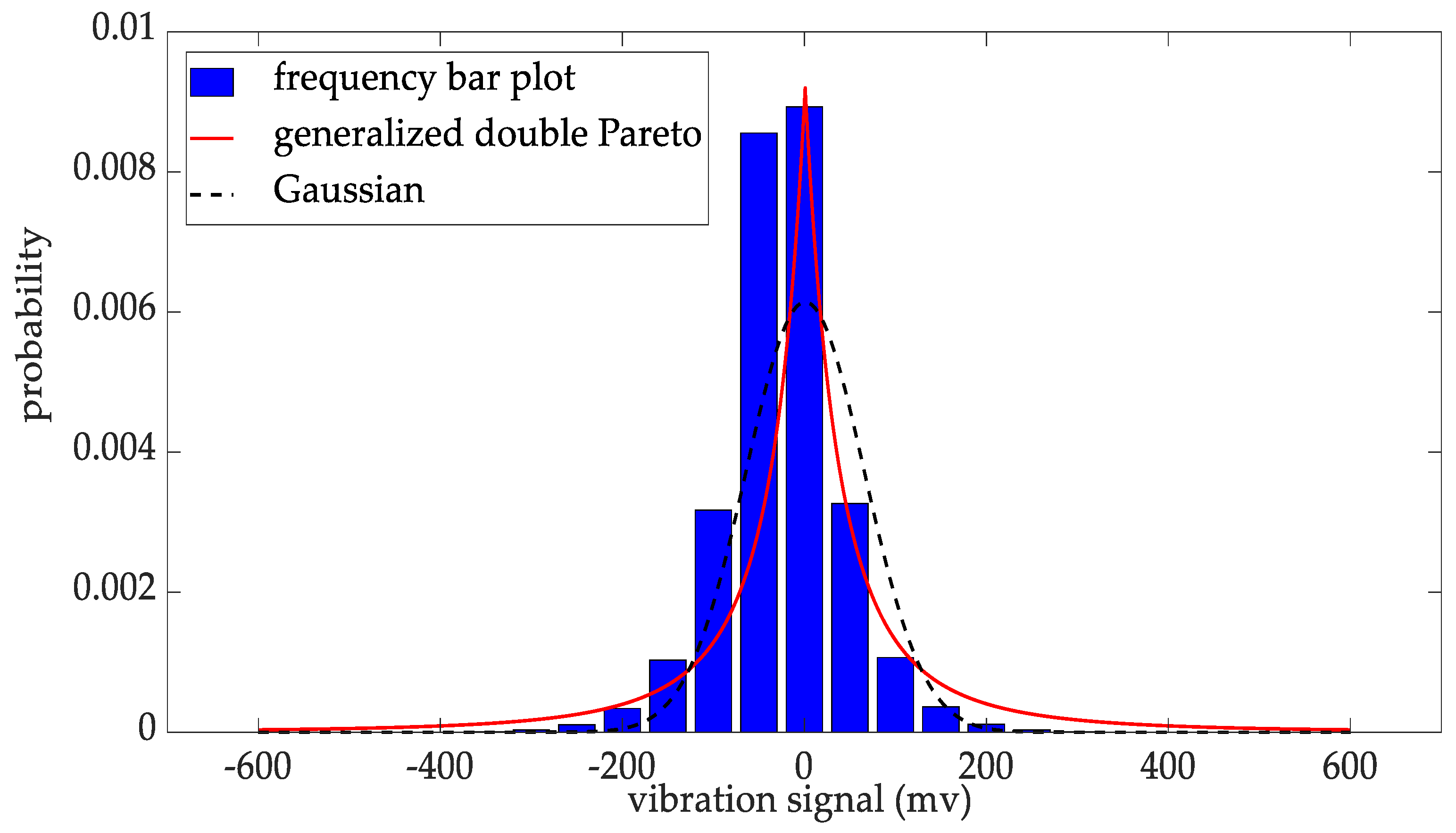
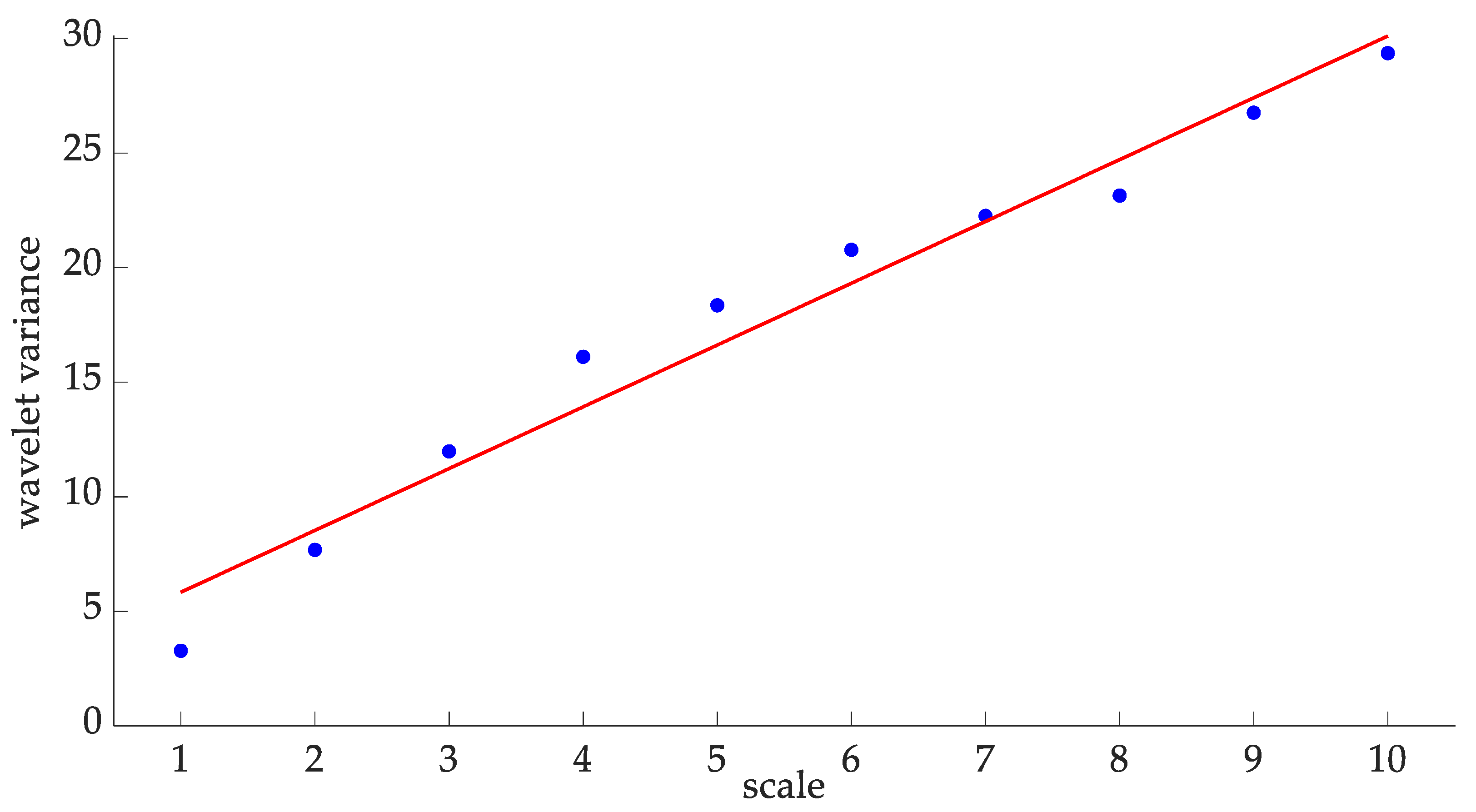
4.3. Statistical Requirements Validation for the Adaptive fGPm
4.4. Performance Evaluation of the Proposed Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| RUL | remaining useful life |
| LSTM | long short-term memory neural network |
| BM–LSTM | Brownian motion–long short-term neural network |
| FBM | fractional Brownian motion |
| fGPm | fractional Generalized Pareto motion |
| HI | health indicator |
| meta-LSTM | meta-long short-term memory neural network |
| meta-pruning | meta-learning with pruning technique |
| probability density function | |
| GDPm | generalized double Pareto motion |
| MA | mean absolute value |
| RMS | root mean square |
| VMD | variational mode decomposition |
| EOL | end of life |
| FT | failure threshold |
| RMSE | root mean squared error |
| MAE | mean absolute error |
| SOA | score of accuracy |
| std | standard deviation |
References
- Jin, X.; Zhang, Z.L.; Ju, W.B. A review on wind power industry and corresponding insurance market in China: Current status and challenges. Renew. Sust. Energy Rev. 2014, 38, 1069–1082. [Google Scholar] [CrossRef]
- Liu, W.Y.; Tang, B.P.; Han, J.G.; Lu, X.N.; Hu, N.N.; He, Z.Z. The structure healthy condition monitoring and fault diagnosis methods in wind turbines: A review. Renew. Sust. Energy Rev. 2014, 44, 466–472. [Google Scholar] [CrossRef]
- Kandukuri, S.T.; Klausen, A.; Karimi, H.R.; Robbersmyr, K.G. A review of diagnostics and prognostics of low-speed machinery towards wind turbine farm-level health management. Renew. Sust. Energy Rev. 2016, 53, 697–708. [Google Scholar] [CrossRef]
- Wang, T.Y.; Han, Q.K.; Chu, F.L.; Feng, Z.P. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Process. 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Bhattacharijee, D.; Bhola, P.; Pan, P.K. A heuristic synthesis of multistage planetary gearbox layout for automotive transmission. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 233, 336–347. [Google Scholar] [CrossRef]
- Li, C.J.; Lee, H. Gear fatigue crack prognosis using embedded model, gear dynamic model and fracture mechanics. Mech. Syst. Signal Process. 2005, 19, 836–846. [Google Scholar] [CrossRef]
- Chen, J.X.; Huang, R.Y.; Chen, Z.Y.; Mao, W.T.; Li, W.H. Transfer learning algorithms for bearing remaining useful life prediction: A comprehensive review from an industrial application perspective. Mech. Syst. Signal Process. 2023, 193, 110239. [Google Scholar] [CrossRef]
- Cárcel, C.R.; Jaramillo, V.H.; Mba, D.; Ottewill, J.R.; Cao, Y. Combination of process and vibration data for improved condition monitoring of industrial systems working under variable operating conditions. Mech. Syst. Signal Process. 2016, 66–67, 699–714. [Google Scholar] [CrossRef]
- Yoshua, B.; Aaron, C.; Pascal, V. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Yann, L.C.; Yoshua, B.; Geoffrey, H. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Yu, J.; Gao, Z.Y. Remaining useful life prediction of planet bearings based on conditional deep recurrent generative adversarial network and action discovery. J. Mech. Sci. Technol. 2021, 35, 21–30. [Google Scholar] [CrossRef]
- Pan, Y.B.; Hong, R.J.; Chen, J.; Wu, W.W. A hybrid DBN-SOM-PF based prognostic approach of remaining useful life for wind turbine gearbox. Renew. Energy 2020, 152, 138–154. [Google Scholar] [CrossRef]
- Zhang, H.W.; Chen, M.Y.; Shang, J.; Yang, C.J.; Sun, Y.X. Stochastic process-based degradation modeling and RUL prediction: From Brownian motion to fractional Brownian motion. Sci. China Inf. Sci. 2021, 64, 171201. [Google Scholar] [CrossRef]
- Chen, X.W.; Liu, Z. A long short-term memory neural network based Wiener process model for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2022, 226, 108651. [Google Scholar] [CrossRef]
- Yu, W.N.; Tu, W.B.; Kim, I.Y.; Mechefske, C. A nonlinear-drift-driven Wiener process model for remaining useful life estimation considering three sources of variability. Reliab. Eng. Syst. Saf. 2021, 212, 107631. [Google Scholar] [CrossRef]
- Zhang, H.W.; Chen, M.Y.; Xi, X.P.; Zhou, D.H. Remaining Useful Life Prediction for Degradation Processes With Long-Range Dependence. IEEE Trans. Reliab. 2017, 66, 1368–1379. [Google Scholar] [CrossRef]
- Bayraktav, E.; Poor, H.V.; Rao, R. Prediction and tracking of long-range dependent sequences. Syst. Control Lett. 2005, 54, 1083–1090. [Google Scholar] [CrossRef]
- Li, X.; Ma, Y. Remaining useful life prediction for lithium-ion battery using dynamic fractional brownian motion degradation model with long-term dependence. J. Power Electron 2022, 22, 2069–2080. [Google Scholar] [CrossRef]
- Song, W.Q.; Duan, S.W.; Chen, D.D.; Zio, E.; Yan, W.D.; Cai, F. Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion. Fractal. Fract. 2022, 6, 471. [Google Scholar] [CrossRef]
- Li, Q.; Li, H.K.; Ma, Z.H.; Liu, X.J.; Guan, X.C.; Zhang, X.L. Performance degradation assessment for mechanical system based on semi-analytical solution of self-similar stable distribution process. Struct. Health Monit. 2023, 0, 23. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.B.; Zhao, Y. An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction. Mech. Syst. Signal Process. 2019, 127, 370–387. [Google Scholar] [CrossRef]
- Lei, Y.G.; Lin, J.; Zuo, M.J.; He, Z.J. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J. Wavelet kernel local Fisher discriminant analysis with particle swarm optimization algorithm for bearing defect classification. IEEE Trans. Instrum. Meas. 2015, 64, 3588–3600. [Google Scholar] [CrossRef]
- Jahan, I.; Castagna, J.; Murphy, M.; Kayali, M.A. Fault detection using principal component analysis of seismic attributes in the Bakken Formation, Williston Basin, North Dakota, USA. Interpret. J. Sub. 2017, 5, T361–T372. [Google Scholar] [CrossRef]
- Saucedo, D.J.J.; Delgado, P.M.; Osornio, R.R.A.; Romero, T.R.D.J. Diagnosis methodology for identifying gearbox wear based on statistical time feature reduction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2711–2722. [Google Scholar] [CrossRef]
- Akrim, A.; Gogu, C.; Vingerhoeds, R.; Salaun, M. Self-Supervised Learning for data scarcity in a fatigue damage prognostic problem. Eng. Appl. Artif. Intel. 2023, 120, 105837. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Lerine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar] [CrossRef]
- Lim, K.; Lee, J.Y.; Carbonell, J.; Poibeau, T. Semi-supervised learning on meta structure: Multi-task tagging and parsing in low-resource scenarios. In Proceedings of the Association for the Advancement of Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020. [Google Scholar] [CrossRef]
- Pan, T.Y.; Zhang, S.; Li, F.D.; Chen, J.L.; Li, A. A meta network pruning framework for remaining useful life prediction of rocket engine bearings with temporal distribution discrepancy. Mech. Syst. Signal Process. 2023, 195, 110271. [Google Scholar] [CrossRef]
- Sun, B.; Li, Y.; Wang, Z.L.; Ren, Y.; Feng, Q.; Yang, D.Z. An improved inverse Gaussian process with random effects and measurement errors for RUL prediction of hydraulic piston pump. Measurement 2021, 173, 108604. [Google Scholar] [CrossRef]
- Armagan, A.; Dunson, D.B.; Lee, J. Generalized Double Pareto Shrinkage. Stat. Sin. 2013, 23, 119–143. [Google Scholar] [CrossRef]
- Song, W.Q.; Deng, W.J.; Chen, D.D.; Jin, R.; Kudreyko, A. Hybrid Approach of Fractional Generalized Pareto Motion and Cosine Similarity Hidden Markov Model for Solar Radiation Forecasting. Fractal. Fract. 2023, 7, 93. [Google Scholar] [CrossRef]
- Lei, Y.G.; Li, N.P.; Guo, L.; Li, N.B.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Hu, L.W.; Wang, W.B.; Ding, G.R. RUL prediction for lithium-ion batteries based on variational mode decomposition and hybrid network model. Signal Image Video Process. 2023, 17, 3109–3117. [Google Scholar] [CrossRef]
- Lazaro, R.; Yurusen, N.Y.; Melero, J.J. Determining Remaining Lifetime of Wind Turbine Gearbox Using a Health Status Indicator Signal. J. Phys. Conf. Ser. 2020, 1618, 022037. [Google Scholar] [CrossRef]
- Marx, D.G. Towards a Hybrid Approach for Diagnostics and Prognostics of Planetary Gearboxes. Master’s Thesis, University of Preroria, Pretoria, South Africa, 2020. [Google Scholar]
- Ghosh, O.; Ghosh, T.; Chatterjee, T.N. Multi technique Analysis of the Solar 10.7 cm Radio Flux Time-Series in Relation to Predictability. Sol. Phys. 2014, 289, 2297–2315. [Google Scholar] [CrossRef]
- Ramirez, J.A.; Echeverria, J.C.; Rodriguez, E. Performance of a high-dimensional R/S method for Hurst exponent estimation. Phys. A 2008, 387, 6452–6462. [Google Scholar] [CrossRef]
- Mondal, D.; Percival, D.B. Wavelet Variance Analysis for Random Fields on a Regular Lattice. IEEE Trans. Image Process. 2012, 21, 537–549. [Google Scholar] [CrossRef]
- Mantalos, P.; Karagrigoriou, A. Bootstrapping the augmented Dickey-Fuller test for unit root using the MDIC. J. Stat. Comput. Sim. 2012, 82, 431–443. [Google Scholar] [CrossRef]
- Deng, W.; Gao, Y.; Chen, J.; Kudreyko, A.; Cattani, C.; Zio, E.; Song, W. Multi-Fractal Weibull Adaptive Model for the Remaining Useful Life Prediction of Electric Vehicle Lithium Batteries. Entropy 2023, 25, 646. [Google Scholar] [CrossRef]





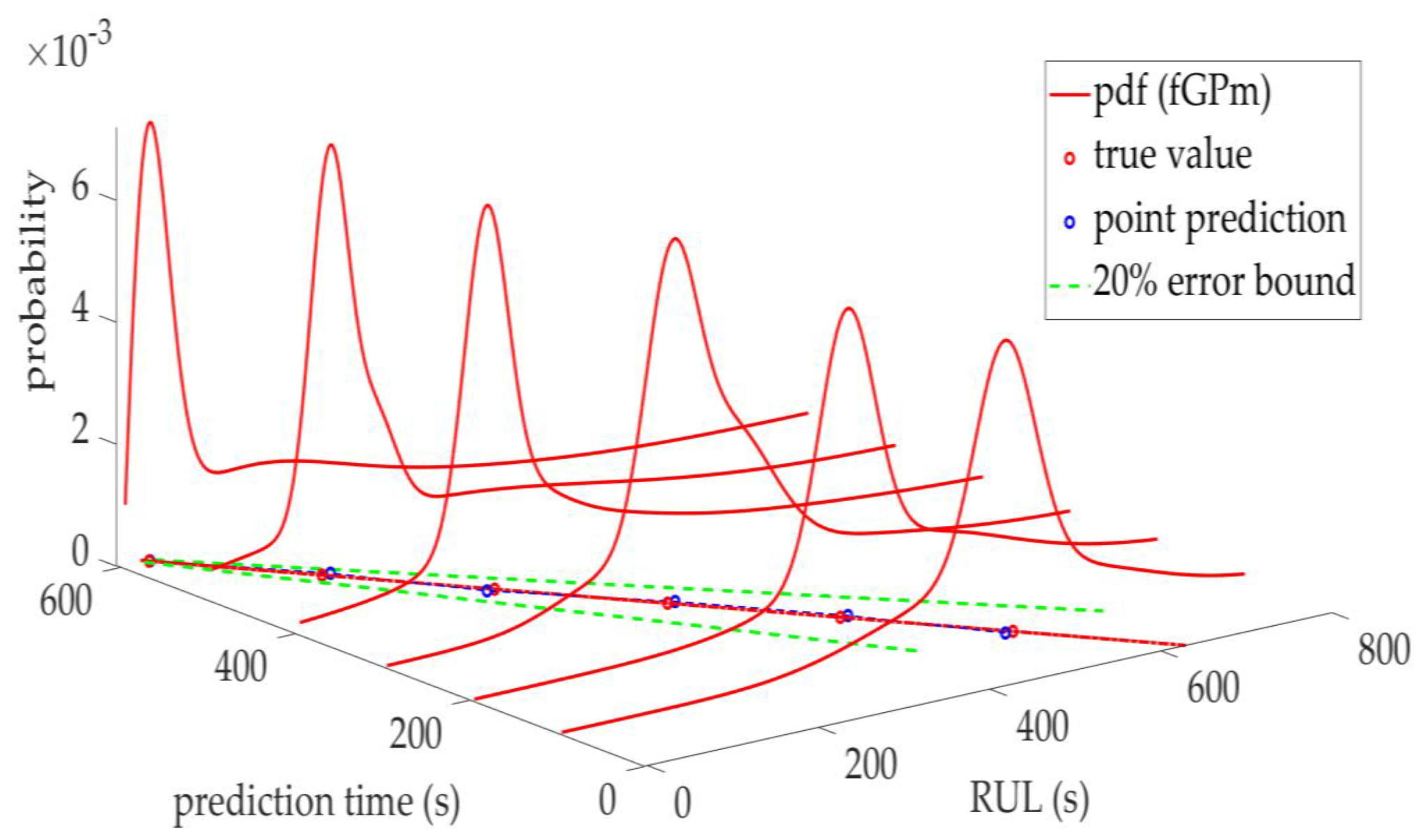
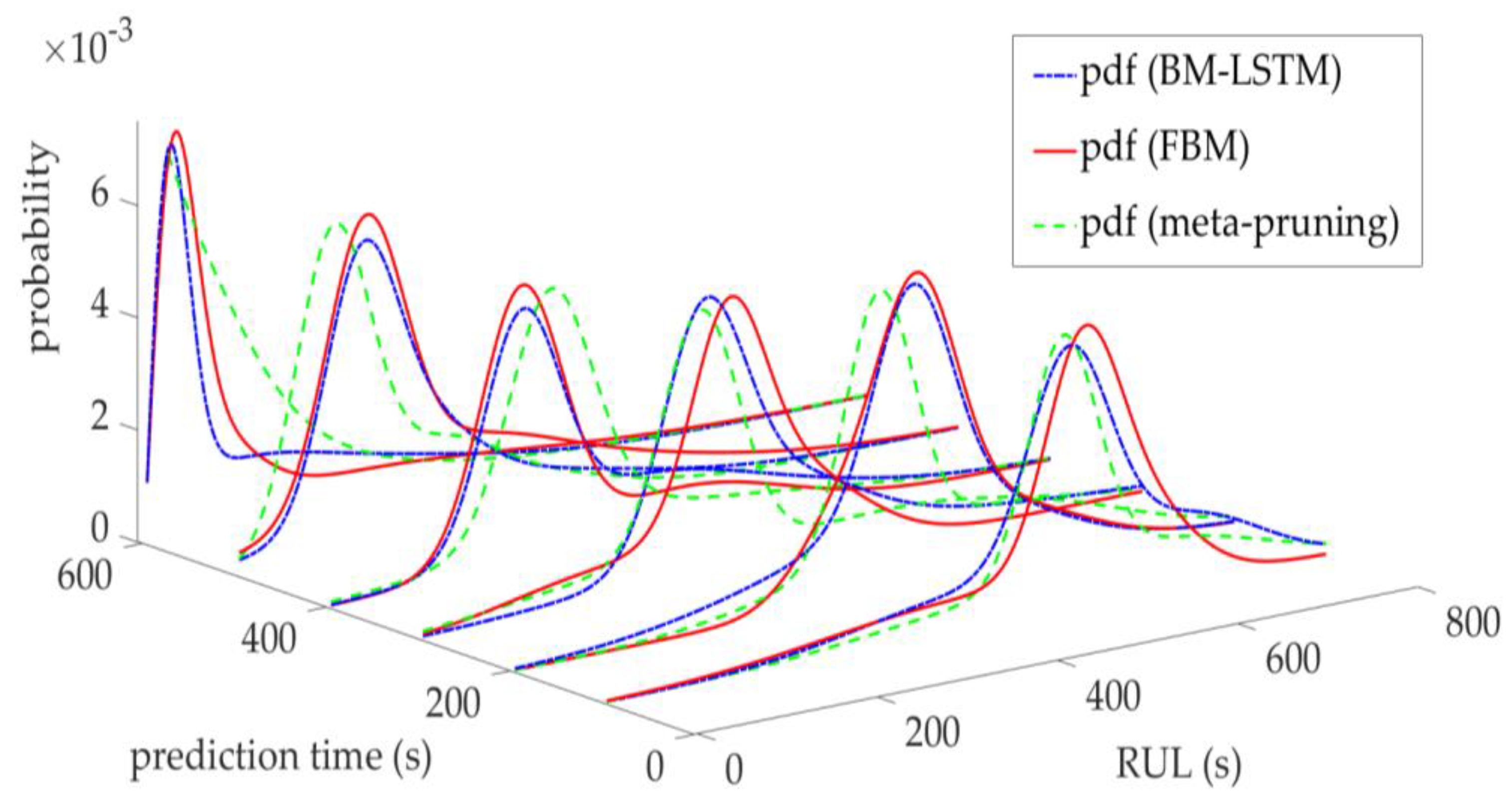
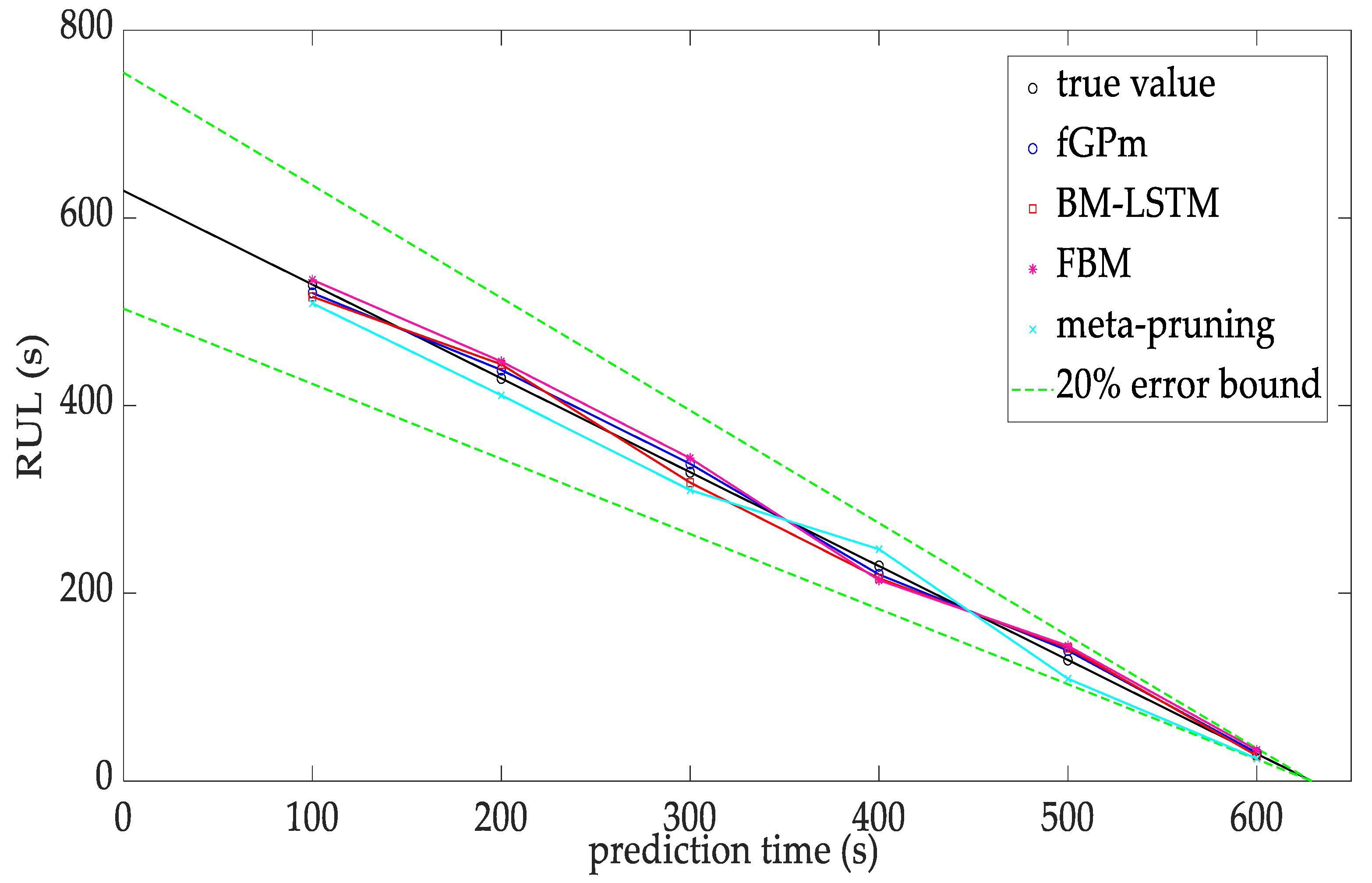
| Range | Variance | MA | RMS | |
|---|---|---|---|---|
| Monotonicity | 0.0456 | 0.1245 | 0.0623 | 0.0923 |
| Robustness | 0.8142 | 0.9835 | 0.7928 | 0.8512 |
| Tradability | 0.4332 | 0.6727 | 0.5216 | 0.5641 |
| fGPm | FBM | BM–LSTM | Meta-Pruning | |
|---|---|---|---|---|
| RMSE | 8.4163 | 13.1656 | 11.9513 | 17.4833 |
| MAE | 7.8333 | 12.2124 | 11.1667 | 16.6667 |
| SOA | 0.7815 | 0.6935 | 0.7186 | 0.5719 |
| std | 0.0842 | 0.2763 | 0.1623 | 0.3651 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Deng, W.; Song, W.; Cheng, W.; Cattani, P.; Villecco, F. Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion. Fractal Fract. 2024, 8, 14. https://doi.org/10.3390/fractalfract8010014
Zheng H, Deng W, Song W, Cheng W, Cattani P, Villecco F. Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion. Fractal and Fractional. 2024; 8(1):14. https://doi.org/10.3390/fractalfract8010014
Chicago/Turabian StyleZheng, Hongqing, Wujin Deng, Wanqing Song, Wei Cheng, Piercarlo Cattani, and Francesco Villecco. 2024. "Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion" Fractal and Fractional 8, no. 1: 14. https://doi.org/10.3390/fractalfract8010014
APA StyleZheng, H., Deng, W., Song, W., Cheng, W., Cattani, P., & Villecco, F. (2024). Remaining Useful Life Prediction of a Planetary Gearbox Based on Meta Representation Learning and Adaptive Fractional Generalized Pareto Motion. Fractal and Fractional, 8(1), 14. https://doi.org/10.3390/fractalfract8010014









