Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects
Abstract
:1. Introduction
- A novel fractional-order hysteresis model with five parameters, including linear and nonlinear components, is proposed to capture the rate-independent hysteresis effect and the main characteristics of PEAs.
- Then, it is proposed to combine the fractional-order creep model with the dynamic model of PEAs and identify the creep parameters and dynamic parameters simultaneously, so as to eliminate dynamic interference and improve the identification accuracy of the creep module.
- Finally, we affirm the verification of the enhanced accuracy achieved by the proposed model in capturing the nonlinear coupled effects of hysteresis and creep, validated through experimental evidence.
2. Fractional-Order Modeling of Hysteresis and Creep for PEAs
2.1. Fractional Calculus Definition and Model Theory
2.2. Features of the Fractional-Order Operator
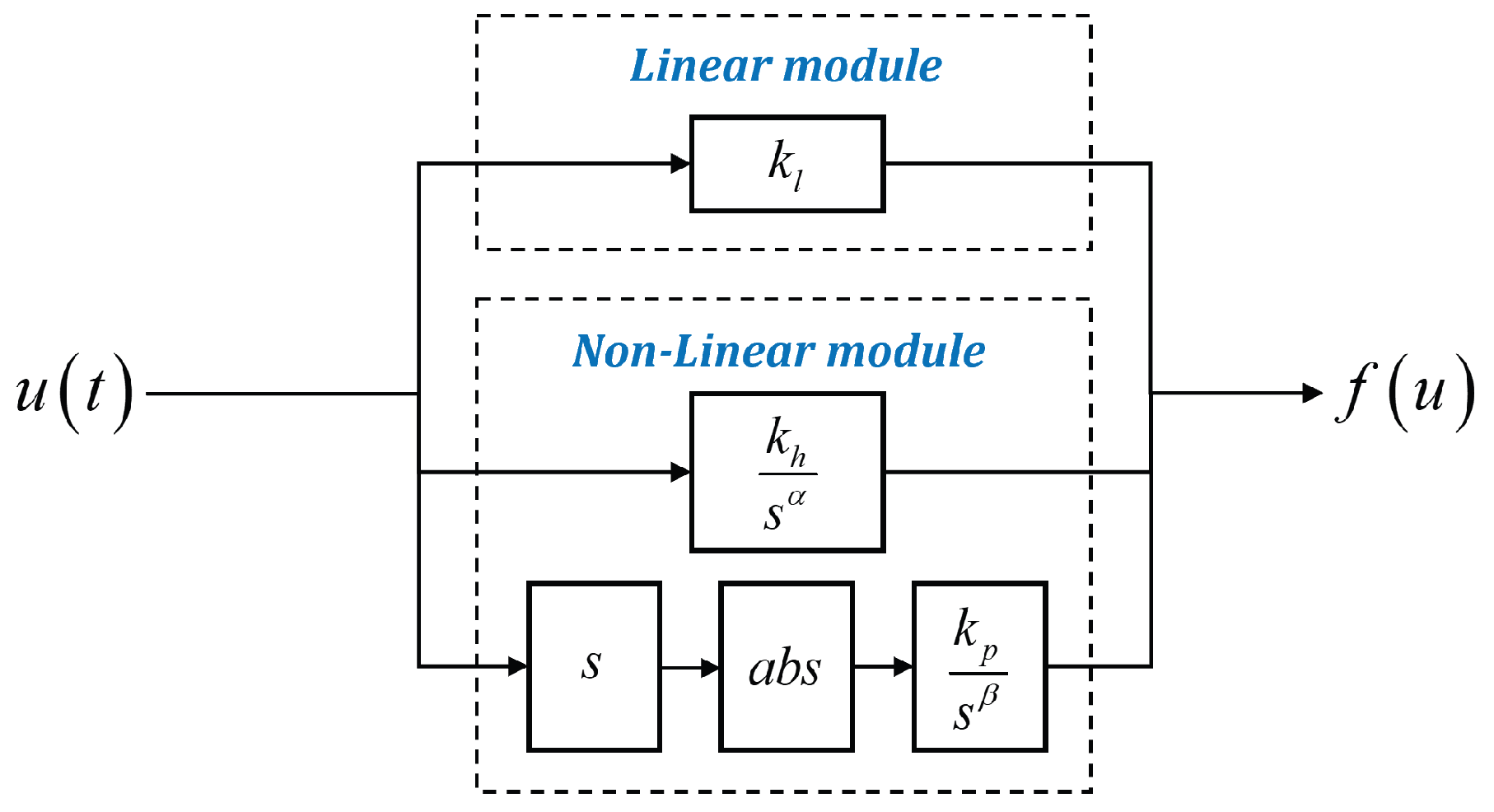
2.3. Fractional-Order Hysteresis Model
2.4. Review of the Fractional-Order Creep Model
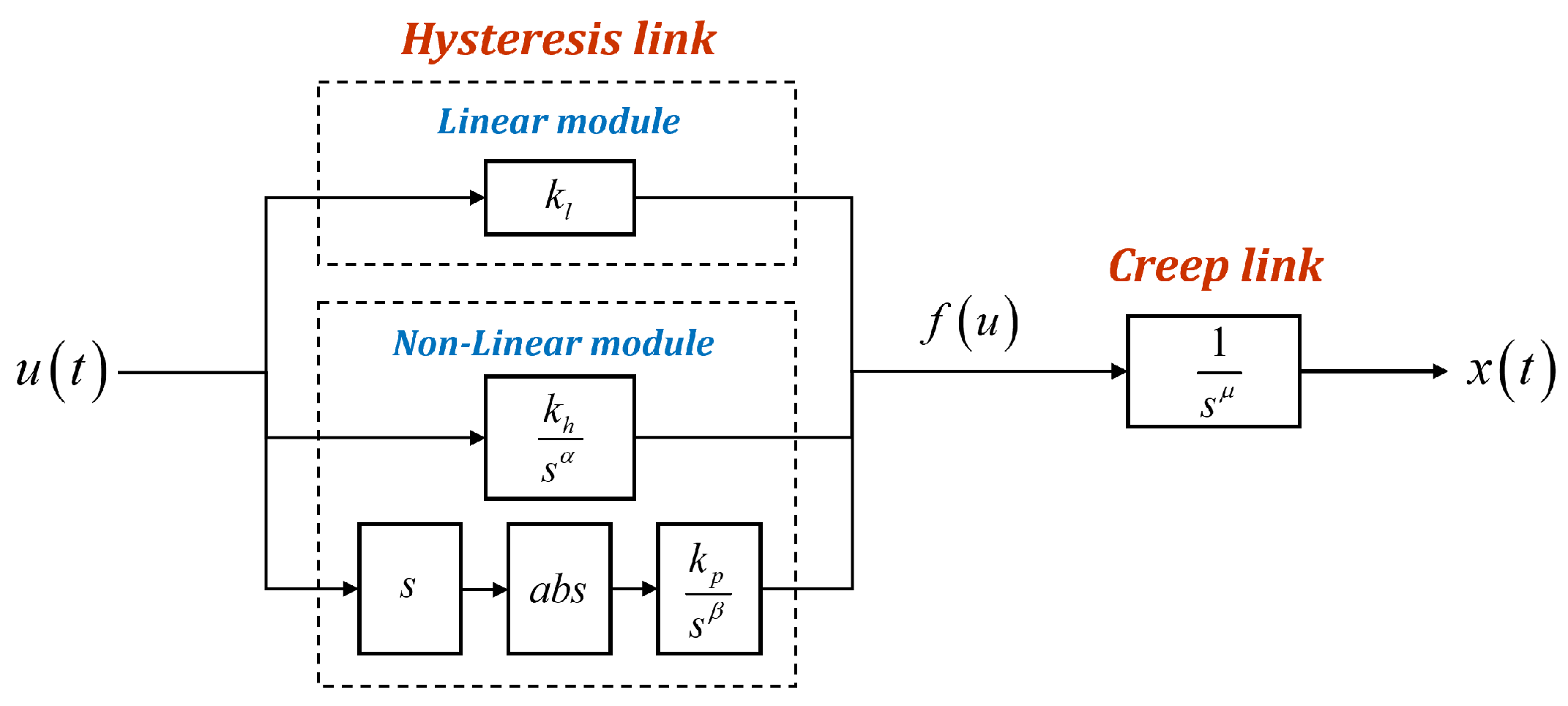
2.5. Fractional-Order Hysteresis and Creep-Coupled Model
3. Properties of the Proposed Models
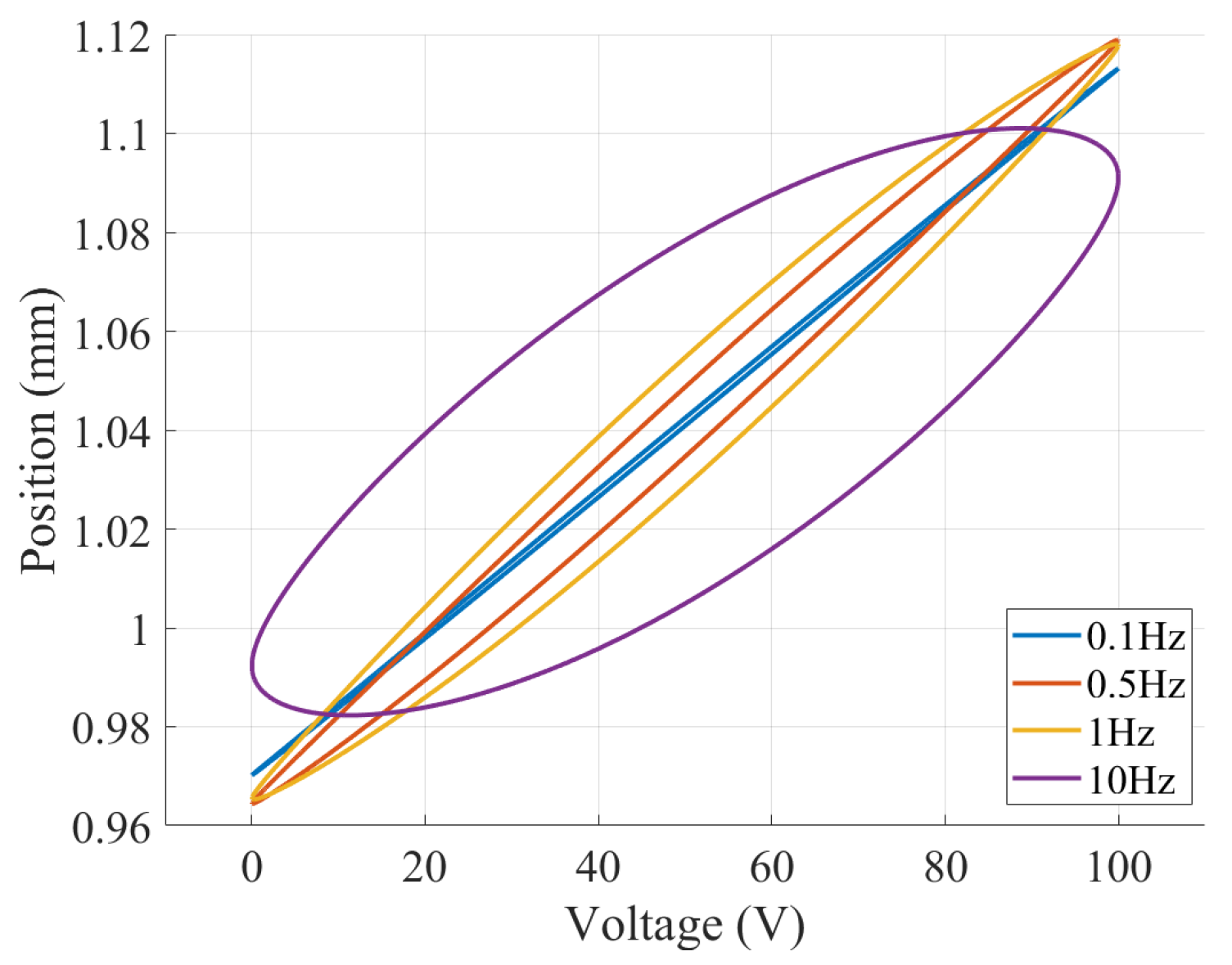
3.1. Properties of the FOH Model
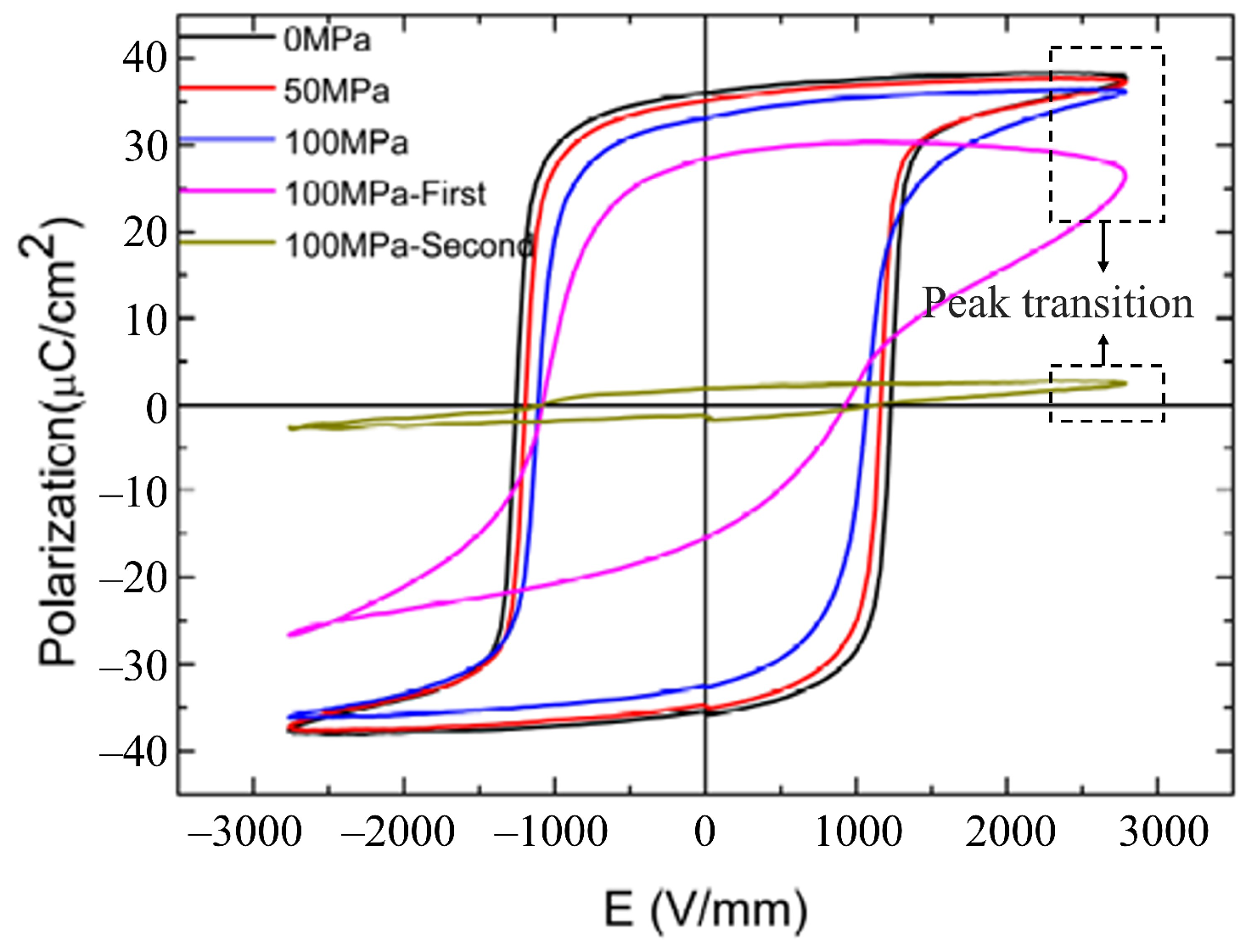
3.1.1. Peak Transition Behavior
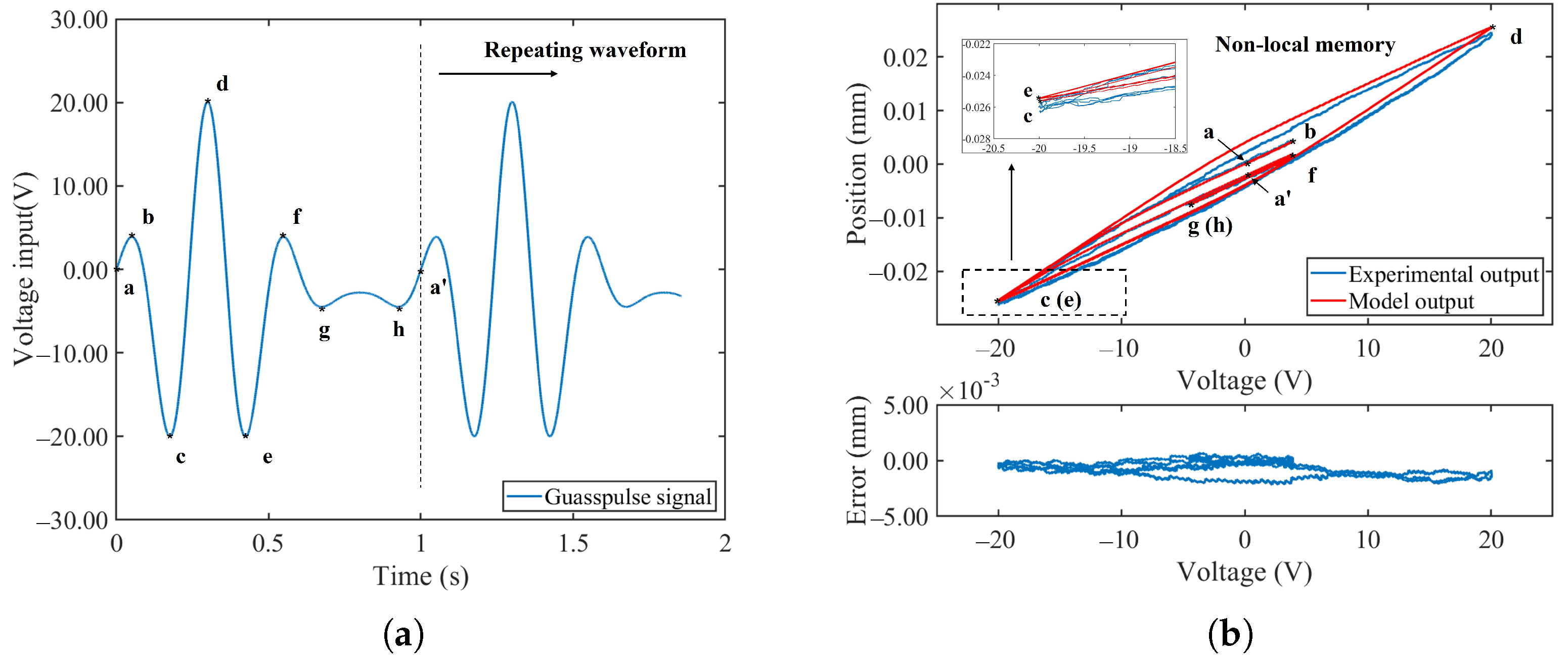
3.1.2. Piezo Lag and Non-Local Memory Effect
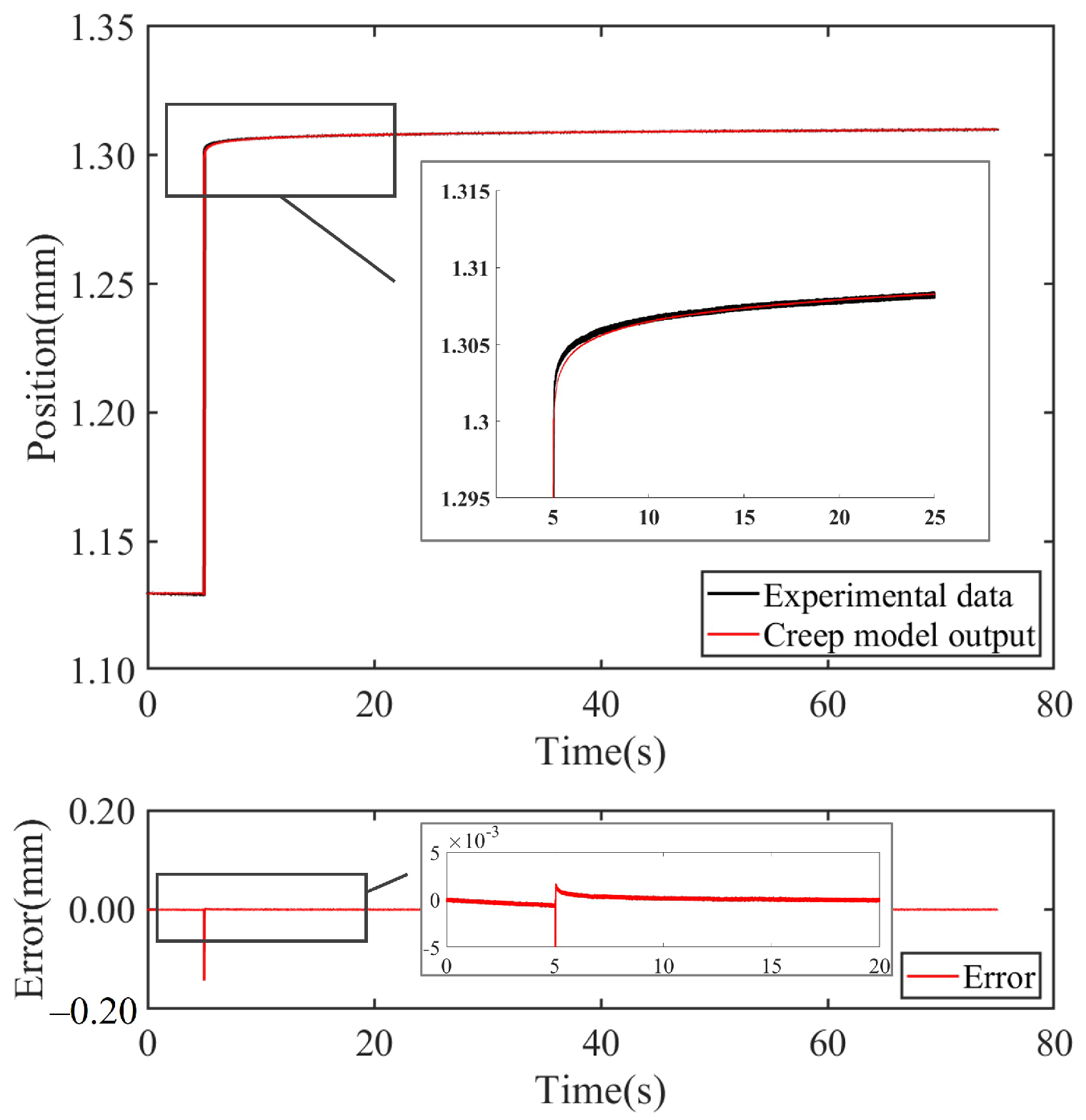
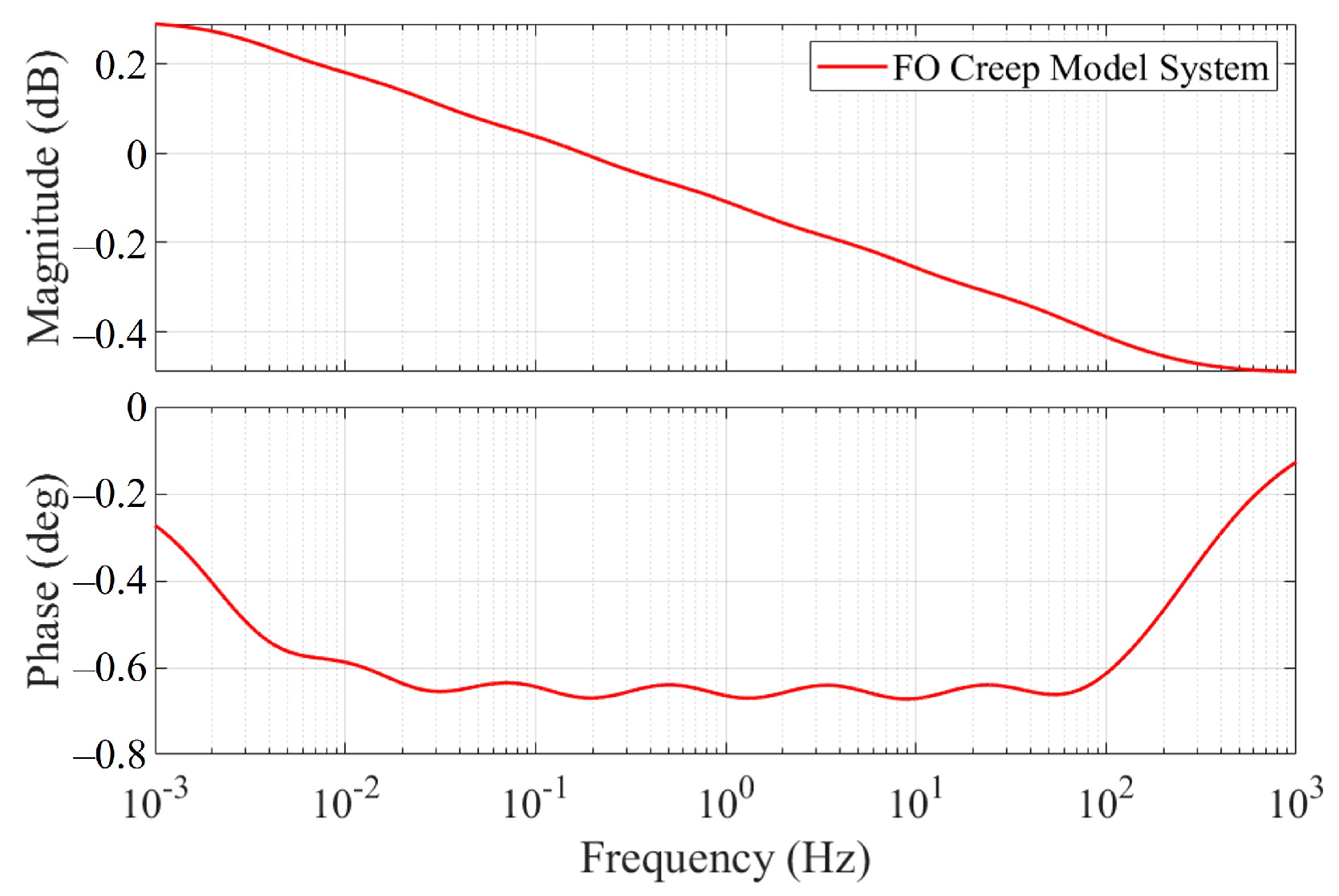
3.2. Properties of the Fractional-Order Creep Model
3.3. Properties of the Coupled Model
4. Identification and Verification of the Fractional-Order Coupled Model
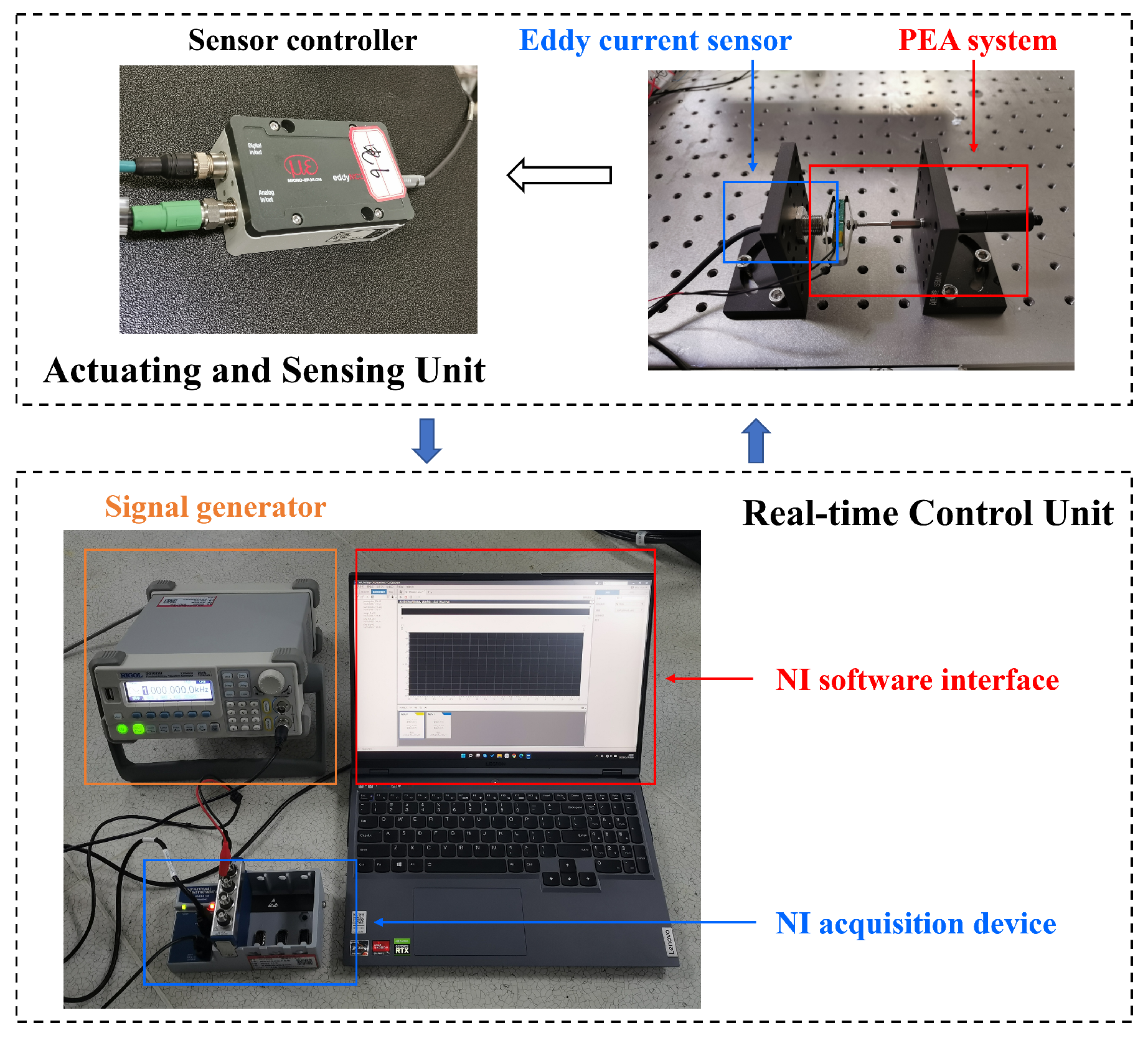
4.1. Experimental Setup
4.2. The FOH Model Parameters Identification
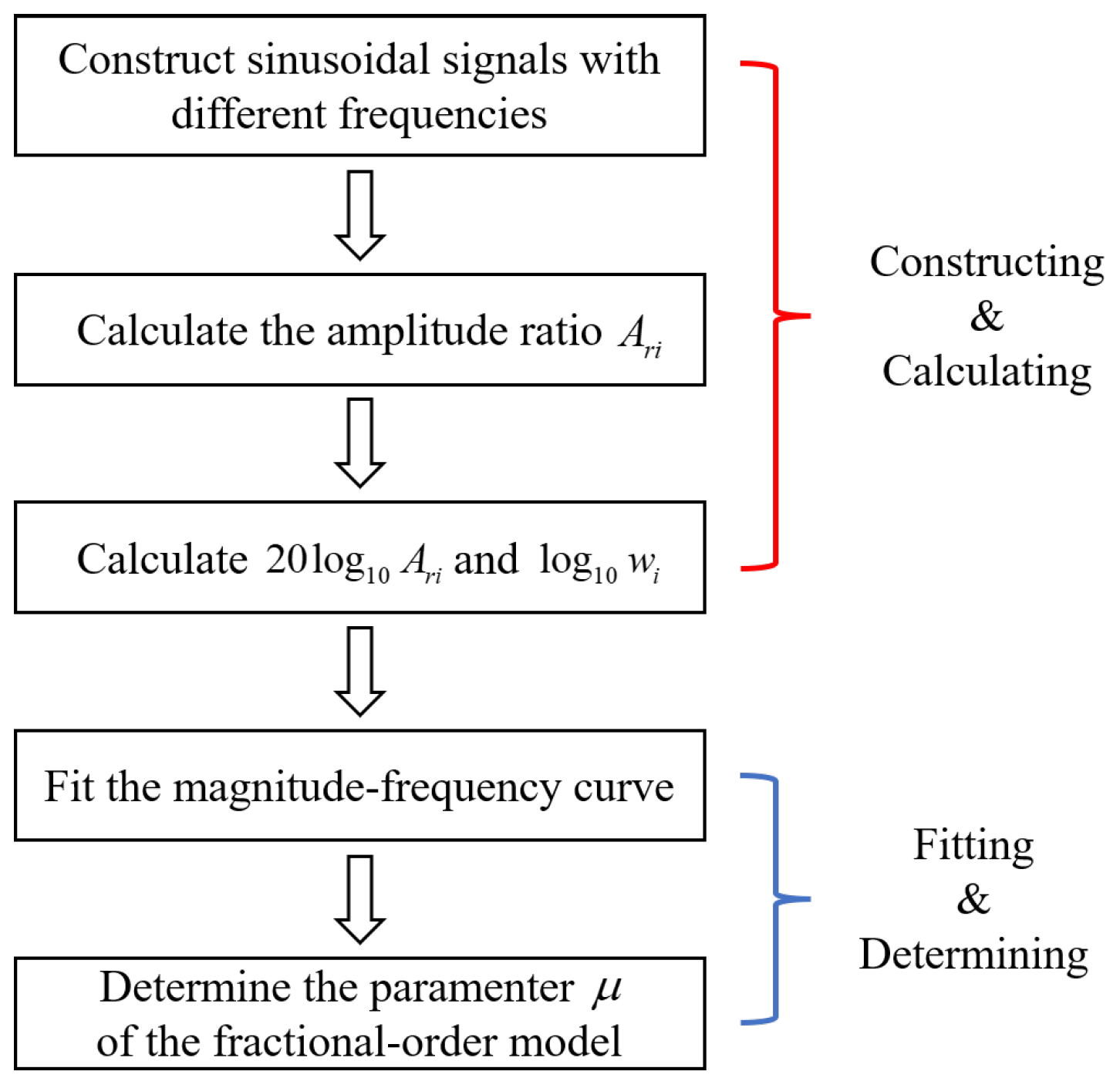
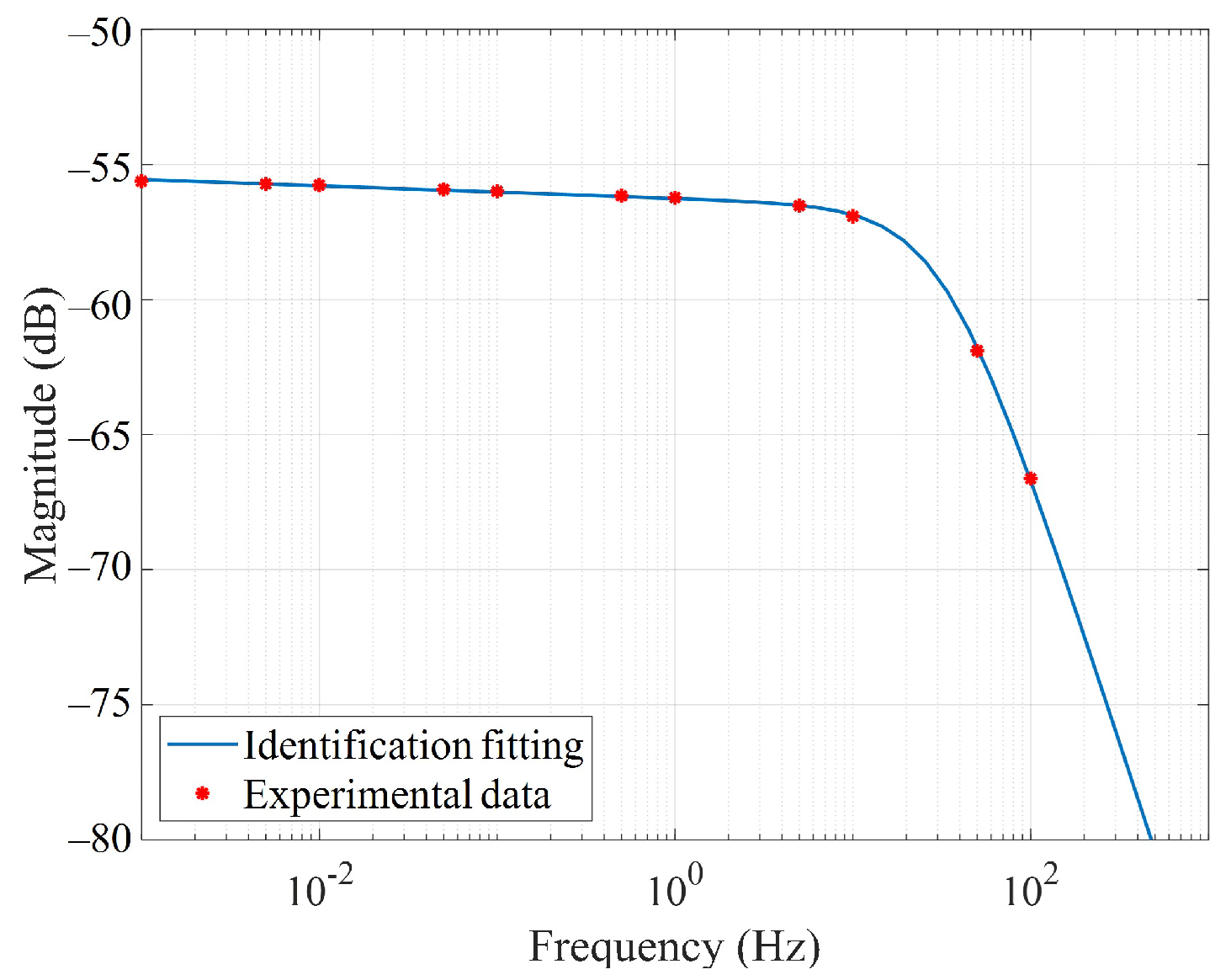
4.3. Fractional-Order Creep Model Parameter Identification
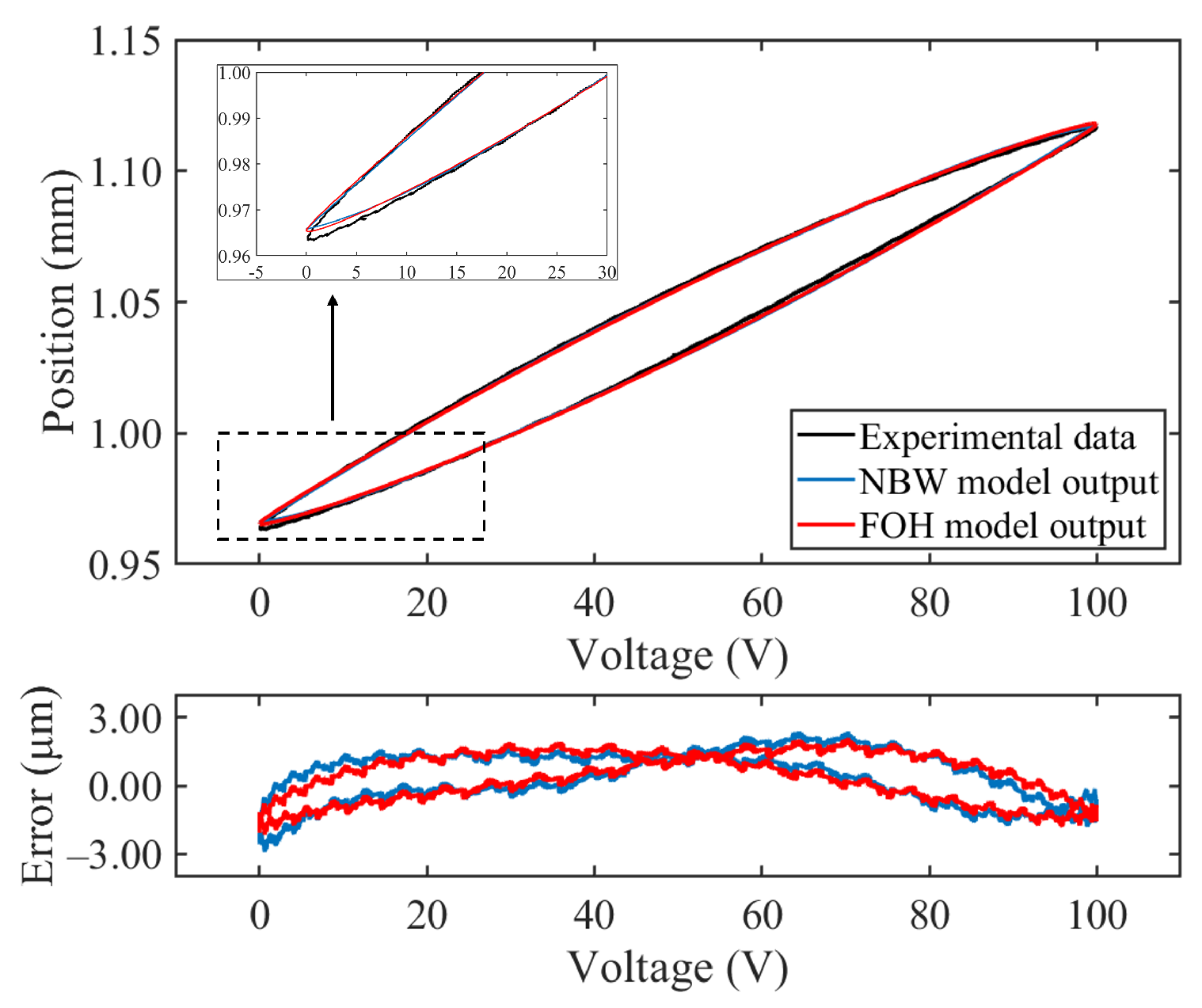
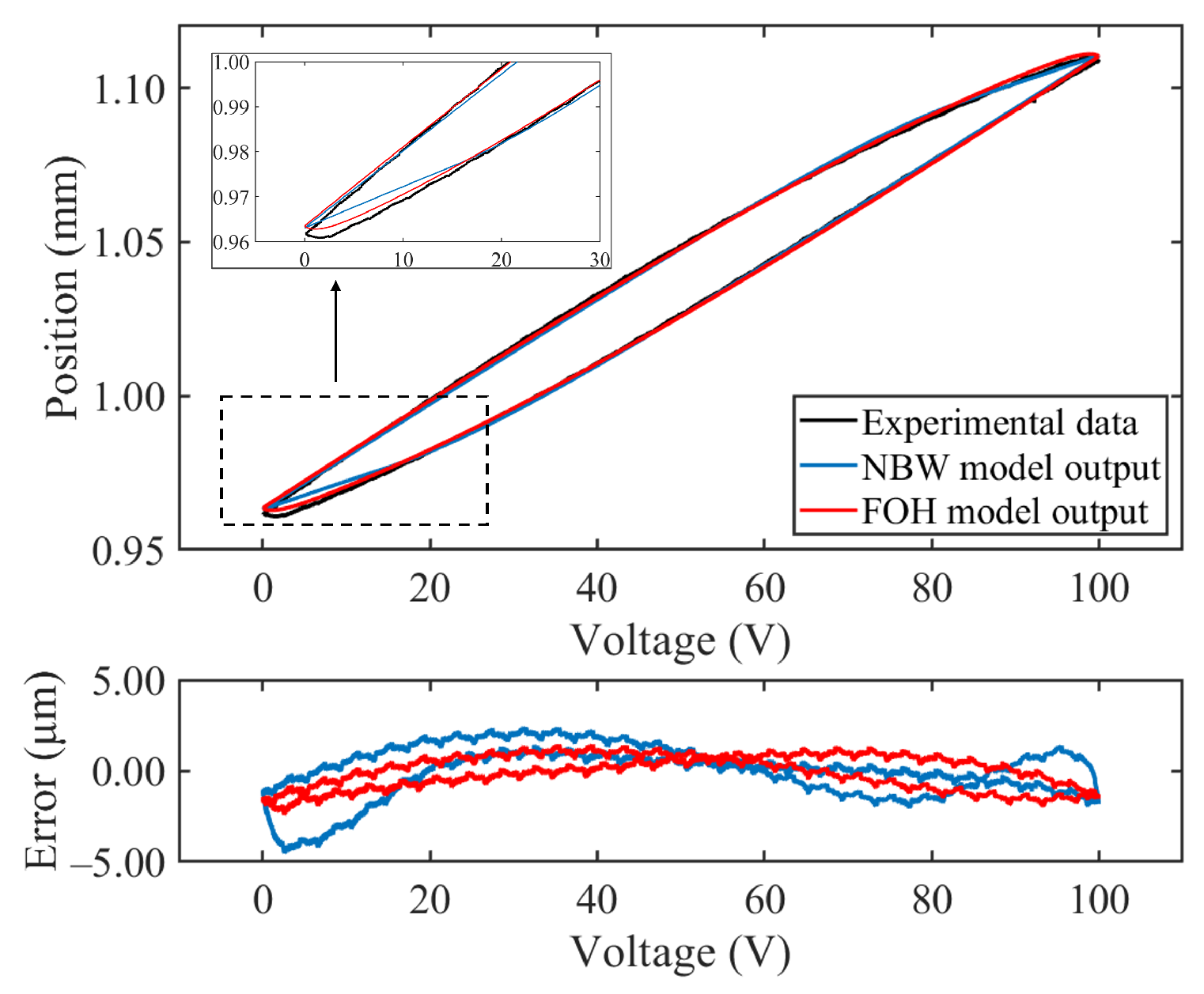
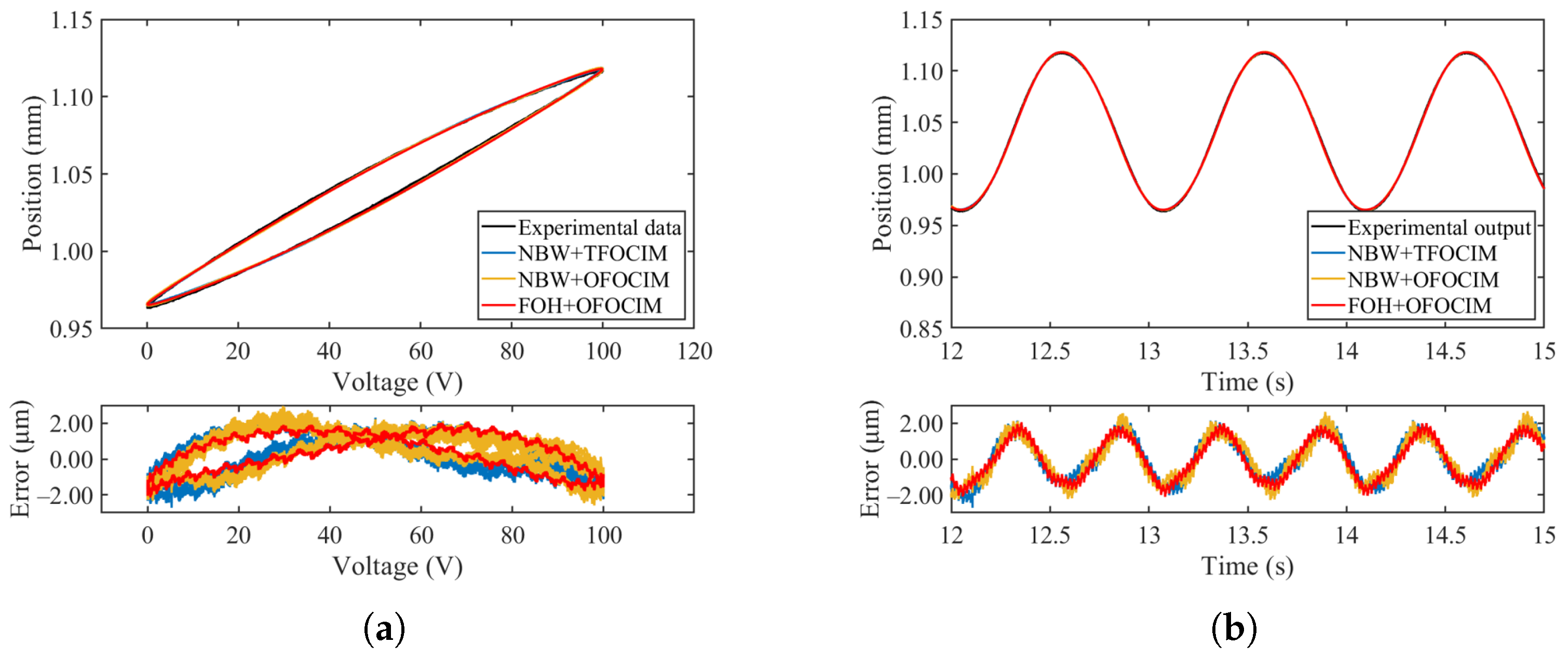
4.4. Experimental Validation of the Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jang, D.D.; Jung, H.J.; Shin, Y.H.; Moon, S.J.; Moon, Y.J.; Oh, J. Feasibility study on a hybrid mount system with air springs and piezo-stack actuators for micro-vibration control. J. Intell. Mater. Syst. Struct. 2012, 23, 515–526. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Q.; Zhang, K.; Shao, L. Design of micro-vibration suppression platform based on piezo-stack array intelligent structure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 799–810. [Google Scholar] [CrossRef]
- Zhiyuan, G.; Muyao, S.; Yiru, W.; Xiaojin, Z. Hybrid De-Jaya Optimized Variable Step-Size and Tap-Length Adaptive Filtering Control Algorithm Active Micro-vibration Control with Piezoelectric Stack Actuator. J. Vib. Eng. Technol. 2022, 10, 887–896. [Google Scholar] [CrossRef]
- Huang, D.; Min, D.; Jian, Y.; Li, Y. Current-cycle iterative learning control for high-precision position tracking of piezoelectric actuator system via active disturbance rejection control for hysteresis compensation. IEEE Trans. Ind. Electron. 2019, 67, 8680–8690. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, L.; Long, Z.; Wang, M.Y. Fuzzy adaptive sliding mode control for the precision position of piezo-actuated nano positioning stage. Int. J. Precis. Eng. Manuf. 2018, 19, 1447–1456. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wu, W.; Falconi, C. Piezotronics and piezo-phototronics with third-generation semiconductors. MRS Bull. 2018, 43, 922–927. [Google Scholar] [CrossRef]
- Sun, C.; Wu, F.; Wallis, D.J.; Shen, M.H.; Yuan, F.; Yang, J.; Wu, J.; Xie, Z.; Liang, D.; Wang, H.; et al. Gallium nitride: A versatile compound semiconductor as novel piezoelectric film for acoustic tweezer in manipulation of cancer cells. IEEE Trans. Electron Devices 2020, 67, 3355–3361. [Google Scholar] [CrossRef]
- Shan, G.; Zhu, M. A piezo stack energy harvester with frequency up-conversion for rail track vibration. Mech. Syst. Signal Process. 2022, 178, 109268. [Google Scholar] [CrossRef]
- Wen, Z.; Ding, Y.; Liu, P.; Ding, H. An efficient identification method for dynamic systems with coupled hysteresis and linear dynamics: Application to piezoelectric-actuated nanopositioning stages. IEEE/ASME Trans. Mechatron. 2019, 24, 326–337. [Google Scholar] [CrossRef]
- Ando, T. High-speed atomic force microscopy. Curr. Opin. Chem. Biol. 2019, 51, 105–112. [Google Scholar] [CrossRef]
- Habibullah; Pota, H.R.; Petersen, I.R.; Rana, M.S. Creep, Hysteresis, and Cross-Coupling Reduction in the High-Precision Positioning of the Piezoelectric Scanner Stage of an Atomic Force Microscope. IEEE Trans. Nanotechnol. 2013, 12, 1125–1134. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Adaptive Sliding Mode Control With Perturbation Estimation and PID Sliding Surface for Motion Tracking of a Piezo-Driven Micromanipulator. IEEE Trans. Control Syst. Technol. 2010, 18, 798–810. [Google Scholar] [CrossRef]
- Grzybek, D.; Sioma, A. Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator. Energies 2022, 15, 8267. [Google Scholar] [CrossRef]
- Richter, H.; Misawa, E.; Lucca, D.; Lu, H. Modeling nonlinear behavior in a piezoelectric actuator. Precis. Eng. 2001, 25, 128–137. [Google Scholar] [CrossRef]
- Grech, C.; Buzio, M.; Pentella, M.; Sammut, N. Dynamic ferromagnetic hysteresis modelling using a Preisach-recurrent neural network model. Materials 2020, 13, 2561. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, S.; Ruderman, M.; Strohla, T.; Bertram, T. Use of Jiles–Atherton and Preisach Hysteresis Models for Inverse Feed-Forward Control. IEEE Trans. Magn. 2010, 46, 3984–3989. [Google Scholar] [CrossRef]
- Li, Z.; Xiong, L.; Tang, L.; Yang, W.; Liu, K.; Mace, B. Modeling and harmonic analysis of energy extracting performance of a piezoelectric nonlinear energy sink system with AC and DC interface circuits. Mech. Syst. Signal Process. 2021, 155, 107609. [Google Scholar] [CrossRef]
- Fujii, F.; Tatebatake, K.; Morita, K.; Shiinoki, T. A Bouc-Wen model-based compensation of the frequency-dependent hysteresis of a piezoelectric actuator exhibiting odd harmonic oscillation. Actuators 2018, 7, 37. [Google Scholar] [CrossRef]
- Habineza, D.; Rakotondrabe, M.; Le Gorrec, Y. Bouc–Wen Modeling and Feedforward Control of Multivariable Hysteresis in Piezoelectric Systems: Application to a 3-DOF Piezotube Scanner. IEEE Trans. Control Syst. Technol. 2015, 23, 1797–1806. [Google Scholar] [CrossRef]
- Xie, S.L.; Liu, H.T.; Mei, J.P.; Gu, G.Y. Modeling and compensation of asymmetric hysteresis for pneumatic artificial muscles with a modified generalized Prandtl–Ishlinskii model. Mechatronics 2018, 52, 49–57. [Google Scholar] [CrossRef]
- Wang, W.; Wang, R.; Chen, Z.; Sang, Z.; Lu, K.; Han, F.; Wang, J.; Ju, B. A new hysteresis modeling and optimization for piezoelectric actuators based on asymmetric Prandtl-Ishlinskii model. Sens. Actuators A Phys. 2020, 316, 112431. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and High Dynamic Compensating the Rate-Dependent Hysteresis of Piezoelectric Actuators via a Novel Modified Inverse Preisach Model. IEEE Trans. Control Syst. Technol. 2013, 21, 1549–1557. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, Y.; Su, M. Modeling of hysteresis in piezoelectric actuators using neural networks. Mech. Syst. Signal Process. 2009, 23, 2699–2711. [Google Scholar] [CrossRef]
- Dang, X.; Tan, Y. RBF neural networks hysteresis modelling for piezoceramic actuator using hybrid model. Mech. Syst. Signal Process. 2007, 21, 430–440. [Google Scholar] [CrossRef]
- Jung, H.; Gweon, D.G. Creep characteristics of piezoelectric actuators. Rev. Sci. Instruments 2000, 71, 1896–1900. [Google Scholar] [CrossRef]
- Changhai, R.; Lining, S. Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sens. Actuators A Phys. 2005, 122, 124–130. [Google Scholar] [CrossRef]
- Georgiou, H.; Mrad, R.B. Dynamic electromechanical drift model for PZT. Mechatronics 2008, 18, 81–89. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M. Motion control of piezoceramic actuators with creep, hysteresis and vibration compensation. Sens. Actuators A Phys. 2013, 197, 76–87. [Google Scholar] [CrossRef]
- Lapchuk, A.; Yun, S.K.; An, S.; Song, J.; Yurlov, V.; Bourim, E.; Yang, H.; Park, H. Creep compensation method in a thin film PZT structure for a spatial optical modulator. Sens. Actuators A Phys. 2011, 167, 406–415. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, X.B. A Survey of Modeling and Control Issues for Piezo-electric Actuators. J. Dyn. Syst. Meas. Control 2014, 137, 014001. [Google Scholar] [CrossRef]
- Liu, L.; Tan, K.K.; Teo, C.S.; Chen, S.L.; Lee, T.H. Development of an Approach Toward Comprehensive Identification of Hysteretic Dynamics in Piezoelectric Actuators. IEEE Trans. Control Syst. Technol. 2013, 21, 1834–1845. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Qi, N. Creep modeling and identification for piezoelectric actuators based on fractional-order system. Mechatronics 2013, 23, 840–847. [Google Scholar] [CrossRef]
- Wen, Z.; Ding, Y.; Liu, P.; Ding, H. Direct integration method for time-delayed control of second-order dynamic systems. J. Dyn. Syst. Meas. Control 2017, 139, 061001. [Google Scholar] [CrossRef]
- Liu, L.; Yun, H.; Li, Q.; Ma, X.; Chen, S.L.; Shen, J. Fractional Order Based Modeling and Identification of Coupled Creep and Hysteresis Effects in Piezoelectric Actuators. IEEE/ASME Trans. Mechatron. 2020, 25, 1036–1044. [Google Scholar] [CrossRef]
- Hilfer, R. Fractional diffusion based on Riemann-Liouville fractional derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Xue, D. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018. [Google Scholar]
- Nonnenmacher, T.F.; Metzler, R. On the Riemann-Liouville fractional calculus and some recent applications. Fractals 1995, 3, 557–566. [Google Scholar] [CrossRef]
- Garg, V.; Singh, K. An improved Grunwald-Letnikov fractional differential mask for image texture enhancement. Int. J. Adv. Comput. Sci. Appl. 2012, 3. [Google Scholar] [CrossRef]
- Chakraborty, M.; Maiti, D.; Konar, A.; Janarthanan, R. A study of the Grunwald-Letnikov definition for minimizing the effects of random noise on fractional order differential equations. In Proceedings of the 2008 4th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 12–14 December 2008; pp. 449–456. [Google Scholar]
- Oustaloup, A.; Moreau, X.; Nouillant, M. The CRONE suspension. Control Eng. Pract. 1996, 4, 1101–1108. [Google Scholar] [CrossRef]
- Sar, E.Y.; Giresunlu, I.B. Fractional differential equations. Pramana J. Phys 2016, 87, 17. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F. Rules for selecting the parameters of Oustaloup recursive approximation for the simulation of linear feedback systems containing PIλDμ controller. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1852–1861. [Google Scholar] [CrossRef]
- Fang, J.; Yin, Z. Dielectric Physics; Science Press: Beijing, China, 1989; pp. 261–303. [Google Scholar]
- Auciello, O.; Scott, J.F.; Ramesh, R. The physics of ferroelectric memories. Phys. Today 1998, 51, 22–27. [Google Scholar] [CrossRef]
- Wang Chunlei, L.J.; Minglei, Z. Piezoelectric Ferroelectric Physics; Science Press of China: Beijing, China, 2009. [Google Scholar]
- Huang, C.; Cai, K.; Wang, Y.; Bai, Y.; Guo, D. Revealing the real high temperature performance and depolarization characteristics of piezoelectric ceramics by combined in situ techniques. J. Mater. Chem. C 2018, 6, 1433–1444. [Google Scholar] [CrossRef]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 121. [Google Scholar]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Ikhouane, F.; Hurtado, J.E.; Rodellar, J. Variation of the hysteresis loop with the Bouc-Wen model parameters. Nonlinear Dyn. 2007, 48, 361–380. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Li, Y.; Yang, X.; Yao, J. A Fractional-Order Normalized Bouc-Wen Model for Piezoelectric Hysteresis Nonlinearity. IEEE/ASME Trans. Mechatron. 2021, 27, 126–136. [Google Scholar] [CrossRef]
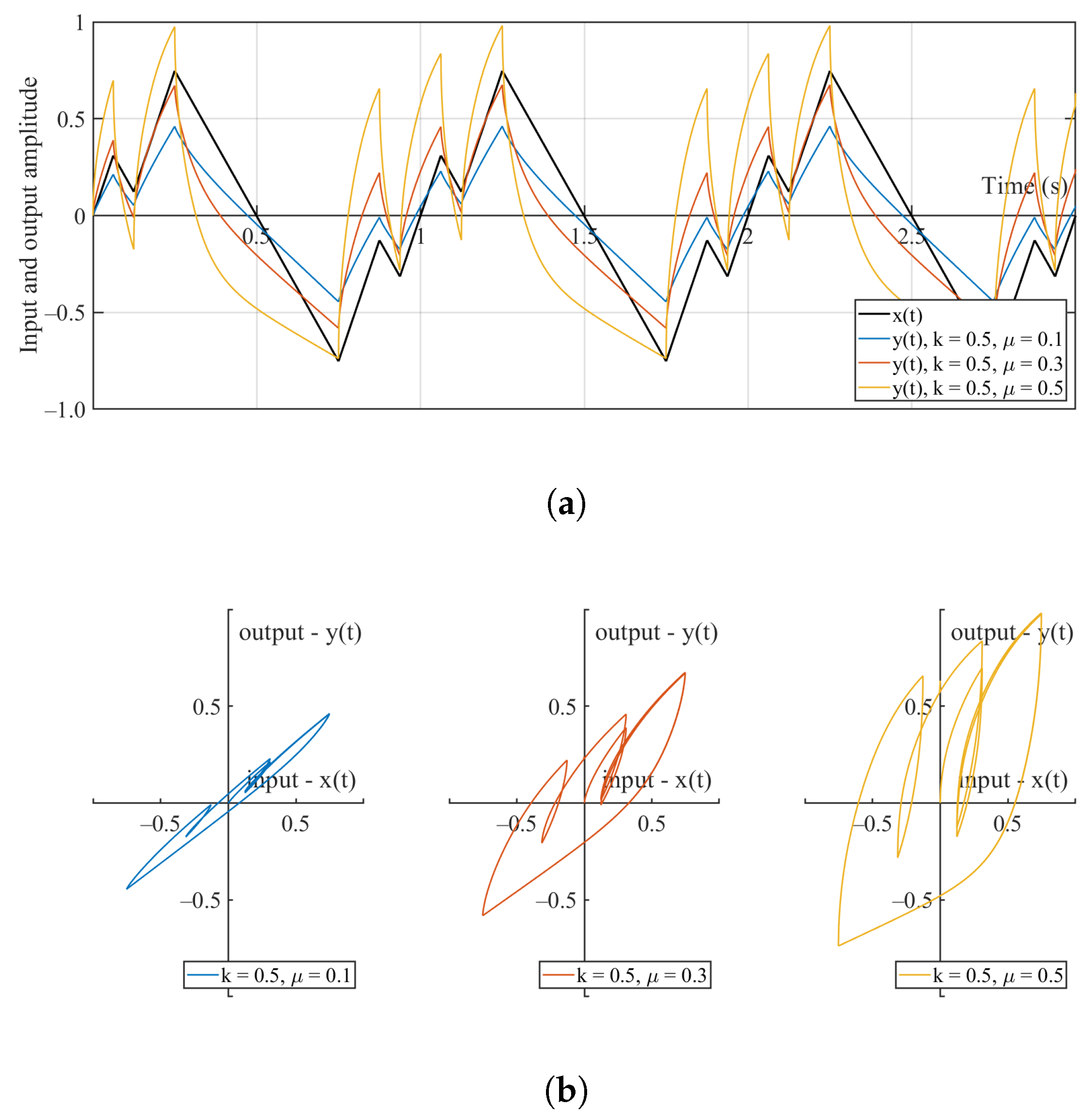
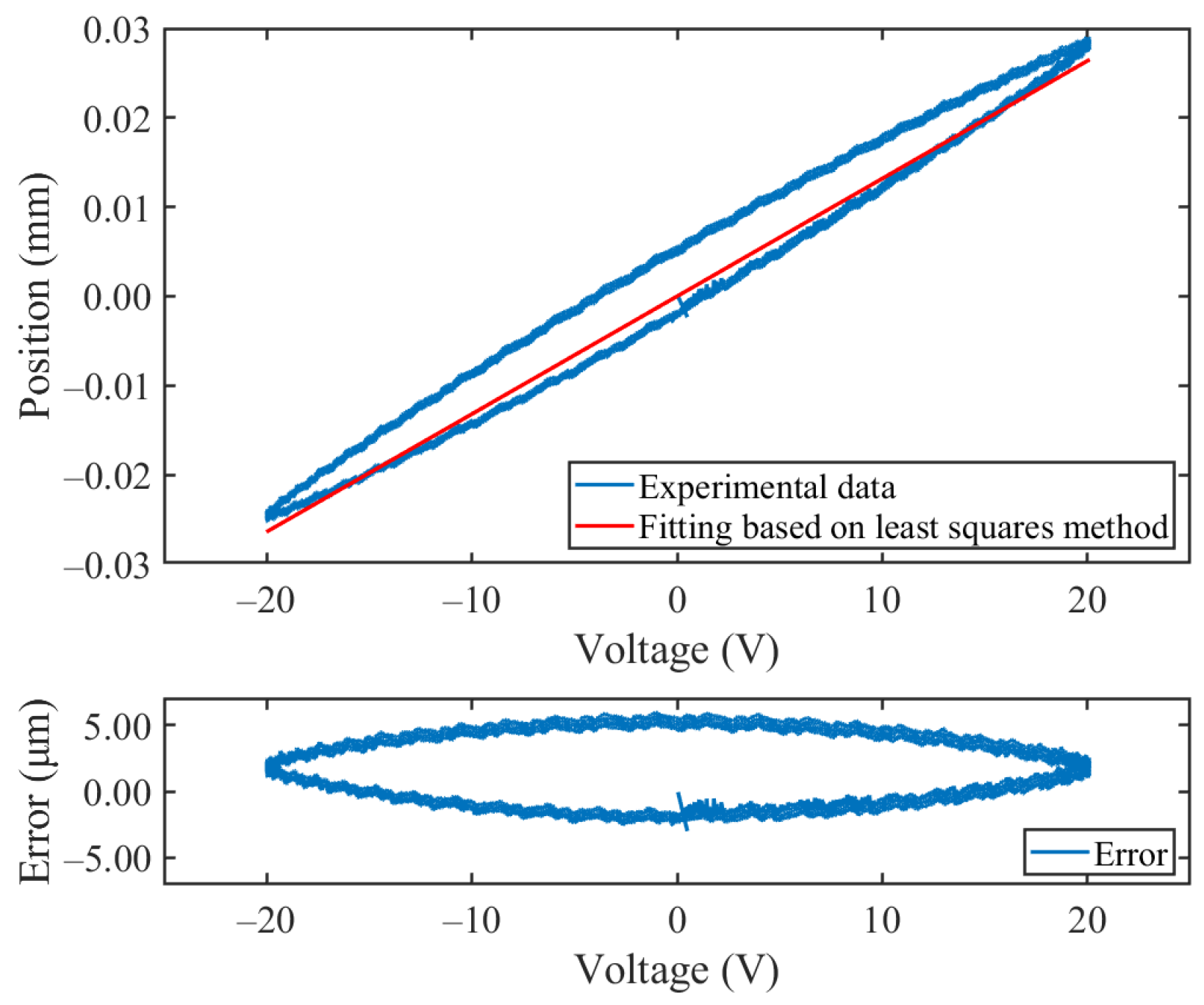
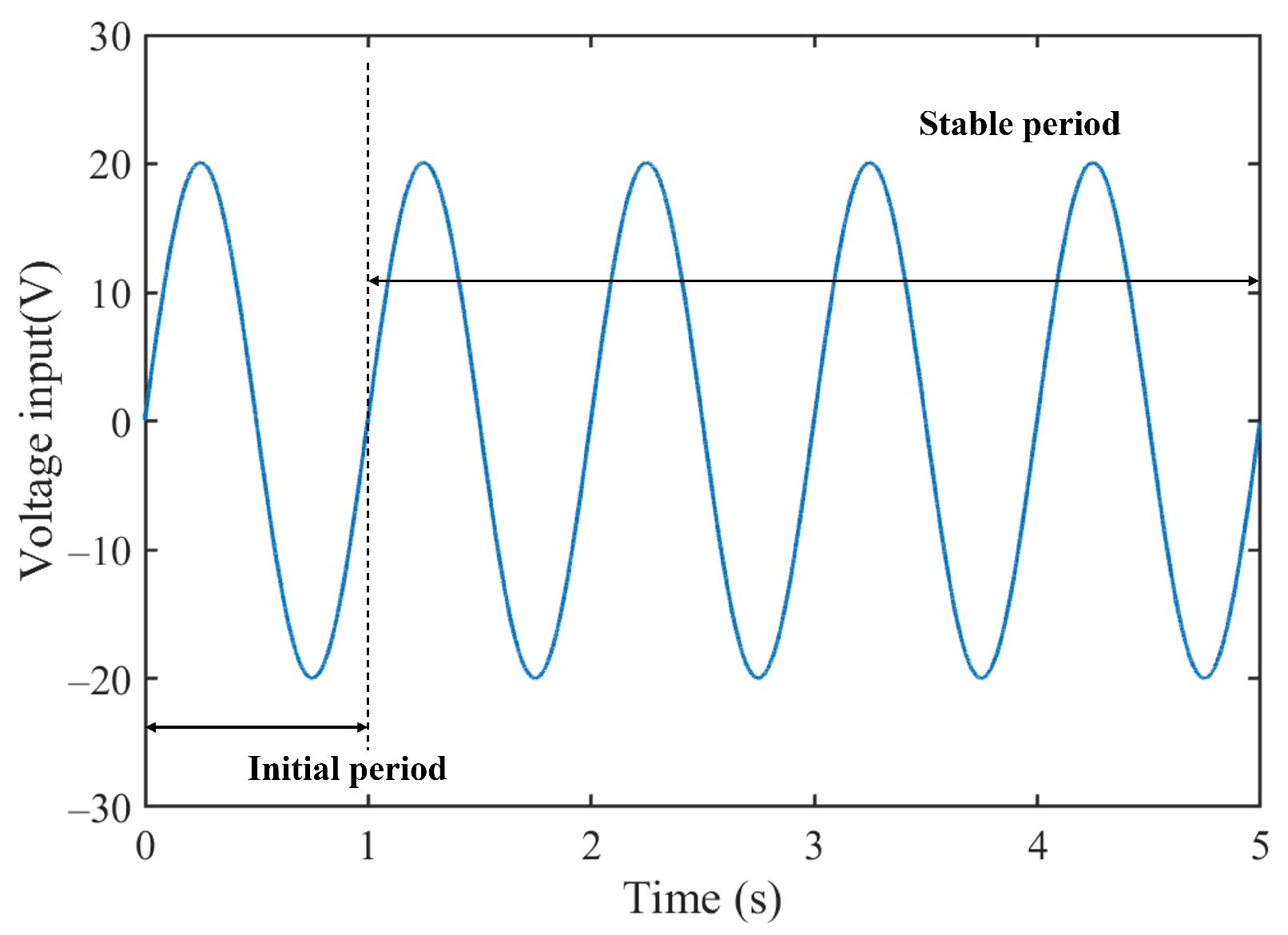
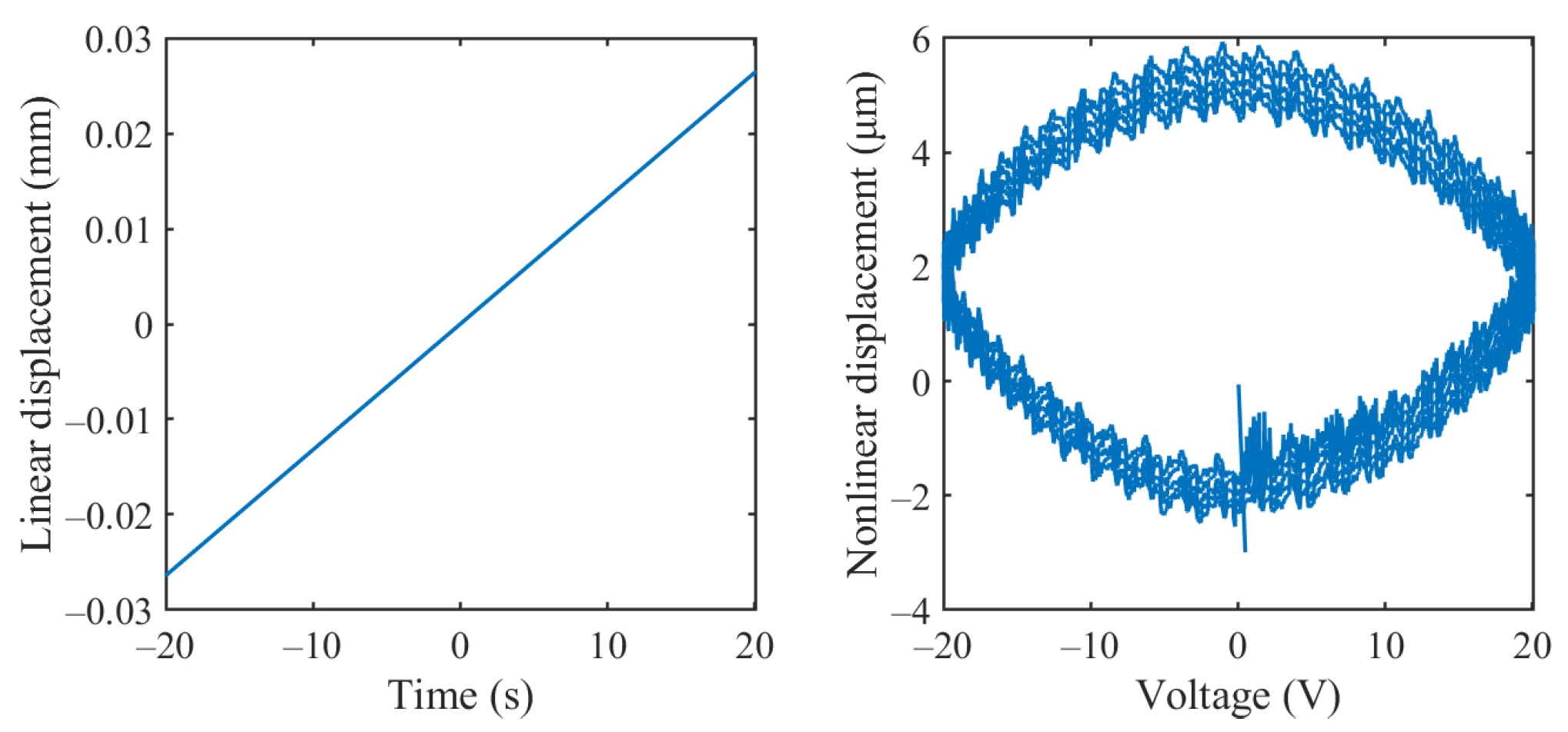



| FOH Model | |
|---|---|
| −0.0017418 | |
| 0.0044141 | |
| 0.02729 | |
| 0.02729 | |
| −0.13501 | |
| 1.11008‰ | |
| NBW Model | |
|---|---|
| 0.0021924 | |
| −0.040845 | |
| 0.19028 | |
| 1.288 | |
| n | 1.6504 |
| 1.1973‰ | |
| Input Signal | Type | ||
|---|---|---|---|
| Sinusoidal input | NBW model | 1.19773e‰ | 0.764227‰ |
| FOH model | 1.11008‰ | 0.708572‰ | |
| Improvement | 7.31801% | 7.28252% | |
| Triangular input | NBW model | 1.35698‰ | 1.208703‰ |
| FOH model | 0.90145‰ | 0.802953‰ | |
| Improvement | 33.56903 % | 33.56904% |
| Coupling Type | ||
|---|---|---|
| NBW + TFOCIM | 1.152877‰ | 0.735807‰ |
| NBW + OFOCIM | 1.152490‰ | 0.735588‰ |
| Improvement | 0.0335682% | 0.029763% |
| FOH + OFOCIM | 1.10993‰ | 0.708479‰ |
| Improvement | 3.7252% | 3.71402% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Luo, Y.; Luo, X.; Chen, Y.; Liu, W. Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects. Fractal Fract. 2024, 8, 3. https://doi.org/10.3390/fractalfract8010003
Xu Y, Luo Y, Luo X, Chen Y, Liu W. Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects. Fractal and Fractional. 2024; 8(1):3. https://doi.org/10.3390/fractalfract8010003
Chicago/Turabian StyleXu, Yifan, Ying Luo, Xin Luo, Yangquan Chen, and Wei Liu. 2024. "Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects" Fractal and Fractional 8, no. 1: 3. https://doi.org/10.3390/fractalfract8010003
APA StyleXu, Y., Luo, Y., Luo, X., Chen, Y., & Liu, W. (2024). Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects. Fractal and Fractional, 8(1), 3. https://doi.org/10.3390/fractalfract8010003







