The Finite Difference Method and Analysis for Simulating the Unsteady Generalized Maxwell Fluid with a Multi-Term Time Fractional Derivative
Abstract
1. Introduction
2. Preliminary Knowledge of the Finite-Difference Method
3. Stability Analysis of the Finite Difference Scheme
4. Convergence Analysis of the Finite Difference Scheme
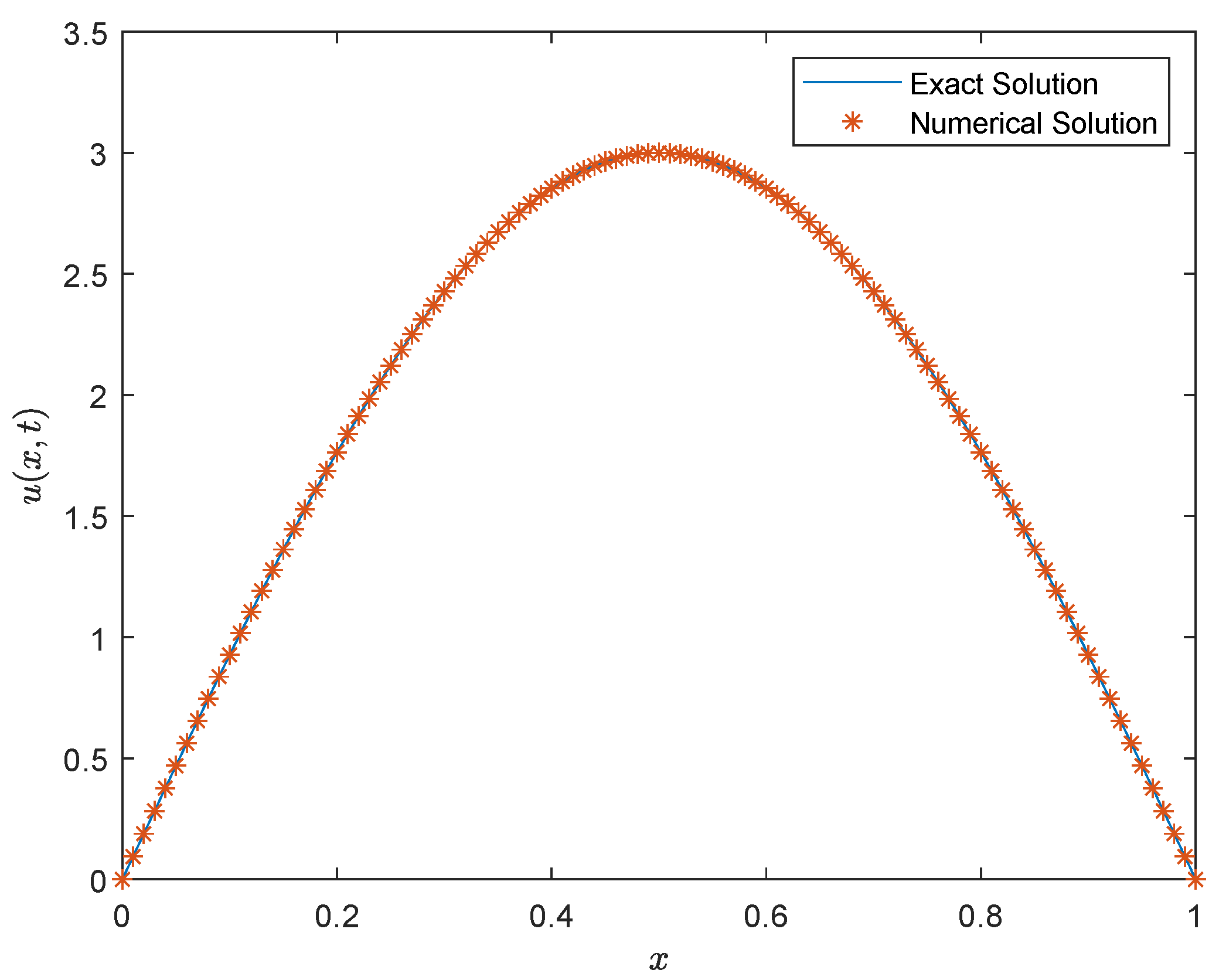
5. Numerical Simulation and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, B.; Zhang, Y.; Zhou, X.; Chen, C.; Li, W. Lattice Boltzmann simulation of two-phase flow involving non-Newtonian fluid in rough channels. Therm. Sci. Eng. Prog. 2019, 10, 309–316. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Nagaraju, K.R.; Kumar Vinay, P.N.; Nadagouda, M.N.; Baeeacer, R.; Sheremet, M.A. Effects of Dufour and Soret mechanisms on MHD mixed convective-radiative non-Newtonian liquid flow and heat transfer over a porous sheet. Therm. Sci. Eng. Prog. 2020, 16, 100459. [Google Scholar] [CrossRef]
- Yanbarisov, R.; Efremov, Y.; Kosheleva, N.; Timashev, P.; Vassilevski, Y. Numerical modelling of multicellular spheroid compression: Viscoelastic fluid vs. viscoelastic solid. Mathematics 2021, 9, 2333. [Google Scholar] [CrossRef]
- Rasheed, A.; Anwar, M.S. Interplay of chemical reacting species in a fractional viscoelastic fluid flow. J. Mol. Liq. 2019, 273, 576–588. [Google Scholar] [CrossRef]
- Li, G.; Lauga, E.; Ardekani, A.M. Microswimming in viscoelastic fluids. J. Non-Newton. Fluid Mech. 2021, 297, 104655. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Three dimensional MHD flow and heat transfer over a stretching/shrinking surface in a viscoelastic fluid with various physical effects. Int. J. Heat Mass Transf. 2014, 78, 150–155. [Google Scholar] [CrossRef]
- Li, B.; Liu, G.; Liu, S.; Chen, L. Research on viscoelastic fluid unsteady flow model based on torque loss correction. Polym. Test. 2021, 93, 106927. [Google Scholar] [CrossRef]
- Turan, O.; Yigit, S.; Chakraborty, N. Mixed convection of power-law fluids in cylindrical enclosures with a cold rotating top cover and a stationary heated bottom wall. Therm. Sci. Eng. Prog. 2020, 18, 100541. [Google Scholar] [CrossRef]
- Kundu, S.; Pani, A.K. Stabilization of Kelvin-Voigt viscoelastic fluid flow model. Appl. Anal. 2019, 98, 2284–2307. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, N.; Sajid, M.; Hayat, T. Heat transfer characteristics in oscillatory hydromagnetic channel flow of Maxwell fluid using Cattaneo-Christov model. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2019, 89, 377–385. [Google Scholar] [CrossRef]
- Khan, M.; Ahmed, A.; Irfan, M.; Ahmed, J. Analysis of Cattaneo-Christov theory for unsteady flow of Maxwell fluid over stretching cylinder. J. Therm. Anal. Calorim. 2021, 144, 145–154. [Google Scholar] [CrossRef]
- Sun, X.; Wang, S.; Zhao, M.; Zhang, Q. Numerical solution of oscillatory flow of Maxwell fluid in a rectangular straight duct. Appl. Math. Mech. 2019, 40, 1647–1656. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.N.; Nadeem, S. Mathematical analysis of heat and mass transfer in a Maxwell fluid with double stratification. Phys. Scr. 2020, 96, 025202. [Google Scholar] [CrossRef]
- Haroon, T.; Siddiqui, A.M.; Ullah, H.; Lu, D. Flow of Maxwell fluid in a channel with uniform porous walls. J. Appl. Anal. Comput. 2021, 11, 1322–1347. [Google Scholar]
- Ahmed, A.; Khan, M.; Zafar, A.; Yasir, M.; Ayub, M. Analysis of Soret-Dufour theory for energy transport in bioconvective flow of Maxwell fluid. Ain Shams Eng. J. 2023, 14, 102045. [Google Scholar] [CrossRef]
- Arora, S.; Mathur, T.; Agarwal, S.; Tiwari, K.; Gupta, P. Applications of fractional calculus in computer vision: A survey. Neurocomputing 2022, 489, 407–428. [Google Scholar] [CrossRef]
- Ikram, M.D.; Imran, M.A.; Chu, Y.; Akgül, A. MHD flow of a Newtonian fluid in symmetric channel with ABC fractional model containing hybrid nanoparticles. Comb. Chem. High Throughput Screen. 2022, 25, 1087–1102. [Google Scholar]
- Abbes, A.; Ouannas, A.; Shawagfeh, N. An incommensurate fractional discrete macroeconomic system: Bifurcation, chaos, and complexity. Chin. Phys. B 2023, 32, 030203. [Google Scholar] [CrossRef]
- Meng, R. Application of fractional calculus to modeling the non-linear behaviors of ferroelectric polymer composites: Viscoelasticity and dielectricity. Membranes 2021, 11, 409. [Google Scholar] [CrossRef]
- Weiss, C.J.; van Bloemen Waanders, B.G.; Antil, H. Fractional operators applied to geophysical electromagnetics. Geophys. J. Int. 2020, 220, 1242–1259. [Google Scholar] [CrossRef]
- Tan, W.; Xu, M. Plane surface suddenly set in motion in a viscoelastic fluid with fractional Maxwell model. Acta Mech. Sin. 2002, 18, 342–349. [Google Scholar]
- Qi, H.; Jin, H. Unsteady rotating flows of a viscoelastic fluid with the fractional Maxwell model between coaxial cylinders. Acta Mech. Sin. 2006, 22, 301–305. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Fetecau, C. Flow of a viscoelastic fluid with the fractional Maxwell model between two side walls perpendicular to a plate. Appl. Math. Comput. 2008, 200, 459–464. [Google Scholar] [CrossRef]
- Razzaq, A.; Seadawy, A.R.; Raza, N. Heat transfer analysis of viscoelastic fluid flow with fractional Maxwell model in the cylindrical geometry. Phys. Scr. 2020, 95, 115220. [Google Scholar] [CrossRef]
- Huang, J.; Chen, L.; Li, S.; Guo, J.; Li, Y. Numerical study for the Performance of Viscoelastic Fluids on Displacing Oil Based on the Fractional-Order Maxwell Model. Polymers 2022, 14, 5381. [Google Scholar] [CrossRef]
- Akyildiz, F.T.; Siginer, D.A. Exact solution of the startup electroosmotic flow of generalized Maxwell fluids in triangular microducts. J. Fluids Eng. 2021, 143, 101302. [Google Scholar] [CrossRef]
- Riaz, M.B.; Atangana, A.; Iftikhar, N. Heat and mass transfer in Maxwell fluid in view of local and non-local differential operators. J. Therm. Anal. Calorim. 2021, 143, 4313–4329. [Google Scholar] [CrossRef]
- Raza, N.; Ullah, M.A. A comparative study of heat transfer analysis of fractional Maxwell fluid by using Caputo and Caputo-Fabrizio derivatives. Can. J. Phys. 2020, 98, 89–101. [Google Scholar] [CrossRef]
- Moosavi, R.; Moltafet, R.; Shekari, Y. Analysis of viscoelastic non-Newtonian fluid over a vertical forward-facing step using the Maxwell fractional model. Appl. Math. Comput. 2021, 401, 126119. [Google Scholar] [CrossRef]
- Saqib, M.; Hanif, H.; Abdeljawad, T.; Khan, I. Heat transfer in MHD flow of maxwell fluid via fractional cattaneo-friedrich model: A finite difference approach. Comput. Mater. Contin. 2020, 65, 1959–1973. [Google Scholar] [CrossRef]
- Moosavi, R.; Moltafet, R.; Lin, C.; Chuang Abel, P. Numerical modeling of fractional viscoelastic non-Newtonian fluids over a backward facing step-Buoyancy driven flow and heat transfer. Therm. Sci. Eng. Prog. 2021, 21, 100767. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, L.; Zhang, X.; Liu, F. Unsteady natural convection boundary layer heat transfer of fractional Maxwell viscoelastic fluid over a vertical plate. Int. J. Heat Mass Transf. 2016, 97, 760–766. [Google Scholar] [CrossRef]
- Fetecau, C.; Athar, M.; Fetecau, C. Unsteady ow of a generalized Maxwell fuid with fractional derivative due to a constantly accelerating plate. Comput. Math. Appl. 2009, 57, 596–603. [Google Scholar]
- Podlubny, I. Fractionsl Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]

| , | Order | Order | ||
| 1/40 | 2.8621 × | 4.0476 × | ||
| 1/80 | 1.4087 × | 1.023 | 1.9922 × | 1.023 |
| 1/160 | 6.9717 × | 1.015 | 9.8594 × | 1.015 |
| 1/320 | 3.4645 × | 1.009 | 4.8995 × | 1.009 |
| 1/640 | 1.7278 × | 1.004 | 2.4434 × | 1.004 |
| , | Order | Order | ||
| 1/40 | 3.1908 × | 4.5125 × | ||
| 1/80 | 1.5587 × | 1.034 | 2.2044 × | 1.034 |
| 1/160 | 7.6515 × | 1.027 | 1.0821 × | 1.027 |
| 1/320 | 3.7717 × | 1.021 | 5.3340 × | 1.021 |
| 1/640 | 1.8668 × | 1.015 | 2.6400 × | 1.015 |
| , | Order | Order | ||
| 1/40 | 2.7492 × | 3.8880 × | ||
| 1/80 | 1.3171 × | 1.061 | 1.8626 × | 1.062 |
| 1/160 | 6.3821 × | 1.045 | 9.0257 × | 1.045 |
| 1/320 | 3.1190 × | 1.033 | 4.4110 × | 1.033 |
| 1/640 | 1.5350 × | 1.023 | 2.1708 × | 1.023 |
| , | Order | Order | ||
| 1/40 | 4.4875 × | 6.3463 × | ||
| 1/80 | 2.17887 × | 1.042 | 3.0813 × | 1.042 |
| 1/160 | 1.0650 × | 1.033 | 1.5061 × | 1.033 |
| 1/320 | 5.2380 × | 1.024 | 7.4077 × | 1.024 |
| 1/640 | 2.5912 × | 1.015 | 3.6646 × | 1.015 |
| , | Order | Order | ||
| 1/40 | 5.3384 × | 7.5497 × | ||
| 1/80 | 2.5484 × | 1.067 | 3.6040 × | 1.067 |
| 1/160 | 1.2232 × | 1.059 | 1.7300 × | 1.059 |
| 1/320 | 5.9084 × | 1.050 | 8.3558 × | 1.050 |
| 1/640 | 2.8727 × | 1.040 | 4.0627 × | 1.040 |
| , | Order | Order | ||
| 1/40 | 5.8816 × | 8.3178 × | ||
| 1/80 | 2.7960 × | 1.073 | 3.9541 × | 1.073 |
| 1/160 | 1.3360 × | 1.066 | 1.8893 × | 1.066 |
| 1/320 | 6.4204 × | 1.057 | 9.0799 × | 1.057 |
| 1/640 | 3.1052 × | 1.048 | 4.3915 × | 1.048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, T.; Zhao, Y. The Finite Difference Method and Analysis for Simulating the Unsteady Generalized Maxwell Fluid with a Multi-Term Time Fractional Derivative. Fractal Fract. 2024, 8, 136. https://doi.org/10.3390/fractalfract8030136
Wang Y, Li T, Zhao Y. The Finite Difference Method and Analysis for Simulating the Unsteady Generalized Maxwell Fluid with a Multi-Term Time Fractional Derivative. Fractal and Fractional. 2024; 8(3):136. https://doi.org/10.3390/fractalfract8030136
Chicago/Turabian StyleWang, Yu, Tianzeng Li, and Yu Zhao. 2024. "The Finite Difference Method and Analysis for Simulating the Unsteady Generalized Maxwell Fluid with a Multi-Term Time Fractional Derivative" Fractal and Fractional 8, no. 3: 136. https://doi.org/10.3390/fractalfract8030136
APA StyleWang, Y., Li, T., & Zhao, Y. (2024). The Finite Difference Method and Analysis for Simulating the Unsteady Generalized Maxwell Fluid with a Multi-Term Time Fractional Derivative. Fractal and Fractional, 8(3), 136. https://doi.org/10.3390/fractalfract8030136







