Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo
Abstract
1. Introduction
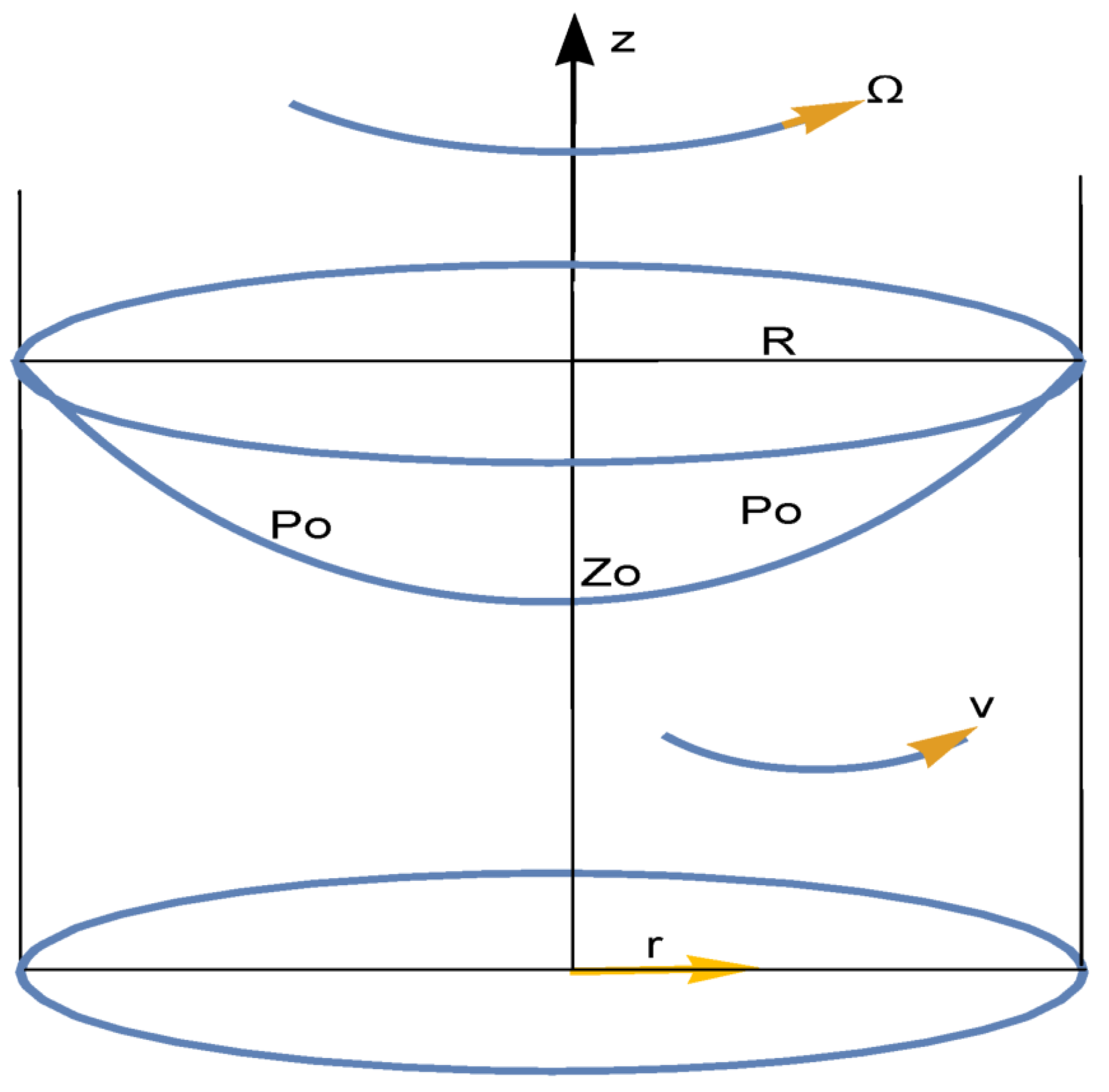
2. Vortex Generation Due to a Rotating Body of Liquid in Fractional Models
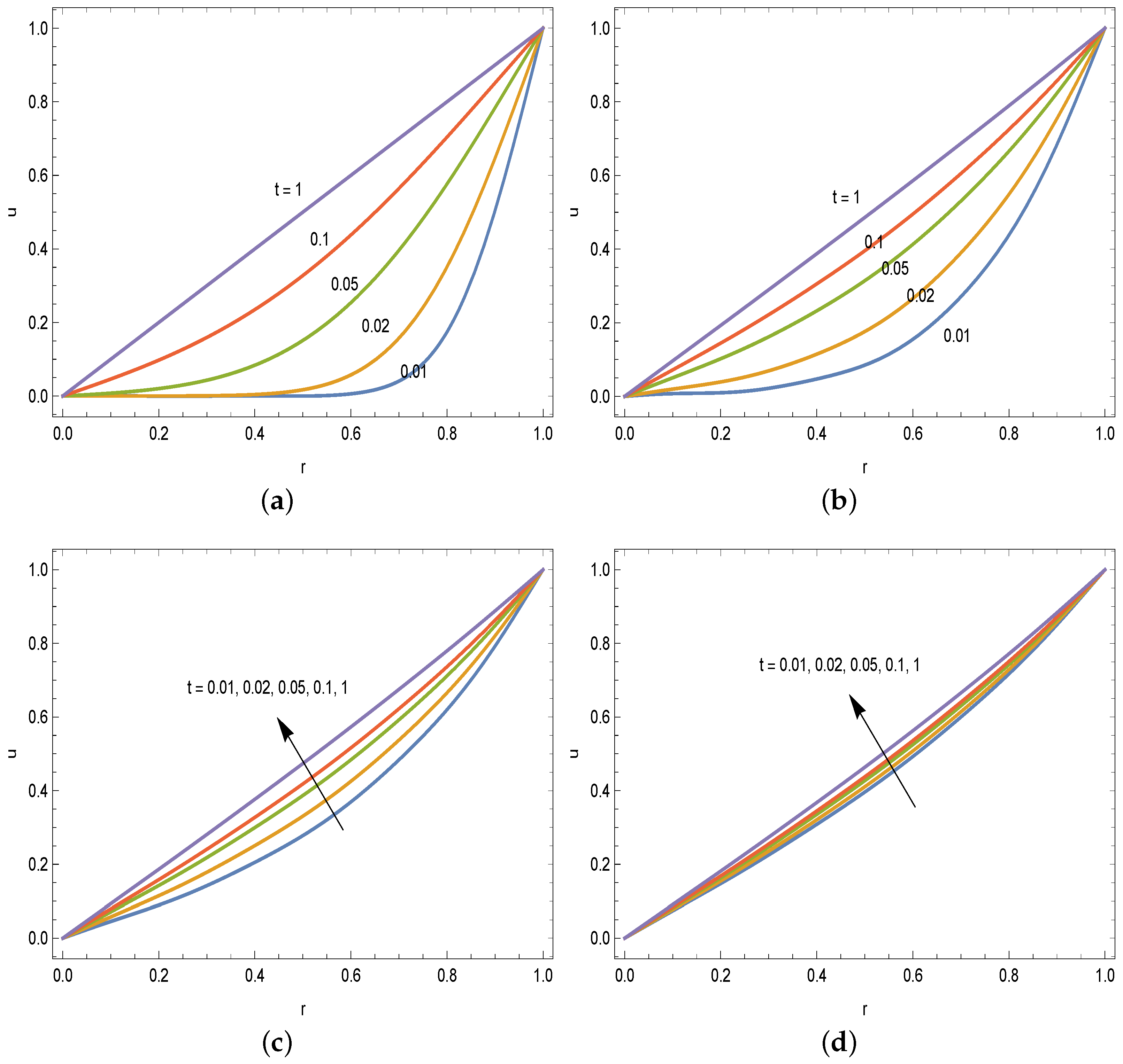
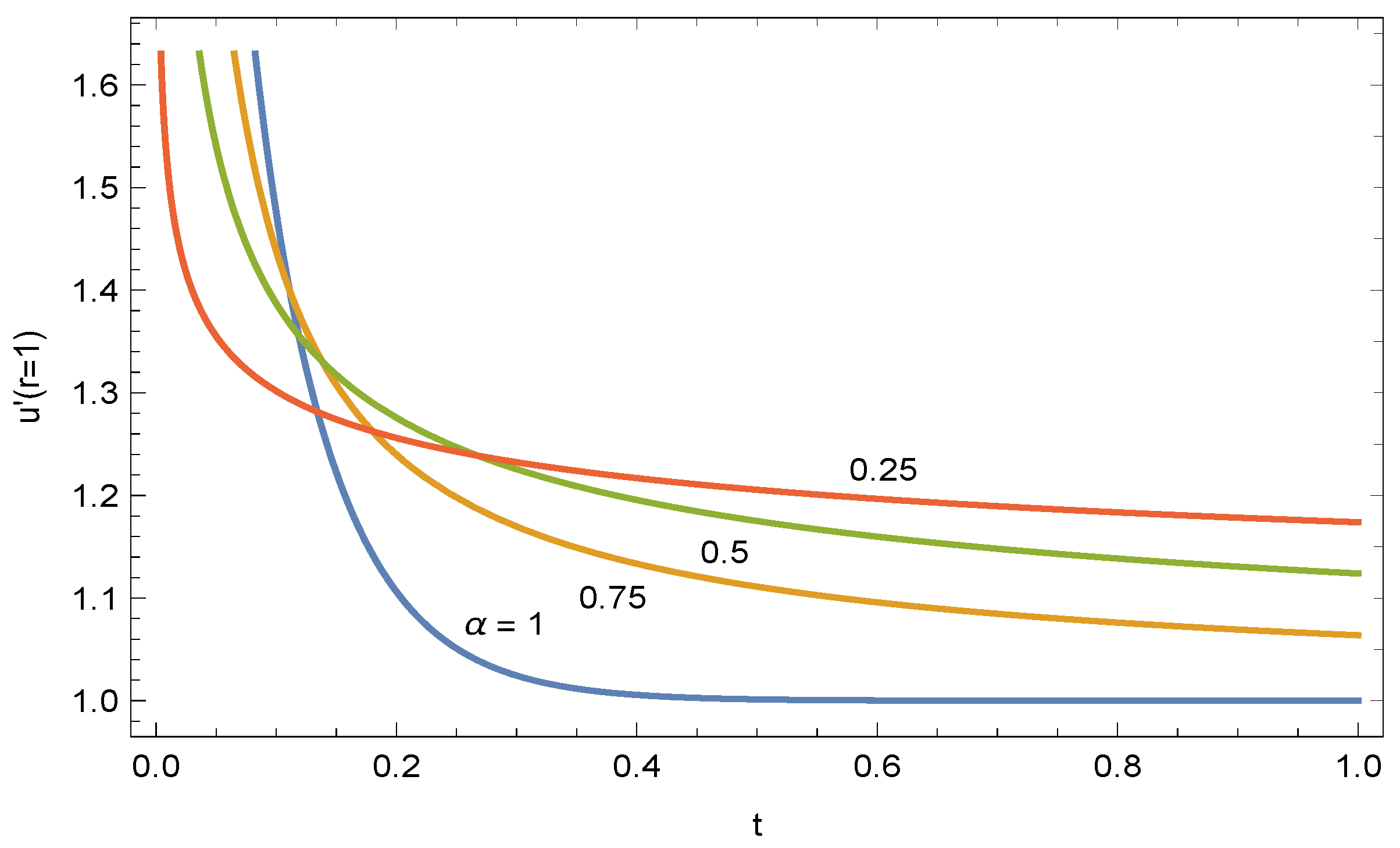
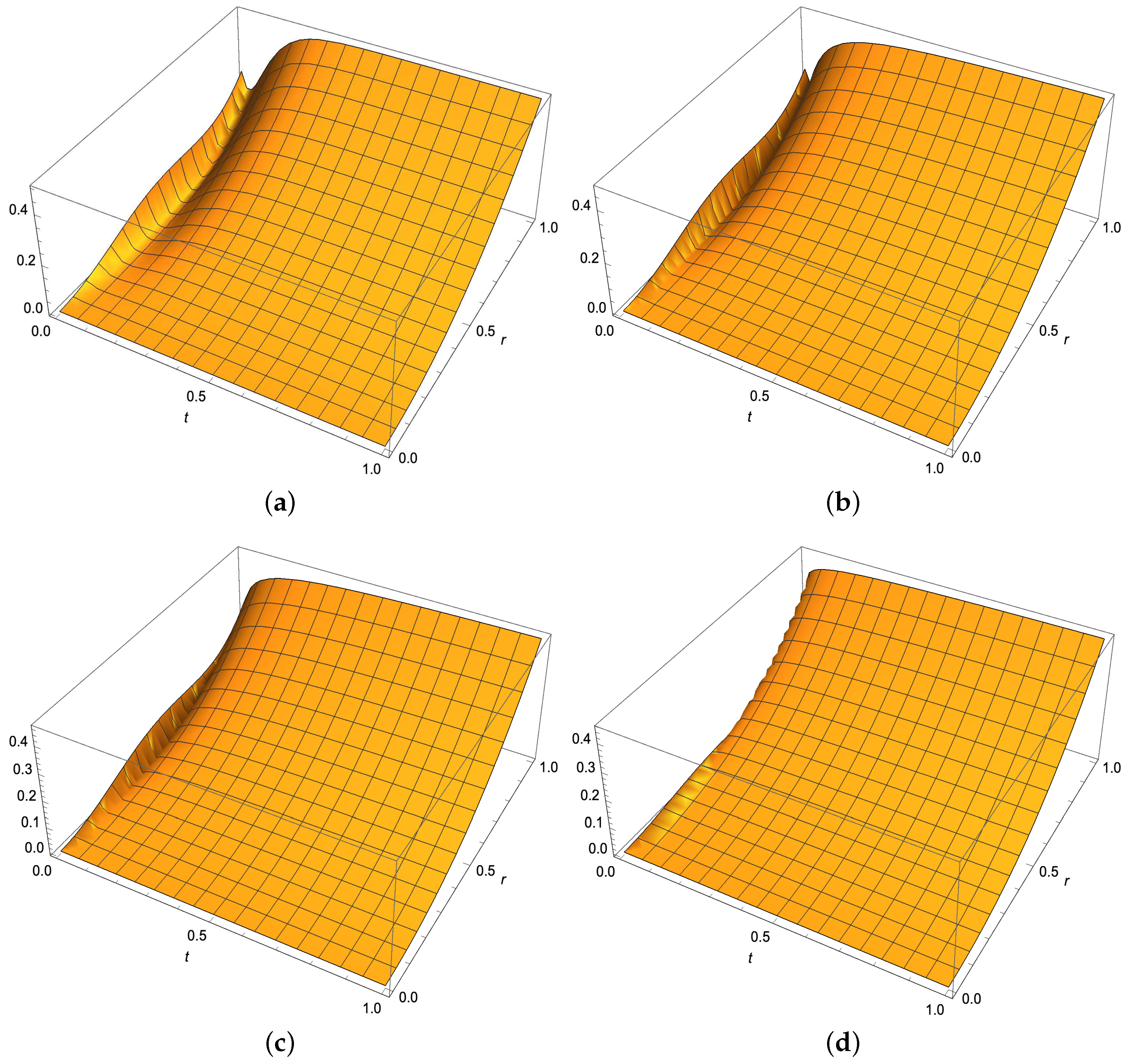
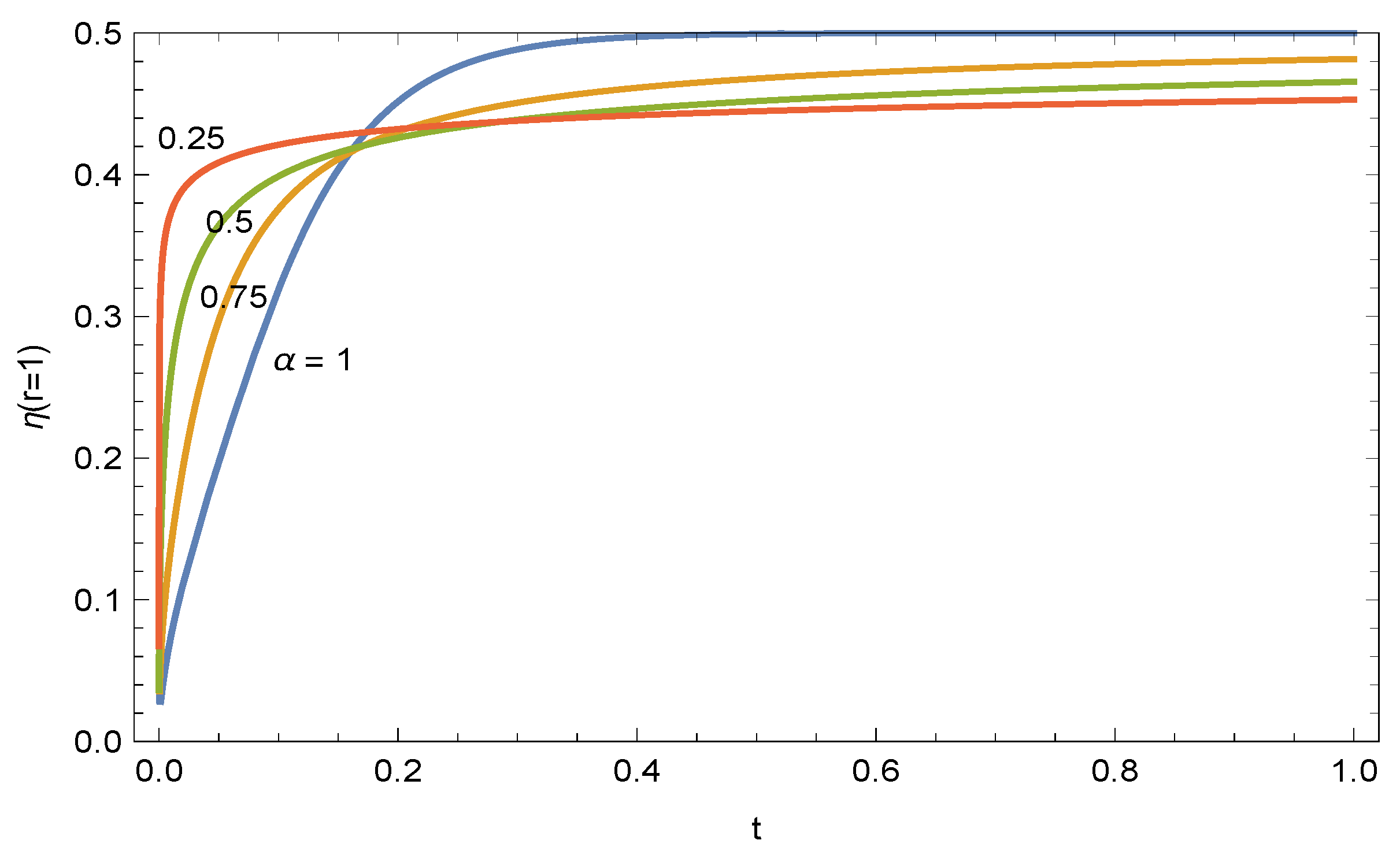
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Altanji, M. Fractional models of falling object with linear and quadratic frictional forces considering Caputo derivative. Chaos Solitons Fractals 2023, 166, 112980. [Google Scholar] [CrossRef]
- Ma, L.; Li, J. A bridge on Lomnitz type creep laws via generalized fractional calculus. Appl. Math. Model. 2023, 116, 786–798. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Transient and passage to steady state in fluid flow and heat transfer within fractional models. Int. Numer. Methods Heat Fluid Flow 2023, 33, 728–750. [Google Scholar] [CrossRef]
- Patel, H.S.; Patel, T.; Pandit, D. An efficient technique for solving fractional-order diffusion equations arising in oil pollution. J. Ocean Eng. Sci. 2022, 8, 1–10. [Google Scholar] [CrossRef]
- Valentim, C.A.; Rabi, J.A.; David, S.A. Fractional Mathematical Oncology: On the potential of non-integer order calculus applied to interdisciplinary models. Biosystems 2021, 204, 104377. [Google Scholar] [CrossRef]
- Keshavarz, M.; Qahremani, E.; Allahviranloo, T. Solving a fuzzy fractional diffusion model for cancer tumor by using fuzzy transforms. Fuzzy Sets Syst. 2022, 443, 198–220. [Google Scholar] [CrossRef]
- Granella, S.J.; Bechlin, T.R.; Christ, D. Moisture diffusion by the fractional-time model in convective drying with ultrasound-ethanol pretreatment of banana slices. Innov. Food Sci. Emerg. Technol. 2022, 76, 102933. [Google Scholar] [CrossRef]
- Sowa, M.; Majka, L.; Wajda, K. Excitation system voltage regulator modeling with the use of fractional calculus. AEU Int. Electron. Commun. 2023, 159, 154471. [Google Scholar] [CrossRef]
- Roul, P.; Rohil, V.; Espinosa-Paredes, G.; Obaidurrahman, K. Numerical simulation of two-dimensional fractional neutron diffusion model describing dynamical behaviour of sodium-cooled fast reactor. Ann. Nucl. Energy 2022, 166, 108709. [Google Scholar] [CrossRef]
- Shaw, S.; Whiteman, J.R. Approximate Fourier series recursion for problems involving temporal fractional calculus. Comput. Methods Appl. Mech. Eng. 2022, 402, 115537. [Google Scholar] [CrossRef]
- Arora, S.; Mathur, T.; Agarwal, S.; Tiwari, K.; Gupta, P. Applications of fractional calculus in computer vision: A survey. Neurocomputing 2022, 489, 407–428. [Google Scholar] [CrossRef]
- Cruz-Lopez, C.A.; Espinosa-Paredes, G.; Francois, J.L. Development of the General Bateman Solution using fractional calculus: A theoretical and algorithmic approach. Comput. Phys. Commun. 2022, 273, 108268. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. Online state of charge and state of power co-estimation of lithium-ion batteries based on fractional-order calculus and model predictive control theory. Appl. Energy 2022, 327, 120009. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, S.; Jing, B.; Yang, C.; Ji, J.; Zhao, Z. Fractional variable-order calculus based state of charge estimation of Li-ion battery using dual fractional order Kalman filter. J. Energy Storage 2022, 52, 104685. [Google Scholar] [CrossRef]
- Ribeiro, J.G.T.; Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Baleanu, D.; Shekari, P.; Torkzadeh, L.; Ranjbar, H.; Jajarmi, A.; Nouri, K. Stability analysis and system properties of Nipah virus transmission: A fractional calculus case study. Chaos Solitons Fractals 2023, 166, 112990. [Google Scholar] [CrossRef]
- Sheng, R.; Zhang, Y.; Sun, W.; Ji, Y.; Zeng, M.; Yao, X.; Dai, Y. Staging Chronic Hepatitis B Related Liver Fibrosis with a Fractional Order Calculus Diffusion Model. Acad. Radiol. 2022, 29, 951–963. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Chen, J.; Zhang, Y.; Guo, Y.; Jiang, M.; Dai, Y.; Yao, X. Differentiating Cytokeratin 19 expression of hepatocellular carcinoma by using multi-b-value diffusion-weighted MR imaging with mono-exponential, stretched exponential, intravoxel incoherent motion, diffusion kurtosis imaging and fractional order calculus models. Eur. J. Radiol. 2022, 150, 110237. [Google Scholar]
- Rabbani, F.; Khraisha, T.; Abbasi, F.; Jafari, G.R. Memory effects on link formation in temporal networks: A fractional calculus approach. Phys. A Stat. Mech. Appl. 2021, 564, 125502. [Google Scholar] [CrossRef]
- Cai, R.Y.; Chen, Y.Q.; Chen, Y.Q.; Kou, C.H. NILT and Prony technique for new definitions of fractional calculus for modeling very slow decay phenomena. IFAC—PapersOnLine 2020, 53, 3689–3694. [Google Scholar] [CrossRef]
- Hejazi, H.A.; Khan, M.I.; Raza, A.; Smida, K.; Khan, S.U.; Tlili, I. Inclined surface slip flow of nanoparticles with subject to mixed convection phenomenon: Fractional calculus applications. J. Indian Chem. Soc. 2022, 99, 100564. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ogam, E.; Berbiche, A.; Depollier, C. Reflection and transmission of transient ultrasonic wave in fractal porous material: Application of fractional calculus. Wave Motion 2021, 106, 102804. [Google Scholar] [CrossRef]
- Costa, F.S.; Oliveira, E.C.; Plata, A.R.G. Fractional Diffusion with Time-Dependent Diffusion Coefficient. Rep. Math. Phys. 2021, 87, 59–79. [Google Scholar] [CrossRef]
- Fahad, H.M.; Fernandez, A. Operational calculus for Caputo fractional calculus with respect to functions and the associated fractional differential equations. Appl. Math. Comput. 2021, 409, 126400. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Geometrically nonlinear analysis of nonlocal plates using fractional calculus. Int. J. Mech. Sci. 2020, 179, 105710. [Google Scholar] [CrossRef]
- Yousri, D.; AbdElaziz, M.; Mirjalilic, S. Fractional-order calculus-based flower pollination algorithm with local search for global optimization and image segmentation. Knowl.-Based Syst. 2020, 197, 105889. [Google Scholar] [CrossRef]
- Wang, H.; Weng, C.; Song, Z.; Cai, J. Research on the law of spatial fractional calculus diffusion equation in the evolution of chaotic economic system. Chaos Solitons Fractals 2020, 131, 109462. [Google Scholar] [CrossRef]
- Bavi, O.; Hosseininia, M.; Heydari, M.M.; Bavi, N. SARS-CoV-2 rate of spread in and across tissue, groundwater and soil: A meshless algorithm for the fractional diffusion equation. Eng. Anal. Bound. Elem. 2022, 138, 108–117. [Google Scholar] [CrossRef]
- Ali, U.; Iqbal, A.; Sohail, M.; Abdullah, F.A.; Khan, Z. Compact implicit difference approximation for time-fractional diffusion-wave equation. Alex. Eng. J. 2022, 61, 4119–4126. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, L.; Hou, J. Solving time fractional Keller–Segel type diffusion equations with symmetry analysis, power series method, invariant subspace method and q-homotopy analysis method. Chin. J. Phys. 2022, 77, 1639–1653. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An Efficient Computational Method for Differential Equations of Fractional Type. CMES Comput. Model. Ineng. Sci. 2022, 133, 47–65. [Google Scholar] [CrossRef]
- Ibraheem, G.H.; Turkyilmazoglu, M.; AL-Jawary, M.A. Novel approximate solution for fractional differential equations by the optimal variational iteration method. J. Comput. Sci. 2022, 64, 101841. [Google Scholar] [CrossRef]
- Kumar, D.; Dubey, V.P.; Dubey, S.; Singh, J.; Alshehri, A.M. Computational analysis of local fractional partial differential equations in realm of fractal calculus. Chaos Solitons Fractals 2023, 167, 113009. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Agarwal, P.; Milovanovic, G.V.; Nisar, S.K. A Fractional Integral Operator Involving the Mittag-Leffler Type with Four Parameters. Facta Univ. Ser. Math. Inform. 2015, 30, 597–605. [Google Scholar]
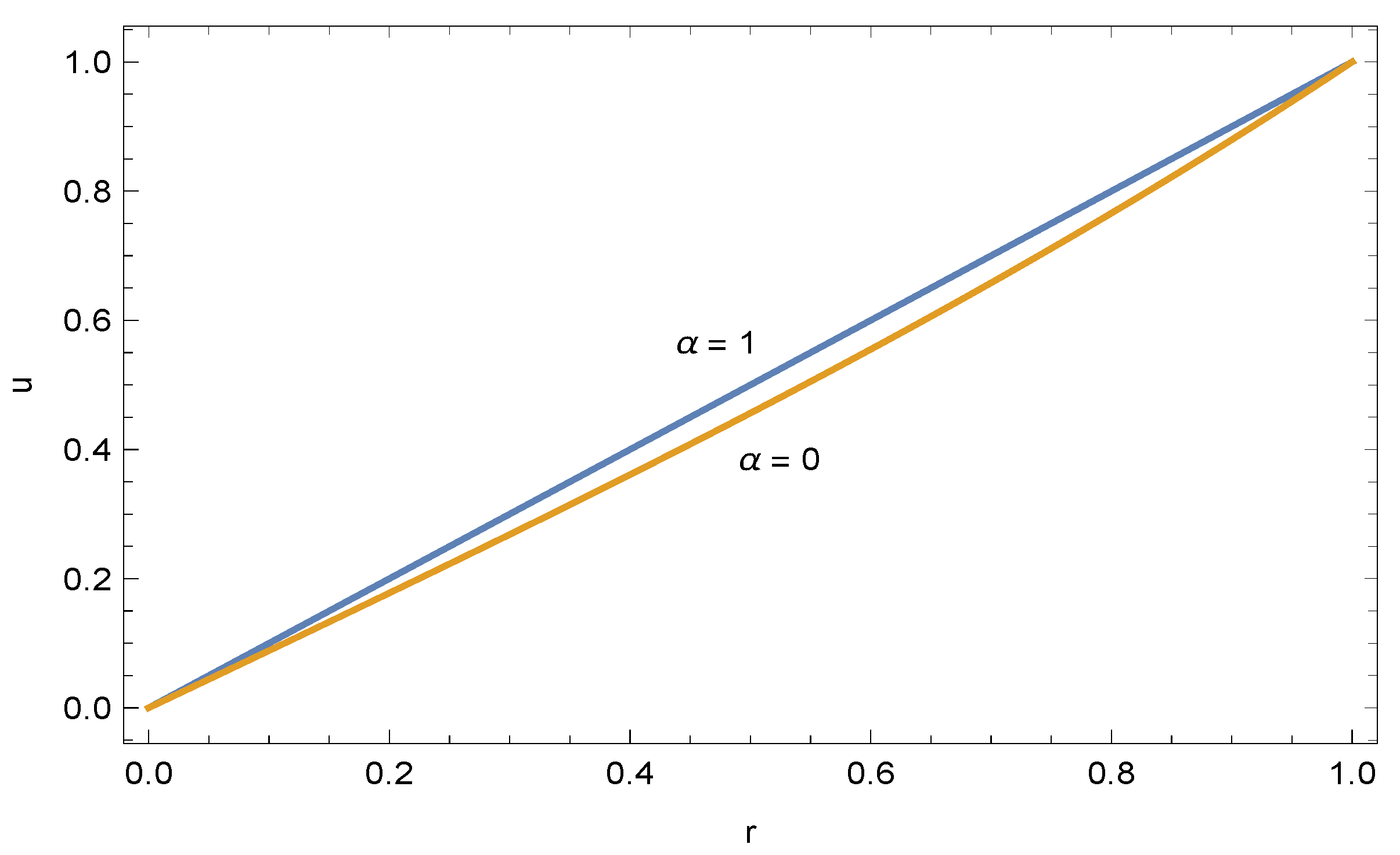
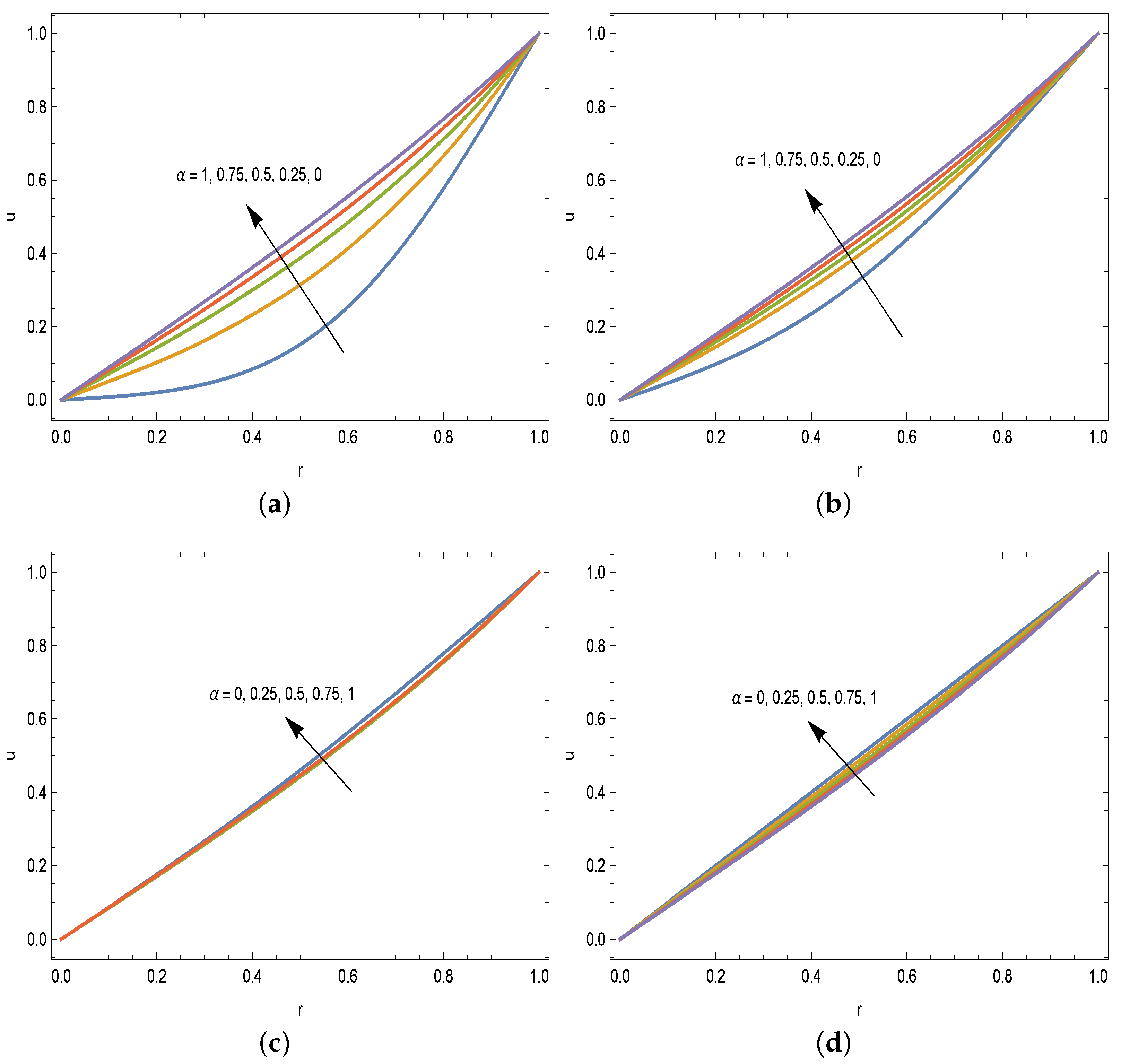

| n | n | ||
|---|---|---|---|
| 1 | 3.83171 | 6 | 19.6159 |
| 2 | 7.01559 | 7 | 22.7601 |
| 3 | 10.1735 | 8 | 25.9037 |
| 4 | 13.3237 | 9 | 29.0468 |
| 5 | 16.4706 | 10 | 32.1897 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turkyilmazoglu, M.; Alofi, A.S. Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo. Fractal Fract. 2024, 8, 231. https://doi.org/10.3390/fractalfract8040231
Turkyilmazoglu M, Alofi AS. Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo. Fractal and Fractional. 2024; 8(4):231. https://doi.org/10.3390/fractalfract8040231
Chicago/Turabian StyleTurkyilmazoglu, Mustafa, and A. S. Alofi. 2024. "Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo" Fractal and Fractional 8, no. 4: 231. https://doi.org/10.3390/fractalfract8040231
APA StyleTurkyilmazoglu, M., & Alofi, A. S. (2024). Liquid Vortex Formation in a Swirling Container Considering Fractional Time Derivative of Caputo. Fractal and Fractional, 8(4), 231. https://doi.org/10.3390/fractalfract8040231






