Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model

Abstract

In this paper, a generalized fractional three-species food chain model with delay is investigated. First, the existence of a positive equilibrium is discussed, and the sufficient conditions for global asymptotic stability are given. Second, through selecting the delay as the bifurcation parameter, we obtain the sufficient condition for this non-control system to generate Hopf bifurcation. Then, a nonlinear delayed feedback controller is skillfully applied to govern the system’s Hopf bifurcation. The results indicate that adjusting the control intensity or the control target’s age can effectively govern the bifurcation dynamics behavior of this system. Last, through application examples and numerical simulations, we confirm the validity and feasibility of the theoretical results, and find that the control strategy is also applicable to eco-epidemiological systems.

1. Introduction

Any population in an ecosystem does not exist in isolation, and certain relationships are bound to exist among different species. Predation, competition, mutualism, and parasitism are the primary population relationships [1]. Predation is widespread in nature and serves as a fundamental prerequisite for sustaining the reproduction and proliferation of biological populations [2,3,4,5]. Studying complex food chains and food web issues is a crucial aspect of ecological research [6,7,8,9]. Delay is prevalent in population systems, for instance, predators may experience gestational delay after consuming prey. Delay reflects inherent population characteristics [10,11,12,13,14]. In comparison to population systems without delay, delayed population systems can exhibit more complex nonlinear dynamical behaviors [15,16,17,18,19,20].

In recent years, the theory of fractional calculus has rapidly advanced and has been extensively used in all kinds of fields, such as population ecology and neural networks [21,22,23,24,25]. Fractional derivative encompasses the entire time domain, whereas the integer derivative only represents characteristics or changes at specific moments. Fractional differential equations are better suited for characterizing the genetic and memory effects in biological systems in comparison to integer derivative [26]. In [27], Li et al. established a fractional population model and utilized the Lyapunov direct method to study the generalized Mittag–Leffler stability of the fractional nonlinear system. In [28], Das and Samanta proposed a fractional (Caputo) three-species food chain model with fear effect and prey shelter to study the stability of delayed and non-delayed system. In [29], Nisar et al. considered the fractional (Atangana–Baleanu–Caputo) delayed food chain model with the Allee effect, analyzed the system solution’s existence and stability utilizing the fixed point theorem, and also applied the Adams–Bashforth–Moulton method to simulate the results of mutual interference between prey and intermediate predator.

The branching problem of ecosystems has also been widely studied by scholars. Hopf bifurcation, an important concept in dynamical system theory, is a bifurcation phenomenon that occurs when a singularity on a two-dimensional central manifold changes from a stable focus to an unstable focus (or from an unstable focus to a stable focus), and generates or vanishes closed trajectories in the vicinity of the singularity [30]. Hopf bifurcation theory is considered to be a classical method for analyzing the generation and disappearance of the periodic solutions of differential equations. Alidousti [31] studied the stability and Hopf bifurcation of a fractional differential system by the Central manifold theorem and Normal form theory. In [32], Wang et al. founded a delayed fractional predator–prey model with intraspecific competition and analyzed system solutions’ existence, uniqueness, stability, and bifurcation behavior. In [33], Rihan et al. examined a fractional-order time-delayed dynamical system with Holling-II type functional response and derived sufficient conditions for inducing a Hopf bifurcation. In [34], Chinnathambi and Rihan established a predator–prey model, and discussed Hopf bifurcation induced by the order of fractional derivative on the basis of stability analysis.

Biological system control plays an important role in maintaining ecosystem balance and species diversity [35,36,37,38,39]. In 1992, K. Pyragas [40] designed a linear feedback controller with delay, aiming at managing bifurcation of the system. The basic idea of the controller is to realize the continuous control of the dynamical system by applying a feedback signal proportional to the gap between the dynamic variable and its delay value. In [41], Jiang et al. implemented a nonlinear feedback controller containing delay in a fractional-order phytoplankton–zooplankton system and proved a Hopf bifurcation triggered through changing the delay and crossing a threshold value. In [42], Huang et al. studied the bifurcation control problem of a incommensurate fractional predator–prey system, and analyzed the conditions of Hopf bifurcation with delay as a bifurcation parameter. The results showed that both the delay and the feedback gain coefficient could suppress the emergence of Hopf bifurcation. Moreover, in [43], Qi H and Zhao W considered the factor of manual intervention and proposed a delayed fractional-order eco-epidemiological model with a feedback controller, which verified the critical role of the controller for the stability of the system.

Currently, there has been extensive research on integer-order food chain models. However, the fractional delay food chain models have received limited attention, especially with general functional responses and nonlinear control. This paper introduces a time-delayed fractional-order food chain model with a general functional response to address this gap. It also deals with the nature of Hopf bifurcation dynamics of the system based on the delay as its bifurcation parameter. Additionally, to address the control issue of the system, a novel nonlinear feedback controller with delay is proposed.

The basic structure of this paper is as follows: In Section 2, we establish the fundamental mathematical model and provide the necessary background knowledge. In Section 3, we select delay as a bifurcation parameter and investigate the stability and Hopf bifurcation issues for both the non-controlled and controlled systems. In Section 4, we test the effectiveness of the theoretical results through application examples and numerical simulations. Final, in Section 5, we present the conclusions and discussion.

2. Preliminaries

This paper considers a generalized fractional-order food chain model with delay

$$\left\{\begin{array}{c}{D}^{\alpha }\mu \left(t\right)=\mu \left(t\right)\left(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right))\right),\hfill \\ D^{\alpha }\nu \left(t\right)=\nu \left(t\right)\left(h_{21}(\mu (t-\tau ),\nu (t-\tau ))-h_{22}\left(\nu \left(t\right)\right)-h_{23}(\nu \left(t\right),\omega \left(t\right))\right),\hfill \\ D^{\alpha }\omega \left(t\right)=\omega \left(t\right)\left(h_{31}(\mu (t-\tau ),\omega (t-\tau ))+h_{32}(\nu (t-\tau ),\omega (t-\tau ))-h_{33}\left(\omega \left(t\right)\right)\right),\hfill \end{array}\right.$$

(1)

here $0<\alpha \le 1$. $\mu \left(t\right)$, $\nu \left(t\right)$, and $\omega \left(t\right)$ represent the density of prey, intermediate predator, and advanced predator. $\tau$ denotes the transformation delay. $D^{\alpha }\xi \left(t\right)$ represents the abbreviation for the Caputo fractional derivative. For simplicity, we define $C^{+}:=C([-\tau ,0],{\mathbb{R}}_{+}^3)$, where $C([-\tau ,0],{\mathbb{R}}_{+}^3)$ is the Banach space of continuous functions mapping $[-\tau ,0]$ into ${\mathbb{R}}_{+}^3$ and ${\mathbb{R}}_{+}^3=\{(x_1,x_2,x_3):x_i\ge 0,i=1,2,3\}$. We suppose that the initial condition for model (1) is

$$\mu \left(\varpi \right)={\varphi }_1\left(\varpi \right),\nu \left(\varpi \right)={\varphi }_2\left(\varpi \right),\omega \left(\varpi \right)={\varphi }_3\left(\varpi \right),\varpi \in [-\tau ,0],\varphi =({\varphi }_1\left(\varpi \right),{\varphi }_2\left(\varpi \right),{\varphi }_3\left(\varpi \right))\in C^{+}.$$

(2)

In the following discussion, we always assume that $h_{ij}(i,j=1,2,3)$ are non-negative and that their partial derivatives are all continuous.

The function $\mu h_{11}\left(\mu \right)$ indicates that the prey population conforms to a logistic growth rate in the absence of a predator population. Since prey are competitive for resources, mates, or territory, then there is $h_{11}^{\prime }\left(\mu \right)<0$.

The function $h_{1i}(·,·)$ for $i=2,3$ is an impact of the predator on the prey per unit of time. Since the prey is preyed upon by the predator, $h_{1i}(·,·)$ is preceded by a negative sign and has $\frac{\partial h_{12}(\mu ,\nu )}{\partial \nu }>0$, $\frac{\partial h_{13}(\mu ,\omega )}{\partial \omega }>0$, $\frac{\partial h_{12}(\mu ,\nu )}{\partial \mu }\le 0$, $\frac{\partial h_{13}(\mu ,\omega )}{\partial \mu }\le 0$.

The function $h_{ii}(·)$ for $i=2,3$ is the decrease of the predator population’s density in unit time due to intraspecific competition or natural mortality, so $h_{ii}(·)$ is also preceded by a negative sign and $h_{22}^{\prime }\left(\nu \right)\ge 0$, $h_{33}^{\prime }\left(\omega \right)\ge 0$.

Functions $h_{23}(\nu ,\omega )$ and $h_{32}(\nu ,\omega )$ are used to characterize the predation phenomenon that exists between two types of the predator, and have $\frac{\partial h_{23}(\nu ,\omega )}{\partial \omega }>0$, $\frac{\partial h_{32}(\nu ,\omega )}{\partial \nu }>0$, $\frac{\partial h_{23}(\nu ,\omega )}{\partial \nu }\le 0$, $\frac{\partial h_{32}(\nu ,\omega )}{\partial \omega }\le 0$.

Functions $h_{21}(\mu ,\nu )$ and $h_{31}(\mu ,\omega )$ describe the energy transfer after prey is captured by the intermediate and the top predator, respectively, and positively affect predator species growth, where $\frac{\partial h_{21}(\mu ,\nu )}{\partial \mu }>0$, $\frac{\partial h_{31}(\mu ,\omega )}{\partial \mu }>0$, $\frac{\partial h_{21}(\mu ,\nu )}{\partial \nu }\le 0$, $\frac{\partial h_{31}(\mu ,\omega )}{\partial \omega }\le 0$.

In a food chain system, many predacious functions [44] satisfy the above conditions. Examples include the Holling-I functional response $\beta xy$, the Holling-II functional response $\frac{\beta xy}{1+\gamma x}$, the proportional-deterministic functional response function $\frac{\beta xy}{N}$, and the ratio-dependent functional response $\frac{\beta xy}{mz+x}$ or $\frac{\beta xy}{mz+y}$, where $\beta$, $\gamma$, m are all numbers greater than zero. In the following discussion, we assume that $h_{ij}(i,j=1,2,3)$ satisfy the above conditions.

2.1. Persistence of the System

Based on reference [45], and considering the biological background of system (1), we make the following hypothesis:

(A1) The survival of the predator population is completely dependent on the prey and will disappear with the extinction of the prey populations, i.e.,

$$\begin{array}{c}{h}_{21}(0,\upsilon )-h_{22}\left(\upsilon \right)-h_{23}(\upsilon ,\omega )<0,h_{31}(0,\omega )+h_{32}(0,\omega )-h_{33}\left(\omega \right)<0.\hfill \end{array}$$

(A2) The prey increases to carrying capacity without predator, i.e.,

$$\begin{array}{c}{h}_{11}\left(0\right)-h_{12}(0,0)-h_{13}(0,0)=h_{11}\left(0\right)>0,{h^{\prime }}_{11}\left(\mu \right)-\frac{\partial h_{12}(\mu ,\upsilon )}{\partial \mu }-\frac{\partial h_{13}(\mu ,\omega )}{\partial \mu }<0,\hfill \end{array}$$

$$\begin{array}{c}\exists K,h_{11}\left(K\right)-h_{12}(K,0)-h_{13}(K,0)=0.\hfill \end{array}$$

(A3) There is no equilibrium point in the $\nu -\omega$ plane.

(A4) The intermediate predator can rely on prey for survival, leading to the existence of a boundary equilibrium, $E_1(e_1,r_1,0)$. Similarly, the top predator can survive by preying only on the lowest-level prey, meaning another boundary equilibrium exists, $E_2(e_2,0,l_2)$.

Proposition 1 

([45]). Let (A1)-(A4) hold. If

$$h_{31}(e_1,0)+h_{32}(r_1,0)-h_{33}\left(0\right)>0,$$

$$h_{21}(e_2,0)-h_{22}\left(0\right)-h_{23}(0,l_2)>0,$$

then, for system (1), there exists at least one positive equilibrium, i.e., system (1) is persistent in infinite time.

Based on the model (1), we design a nonlinear delayed feedback controller to control the bifurcation in the system to obtain the required dynamic behavior. Here, we choose to introduce the delayed feedback controller $\mathrm{\Phi }\left(t\right)=k{e}^{-d\sigma }(\nu \left(t\right)-\nu (t-\sigma ))$ in the intermediate predator (where k, $\sigma$ and d denote the control intensity, the control target’s age, and the intermediate predator’s reduction rate in unit time, respectively), which yields the following dynamical system:

$$\left\{\begin{array}{c}{D}^{\alpha }\mu \left(t\right)=\mu \left(t\right)\left(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right))\right),\hfill \\ D^{\alpha }\nu \left(t\right)=\nu \left(t\right)\left(h_{21}(\mu (t-\tau ),\nu (t-\tau ))-h_{22}\left(\nu \left(t\right)\right)-h_{23}(\nu \left(t\right),\omega \left(t\right))\right)+k{e}^{-d\sigma }(\nu \left(t\right)-\nu (t-\sigma )),\hfill \\ D^{\alpha }\omega \left(t\right)=\omega \left(t\right)\left(h_{31}(\mu (t-\tau ),\omega (t-\tau ))+h_{32}(\nu (t-\tau ),\omega (t-\tau ))-h_{33}\left(\omega \left(t\right)\right)\right),\hfill \end{array}\right.$$

(3)

where the initial value is $\mu \left(\varpi \right)={\varphi }_1\left(\varpi \right),\nu \left(\varpi \right)={\varphi }_2\left(\varpi \right),\omega \left(\varpi \right)={\varphi }_3\left(\varpi \right)$, $\varpi \in [-max(\tau ,\sigma ),0]$. The research is grounded in the theory of the Caputo fractional derivative.

2.2. The Well-Posedness of System (1)

It is not difficult to verify that the right side of Equation (1) satisfies the local Lipschitz condition, and therefore, can be obtained

Theorem 1. 

For any given initial value $\varphi =({\varphi }_1\left(\varpi \right),{\varphi }_2\left(\varpi \right),{\varphi }_3\left(\varpi \right))$, when $t\ge 0$, the system (1) has a unique solution $X\left(t\right)=\left(\mu \right(t),\nu (t),\omega (t\left)\right)$.

Considering the biological significance of this system, we are only interested in non-negative solutions. The below result guarantees the non-negativity of the solutions of system (1).

Theorem 2. 

All solutions of system (1) are non-negative.

Proof. 

Suppose that there exists a constant $t_1>t_0$, $t_1^{+}>t_1$ and that $t_1^{+}$ is close enough to $t_1$ such that

$$\left\{\begin{array}{c}\mu \left(t\right)>0,t_0<t<t_1,\hfill \\ \mu \left(t_1\right)=0,\hfill \\ \mu \left(t_1^{+}\right)<0.\hfill \end{array}\right.$$

There are two possible situations as follows:

(1) If $D^{\alpha }\mu \left(t\right)\ge 0$ for all $t\in \left[t_1,t_1^{+}\right]$, by relying on Theorem 1 in [46], it follows that $\mu \left(t\right)$ is a non-decreasing function for any $t\in \left[t_1,t_1^{+}\right]$, then $\mu \left(t_1^{+}\right)\ge 0$. It contradicts the assumption.

(2) If $D^{\alpha }\mu \left(t\right)\le 0$ for all $t\in \left[t_1,t_1^{+}\right]$, from the first equality of Equation (1), we get

$$\begin{array}{cc}\hfill D^{\alpha }\mu \left(t\right)=& \mu \left(t\right)(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right)))\hfill \\ \hfill \ge & \mu \left(t\right)·max\left(h_{11}\left(\mu \left(t\right)\right)\right).\hfill \end{array}$$

Define $N=max\left(h_{11}\left(\mu \left(t\right)\right)\right)$, then

$$D^{\alpha }\mu \left(t\right)\ge \mu \left(t\right)N.$$

Applying the Laplace transform to the above inequality, we have that

$$\mu \left(t\right)\ge \mu \left(t_1\right)E_{\alpha }\left(N{(t-t_1)}^{\alpha }\right),t\in \left[t_1,t_1^{+}\right].$$

Thus, for any $t>t_1$, we have $\mu \left(t\right)\ge 0$ inconsistent with the above assumption. Combining both cases (1) and (2), we conclude that $\mu \left(t\right)$ is non-negative.

In the same way, we can justify that $\nu \left(t\right)$ and $\omega \left(t\right)$ are also non-negative. □

3. Main Results

We know that there exists one positive equilibrium point of the system (1), assuming that its positive equilibrium is $\hat{E}(\hat{\mu },\hat{\nu },\hat{\omega })$. Let $P_1\left(t\right)=\mu \left(t\right)-\hat{\mu },P_2\left(t\right)=\nu \left(t\right)-\hat{\nu }$, and $P_3\left(t\right)=\omega \left(t\right)-\hat{\omega }$, through variable transformation, and combined with system (1), we can obtain the linearized system as follows:

$$\left\{\begin{array}{c}{D}^{\alpha }{P}_1\left(t\right)=\left(a_{11}-a_{12}-a_{13}\right)\hat{\mu }{P}_1\left(t\right)-{\overline{a}}_{12}\hat{\mu }{P}_2\left(t\right)-{\overline{a}}_{13}\hat{\mu }{P}_3\left(t\right),\hfill \\ D^{\alpha }{P}_2\left(t\right)=a_{21}\hat{\nu }{P}_1(t-\tau )-(a_{22}\hat{\nu }+a_{23}\hat{\nu })P_2\left(t\right)+{\overline{a}}_{21}\hat{\nu }{P}_2(t-\tau )-{\overline{a}}_{23}\hat{\nu }{P}_3\left(t\right),\hfill \\ D^{\alpha }{P}_3\left(t\right)=a_{31}\hat{\omega }{P}_1(t-\tau )+a_{32}\hat{\omega }{P}_2(t-\tau )-a_{33}\hat{\omega }{P}_3\left(t\right)+({\overline{a}}_{31}\hat{\omega }+{\overline{a}}_{32}\hat{\omega })P_3(t-\tau ),\hfill \end{array}\right.$$

(4)

where

$$\begin{array}{ccccc}\hfill {h^{\prime }}_{11}\left(\hat{\mu }\right)=a_{11},& \hfill \frac{\partial h_{12}}{\partial \mu }(\hat{\mu },\hat{\nu })=a_{12},& \hfill \frac{\partial h_{12}}{\partial \nu }(\hat{\mu },\hat{\nu })={\overline{a}}_{12},& \hfill \frac{\partial h_{13}}{\partial \mu }(\hat{\mu },\hat{\omega })=a_{13},& \hfill \frac{\partial h_{13}}{\partial \omega }(\hat{\mu },\hat{\omega })={\overline{a}}_{13},\\ \hfill {h^{\prime }}_{22}\left(\hat{\nu }\right)=a_{22},& \hfill \frac{\partial h_{21}}{\partial \mu (t-\tau )}(\hat{\mu },\hat{\nu })=a_{21},& \hfill \frac{\partial h_{21}}{\partial \nu (t-\tau )}(\hat{\mu },\hat{\nu })={\overline{a}}_{21},& \hfill \frac{\partial h_{23}}{\partial \nu }(\hat{\nu },\hat{\omega })=a_{23},& \hfill \frac{\partial h_{23}}{\partial \omega }(\hat{\nu },\hat{\omega })={\overline{a}}_{23},\\ \hfill {h^{\prime }}_{33}\left(\hat{\omega }\right)=a_{33},& \hfill \frac{\partial h_{31}}{\partial \mu (t-\tau )}(\hat{\mu },\hat{\omega })=a_{31},& \hfill \frac{\partial h_{31}}{\partial \omega (t-\tau )}(\hat{\mu },\hat{\omega })={\overline{a}}_{31},& \hfill \frac{\partial h_{32}}{\partial \nu (t-\tau )}(\hat{\nu },\hat{\omega })=a_{32},& \hfill \frac{\partial h_{32}}{\partial \omega (t-\tau )}(\hat{\nu },\hat{\omega })={\overline{a}}_{32}.\end{array}$$

(5)

Then, in order to study the stability of the system, we perform a Laplace transform on Equation (4) to obtain its characteristic matrix $\mathsf{\Delta }\left(s\right)$ at the positive equilibrium $\hat{E}(\hat{\mu },\hat{\nu },\hat{\omega })$.

$$\mathsf{\Delta }\left(s\right)=\left[\begin{array}{ccc}{s}^{\alpha }-(a_{11}-a_{12}-a_{13})\hat{\mu }& {\overline{a}}_{12}\hat{\mu }& {\overline{a}}_{13}\hat{\mu }\\ -a_{21}\hat{\nu }{e}^{-s\tau }& s^{\alpha }+(a_{22}+a_{23})\hat{\nu }-{\overline{a}}_{21}\hat{\nu }{e}^{-s\tau }& {\overline{a}}_{23}\hat{\nu }\\ -a_{31}\hat{\omega }{e}^{-s\tau }& -a_{32}\hat{\omega }{e}^{-s\tau }& s^{\alpha }+a_{33}\hat{\omega }-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{e}^{-s\tau }\end{array}\right].$$

(6)

3.1. Dynamic Analysis of the System (1) without Delay

First, we study the delay-free system

$$\left\{\begin{array}{c}{D}^{\alpha }\mu \left(t\right)=\mu \left(t\right)\left(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right))\right),\hfill \\ D^{\alpha }\nu \left(t\right)=\nu \left(t\right)\left(h_{21}(\mu \left(t\right),\nu \left(t\right))-h_{22}\left(\nu \left(t\right)\right)-h_{23}(\nu \left(t\right),\omega \left(t\right))\right),\hfill \\ D^{\alpha }\omega \left(t\right)=\omega \left(t\right)\left(h_{31}(\mu \left(t\right),\omega \left(t\right))+h_{32}(\nu \left(t\right),\omega \left(t\right))-h_{33}\left(\omega \left(t\right)\right)\right).\hfill \end{array}\right.$$

(7)

The Jacobian matrix of the system (7) at the positive equilibrium $\hat{E}$ is

$$J=\left[\begin{array}{ccc}(a_{11}-a_{12}-a_{13})\hat{\mu }& -{\overline{a}}_{12}\hat{\mu }& -{\overline{a}}_{13}\hat{\mu }\\ a_{21}\hat{\nu }& ({\overline{a}}_{21}-a_{22}-a_{23})\hat{\nu }& -{\overline{a}}_{23}\hat{\nu }\\ a_{31}\hat{\omega }& a_{32}\hat{\omega }& ({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})\hat{\omega }\end{array}\right].$$

Theorem 3. 

If $\left[{\mathbb{H}}_1\right]$ and $\left[{\mathbb{H}}_2\right]$ are established, the positive equilibrium $\hat{E}$ of the fractional system (7) is locally asymptotically stable. $\left[{\mathbb{H}}_1\right]$ and $\left[{\mathbb{H}}_2\right]$ are given during the proof.

Proof. 

Let $\lambda =s^{\alpha }$, the characteristic equation at the positive equilibrium $\hat{E}$ can be simplified to

$${\lambda }^3+p_1{\lambda }^2+p_2\lambda +p_3=0,$$

(8)

where

$$\begin{array}{cc}\hfill p_1=& -(a_{11}-a_{12}-a_{13})\hat{\mu }-({\overline{a}}_{21}-a_{22}-a_{23})\hat{\nu }-({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})\hat{\omega },\hfill \\ \hfill p_2=& ((a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})+{\overline{a}}_{12}{a}_{21})\hat{\mu }\hat{\nu }+(({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})\hfill \\ \hfill & +{\overline{a}}_{23}{a}_{32})\hat{\nu }\hat{\omega }+((a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{13}{a}_{31})\hat{\mu }\hat{\omega },\hfill \\ \hfill p_3=& ({\overline{a}}_{13}{a}_{21}{a}_{32}-{\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}-{\overline{a}}_{13}{a}_{31}({\overline{a}}_{21}-a_{22}-a_{23})-{\overline{a}}_{23}{a}_{32}(a_{11}-a_{12}-a_{13})\hfill \\ \hfill & -{\overline{a}}_{12}{a}_{21}({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})-(a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33}))\hat{\mu }\hat{\nu }\hat{\omega }.\hfill \end{array}$$

According the qualification of model (1) to the functions $h_{ij}(i,j=1,2,3)$ (in the Preliminaries section), and combined with the formula (5), we know $a_{11}<0$, $a_{12}\le 0$, ${\overline{a}}_{12}>0$, $a_{13}\le 0$, ${\overline{a}}_{13}>0$, $a_{22}>0$, $a_{23}\le 0$, ${\overline{a}}_{23}>0$, $a_{32}>0$, ${\overline{a}}_{32}\le 0$, $a_{33}>0$, $a_{21}>0$, ${\overline{a}}_{21}\le 0$, $a_{31}>0$, ${\overline{a}}_{31}\le 0$, thus, ${\overline{a}}_{31}+{\overline{a}}_{32}-a_{33}<0$. Define the following formulas

$$\begin{array}{cc}\hfill & \left[{\mathbb{H}}_1\right]:{\overline{a}}_{21}-a_{22}-a_{23}<0,a_{11}-a_{12}-a_{13}<0,\hfill \\ \hfill & \left[{\mathbb{H}}_2\right]:p_1{p}_2>p_3>0.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill p_1=& -(a_{11}-a_{12}-a_{13})\hat{\mu }-({\overline{a}}_{21}-a_{22}-a_{23})\hat{\nu }-({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})\hat{\omega }>0,\hfill \\ \hfill p_2=& ((a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})+{\overline{a}}_{12}{a}_{21})\hat{\mu }\hat{\nu }+(({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{23}{a}_{32})\hat{\nu }\hat{\omega }\hfill \\ \hfill & +((a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{13}{a}_{31})\hat{\mu }\hat{\omega }>0,\hfill \\ \hfill p_3=& ({\overline{a}}_{13}{a}_{21}{a}_{32}-{\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}-{\overline{a}}_{13}{a}_{31}({\overline{a}}_{21}-a_{22}-a_{23})-{\overline{a}}_{23}{a}_{32}(a_{11}-a_{12}-a_{13})\hfill \\ \hfill & -{\overline{a}}_{12}{a}_{21}({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})-(a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33}))\hat{\mu }\hat{\nu }\hat{\omega }>0,\hfill \\ \hfill p_1{p}_2-p_3=& -(a_{11}-a_{12}-a_{13})[(a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})+{\overline{a}}_{12}{a}_{21}]{\hat{\mu }}^2\hat{\nu }\hfill \\ \hfill & -({\overline{a}}_{21}-a_{22}-a_{23})[(a_{11}-a_{12}-a_{13})({\overline{a}}_{21}-a_{22}-a_{23})+{\overline{a}}_{12}{a}_{21}]\hat{\mu }{\hat{\nu }}^2\hfill \\ \hfill & -({\overline{a}}_{21}-a_{22}-a_{23})[({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{23}{a}_{32}]{\hat{\nu }}^2\hat{\omega }\hfill \\ \hfill & -({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})[({\overline{a}}_{21}-a_{22}-a_{23})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{23}{a}_{32}]\hat{\nu }{\hat{\omega }}^2\hfill \\ \hfill & -(a_{11}-a_{12}-a_{13})[(a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{13}{a}_{31}]{\hat{\mu }}^2\hat{\omega }\hfill \\ \hfill & -({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})[(a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+{\overline{a}}_{13}{a}_{31}]\hat{\mu }{\hat{\omega }}^2\hfill \\ \hfill & -[{\overline{a}}_{13}{a}_{21}{a}_{32}-{\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}+2(a_{11}-a_{12}-a_{13})(a_{22}+a_{23}-{\overline{a}}_{21})(a_{33}-{\overline{a}}_{31}-{\overline{a}}_{32})]\hat{\mu }\hat{\nu }\hat{\omega }>0.\hfill \end{array}$$

Thus, under assumptions $\left[{\mathbb{H}}_1\right]$ and $\left[{\mathbb{H}}_2\right]$, we have $H_1=p_1>0$, $H_2=p_1{p}_2-p_3>0$, and $H_3=p_3(p_1{p}_2-p_3)>0$, which satisfies the Hurwitz criterion that all roots of the characteristic equation have negative real parts, i.e., $|arg\left(s_{1,2,3}^{\alpha }\right)|>\frac{\alpha \pi }{2}$ hold. Through this argument, the positive equilibrium $\hat{E}$ of the delay-free system (7) is locally asymptotically stable. □

Theorem 4. 

Assuming that the positive equilibrium $\hat{E}$ of the system (7) satisfies conditions $\left[{\mathbb{H}}_1\right]$ and $\left[{\mathbb{H}}_3\right]:{\overline{a}}_{13}{a}_{21}{a}_{32}={\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}$, then $\hat{E}$ is globally asymptotically stable.

Proof. 

At the positive equilibrium $\hat{E}=(\hat{\mu },\hat{\nu },\hat{\omega })$, we have

$$\left\{\begin{array}{c}{h}_{11}\left(\hat{\mu }\right)-h_{12}(\hat{\mu },\hat{\nu })-h_{13}(\hat{\mu },\hat{\omega })=0,\hfill \\ h_{21}(\hat{\mu },\hat{\nu })-h_{22}\left(\hat{\nu }\right)-h_{23}(\hat{\nu },\hat{\omega })=0,\hfill \\ h_{31}(\hat{\mu },\hat{\omega })+h_{32}(\hat{\nu },\hat{\omega })-h_{33}\left(\hat{\omega }\right)=0.\hfill \end{array}\right.$$

Define the Lyapunov function

$$V(\mu ,\nu ,\omega )=f_1(\mu -\hat{\mu }-\hat{\mu }ln\frac{\mu }{\hat{\mu }})+f_2(\nu -\hat{\nu }-\hat{\nu }ln\frac{\nu }{\hat{\nu }})+f_3(\omega -\hat{\omega }-\hat{\omega }ln\frac{\omega }{\hat{\omega }}),$$

(9)

where $f_i(i=1,2,3)$ are constants, given by the later calculation. Through Lemma 1 of [47] and the continuity of the partial derivative of $h_{ij}(i,j=1,2,3)$, we have

$$\begin{array}{cc}\hfill D^{\alpha }V\le & f_1(\mu -\hat{\mu })(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right)))+f_2(\nu -\hat{\nu })\left(h_{21}(\mu \left(t\right),\nu \left(t\right))\right)\hfill \\ \hfill & -h_{22}\left(\nu \left(t\right)\right)-h_{23}(\nu \left(t\right),\omega \left(t\right))+f_3(\omega -\hat{\omega })(h_{31}(\mu \left(t\right),\omega \left(t\right))+h_{32}(\nu \left(t\right),\omega \left(t\right))-h_{33}\left(\omega \left(t\right)\right))\hfill \\ \hfill =& f_1(\mu -\hat{\mu })(h_{11}\left(\mu \left(t\right)\right)-h_{12}(\mu \left(t\right),\nu \left(t\right))-h_{13}(\mu \left(t\right),\omega \left(t\right))-(h_{11}\left(\hat{\mu }\right)-h_{12}(\hat{\mu },\hat{\nu })-h_{13}(\hat{\mu },\hat{\omega })))\hfill \\ \hfill & +f_2(\nu -\hat{\nu })(h_{21}(\mu \left(t\right),\nu \left(t\right))-h_{22}\left(\nu \left(t\right)\right)-h_{23}(\nu \left(t\right),\omega \left(t\right)))-(h_{21}(\hat{\mu },\hat{\nu })-h_{22}\left(\hat{\nu }\right)-h_{23}(\hat{\nu },\hat{\omega }))\hfill \\ \hfill & +f_3(\omega -\hat{\omega })(h_{31}(\mu \left(t\right),\omega \left(t\right))+h_{32}(\nu \left(t\right),\omega \left(t\right))-h_{33}\left(\omega \left(t\right)\right))-(h_{31}(\hat{\mu },\hat{\omega })+h_{32}(\hat{\nu },\hat{\omega })-h_{33}\left(\hat{\omega }\right))\hfill \\ \hfill =& f_1(\mu -\hat{\mu })[(\mu -\hat{\mu }){h^{\prime }}_{11}\left(\hat{\mu }\right)+{\gamma }_1]+f_1(\mu -\hat{\mu })[-(\mu -\hat{\mu })\frac{\partial h_{12}}{\partial \mu }(\hat{\mu },\hat{\nu })-(\nu -\hat{\nu })\frac{\partial h_{12}}{\partial \nu }(\hat{\mu },\hat{\nu })+{\alpha }_1]\hfill \\ \hfill & +f_1(\mu -\hat{\mu })[-(\mu -\hat{\mu })\frac{\partial h_{13}}{\partial \mu }(\hat{\mu },\hat{\omega })-(\omega -\hat{\omega })\frac{\partial h_{13}}{\partial \omega }(\hat{\mu },\hat{\omega })+{\beta }_1]+f_2(\nu -\hat{\nu })[(\mu -\hat{\mu })\frac{\partial h_{21}}{\partial \mu }(\hat{\mu },\hat{\nu })\hfill \\ \hfill & +(\nu -\hat{\nu })\frac{\partial h_{21}}{\partial \nu }(\hat{\mu },\hat{\nu })+{\alpha }_2]+f_2(\nu -\hat{\nu })[-(\nu -\hat{\nu })\frac{\partial h_{23}}{\partial \nu }(\hat{\nu },\hat{\omega })-(\omega -\hat{\omega })\frac{\partial h_{23}}{\partial \omega }(\hat{\nu },\hat{\omega })+{\beta }_2]\hfill \\ \hfill & +f_2(\nu -\hat{\nu })[-(\nu -\hat{\nu }){h^{\prime }}_{22}\left(\hat{\nu }\right)+{\gamma }_2]+f_3(\omega -\hat{\omega })[(\mu -\hat{\mu })\frac{\partial h_{31}}{\partial \mu }(\hat{\mu },\hat{\omega })+(\omega -\hat{\omega })\frac{\partial h_{31}}{\partial \omega }(\hat{\mu },\hat{\omega })+{\alpha }_3]\hfill \\ \hfill & +f_3(\omega -\hat{\omega })[(\nu -\hat{\nu })\frac{\partial h_{32}}{\partial \nu }(\hat{\nu },\hat{\omega })+(\omega -\hat{\omega })\frac{\partial h_{32}}{\partial \omega }(\hat{\nu },\hat{\omega })+{\beta }_3]+f_3(\omega -\hat{\omega })[-(\omega -\hat{\omega }){h^{\prime }}_{33}\left(\hat{\omega }\right)+{\gamma }_3],\hfill \end{array}$$

where ${\alpha }_i$, ${\beta }_i$ and ${\gamma }_i(i=1,2,3)$ are infinitesimals of higher order with respect to distance. So we can obtain

$$\begin{array}{cc}\hfill D^{\alpha }V\le & f_1{(\mu -\hat{\mu })}^2(a_{11}-a_{12}-a_{13})+f_2{(\nu -\hat{\nu })}^2({\overline{a}}_{21}-a_{22}-a_{23})\hfill \\ \hfill & +f_3{(\omega -\hat{\omega })}^2({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})+(f_2{a}_{21}-f_1{\overline{a}}_{12})(\mu -\hat{\mu })(\nu -\hat{\nu })\hfill \\ \hfill & +(f_3{a}_{31}-f_1{\overline{a}}_{13})(\mu -\hat{\mu })(\omega -\hat{\omega })+(f_3{a}_{32}-f_2{\overline{a}}_{23})(\nu -\hat{\nu })(\omega -\hat{\omega }).\hfill \end{array}$$

If $\left[{\mathbb{H}}_3\right]:{\overline{a}}_{13}{a}_{21}{a}_{32}={\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}$ and $\left[{\mathbb{H}}_1\right]:{\overline{a}}_{21}-a_{22}-a_{23}<0$ are held, we consider $f_1=\frac{a_{31}{\overline{a}}_{23}}{{\overline{a}}_{13}}=\frac{a_{21}{a}_{32}}{{\overline{a}}_{12}}$, $f_2=a_{32}$, and $f_3={\overline{a}}_{23}$, then we have

$$\begin{array}{cc}\hfill D^{\alpha }V\le & f_1{(\mu -\hat{\mu })}^2(a_{11}-a_{12}-a_{13})+f_2{(\nu -\hat{\nu })}^2({\overline{a}}_{21}-a_{22}-a_{23})+f_3{(\omega -\hat{\omega })}^2({\overline{a}}_{31}+{\overline{a}}_{32}-a_{33})\le 0.\hfill \end{array}$$

When $\left[{\mathbb{H}}_3\right]$ holds, $\left[{\mathbb{H}}_2\right]$ also follows, and by Theorem 3, if $\left[{\mathbb{H}}_1\right]$ is satisfied, then $\hat{E}$ is locally asymptotically stable. From $\left[{\mathbb{H}}_1\right]$ and $\left[{\mathbb{H}}_3\right]$, we obtain $D^{\alpha }V\le 0$. Furthermore, utilizing LasSalle’s invariant set principle for differential system (7), $\hat{E}$ is globally asymptotically stable, thereby concluding the proof of Theorem 4. □

3.2. Dynamic Analysis of the System (1) with Delay

Next, we study the delayed fractional system (1), where systems (1) and (7) have the same equilibrium. The stability of the fractional system needs to be revisited due to the effect of delay $\tau$. We calculate the critical value of bifurcation with delay $\tau$ serving as a branch parameter and explore the sufficient condition leading to a Hopf bifurcation.

When $\tau >0$, the characteristic equation of the non-controlled system (1) at the equilibrium $\hat{E}$ is organized as follows:

$$M_1\left(s\right)+M_2\left(s\right)e^{-s\tau }+M_3\left(s\right)e^{-2s\tau }=0,$$

(10)

where

$$\begin{array}{cc}{M}_1\left(s\right)=& s^{3\alpha }+((a_{22}+a_{23})\hat{\nu }-(a_{11}-a_{12}-a_{13})\hat{\mu }+a_{33}\hat{\omega })s^{2\alpha }+\left[a_{33}\right((a_{22}+a_{23})\hat{\nu }\hat{\omega }\hfill \\ & -(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega })-(a_{22}+a_{23})(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\nu }]s^{\alpha }\hfill \\ & -(a_{22}+a_{23})(a_{11}-a_{12}-a_{13})a_{33}\hat{\mu }\hat{\nu }\hat{\omega },\hfill \\ M_2\left(s\right)=& (-{\overline{a}}_{21}\hat{\nu }-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega })s^{2\alpha }+[({\overline{a}}_{12}{a}_{21}+{\overline{a}}_{21}(a_{11}-a_{12}-a_{13}))\hat{\mu }\hat{\nu }+({\overline{a}}_{23}{a}_{32}-{\overline{a}}_{21}{a}_{33}\hfill \\ & -({\overline{a}}_{31}+{\overline{a}}_{32})(a_{22}+a_{23}))\hat{\nu }\hat{\omega }+((a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32})+{\overline{a}}_{13}{a}_{31}\left)\hat{\mu }\hat{\omega }\right]s^{\alpha }\hfill \\ & +\left[(a_{11}-a_{12}-a_{13})\right((a_{22}+a_{23})({\overline{a}}_{31}+{\overline{a}}_{32})+{\overline{a}}_{21}{a}_{33}-{\overline{a}}_{23}{a}_{32})+{\overline{a}}_{12}{a}_{21}{a}_{33}\hfill \\ & +{\overline{a}}_{13}{a}_{31}(a_{22}+a_{23})-{\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}]\hat{\mu }\hat{\nu }\hat{\omega },\hfill \\ M_3\left(s\right)=& {\overline{a}}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\nu }\hat{\omega }{s}^{\alpha }+({\overline{a}}_{13}{a}_{21}{a}_{32}-{\overline{a}}_{13}{\overline{a}}_{21}{a}_{31}-{\overline{a}}_{12}{a}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})\hfill \\ & -{\overline{a}}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})(a_{11}-a_{12}-a_{13}))\hat{\mu }\hat{\nu }\hat{\omega }.\hfill \end{array}$$

Multiplying both sides of the equation by $e^{s\tau }$, then we obtain

$$M_1\left(s\right)e^{s\tau }+M_2\left(s\right)+M_3\left(s\right)e^{-s\tau }=0.$$

(11)

Assuming $s=i\rho (\rho >0)$ represents a purely imaginary root of Equation (11), then separating the real and imaginary parts of the above equation, we obtain the following system of equations

$$\left\{\begin{array}{c}(M_1^R+M_3^R)cos\rho \tau +(M_3^I-M_1^I)sin\rho \tau =-M_2^R,\hfill \\ (M_1^I+M_3^I)cos\rho \tau +(M_1^R-M_3^R)sin\rho \tau =-M_2^I,\hfill \end{array}\right.$$

(12)

where

$$\begin{array}{cc}\hfill M_1^R=& {\rho }^{3\alpha }cos\frac{3\alpha \pi }{2}+((a_{22}+a_{23})\hat{\nu }-(a_{11}-a_{12}-a_{13})\hat{\mu }+a_{33}\hat{\omega }){\rho }^{2\alpha }cos\alpha \pi +\left(a_{33}\right((a_{22}+a_{23})\hat{\nu }\hat{\omega }\hfill \\ \hfill & -(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega })-(a_{22}+a_{23})(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\nu }){\rho }^{\alpha }cos\frac{\alpha \pi }{2}\hfill \\ \hfill & -(a_{22}+a_{23})(a_{11}-a_{12}-a_{13})a_{33}\hat{\mu }\hat{\nu }\hat{\omega },\hfill \\ \hfill M_1^I=& {\rho }^{3\alpha }sin\frac{3\alpha \pi }{2}+((a_{22}+a_{23})\hat{\nu }-(a_{11}-a_{12}-a_{13})\hat{\mu }+a_{33}\hat{\omega }){\rho }^{2\alpha }sin\alpha \pi +\left(a_{33}\right((a_{22}+a_{23})\hat{\nu }\hat{\omega }\hfill \\ \hfill & -(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega })-(a_{22}+a_{23})(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\nu }){\rho }^{\alpha }sin\frac{\alpha \pi }{2},\hfill \\ \hfill M_2^R=& (-{\overline{a}}_{21}\hat{\nu }-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }){\rho }^{2\alpha }cos\alpha \pi +[({\overline{a}}_{12}{a}_{21}+{\overline{a}}_{21}(a_{11}-a_{12}-a_{13}))\hat{\mu }\hat{\nu }+({\overline{a}}_{23}{a}_{32}-{\overline{a}}_{21}{a}_{33}\hfill \\ \hfill & -({\overline{a}}_{31}+{\overline{a}}_{32})(a_{22}+a_{23}))\hat{\nu }\hat{\omega }+((a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32})+{\overline{a}}_{13}{a}_{31})\hat{\mu }\hat{\omega }]{\rho }^{\alpha }cos\frac{\alpha \pi }{2}\hfill \\ \hfill & +[(a_{11}-a_{12}-a_{13})((a_{22}+a_{23})({\overline{a}}_{31}+{\overline{a}}_{32})+{\overline{a}}_{21}{a}_{33}-{\overline{a}}_{23}{a}_{32})+{\overline{a}}_{12}{a}_{21}{a}_{33}\hfill \\ \hfill & +{\overline{a}}_{13}{a}_{31}(a_{22}+a_{23})-{\overline{a}}_{12}{\overline{a}}_{23}{a}_{31}]\hat{\mu }\hat{\nu }\hat{\omega },\hfill \\ \hfill M_2^I=& (-{\overline{a}}_{21}\hat{\nu }-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }){\rho }^{2\alpha }sin\alpha \pi +[({\overline{a}}_{12}{a}_{21}+{\overline{a}}_{21}(a_{11}-a_{12}-a_{13}))\hat{\mu }\hat{\nu }+({\overline{a}}_{23}{a}_{32}-{\overline{a}}_{21}{a}_{33}\hfill \\ \hfill & -({\overline{a}}_{31}+{\overline{a}}_{32})(a_{22}+a_{23}))\hat{\nu }\hat{\omega }+((a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32})+{\overline{a}}_{13}{a}_{31})\hat{\mu }\hat{\omega }]{\rho }^{\alpha }sin\frac{\alpha \pi }{2},\hfill \\ \hfill M_3^R=& {\overline{a}}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\nu }\hat{\omega }{\rho }^{\alpha }cos\frac{\alpha \pi }{2}+({\overline{a}}_{13}{a}_{21}{a}_{32}-{\overline{a}}_{13}{\overline{a}}_{21}{a}_{31}-{\overline{a}}_{12}{a}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})\hfill \\ \hfill & -({\overline{a}}_{31}+{\overline{a}}_{32}){\overline{a}}_{21}(a_{11}-a_{12}-a_{13}))\hat{\mu }\hat{\nu }\hat{\omega },\hfill \\ \hfill M_3^I=& {\overline{a}}_{21}({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\nu }\hat{\omega }{\rho }^{\alpha }sin\frac{\alpha \pi }{2}.\hfill \end{array}$$

By solving the Equation (12), we derive that

$$\left\{\begin{array}{c}cos\rho \tau =\frac{M_2^I(M_3^I-M_1^I)-M_2^R(M_1^R-M_3^R)}{{\left(M_1^R\right)}^2+{\left(M_1^I\right)}^2-{\left(M_3^R\right)}^2-{\left(M_3^I\right)}^2}\equiv {\phi }_1\left(\rho \right),\hfill \\ sin\rho \tau =\frac{M_2^R(M_3^I+M_1^I)-M_2^I(M_1^R+M_3^R)}{{\left(M_1^R\right)}^2+{\left(M_1^I\right)}^2-{\left(M_3^R\right)}^2-{\left(M_3^I\right)}^2}\equiv {\phi }_2\left(\rho \right).\hfill \end{array}\right.$$

(13)

Making ${\rho }_1$ is a positive real root of equation ${\phi }_1^2\left(\rho \right)+{\phi }_2^2\left(\rho \right)=1$, then based on the Equation (13), it is obtained that

$${\tau }^{\left(k\right)}=\frac{1}{{\rho }_1}[arccos\frac{M_2^I(M_3^I-M_1^I)-M_2^R(M_1^R-M_3^R)}{{\left(M_1^R\right)}^2+{\left(M_1^I\right)}^2-{\left(M_3^R\right)}^2-{\left(M_3^I\right)}^2}+2k\pi ],k=0,1,2,\cdots .$$

Define the bifurcation point

$${\tau }_0=min\left\{{\tau }^{\left(k\right)}\right\},k=0,1,2,\cdots .$$

Using the chain rule to differentiate both sides of (10) regarding $\tau$, then

$${M_1}^{\prime }\left(s\right)\frac{ds}{d\tau }+\left[{M_2}^{\prime }\left(s\right)\frac{ds}{d\tau }{e}^{-s\tau }+M_2\left(s\right)e^{-s\tau }(-\tau \frac{ds}{d\tau }-s)\right]+\left[{M_3}^{\prime }\left(s\right)\frac{ds}{d\tau }{e}^{-2s\tau }+M_3\left(s\right)e^{-2s\tau }(-2\tau \frac{ds}{d\tau }-2s)\right]=0.$$

Processing the above equation gets

$$Re\left[{\displaystyle \frac{ds}{d\tau }}\right]{|}_{(\rho ={\rho }_1,\tau ={\tau }_0)}={\displaystyle \frac{{\mathrm{\Lambda }}_1{\mathsf{\Delta }}_1+{\mathrm{\Lambda }}_2{\mathsf{\Delta }}_2}{{\mathsf{\Delta }}_1^2+{\mathsf{\Delta }}_2^2}},$$

(14)

where

$$\begin{array}{cc}\hfill {\mathrm{\Lambda }}_1=& {\rho }_1(M_2^{R}sin{\rho }_1{\tau }_0-M_2^{I}cos{\rho }_1{\tau }_0+2M_3^{R}sin2{\rho }_1{\tau }_0-2M_3^{I}cos2{\rho }_1{\tau }_0),\hfill \\ \hfill {\mathrm{\Lambda }}_2=& {\rho }_1(M_2^{R}cos{\rho }_1{\tau }_0+M_2^{I}sin{\rho }_1{\tau }_0+2M_3^{R}cos2{\rho }_1{\tau }_0+2M_3^{I}sin2{\rho }_1{\tau }_0),\hfill \\ \hfill {\mathsf{\Delta }}_1=& M_1^{\prime R}+(M_2^{\prime R}-{\tau }_0{M}_2^R)cos{\rho }_1{\tau }_0+(M_2^{\prime I}-{\tau }_0{M}_2^I)sin{\rho }_1{\tau }_0\hfill \\ \hfill & +(M_3^{\prime R}-2{\tau }_0{M}_3^R)cos2{\rho }_1{\tau }_0+(M_3^{\prime I}-2{\tau }_0{M}_3^I)sin2{\rho }_1{\tau }_0,\hfill \\ \hfill {\mathsf{\Delta }}_2=& M_1^{\prime I}+(M_2^{\prime I}-{\tau }_0{M}_2^I)cos{\rho }_1{\tau }_0-(M_2^{\prime R}-{\tau }_0{M}_2^R)sin{\rho }_1{\tau }_0\hfill \\ \hfill & +(M_3^{\prime I}-2{\tau }_0{M}_3^I)cos2{\rho }_1{\tau }_0-(M_3^{\prime R}-2{\tau }_0{M}_3^R)sin2{\rho }_1{\tau }_0.\hfill \end{array}$$

If $\left[{\mathbb{H}}_4\right]:{\displaystyle \frac{{\mathrm{\Lambda }}_1{\mathsf{\Delta }}_1+{\mathrm{\Lambda }}_2{\mathsf{\Delta }}_2}{{\mathsf{\Delta }}_1^2+{\mathsf{\Delta }}_2^2}}>0$, it shows that the transversality condition $Re\left[{\displaystyle \frac{ds}{d\tau }}\right]{|}_{(\rho ={\rho }_1,\tau ={\tau }_0)}$

$>0$ holds. Thus, we receive the following theorem:

Theorem 5. 

Assuming condition $\left[{\mathbb{H}}_4\right]$ is true, then

$\left(i\right)$ If $\tau \in [0,{\tau }_0)$, Equation (10) has all roots with negative real parts, then the positive equilibrium $\hat{E}$ is locally asymptotically stable;

$\left(ii\right)$ If $\tau ={\tau }_0$, Equation (10) has a purely imaginary root, and system (1) exhibits a Hopf bifurcation at the positive equilibrium $\hat{E}$, which implies it has a branch of periodic solution bifurcating from $\hat{E}$ near $\tau ={\tau }_0$;

$\left(iii\right)$ If $\tau >{\tau }_0$, Equation (10) has at least one root with a positive real part, then the positive equilibrium $\hat{E}$ is unstable.

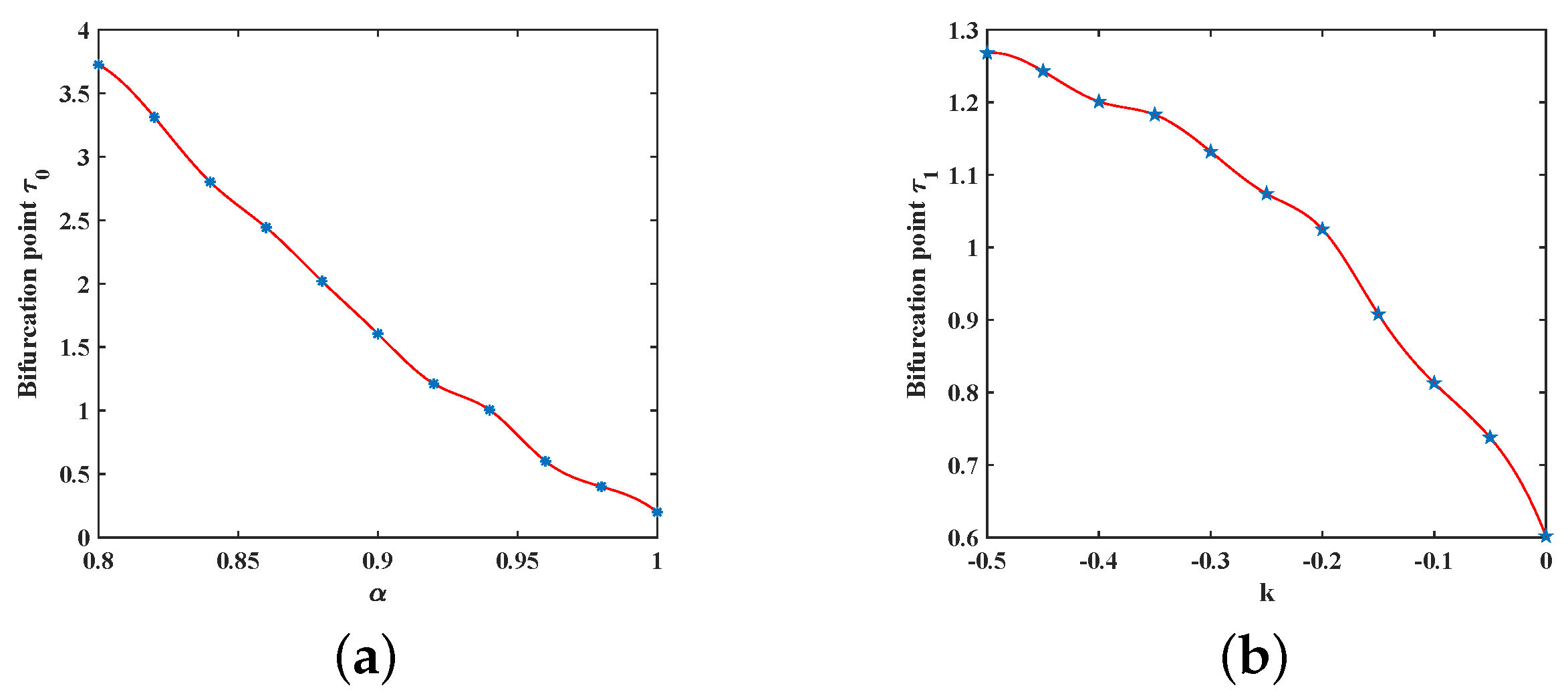
3.3. Bifurcation Dynamics in the System (3) with Control

Artificially controlling population dynamics systems enables human to better protect populations and more effectively exploit resources. In this section, we make it possible to achieve an increase in the system’s stability range of the system by designing a nonlinear feedback control strategy containing delay. For the control system (3), we select $\tau$ and $\sigma$ as the key parameters, research the stability and branch of the controlled system (3), and precisely discuss the threshold bifurcation value.

To better investigate the system’s stability, it is relatively easy to obtain the characterization matrix $\mathrm{\Lambda }\left(s\right)$ of the system (3) at $\hat{E}$ as

$$\mathrm{\Lambda }\left(s\right)=\left[\begin{array}{ccc}{s}^{\alpha }-(a_{11}-a_{12}-a_{13})\hat{\mu }& {\overline{a}}_{12}\hat{\mu }& {\overline{a}}_{13}\hat{\mu }\\ -a_{21}\hat{\nu }{e}^{-s\tau }& s^{\alpha }+(a_{22}+a_{23})\hat{\nu }-{\overline{a}}_{21}\hat{\nu }{e}^{-s\tau }+F\left(s\right)& {\overline{a}}_{23}\hat{\nu }\\ -a_{31}\hat{\omega }{e}^{-s\tau }& -a_{32}\hat{\omega }{e}^{-s\tau }& s^{\alpha }+Y\left(s\right)\end{array}\right],$$

(15)

where $F\left(s\right)=-k{e}^{-d\sigma }+k{e}^{-d\sigma }{e}^{-s\sigma }$, $Y\left(s\right)=a_{33}\hat{\omega }-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{e}^{-s\tau }$.

3.3.1. Bifurcation Dynamics Due to Delay $\tau$ in System (3) with Control

Theorem 6. 

Assuming condition $\left[{\mathbb{H}}_5\right]$ is established, which is given in the proof, we can draw the following conclusions:

$\left(i\right)$ If $\tau \in [0,{\tau }_1)$, all roots of Equation (16) have negative real parts, ensuring local asymptotic stability of the equilibrium $\hat{E}$ in the control system (3);

$\left(ii\right)$ If $\tau ={\tau }_1$, one root of Equation (16) is a pure imaginary number, then the control system (3) undergoes a Hopf bifurcation at the positive equilibrium $\hat{E}$;

$\left(iii\right)$ If $\tau >{\tau }_1$, at least one root of Equation (16) has a positive real part, rendering the equilibrium $\hat{E}$ in the control system (3) unstable.

Proof. 

The characteristic equation of the system (3) at the positive equilibrium $\hat{E}$ is

$$W_1\left(s\right)+W_2\left(s\right)e^{-s\tau }+W_3\left(s\right)e^{-2s\tau }=0,$$

(16)

where

$$\begin{array}{cc}\hfill U\left(s\right)& =s^{2\alpha }+(a_{33}\hat{\omega }-(a_{11}-a_{12}-a_{13})\hat{\mu })s^{\alpha }-a_{33}(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega },\hfill \\ \hfill N\left(s\right)& =-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{s}^{\alpha }+({\overline{a}}_{13}{a}_{31}+(a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}))\hat{\mu }\hat{\omega },\hfill \\ \hfill W_1\left(s\right)& =M_1\left(s\right)+k{e}^{-d\sigma }(e^{-s\sigma }-1)U\left(s\right),\hfill \\ \hfill W_2\left(s\right)& =M_2\left(s\right)+k{e}^{-d\sigma }(e^{-s\sigma }-1)N\left(s\right),\hfill \\ \hfill W_3\left(s\right)& =M_3\left(s\right).\hfill \end{array}$$

The equation is then organized as

$$W_1\left(s\right)e^{s\tau }+W_2\left(s\right)+W_3\left(s\right)e^{-s\tau }=0.$$

(17)

Assume that there exists a purely imaginary root $s=i\eta (\eta >0)$ of Equation (17), and substitute s into Equation (17) can be obtained

$$\left\{\begin{array}{c}(W_1^R+W_3^R)cos\eta \tau +(W_3^I-W_1^I)sin\eta \tau =-W_2^R,\hfill \\ (W_1^I+W_3^I)cos\eta \tau +(W_1^R-W_3^R)sin\eta \tau =-W_2^I,\hfill \end{array}\right.$$

(18)

where

$$\begin{array}{cc}\hfill U_R=& {\eta }^{2\alpha }cos\alpha \pi +(a_{33}\hat{\omega }-(a_{11}-a_{12}-a_{13})\hat{\mu }){\eta }^{\alpha }cos\frac{\alpha \pi }{2}-a_{33}(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega },\hfill \\ \hfill U_I=& {\eta }^{2\alpha }sin\alpha \pi +(a_{33}\hat{\omega }-(a_{11}-a_{12}-a_{13})\hat{\mu }){\eta }^{\alpha }sin\frac{\alpha \pi }{2},\hfill \\ \hfill N_R=& -({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{\eta }^{\alpha }cos\frac{\alpha \pi }{2}+({\overline{a}}_{13}{a}_{31}+(a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}))\hat{\mu }\hat{\omega },\hfill \\ \hfill N_I=& -({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{\eta }^{\alpha }sin\frac{\alpha \pi }{2},\hfill \end{array}$$

$$\begin{array}{cc}\hfill W_1^R=& M_1^R+k{e}^{-d\sigma }(U_{R}cos\eta \sigma +U_{I}sin\eta \sigma )-k{U}_R{e}^{-d\sigma },\hfill \\ \hfill W_1^I=& M_1^I+k{e}^{-d\sigma }(U_{I}cos\eta \sigma -U_{R}sin\eta \sigma )-k{U}_I{e}^{-d\sigma },\hfill \\ \hfill W_2^R=& M_2^R+k{e}^{-d\sigma }(N_{R}cos\eta \sigma +N_{I}sin\eta \sigma )-k{N}_R{e}^{-d\sigma },\hfill \\ \hfill W_2^I=& M_2^I+k{e}^{-d\sigma }(N_{I}cos\eta \sigma -N_{R}sin\eta \sigma )-k{N}_I{e}^{-d\sigma },\hfill \\ \hfill W_3^R=& M_3^R,W_3^I=M_3^I.\hfill \end{array}$$

Considering Equation (18), we get

$$\left\{\begin{array}{c}cos\eta \tau =\frac{{\mathrm{\Phi }}_1\left(\eta \right)}{{\mathrm{\Phi }}_3\left(\eta \right)},\hfill \\ sin\eta \tau =\frac{{\mathrm{\Phi }}_2\left(\eta \right)}{{\mathrm{\Phi }}_3\left(\eta \right)},\hfill \end{array}\right.$$

(19)

where

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_1\left(\eta \right)=& W_2^I(W_3^I-W_1^I)-W_2^R(W_1^R-W_3^R),\hfill \\ \hfill {\mathrm{\Phi }}_2\left(\eta \right)=& W_2^R(W_3^I+W_1^I)-W_2^I(W_1^R+W_3^R),\hfill \\ \hfill {\mathrm{\Phi }}_3\left(\eta \right)=& {\left(W_1^R\right)}^2+{\left(W_1^I\right)}^2-{\left(W_3^R\right)}^2-{\left(W_3^I\right)}^2.\hfill \end{array}$$

By means of Equation (19), it procures that

$${\mathrm{\Phi }}_3^2\left(\eta \right)={\mathrm{\Phi }}_1^2\left(\eta \right)+{\mathrm{\Phi }}_2^2\left(\eta \right).$$

(20)

Meanwhile, it can be defined from Equation (20) that

$$\mathrm{\Phi }\left(\eta \right)={\mathrm{\Phi }}_1^2\left(\eta \right)+{\mathrm{\Phi }}_2^2\left(\eta \right)-{\mathrm{\Phi }}_3^2\left(\eta \right)=0.$$

(21)

Assuming that there exists a positive real root ${\eta }_1$ of Equation (21), substituting this into the first equation of (19) we have

$${\tau }^{\left(k\right)}=\frac{1}{{\eta }_1}[arccos\frac{{\mathrm{\Phi }}_1\left({\eta }_1\right)}{{\mathrm{\Phi }}_3\left({\eta }_1\right)}+2k\pi ],k=0,1,2,\cdots .$$

We define the bifurcation of the fractional system (3) as follows:

$${\tau }_1=min\left\{{\tau }^{\left(k\right)}\right\},k=0,1,2,\cdots .$$

Using the chain rule to differentiate both sides of (16) regarding $\tau$, then

$${W_1}^{\prime }\left(s\right)\frac{ds}{d\tau }+\left[{W_2}^{\prime }\left(s\right)\frac{ds}{d\tau }{e}^{-s\tau }+W_2\left(s\right)e^{-s\tau }(-\tau \frac{ds}{d\tau }-s)\right]+\left[{W_3}^{\prime }\left(s\right)\frac{ds}{d\tau }{e}^{-2s\tau }+W_3\left(s\right)e^{-2s\tau }(-2\tau \frac{ds}{d\tau }-2s)\right]=0.$$

Processing the above equation gets

$$Re\left[{\displaystyle \frac{ds}{d\tau }}\right]{|}_{(\eta ={\eta }_1,\tau ={\tau }_1)}={\displaystyle \frac{{\mathrm{\Pi }}_1{\mathrm{\Gamma }}_1+{\mathrm{\Pi }}_2{\mathrm{\Gamma }}_2}{{\mathrm{\Gamma }}_1^2+{\mathrm{\Gamma }}_2^2}},$$

(22)

where

$$\begin{array}{cc}\hfill {\mathrm{\Pi }}_1=& {\eta }_1(W_2^{R}sin{\eta }_1{\tau }_1-W_2^{I}cos{\eta }_1{\tau }_1+2W_3^{R}sin2{\eta }_1{\tau }_1-2W_3^{I}cos2{\eta }_1{\tau }_1),\hfill \\ \hfill {\mathrm{\Pi }}_2=& {\eta }_1(W_2^{R}cos{\eta }_1{\tau }_1+W_2^{I}sin{\eta }_1{\tau }_1+2W_3^{R}cos2{\eta }_1{\tau }_1+2W_3^{I}sin2{\eta }_1{\tau }_1),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_1=& W_1^{\prime R}+(W_2^{\prime R}-{\tau }_1{W}_2^R)cos{\eta }_1{\tau }_1+(W_2^{\prime I}-{\tau }_1{W}_2^I)sin{\eta }_1{\tau }_1\hfill \\ \hfill & +(W_3^{\prime R}-2{\tau }_1{W}_3^R)cos2{\eta }_1{\tau }_1+(W_3^{\prime I}-2{\tau }_1{W}_3^I)sin2{\eta }_1{\tau }_1,\hfill \\ \hfill {\mathrm{\Gamma }}_2=& W_1^{\prime I}+(W_2^{\prime I}-{\tau }_1{W}_2^I)cos{\eta }_1{\tau }_1-(W_2^{\prime R}-{\tau }_1{W}_2^R)sin{\eta }_1{\tau }_1\hfill \\ \hfill & +(W_3^{\prime I}-2{\tau }_1{W}_3^I)cos2{\eta }_1{\tau }_1-(W_3^{\prime R}-2{\tau }_1{W}_3^R)sin2{\eta }_1{\tau }_1.\hfill \end{array}$$

Under $\left[{\mathbb{H}}_5\right]:{\displaystyle \frac{{\mathrm{\Pi }}_1{\mathrm{\Gamma }}_1+{\mathrm{\Pi }}_2{\mathrm{\Gamma }}_2}{{\mathrm{\Gamma }}_1^2+{\mathrm{\Gamma }}_2^2}}>0$, the transversality condition is $Re\left[{\displaystyle \frac{ds}{d\tau }}\right]{|}_{(\eta ={\eta }_1,\tau ={\tau }_1)}>0$. Thus we complete the proof of the theorem. □

3.3.2. Bifurcation Dynamics Due to Feedback Delay $\sigma$ in System (3) with Control

Theorem 7. 

If the transversality condition $\left[{\mathbb{H}}_6\right]$ is satisfied, we can conclude the following:

$\left(i\right)$ If $\sigma \in [0,{\sigma }_1)$, the local asymptotic stability of the positive equilibrium $\hat{E}$ in the controlled system (3) is established;

$\left(ii\right)$ If $\sigma ={\sigma }_1$, the fractional system (3) undergoes a Hopf bifurcation, meaning a bifurcation to a periodic solution is generated from $\hat{E}$ near $\sigma ={\sigma }_1$;

$\left(iii\right)$ If $\sigma >{\sigma }_1$, the positive equilibrium $\hat{E}$ in the controlled system (3) becomes unstable.

Proof. 

Rearrange the characteristic equation of the controlled system at the positive equilibrium $\hat{E}$ into the following form

$$Q\left(s\right)-kP\left(s\right)e^{-d\sigma }+kP\left(s\right)e^{-d\sigma }{e}^{-s\sigma }=0,$$

(23)

where

$$\begin{array}{cc}\hfill Q\left(s\right)=& M_1\left(s\right)+M_2\left(s\right)e^{-s\tau }+M_3\left(s\right)e^{-2s\tau },\hfill \\ \hfill P\left(s\right)=& s^{2\alpha }+(a_{33}\hat{\omega }-(a_{11}-a_{12}-a_{13})\hat{\mu })s^{\alpha }-a_{33}(a_{11}-a_{12}-a_{13})\hat{\mu }\hat{\omega }\hfill \\ \hfill & +(-({\overline{a}}_{31}+{\overline{a}}_{32})\hat{\omega }{s}^{\alpha }+({\overline{a}}_{13}{a}_{31}+(a_{11}-a_{12}-a_{13})({\overline{a}}_{31}+{\overline{a}}_{32}))\hat{\mu }\hat{\omega })e^{-s\tau }.\hfill \end{array}$$

Suppose that the characteristic Equation (23) has a purely imaginary root $s=i\xi (\xi >0)$, substituting s into Equation (23) and separating their imaginary and real parts, we get

$$\left\{\begin{array}{c}{Q}_R-k{P}_R{e}^{-d\sigma }+k{e}^{-d\sigma }{P}_{R}cos\xi \sigma +k{e}^{-d\sigma }{P}_{I}sin\xi \sigma =0,\hfill \\ Q_I-k{P}_I{e}^{-d\sigma }+k{e}^{-d\sigma }{P}_{I}cos\xi \sigma -k{e}^{-d\sigma }{P}_{R}sin\xi \sigma =0,\hfill \end{array}\right.$$

(24)

where

$$\begin{array}{cc}\hfill Q_R=& M_1^R+M_2^{R}cos\xi \tau +M_2^{I}sin\xi \tau +M_3^{R}cos2\xi \tau +M_3^{I}sin2\xi \tau ,\hfill \\ \hfill Q_I=& M_1^I+M_2^{I}cos\xi \tau -M_2^{R}sin\xi \tau +M_3^{I}cos2\xi \tau -M_3^{R}sin2\xi \tau ,\hfill \\ \hfill P_R=& U_R+N_{R}cos\xi \tau +N_{I}sin\xi \tau ,\hfill \\ \hfill P_I=& U_I+N_{R}cos\xi \tau -N_{R}sin\xi \tau .\hfill \end{array}$$

$U_R$, $U_I$, $N_R$, and $N_I$ have already been defined in the proof of Theorem 6. By the aid of Equation (24), we have

$$\left\{\begin{array}{cc}cos\xi \sigma =\hfill & 1-\frac{e^{d\sigma (P_R{Q}_R+P_I{Q}_I)}}{k(P_R^2+P_I^2)}={\mathrm{{\rm Y}}}_1\left(\xi \right),\hfill \\ sin\xi \sigma =\hfill & \frac{e^{d\sigma (P_R{Q}_I-P_I{Q}_R)}}{k(P_R^2+P_I^2)}={\mathrm{{\rm Y}}}_2\left(\xi \right).\hfill \end{array}\right.$$

(25)

In the meantime, from the Equation (25), we can calculate

$$I(\xi ,\sigma )=e^{d\sigma }(Q_R^2+Q_I^2)-2k(P_R{Q}_R+P_I{Q}_I)=0.$$

(26)

Assuming a positive real root ${\xi }_1$ for $I(\xi ,\sigma )=0$, then

$${\sigma }^k=\frac{1}{{\xi }_1}[arccos{\mathrm{{\rm Y}}}_1\left({\xi }_1\right)+2k\pi ],k=0,1,2,\cdots .$$

Select the bifurcation point ${\sigma }_1=min\left\{{\sigma }^k,k=0,1,2,\cdots \right\}$, and then differentiate both sides of Equation (23) with respect to $\sigma$. We have

$$Q^{\prime }\left(s\right)\frac{\mathrm{d}s}{\mathrm{d}\sigma }+dkP\left(s\right)e^{-d\sigma }-k{P}^{\prime }\left(s\right)e^{-d\sigma }\frac{\mathrm{d}s}{\mathrm{d}\sigma }-dkP\left(s\right)e^{-d\sigma }{e}^{-s\sigma }+k{P}^{\prime }\left(s\right)e^{-d\sigma }{e}^{-s\sigma }\frac{\mathrm{d}s}{\mathrm{d}\sigma }+kP\left(s\right)e^{-d\sigma }{e}^{-s\sigma }(-\sigma \frac{\mathrm{d}s}{\mathrm{d}\sigma }-s)=0.$$

Solving the above equation gives

$$\frac{\mathrm{d}s}{\mathrm{d}\sigma }=\frac{\mathrm{\Xi }\left(s\right)}{\mathrm{\Sigma }\left(s\right)}.$$

(27)

Define the real and imaginary parts of $\mathrm{\Xi }\left(s\right)$ as ${\mathrm{\Xi }}_R$, ${\mathrm{\Xi }}_I$, and the real and imaginary parts of $\mathrm{\Sigma }\left(s\right)$ as ${\mathrm{\Sigma }}_R$, ${\mathrm{\Sigma }}_I$, respectively. Based on the preceding analysis, we can derive that

$$Re\left[{\displaystyle \frac{ds}{d\sigma }}\right]{|}_{(\xi ={\xi }_1,\sigma ={\sigma }_1)}={\displaystyle \frac{{\mathrm{\Xi }}_R{\mathrm{\Sigma }}_R+{\mathrm{\Xi }}_I{\mathrm{\Sigma }}_I}{{\mathrm{\Sigma }}_R^2+{\mathrm{\Sigma }}_I^2}},$$

(28)

where

$$\begin{array}{cc}\hfill & {\mathrm{\Xi }}_R=k{e}^{-d\sigma }(P_R({\xi }_{1}sin{\xi }_1{\sigma }_1+dcos{\xi }_1{\sigma }_1-d)-P_I({\xi }_{1}cos{\xi }_1{\sigma }_1-dsin{\xi }_1{\sigma }_1)),\hfill \\ \hfill & {\mathrm{\Xi }}_I=k{e}^{-d\sigma }(P_I({\xi }_{1}sin{\xi }_1{\sigma }_1+dcos{\xi }_1{\sigma }_1-d)+P_R({\xi }_{1}cos{\xi }_1{\sigma }_1-dsin{\xi }_1{\sigma }_1)),\hfill \\ \hfill & {\mathrm{\Sigma }}_R=Q^{\prime R\left(s\right)}+k{e}^{-d{\sigma }_1}(P^{\prime R}\left(s\right)cos{\xi }_1{\sigma }_1+P^{\prime I}\left(s\right)sin{\xi }_1{\sigma }_1-P^{\prime R}\left(s\right)-{\sigma }_1(P_{R}cos{\xi }_1{\sigma }_1+P_{I}sin{\xi }_1{\sigma }_1)),\hfill \\ \hfill & {\mathrm{\Sigma }}_I=Q^{\prime I\left(s\right)}+k{e}^{-d{\sigma }_1}(P^{\prime I}\left(s\right)cos{\xi }_1{\sigma }_1-P^{\prime R}\left(s\right)sin{\xi }_1{\sigma }_1-P^{\prime I}\left(s\right)-{\sigma }_1(P_{I}cos{\xi }_1{\sigma }_1-P_{R}sin{\xi }_1{\sigma }_1)).\hfill \end{array}$$

As a result, under the condition of $\left[{\mathbb{H}}_6\right]:$${\displaystyle \frac{{\mathrm{\Xi }}_R{\mathrm{\Sigma }}_R+{\mathrm{\Xi }}_I{\mathrm{\Sigma }}_I}{{\mathrm{\Sigma }}_R^2+{\mathrm{\Sigma }}_I^2}}>0$, we conclude that the transversality condition is $Re\left[{\displaystyle \frac{ds}{d\sigma }}\right]{|}_{(\xi ={\xi }_1,\sigma ={\sigma }_1)}>0$. The analysis above confirms Theorem 7. □

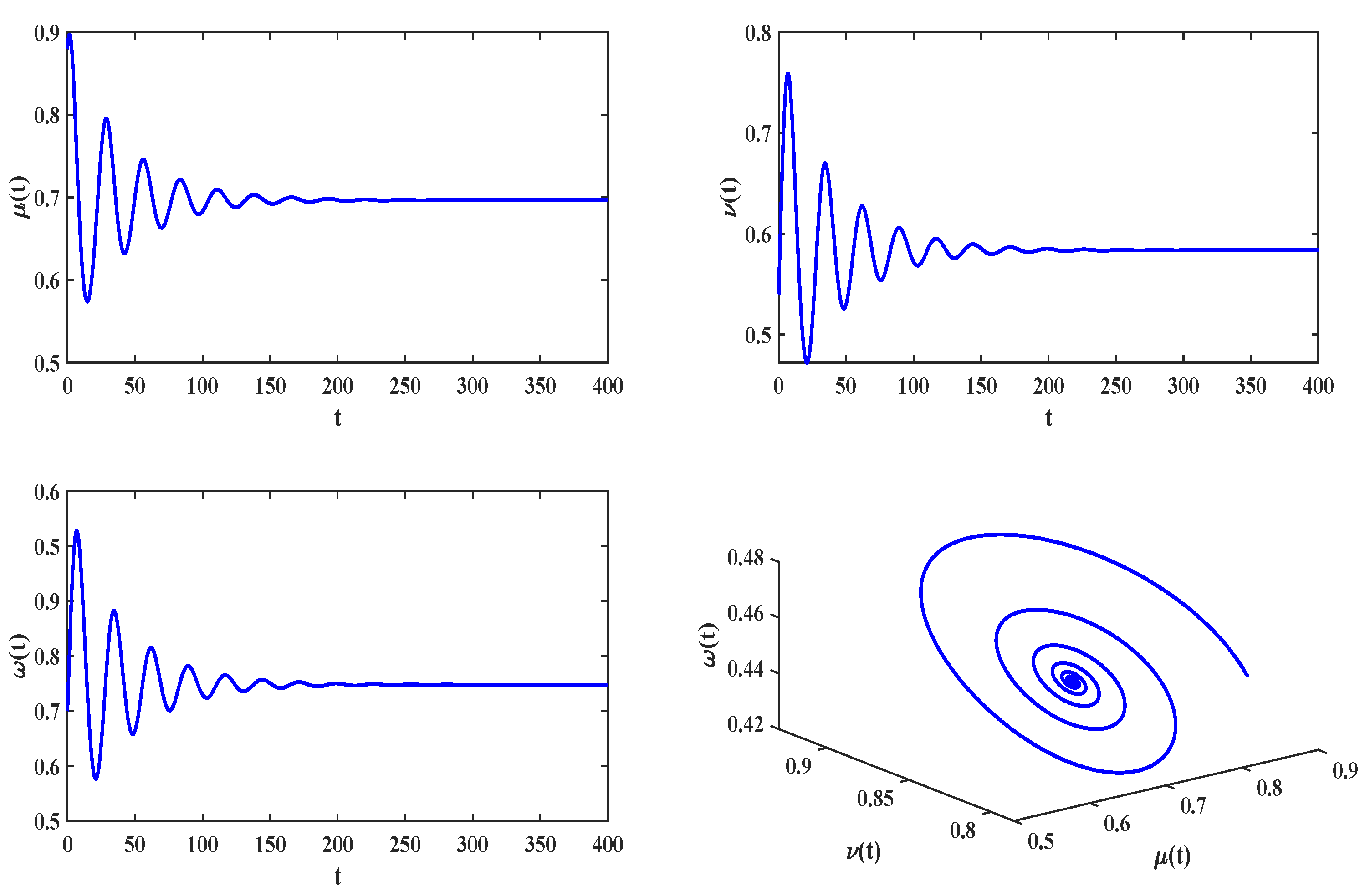
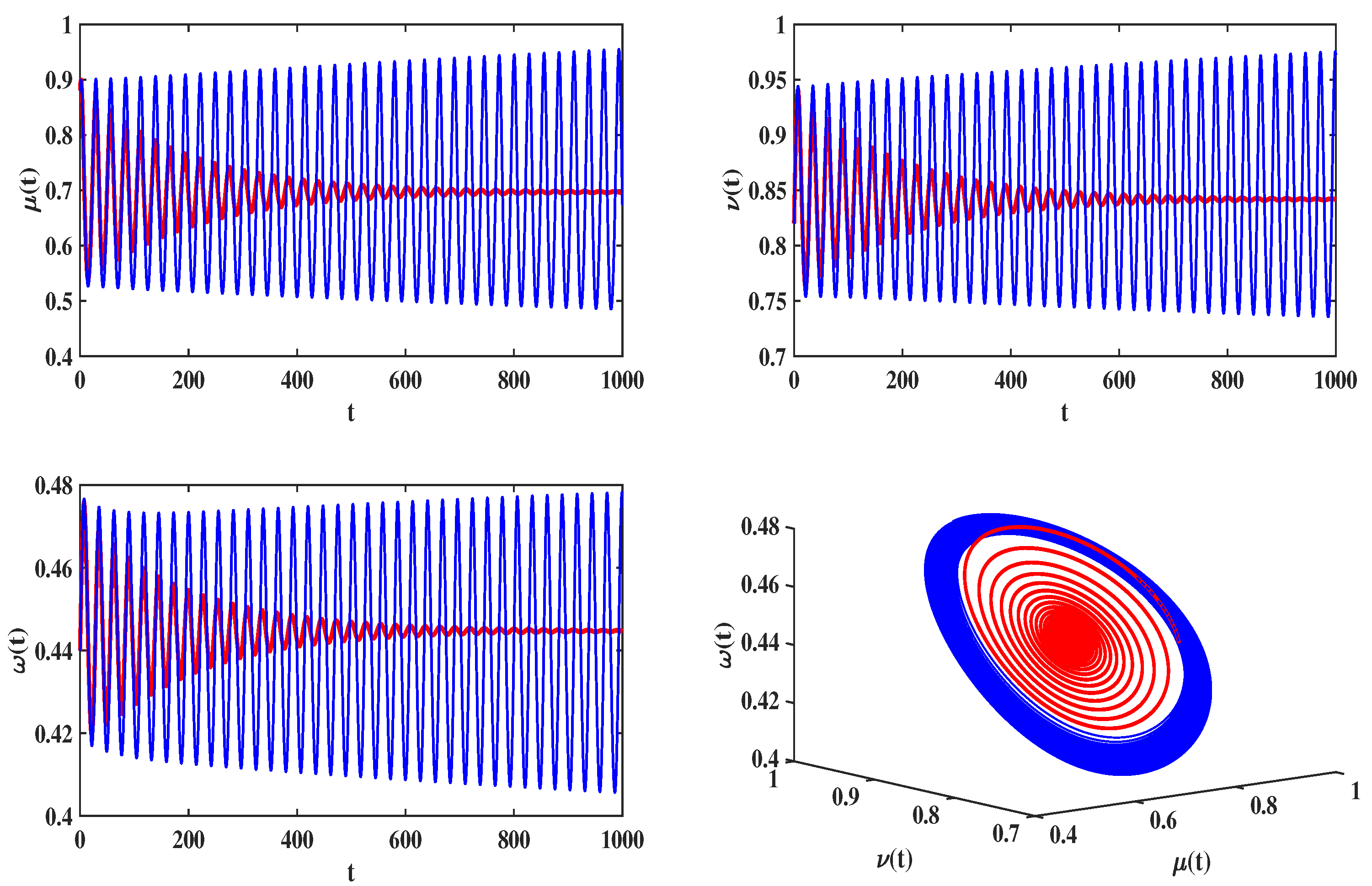
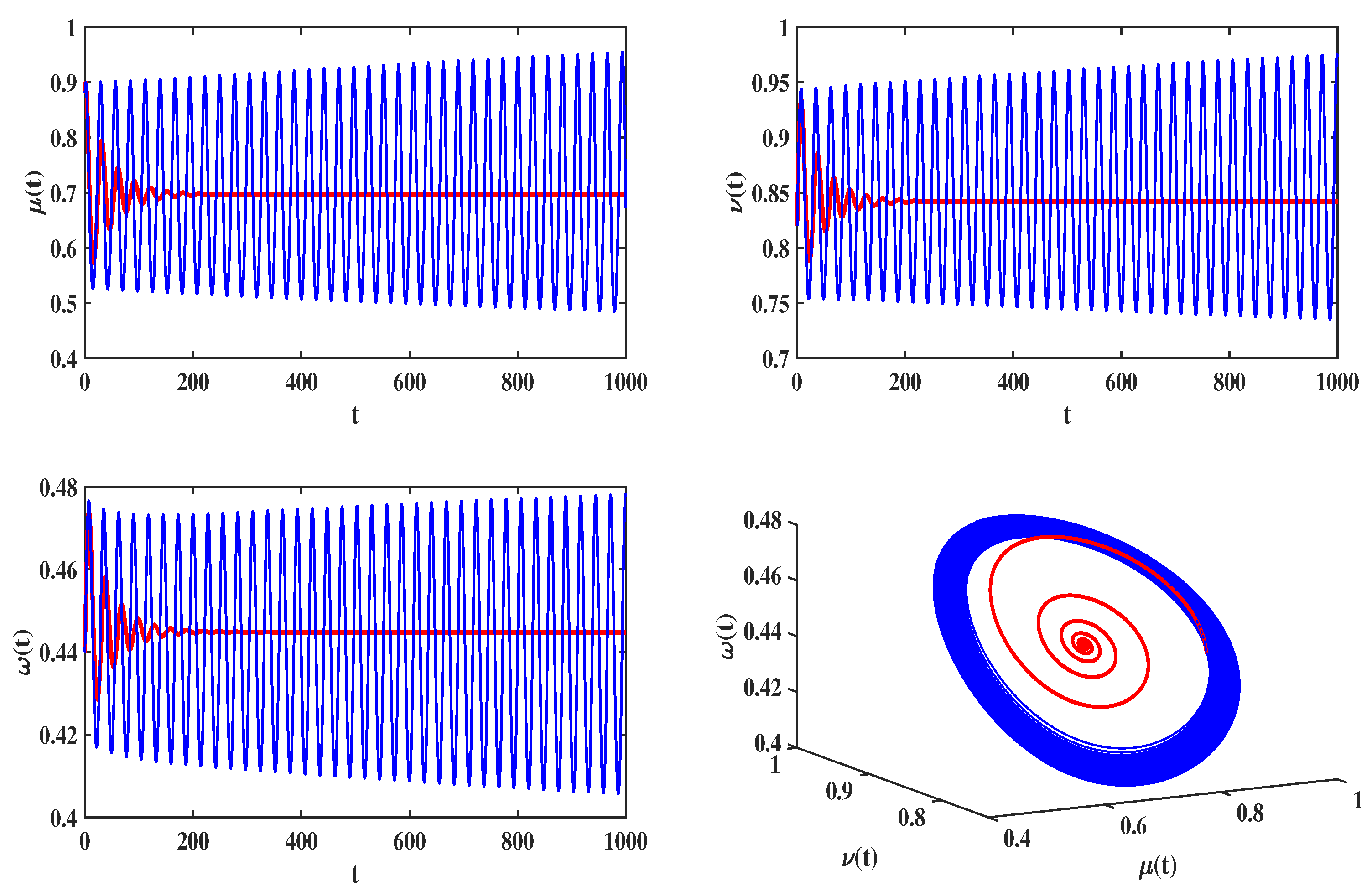
4. Practical Applications and Numerical Simulations

In this section, numerical simulations are performed by using the Adams–Bashforth–Moulton method [48,49]. We provide two application examples to confirm the validity and biological feasibility of theoretical results for system’s stability and Hopf bifurcation.

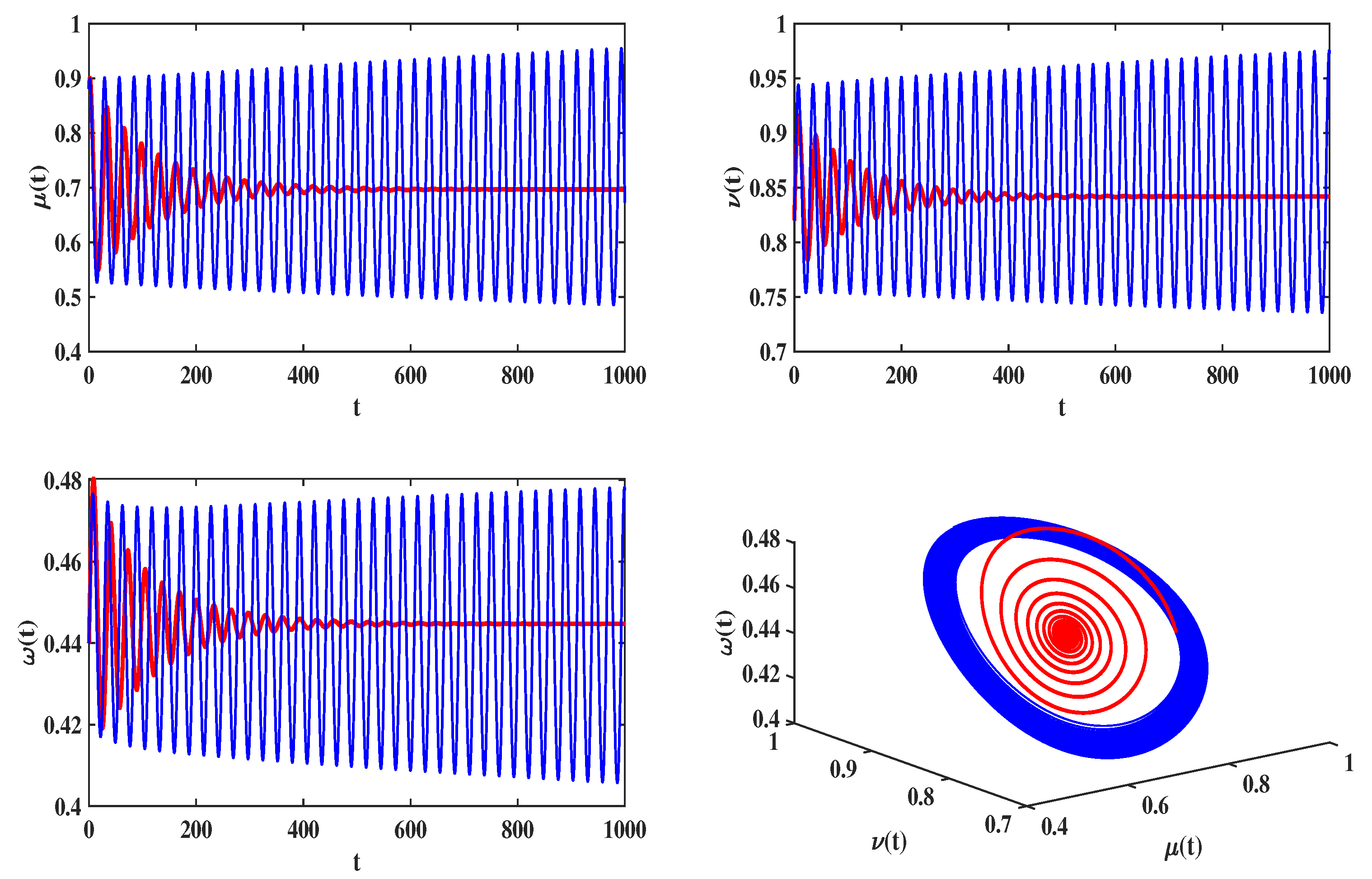
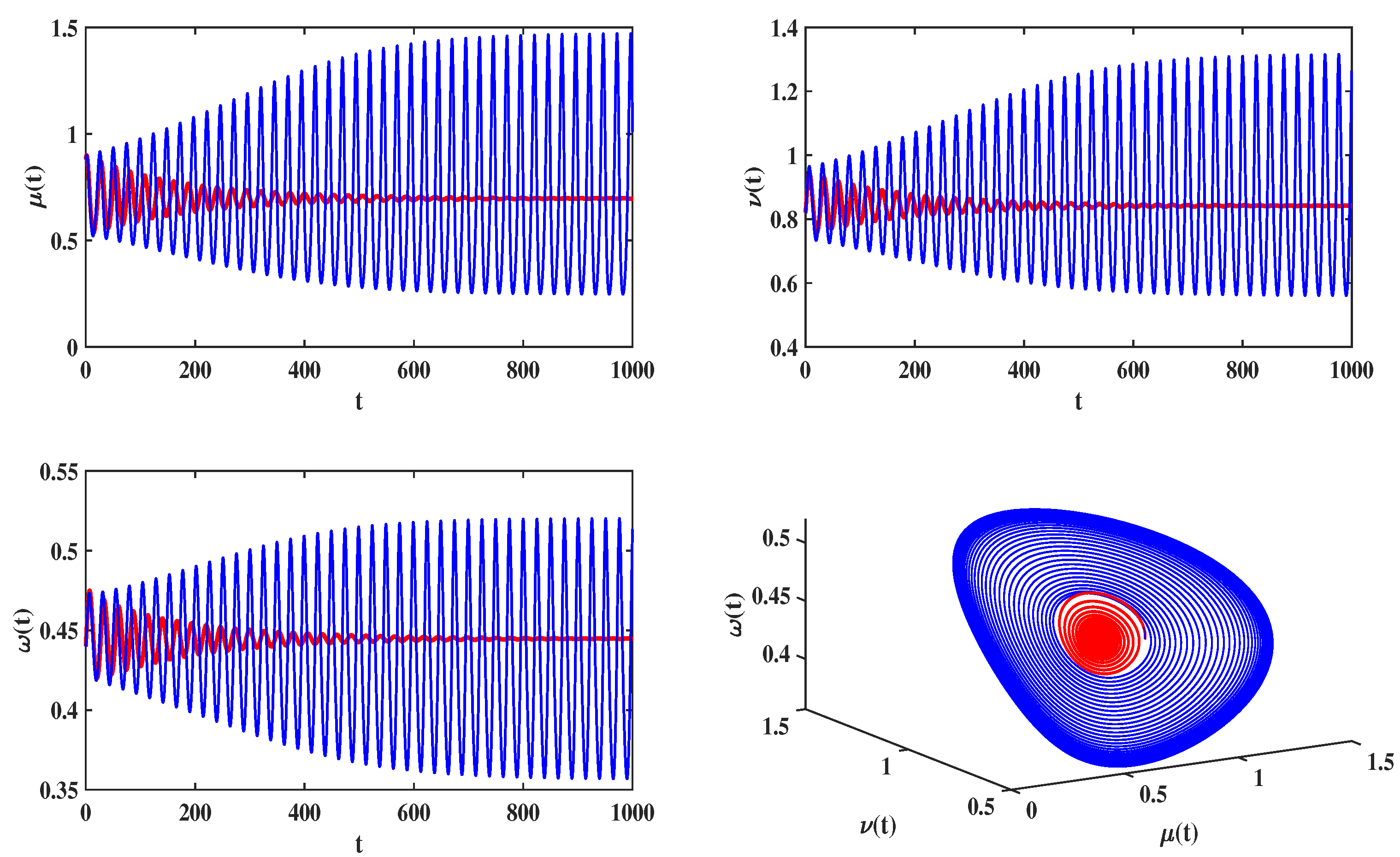
4.1. Delayed Feedback Control for a Food Chain Model

We consider the following fractional three-species food chain model with delay

$$\left\{\begin{array}{c}{D}^{\alpha }\mu \left(t\right)=\mu \left(t\right)\left(0.7(1-\frac{1}{18}\mu \left(t\right))-\frac{0.6\nu \left(t\right)}{1+0.125\mu \left(t\right)}-\frac{0.55\omega \left(t\right)}{1+0.25\mu \left(t\right)}\right),\hfill \\ D^{\alpha }\nu \left(t\right)=\nu \left(t\right)\left(\frac{0.18\mu (t-\tau )}{1+0.125\mu (t-\tau )}-\frac{0.15\omega \left(t\right)}{1+0.3\nu \left(t\right)}-0.05\nu \left(t\right)-0.02\right)+k{e}^{-0.02\sigma }(\nu \left(t\right)-\nu (t-\sigma )),\hfill \\ D^{\alpha }\omega \left(t\right)=\omega \left(t\right)\left(\frac{0.124\mu (t-\tau )}{1+0.25\mu (t-\tau )}+\frac{0.075\nu (t-\tau )}{1+0.3\nu (t-\tau )}-0.18\omega \left(t\right)-0.02\right).\hfill \end{array}\right.$$

(29)

where $\mu \left(t\right)$, $\nu \left(t\right)$, and $\omega \left(t\right)$ represent the density of prey, intermediate predator, and advanced predator, respectively. We define its initial condition as $\mu \left(t\right)=0.88,\nu \left(t\right)=0.82,\omega \left(t\right)=0.44,t\in \left[-\tau ,0\right]$. By calculating, we obtain the positive equilibrium of the system is $\hat{E}(0.697,0.842,0.445)$. In the discussion below, we fix $\alpha =0.96$ without any special remarks.

When $k=0$ or $\sigma =0$, we deal with the fractional system (29) without a controller.

When $\tau =0$, the delay-free system (29) satisfies the conditions of Theorems 3 and 4, then the system (29) is globally asymptotically stable at $\hat{E}$. Figure 1 illustrates the conclusion.

Next, when $\tau >0$, we can calculate that the critical value of the system to generate a Hopf bifurcation is ${\tau }_0=0.602$. Thus, from Figure 2, we can also observe that the system (29) is locally asymptotically stable at $\hat{E}$ when $\tau =0.51<{\tau }_0$, producing a periodic solution when $\tau ={\tau }_0$ and unstable when $\tau =0.8>{\tau }_0$.

To investigate whether the change in the order value causes a difference in the system’s stability, in Figure 3, we fix $\tau =0.8$, then take $\alpha =0.9$ and $\alpha =0.96$, respectively, which are observed to exhibit stable and unstable states. So, the change in the value of order also causes a difference in the system’s stability.

Remark 1. 

To better illustrate that the fractional order suppresses the oscillatory behavior of a system, we show the corresponding bifurcation thresholds from $\alpha =0.8$ to $\alpha =1$ in Figure 4a. The results indicate that the smaller order of the system has a better bifurcation suppression effect, which means that the fractional system has a wider stable region.

When $k\ne 0$ and $\sigma \ne 0$, we discuss the fractional system (29) with a delay controller.

(i) Initially, we discuss the influence of delay $\tau$ on the bifurcation behavior of system (29). In Figure 3, when $\tau =0.8$, the non-control system is unstable. Let $k=$−0.2, $\sigma =4$, the controlled system can reach a steady state due to $\tau =0.8<{\tau }_1=1.025$, where ${\tau }_1$ is the bifurcation point of system (29) (see Figure 5). When $\tau ={\tau }_1$, it causes a Hopf bifurcation and is accompanied by generating a periodic solution near $\hat{E}$. The above is consistent with the conclusion of Theorem 6. Therefore, choosing an appropriate controller can effectively suppress oscillatory behavior in the system.

(ii) Subsequently, we examine how the feedback control gain k influences the bifurcation behavior of system (29). Fixing $\sigma =4$, changing the feedback gain k within a certain range will also change the corresponding system’s bifurcation critical values (as shown in Figure 4b). Therefore, the selection of a feedback gain factor also influences the system’s stability.

(iii) Ultimately, we explore how the feedback control delay $\sigma$ impacts the bifurcation behavior of system (29). Fixing $k=0.15$ and $\tau =0.45$, we compute the critical value ${\sigma }_1=1.832$, at which the system undergoes a Hopf bifurcation and generates a periodic solution branch near $\hat{E}$. When $\sigma =0.5<{\sigma }_1$, the system is stable at $\hat{E}$. When $\sigma =2.25>{\sigma }_1$, $\hat{E}$ is unstable (as shown in Figure 6). The conclusion is consistent with Theorem 7.

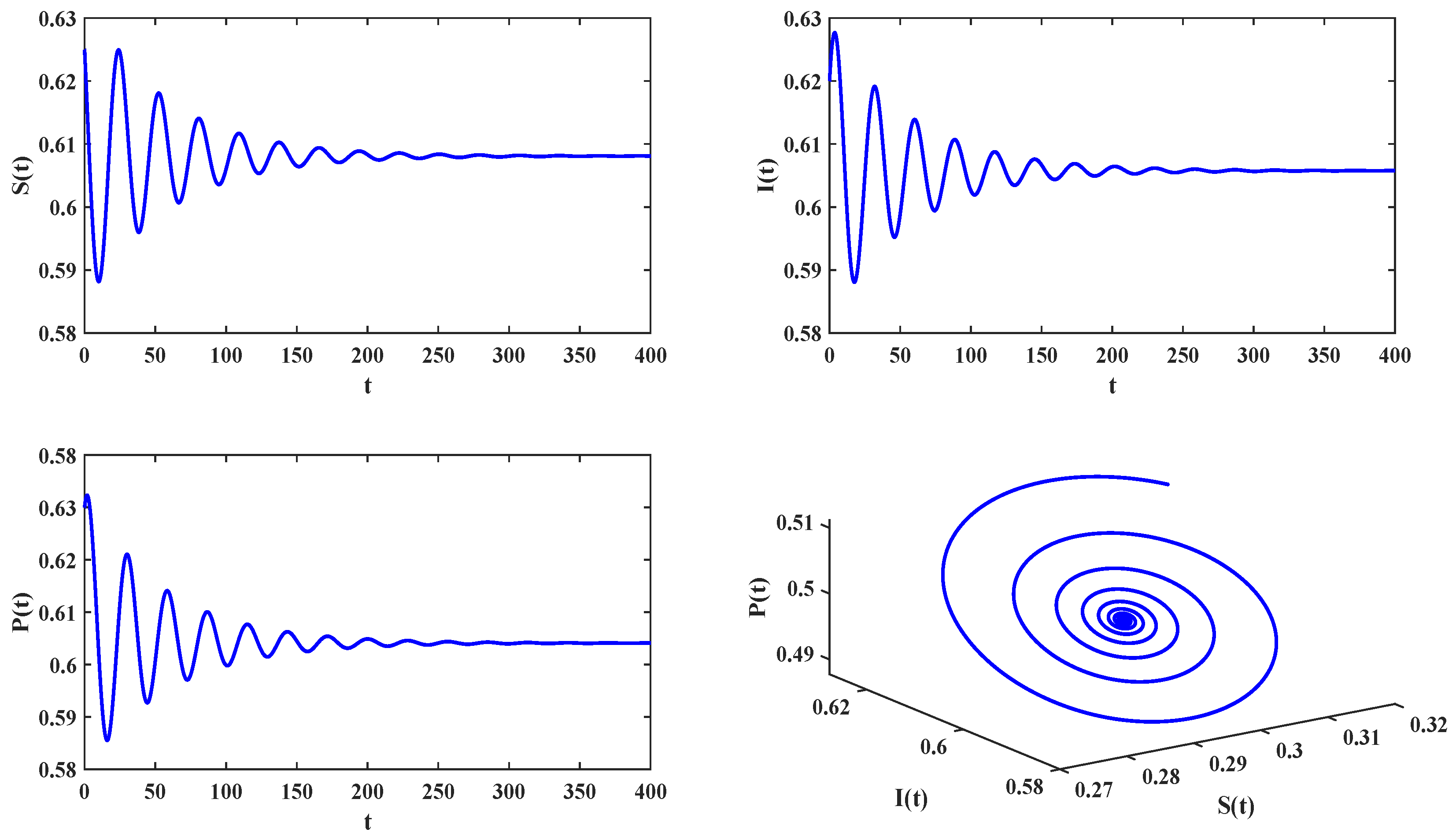
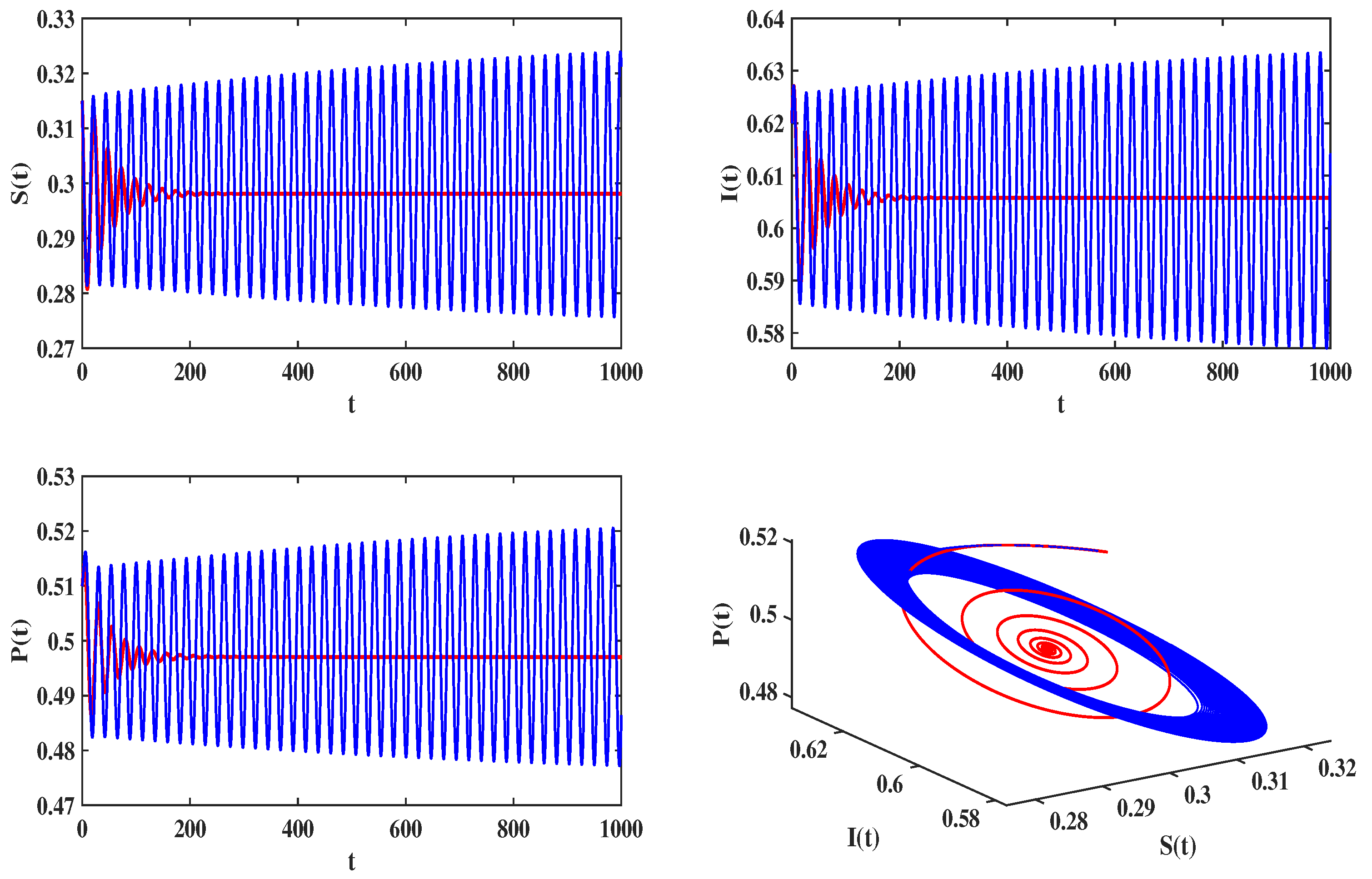
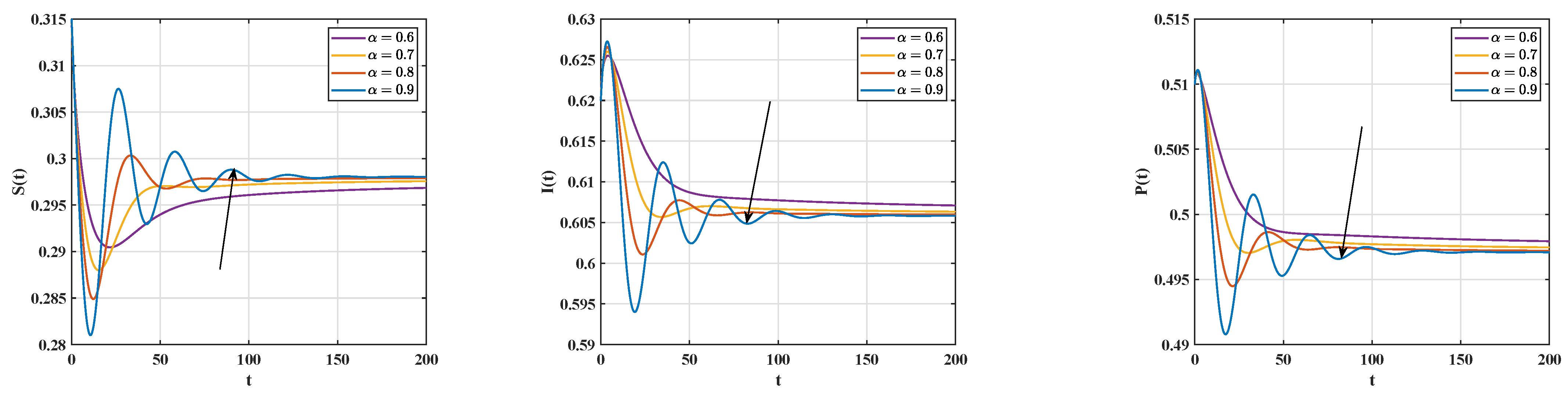
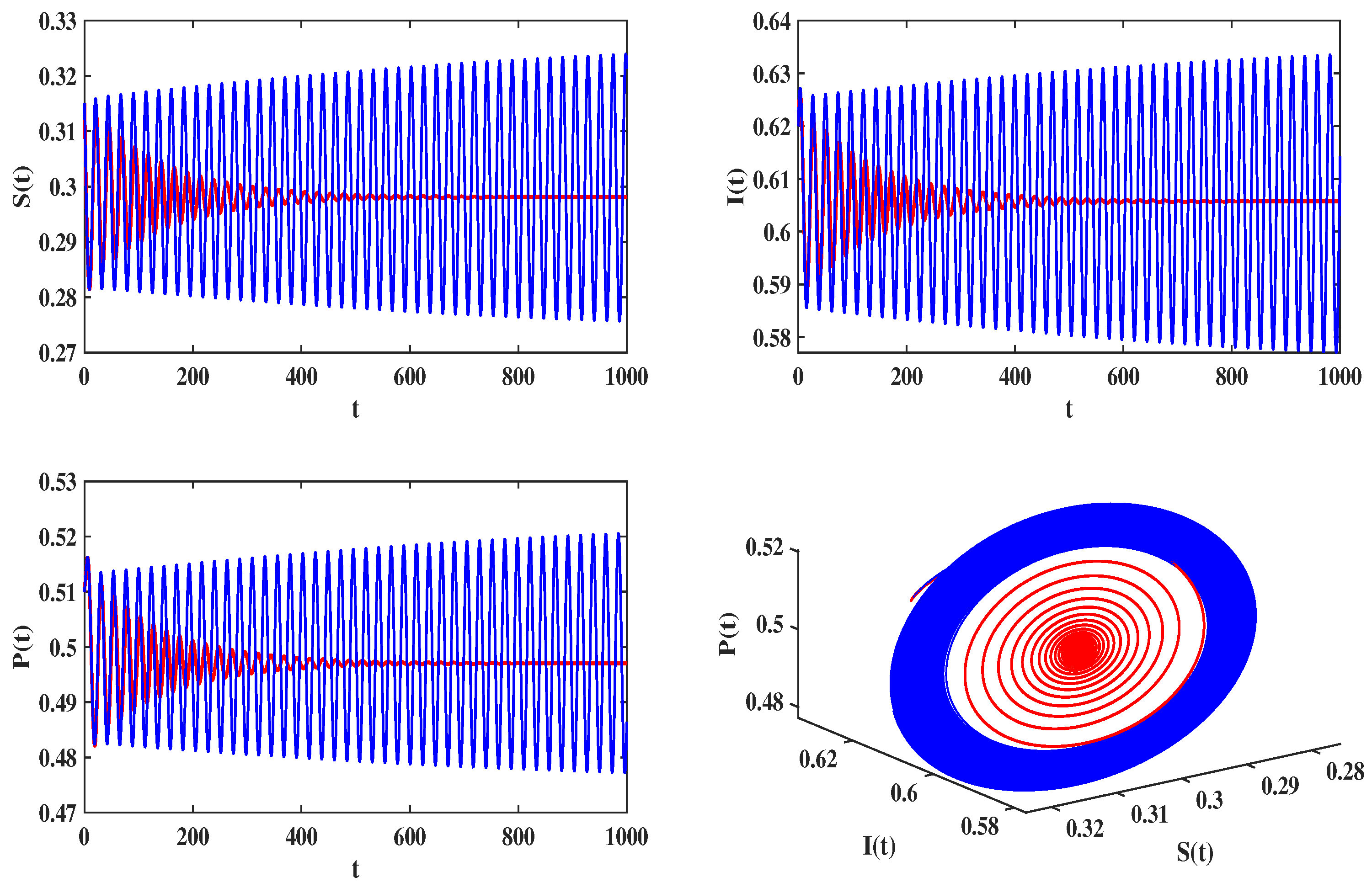
4.2. Delayed Feedback Control in an Eco-Epidemiologic System

In the above study, we discussed the stability and Hopf bifurcation of a delayed fractional food chain model. Through observation, it is found that the above conclusions are still applicable to the eco-epidemiological system. It also provides novel control strategy for the spread of disease. For instance, $S\left(t\right)$, $I\left(t\right)$, and $P\left(t\right)$ denote the population density of susceptible prey, diseased prey, and predator, respectively. We consider the following fractional eco-epidemiological system

$$\left\{\begin{array}{c}{D}^{\alpha }S\left(t\right)=S\left(t\right)\left(1-S\left(t\right)-\frac{1.5I\left(t\right)}{1+3S\left(t\right)}-\frac{0.8P\left(t\right)}{3P\left(t\right)+S\left(t\right)}\right),\hfill \\ D^{\alpha }I\left(t\right)=I\left(t\right)\left(\frac{1.5S\left(t\right)}{1+3S\left(t\right)}-0.05-\frac{0.45P\left(t\right)}{1.2P\left(t\right)+I\left(t\right)}\right)+k{e}^{-0.05\sigma }(I\left(t\right)-I(t-\sigma )),\hfill \\ D^{\alpha }P\left(t\right)=P\left(t\right)\left(\frac{0.64S(t-\tau )}{3P(t-\tau )+S(t-\tau )}+\frac{0.225I(t-\tau )}{1.2P(t-\tau )+I(t-\tau )}-0.22\right).\hfill \end{array}\right.$$

(30)

where the initial condition is $S\left(t\right)=0.315,I\left(t\right)=0.620,P\left(t\right)=0.510,t\in \left[-\tau ,0\right]$. After computation, system (30) has a unique positive equilibrium $\hat{E}(0.298,0.606,0.497)$. In general, we take $\alpha =0.96$.

First, we consider the non-controlled system when $k=0$ or $\sigma =0$.

The fractional system’s positive equilibrium $\hat{E}$ is globally asymptotically stable for $\tau =0$ (refer to Figure 7). After computing ${\tau }_0=4.253$, $\hat{E}$ is asymptotically stable for $\tau <4.253$ and unstable for $\tau >4.253$ (refer to Figure 8). As in example 1, the order affects the system’s stability. The system is stable and unstable when $\alpha =0.9$ and $\alpha =0.96$, respectively (see Figure 9).

Remark 2. 

At $\tau =0$, Figure 10 simulates the solutions of the non-controlled system for various values of the order α. Obviously, we can observe the order’s effect on the convergence speed. As the order α decreases, the memory effect of the system increases, which slows the rate of convergence, which means that it takes longer for the predator to eradicate the disease. We can observe that as the order α approaches 1, the solution of the fractional-order system more closely resembles the pattern of an integer-order system (all the directions indicated by the arrows in the figure, in which the order α increases).

Next, we consider the epidemic system (30) with a feedback controller when $k\ne 0$ and $\sigma \ne 0$.

By introducing the feedback delay controller with fixed $k=$−0.2 and $\sigma =0.9$ into the system, the original system achieves a state transition from oscillatory to stable (see Figure 11). We calculate ${\sigma }_1=12.837$. It is observed that the positive equilibrium $\hat{E}$ of the fractional delayed system is asymptotically stable for $\sigma <12.837$ and unstable for $\sigma >12.837$ (see Figure 12). They both verify the validity of the theoretical results.

Remark 3. 

The conclusions in the food chain model described above still apply to the eco-epidemiological model. The rational intervention and control of eco-epidemiological systems are particularly important to prevent infectious diseases from causing serious damage or even extinction to plant and animal populations. In the eco-epidemiological system, we design a nonlinear feedback control strategy with delay to make the system reach a stable state faster, inhibit its oscillation phenomenon, and finally obtain the ideal behavior.

5. Conclusions and Discussion

In this paper, we incorporate a delayed nonlinear feedback controller into the predator–prey system and establish a fractional food chain model with a general functional response. Initially, the stability of the nontrivial equilibrium and the Hopf bifurcation in the non-controlled system are analyzed. We also discuss the effects of delay and fractional order on system stability, revealing that fractional systems have a broader stability region and effectively suppress systems oscillation compared to integer systems. Additionally, by appropriately adjusting the delay, a smooth transition from an unstable to a stable state in the system can be achieved. Subsequently, we investigate the fractional system with a nonlinear delayed controller, obtaining threshold values for Hopf bifurcation occurrence by considering delay as bifurcation parameter. Notably, the introduction of the controller modifies the stability region of the original non-controlled system and enables effective bifurcation control. Finally, the introduced control strategy is effective in combating disease prevalence in the ecosystem. Considering the effectiveness of the nonlinear delay feedback controller for controlling the balance of the system, its application in different fields is still the exploration direction of future work.