Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model
Abstract
:1. Introduction
2. Preliminaries
2.1. Persistence of the System
2.2. The Well-Posedness of System (1)
3. Main Results
3.1. Dynamic Analysis of the System (1) without Delay
3.2. Dynamic Analysis of the System (1) with Delay
3.3. Bifurcation Dynamics in the System (3) with Control
3.3.1. Bifurcation Dynamics Due to Delay in System (3) with Control
3.3.2. Bifurcation Dynamics Due to Feedback Delay in System (3) with Control
4. Practical Applications and Numerical Simulations
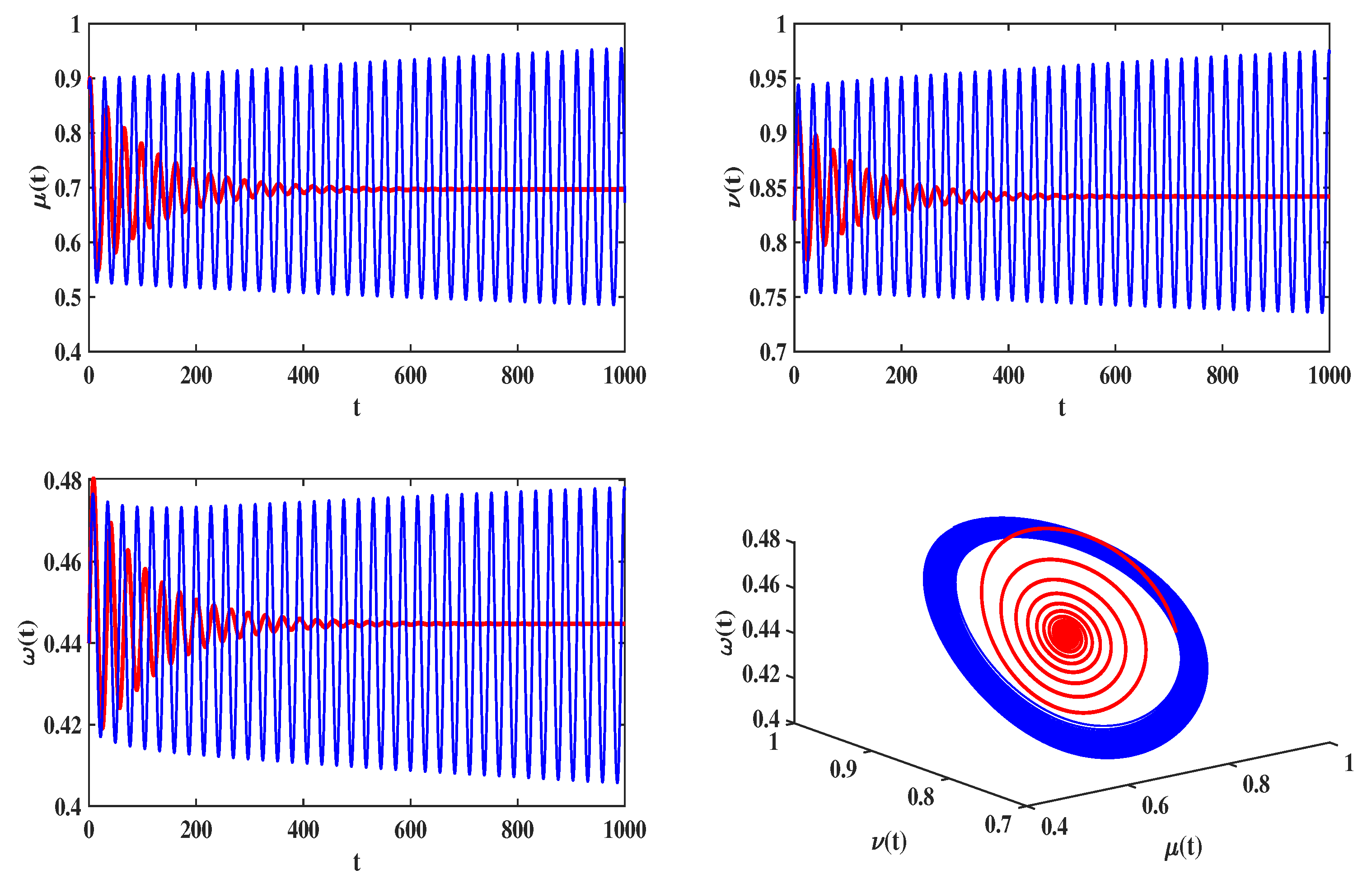
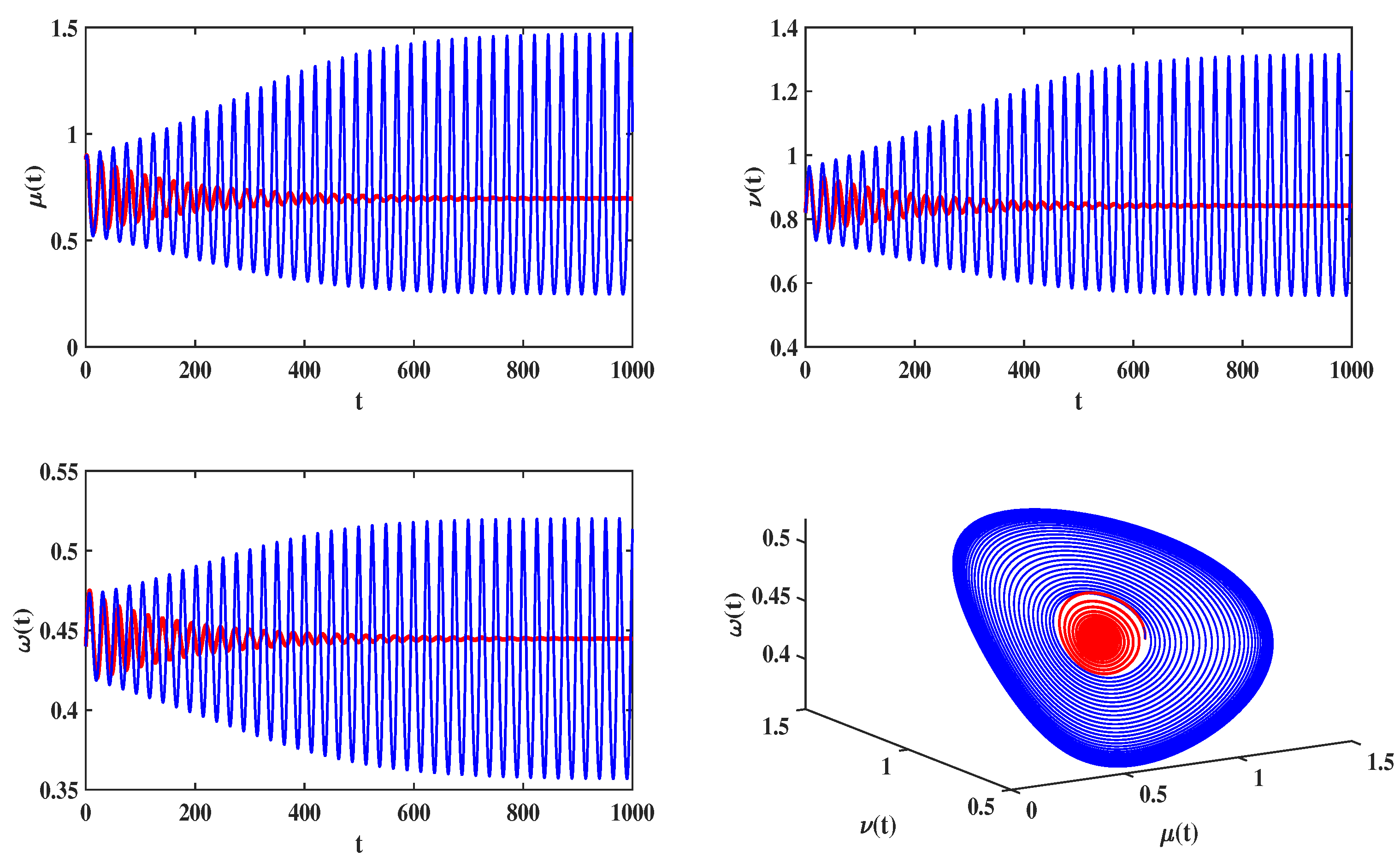
4.1. Delayed Feedback Control for a Food Chain Model
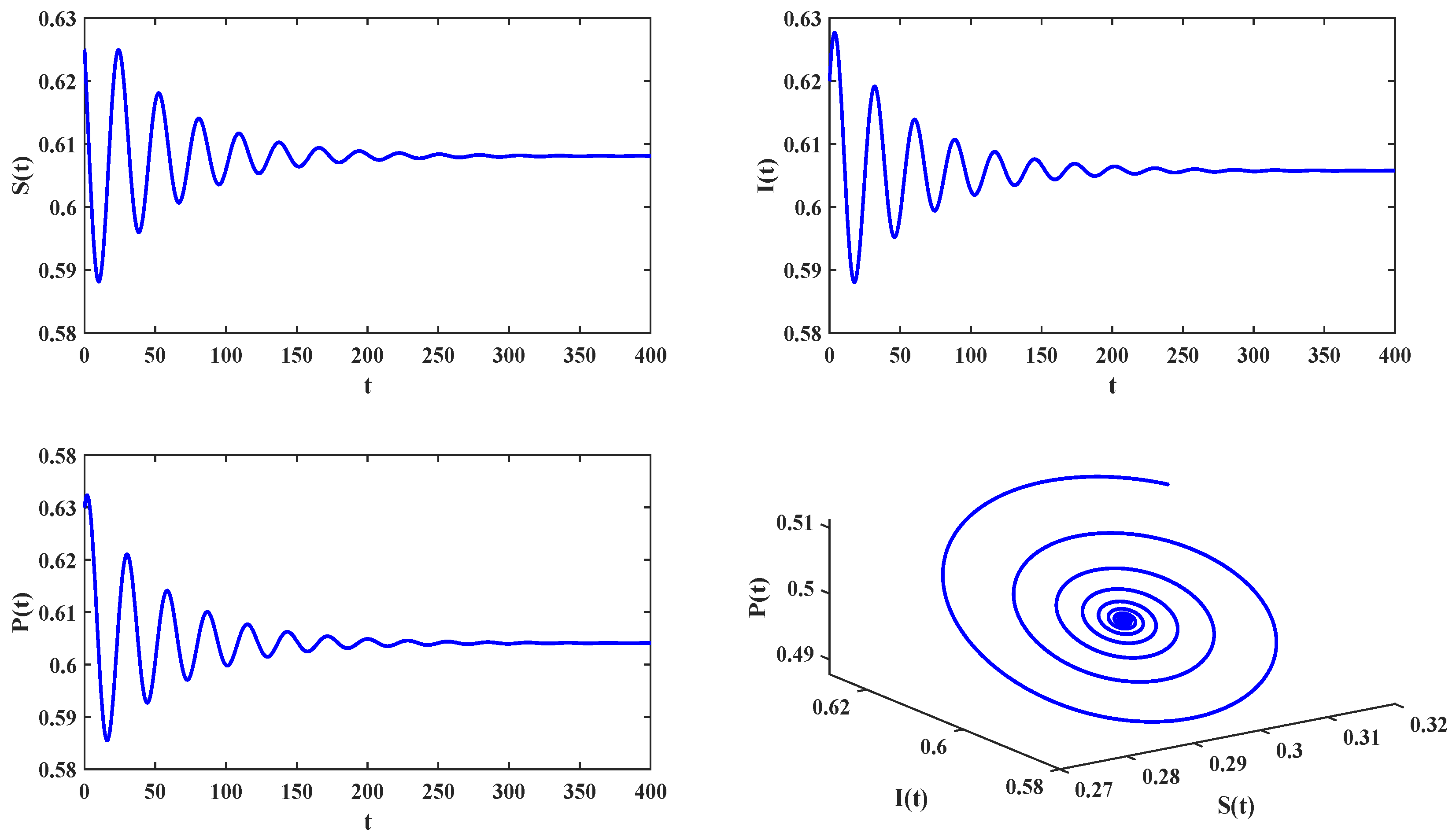
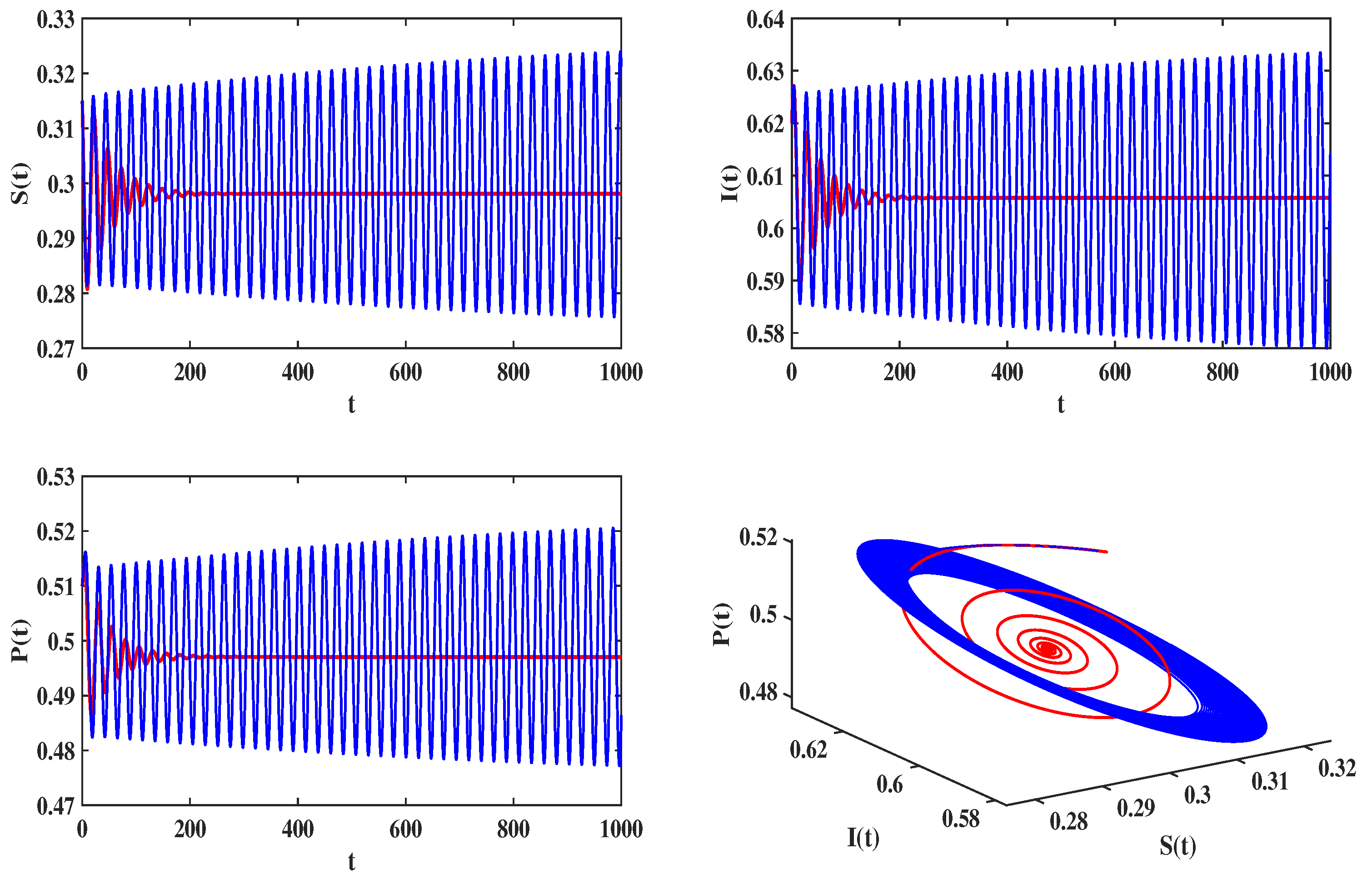
4.2. Delayed Feedback Control in an Eco-Epidemiologic System
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.Q. Dynamical Systems in Population Biology; Springer: New York, NY, USA, 2003. [Google Scholar]
- Haque, M. A detailed study of the Beddington-DeAngelis predator-prey model. Math. Biosci. 2011, 234, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Gazi, N.H.; Bandyopadhyay, M. Effect of time delay on a harvested predator-prey model. J. Appl. Math. Comput. 2008, 26, 263–280. [Google Scholar] [CrossRef]
- Mougi, A.; Iwasa, Y. Evolution towards oscillation or stability in a predator-prey system. Proc. R. Soc. B. 2010, 277, 3163–3171. [Google Scholar] [CrossRef] [PubMed]
- Mougi, A.; Kishida, O. Reciprocal phenotypic plasticity can lead to stable predator-prey interaction. J. Anim. Ecol. 2009, 78, 1172–1181. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Qiao, Y.; Huang, L.; Agarwal, R. Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 2018, 186. [Google Scholar] [CrossRef]
- Sahoo, B.; Poria, S. The chaos and control of a food chain model supplying additional food to top-predator. Chaos Solitons Fractals. 2014, 58, 52–64. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, S.; Zhang, T. Global dynamics of a predator-prey model with defense mechanism for prey. Appl. Math. Lett. 2016, 62, 42–48. [Google Scholar] [CrossRef]
- Jana, D.; Agrawal, R.; Upadhyay, R.K. Top-predator interference and gestation delay as determinants of the dynamics of a realistic model food chain. Chaos Solitons Fractals. 2014, 69, 50–63. [Google Scholar] [CrossRef]
- Zhang, F.; Li, Y. Stability and Hopf bifurcation of a delayed-diffusive predator-prey model with hyperbolic mortality and nonlinear prey harvesting. Nonlinear Dyn. 2017, 88, 1397–1412. [Google Scholar] [CrossRef]
- Song, C.; Li, N. Dynamic analysis and bifurcation control of a delayed fractional-order eco-epidemiological migratory bird model with fear effect. Int. J. Biomath. 2023, 2350022. [Google Scholar] [CrossRef]
- Hu, H.; Huang, L. Stability and Hopf bifurcation in a delayed predator-prey system with stage structure for prey. Nonlinear. Anal. Real. World Appl. 2010, 11, 2757–2769. [Google Scholar] [CrossRef]
- Zhang, T.; Meng, X.; Zhang, T.; Song, Y. Global dynamics for a new high-dimensional SIR model with distributed delay. Appl. Math. Comput. 2012, 218, 11806–11819. [Google Scholar] [CrossRef]
- Gan, Q.; Xu, R.; Yang, P. Bifurcation and chaos in a ratio-dependent predator-prey system with time delay. Chaos Solitons Fractals. 2009, 39, 1883–1895. [Google Scholar] [CrossRef]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Celik, C. The stability and Hopf bifurcation for a predator-prey system with time delay. Chaos Solitons Fractals. 2008, 37, 87–99. [Google Scholar] [CrossRef]
- Qi, H.; Zhao, W. Bifurcation control strategy for a delayed fractional-order population dynamics model with incommensurate orders. J. Biol. Syst. 2023, 31, 993–1013. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Yao, L. Bifurcation insight for a fractional-order stage-structured predator-prey system incorporating mixed time delays. Math. Methods Appl. Sci. 2023, 46, 9103–9118. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D. Influence of the fear factor on the dynamics of a stochastic predator-prey model. Appl. Math. Lett. 2021, 112, 106756. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals. 2020, 135, 109811. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z.; Li, Y. Nonlinear dynamics and chaos in a simplified memristor-based fractional-order neural network with discontinuous memductance function. Nonlinear Dyn. 2018, 93, 611–627. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M. Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos Solitons Fractals. 2016, 87, 19–29. [Google Scholar] [CrossRef]
- Bao, H.; Cao, J.; Kurths, J. State estimation of fractional-order delayed memristive neural networks. Nonlinear Dyn. 2018, 94, 1215–1225. [Google Scholar] [CrossRef]
- Cermak, J.; Dosla, Z.; Kisela, T. Fractional differential equations with a constant delay: Stability and asymptotics of solutions. Appl. Math. Comput. 2017, 298, 336–350. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Singapore, 2021. [Google Scholar]
- Li, Y.; Chen, Y.Q. Podlubny I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.P. A delayed fractional order food chain model with fear effect and prey refuge. Math. Comput. Simul. 2020, 178, 218–245. [Google Scholar] [CrossRef]
- Nisar, K.S.; Rahman, M.U.; Laouini, G.; Shutaywi, M.; Arfan, M. On nonlinear fractional-order mathematical model of food-chain. Fractals 2022, 30, 2240014. [Google Scholar] [CrossRef]
- Hale, J.K.; Kocak, H. Dynamics and Bifurcations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Alidousti, J. Stability and bifurcation analysis for a fractional prey-predator scavenger model. Appl. Math. Model. 2020, 81, 342–355. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Lu, J.; Li, Y. Stability and bifurcation of a delayed generalized fractional-order prey-predator model with interspecific competition. Appl. Math. Comput. 2019, 347, 360–369. [Google Scholar] [CrossRef]
- Rihan, F.A.; Lakshmanan, S.; Hashish, A.H.; Rakkiyappan, R.; Ahmed, E. Fractional-order delayed predator-prey systems with Holling type-II functional response. Nonlinear Dyn. 2015, 80, 777–789. [Google Scholar] [CrossRef]
- Chinnathambi, R.; Rihan, F.A. Stability of fractional-order prey-predator system with time-delay and Monod-Haldane functional response. Nonlinear Dyn. 2018, 92, 1637–1648. [Google Scholar] [CrossRef]
- Liu, L.; Meng, X.; Zhang, T. Optimal control strategy for an impulsive stochastic competition system with time delays and jumps. Phys. A. 2017, 477, 99–113. [Google Scholar] [CrossRef]
- Sun, D.; Li, Q.; Zhao, W. Stability and optimal control of a fractional SEQIR epidemic model with saturated incidence rate. Fractal Fract. 2023, 7, 533. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, Y.; Dai, Y. Bifurcation analysis and control of chaos for a hybrid ratio-dependent three species food chain. Appl. Math. Comput. 2011, 218, 1533–1546. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, T.; Tian, Y. Dynamics analysis and control optimization of a pest management predator-prey model with an integrated control strategy. Appl. Math. Comput. 2017, 292, 253–271. [Google Scholar] [CrossRef]
- Liu, X.; Fang, H. Periodic pulse control of Hopf bifurcation in a fractional-order delay predator-prey model incorporating a prey refuge. Adv. Differ. Equ. 2019, 2019, 1–30. [Google Scholar] [CrossRef]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A. 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhao, Y.; Bai, X.; Zhang, Z. Bifurcation and control of a planktonic ecological system with double delays by delayed feedback control. J. Frankl. Inst. 2021, 358, 3609–3632. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Alsaadi, F.E. Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders. Appl. Math. Comput. 2017, 293, 293–310. [Google Scholar] [CrossRef]
- Qi, H.; Zhao, W. Stability and bifurcation control analysis of a delayed fractional-order eco-epidemiological system. Eur. Phys. J. Plus. 2022, 137, 934. [Google Scholar] [CrossRef] [PubMed]
- Ellner, S.P.; Guckenheimer, J. Dynamic Models in Biology; Princeton University Press: Princeton, NY, USA, 2006. [Google Scholar]
- Freedman, H.I.; Waltman, P. Persistence in models of three interacting predator-prey populations. Math. Biosci. 1984, 68, 213–231. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Li, Q.; Sun, D.; Liu, H.; Zhao, W. Stability and bifurcation control of a delayed fractional eco-epidemiological system with saturated incidence. Results Phys. 2023, 54, 107019. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liu, H.; Zhao, W.; Meng, X. Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model. Fractal Fract. 2024, 8, 232. https://doi.org/10.3390/fractalfract8040232
Li Q, Liu H, Zhao W, Meng X. Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model. Fractal and Fractional. 2024; 8(4):232. https://doi.org/10.3390/fractalfract8040232
Chicago/Turabian StyleLi, Qing, Hongxia Liu, Wencai Zhao, and Xinzhu Meng. 2024. "Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model" Fractal and Fractional 8, no. 4: 232. https://doi.org/10.3390/fractalfract8040232
APA StyleLi, Q., Liu, H., Zhao, W., & Meng, X. (2024). Stability and Bifurcation Control for a Generalized Delayed Fractional Food Chain Model. Fractal and Fractional, 8(4), 232. https://doi.org/10.3390/fractalfract8040232






