The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator

Abstract

This study proposes a fractional-order model in the Caputo sense to describe the interaction between tumor and immune macrophages by assuming that the pro-tumor macrophages induce a Holling type-II response to the tumor. Then, the basic properties of the solutions to the model are studied. Local stability analysis is conducted at each of the equilibria in the model, and a numerical study is performed with varying activation rates of type-II or pro-tumor macrophages and the order of the fractional operator. The numerical findings suggest that type-I or anti-tumor macrophages can stabilize the system if the activation rate of type-II or pro-tumor macrophages is low. Still, for a higher value of the activation rate for type-II or pro-tumor macrophages, the proliferation of tumor cells is uncontrollable and the system becomes unstable. Furthermore, the stability of the system decreases as the order of the fractional operator increases.

1. Introduction and Background

Mathematical models in cancer research play a crucial role in controlling the disease and predicting the efficacy of cancer treatment through obtaining the optimum amount of drug. Cancer is a disease that occurs due to the appearance of malignant tumors in the human body. While malignant tumor cells are developed, various chemokines, cytokines, and cells of the immune system are responsible for promoting or resisting the tumor [1]. At the early stage of the tumor, natural killer (NK) and CD8⁺ T cells are responsible for eliminating more immunogenic tumor cells [2]. After the first phase of elimination, less immunogenic tumor cells are detectable and can increase by invading the immune system. At this stage, tumor cells interact with dendritic cells (DCs), B cells, neutrophils, CD4⁺ T cells, antibodies, and macrophages of the immune system [3,4]. Several mathematical studies have been performed to assess the roles of immune effector cells, such as natural killer (NK) cells, CD8⁺ T cells, dendritic cells (DCs), B cells, and CD4⁺ T cells, in tumor development and elimination processes [5,6,7,8,9,10,11,12,13,14]. Pillis et al. [15] formulated a valid mathematical model to describe the functions of NK and CD8⁺ T cells in tumor–immune interactions. The role of cytotoxic T lymphocytes in tumor regression processes was explored in Refs. [16,17,18]. Li et al. [19] described the association between cancer cells and endothelial cells, considering the angiogenic growth factors secreted by the tumor that help the tumor grow. The immune response of CD4⁺ anti-tumor Th1 and Th2 cells against skin tumors was discussed in Ref. [20]. In Ref. [21], the effect of immune antibodies in cancer suppression has been discussed, and it was suggested that antibody therapy may also be used in cancer treatment. Makhlouf et al. [22] studied the role of CD4⁺ T cells that secrete cytokines for killing tumor cells in the tumor progression stage and propounded that CD4⁺ T cell therapy would also be used for eliminating tumors. A mathematical study [23] has been performed to discuss the interaction between tumor cells and immune T lymphocytes, which revealed that the flow rate of mature T lymphocytes plays a crucial role in controlling tumor growth.

However, a few modeling studies have discussed the interaction between tumors and immune macrophages [24,25,26,27,28]. Macrophages are innate immune cells that show two kinds of responses to tumor cells. Type-I or anti-tumor macrophages suppress tumor growth through secreting IL-4 or IL-13. Type-II or pro-tumor macrophages help the proliferation of tumor cells by driving LPS, or interferon-$\gamma$ [29]. Thus, it is necessary to explore the dual role of both macrophages in the processes of tumor regression and proliferation. To describe tumor–macrophage interactions, a mathematical model was analyzed in Ref. [30], which suggests that tumor dormancy is associated with an increase in the clonal heterogeneity of tumor cells and the phenotypic heterogeneity of macrophages. Shu et al. [31] revealed that not only the direct activation of anti-tumor and pro-tumor macrophages destroy tumor cells, but also the combined effect of the transition between both macrophages. In Ref. [32], a spatiotemporal brain tumor model was proposed to examine the associations among glioma cells, macrophages, and immune cells. The effect of time delay on the activation of pro-tumor macrophages in tumor–macrophage interactions were studied in Ref. [33]. The saturated response of M2 macrophages due to tumor cells was explored in Ref. [34], which demonstrated that tumor cells quickly spread in the body for a relatively higher activation rate of M2 macrophages.

To date, fractional calculus has been widely used to formulate mathematical models in various fields due to its memory effect [35,36,37,38], including in cancer research too [39,40,41,42,43,44]. Farman et al. [45] proposed a fractal fractional-order model to study the association between cancer cells, IL-12 cytokines, and anti-PD-L1 inhibitors. The effects of CD8⁺ T cells, dendritic cells (DCs), IL-2, and CD4⁺ T cells on the dynamics of cancer cells to the fractal order was observed in Ref. [46]. In Ref. [47], the role of immune macrophages was investigated by analyzing a fractional-order mathematical model for lung cancer in the presence of normal cells. A Caputo-type fractional-order tumor–macrophage interaction model has been investigated in Ref. [48], to observe the stability and Hopf bifurcation of the model under the influence of multiple time delays. Padder et al. [49] observed the effect of fractional order on the dynamics of tumor–immune macrophage interactions. The efficacy of the combined therapy of surgery and immunotherapy for treating lung cancer with varying fractional orders was investigated in Ref. [50]. Thus, based on the above literature, in this study, we formulated a fractional-order model in the Caputo sense that describes the tumor–macrophage interaction. The remainder of this study is assembled in the following manner: In Section 2, we formulate our fractional-order tumor–macrophages model and study the characteristics of the solutions of the model. The local stability of the model is investigated in Section 3. Numerical studies of the model are performed in Section 4. Section 5 deals with concluding remarks.

2. The Model

Before formulating our proposed model, we define the Caputo fractional derivative and the corresponding integral.

Definition 1

([51,52]). For $\Psi :[a,b]\to \mathbf{R}$, $n-1<v\le n$, and $n\in \mathbf{N}$, the Caputo fractional derivative of order v is expressed as

$${ }^c{D}_t^v\Psi \left(t\right)=\frac{1}{\Gamma (n-v)}{\int }_a^t{\Psi }^{\left(n\right)}\left(s\right){(t-s)}^{n-v-1}ds.$$

(1)

Furthermore, the associated fractional integral can be presented as

$${ }^c{I}_t^v\Psi \left(t\right)=\frac{1}{\Gamma \left(v\right)}{\int }_a^t\Psi \left(s\right){(t-s)}^{v-1}ds.$$

(2)

Here, we formulate a fractional-order tumor–macrophages interaction model by modifying the model proposed in Refs. [31,34]. The modification is made on account of the saturated response of pro-tumor macrophages. Suppose $M\left(t\right)$, $A\left(t\right)$, and $P\left(t\right)$ denote the number of malignant tumor cells, type-I or anti-tumor macrophages, and type-II or pro-tumor macrophages at time $t>0$, respectively. Then, the proposed model takes on the following form:

$$\left\{\begin{array}{cc}\hfill \frac{dM}{dt}& =a_{1}M(1-b_{1}M)-c_{1}MA+c_{2}MP\hfill \\ \hfill \frac{dA}{dt}& =a_{2}MA-b_{2}A-d_{1}A+d_{2}P\hfill \\ \hfill \frac{dP}{dt}& =\frac{a_{3}MP}{g+M}-b_{3}P+d_{1}A-d_{2}P.\hfill \end{array}\right.$$

(3)

Here, $a_{1}M(1-b_{1}M)$ denotes the logistic growth of malignant tumor cells with a proliferation rate $a_1$ and carrying capacity $\frac{1}{b_1}$. Due to the presence of type-I macrophages, the tumor cells die off at a rate of $c_1$ and, due to the presence of type-II macrophages, the tumor cells can increase at a rate of $c_2$. The term $a_{2}MA$ denotes the activation of type-I macrophages by pro-inflammatory cytokines due to the presence of tumor cells at the rate $a_2$. Furthermore, $b_2$ is the natural mortality rate of type-I macrophages, $d_1$ is the transition rate for type-I macrophages to type-II macrophages, and $d_2$ is the transition rate for type-II macrophages to type-I macrophages. It is evident that, due to the presence of tumor cells, the type-II macrophages can be increased through the stimulation of tumor cells. We account for this response using a nonlinear term $\frac{a_{3}MP}{g+M}$, where $a_3$ is the activation rate of type-II macrophages and g is the threshold rate of type-II macrophages [53,54]. The natural mortality rate of type-II macrophages is denoted by $b_3$.

The initial condition corresponding to the system (3) is considered as:

$$T\left(0\right)=T_0\ge 0,A\left(0\right)=A_0\ge 0,P\left(0\right)=P_0\ge 0.$$

(4)

We refer to Ref. [31] for a detailed description, including the values and units of the parameters, of the model represented by (3).

To investigate the basic characteristics of the solutions, along with the linear stability of the proposed model (3), we transform the model (3) to its dimensionless form through assuming $x=\frac{M}{M\left(0\right)}$, $y=\frac{A}{A\left(0\right)}$, $z=\frac{P}{P\left(0\right)}$ and $\tau =a_{2}M\left(0\right)t$. Taking ${ }^c{D}_t^v$ as the Caputo fractional differential with fractional order $v\in (0,1]$ and $t\in (0,T]$, then the model (3) becomes

$$\left\{\begin{array}{cc}\hfill { }^c{D}_t^{v}x\left(t\right)& ={\alpha }^{v}x(1-{\beta }^{v}x)-{\gamma }_1^{v}xy+{\gamma }_2^{v}xz\hfill \\ \hfill { }^c{D}_t^{v}y\left(t\right)& =xy-{\eta }^{v}y-{\delta }_1^{v}y+{\delta }_2^{v}z\hfill \\ \hfill { }^c{D}_t^{v}z\left(t\right)& =\frac{{\rho }^{v}xz}{{\sigma }^v+x}-{\mu }^{v}z+{\delta }_1^{v}y-{\delta }_2^{v}z,\hfill \end{array}\right.$$

(5)

where $\alpha =\frac{a_1}{a_{2}M\left(0\right)}$, $\beta =b_{1}M\left(0\right)$, ${\gamma }_1=\frac{c_1}{a_2}$, ${\gamma }_2=\frac{c_2}{a_2}$, $\eta =\frac{b_2}{a_{2}M\left(0\right)}$, ${\delta }_1=\frac{d_1}{a_{2}M\left(0\right)}$, ${\delta }_2=\frac{d_2}{a_{2}M\left(0\right)}$, $\rho =\frac{a_3}{a_{2}M\left(0\right)}$, $\sigma =\frac{g}{M\left(0\right)}$, and $\mu =\frac{b_3}{a_{2}M\left(0\right)}$. The new state variables $x\left(t\right)$, $y\left(t\right)$, and $z\left(t\right)$ denote the number of malignant tumor cells, type-I macrophages, and type-II immune macrophages at time $t>0$, respectively. The model (5) reduces to an integer-order model when $v\to 1$. Furthermore, the initial condition corresponding to the system (5) is

$$x\left(0\right)=x_0\ge 0,y\left(0\right)=y_0\ge 0,z\left(0\right)=z_0\ge 0.$$

(6)

The model (5) can be expressed as

$${ }^c{D}_t^{v}W\left(t\right)=G\left[W\left(t\right)\right],t\in (0,T],W\left(0\right)=W_0,$$

(7)

where

$$W=\left(\begin{array}{c}x\\ y\\ z\end{array}\right),W_0=\left(\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right),G\left(W\right)=\left(\begin{array}{c}{\alpha }^{v}x(1-{\beta }^{v}x)-{\gamma }_1^{v}xy+{\gamma }_2^{v}xz\\ xy-{\eta }^{v}y-{\delta }_1^{v}y+{\delta }_2^{v}z\\ \frac{{\rho }^{v}xz}{{\sigma }^v+x}-{\mu }^{v}z+{\delta }_1^{v}y-{\delta }_2^{v}z\end{array}\right).$$

For G, we define a supremum norm as

$$\left|\right|G\left|\right|=\underset{t\in (0,T]}{sup}\left|G\left(t\right)\right|$$

and, for the matrix $B=\left[b_{ij}\left(t\right)\right]$, we define a norm as

$$\left|\right|B\left|\right|=\sum _{i,j}\underset{t\in (0,T]}{sup}\left|b_{ij}\left(t\right)\right|.$$

Now, using the definition of the Caputo fractional derivative (1), the solution of the system (7) has the following form:

$$W\left(t\right)=W_0+\frac{1}{\Gamma \left(v\right)}{\int }_0^t{(t-s)}^{v-1}F\left(W\left(s\right)\right)ds=\Theta \left(W\right).$$

This gives the equality

$$\Theta \left(W_1\right)-\Theta \left(W_2\right)=\frac{1}{\Gamma \left(v\right)}{\int }_0^t{(t-s)}^{v-1}(G\left(W_1\left(s\right)\right)-G\left(W_2\left(s\right)\right))ds.$$

Hence, we have

$$\begin{array}{cc}\hfill \left|\right|\Theta \left(W_1\right)-\Theta \left(W_2\right)\left|\right|& =\frac{1}{\Gamma \left(v\right)}\left|\right|{\int }_0^t{(t-s)}^{v-1}(G\left(W_1\left(s\right)\right)-G\left(W_2\left(s\right)\right))ds\left|\right|\hfill \\ \hfill & \le \frac{1}{\Gamma \left(v\right)}{\int }_0^t{(t-s)}^{v-1}\left|\right|(G\left(W_1\left(s\right)\right)-G\left(W_2\left(s\right)\right))\left|\right|ds\hfill \\ \hfill & \le \varphi \left|\right|W_1-W_2\left|\right|,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \varphi & =L^v\max \left\{\left({\alpha }^v+(2{\alpha }^v{\beta }^v+{\gamma }_1^v+{\gamma }_2^v)\xi \right),(\xi +\eta +{\delta }_1),\left({\delta }_2^v+{\rho }^v(1-\frac{{\sigma }^v}{\xi })\right)\right\},\hfill \\ \hfill L^v& =\frac{T^v}{\Gamma (v+1)},\hfill \\ \hfill \mathrm{and}\Omega & =\left\{\right(x,y,z):\max (\left|x\right|,\left|y\right|,\left|z\right|\left)\right\}\le \xi .\hfill \end{array}$$

Therefore, a unique solution exists for the system (7) if the mapping $\Theta \left(W\right)$ is a contraction mapping; that is, if $\varphi <1$ [55]. Thus, we obtain the following results:

Theorem 1.

There exists a unique solution for the system (7) corresponding to the initial condition $W\left(0\right)=W_0$ in the region $\Omega \times (0,T]$, where $t\in (0,T]$, $\Omega =\left\{\right(x,y,z):\max (\left|x\right|,\left|y\right|,\left|z\right|\left)\right\}\le \eta$, if

$$L^{v}max\left\{\left({\alpha }^v+(2{\alpha }^v{\beta }^v+{\gamma }_1^v+{\gamma }_2^v)\xi \right),(\xi +\eta +{\delta }_1),\left({\delta }_2^v+{\rho }^v(1-\frac{{\sigma }^v}{\xi })\right)\right\}<1,$$

where $L^v=\frac{T^v}{\Gamma (v+1)}$.

Again, it is clear that

$$\left\{\begin{array}{cc}\hfill { }^c{D}_t^v{x\left(t\right)|}_{x=0}& =0\hfill \\ \hfill { }^c{D}_t^v{y\left(t\right)|}_{y=0}& ={\delta }_2^{v}z\ge 0,\mathrm{where} z\left(t\right)\ge 0,{\delta }_2>0\hfill \\ \hfill { }^c{D}_t^v{z\left(t\right)|}_{z=0}& ={\delta }_1^{v}y\ge 0,\mathrm{where} y\left(t\right)\ge 0,{\delta }_1>0.\hfill \end{array}\right.$$

(8)

Thus, on each plane bounding the non-negative octant, the vector field points into ${\mathbf{R}}_{+}^3$. Thus, the solution will remain in ${\mathbf{R}}_{+}^3$ [56]. Therefore, we can state the following result:

Theorem 2.

All solutions of the considered fractional-order system (5) remain in ${\mathbf{R}}_{+}^3$.

3. Local Stability

To check the stability of the system (5), we solve ${ }^c{D}_t^{v}x\left(t\right)=0$, ${ }^c{D}_t^{v}y\left(t\right)=0$, ${ }^c{D}_t^{v}z\left(t\right)=0$ to find the equilibrium points of the system (5).

We found three biologically valid equilibrium points for the system (5), and the corresponding stability analysis is as follows:

• Suppose there are no tumor cells in the body, then the macrophages do not emerge in the body in action; thus, in this sense, we take $y=0$ and $z=0$. Then, we get the tumor-free trivial equilibrium as $E_1^v=(0,0,0)$, which always exists.
  The Jacobian matrix of the system (5) evaluated at the tumor-free equilibrium $E_1^v=(0,0,0)$ is:

  $$J_{E_1^v}=\left(\begin{array}{ccc}{\alpha }^v& 0& 0\\ 0& -{\eta }^v-{\delta }_1^v& {\delta }_2^v\\ 0& {\delta }_1^v& -{\mu }^v-{\delta }_2^v\end{array}\right).$$

  (9)

  It is clear that ${\alpha }^v$ is one of the eigenvalues of the matrix (9), while the other two eigenvalues are the roots of the following equation:

  $${\lambda }^2+({\eta }^v+{\delta }_1^v+{\mu }^v+{\delta }_2^v)\lambda +{\eta }^v{\mu }^v+{\eta }^v{\delta }_2^v+{\mu }^v{\delta }_1^v=0.$$

  (10)

  As one eigenvalue of the matrix (9) is ${\alpha }^v>0$, this implies the instability of the tumor-free trivial equilibrium $E_1^v=(0,0,0)$. Thus, we can state this result as follows:

  Theorem 3.

  The tumor-free trivial equilibrium $E_1^v=(0,0,0)$ always exists and shows unstable behavior.
• Suppose there are tumor cells in the body; however, the macrophages have not emerged in the body in action yet. Thus, in this sense, we take $y=0$ and $z=0$. Then, we have found the tumor dominant equilibrium as $E_2^v=(\frac{1}{{\beta }^v},0,0)$, which also always exists.
  The Jacobian matrix of the system (5) evaluated at tumor dominant equilibrium $E_2^v=(\frac{1}{{\beta }^v},0,0)$ is:

  $$J_{E_2^v}=\left(\begin{array}{ccc}-{\alpha }^v& 0& 0\\ 0& \frac{1}{{\beta }^v}-{\eta }^v-{\delta }_1^v& {\delta }_2^v\\ 0& {\delta }_1^v& \frac{{\rho }^v}{{\beta }^v{\sigma }^v+1}-{\mu }^v-{\delta }_2^v\end{array}\right).$$

  (11)

  Clearly, $-{\alpha }^v$ is an eigenvalue of the matrix (11), while the other two eigenvalues will be the roots of the following equation:

  $$\begin{array}{cc}\hfill {\lambda }^2+({\eta }^v+{\delta }_1^v+{\mu }^v+{\delta }_2^v-\frac{1}{{\beta }^v}-\frac{{\rho }^v}{{\beta }^v{\sigma }^v+1})\lambda +[(\frac{1}{{\beta }^v}-{\eta }^v-{\delta }_1^v)& \\ \hfill (\frac{{\rho }^v}{{\beta }^v{\sigma }^v+1}-{\mu }^v-{\delta }_2^v)-{\delta }_1^v{\delta }_2^v]=0.\end{array}$$

  (12)

  As $-{\alpha }^v<0$, for the stability of the system (5), the Equation (12) must have all negative roots. Equation (12) possesses both roots as negative if the following conditions hold:

  $$\left\{\begin{array}{cc}\hfill {\eta }^v+{\delta }_1^v+{\mu }^v+{\delta }_2^v-\frac{1}{{\beta }^v}-\frac{{\rho }^v}{{\beta }^v{\sigma }^v+1}& >0,\mathrm{and}\hfill \\ \hfill (\frac{1}{{\beta }^v}-{\eta }^v-{\delta }_1^v)(\frac{{\rho }^v}{{\beta }^v{\sigma }^v+1}-{\mu }^v-{\delta }_2^v)-{\delta }_1^v{\delta }_2^v& >0.\hfill \end{array}\right.$$

  (13)

  Thus, we can state the following theorem:

  Theorem 4.

  The tumor-dominant equilibrium $E_2^v=(\frac{1}{{\beta }^v},0,0)$ always exists and it is asymptotically stable if ${\eta }^v+{\delta }_1^v+{\mu }^v+{\delta }_2^v>\frac{1}{{\beta }^v}+\frac{{\rho }^v}{{\beta }^v{\sigma }^v+1}$ and $\frac{{\rho }^v}{{\beta }^v({\beta }^v{\sigma }^v+1)}+{\eta }^v{\mu }^v+{\eta }^v{\delta }_2^v+{\delta }_1^v{\mu }^v>\frac{{\mu }^v+{\delta }_2^v}{{\beta }^v}+\frac{({\eta }^v+{\delta }_1^v){\rho }^v}{{\beta }^v{\sigma }^v+1}$; otherwise, it is unstable.
• Suppose that all three cells emerge in the body at the same time. Then, for $x\ne 0$ and $x\ne \frac{1}{{\beta }^v}$, we obtain the co-axial equilibrium as

  $$\begin{array}{cc}\hfill E_3^v(x^{*},y^{*},z^{*})& =\hfill \\ & E_3^v\left(x^{*},\frac{{\alpha }^v{\delta }_2^v(1-{\beta }^v{x}^{*})}{{\gamma }_1^v{\delta }_2^v+{\gamma }_2^v(x^{*}-{\eta }^v-{\delta }_1^v)},\frac{({\delta }_1^v+{\eta }^v-x^{*}){\alpha }^v(1-{\beta }^v{x}^{*})}{{\gamma }_1^v{\delta }_2^v+{\gamma }_2^v(x^{*}-{\eta }^v-{\delta }_1^v)}\right),\hfill \end{array}$$

  (14)

  where $x^{*}$ is given by the following equation:

  $$\begin{array}{cc}\hfill ({\rho }^v-{\mu }^v-{\delta }_2^v)x^2-\{{\rho }^v{\eta }^v+{\rho }^v{\delta }_1^v+{\mu }^v{\sigma }^v+{\delta }_2^v{\sigma }^v-{\delta }_1^v{\mu }^v-{\eta }^v{\mu }^v-{\eta }^v{\delta }_2^v\}x& \\ \hfill +({\delta }_1^v{\mu }^v+{\eta }^v{\mu }^v+{\eta }^v{\delta }_2^v)\sigma =0.\end{array}$$

  (15)

  For positive $x^{*}$, we must have the discriminant of the Equation (15) greater than zero and

  $${\eta }^v+{\delta }_1^v-\frac{{\gamma }_1^v{\delta }_2^v}{{\gamma }_2^v}<x^{*}<{\eta }^v+{\delta }_1^v<\frac{1}{{\beta }^v}.$$

  Now, we investigate the stability of the system (5) around the co-axial equilibrium $E_3^v(x^{*},y^{*},z^{*})$. For $x\ne 0$ and $x\ne \frac{1}{{\beta }^v}$, we obtain the following relations at the co-axial equilibrium $E_3^v(x^{*},y^{*},z^{*})$:

  $$\left\{\begin{array}{cc}\hfill {\alpha }^v+{\gamma }_2^v{z}^{*}& ={\alpha }^v{\beta }^v{x}^{*}+{\gamma }_1^v{y}^{*},\hfill \\ \hfill x^{*}-{\eta }^v-{\delta }_1^v& =-\frac{{\delta }_2^v{z}^{*}}{y^{*}},\hfill \\ \hfill \frac{{\rho }^v{x}^{*}}{{\sigma }^v+x^{*}}-{\mu }^v-{\delta }_2^v& =-\frac{{\delta }_1^v{y}^{*}}{z^{*}}.\hfill \end{array}\right.$$

  (16)

  Using the relations (16), we obtain the Jacobian matrix at co-axial equilibrium $E_3^v(x^{*},y^{*},z^{*})$ as:

  $$J_{E_3^v}=\left(\begin{array}{ccc}-{\alpha }^v{\beta }^v{x}^{*}& -{\gamma }_1^v{x}^{*}& -{\gamma }_2^v{x}^{*}\\ y^{*}& -\frac{{\delta }_2^v{z}^{*}}{y^{*}}& {\delta }_2^v\\ \frac{{\rho }^v{\sigma }^v{z}^{*}}{{({\sigma }^v+x^{*})}^2}& {\delta }_1^v& -\frac{{\delta }_1^v{y}^{*}}{z^{*}}\end{array}\right).$$

  (17)

  The eigenvalues of the Jacobian (17) are the roots of the following equation:

  $${\lambda }^3+{\Phi }_1{\lambda }^2+{\Phi }_2\lambda +{\Phi }_3=0,$$

  (18)

  where

  $$\begin{array}{cc}\hfill {\Phi }_1& ={\alpha }^v{\beta }^v{x}^{*}+\frac{{\delta }_2^v{z}^{*}}{y^{*}}+\frac{{\delta }_1{y}^{*}}{z^{*}},\hfill \\ \hfill {\Phi }_2& ={\alpha }^v{\beta }^v{x}^{*}(\frac{{\delta }_1{y}^{*}}{z^{*}}+\frac{{\delta }_2^v{z}^{*}}{y^{*}})+x^{*}\left[{\gamma }_1^v{y}^{*}-\frac{{\rho }^v{\sigma }^v{\gamma }_2^v{z}^{*}}{{({\sigma }^v+x^{*})}^2}\right],\hfill \\ \hfill {\Phi }_3& ={\alpha }^v{x}^{*}(1-{\beta }^v{x}^{*})\left[\frac{{\rho }^v{\delta }_2^v{\sigma }^v{z}^{*}}{y^{*}{({\sigma }^v+x^{*})}^2}+\frac{{\delta }_1^v{y}^{*}}{z^{*}}\right].\hfill \end{array}$$

  According to the Routh–Hurwitz criterion, the system (5) is locally asymptotically stable if all the roots of the Equation (18) are negative or have negative real parts; that is, if

  $${\Phi }_1>0,{\Phi }_2>0,{\Phi }_3>0\mathrm{and}{\Phi }_1{\Phi }_2-{\Phi }_3>0,$$

  (19)

  which implies that $x^{*}<\frac{1}{{\beta }^v}$ and

  $$\begin{array}{ccc}\hfill [{\alpha }^v{\beta }^v{x}^{*}+\frac{{\delta }_2^v{z}^{*}}{y^{*}}+\frac{{\delta }_1{y}^{*}}{z^{*}}][{\alpha }^v{\beta }^v{x}^{*}(\frac{{\delta }_1{y}^{*}}{z^{*}}+\frac{{\delta }_2^v{z}^{*}}{y^{*}})+& x^{*}[{\gamma }_1^v{y}^{*}-\frac{{\rho }^v{\sigma }^v{\gamma }_2^v{z}^{*}}{{({\sigma }^v+x^{*})}^2}]]\hfill & \\ \hfill >{\alpha }^v{x}^{*}(1-{\beta }^v{x}^{*})[\frac{{\rho }^v{\delta }_2^v{\sigma }^v{z}^{*}}{y^{*}{({\sigma }^v+x^{*})}^2}+\frac{{\delta }_1^v{y}^{*}}{z^{*}}].\end{array}$$

  Thus, we can state the following result:

  Theorem 5.

  There exists a positive co-axial equilibrium $E_3^v(x^{*},y^{*},z^{*})$ for the system (5) if

  $${\eta }^v+{\delta }_1^v-\frac{{\gamma }_1^v{\delta }_2^v}{{\gamma }_2^v}<x^{*}<{\eta }^v+{\delta }_1^v<\frac{1}{{\beta }^v},$$

  and it is locally asymptotically stable if $x^{*}<\frac{1}{{\beta }^v}$ and

  $$\begin{array}{ccc}\hfill [{\alpha }^v{\beta }^v{x}^{*}+\frac{{\delta }_2^v{z}^{*}}{y^{*}}+\frac{{\delta }_1{y}^{*}}{z^{*}}][{\alpha }^v{\beta }^v{x}^{*}(\frac{{\delta }_1{y}^{*}}{z^{*}}+\frac{{\delta }_2^v{z}^{*}}{y^{*}})+& x^{*}[{\gamma }_1^v{y}^{*}-\frac{{\rho }^v{\sigma }^v{\gamma }_2^v{z}^{*}}{{({\sigma }^v+x^{*})}^2}]]\hfill & \\ \hfill >{\alpha }^v{x}^{*}(1-{\beta }^v{x}^{*})[\frac{{\rho }^v{\delta }_2^v{\sigma }^v{z}^{*}}{y^{*}{({\sigma }^v+x^{*})}^2}+\frac{{\delta }_1^v{y}^{*}}{z^{*}}].\end{array}$$

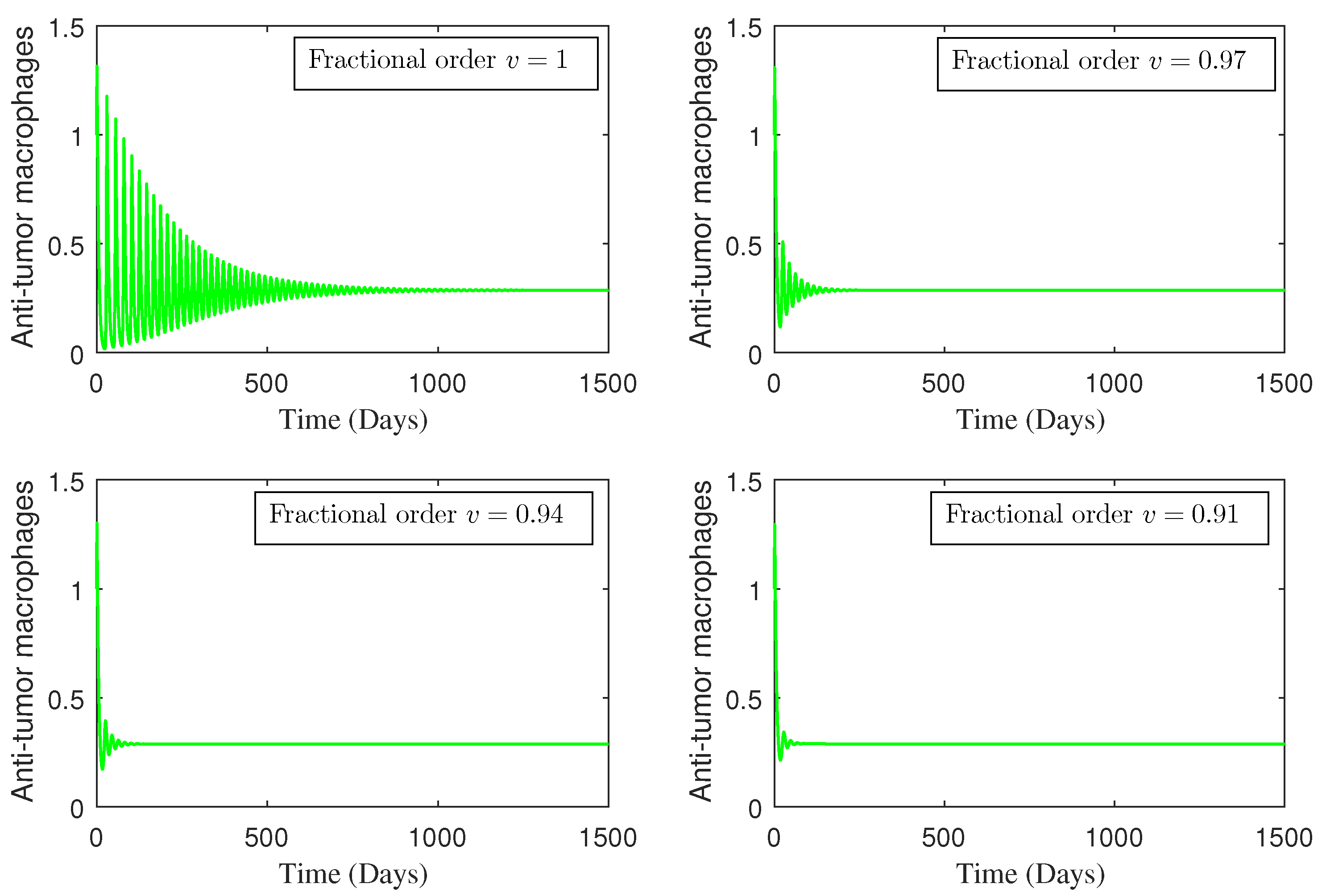
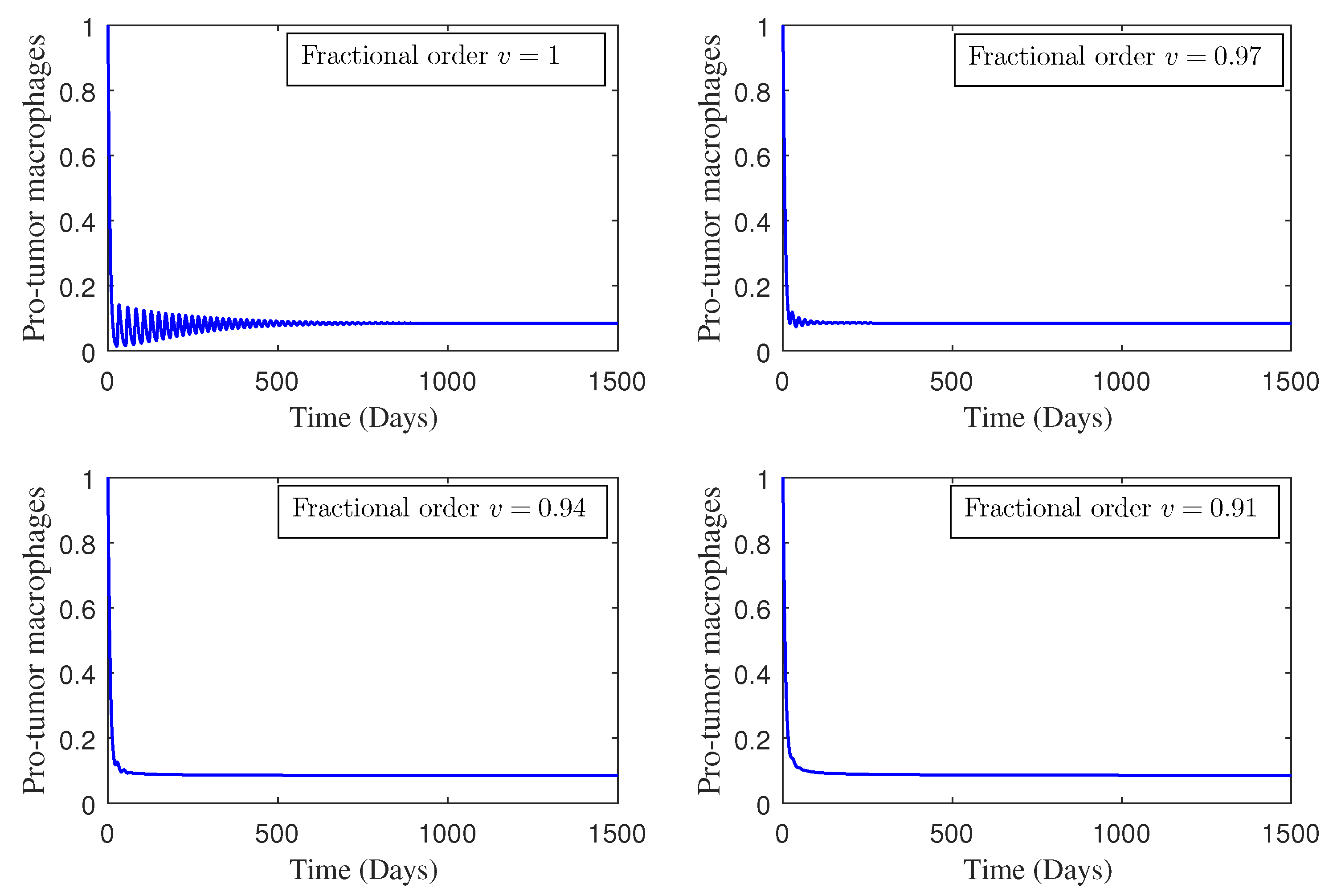
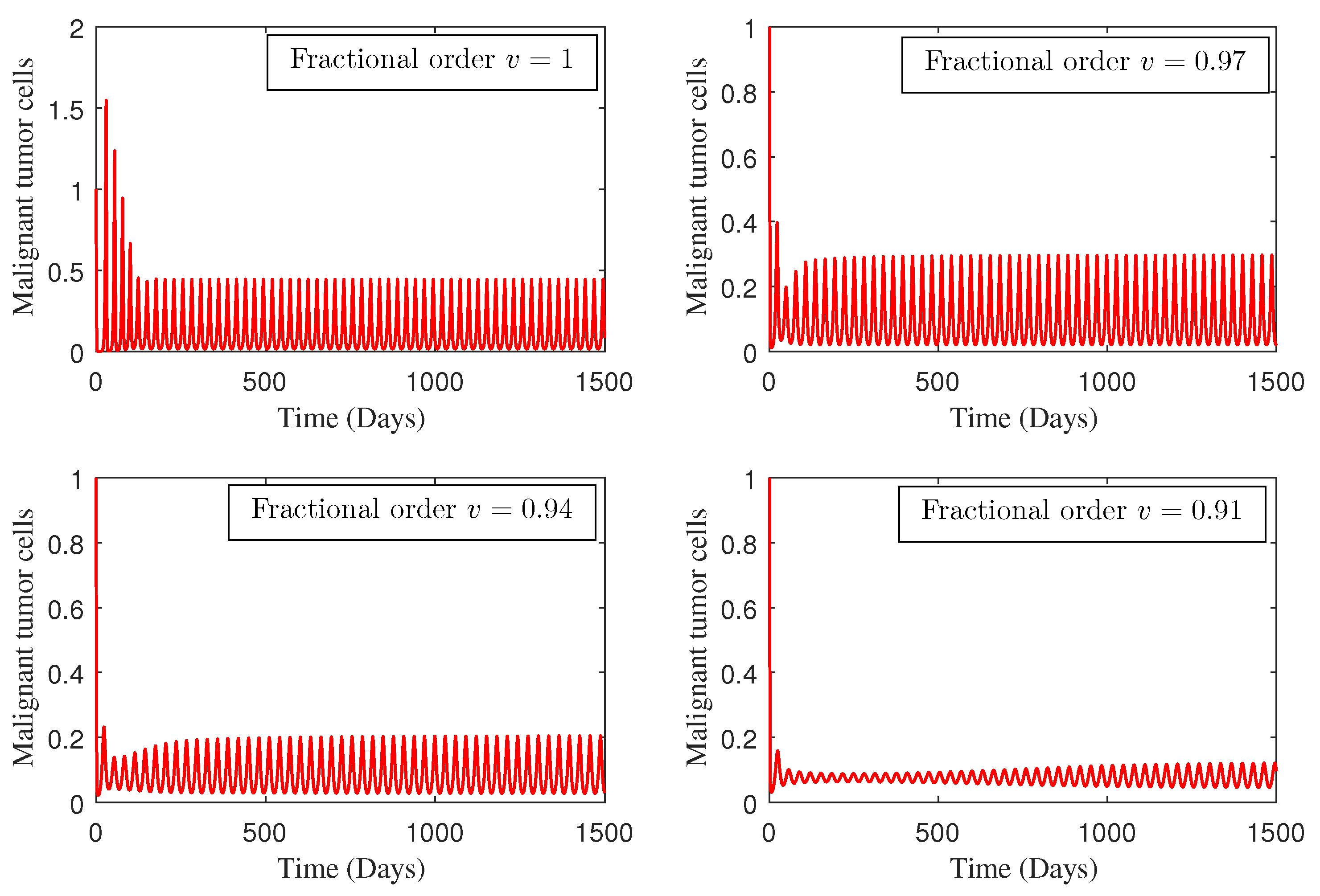
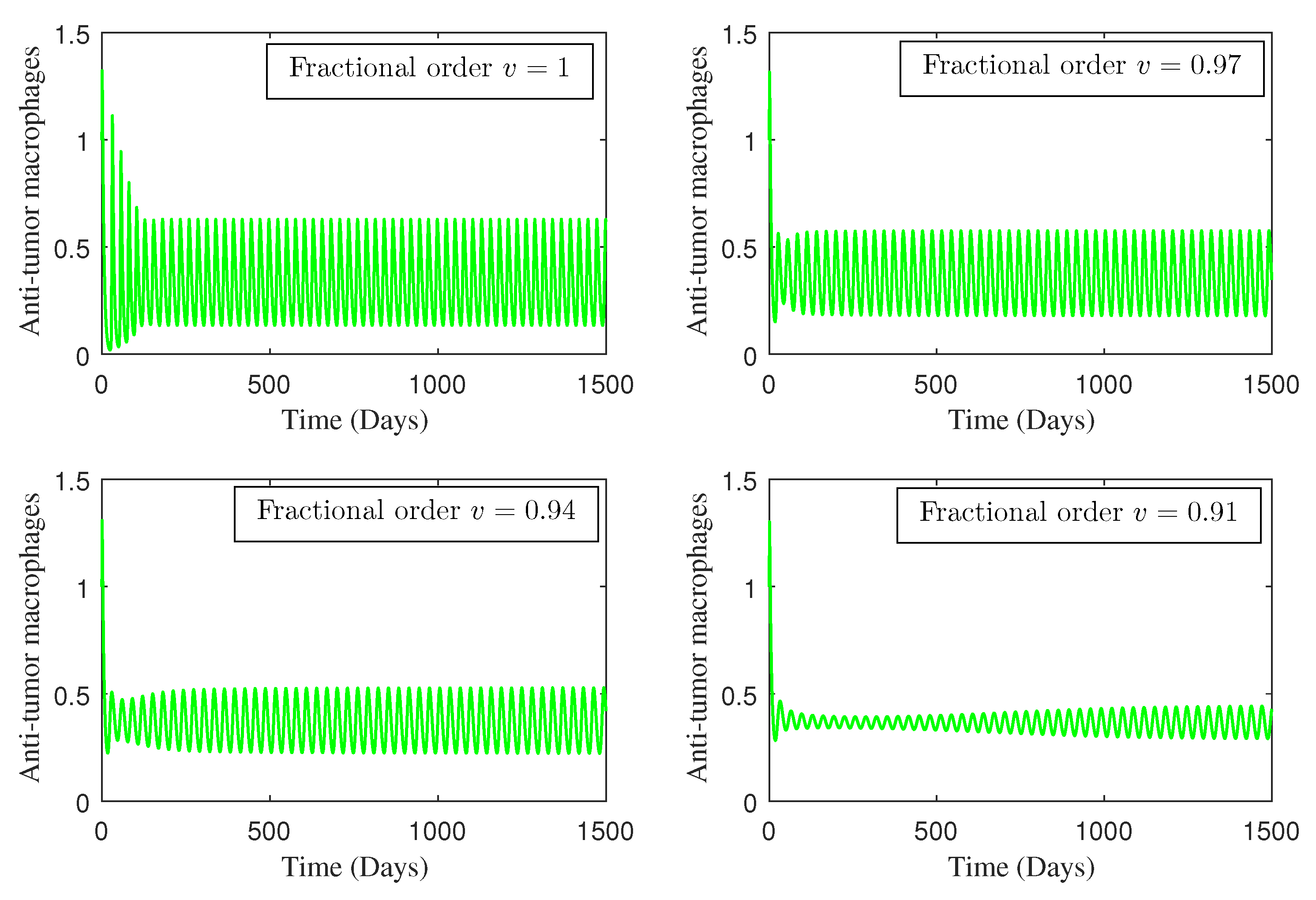
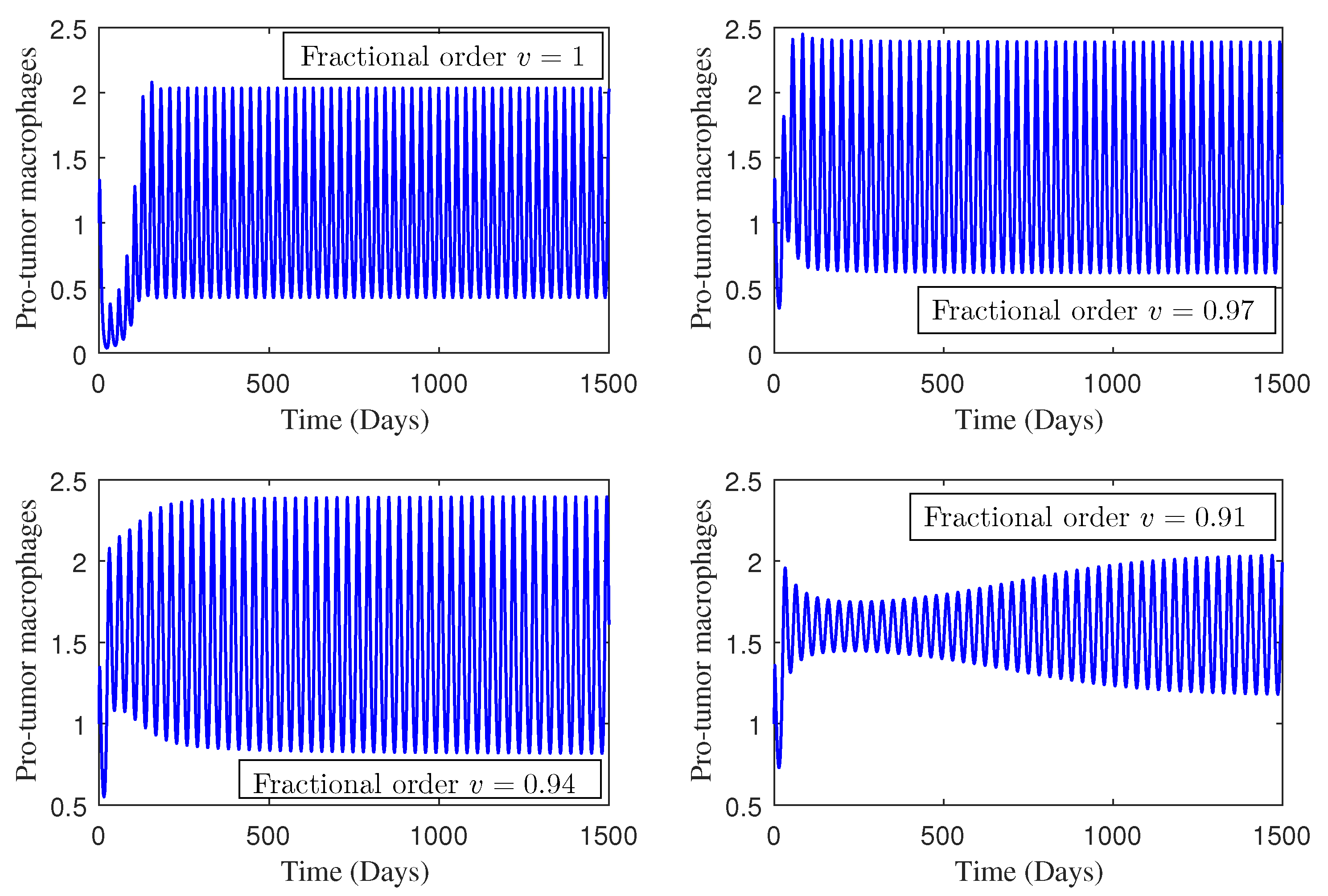
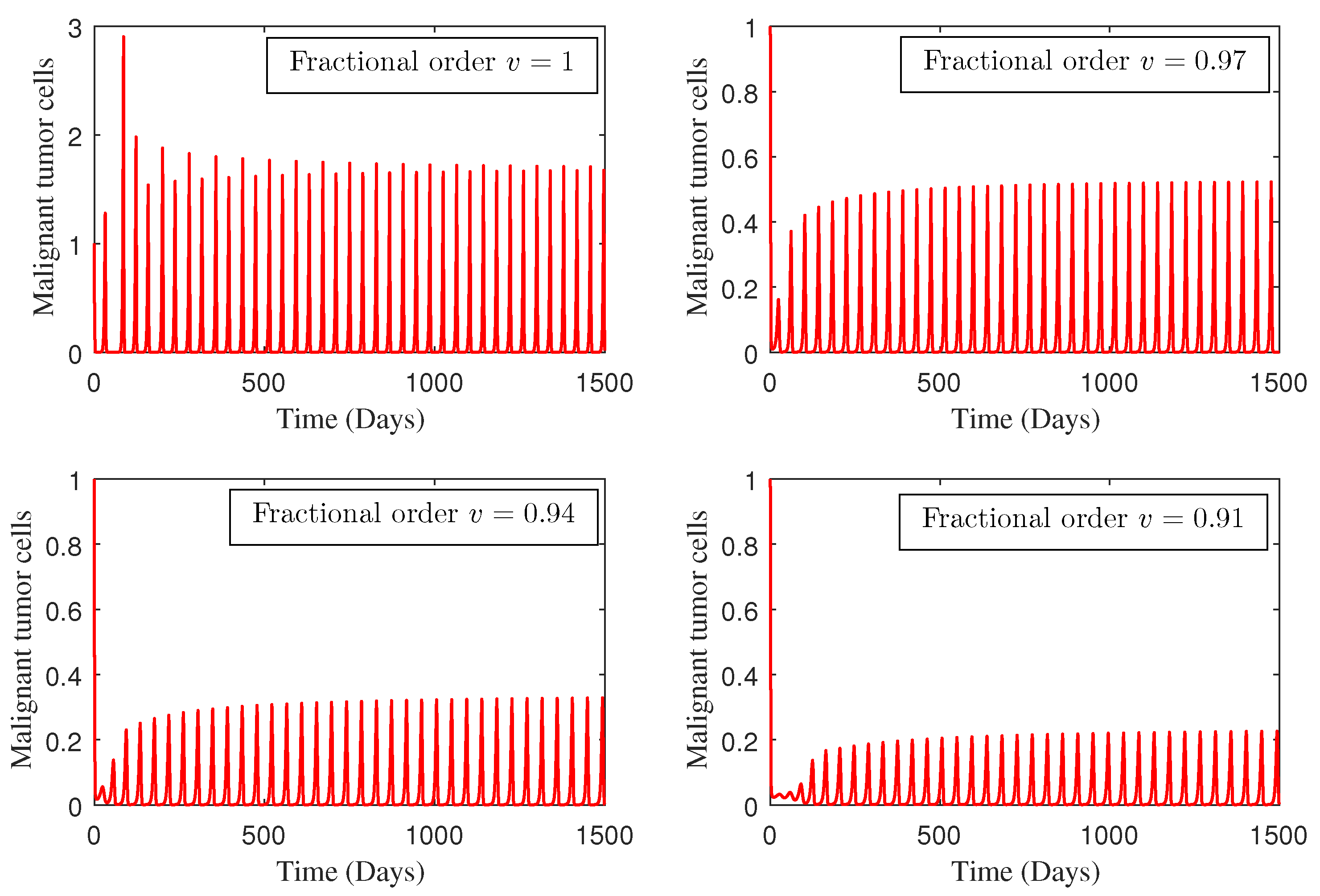
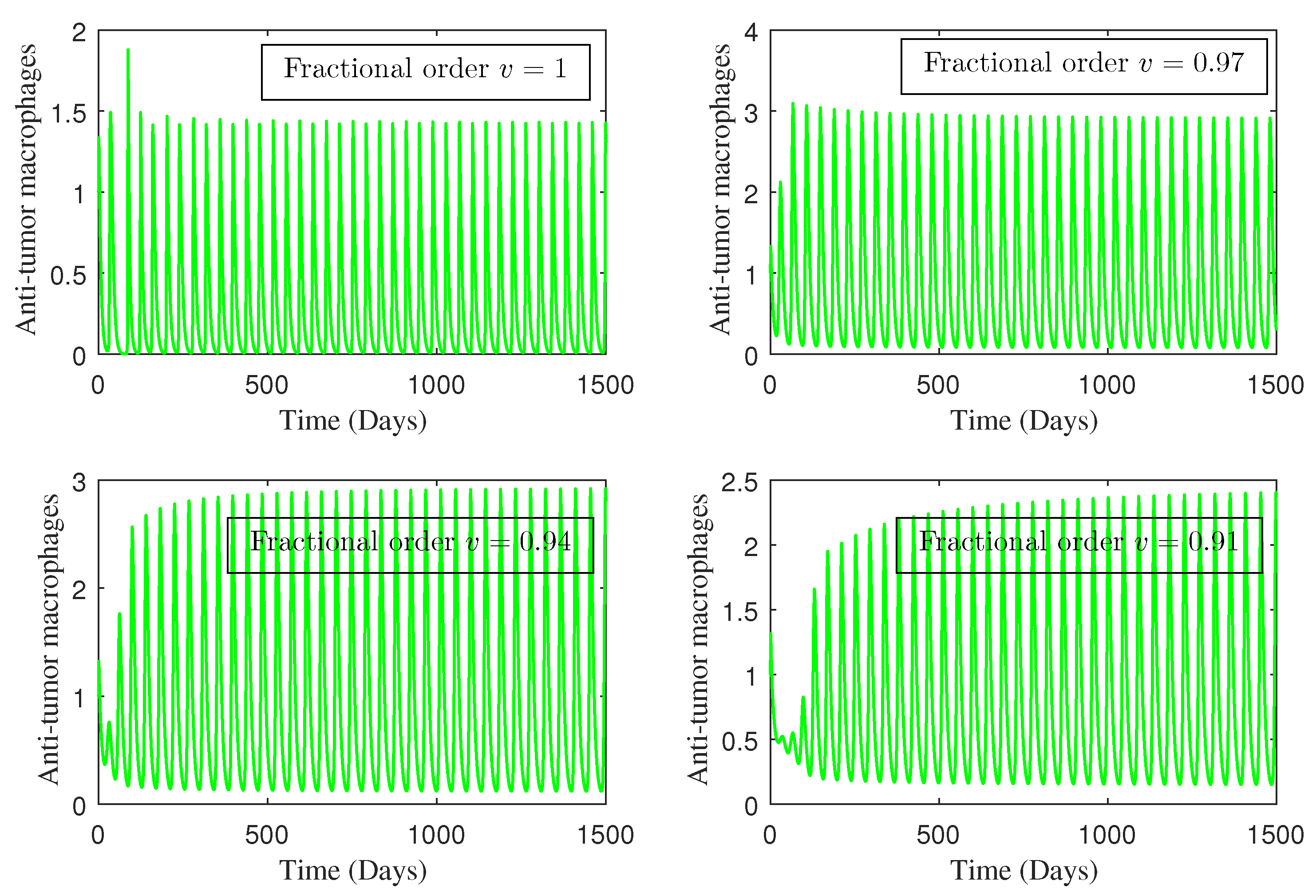
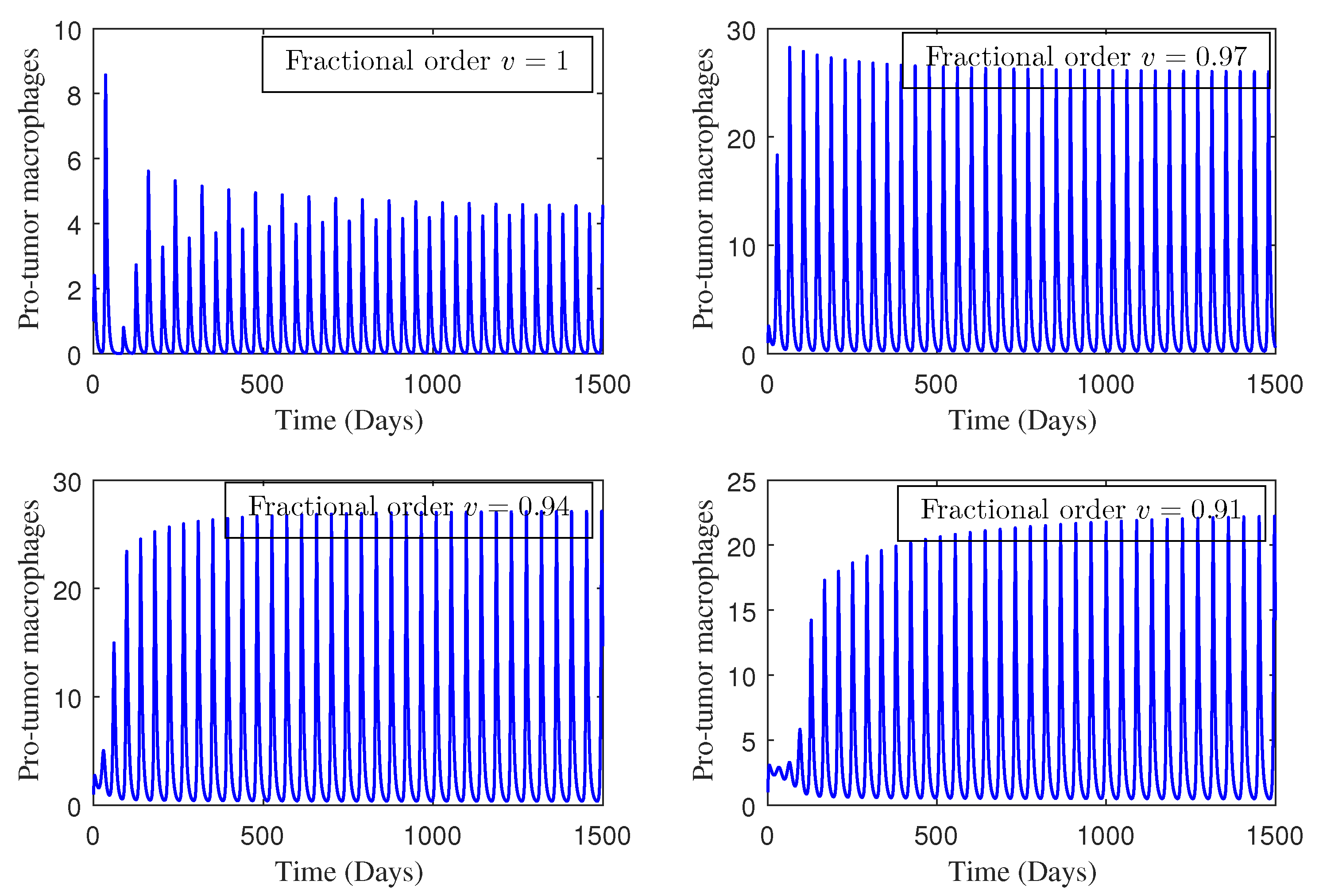
4. Numerical Study

This section is devoted to a numerical study of the proposed model for verification of the analytical findings. To observe the effect of the fractional order v on the stability of the model (5), we arbitrarily take four values for v as follows: $0.91$, $0.94$, $0.97$, and 1. We set the values of the non-dimension parameters in the numerical study as follows: $\alpha =0.565$, $\beta =5\times {10}^{-4}$, ${\gamma }_1=2$, ${\gamma }_2=0.1$, $\eta =0.2$, ${\delta }_1=0.05$, ${\delta }_2=0.04$, $\sigma =0.1$ (assumed), and $\mu =0.2$. The parameter values were chosen arbitrarily and based on the previous literature [31,34].

We also varied the parameter $\rho$ to observe the effect of the activation rate of type-II macrophages due to the emergence of tumor cells on the system (5). For this purpose, we assumed that the range of $\rho$ is $[0,1.1]$ and considered three cases: (i) $\rho =0.1$ (low activation rate of type-II macrophages), (ii) $\rho =0.5358$ (medium activation rate of type-II macrophages), and (iii) $\rho =1.062$ (high activation rate of type-II macrophages).

In Figure 1, Figure 2 and Figure 3, we show the densities of malignant tumor cells $x\left(t\right)$, type-I macrophages $y\left(t\right)$, and type-II macrophages $z\left(t\right)$ when the activation rate of type-II macrophages due to the emergence of tumor cells is low (i.e., $\rho =0.1$). It can be observed that all three cell populations tend to be stable as time increases. However, the cell populations show oscillatory behavior initially, while the order of the fractional derivative increases. This means that, even if the type-II macrophages activate at a slow rate, the type-I macrophages can keep the system stable around the positive co-axial equilibrium $E_3^v(x^{*},y^{*},z^{*})$. In

Table 1. Stability of the system for the case $\rho =0.1$.

Equilibrium Point	Eigenvalues	Stability
$E_1^v(0,0,0)$	$-0.2000,-0.2900,0.5650$	unstable
$E_2^v(2000,0,0)$	$-0.1400,1999.7500,-0.565$	unstable
$E_3^v(0.2382,0.2867,0.0845)$	$-0.0034+0.37\iota ,-0.0034-0.37\iota ,-0.1745$	asymptotically stable

, we show the stability of the system (5) around its equilibrium point based on the eigenvalues of the corresponding Jacobian of the system (5).

In Figure 4, Figure 5 and Figure 6, we show the densities of malignant tumor cells $x\left(t\right)$, type-I macrophages $y\left(t\right)$, and type-II macrophages $z\left(t\right)$ when the activation rate of type-II macrophages due to the emergence of tumor cells is medium (i.e., $\rho =0.5358$). It can be observed that all three cell populations show periodic oscillatory behavior, with this behavior increasing as the order of the fractional derivative increases. This result suggests that, for a medium activation rate of type-II macrophages, the type-I macrophages compete with the malignant tumor cells and type-II macrophages to stabilize the system for which periodic solutions are observed. In

Table 2. Stability of the system for the case $\rho =0.5358$.

Equilibrium Point	Eigenvalues	Stability
$E_1^v(0,0,0)$	$-0.2000,-0.2900,0.5650$	unstable
$E_2^v(2000,0,0)$	$0.2958,1999.7500,-0.565$	unstable
$E_3^v(0.0744,0.3619,1.5887)$	$0.0268+0.30\iota ,0.0268-0.30\iota ,-0.2406$	unstable

, we show the stability of the system (5) around its equilibrium point, based on the eigenvalues of the corresponding Jacobian of the system (5).

In Figure 7, Figure 8 and Figure 9, we show the densities of malignant tumor cells $x\left(t\right)$, type-I macrophages $y\left(t\right)$, and type-II macrophages $z\left(t\right)$ when the activation rate of type-II macrophages due to the emergence of tumor cells is high (i.e., $\rho =1.062$). It can be observed that all three cell populations show high periodic oscillatory behavior, where this behavior increases as the order of the fractional derivative increases. This finding suggests that, when there is a high activation rate of pro-tumor macrophages, the type-I macrophages compete with the malignant tumor cells and type-II macrophages to keep the system stable, which is why high periodic solutions are seen. In

Table 3. Stability of the system for the case $\rho =1.062$.

Equilibrium Point	Eigenvalues	Stability
$E_1^v(0,0,0)$	$-0.2000,-0.2900,0.5650$	unstable
$E_2^v(2000,0,0)$	$0.8220,1999.7500,-0.565$	unstable
$E_3^v(0.0280,0.3911,2.1728)$	$0.0675+0.33\iota ,0.0675-0.33\iota ,-0.3662$	unstable

, we show the stability of the system (5) around its equilibrium point, based on the eigenvalues of the corresponding Jacobian of the system (5).

It can be observed, from the above scenarios, that the oscillatory behavior of the system (5) increases as the order of the fractional derivative increases, and that each order depends on its previous order, which verifies the memory effect of the fractional operator. Furthermore, $\rho$ (i.e., the activation rate of pro-tumor macrophages due to the emergence of tumor cells) highly impacts the stability of the system (5), as it affects the proliferation of tumor cells. The proliferation of tumor cells is relatively slow. At the same time, when the activation rate of type-II macrophages is low, the type-I macrophages can stabilize the system to the co-axial equilibrium point. When the activation rate of type-II macrophages increases to a medium value, the proliferation of tumor cells also increases, which results in mild competition among all three cell populations, and the system presents an unstable periodic solution around the co-axial equilibrium point. However, with further increases in the activation rate of type-II macrophages to a high value, the proliferation of tumor cells is very high and the type-I macrophages compete with the other two cells. Still, they cannot suppress the growth of tumor cells, which may result in the disease persisting in the body.

5. Conclusions

In this study, we developed a fractional-order mathematical model in the Caputo sense that describes the interactions between tumors and immune macrophages. The main objective of the work was to describe the role of the activation rate of type-II macrophages and to observe the effect of fractional order on the model. First, we examined the fundamental properties of the model’s solutions. The local stability of the model was checked at each of the biologically feasible equilibria, and it was found that the tumor-free equilibrium presents unstable behavior, whereas the tumor-dominant and co-axial equilibria show stable behavior, provided that certain conditions hold. A numerical study was conducted by varying the activation rates of type-II macrophages and the order of the fractional operator. The numerical findings suggest that type-I macrophages can stabilize the system if the activation rate of type-II macrophages is low. However, with a higher activation rate of type-II macrophages, the proliferation of tumor cells becomes uncontrollable and the system is unstable. Furthermore, the stability of the system decreases as the order of the fractional operator increases.

Comparing our results with those of a previous study [31], we noticed that, while pro-tumor macrophages respond to the tumor in the Holling type-II form, the system shows oscillatory behavior for a lower value of activation rate of pro-tumor macrophages than the value obtained in Ref. [31]. Additionally, in comparison with Refs. [34,48], we discussed the effect of the saturated response of M2 macrophages due to tumor cells in a fractional-order tumor–macrophages model in the Caputo sense. The results of this study will be beneficial for clinicians and oncologists to develop treatments that target the immune macrophages to control the abnormal growth of tumor cells.

One of the main limitations of this study is that the type-I macrophages can also respond to the tumor in the Holling type-II form. Considering this fact, one could extend this study. Furthermore, the model could be extended using other families of fractional operators, such as the Caputo–Fabrizio fractional operator, conformable and $\beta$-conformable fractional operators in the Liouville–Caputo (LC) sense, and the Atangana–Baleanu fractional operator with different kernels. For example, the model with Caputo–Fabrizio fractional operator can be expressed as:

$$\left\{\begin{array}{cc}\hfill { }^{CF}{D}_t^{v}x\left(t\right)& ={\alpha }^{v}x(1-{\beta }^{v}x)-{\gamma }_1^{v}xy+{\gamma }_2^{v}xz\hfill \\ \hfill { }^c{D}_t^{v}y\left(t\right)& =xy-{\eta }^{v}y-{\delta }_1^{v}y+{\delta }_2^{v}z\hfill \\ \hfill { }^c{D}_t^{v}z\left(t\right)& =\frac{{\rho }^{v}xz}{{\sigma }^v+x}-{\mu }^{v}z+{\delta }_1^{v}y-{\delta }_2^{v}z,\hfill \end{array}\right.$$

(20)

and the model with Caputo–Fabrizio fractional operator can be expressed as:

$$\left\{\begin{array}{cc}\hfill { }^{ABC}{D}_t^{v}x\left(t\right)& ={\alpha }^{v}x(1-{\beta }^{v}x)-{\gamma }_1^{v}xy+{\gamma }_2^{v}xz\hfill \\ \hfill { }^{ABC}{D}_t^{v}y\left(t\right)& =xy-{\eta }^{v}y-{\delta }_1^{v}y+{\delta }_2^{v}z\hfill \\ \hfill { }^{ABC}{D}_t^{v}z\left(t\right)& =\frac{{\rho }^{v}xz}{{\sigma }^v+x}-{\mu }^{v}z+{\delta }_1^{v}y-{\delta }_2^{v}z.\hfill \end{array}\right.$$

(21)

We hope to carry out works to address the above limitations and focus on extension of the proposed model in the future.