The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator
Abstract
1. Introduction and Background
2. The Model
3. Local Stability
- Suppose there are no tumor cells in the body, then the macrophages do not emerge in the body in action; thus, in this sense, we take and . Then, we get the tumor-free trivial equilibrium as , which always exists.The Jacobian matrix of the system (5) evaluated at the tumor-free equilibrium is:It is clear that is one of the eigenvalues of the matrix (9), while the other two eigenvalues are the roots of the following equation:As one eigenvalue of the matrix (9) is , this implies the instability of the tumor-free trivial equilibrium . Thus, we can state this result as follows:Theorem 3.The tumor-free trivial equilibrium always exists and shows unstable behavior.
- Suppose there are tumor cells in the body; however, the macrophages have not emerged in the body in action yet. Thus, in this sense, we take and . Then, we have found the tumor dominant equilibrium as , which also always exists.The Jacobian matrix of the system (5) evaluated at tumor dominant equilibrium is:Clearly, is an eigenvalue of the matrix (11), while the other two eigenvalues will be the roots of the following equation:As , for the stability of the system (5), the Equation (12) must have all negative roots. Equation (12) possesses both roots as negative if the following conditions hold:Thus, we can state the following theorem:Theorem 4.The tumor-dominant equilibrium always exists and it is asymptotically stable if and ; otherwise, it is unstable.
- Suppose that all three cells emerge in the body at the same time. Then, for and , we obtain the co-axial equilibrium aswhere is given by the following equation:For positive , we must have the discriminant of the Equation (15) greater than zero andNow, we investigate the stability of the system (5) around the co-axial equilibrium . For and , we obtain the following relations at the co-axial equilibrium :Using the relations (16), we obtain the Jacobian matrix at co-axial equilibrium as:The eigenvalues of the Jacobian (17) are the roots of the following equation:whereAccording to the Routh–Hurwitz criterion, the system (5) is locally asymptotically stable if all the roots of the Equation (18) are negative or have negative real parts; that is, ifwhich implies that andThus, we can state the following result:Theorem 5.There exists a positive co-axial equilibrium for the system (5) ifand it is locally asymptotically stable if and
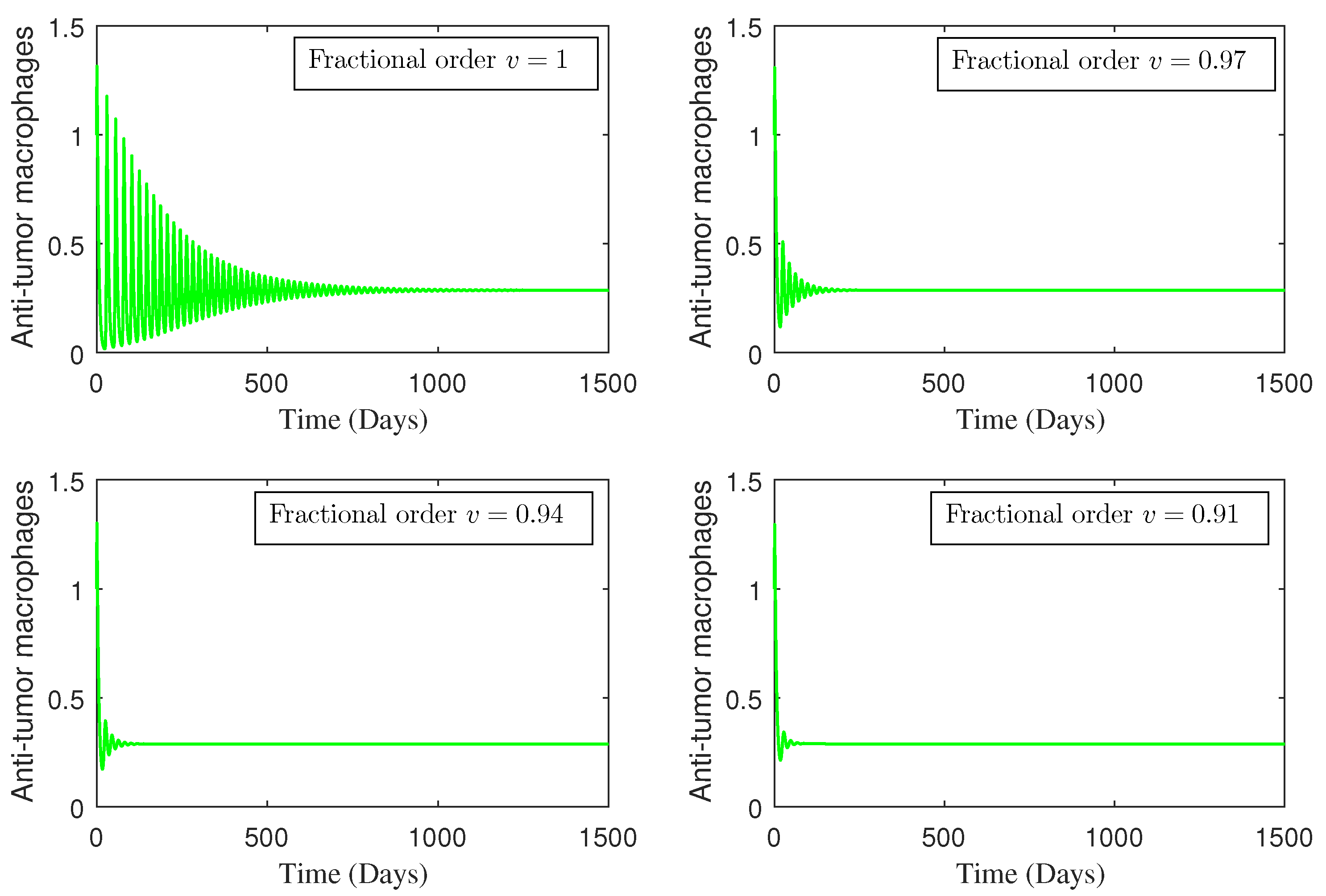
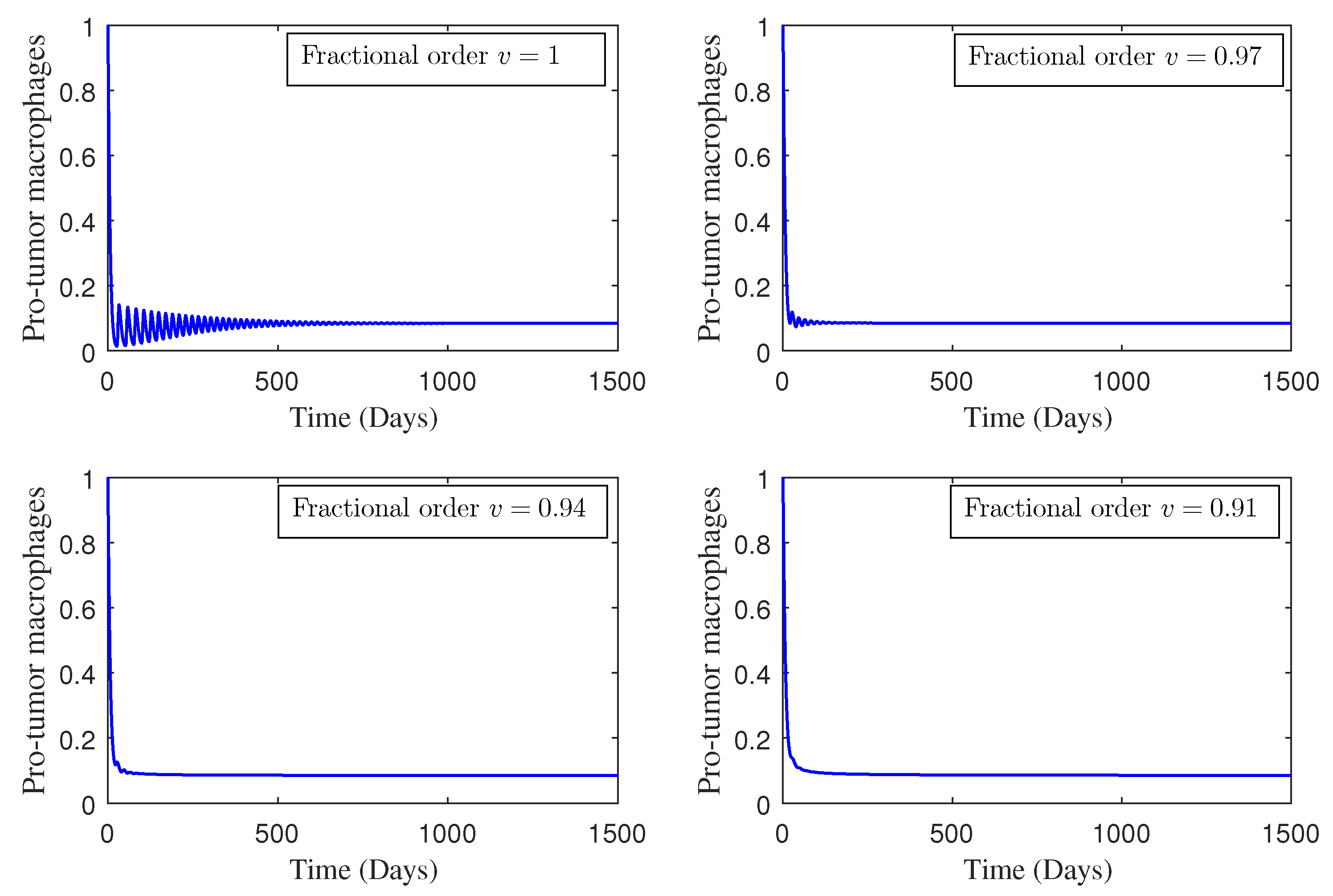
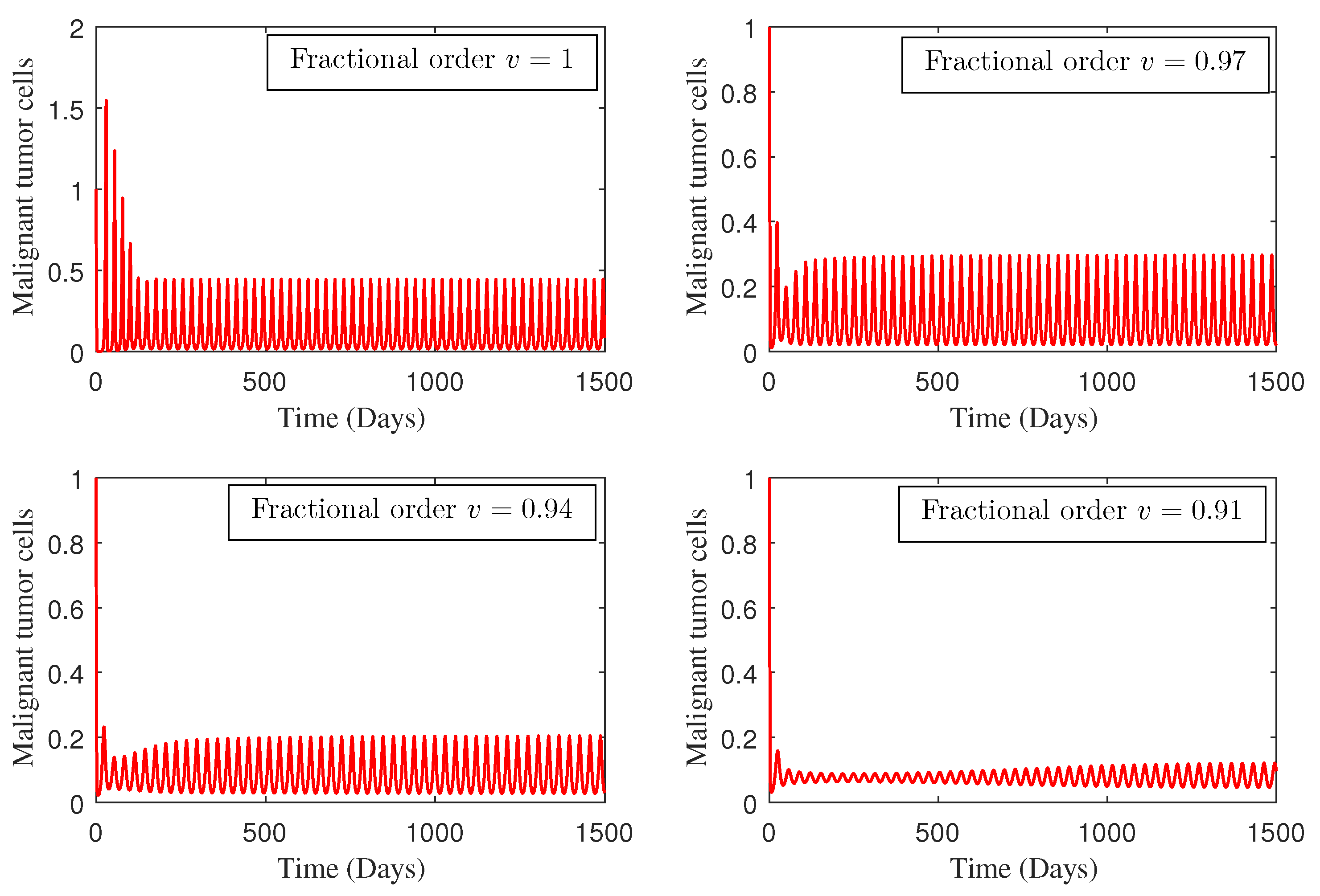
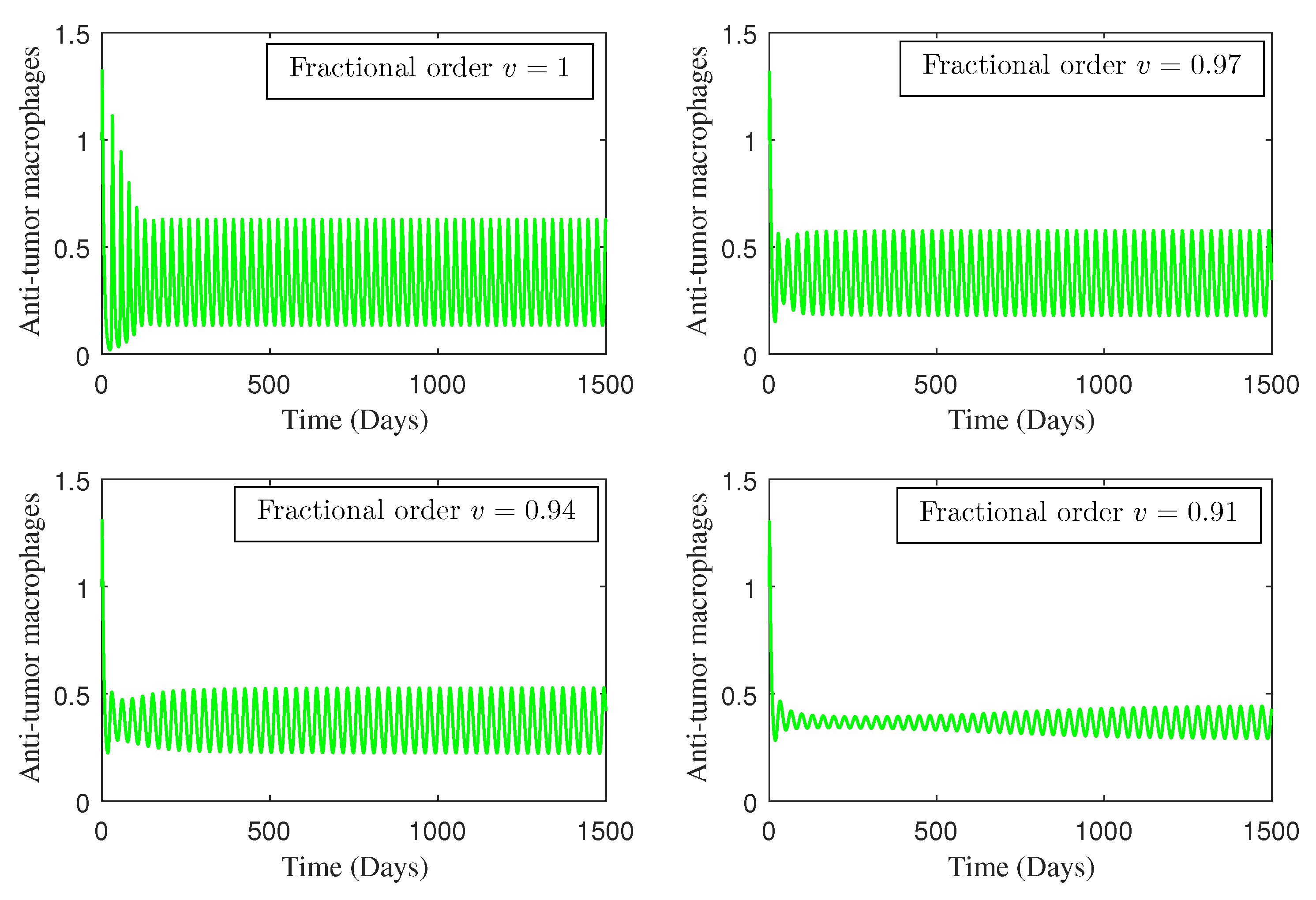
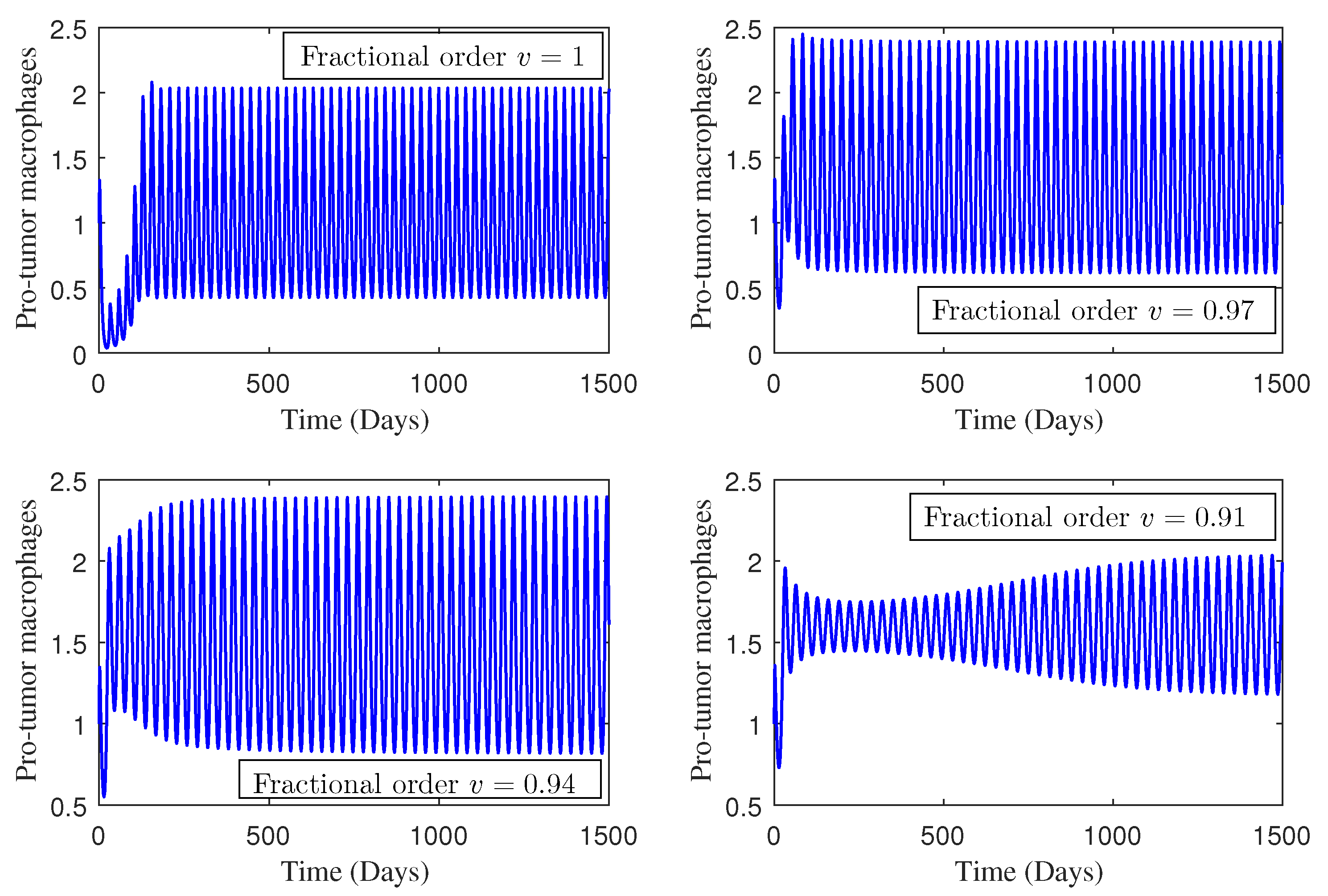
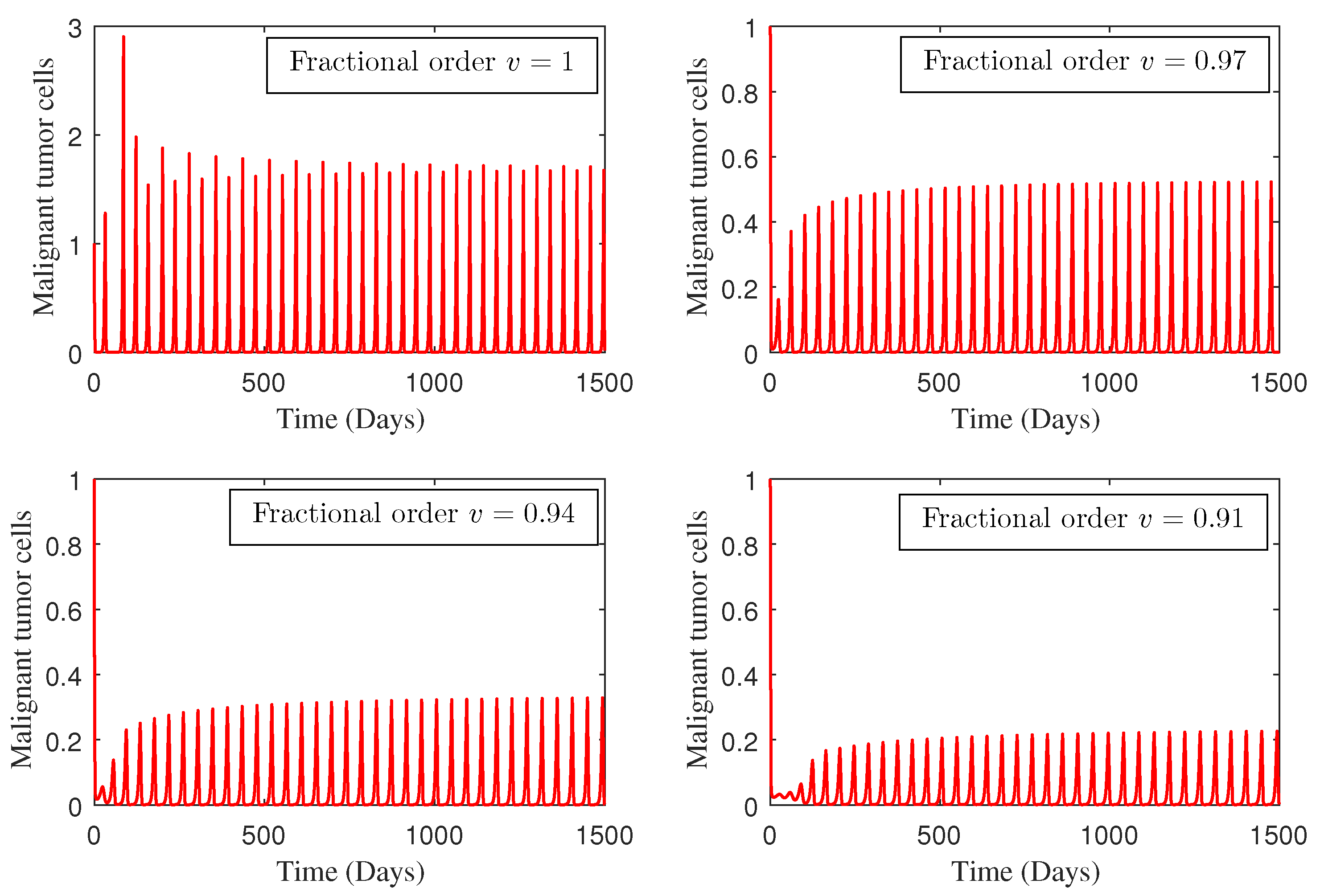
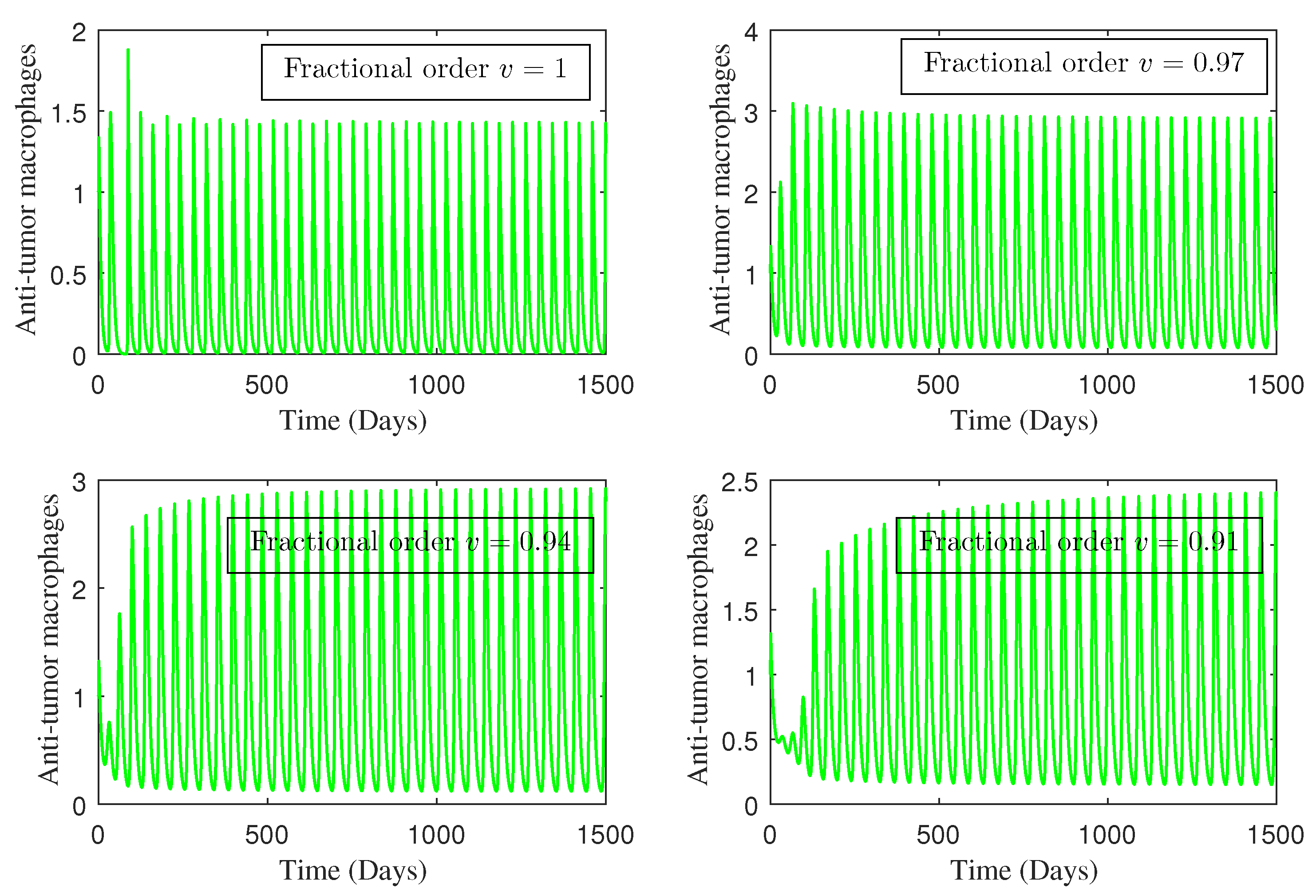
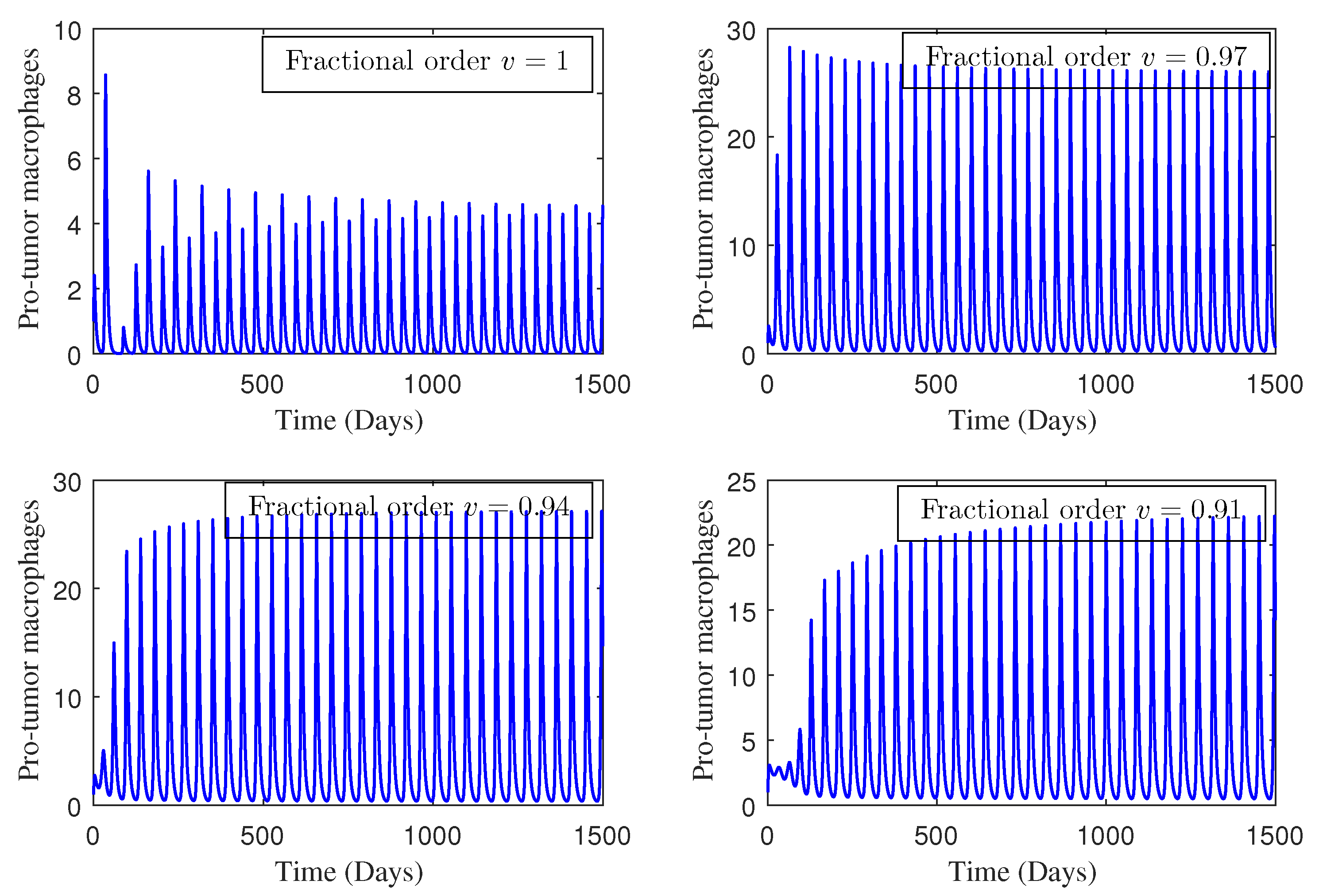
4. Numerical Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shelton, S.E.; Nguyen, H.T.; Barbie, D.A.; Kamm, R.D. Engineering approaches for studying immune-tumor cell interactions and immunotherapy. iScience 2020, 24, 101985. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, H.; Hagerling, C.; Werb, Z. Roles of the immune system in cancer: From tumor initiation to metastatic progression. Genes Dev. 2018, 32, 1267–1284. [Google Scholar] [CrossRef] [PubMed]
- Mengus, C.; Muraro, M.G.; Mele, V.; Amicarella, F.; Manfredonia, C.; Foglietta, F.; Muenst, S.; Soysal, S.D.; Iezzi, G.; Spagnoli, G.C. In vitro modeling of tumor-immune system interaction. ACS Biomater. Sci. Eng. 2018, 4, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Akhmetzyanova, I.; Zelinskyy, G.; Schimmer, S.; Brandau, S.; Altenhoff, P.; Sparwasser, T.; Dittmer, U. Tumor-specific CD4+ T cells develop cytotoxic activity and eliminate virus-induced tumor cells in the absence of regulatory T cells. Cancer Immunol. Immunother. 2013, 62, 257–271. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dehingia, K.; Das, P.; Upadhyay, R.K.; Misra, A.K.; Rihan, F.A.; Hosseini, K. Modelling and analysis of delayed tumour–immune system with hunting T-cells. Math. Comput. Simul. 2023, 203, 669–684. [Google Scholar] [CrossRef]
- Anderson, A.R.; Chaplain, M.A. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull. Math. Biol. 1998, 60, 857–899. [Google Scholar] [CrossRef] [PubMed]
- Arlotti, L.; Gamba, A.; Lachowicz, M. A kinetic model of tumor/immune system cellular interactions. J. Theor. Med. 2002, 4, 39–50. [Google Scholar] [CrossRef]
- Galach, M. Dynamics of the tumor-immune system competition-the effect of time delay. Int. J. Appl. Math. Comput. Sci. 2003, 13, 395–406. [Google Scholar]
- Araujo, R. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef]
- Enderling, H.; Chaplain, M.A.J. Mathematical modeling of tumor growth and treatment. Curr. Pharm. Des. 2014, 20, 4934–4940. [Google Scholar] [CrossRef]
- Chrobak, J.M.; Herrero, H. A mathematical model of induced cancer-adaptive immune system competition. J. Biol. Syst. 2011, 19, 521–532. [Google Scholar] [CrossRef]
- Eftimie, R.; Bramson, J.L.; Earn, D.J.D. Interactions between the immune system and cancer: A brief review of non-spatial mathematical models. Bull. Math. Biol. 2011, 73, 2–32. [Google Scholar] [CrossRef] [PubMed]
- Arabameri, A.; Asemani, D.; Hajati, J. Mathematical modeling of in-vivo tumor-immune interactions for the cancer immu-notherapy using matured dendritic cells. J. Biol. Syst. 2018, 26, 167–188. [Google Scholar] [CrossRef]
- Mahlbacher, G.E.; Reihmer, K.C.; Frieboes, H.B. Mathematical modeling of tumor-immune cell interactions. J. Theor. Biol. 2019, 469, 47–60. [Google Scholar] [CrossRef]
- de Pillis, L.G.; Radunskaya, A.E.; Wiseman, C.L. A validated mathematical model of cell-mediated immune response to tumor growth. Cancer Res. 2005, 65, 7950–7958. [Google Scholar] [CrossRef]
- Sarkar, R.; Banerjee, S. Cancer self remision and tumor stability—A stochastic approach. Math. Biosci. 2005, 196, 65–81. [Google Scholar] [CrossRef]
- Banerjee, S.; Sarkar, R.R. Delay-induced model for tumor–immune interaction and control of malignant tumor growth. Biosystems 2008, 91, 268–288. [Google Scholar] [CrossRef] [PubMed]
- Dritschel, H.; Waters, S.L.; Roller, A.; Byrne, H.M. A mathematical model of cytotoxic and helper T cell interactions in a tumour microenvironment. Lett. Biomath. 2018, 5 (Suppl. 1), S36–S68. [Google Scholar] [CrossRef]
- Li, D.; Ma, W.; Guo, S. Stability of a mathematical model of tumor-induced angiogenesis. Nonlinear Anal. Model. Control. 2016, 21, 325–344. [Google Scholar] [CrossRef]
- Eftimie, R.; Bramson, J.L.; Earn, D.J.D. Modeling anti-tumor Th1 and Th2 immunity in the rejection of melanoma. J. Theor. Biol. 2010, 265, 467–480. [Google Scholar] [CrossRef]
- Ghosh, S.; Banerjee, S. Mathematical modeling of cancer–immune system, considering the role of antibodies. Theor. Biosci. 2018, 137, 67–78. [Google Scholar] [CrossRef]
- Makhlouf, A.M.; El-Shennawy, L.; Elkaranshawy, H.A. Mathematical modelling for the role of CD4+T cells in tumor-immune interactions. Comput. Math. Methods Med. 2020, 1, 7187602. [Google Scholar] [CrossRef]
- Pang, L.; Liu, S.; Zhang, X.; Tian, T. Mathematical modeling and dynamic analysis of anti-tumor immune response. J. Appl. Math. Comput. 2019, 62, 473–488. [Google Scholar] [CrossRef]
- Boer, R.J.D.; Hogeweg, P.; Dullens, H.F.; Weger, R.A.D.; Otter, W.D. Macrophage T lymphocyte interactions in the anti-tumor immune response: A mathematical model. J. Immunol. 1985, 134, 2748–2758. [Google Scholar] [CrossRef]
- Owen, M.R.; Sherratt, J.A. Mathematical modelling of macrophage dynamics in tumours. Math. Models Methods Appl. Sci. 1999, 9, 513–539. [Google Scholar] [CrossRef]
- Webb, S.D.; Owen, M.R.; Byrne, H.M.; Murdoch, C.; Lewis, C.E. Macrophage-based anti-cancer therapy: Modelling different modes of tumour targeting. Bull. Math. Biol. 2007, 69, 1747–1776. [Google Scholar] [CrossRef]
- Shojaee, P.; Mornata, F.; Deutsch, A.; Locati, M.; Hatzikirou, H. The impact of tumor associated macrophages on tumor biology under the lens of mathematical modelling: A review. Front. Immunol. 2022, 13, 1050067. [Google Scholar] [CrossRef] [PubMed]
- Mahlbacher, G.E.; Curtis, L.T.; Lowengrub, J.; Frieboes, H.B. Mathematical modeling of tumor-associated macrophage in-teractions with the cancer microenvironment. J. Immunother. Cancer 2018, 6, 10. [Google Scholar] [CrossRef]
- Mantovani, A.; Sozzani, S.; Locati, M.; Allavena, P.; Sica, A. Macrophage polarization: Tumor-associated macrophages as a paradigm for polarized M2 mononuclear phagocytes. Trends Immunol. 2002, 23, 549–555. [Google Scholar] [CrossRef]
- Eftimie, R.; Gibell, L. A kinetic theory approach for modelling tumour and macrophages heterogeneity and plasticity during cancer progression. Math. Models Methods Appl. Sci. 2020, 30, 659–683. [Google Scholar] [CrossRef]
- Shu, Y.; Huang, J.; Dong, Y.; Takeuchi, Y. Mathematical modeling and bifurcation analysis of pro-and anti-tumor macrophages. Appl. Math. Model. 2020, 88, 758–773. [Google Scholar] [CrossRef]
- Khajanchi, S.; Nieto, J.J. Spatiotemporal dynamics of a glioma immune interaction model. Sci. Rep. 2021, 11, 22385. [Google Scholar] [CrossRef] [PubMed]
- Dehingia, K.; Hosseini, K.; Salahshour, S.; Baleanu, D. A detailed study on a tumor model with delayed growth of pro-tumor macrophages. Int. J. Appl. Comput. Math. 2022, 8, 245. [Google Scholar] [CrossRef]
- Dehingia, K.; Alharbi, Y.; Pandey, V. A mathematical tumor growth model for exploring saturated response of M2 macro-phages. Healthc. Anal. 2024, 5, 100306. [Google Scholar] [CrossRef]
- Rihan, F.A. Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Baleanu, D. On the fractional model of Fokker-Planck equations with two different operators. AIMS Math. 2020, 5, 236–248. [Google Scholar] [CrossRef]
- Tarasov, V.E. Mathematical Economics: Application of Fractional Calculus; MDPI: Basel, Switzerland, 2020. [Google Scholar] [CrossRef]
- Baleanu, D.; Agarwal, R.P. Fractional calculus in the sky. Adv. Differ. Equ. 2021, 2021, 117. [Google Scholar] [CrossRef]
- Ahmed, E.; Hashis, A.H.; Rihan, F.A. On fractional order cancer model. J. Fract. Calc. Appl. 2012, 3, 1–6. [Google Scholar]
- Arshad, S.; Baleanu, D.; Huang, J.; Tang, Y.; Qurashi, M.M.A. Dynamical analysis of fractional order model of immunogenic tumors. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Gömez-Aguilar, J.F.; Löpez-Löpez, M.G.; Alvarado-Martïnez, V.M.; Baleanu, D.; Khan, H. Chaos in a cancer model via frac-tional derivatives with exponential decay and Mittag-Leffler law. Entropy 2017, 19, 681. [Google Scholar] [CrossRef]
- Balcı, E.; Öztürk, Ï.; Kartal, S. Dynamical behaviour of fractional order tumor model with Caputo and conformable fractional derivative. Chaos Solit. Fractals 2019, 123, 43–51. [Google Scholar] [CrossRef]
- Ucar, E.; Özdemir, N.; Altun, E. Fractional order model of immune cells influenced by cancer cells. Math. Model. Nat. Phenom. 2019, 14, 308. [Google Scholar] [CrossRef]
- Özköse, F.; Yilmaz, S.; Yavuz, M.; Öztürk, I.; Senel, M.T.; Bagci, B.S.; Dogan, M.; Önal, Ö. A fractional modeling of tumor–immune system interaction related to lung cancer with real data. Eur. Phys. J. Plus 2022, 137, 40. [Google Scholar] [CrossRef]
- Farman, M.; Ahmad, A.; Akgül, A.; Saleem, M.U.; Nisar, K.S.; Vijayakumar, V. Dynamical behavior of tumor-immune system with fractal-fractional operator. AIMS Math. 2022, 7, 8751–8773. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Abdeljawad, T.; Akgül, A.; Mlaiki, N. Analysis of fractal-fractional model of tumor-immune interaction. Results Phys. 2021, 25, 104178. [Google Scholar] [CrossRef]
- Hassani, H.; Avazzadeh, Z.; Agarwal, P.; Mehrabi, S.; Ebadi, M.J.; Dahaghin, M.S.; Naraghirad, E. A study on fractional tu-mor-immune interaction model related to lung cancer via generalized Laguerre polynomials. BMC Med. Res. Methodol. 2023, 23, 189. [Google Scholar] [CrossRef] [PubMed]
- Padder, A.; Mokkedem, F.Z.; Lotfi, E.M. Stability and bifurcation analysis of fractional-order tumor–macrophages interaction model with multi-delays. Math. Meth. Appl. Sci. 2024, 47, 6143–6171. [Google Scholar] [CrossRef]
- Padder, A.; Almutairi, L.; Qureshi, S.; Soomro, A.; Afroz, A.; Hincal, E.; Tassaddiq, A. Dynamical analysis of generalized tumor model with Caputo fractional-order derivative. Fractal Fract. 2023, 7, 258. [Google Scholar] [CrossRef]
- Amilo, D.; Kaymakamzade, B.; Hincal, E. A fractional-order mathematical model for lung cancer incorporating integrated therapeutic approaches. Sci. Rep. 2023, 13, 12426. [Google Scholar] [CrossRef] [PubMed]
- Jajarmi, A.; Baleanu, D. A new fractional analysis on the interaction of HIV with CD4+T-cells. Chaos Solit. Fractals 2018, 113, 221–229. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, L.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter es-timation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
- Dehingia, K.; Sarmah, H.K.; Alharbi, Y.; Hosseini, K. Mathematical analysis of a cancer model with time-delay in tu-mor-immune interaction and stimulation processes. Adv. Differ. Equ. 2021, 2021, 473. [Google Scholar] [CrossRef] [PubMed]
- Arshad, S.; Yildiz, T.A.; Baleanu, D.; Tang, Y. The role of obesity in fractional order tumor-immune model. Politehn. Univ. Bucharest Sci. Bull. Ser. A Appl. Math. Phys 2020, 82, 181–196. [Google Scholar]
- Khan, N.; Ali, A.; Ullah, A.; Khan, Z.A. Mathematical analysis of neurological disorder under fractional order derivative. AIMS Math. 2023, 8, 18846–18865. [Google Scholar] [CrossRef]

| Equilibrium Point | Eigenvalues | Stability |
|---|---|---|
| unstable | ||
| unstable | ||
| asymptotically stable |
| Equilibrium Point | Eigenvalues | Stability |
|---|---|---|
| unstable | ||
| unstable | ||
| unstable |
| Equilibrium Point | Eigenvalues | Stability |
|---|---|---|
| unstable | ||
| unstable | ||
| unstable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehingia, K.; Boulaaras, S. The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator. Fractal Fract. 2024, 8, 394. https://doi.org/10.3390/fractalfract8070394
Dehingia K, Boulaaras S. The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator. Fractal and Fractional. 2024; 8(7):394. https://doi.org/10.3390/fractalfract8070394
Chicago/Turabian StyleDehingia, Kaushik, and Salah Boulaaras. 2024. "The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator" Fractal and Fractional 8, no. 7: 394. https://doi.org/10.3390/fractalfract8070394
APA StyleDehingia, K., & Boulaaras, S. (2024). The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator. Fractal and Fractional, 8(7), 394. https://doi.org/10.3390/fractalfract8070394






