Fixed-Point Results in Fuzzy S-Metric Space with Applications to Fractals and Satellite Web Coupling Problem

Abstract

In this manuscript, we introduce the concept of fuzzy S-metric spaces and study some of their characteristics. We prove a fixed-point theorem for a self-mapping on a complete fuzzy S-metric space. To illustrate the versatility of our new ideas and related fixed-point theorems, we give examples to illustrate their use in a variety of domains, including fractal formation. These examples illustrate how the fuzzy S-contraction can be applied to iterated function systems, enabling the exploration of fractal forms under diverse contractive conditions. In addition, we solve the satellite web coupling problem by employing this coherent framework.

1. Introduction

Finding the distance between two or more objects that may be difficult to measure precisely is a requirement in many real-world scenarios. As a result, we need a suitable metric to model different practical difficulties. There are a number of methods for more accurate distance measurement that are being used to expand the scope of fixed-point (FP) theory research. In the theory of fixed points, both unique and non-unique FP conclusions have been extensively studied from various angles using different metrics. In many branches of mathematics, including applied mathematics, topology, and analysis, metric spaces (MSs) are crucial. Thus, a number of FP results were discovered after studying various generalizations of MSs. Numerous authors have studied the FP theory in generalized metric space. For instance, the notions of 2-MSs and D-MSs were first proposed by Gahler [1] and Dhage [2], respectively; however, other writers noted that these attempts are invalid (see [3,4]). An S-metric space (S-MS) was first proposed by Sedghi et al. [5] in 2012, and it was demonstrated that this concept represents a generalization of an MS. Furthermore, they established some FP theorems on S-metric spaces and demonstrated certain features of these spaces. In Ref. [6], Sedghi and Dung generalized their own work and derived numerous analogues of FP theorems in S-MSs. The fuzzy set idea was initially presented by Lotfi A. Zadeh in 1965 [7]. The term “fuzzy” refers to vagueness or ambiguity. Fuzziness arises when the boundaries of a piece of information are not precisely defined. Fuzzy sets are characterized by elements that possess varying degrees of membership, serving as a generalization of the traditional concept of a set. Numerous researchers have proposed different approaches to defining fuzzy metric spaces. The fuzzy perspective on distance is based on the idea that the distance between two points is a fuzzy concept instead of a definite real value that can be calculated or estimated. Building on these ideas of fuzziness and ambiguity in the closeness of objects, in 1975, Kramosil and Michalek defined fuzzy metric space (FMS) and introduced related concepts [8]. George and Veeramani [9] proposed and examined a concept of fuzzy metric space based on continuous t-norm (CTN). Their approach represents a refined and appealing variation of the frameworks earlier introduced by Kramosil and Michalek [8] as well as Kaleva and Seikkala [10]. Grabiec, M. [11] was the pioneer in exploring fixed-point theory within FMSs and developed a fuzzy analog of Banach’s principle. He integrated the idea of contraction into the structure of fuzzy metrics, laying the foundation for concepts such as sequence convergence, Cauchy sequences, and completeness in this framework. Zahid [12] also presents new modifications in fixed-point theory.

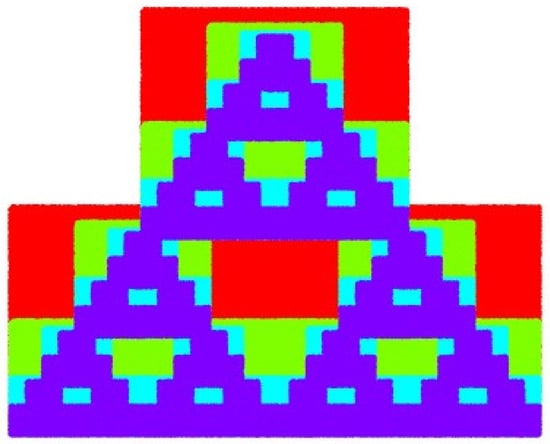
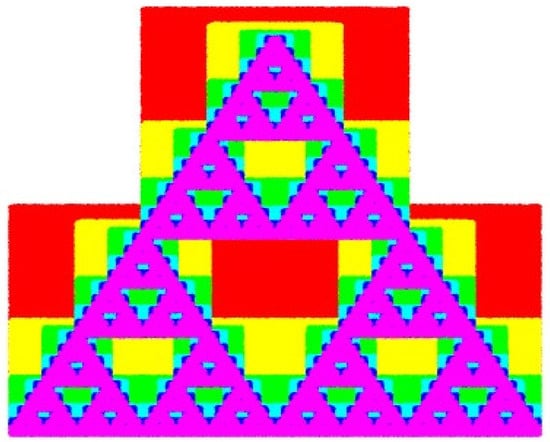
Since self-similar sets offer a potent means of incorporating a broad variety of physical phenomena into mathematical models, they are crucial to the study of fractals. Hutchinson’s seminal study [13] made a significant advance in this subject, exploring concepts of self-similarity. Iterated function systems (IFSs), which were developed as a result of his pioneering work, are now a crucial tool for producing self-similar fractals. Hutchinson’s groundbreaking work was further supported by Barnsley [14]. Iterated function systems (i.f.ss) are introduced as a unified way of generating a broad class of fractals. These fractals are often attractors for i.f.ss and occur as the supports of probability measures associated with functional equations. Zahid et al. [15] introduced a novel iterated function system (IFS) called the F-Proximal Iterated Function System (F-PIFS) and proposed a new technique for generating fractals. Unlike traditional methods that produce a single fractal, their approach enables the simultaneous generation of two fractals, opening a new direction in fractal theory. Recently, in 2024, Shaheryar et al. [16] introduced fuzzy enriched contraction and generating fractals using this generalized contraction.

Fixed-point theory plays a crucial role in various scientific and engineering applications. The Gaussian Decomposition Algorithm [17] relies on iterative refinements for signal decomposition, ensuring convergence through fixed-point principles. In echo signal detection [18], contraction mappings aid in filtering weak signals from noise. The information transmission model [19] benefits from fixed-point methods in optimizing error correction and data efficiency. Additionally, optical structures for lightweight materials [20] use fixed-point approaches to stabilize wave propagation and optimize optical networks. These applications highlight the significance of fixed-point theory in signal processing, communications, and material design.

Fuzzy metric spaces have been extensively studied due to their applicability in various domains such as image processing, decision-making, and complex network modeling. However, conventional fuzzy metric spaces often exhibit limitations when dealing with multi-point relationships and dynamic systems. Traditional fuzzy metric spaces primarily focus on pairwise distance measures, which may not adequately capture interactions in scenarios where three or more elements interact simultaneously. To overcome these limitations, we introduce the fuzzy S-metric space (FS-MS), which extends the traditional fuzzy metric structure by incorporating a three-point distance measure. This modification is particularly useful in applications such as fractals and satellite web coupling, where multi-point dependencies play a crucial role in defining structural and topological properties. In fractals, distance measures must accommodate self-similarity and iterative transformations, which FS-MS effectively models through its generalized inequality condition. Similarly, in satellite web coupling, the interaction between multiple nodes in a dynamic network requires a robust and flexible metric, which FS-MS provides by enforcing associativity via the composition property. Thus, FS-MS provides a more robust framework for analyzing fractal structures and satellite web systems, making it an indispensable tool in these contexts.

In order to integrate the idea of fuzzy S-contractions within complete fuzzy S-MSs, we introduce a new metric space, called the fuzzy S-metric space, which generalizes both the fuzzy metric space and the S-metric space. Additionally, we propose a novel S-iterated function system (S-IFS) along with its associated H–B operator. We aim to prove the existence of a single attractor for the S-IFS by utilizing the proven FP theorem. In order to clarify the suggested architecture, we offer a tangible illustration that demonstrates how fuzzy S-contractions are used to create fractals. We hope to highlight the effectiveness of our method in producing complex geometric objects with self-similar qualities through this example demonstration. In conclusion, by presenting the idea of fuzzy S-contractions, this study seeks to improve our understanding and use of fuzzy S-contraction mappings. By investigating their characteristics and using them in the context of S-IFS, we want to further the study of fractal geometry and offer important new perspectives on the creation of intricate fractal designs.

2. Preliminaries

In this section, we discuss some basic definitions from the existing literature.

Definition 1.

([21]). An operation that is binary $⊠:[0,1]\times [0,1]\to [0,1]$ is referred to as a CTN if the binary operation ⊠ is associative, commutative, and continuous, and also if ⊠ satisfies the boundary condition, i.e.,

$\mathfrak{x}⊠1=\mathfrak{x}\forall \mathfrak{x}\in [0,1]$, and ⊠ is monotonic, i.e., $\mathfrak{x}⊠\mathfrak{y}\le \gamma ⊠\varkappa \mathit{whenever}\mathfrak{x}\le \gamma \mathit{and}$$\mathfrak{y}\le \varkappa ,\mathit{for}\mathit{each}\mathfrak{x},\mathfrak{y},\gamma ,\varkappa \in [0,1].$

Definition 2.

([5]). Let Ω be a non-empty set. A function $S:{\Omega }^3\to [0,\infty )$ that meets the following criteria is an S-metric on Ω . For any $\zeta ,\eta ,\gamma ,\mathfrak{a}\in \Omega$,

• $S(\zeta ,\eta ,\gamma )\ge 0$,
• $S(\zeta ,\eta ,\gamma )=0\iff \zeta =\eta =\gamma$,
• $S(\zeta ,\eta ,\gamma )\le S(\zeta ,\zeta ,\mathfrak{a})+S(\eta ,\eta ,\mathfrak{a})+S(\gamma ,\gamma ,\mathfrak{a}).$

The pair $(\Omega ,S)$ is called an S-metric space.

Definition 3.

The 3-tuple $(\Omega ,M_S,⊠)$ is a fuzzy S-metric space (FS-MS) if Ω is an arbitrary set, ⊠ is a CTN, and $M_S$ is a fuzzy set on ${\Omega }^3\times (0,\infty )$ that fulfills the requirements listed below:

• $M_S(\zeta ,\eta ,\gamma ,\theta )>0,$
• $M_S(\zeta ,\eta ,\gamma ,\theta )=1\forall \theta >0$⇔$\zeta =\eta =\gamma$,
• $M_S(\zeta ,\eta ,\gamma ,\theta +u+v)\ge M_S(\zeta ,\zeta ,a,\theta )⊠M_S(\eta ,\eta ,a,u)⊠M_S(\gamma ,\gamma ,a,v).$
• $M_S(\zeta ,\eta ,\gamma ,·):(0,\infty )\to [0,1]$ is left-continuous and non-decreasing for all $\zeta ,\eta ,\gamma ,a\in \Omega$ and $\theta ,u,v>0$.

Definition 4.

A sequence $\left\{{\zeta }_n\right\}$ in an FS-MS converges to $\zeta \in \Omega$

if ${lim}_{n\to \infty }{M}_S({\zeta }_n,{\zeta }_n,\zeta ,\theta )=1$ for each $\theta >0$. A sequence $\left\{{\zeta }_n\right\}$ in an FS-MS is Cauchy if ${lim}_{n\to \infty }{M}_S({\zeta }_n,{\zeta }_n,{\zeta }_{n+m},\theta )=1$ for each $\theta >0$ and $m>0$.

An FS-MS is said to be complete if every Cauchy sequence is convergent in it.

Lemma 1.

In an FS-MS, we also have $M_S(\zeta ,\zeta ,\eta ,\theta )=M_S(\eta ,\eta ,\zeta ,\theta )$.

Proof. 

According to fuzzy S-metric space’s third condition, we obtain

$$\begin{array}{cc}\hfill M_S(\zeta ,\zeta ,\eta ,\theta )& \ge M_S(\zeta ,\zeta ,\zeta ,\theta -2\theta )⊠M_S(\zeta ,\zeta ,\zeta ,\theta )⊠M_S(\eta ,\eta ,\zeta ,\theta ),\hfill \\ & =1⊠1⊠M_S(\eta ,\eta ,\zeta ,\theta ),\hfill \\ & =M_S(\eta ,\eta ,\zeta ,\theta ).\hfill \end{array}$$

(1)

Also,

$$\begin{array}{cc}\hfill M_S(\eta ,\eta ,\zeta ,\theta )& \ge M_S(\eta ,\eta ,\eta ,\theta -2\theta )⊠M_S(\eta ,\eta ,\eta ,\theta )⊠M_S(\zeta ,\zeta ,\eta ,\theta ),\hfill \\ & =1⊠1⊠M_S(\zeta ,\zeta ,\eta ,\theta ),\hfill \\ & =M_S(\zeta ,\zeta ,\eta ,\theta ).\hfill \end{array}$$

(2)

From (1) and (2), we obtain $M_S(\zeta ,\zeta ,\eta ,\theta )=M_S(\eta ,\eta ,\zeta ,\theta )$. □

Definition 5.

Let $(\Omega ,M_S,⊠)$ be an FS-MS. A fuzzy S-contraction is defined as a mapping $F:\Omega \to \Omega$ if there is a constant $0<\alpha <1$ such that

$$M_S(F\zeta ,F\zeta ,F\eta ,\alpha \theta )\ge M_S(\zeta ,\zeta ,\eta ,\theta ),\forall \zeta ,\eta ,\in \Omega .$$

(3)

Theorem 1.

Let $(\Omega ,M_S,⊠)$ be a complete FS-MS such that

$$\underset{\theta \to \infty }{lim}{M}_S(\zeta ,\eta ,\gamma ,\theta )=1\forall \zeta ,\eta ,\gamma \in \Omega .$$

(4)

Let $F:\Omega \to \Omega$ be a fuzzy S-contraction on Ω. Then, F has a unique fixed point.

Proof. 

Let $\zeta \in \Omega$ and ${\zeta }_n=F^n\left(\zeta \right)$$(n\in \mathbb{N})$. Then,

$$\begin{array}{cc}\hfill M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},\theta \right)& \ge M_S\left({\zeta }_{n-1},{\zeta }_{n-1},{\zeta }_n,{\displaystyle \frac{\theta }{\alpha }}\right),\hfill \\ & \ge M_S\left({\zeta }_{n-2},{\zeta }_{n-2},{\zeta }_{n-1},{\displaystyle \frac{\theta }{{\alpha }^2}}\right),\hfill \\ & \ge M_S\left({\zeta }_{n-3},{\zeta }_{n-3},{\zeta }_{n-2},{\displaystyle \frac{\theta }{{\alpha }^3}}\right),\hfill \\ & ⋮\hfill \\ & \ge M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^n}}\right),\hfill \end{array}$$

which implies that

$$M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},\theta \right)\ge M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^n}}\right).$$

(5)

Thus, for any positive integer, m we have

$$\begin{array}{cc}\hfill M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+m},\theta \right)& \ge M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_{n+m},{\zeta }_{n+m},{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right),\hfill \\ & \ge M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_{n+m},{\zeta }_{n+m},{\zeta }_{n+2},{\displaystyle \frac{\theta }{m}}\right),\hfill \\ & ⊠M_S\left({\zeta }_{n+m},{\zeta }_{n+m},{\zeta }_{n+2},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_{n+1},{\zeta }_{n+1},{\zeta }_{n+2},{\displaystyle \frac{\theta }{m}}\right),\hfill \\ & ⋮\hfill \\ & \ge M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_n,{\zeta }_n,{\zeta }_{n+1},{\displaystyle \frac{\theta }{m}}\right)⊠M_S\left({\zeta }_{n+1},{\zeta }_{n+1},{\zeta }_{n+2},{\displaystyle \frac{\theta }{m}}\right),\hfill \\ \hfill & ⊠M_S\left({\zeta }_{n+2},{\zeta }_{n+2},{\zeta }_{n+3},{\displaystyle \frac{\theta }{m}}\right)⊠\cdots ⊠M_S\left({\zeta }_{n+m},{\zeta }_{n+m},{\zeta }_{n+m-1},{\displaystyle \frac{\theta }{m}}\right),\hfill \\ & \ge M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^{n}m}}\right)⊠M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^{n}m}}\right)⊠M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^{n+1}m}}\right),\hfill \\ & ⊠M_S\left(\zeta ,\zeta ,{\zeta }_1,{\displaystyle \frac{\theta }{{\alpha }^{n+2}m}}\right)⊠\cdots ⊠M_S\left({\zeta }_1,{\zeta }_1,{\zeta }_o,{\displaystyle \frac{\theta }{{\alpha }^{n+m-1}m}}\right).\hfill \end{array}$$

By (5), according to (4), we now have

$$\underset{n\to \infty }{lim}{M}_S({\zeta }_n,{\zeta }_n,{\zeta }_{n+m},\theta )\ge 1⊠1⊠\cdots ⊠1=1,$$

i.e., $\left\{{\zeta }_n\right\}$ is a Cauchy sequence. Consequently, it converges in the complete FS-MS. Let us indicate

$$\mathfrak{p}=\underset{n\to \infty }{lim}{\zeta }_n.$$

We will now demonstrate that $\mathfrak{p}$ is an FP of F. Thus, we have

$$\begin{array}{cc}\hfill M_S(F\mathfrak{p},F\mathfrak{p},\mathfrak{p},\theta )& \ge M_S\left(F\mathfrak{p},F\mathfrak{p},F{\zeta }_n,{\displaystyle \frac{\theta }{2}}\right)⊠M_S\left(F\mathfrak{p},F\mathfrak{p},F{\zeta }_n,{\displaystyle \frac{\theta }{2}}\right)⊠M_S\left(\mathfrak{p},\mathfrak{p},{\zeta }_n,{\displaystyle \frac{\theta }{2}}\right),\hfill \\ & \ge M_S\left(\mathfrak{p},\mathfrak{p},{\zeta }_n,{\displaystyle \frac{\theta }{2\alpha }}\right)⊠M_S\left(\mathfrak{p},\mathfrak{p},{\zeta }_n,{\displaystyle \frac{\theta }{2\alpha }}\right)⊠M_S\left(\mathfrak{p},\mathfrak{p},{\zeta }_n,{\displaystyle \frac{\theta }{2}}\right).\hfill \end{array}$$

Taking $n\to \infty$, we obtain

$$M_S(F\mathfrak{p},F\mathfrak{p},\mathfrak{p},\theta )\ge 1⊠1⊠1=1,$$

which implies that

$$M(F\mathfrak{p},F\mathfrak{p},\mathfrak{p},\theta )=1.$$

Thus, we can deduce that $\mathfrak{p}=F\mathfrak{p}$. It remains to be verified that $\mathfrak{p}$ is a unique FP of F. For this, let $w\in \Omega$ such that $w=Fw$. Then,

$$\begin{array}{cc}\hfill 1\ge M_S(w,w,\mathfrak{p},\theta )& =M_S(Fw,Fw,F\mathfrak{p},\theta )\ge M_S(w,w,y,{\displaystyle \frac{\theta }{\alpha }})=M_S\left(Fw,Fw,F\mathfrak{p},{\displaystyle \frac{\theta }{\alpha }}\right),\hfill \\ & \ge M_S\left(w,w,\mathfrak{p},{\displaystyle \frac{\theta }{{\alpha }^2}}\right)\ge \cdots \ge M_S(w,w,\mathfrak{p},{\displaystyle \frac{\theta }{{\alpha }^n}}),\hfill \end{array}$$

taking $n\to \infty$ we obtain

$$1\le M_S(w,w,\mathfrak{p},\theta )\le 1$$

which implies that $w=\mathfrak{p}$. This concludes the proof. □

This theorem in the framework of FS-MS extends classical results by generalizing the contraction mapping principle to a multi-point setting. Unlike traditional fixed-point theorems, which are primarily based on pairwise distances, this theorem introduces a new contraction condition incorporating three-point distance measures. This advancement is crucial for applications requiring a more flexible and robust structure, such as dynamic networks and fractal-based models.

Example 1.

The ordinary multiplication for every $a,b\in [0,1]$ is defined as $a⊠b=a·b$. Let $M_S$ be the function defined on $\Omega \times \Omega \times \Omega \times (0,\infty )$ by

$$M_S(\zeta ,\eta ,\gamma ,\theta )={\displaystyle \frac{\theta }{\theta +S(\zeta ,\eta ,\gamma )}},$$

for all $\zeta ,\eta ,\gamma \in \Omega$ and $\theta >0$. Then $(\Omega ,M_S,⊠)$ is an FS-MS called standard FS-MS, and $M_S$ is called the standard fuzzy S-metric induced by the S-metric. We only need to verify the triangle inequality, as the other properties are straightforward to check.

$$\begin{array}{cc}\hfill M_S(\zeta ,\zeta ,a,\theta )·M_S(\eta ,\eta ,a,u)·M_S(\gamma ,\gamma ,a,v)& ={\displaystyle \frac{\theta }{\theta +S(\zeta ,\zeta ,a)}}·{\displaystyle \frac{u}{u+S(\eta ,\eta ,a)}}·{\displaystyle \frac{v}{v+S(\gamma ,\gamma ,a)}}\hfill \\ & ={\displaystyle \frac{1}{1+\frac{S(\zeta ,\zeta ,a)}{\theta }}}·{\displaystyle \frac{1}{1+\frac{S(\eta ,\eta ,a)}{u}}}·{\displaystyle \frac{1}{1+\frac{S(\gamma ,\gamma ,a)}{v}}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{1+\frac{S(\zeta ,\zeta ,a)}{\theta +u+v}}}·{\displaystyle \frac{1}{1+\frac{S(\eta ,\eta ,a)}{\theta +u+v}}}·{\displaystyle \frac{1}{1+\frac{S(\gamma ,\gamma ,a)}{\theta +u+v}}}\hfill \\ & \le {\displaystyle \frac{1}{1+\frac{S(\zeta ,\zeta ,a)+S(\eta ,\eta ,a)+S(\gamma ,\gamma ,a)}{\theta +u+v}}}\hfill \\ & ={\displaystyle \frac{\theta +u+v}{\theta +u+v+S(\zeta ,\zeta ,a)+S(\eta ,\eta ,a)+S(\gamma ,\gamma ,a)}}\hfill \\ & \le {\displaystyle \frac{\theta +u+v}{\theta +u+v+S(\zeta ,\eta ,\gamma )}}\hfill \\ & =M_S(\zeta ,\eta ,\gamma ,\theta +u+v),\hfill \end{array}$$

for all $\zeta ,\eta ,\gamma \in \Omega$ and $\theta ,u,v>0$.

Example 2.

Let $\Omega =\mathbb{R}$; then, $S(\zeta ,\eta ,\gamma )=|\zeta -\gamma |+|\eta -\gamma |$ is an S-MS. Let $(\Omega ,M_S,⊠)$ be an FS-MS defined by

$$M_S(\zeta ,\eta ,\gamma ,\theta )={\displaystyle \frac{\theta }{\theta +S(\zeta ,\eta ,\gamma )}}.$$

Let $F:\Omega \to \Omega$ be a mapping defined by $F\left(\zeta \right)={\displaystyle \frac{1}{2}}\zeta$. We are going to show that F is a fuzzy S-contraction on Ω. We have

$$\begin{array}{cc}\hfill M_S(F\zeta ,F\zeta ,F\eta ,\alpha \theta )& ={\displaystyle \frac{\alpha \theta }{\alpha \theta +S(F\zeta ,F\zeta ,F\eta )}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +|F\zeta -F\eta |+|F\zeta -F\eta |}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}(|\zeta -\eta |+|\zeta -\eta |)}},\hfill \end{array}$$

and for $\alpha ={\displaystyle \frac{1}{2}}$, we obtain

$$\begin{array}{cc}\hfill M_S\left(F\zeta ,F\zeta ,F\eta ,{\displaystyle \frac{1}{2}}\theta \right)& ={\displaystyle \frac{\theta }{\theta +\left(\right|\zeta -\eta |+|\zeta -\eta \left|\right)}}\hfill \\ & ={\displaystyle \frac{\theta }{\theta +S(\zeta ,\zeta ,\eta )}}\hfill \\ & =M_S(\zeta ,\zeta ,\eta ,\theta ).\hfill \end{array}$$

Thus, F is a fuzzy S-contraction on Ω. So by Theorem (1), F has a unique FP which is $\zeta =0$.

3. Topology Induced by a Fuzzy S-Metric

Definition 6.

Let $(\Omega ,M_S,⊠)$ be an FS-MS. We define an open ball $B_S(\zeta ,\mathfrak{r},\theta )$ with center $\zeta \in \Omega$ and radius $\mathfrak{r}$, $0<\mathfrak{r}<1$ and $\theta >0$ as

$$B_S(\zeta ,\mathfrak{r},\theta )=\{\eta \in \Omega :M_S(\eta ,\eta ,\zeta ,\theta )>1-\mathfrak{r}\}.$$

Proposition 1.

Every open ball in an FS-MS is an open set.

Proof. 

Consider an open ball $B_S(\zeta ,\mathfrak{r},\theta )$. Now,

$$\eta \in B_S(\zeta ,\mathfrak{r},\theta )\Rightarrow M_S(\eta ,\eta ,\zeta ,\theta )>1-\mathfrak{r}.$$

Since $M_S(\eta ,\eta ,\zeta ,\theta )>1-\zeta$, we can find a ${\theta }_o$, $0<{\theta }_o<\theta$ such that

$M_S(\eta ,\eta ,\zeta ,{\theta }_o)>1-\mathfrak{r}$. Let ${\mathfrak{r}}_o=M_S(\eta ,\eta ,\zeta ,{\theta }_o)>1-\mathfrak{r}$. Since ${\mathfrak{r}}_o>1-\mathfrak{r}$, we may discover a $\mathfrak{s}$, $0<\mathfrak{s}<1$, s.t ${\mathfrak{r}}_o>1-\mathfrak{s}>1-\mathfrak{r}$. We can now find ${\mathfrak{r}}_1$, $0<{\mathfrak{r}}_1<1$ s.t ${\mathfrak{r}}_o⊠{\mathfrak{r}}_1⊠{\mathfrak{r}}_1\ge 1-\mathfrak{s}$ for a given ${\mathfrak{r}}_o$ and $\mathfrak{s}$ s.t ${\mathfrak{r}}_o>1-\mathfrak{s}$. The ball $B_S(\eta ,1-{\mathfrak{r}}_1,\theta -2{\theta }_o)$ is now being considered. We assert that

$$B_S(\eta ,1-{\mathfrak{r}}_1,\theta -2{\theta }_o)\subset B_S(\zeta ,\mathfrak{r},\theta ).$$

Now, let $\gamma \in B_S(\eta ,1-{\mathfrak{r}}_1,\theta -2{\theta }_o)\Rightarrow M_S(\gamma ,\gamma ,\eta ,\theta -2{\theta }_o)>{\mathfrak{r}}_1.$

Therefore,

$$\begin{array}{cc}\hfill M_S(\gamma ,\gamma ,\zeta ,\theta )& \ge M_S(\gamma ,\gamma ,\eta ,\theta -2{\theta }_o)⊠M_S(\gamma ,\gamma ,\eta ,{\theta }_o)⊠M_S(\zeta ,\zeta ,\eta ,{\theta }_o)\hfill \\ & \ge {\mathfrak{r}}_1⊠{\mathfrak{r}}_1⊠M_S(\eta ,\eta ,\zeta ,{\theta }_o)\hfill \\ & \ge {\mathfrak{r}}_1⊠{\mathfrak{r}}_1⊠{\mathfrak{r}}_o\hfill \\ & \ge 1-\mathfrak{s}\hfill \\ & >1-\mathfrak{r}.\hfill \end{array}$$

Therefore, $\gamma \in B_S(\zeta ,\mathfrak{r},\theta )$. Hence, $B_S(\eta ,1-{\mathfrak{r}}_1,\theta -2{\theta }_o)\subset B_S(\zeta ,\mathfrak{r},\theta )$. □

Result 1.

Let $(\Omega ,M_S,⊠)$ be an FS-MS. Define

$$\tau =\{U\subset \Omega :\zeta \in U\mathit{if}\mathit{and}\mathit{only}\mathit{if}\mathit{there}\mathit{exist}\theta >0\mathit{and}\mathfrak{r},0<\mathfrak{r}<1s.t{B}_S(\zeta ,\mathfrak{r},\theta )\subset U\}.$$

Then, τ is a topology on Ω.

Theorem 2.

Every FS-MS is Hausdorff.

Proof. 

Let $(\Omega ,M_S,⊠)$ be the given FS-MS. Let $\zeta ,\eta$ be the two distinct points of $\Omega$. Then, $0<M_S(\zeta ,\zeta ,\eta ,\theta )<1$. For some $\mathfrak{r}$, $0<\mathfrak{r}<1$, let $M_S(\zeta ,\zeta ,\eta ,\theta )=\mathfrak{r}$. We can find a ${\mathfrak{r}}_1$ s.t ${\mathfrak{r}}_1⊠{\mathfrak{r}}_1⊠{\mathfrak{r}}_1\ge {\mathfrak{r}}_o$ for each ${\mathfrak{r}}_o$, $\mathfrak{r}<{\mathfrak{r}}_o<1$. Now, consider the open balls $B_S(\zeta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta )$ and $B_S(\eta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta )$. Clearly,

$$B_S(\zeta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta )\cap B_S(\eta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta )=\varnothing .$$

If there exists

$$\gamma \in B_S(\zeta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta )\cap B_S(\eta ,1-{\mathfrak{r}}_1,{\displaystyle \frac{1}{3}}\theta ),$$

then

$$\begin{array}{cc}\hfill \mathfrak{r}& =M_S(\zeta ,\zeta ,\eta ,\theta )\hfill \\ & \ge M_S(\zeta ,\zeta ,\gamma ,{\displaystyle \frac{1}{3}}\theta )⊠M_S(\zeta ,\zeta ,\gamma ,{\displaystyle \frac{1}{3}}\theta )⊠M_S(\eta ,\eta ,\gamma ,{\displaystyle \frac{1}{3}}\theta )\hfill \\ & =M_S(\gamma ,\gamma ,\zeta ,{\displaystyle \frac{1}{3}}\theta )⊠M_S(\gamma ,\gamma ,\zeta ,{\displaystyle \frac{1}{3}}\theta )⊠M_S(\gamma ,\gamma ,\eta ,{\displaystyle \frac{1}{3}}\theta )\hfill \\ & \ge {\mathfrak{r}}_1⊠{\mathfrak{r}}_1⊠{\mathfrak{r}}_1>{\mathfrak{r}}_o\hfill \\ & >\mathfrak{r}\hfill \end{array}$$

which is a contradiction. Therefore, $(\Omega ,M_S,⊠)$ is a Hausdorff. □

Definition 7.

Let $(\Omega ,M_S,⊠)$ be an FS-MS and let τ be the topology induced by the FS-MS. The symbol $\mathfrak{C}(\Omega )$ will be used to indicate the collection of all compact subsets of Ω that are not empty. We define Hausdorff FS-MS ${\mathcal{H}}_S$, for $\mathcal{N},\mathcal{O},\mathcal{P}\in \mathfrak{C}(\Omega )$ as

$${\mathcal{H}}_S(\mathcal{N},\mathcal{O},\mathcal{P},\theta )=min\{D_S(\mathcal{N},\mathcal{O}),D_S(\mathcal{O},\mathcal{P}),D_S(\mathcal{P},\mathcal{N})\}.$$

where, $D_S(\mathcal{N},\mathcal{O})$= min$\{M_S(\mathcal{N},\mathcal{O},\mathcal{O},\theta ),M_S(\mathcal{O},\mathcal{N},\mathcal{N},\theta )\}.$

Thus, ${\mathcal{H}}_S$ is a Hausdorff fuzzy S-metric on $\mathfrak{C}(\Omega )$, making $(\mathfrak{C}(\Omega ),{\mathcal{H}}_S,⊠)$ a Hausdorff FS-MS. It should be noted that the Hausdorff FS-MS is complete, provided that the FS-MS $(\Omega ,M_S,⊠)$ is complete.

Lemma 2.

Let $F:\Omega \to \Omega$ be a fuzzy S-contraction on the FS-MS $(\Omega ,M_S,⊠)$. Then, $F:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ defined by

$$F\left(\mathcal{N}\right)=\left\{F\right(\mathfrak{x}):\mathfrak{x}\in \mathcal{N}\}\forall \mathcal{N}\in \mathfrak{C}(\Omega )$$

is a fuzzy S-contraction on $(\mathfrak{C}(\Omega ),{\mathcal{H}}_S,⊠)$.

Proof. 

Suppose $F:\Omega \to \Omega$ be a fuzzy S-contraction on the fuzzy S-metric space $(\Omega ,M_S,⊠)$. Then,

$$M_S(F\zeta ,F\zeta ,F\eta ,\alpha \theta )\ge M_S(\zeta ,\zeta ,\eta ,\theta ),$$

for all $\zeta ,\eta \in \Omega$, since $F:\Omega \to \Omega$ is a fuzzy S-contraction. So F maps $\mathfrak{C}(\Omega )$ into itself. We will demonstrate that $F:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ is a fuzzy S-contraction on $(\mathfrak{C}(\Omega ),{\mathcal{H}}_S,⊠)$. Let, for any $\mathcal{N},\mathcal{O}\in \mathfrak{C}(\Omega )$ and $\theta >0$, us have

$${\mathcal{H}}_S(F\mathcal{N},F\mathcal{N},F\mathcal{O},\alpha \theta )=min\{D_S(F\mathcal{N},F\mathcal{N}),D_S(F\mathcal{N},F\mathcal{O}),D_S(F\mathcal{O},F\mathcal{N})\}.$$

(6)

$$\begin{array}{cc}\hfill D_S(F\mathcal{N},F\mathcal{N})& =min\{mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(F\mathfrak{x},F\mathfrak{x},F\mathfrak{x},\alpha \theta ),mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(F\mathfrak{x},F\mathfrak{x},F\mathfrak{x},\alpha \theta )\}\hfill \\ & \ge min\{mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(\mathfrak{x},\mathfrak{x},\mathfrak{x},\theta ),mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(\mathfrak{x},\mathfrak{x},\mathfrak{x},\theta )\}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill D_S(F\mathcal{N},F\mathcal{O})& =min\{mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{y}\in \mathcal{O}}{M}_S(F\mathfrak{x},F\mathfrak{y},F\mathfrak{y},\alpha \theta ),mi{n}_{\mathfrak{y}\in \mathcal{O}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(F\mathfrak{y},F\mathfrak{x},F\mathfrak{x},\alpha \theta )\}\hfill \\ & \ge min\{mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{y}\in \mathcal{O}}{M}_S(\mathfrak{x},\mathfrak{y},\mathfrak{y},\theta ),mi{n}_{\mathfrak{y}\in \mathcal{O}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(\mathfrak{y},\mathfrak{x},\mathfrak{x},\theta )\}.\hfill \end{array}$$

Similarly,

$$\begin{array}{c}\hfill D_S(F\mathcal{O},F\mathcal{N})\ge min\{mi{n}_{\mathfrak{y}\in \mathcal{O}}ma{x}_{\mathfrak{x}\in \mathcal{N}}{M}_S(\mathfrak{y},\mathfrak{x},\mathfrak{x},\theta ),mi{n}_{\mathfrak{x}\in \mathcal{N}}ma{x}_{\mathfrak{y}\in \mathcal{O}}{M}_S(\mathfrak{x},\mathfrak{y},\mathfrak{y},\theta )\}.\end{array}$$

Equation (6) implies that

$${\mathcal{H}}_S(F\mathcal{N},F\mathcal{N},F\mathcal{O},\alpha \theta )\ge {\mathcal{H}}_S(\mathcal{N},\mathcal{N},\mathcal{O},\theta ).$$

Thus, $F:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ is a fuzzy S-contraction on $(\mathfrak{C}(\Omega ),{\mathcal{H}}_S,⊠)$. □

Definition 8.

Let $(\Omega ,M_S,⊠)$ be an FS-MS and $\{F_i:\Omega \to \Omega :i=1,2,3,\cdots ,N\}$ be a family of fuzzy S-contractions. The operator $W:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ defined by

$$W\left(\mathcal{M}\right)=\bigcup _{i=1}^N{F}_i\left(\mathcal{M}\right),$$

for all $\mathcal{M}\in \mathfrak{C}(\Omega )$, is a fuzzy S-Hutchinson–Barnsley (S-H-B) operator.

Definition 9.

Let $(\Omega ,M_S,⊠)$ be a complete FS-MS and $\{F_i:\Omega \to \Omega :i=1,2,3,\cdots ,N\}$ be fuzzy S-contractions; then, $(\Omega ,F_1,F_2,F_3,\cdots ,F_N)$ is called a fuzzy S-iterated function system (S-IFS).

Definition 10.

A compact non-empty set $\mathcal{A}$ is considered an attractor of fuzzy S-IFS if it satisfies $\mathcal{A}=W\left(\mathcal{A}\right)={\bigcup }_{i=1}^N{F}_i\left(\mathcal{A}\right)$ and can be expressed as $\mathcal{A}={lim}_{n\to \infty }{W}^n\left(\mathcal{B}\right)$ where $\mathcal{B}\in \mathfrak{C}(\Omega )$.

Theorem 3.

Let $(\Omega ,M_S,⊠)$ be an FS-MS and $\{F_i:\Omega \to \Omega :i=1,2,3,\cdots ,N\}$ be a family of fuzzy S-contraction. The operator $W:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ is defined by

$$W\left(\mathcal{M}\right)=\bigcup _{i=1}^N{F}_i\left(\mathcal{M}\right),$$

for all $\mathcal{M}\in \mathfrak{C}(\Omega )$. Then, W is fuzzy S-contraction on $\mathfrak{C}(\Omega )$.

Proof. 

Proving the statement for $N=2$ is sufficient. Let $F_1,F_1:\Omega \to \Omega$ be two fuzzy S-contractions. So, $F_1$ and $F_1$ will map $\mathfrak{C}(\Omega )$ into itself. Take $\mathcal{N},\mathcal{O}\in \mathfrak{C}(\Omega )$ with ${\mathcal{H}}_S\left(W\left(\mathcal{N}\right),W\left(\mathcal{N}\right),W\left(\mathcal{O}\right),\theta \right)\ne 0$ and $\theta >0$. Then, lemma (2) makes it clear that

$$\begin{array}{cc}\hfill {\mathcal{H}}_S\left(W\left(\mathcal{N}\right),W\left(\mathcal{N}\right),W\left(\mathcal{O}\right),\alpha \theta \right)& ={\mathcal{H}}_S\left((F_1\cup F_2)\left(\mathcal{N}\right),(F_1\cup F_2)\left(\mathcal{N}\right),(F_1\cup F_2)\left(\mathcal{O}\right),\alpha \theta \right)\hfill \\ \hfill & \ge min\left\{\begin{array}{c}{\mathcal{H}}_S\left(F_1\left(\mathcal{N}\right),F_1\left(\mathcal{N}\right),F_1\left(\mathcal{O}\right),\alpha \theta \right)\\ {\mathcal{H}}_S\left(F_2\left(\mathcal{N}\right),F_2\left(\mathcal{N}\right),F_2\left(\mathcal{O}\right),\alpha \theta \right)\end{array}\right\},\hfill \\ \hfill & \ge min\{{\mathcal{H}}_S(\mathcal{N},\mathcal{N},\mathcal{O},\theta ),{\mathcal{H}}_S(\mathcal{N},\mathcal{N},\mathcal{O},\theta )\}\hfill \\ & ={\mathcal{H}}_S(\mathcal{N},\mathcal{N},\mathcal{O},\theta ).\hfill \end{array}$$

Similarly, it can be proven for any natural number N.

Hence, W is fuzzy S-contraction on $\mathfrak{C}(\Omega )$. □

Theorem 4.

Let $(\Omega ,M_S,⊠)$ be a complete FS-MS and $\{F_i:\Omega \to \Omega :i=1,2,3,\cdots ,N\}$ be a family of fuzzy S-contractions. The operator $W:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$, which is defined by

$$W\left(\mathcal{M}\right)=\bigcup _{i=1}^N{F}_i\left(\mathcal{M}\right),$$

for all $\mathcal{M}\in \mathfrak{C}(\Omega )$. Then, W has a unique fixed $\mathcal{A}\in \mathfrak{C}(\Omega )$, i.e., $\mathcal{A}=W\left(\mathcal{A}\right)$.

Proof. 

From Theorem 3, $W:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ is a fuzzy S-contraction on $\mathfrak{C}(\Omega )$. Also, $(\mathfrak{C}(\Omega ),{\mathcal{H}}_S,⊠)$ is a complete FS-MS, as implied by the completeness of $(\Omega ,M_S,⊠)$. Thus, by Theorem 1, W has a unique FP $\mathcal{A}\in \mathfrak{C}(\Omega )$, i.e., $\mathcal{A}=W\left(\mathcal{A}\right)$. □

Example 3.

Let $\Omega ={\mathbb{R}}^2$; then, $S(\zeta ,\eta ,\gamma )=\left|\right|\zeta -\gamma \left|\right|+\left|\right|\eta -\gamma \left|\right|$ is an S-MS, and $\left|\right|·\left|\right|$ denotes the Euclidean norm on ${\mathbb{R}}^2.$ Let $(\Omega ,M_S,⊠)$ be an FS-MS defined by

$$M_S(\zeta ,\eta ,\gamma ,\theta )={\displaystyle \frac{\theta }{\theta +S(\zeta ,\eta ,\gamma )}}.$$

Let $F_1,F_2,F_3:\Omega \to \Omega$, defined by

$F_1(\zeta ,\eta )=({\displaystyle \frac{\zeta }{2}},{\displaystyle \frac{\eta }{2}}),F_2(\zeta ,\eta )=({\displaystyle \frac{\zeta }{2}}+{\displaystyle \frac{1}{2}},{\displaystyle \frac{\eta }{2}}),$ and $F_3(\zeta ,\eta )=({\displaystyle \frac{\zeta }{2}}+{\displaystyle \frac{1}{4}},{\displaystyle \frac{\eta }{2}}+{\displaystyle \frac{\sqrt{3}}{4}})$.

We are going to show that $F_1,F_2$ and $F_3$ are fuzzy S-contractions on Ω .

$$\begin{array}{cc}\hfill M_S(F_1\zeta ,F_1\zeta ,F_1\eta ,\alpha \theta )& ={\displaystyle \frac{\alpha \theta }{\alpha \theta +S(F_1\zeta ,F_1\zeta ,F_1\eta )}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\left||F_1\zeta -F_1\eta |\right|+\left||F_1\zeta -F_1\eta |\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\right|\zeta -\eta \left|\right|+\left|\right|\zeta -\eta \left|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}S(\zeta ,\zeta ,\eta )}},\hfill \end{array}$$

for $\alpha ={\displaystyle \frac{1}{2}}$ we obtain $M_S(F_1\zeta ,F_1\zeta ,F_1\eta ,{\displaystyle \frac{1}{2}}\theta )={\displaystyle \frac{\theta }{\theta +S(\zeta ,\zeta ,\eta )}}=M_S(\zeta ,\zeta ,\eta ,\theta )$. Thus, $F_1$ is a fuzzy S-contraction on Ω. Now, consider

$$\begin{array}{cc}\hfill M_S(F_2\zeta ,F_2\zeta ,F_2\eta ,\alpha \theta )& ={\displaystyle \frac{\alpha \theta }{\alpha \theta +S(F_2\zeta ,F_2\zeta ,F_2\eta )}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\left||F_2\zeta -F_2\eta |\right|+\left||F_2\zeta -F_2\eta |\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\left||(\frac{{\zeta }_1}{2}+\frac{1}{2},\frac{{\eta }_1}{2})-(\frac{{\zeta }_2}{2}+\frac{1}{2},\frac{{\eta }_2}{2})|\right|+\left||(\frac{{\zeta }_1}{2}+\frac{1}{2},\frac{{\eta }_1}{2})-(\frac{{\zeta }_2}{2}+\frac{1}{2},\frac{{\eta }_2}{2})|\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\right|\zeta -\eta \left|\right|+\left|\right|\zeta -\eta \left|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}S(\zeta ,\zeta ,\eta )}},\hfill \end{array}$$

for $\alpha ={\displaystyle \frac{1}{2}}$, we obtain

$$\begin{array}{cc}\hfill M_S(F_2\zeta ,F_2\zeta ,F_2\eta ,{\displaystyle \frac{1}{2}}\theta )& ={\displaystyle \frac{\theta }{\theta +S(\zeta ,\zeta ,\eta )}}\hfill \\ & =M_S(\zeta ,\zeta ,\eta ,\theta ).\hfill \end{array}$$

Thus, $F_2$ is a fuzzy S-contraction on Ω.

And similarly,

$$\begin{array}{cc}\hfill M_S(F_3\zeta ,F_3\zeta ,F_3\eta ,\alpha \theta )& ={\displaystyle \frac{\alpha \theta }{\alpha \theta +S(F_3\zeta ,F_3\zeta ,F3\eta )}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\left||F_3\zeta -F_3\eta |\right|+\left||F_3\zeta -F_3\eta |\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2\left||(\frac{{\zeta }_1}{2}+\frac{1}{4},\frac{{\eta }_1}{2}+\frac{\sqrt{3}}{4})-(\frac{{\zeta }_2}{2}+\frac{1}{4},\frac{{\eta }_2}{2}+\frac{\sqrt{3}}{4})|\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\frac{1}{2}\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|+\left|\left|({\zeta }_1-{\zeta }_2,{\eta }_1-{\eta }_2)\right|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}\left(\left|\right|\zeta -\eta \left|\right|+\left|\right|\zeta -\eta \left|\right|\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{1}{2}S(\zeta ,\zeta ,\eta )}},\hfill \end{array}$$

for $\alpha ={\displaystyle \frac{1}{2}}$, we obtain

$$\begin{array}{cc}\hfill M_S(F_3\zeta ,F_3\zeta ,F_3\eta ,{\displaystyle \frac{1}{2}}\theta )& ={\displaystyle \frac{\theta }{\theta +S(\zeta ,\zeta ,\eta )}}\hfill \\ & =M_S(\zeta ,\zeta ,\eta ,\theta ).\hfill \end{array}$$

Thus, $F_1,F_2,F_3$ are a fuzzy S-contractions on Ω.

Consider the S-IFS $\{X,F_1,F_2,F_3\}$ with the mapping $W:\mathfrak{C}(\Omega )\to \mathfrak{C}(\Omega )$ given as

$$W\left(\mathcal{U}\right)=\bigcup _{i=1}^3{F}_i\left(\mathcal{U}\right),$$

for all $\mathcal{U}\in \mathfrak{C}\left({\mathbb{R}}^2\right)$. Then, by Theorem 3,

$${\mathcal{H}}_S\left(W\left(\mathcal{N}\right),W\left(\mathcal{N}\right),W\left(\mathcal{O}\right),\alpha \theta \right)\ge {\mathcal{H}}_S(\mathcal{N},\mathcal{N},\mathcal{O},\theta ).$$

Additionally, for any initial set ${\mathcal{L}}_o\in \mathfrak{C}\left({\mathbb{R}}^2\right)$, the sequence of compact set $\{{\mathcal{L}}_o,W\left({\mathcal{L}}_o\right),W^2\left({\mathcal{L}}_o\right),\cdots \}$ is convergent, i.e., $\mathcal{A}={lim}_{n\to \infty }{W}^n\left({\mathcal{L}}_o\right)$.

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 shows how W converges to the IFS attractor in the example.

Figure 1. ${\mathcal{L}}_o$.

Figure 2. $W\left({\mathcal{L}}_o\right)$.

Figure 3. $W^2\left({\mathcal{L}}_o\right)$.

Figure 4. $W^3\left({\mathcal{L}}_o\right)$.

Figure 5. $W^4\left({\mathcal{L}}_o\right)$.

4. Application to a Satellite Web Coupling Problem

Fixed-point theory has found numerous applications in various fields, including optimization, control systems, and nonlinear analysis. One emerging application is in satellite web coupling, which involves optimizing and stabilizing satellite networks for communication, navigation, and remote sensing. Recent studies have shown that fixed-point principles can play a crucial role in designing algorithms for satellite trajectory optimization and inter-satellite link stability [22,23,24,25,26,27,28].

Inspired by the use of FP approaches in several real-world scenarios, we apply Theorem 1 to solve a satellite web coupling boundary value problem. A thin sheet joining two cylindrical satellites might be thought of as a satellite web connection. The radiation problem brought on by the web coupling between two satellites leads to the following non-linear boundary value problem:

$$-{\displaystyle \frac{d^2\mathfrak{w}}{d{\kappa }^2}}=\mu {\mathfrak{w}}^4,0<\kappa <1,\mathfrak{w}\left(0\right)=\mathfrak{w}\left(1\right)=0,$$

(7)

where $\mathfrak{w}\left(\kappa \right)$ represents the radiation temperature at any given position $\kappa \in [0,1],$$\mu ={\displaystyle \frac{2a{\mathfrak{l}}^2{K}^3}{\xi h}}>0$ is a positive, non-dimensional constant, whereas heat is emitted into space from the web’s surface at a temperature of zero. The constant absolute temperature of both satellites is denoted by K. $\mathfrak{l}$ separates the two satellites, a is a positive constant that characterizes the radiation properties of the web’s surface, the factor 2 is required since radiation originates from both the top and bottom surfaces, $\xi$ is thermal conductivity, and h is the thickness.

The Green function

$$\mathfrak{G}(\kappa ,\xi )=\left\{\begin{array}{cc}\kappa (1-\xi ),\hfill & 0<\kappa <\xi ,\hfill \\ \xi (1-\kappa ),\hfill & \xi <\kappa <1.\hfill \end{array}\right.$$

Problem (7) is equivalent to

$$\begin{array}{c}\hfill \mathfrak{w}\left(\kappa \right)=1-\mu {\int }_0^1\mathfrak{G}(\kappa ,\xi ){\mathfrak{w}}^4\left(\xi \right)d\xi .\end{array}$$

Let $\Omega =\mathcal{R}[0,1]$ be a collection of functions on $[0,1]$ that are Riemann-integrable. Define an S-MS $S:\Omega \times \Omega \times \Omega \to {\mathbb{R}}^{+}$ by $S(\mathfrak{w},\mathfrak{u},\mathfrak{v})=|\mathfrak{w}-\mathfrak{v}|+|\mathfrak{u}-\mathfrak{v}|$. Clearly, $(\Omega ,S)$ is a complete S-MS, and ${\left|\left|\mathfrak{w}\right|\right|}_{\infty }=su{p}_{\kappa \in [0,1]}\left|\mathfrak{w}\left(\kappa \right)\right|$. Then $(\Omega ,M_S,⊠)$ is an FS-MS defined by

$$M_S(\mathfrak{w},\mathfrak{u},\mathfrak{v},\theta )={\displaystyle \frac{\theta }{\theta +S(\mathfrak{w},\mathfrak{u},\mathfrak{v})}},$$

and clearly, $(\Omega ,M_S,⊠)$ is a complete FS-MS as implied by the completeness of $(\Omega ,S)$.

Theorem 5.

Let $F:\Omega \to \Omega$ be a self map in a complete FS-MS $(\Omega ,M_S,⊠)$, satisfying

$${\left||\mathfrak{w}\left(\kappa \right)-\mathfrak{v}\left(\kappa \right)|\right|}_{\infty }>0\Rightarrow {\left|\left|({\mathfrak{w}}^2\left(\xi \right)+{\mathfrak{v}}^2\left(\xi \right))(\mathfrak{w}\left(\xi \right)+\mathfrak{w}\left(\xi \right))\right|\right|}_{\infty }\le {\displaystyle \frac{\mathfrak{k}}{\mu }},\mathfrak{k}\in (0,8).$$

(8)

Then, there is a unique solution to the satellite web coupling boundary value problem (7).

Proof. 

Define a self map $F:\Omega \to \Omega$ by

$$F\mathfrak{w}\left(\kappa \right)=1-\mu {\int }_0^1\mathfrak{G}(\kappa ,\xi ){\mathfrak{w}}^4\left(\xi \right)d\xi ,\xi \in [0,1].$$

A fixed point of a self map F is obviously a solution to the satellite web coupling problem (7).

Now,

$$\begin{array}{cc}\hfill & M_S(F\mathfrak{w}\left(\kappa \right),F\mathfrak{w}\left(\kappa \right),F\mathfrak{v}\left(\kappa \right),\alpha \theta )\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +S\left(F\mathfrak{w}\right(\kappa ),F\mathfrak{w}(\kappa ),F\mathfrak{v}(\kappa \left)\right)}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2\left|F\mathfrak{w}\right(\kappa )-F\mathfrak{v}(\kappa \left)\right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2|1-\mu {\int }_0^1\mathfrak{G}(\kappa ,\xi ){\mathfrak{w}}^4\left(\xi \right)d\xi -1+\mu {\int }_0^1\mathfrak{G}(\kappa ,\xi ){\mathfrak{v}}^4\left(\xi \right)d\xi |}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2\mu \left|{\int }_0^1\left({\mathfrak{v}}^4\left(\xi \right)-{\mathfrak{w}}^4\left(\xi \right)\right)\mathfrak{G}(\kappa ,\xi )d\xi \right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2\mu \left|{\int }_0^1\left({\mathfrak{v}}^2\left(\xi \right)+{\mathfrak{w}}^2\left(\xi \right)\right)\left(\mathfrak{v}\left(\xi \right)+\mathfrak{w}\left(\xi \right)\right)\left(\mathfrak{v}\left(\xi \right)-\mathfrak{w}\left(\xi \right)\right)\mathfrak{G}(\kappa ,\xi )d\xi \right|}}\hfill \\ & ={\displaystyle \frac{\alpha \theta }{\alpha \theta +2\mu {\left||\mathfrak{w}\left(\kappa \right)-\mathfrak{v}\left(\kappa \right)|\right|}_{\infty }{\left|\left|\left({\mathfrak{w}}^2\left(\kappa \right)+{\mathfrak{v}}^2\left(\kappa \right)\right)\left(\mathfrak{w}\left(\kappa \right)+\mathfrak{v}\left(\kappa \right)\right)\right|\right|}_{\infty }{\int }_0^1\mathfrak{G}(\kappa ,\xi )d\xi }}\hfill \\ & \ge {\displaystyle \frac{\alpha \theta }{\alpha \theta +2\mathfrak{k}{\left||\mathfrak{w}\left(\kappa \right)-\mathfrak{v}\left(\kappa \right)|\right|}_{\infty }\left[{\int }_0^{\kappa }\xi (1-\kappa )d\xi +{\int }_{\kappa }^1\kappa (1-\xi )d\xi \right]}}\hfill \\ & \ge {\displaystyle \frac{\alpha \theta }{\alpha \theta +\frac{\mathfrak{k}}{8}{\left||\mathfrak{w}\left(\kappa \right)-\mathfrak{v}\left(\kappa \right)|\right|}_{\infty }}},\hfill \end{array}$$

for $\alpha ={\displaystyle \frac{\mathfrak{k}}{8}}$ we obtain

$$\begin{array}{cc}\hfill M_S\left(F\mathfrak{w}\left(\kappa \right),F\mathfrak{w}\left(\kappa \right),F\mathfrak{v}\left(\kappa \right),{\displaystyle \frac{\mathfrak{k}}{8}}\theta \right)& \ge {\displaystyle \frac{\theta }{\theta +{\left||\mathfrak{w}\left(\kappa \right)-\mathfrak{v}\left(\kappa \right)|\right|}_{\infty }}}\hfill \\ & ={\displaystyle \frac{\theta }{\theta +S\left(\mathfrak{w}\right(\kappa ),\mathfrak{w}(\kappa ),\mathfrak{v}(\kappa \left)\right)}}\hfill \\ & =M_S(\mathfrak{w}\left(\kappa \right),\mathfrak{w}\left(\kappa \right),\mathfrak{v}\left(\kappa \right),\theta ).\hfill \end{array}$$

Therefore, Theorem 1 postulates are all verified. Because of this, F has a unique FP, and there is a unique solution to the satellite web coupling problem (7). □

Remark 1.

Theorems 1–5 establish key results in fuzzy S-metric spaces (FS-MS) by proving the existence and uniqueness of fixed points for fuzzy S-contractions. Theorem 1 ensures a unique fixed point for a single fuzzy S-contraction, while Theorems 3 and 4 extend this to a family of such contractions, demonstrating the contraction property and the existence of a unique fixed point in a complete FS-MS. Theorem 2 guarantees the Hausdorff property of FS-MS, supporting the validity of these results. Finally, Theorem 5 applies the fuzzy S-contraction framework to a boundary value problem, highlighting its significance in applied mathematics.

5. Conclusions

In this study, we introduced the concept of fuzzy S-metric spaces and explored their fundamental characteristics. By establishing a fixed-point theorem for self-mappings on complete fuzzy S-metric spaces, we provided a significant theoretical contribution to the field. To illustrate the versatility and applicability of our results, we presented examples demonstrating how fuzzy S-contractions can be effectively employed in fractal generation via iterated function systems under varying contractive conditions. Additionally, we applied our framework to solve the satellite web coupling problem, highlighting its potential for addressing complex, real-world challenges. These findings not only extend the scope of fuzzy metric spaces but also pave the way for future research and innovative applications in fuzzy systems, optimization, and nonlinear analysis.