Fractal Characteristics of Wind Speed Time Series Under Typhoon Climate in Southeastern China
Abstract
:1. Introduction
2. Data Sources and Processing
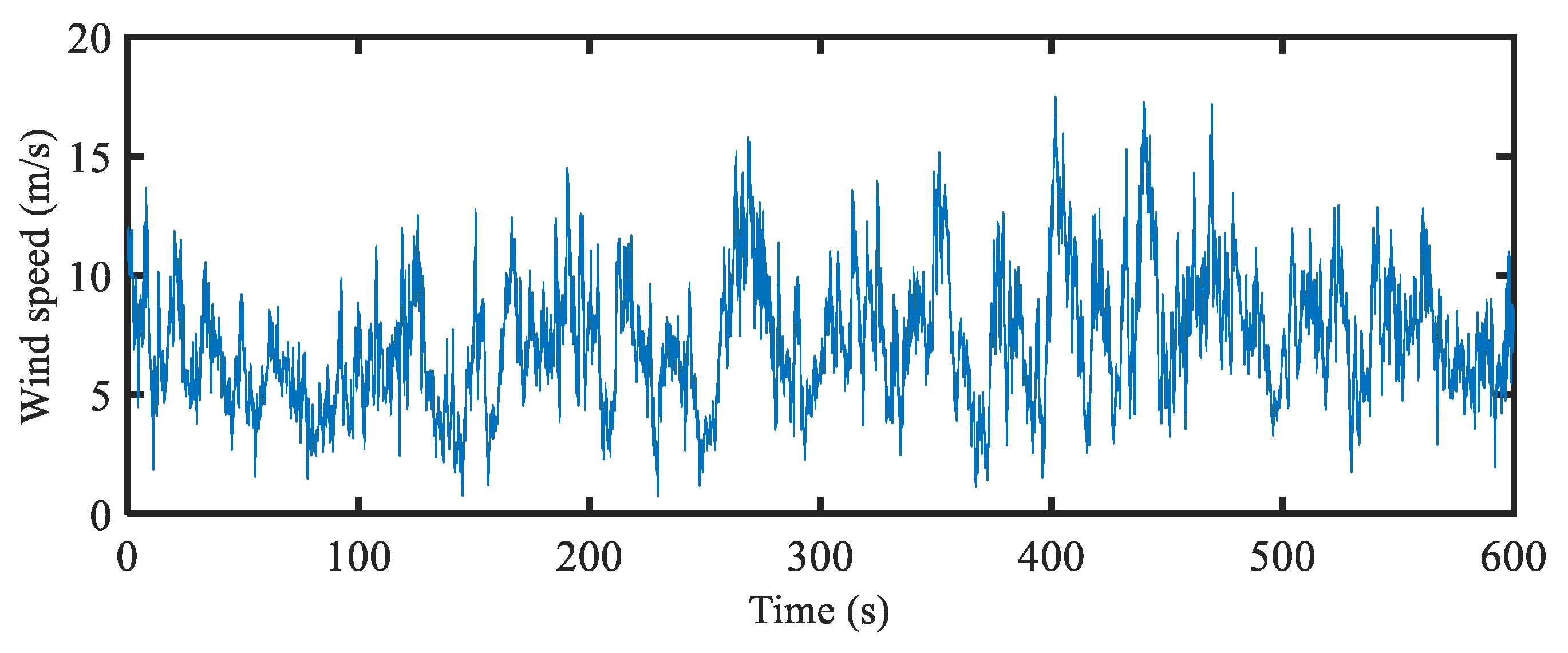
2.1. Experiment Site and Instruments
2.2. Data Control and Filtering
3. Fractal Analysis
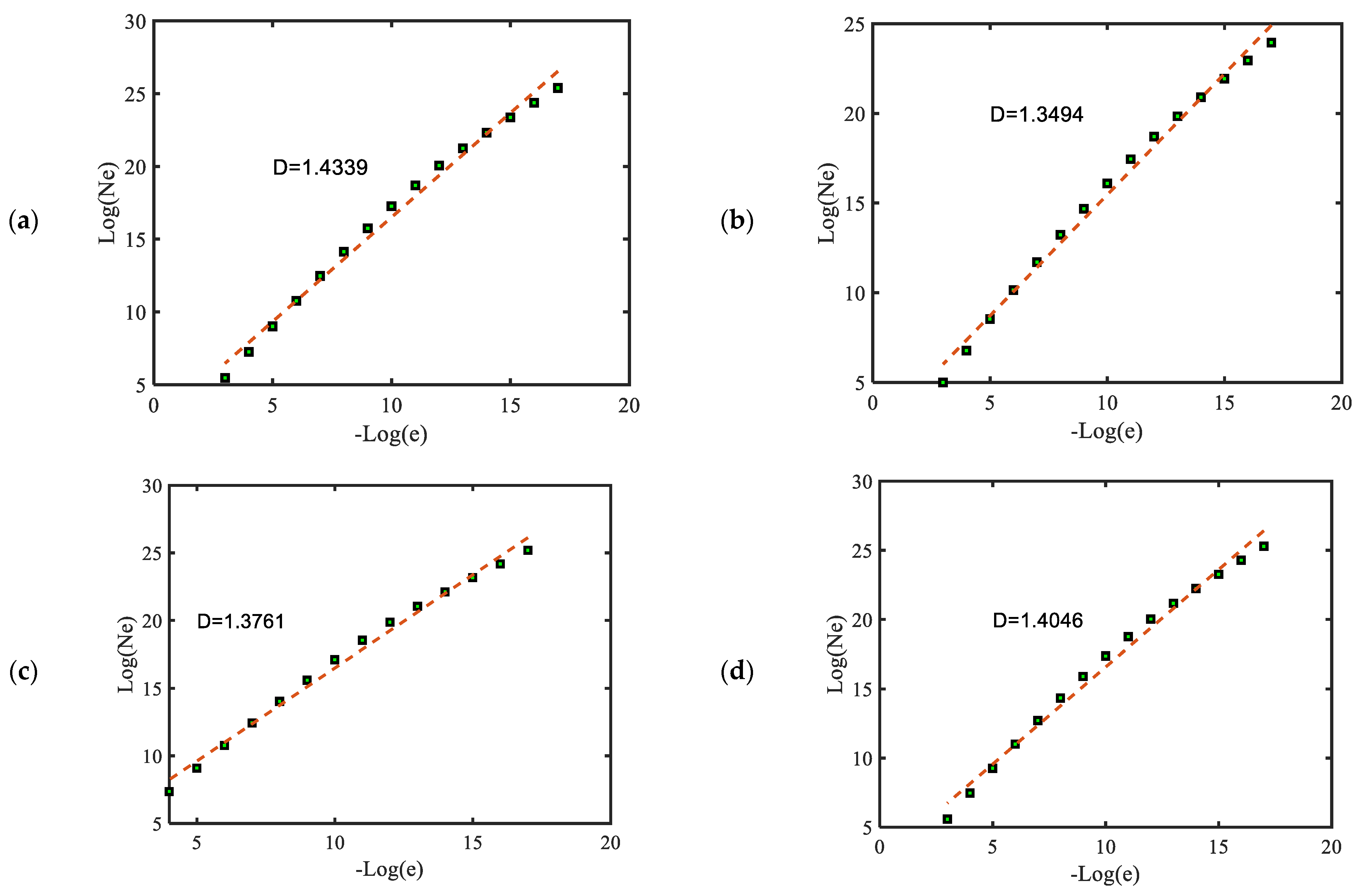
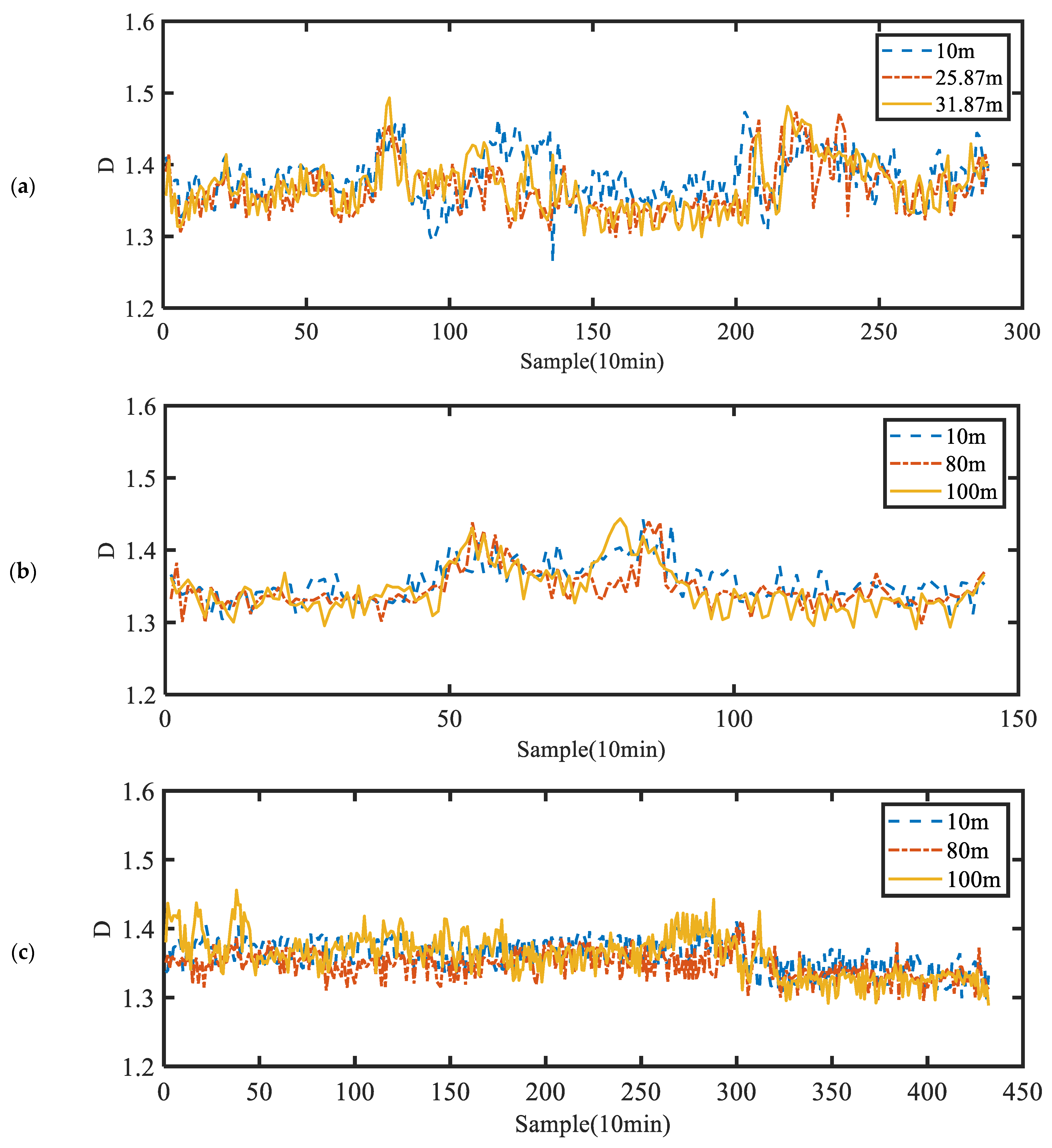
3.1. Box-Counting Method
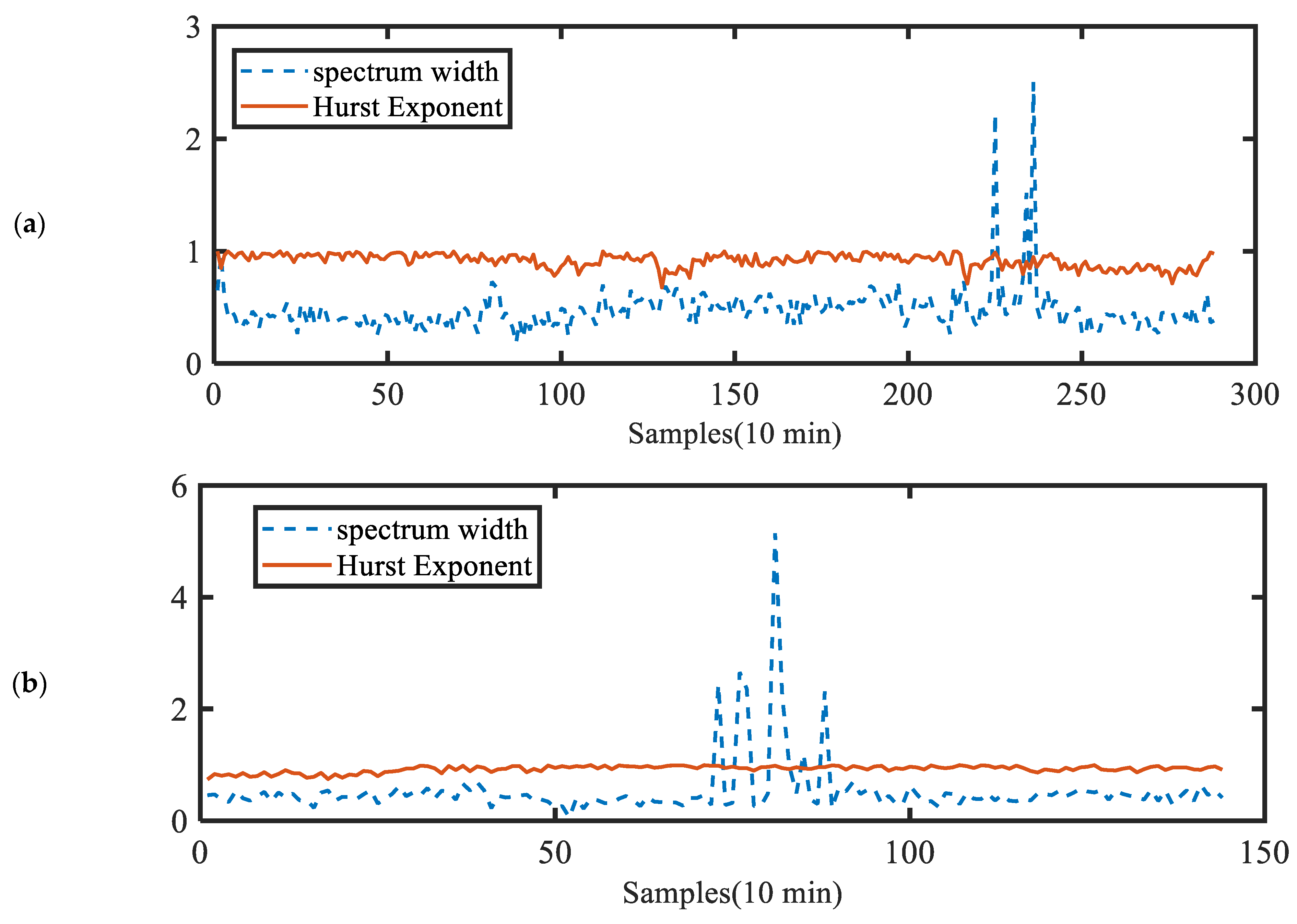
- When H = 0.5 and the fractal dimension D is 1.5, the wind speed series is random and unpredictable. This is called a Brownian time series or a random walk. Time series with such characteristics are often considered white noise.
- When 0 < H < 0.5, the fractal dimension is larger than 1.5, and the wind speed series shows anti-persistence, indicating that the wind speeds have a long-term negative autocorrelation and long-term conversion between high and low in the future.
- When 0.5 < H < 1.0, the fractal dimension is between 1 and 1.5, the wind speeds have a long-term positive autocorrelation, and there is another high value for a long period of time.
- When H = 1, the fractal dimension equals 1, indicating that the wind speed is strongly predictable.
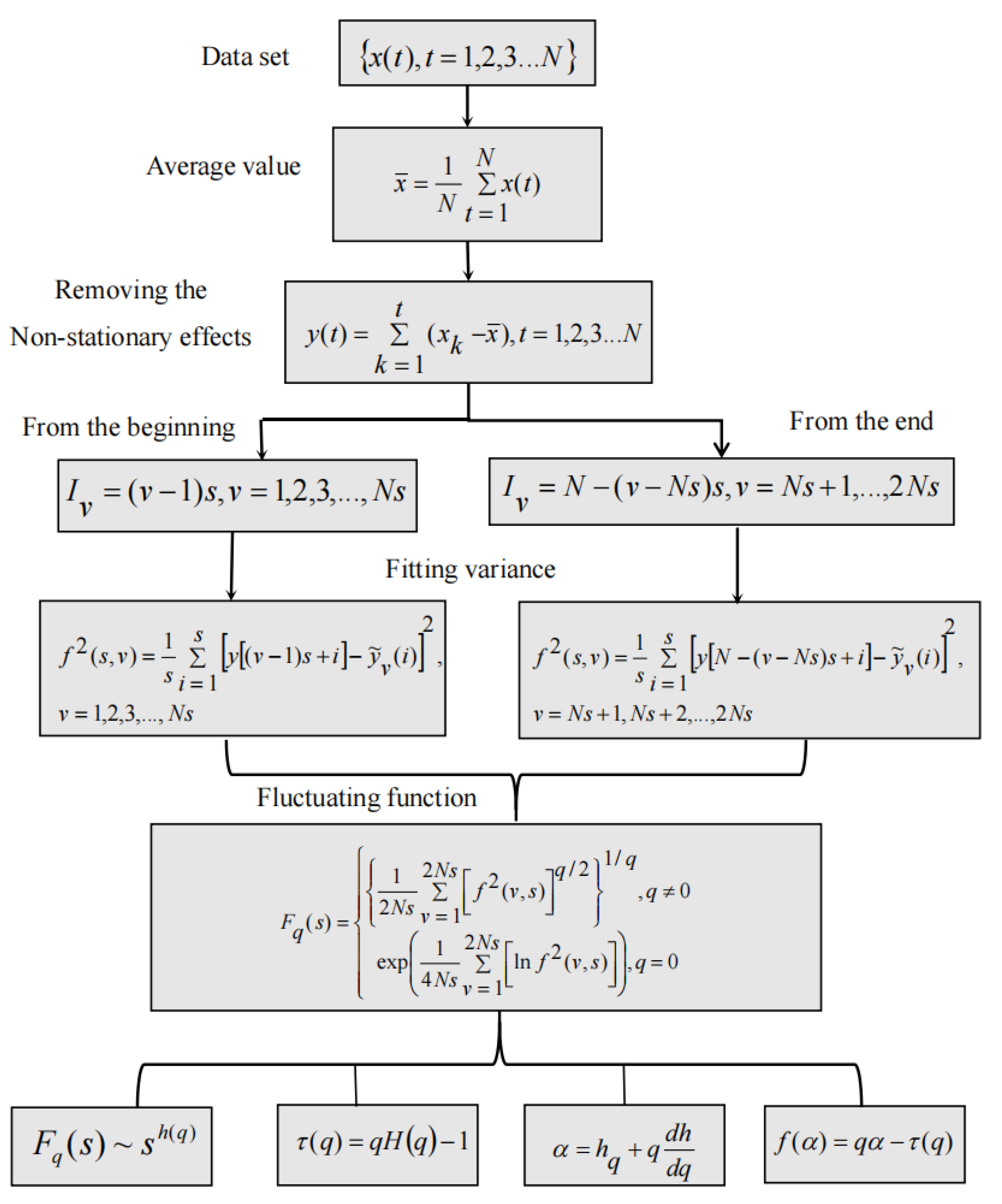
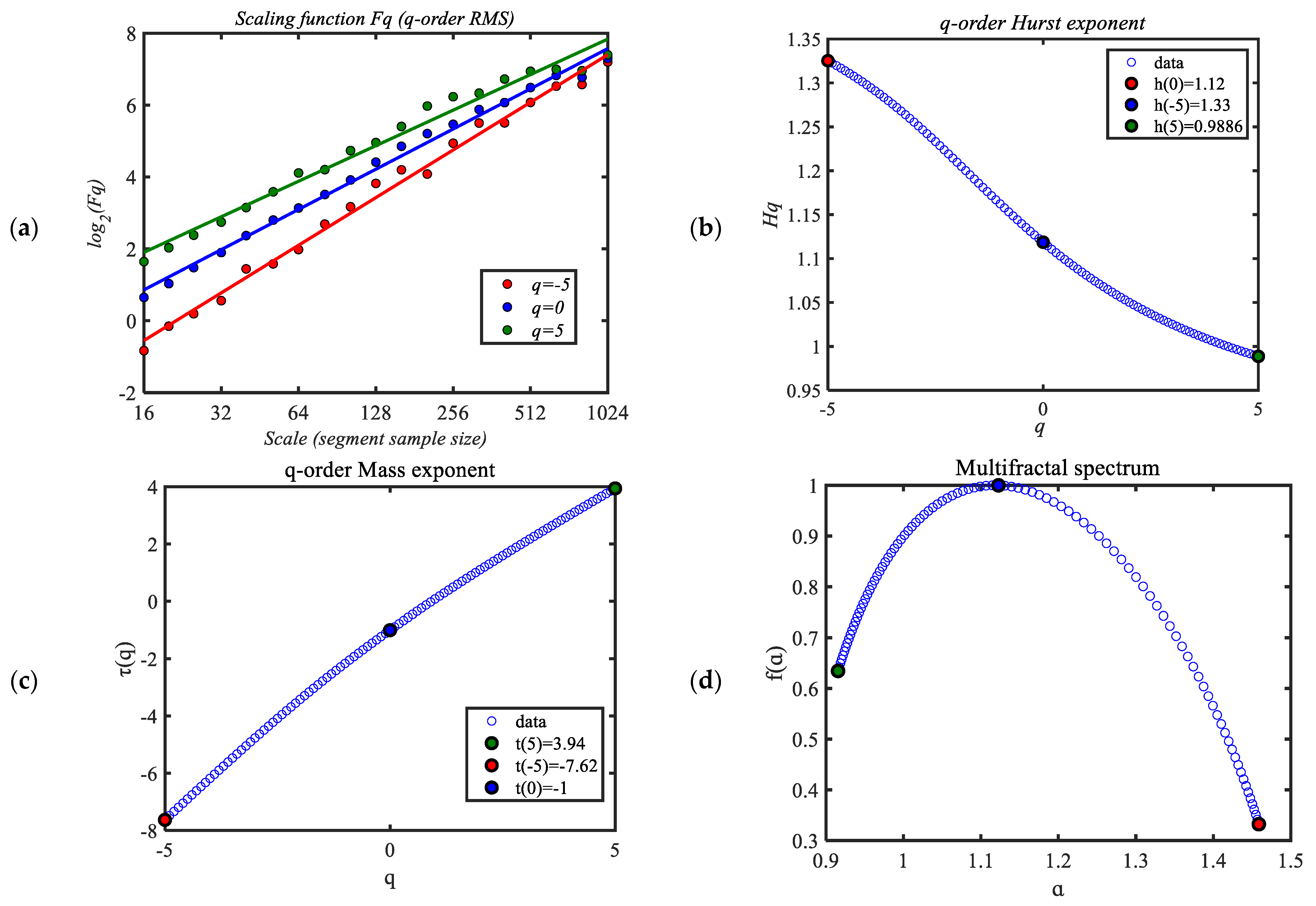
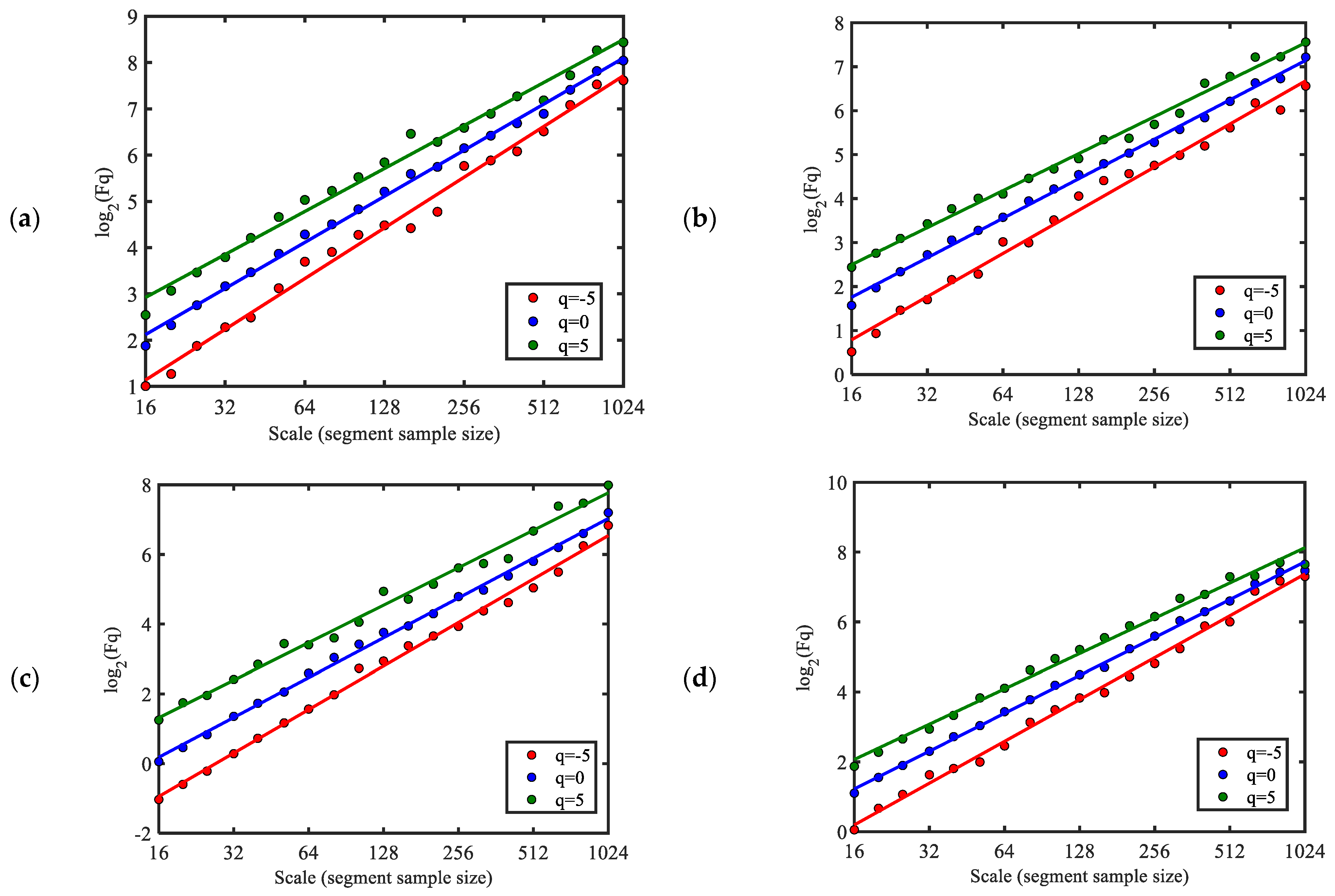
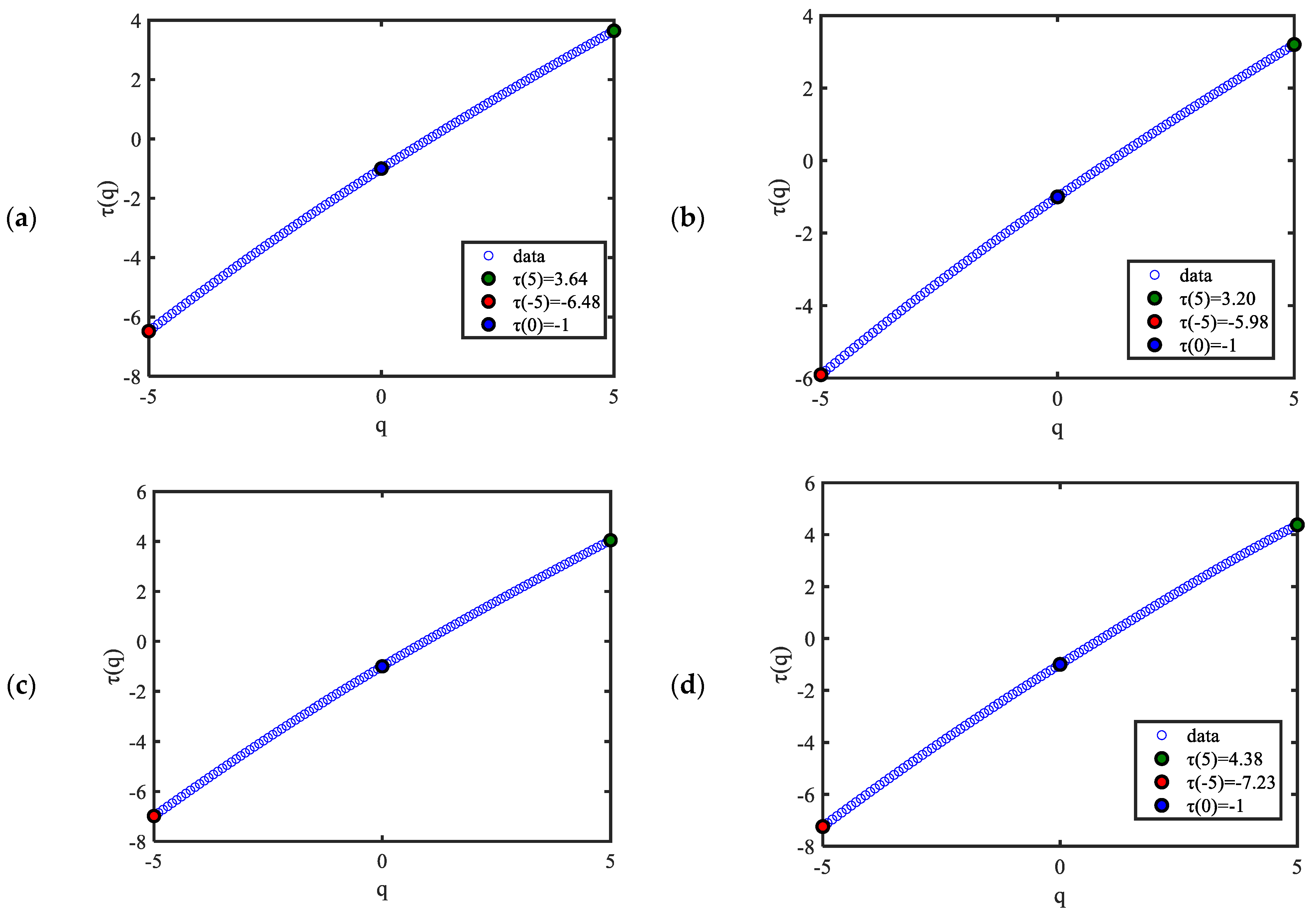
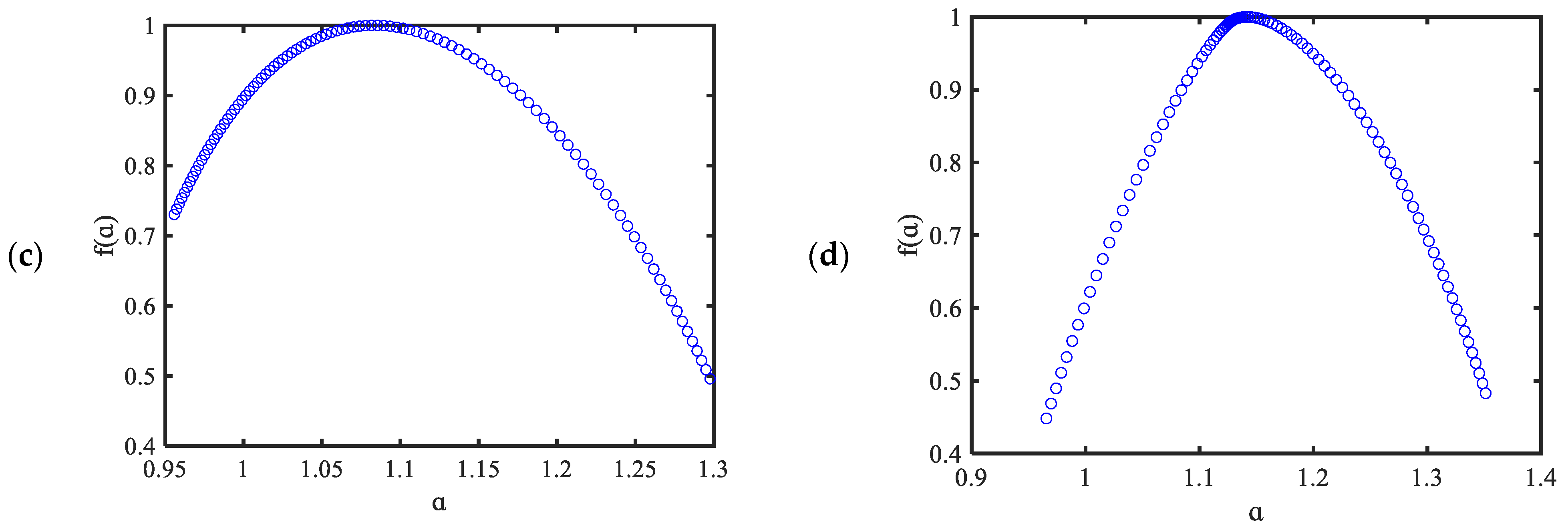
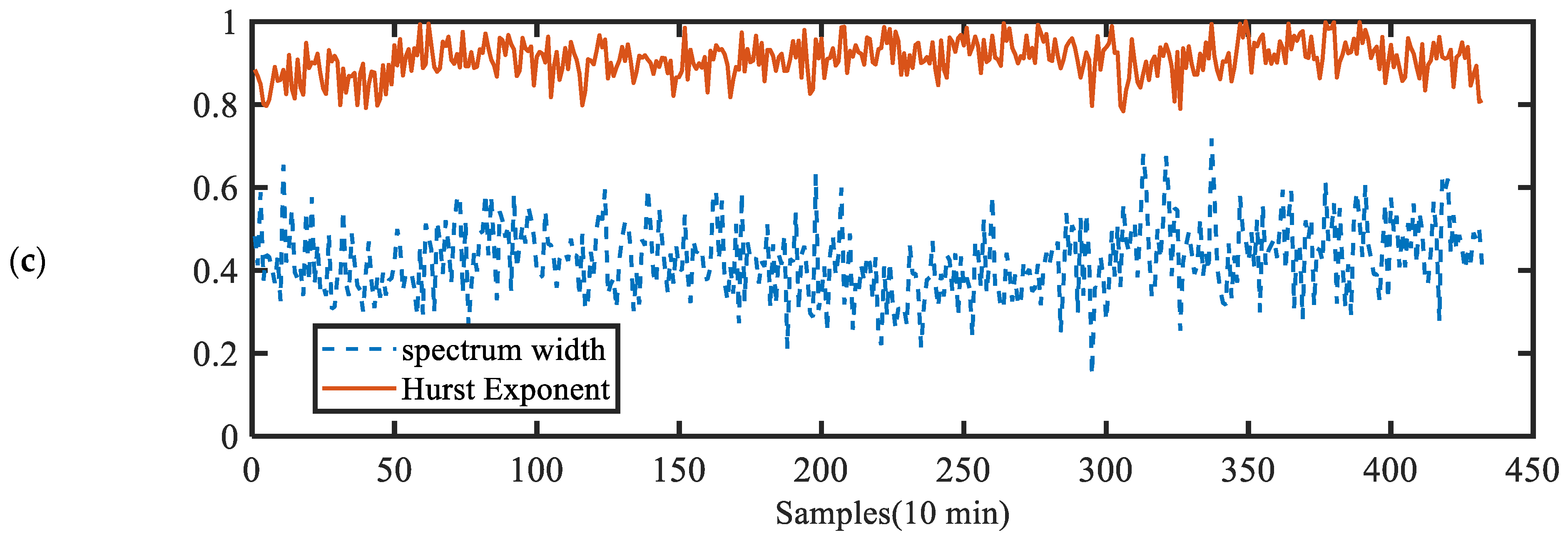
3.2. Multifractal Analysis: Multifractal Detrended Fluctuation Analysis (MFDFA)
4. Conclusions
- Based on the measured data and data control method, the wind speeds of the four typhoon processes Nesat, Haitang, Maria, and Bailu were obtained for fractal analysis.
- In the box-counting method, the fractal dimensions generally vary between 1.3 and 1.5. The fractal dimensions differ with different measurement sites due to the influence of terrain conditions. The fractal dimensions slightly vary with measurement height. The maximum fractal dimension values occur when a typhoon makes landfall, indicating the complexity of wind speeds during typhoon landfall.
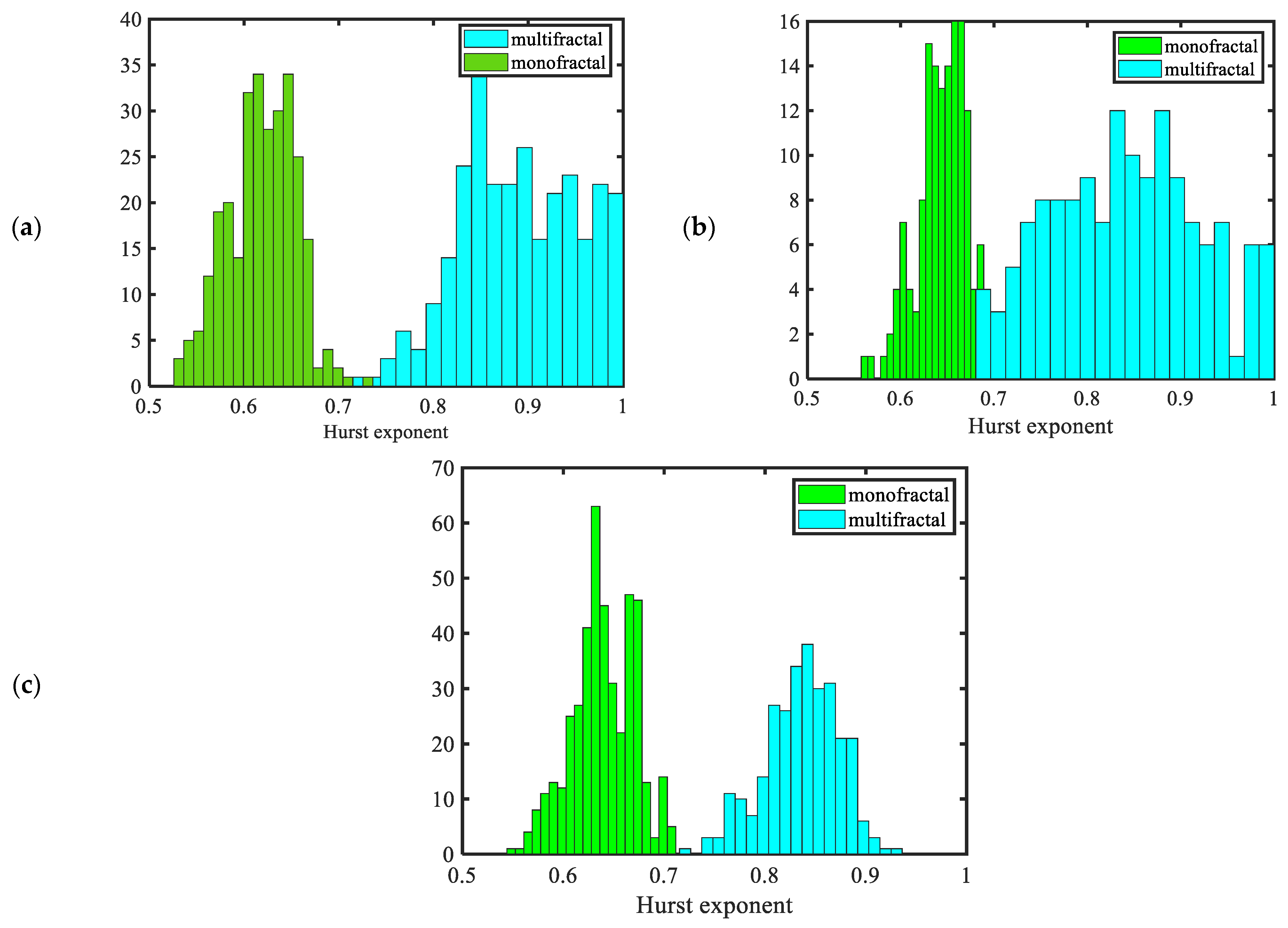
- Multifractality can be found in typhoon wind speeds as the fractal dimensions change with scale by multifractal detrended fluctuation analysis. When selecting the physical parameters of a typhoon simulation model, it is vital to consider multi-fractality.
- In the MFDFA, the fractal parameters are generally greater than those that are determined by monofractal analysis, with Hurst exponents greater than 0.5 indicating that the original wind speed series are persistent.
- Fractal analysis is vital for explaining the inner dynamic nature of turbulence. This research can provide a reference for future typhoon predictions, such as typhoon simulations and the development of predictive models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, L.; Chen, W.; Wang, B.; Zhi, S.; Liu, A. Characteristics of wind profiles in the landfalling typhoon boundary layer. J. Wind Eng. Ind. Aerodyn. 2016, 149, 77–88. [Google Scholar]
- Lin, L.; Chen, K.; Xia, D.; Wang, H.; Hu, H.; He, F. Analysis on the wind characteristics under typhoon climate at the southeast coast of China. J. Wind Eng. Ind. Aerodyn. 2018, 182, 37–48. [Google Scholar]
- Xia, D.; Dai, L.; Lin, L.; Wang, H.; Hu, H. A Field Measurement Based Wind Characteristics Analysis of a Typhoon in Near-Ground Boundary Layer. Atmosphere 2021, 12, 873. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Wang, H. Numerical Simulation Analysis of Typhoon Moving Track on Sea Surface Cooling. J. Phys. Conf. Ser. 2024, 2718, 012002. [Google Scholar]
- Pang, S.; Li, J.; Guo, T.; Ma, X. Influence of the Species Number of Hydrometeors on Numerical Simulation of the Super Typhoon Mujigae in 2015. Asia-Pac. J. Atmos. Sci. 2023, 60, 29–47. [Google Scholar]
- Tao, T.Y.; Wang, H.; Wu, T. Stationary and non-stationary analysis on the wind characteristics of a tropical storm. Smart Struct. Syst. 2016, 17, 1067–1085. [Google Scholar]
- He, X.; Qin, H.; Tao, T.; Liu, W.; Wang, H. Measurement of Non-Stationary Characteristics of a Landfall Typhoon at the Jiangyin Bridge Site. Sensors 2017, 17, 2186. [Google Scholar] [CrossRef]
- Fang, G.S.; Zhao, L.; Cao, S.Y.; Ge, Y.J.; Pang, W.C. A novel analytical model for wind field simulation under typhoon boundary layer considering multi-field correlation and height-dependency. J. Wind. Eng. Ind. Aerod. 2018, 175, 77–89. [Google Scholar]
- Jin, J.; Wang, B.; Yu, M.; Liu, J.; Wang, W. A Novel Self-Adaptive Wind Speed Prediction Model Considering Atmospheric Motion and Fractal Feature. IEEE Access 2020, 8, 215892–215903. [Google Scholar]
- Breslin, M.; Belward, J. Fractal dimensions for rainfall time series. Math. Comput. Simulat. 1999, 48, 437–446. [Google Scholar]
- Ribeiro, M.B.; Miguelote, A.Y. Fractals and the distribution of galaxies. Braz. J. Phys. 1998, 28, 132–160. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kavasseri, R.G.; Nagarajan, R. A multifractal description of wind speed records. Chaos Solitons Fractals 2005, 24, 165–173. [Google Scholar] [CrossRef]
- Feng, T.; Fu, Z.; Deng, X.; Mao, J. A brief description to different multi-fractal behaviors of daily wind speed records over China. Phys. Lett. A 2009, 45, 4134–4141. [Google Scholar] [CrossRef]
- Chang, T.; Ko, H.-H.; Liu, F.; Chen, P.; Chang, Y.; Liang, Y.-H.; Jang, H.-Y.; Lin, T.-C.; Chen, Y.-H. Fractal dimension of wind speed time series. Appl. Energy 2012, 93, 742–749. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, S.; Guariso, G. Fractal order evidences in wind speed time series. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications, Catania, Italy, 23–25 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Laib, M.; Golay, J.; Telesca, L.; Kanevski, M. Multifractal analysis of the time series of daily means of wind speed in complex regions. Chaos Solitons Fractals 2018, 109, 118–127. [Google Scholar] [CrossRef]
- Balkissoon, S.; Fox, N. Anthony LupoFractal characteristics of tall tower wind speeds in Missouri. Renew. Energy 2020, 154, 1346–1356. [Google Scholar] [CrossRef]
- Cui, B.; Huang, P.; Xie, W. Fractal dimension characteristics of wind speed time series under typhoon climate. J. Wind. Eng. Ind. Aerodyn. 2022, 229, 105144. [Google Scholar] [CrossRef]
- Liang, J.; Li, L.; Chan, P.W.; Zhang, L.; Lu, C. Honglong Yang, Fractal dimension characterization of wind speed in typhoons and severe convective weather events based on box dimension analysis. Chaos Solitons Fractals 2024, 186, 115301. [Google Scholar] [CrossRef]
- Shu, Z.R.; Chan, P.W.; Li, Q.S.; He, Y.C.; Yan, B.W. Quantitative assessment of offshore wind speed variability using fractal analysis. Wind. Struct. 2020, 31, 363–371. [Google Scholar]
- Malinverno, A. A simple method to estimate the fractal dimension of a self-affine series. Geophys. Res. Lett. 1990, 17, 1953–1956. [Google Scholar] [CrossRef]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar] [CrossRef]
- Espen, A.F. Ihlen Multifractal analyses of response time series: A comparative study. Behav. Res. Methods 2013, 45, 928–945. [Google Scholar]
- Gu, G.; Zhou, W. Detrending moving average algorithm for multifractals. Phys. Rev. E 2010, 82, 011136. [Google Scholar] [CrossRef]
- Zhao, G.; Deng, Q.; Li, X.; Dong, L.; Chen, G.; Zhang, C. Recognition of microseismic waveforms based on EMD and morphological fractal dimension. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 162–167. [Google Scholar]
- Cadenas, E.; Campos-Amezcua, R.; Rivera, W.; Espinosa-Medina, M.A.; Mendez-Gordillo, A.R.; Rangel, E.; Tena, J. Wind speed variability study based on the Hurst coefficient and fractal dimensional analysis. Energy Sci. Eng. 2019, 7, 361–378. [Google Scholar] [CrossRef]
- Harrouni, S.; Guessoum, A. Using fractal dimension to quantify long-range persistence in global solar radiation. Chaos Soliton Fract 2009, 41, 1520–1530. [Google Scholar] [CrossRef]
- de Figueiredo, B.C.L.; Moreira, G.R.; Stosic, B.; Stosic, T. Multifractal analysis of hourly wind speed records in petrolina, northeast Brazil. Rev. Bras. Biom. 2014, 32, 599–608. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Movahed, M.S.; Jafari, G.; Ghasemi, F.; Rahvar, S.; Tabar, M.R.R. Multifractal detrended fluctuation analysis of sunspot time series. J. Stat. Mech. Theor. Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef]



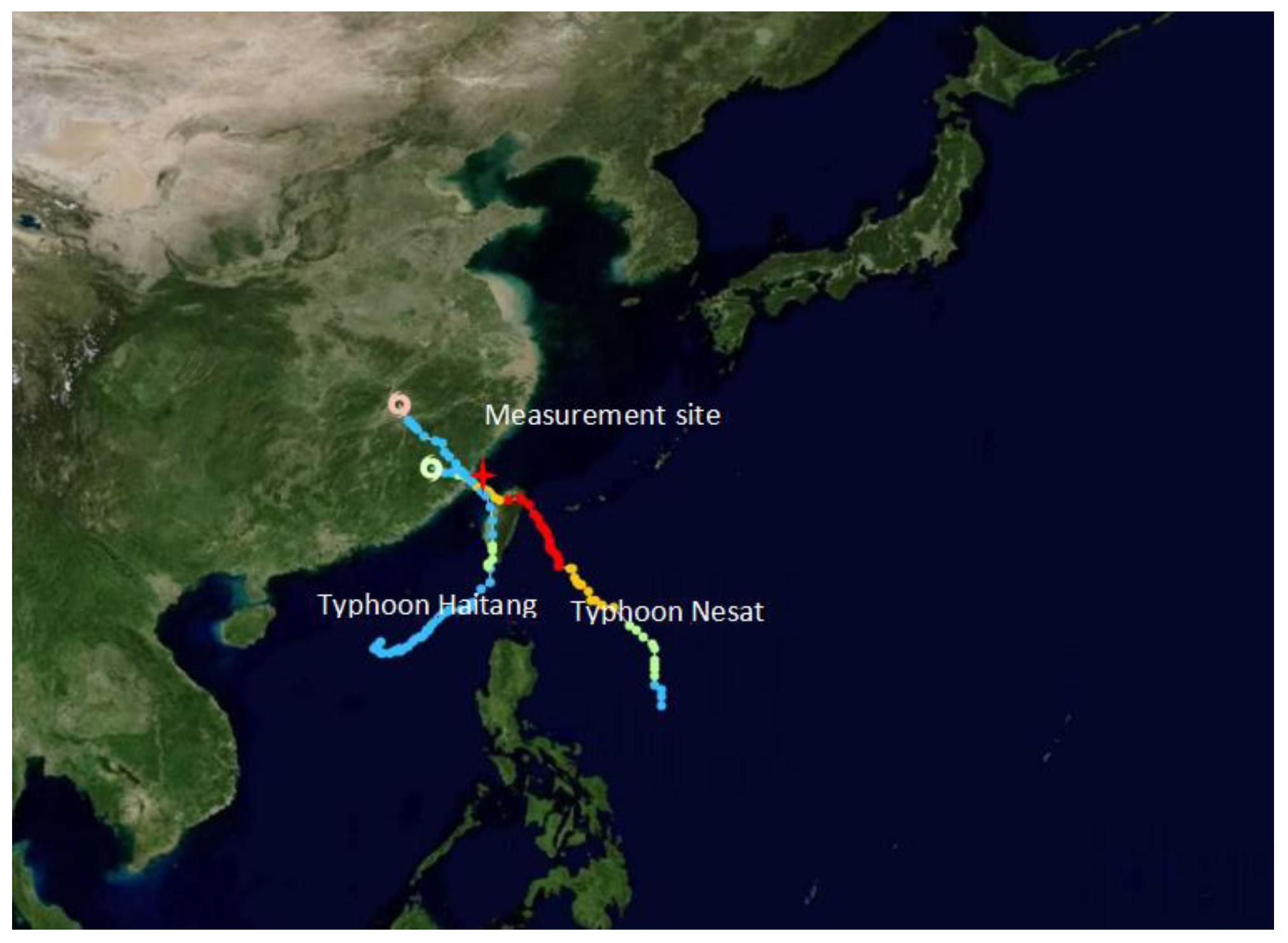
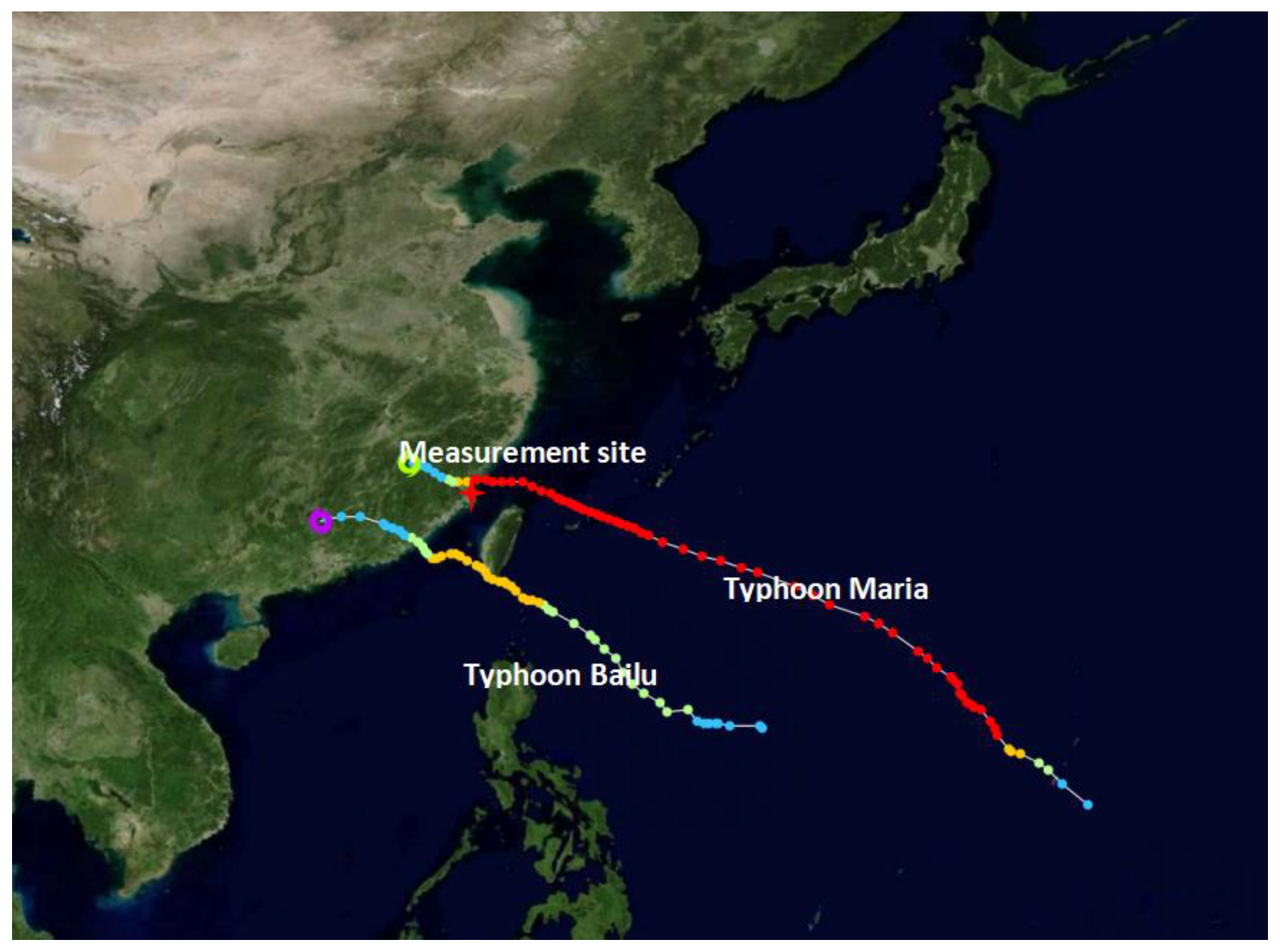
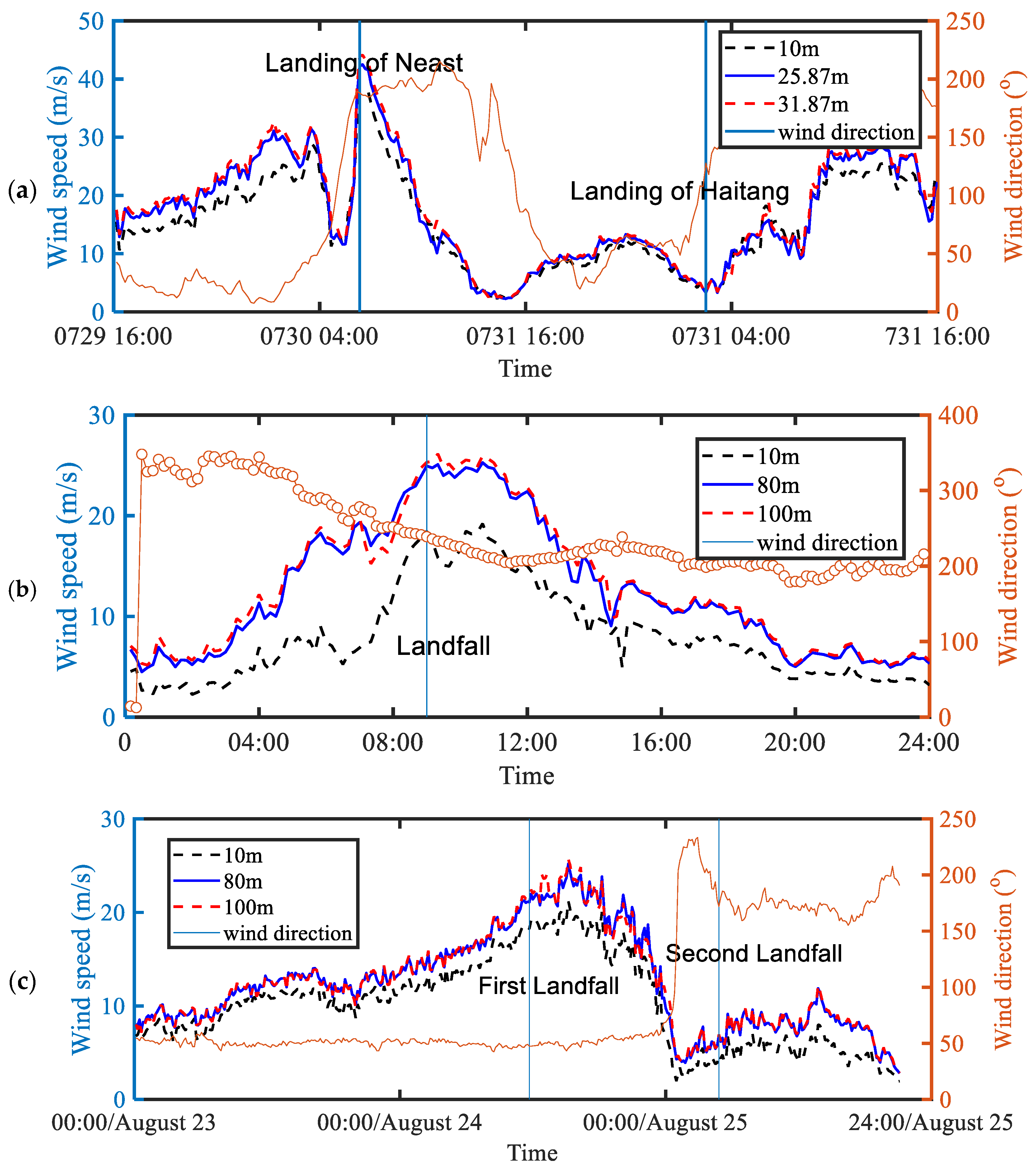


| Typhoon | Landing time | Station | Measurement Height | Maximum Wind Speed at Height 10 m |
|---|---|---|---|---|
| Nesat | 2016.07.29–2016.07.30 | Wangye Shan Island | 10 m, 25.87 m, 31.87 m | 37.8 m/s |
| Haitang | 2016.07.30–2016.07.31 | Wangye Shan Island | 10 m, 25.87 m, 31.87 m | 25.4 m/s |
| Maria | 2018.07.11–2018.07.11 | Yutou Island | 10 m, 80 m, 100 m | 26.13 m/s |
| Bailu | 2019.08.23–2019.08.24 | Yutou Island | 10 m, 80 m, 100 m | 25.69 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Yu, W.; Lin, L.; Lin, X.; Hu, Y. Fractal Characteristics of Wind Speed Time Series Under Typhoon Climate in Southeastern China. Fractal Fract. 2025, 9, 175. https://doi.org/10.3390/fractalfract9030175
Xia D, Yu W, Lin L, Lin X, Hu Y. Fractal Characteristics of Wind Speed Time Series Under Typhoon Climate in Southeastern China. Fractal and Fractional. 2025; 9(3):175. https://doi.org/10.3390/fractalfract9030175
Chicago/Turabian StyleXia, Dandan, Wanghua Yu, Li Lin, Xiaobo Lin, and Yu Hu. 2025. "Fractal Characteristics of Wind Speed Time Series Under Typhoon Climate in Southeastern China" Fractal and Fractional 9, no. 3: 175. https://doi.org/10.3390/fractalfract9030175
APA StyleXia, D., Yu, W., Lin, L., Lin, X., & Hu, Y. (2025). Fractal Characteristics of Wind Speed Time Series Under Typhoon Climate in Southeastern China. Fractal and Fractional, 9(3), 175. https://doi.org/10.3390/fractalfract9030175





