Revisiting the Consolidation Model by Taking the Rheological Characteristic and Abnormal Diffusion Process into Account
Abstract
1. Introduction
2. Fractional Derivative-Based Model
2.1. Basics of Fractional Calculus
2.2. Fractional Derivative Merchant Model
2.3. Fractional Derivative-Based Darcy Model
3. One-Dimension Consolidation Model of Rheological Soils
3.1. Governing Equations, Boundary Conditions and Initial Conditions
- (1)
- Deformation of the soil skeleton is governed by FDMM;
- (2)
- Water flow through an isotropic homogeneous layer is governed by FDDM.
3.2. Time-Dependent Load
4. Numerical Solution to the 1D Rheological Consolidation Model
4.1. Forward Time-Centered Space Scheme
4.2. Matrix Form of Finite Difference Format
4.3. Verification of the Model and FTCS Algorithm
5. Parametric Study and Discussion
5.1. Influence of the Loading Rate
5.2. Influence of the FDMM Parameters
5.2.1. Influence of the Fractional Order
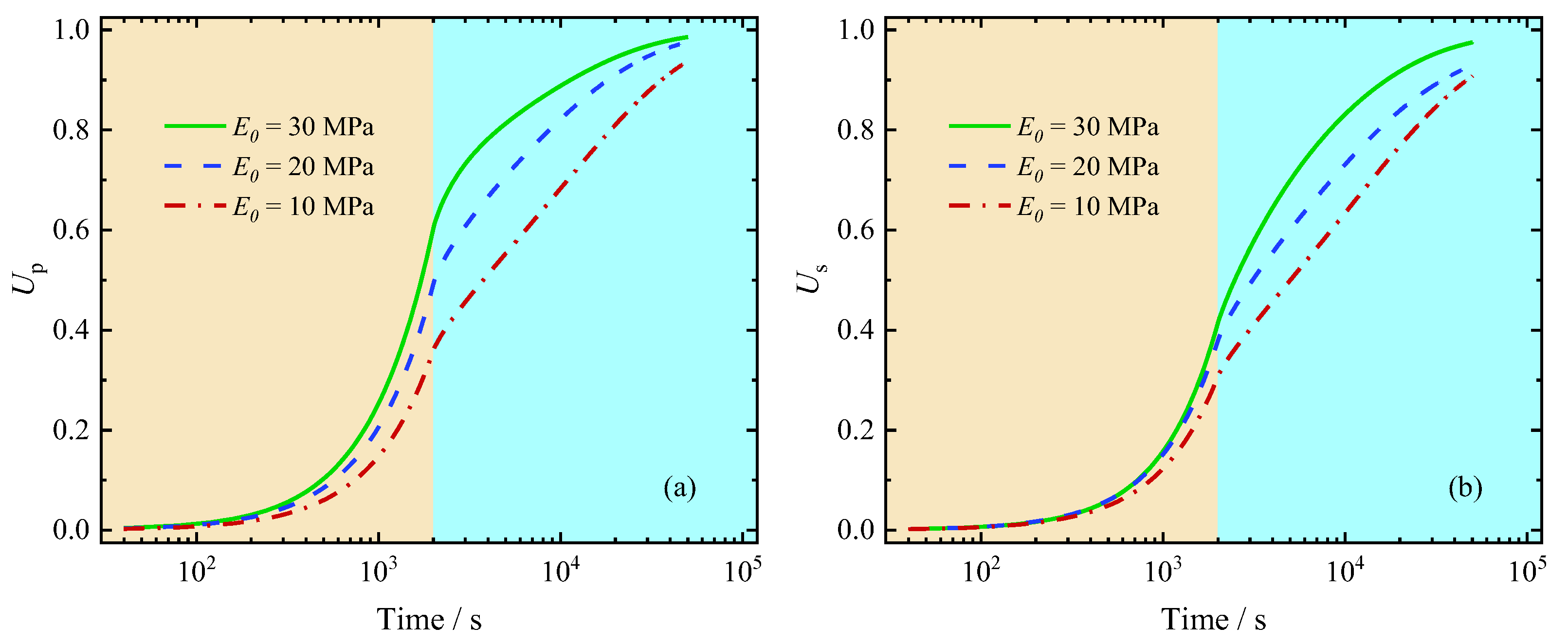
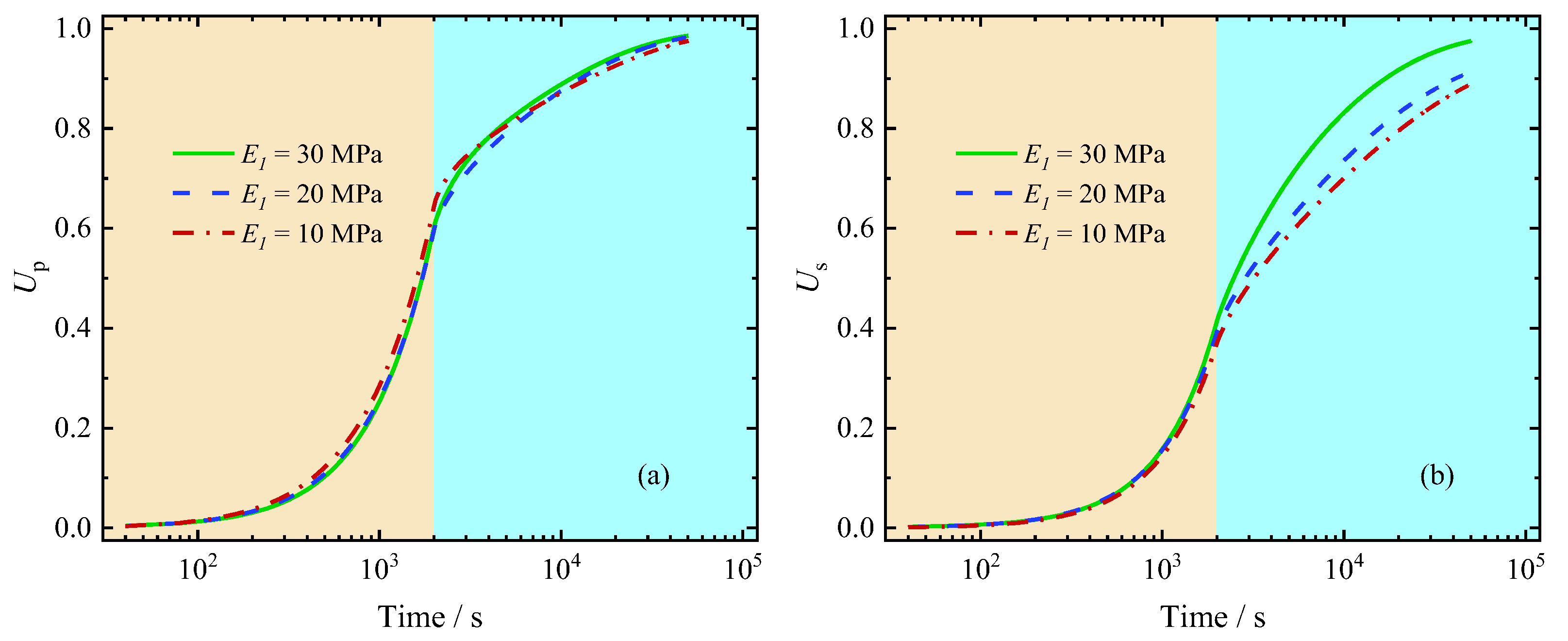
5.2.2. Influence of the Elastic Modulus
5.2.3. Influence of the Elastic Modulus
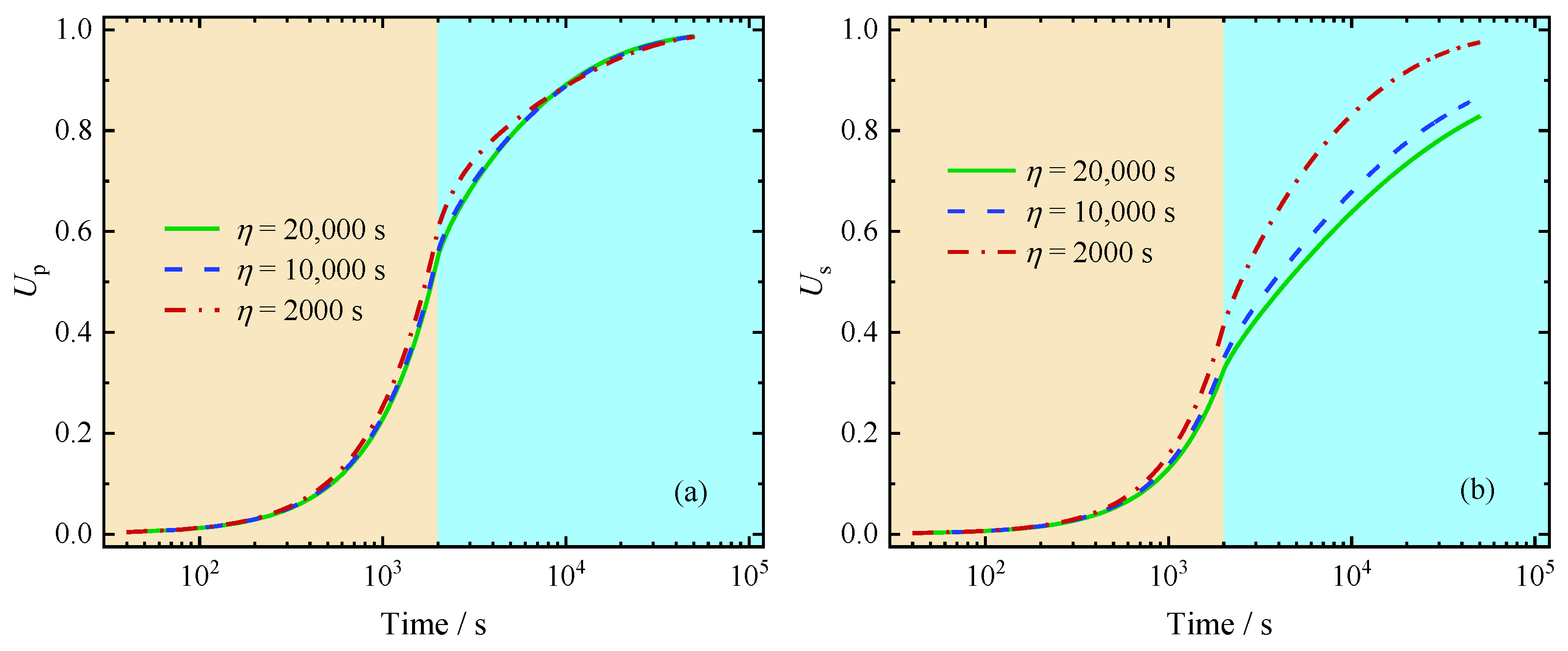
5.2.4. Influence of the Viscosity Time
5.3. Influence of the FDDM Parameters
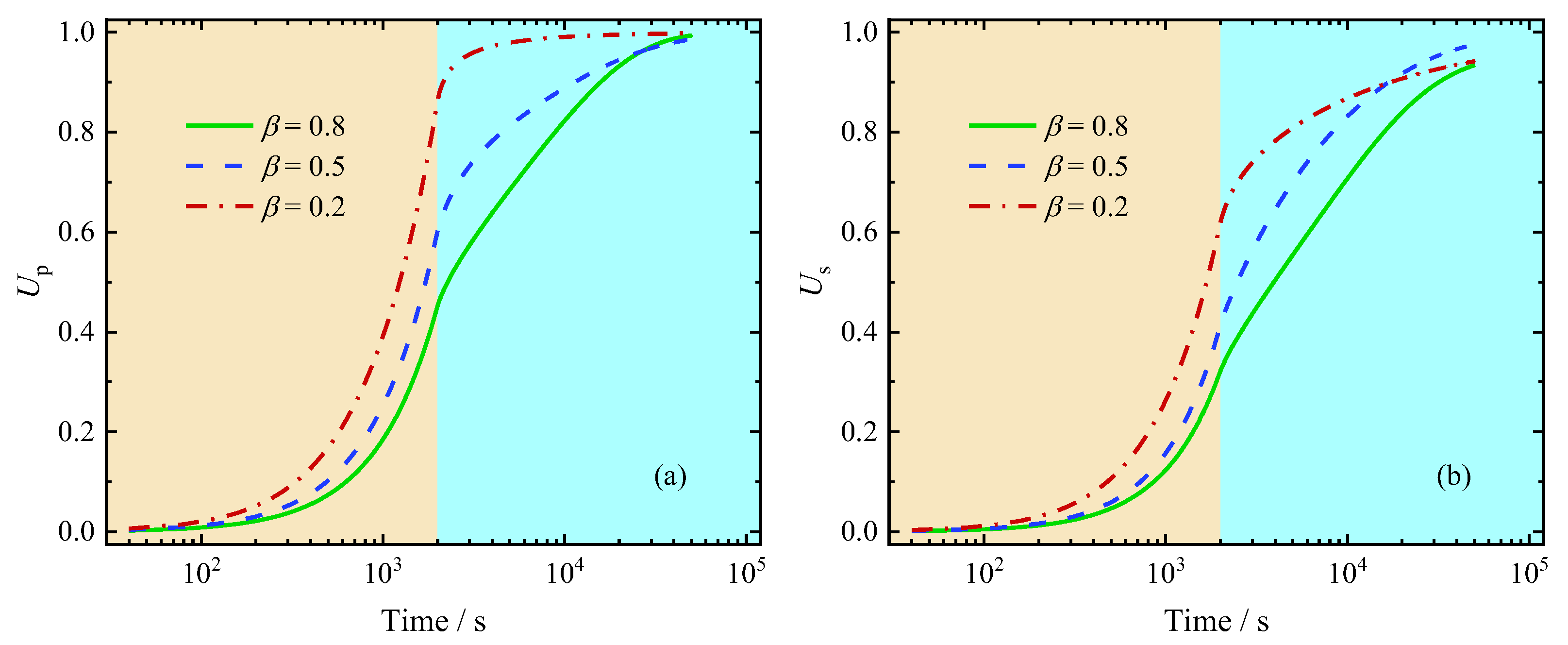
5.3.1. Influence of the Fractional Order
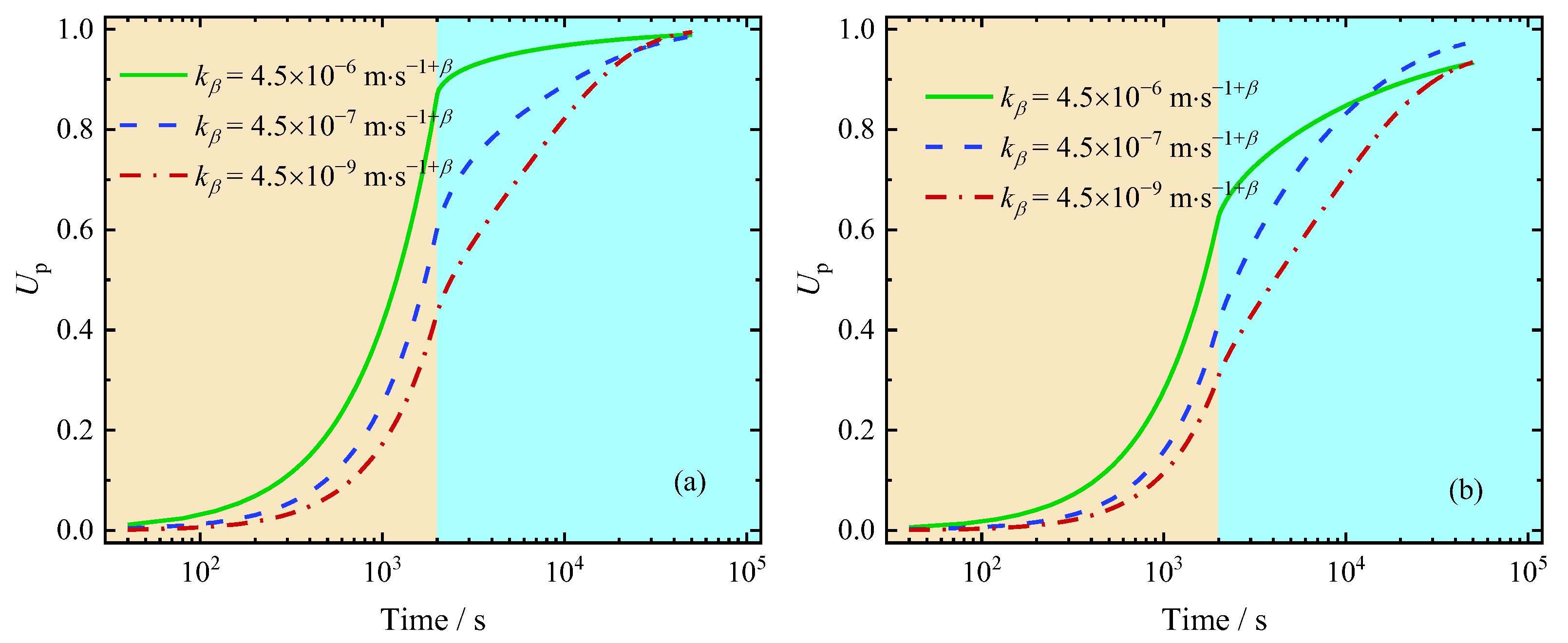
5.3.2. Influence of the Abnormal Permeability Coefficient
6. Discussion
7. Conclusions
- (1)
- Throughout the consolidation process, consistently exceeds , indicating that the excess pore pressure dissipation process occurs ahead of soil settlement. This phenomenon becomes more pronounced as , and decrease, while and increase. Furthermore, a higher loading rate results in greater degrees of consolidation during the loading stage but a slower consolidation rate in the holding stage.
- (2)
- The impact of elastic modulus and the viscosity time on the consolidation process is primarily observed in the soil settlement during the holding stage. As increases or decreases, the soil settlement rate increases, reflecting the critical role of viscoelastic properties in long-term consolidation behavior.
- (3)
- Both in the loading and holding stages, significantly impacts excess pore pressure dissipation and settlement rates, with an increase in accelerating both. In contrast, affects only the settlement rate during the holding stage, where a higher speeds up soil settlement. This difference can be attributed to the fact that changes in influence the elastic deformation of the soil, while changes in primarily affect its viscous deformation.
- (4)
- With the decrease in and the increase in , the consolidation rate of the soil accelerates in the early and middle stages of the consolidation process but slows down in the final stage. Between the two permeability coefficients, and , predominantly governs the consolidation rate, suggesting that traditional permeability remains a key factor even in the presence of memory effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Terzaghi, K. Theory of consolidation. In Theoretical Soil Mechanics; John Wiley& Sons: New York, NY, USA, 1943; pp. 265–296. [Google Scholar]
- Yuan, J.; Ye, L.; Hu, G.; Ying-Guang, F. Experimental study on the influence of granulometric and material compositions on soil rheological properties. Soil Mech. Found. Eng. 2020, 57, 35–42. [Google Scholar] [CrossRef]
- Ter-Martirosyan, Z.; Ter-Martirosyan, A. Rheological properties of soil subject to shear. Soil Mech. Found. Eng. 2013, 49, 219. [Google Scholar] [CrossRef]
- Lanes, R.M.; Greco, M.; Almeida, V.D. Viscoelastic soil–structure interaction procedure for building on footing foundations considering consolidation settlements. Buildings 2023, 13, 813. [Google Scholar] [CrossRef]
- Ter-Martirosyan, Z.G.; Ter-Martirosyan, A.Z.; Kurilin, N.O. Predicting the settlement and long-term bearing capacity of a base of foundation of finite width. Soil Mech. Found. Eng. 2021, 58, 190–195. [Google Scholar] [CrossRef]
- Huang, W.; Wen, K.; Deng, X.; Li, J.; Jiang, Z.; Li, Y.; Li, L.; Amini, F. Constitutive model of lateral unloading creep of soft soil under excess pore water pressure. Math. Probl. Eng. 2020, 2020, 5017546. [Google Scholar] [CrossRef]
- Yu, Y.-Y.; Luo, C.-L.; Cui, W.-H.; Tao, J.-Y.; Zhang, T.-H. Study on creep characteristics and component model of saline soil in hexi corridor. Sci. Rep. 2023, 13, 18067. [Google Scholar] [CrossRef]
- Ding, P.; Xu, R.; Ju, L.; Qiu, Z.; Cheng, G.; Zhan, X. Semi-analytical analysis of fractional derivative rheological consolidation considering the effect of self-weight stress. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1049–1066. [Google Scholar] [CrossRef]
- Wang, P.; Tang, Y.; Ren, P.; Zhang, H. An isochronous stress ratio logarithmic strain curve based clay creep model considering the effects of hardening and damage. Sci. Rep. 2024, 14, 7057. [Google Scholar] [CrossRef]
- Huang, M.; Lv, C.; Zhou, S.; Zhou, S.; Kang, J. One-dimensional consolidation of viscoelastic soils incorporating Caputo-Fabrizio fractional derivative. Appl. Sci. 2021, 11, 927. [Google Scholar] [CrossRef]
- Wang, L.; Chen, H.; Liu, S.; Yu, Y. Rheological consolidation analysis of saturated clay ground under cyclic loading based on the fractional order Kelvin model. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 1814–1832. [Google Scholar] [CrossRef]
- Ding, P.; Xu, R.; Zhu, Y.; Wen, M. Fractional derivative modelling for rheological consolidation of multilayered soil under time-dependent loadings and continuous permeable boundary conditions. Acta Geotech. 2022, 17, 2287–2304. [Google Scholar] [CrossRef]
- Hu, S.; Li, X.; Bai, B.; Shi, L.; Liu, M.; Wu, H. A modified true triaxial apparatus for measuring mechanical properties of sandstone coupled with Co2-H2o biphase fluid. Greenh. Gases Sci. Technol. 2017, 7, 78–91. [Google Scholar] [CrossRef]
- Han, Z.; Li, J.; Li, Y.; Gu, X.; Chen, X.; Wei, C. Assessment of the size selectivity of eroded sediment in a partially saturated sandy loam soil using scouring experiments. Catena 2021, 201, 105234. [Google Scholar] [CrossRef]
- Ranaivomanana, H.; Razakamanantsoa, A.; Amiri, O. Permeability prediction of soils including degree of compaction and microstructure. Int. J. Geomech. 2017, 17, 04016107. [Google Scholar] [CrossRef]
- van Verseveld, C.J.W.; Gebert, J. Effect of compaction and soil moisture on the effective permeability of sands for use in methane oxidation systems. Waste Manag. 2020, 107, 44–53. [Google Scholar] [CrossRef]
- Xie, J.; Li, Q.; Li, T.; Zhao, Z. Lattice boltzmann simulation of non-darcy flow in stochastically generated three-dimensional granular porous media. J. Porous Media 2021, 24, 93–104. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, C.; Oh, J. Assessments of the effects of various fracture surface morphology on single fracture flow: A review. Int. J. Min. Sci. Technol. 2023, 33, 1–29. [Google Scholar] [CrossRef]
- Muzemder, A.T.M.S.H.; Singh, K. Intra-pore tortuosity and diverging-converging pore geometry controls on flow enhancement due to liquid boundary slip. J. Hydrol. 2021, 598, 126475. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S.; Zhang, S.Q. Modeling non-Darcian flow and solute transport in porous media with the Caputo–Fabrizio derivative. Appl. Math. Model. 2019, 68, 603–615. [Google Scholar] [CrossRef]
- Di Giuseppe, E.; Moroni, M.; Caputo, M. Flux in porous media with memory: Models and experiments. Transp. Porous Media 2010, 83, 479–500. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, H.-w.; Zhuo, Z.; Xue, D.-j.; Yang, S. Finite difference method for space-fractional seepage process in unsaturated soil. Chin. J. Geotech. Eng. 2020, 42, 1759–1764. [Google Scholar]
- Kim, P.; Kim, H.-S.; Pak, C.-U.; Paek, C.-H.; Ri, G.-H.; Myong, H.-B. Analytical solution for one-dimensional nonlinear consolidation of saturated multi-layered soil under time-dependent loading. J. Ocean Eng. Sci. 2021, 6, 21–29. [Google Scholar] [CrossRef]
- Cui, P.; Cao, W.; Lin, C.; Liu, Y.; Chen, M.; Zhang, J. 1d elastic viscoplastic consolidation analysis of bi-layered soft ground under time-dependent drainage boundary and ramp load. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 55–77. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Alaimo, G.; Piccolo, V.; Cutolo, A.; Deseri, L.; Fraldi, M.; Zingales, M. A fractional order theory of poroelasticity. Mech. Res. Commun. 2019, 100, 103395. [Google Scholar] [CrossRef]
- Iaffaldano, G.; Caputo, M.; Martino, S. Experimental and theoretical memory diffusion of water in sand. Hydrol. Earth Syst. Sci. 2006, 10, 93–100. [Google Scholar] [CrossRef]
- Zhang, Y.-N.; Sun, Z.-Z.; Wu, H.-W. Error estimates of Crank–Nicolson-type difference schemes for the subdiffusion equation. SIAM J. Numer. Anal. 2011, 49, 2302–2322. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Q. One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin’s model. Rock Soil Mech. 2017, 38, 3680–3687, 3697. [Google Scholar]
- Hanna, D.; Sivakugan, N.; Lovisa, J. Simple approach to consolidation due to constant rate loading in clays. Int. J. Geomech. 2013, 13, 193–196. [Google Scholar] [CrossRef]
- Cui, P.; Liu, Z.-Y.; Zhang, J.-C.; Fan, Z.-C. Analysis of one-dimensional rheological consolidation of double-layered soil with fractional derivative Merchant model and non-Darcian flow described by non-Newtonian index Merchant. J. Cent. South Univ. 2021, 28, 284–296. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, P.; Zhang, J.; Xia, Y. Consolidation analysis of ideal sand-drained ground with fractional-derivative Merchant model and non-Darcian flow described by non-Newtonian index. Math. Probl. Eng. 2019, 2019, 5359076. [Google Scholar] [CrossRef]
- Zhang, S.; Pei, H. Determining the bound water content of montmorillonite from molecular simulations. Eng. Geol. 2021, 294, 106353. [Google Scholar] [CrossRef]


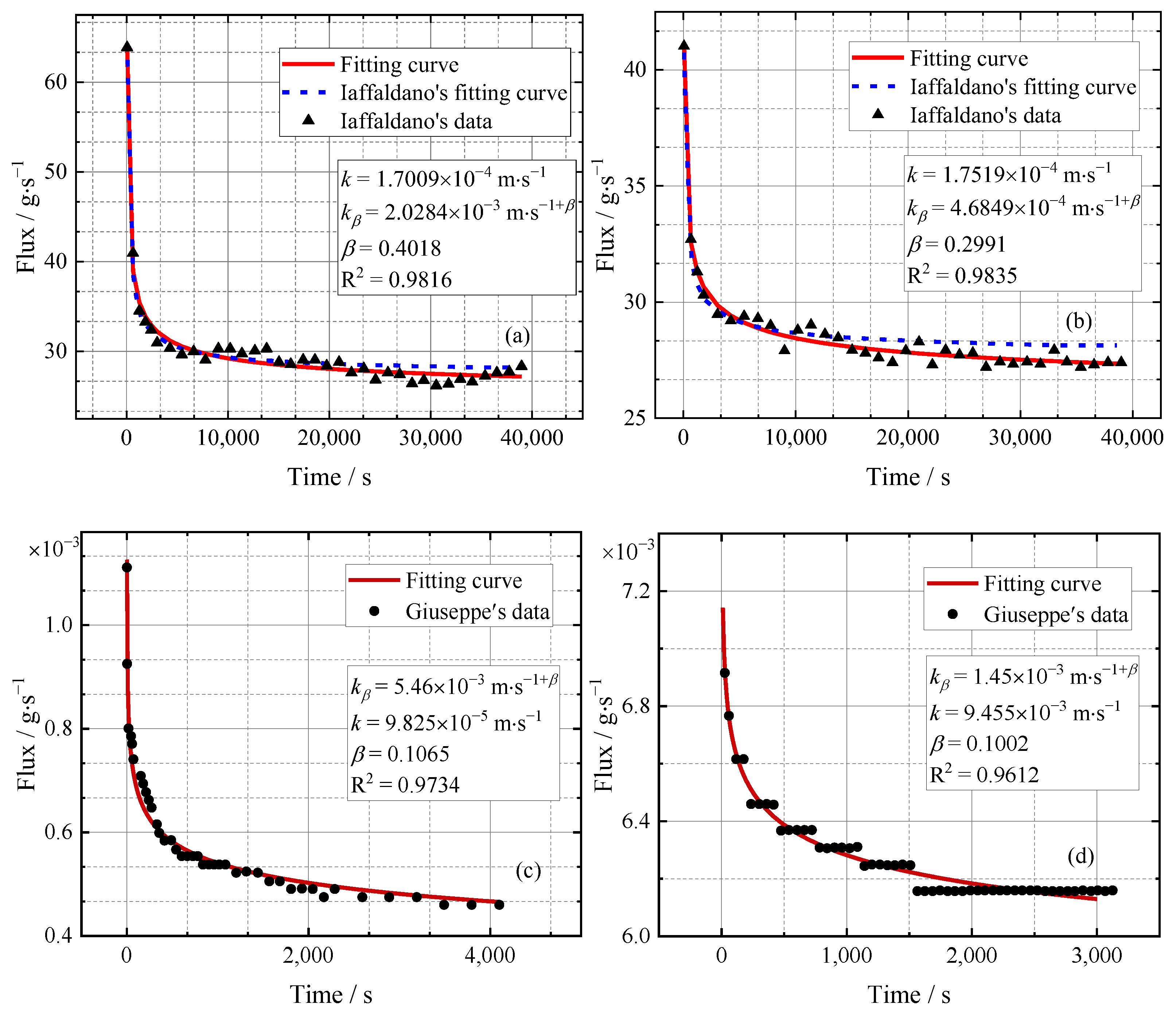


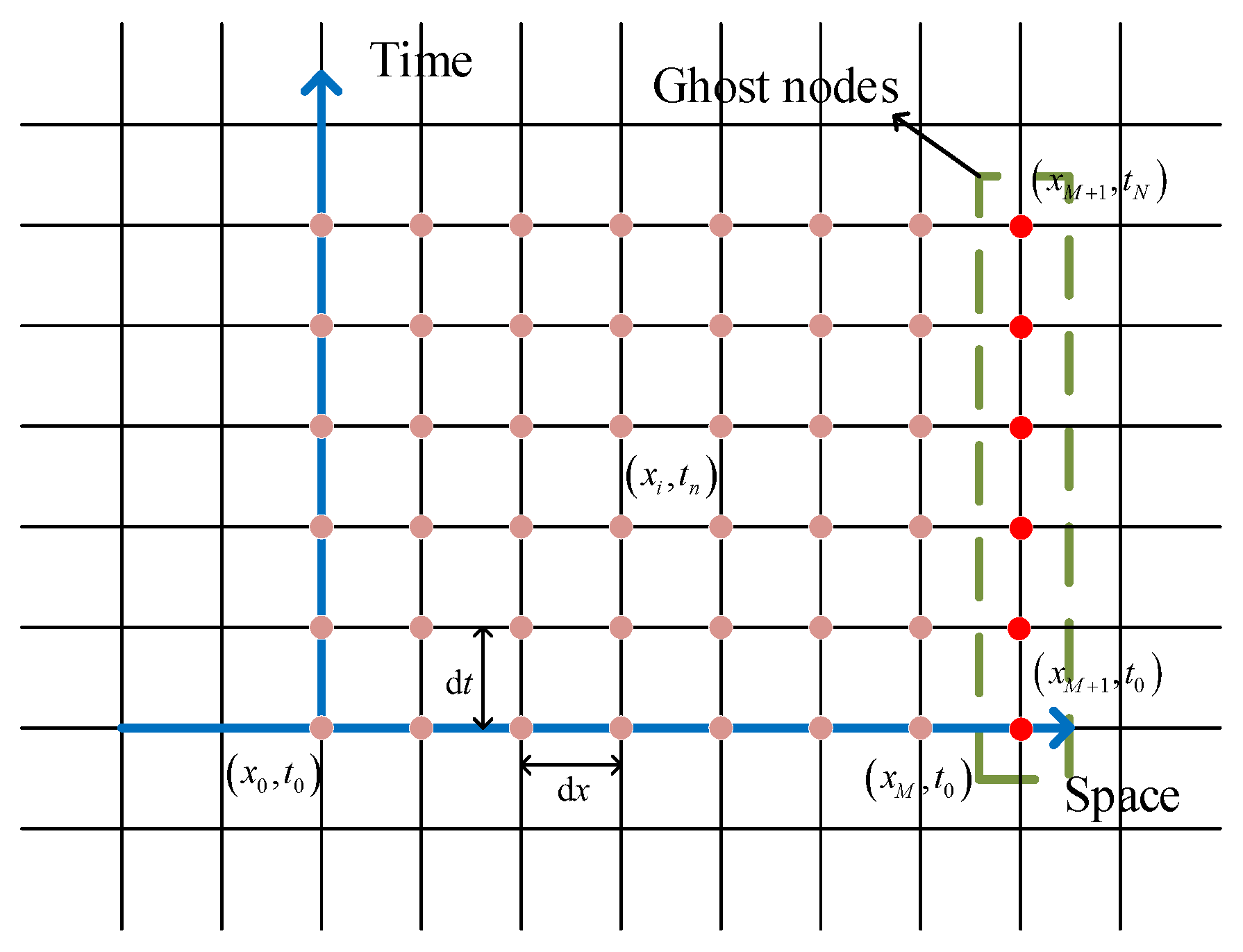

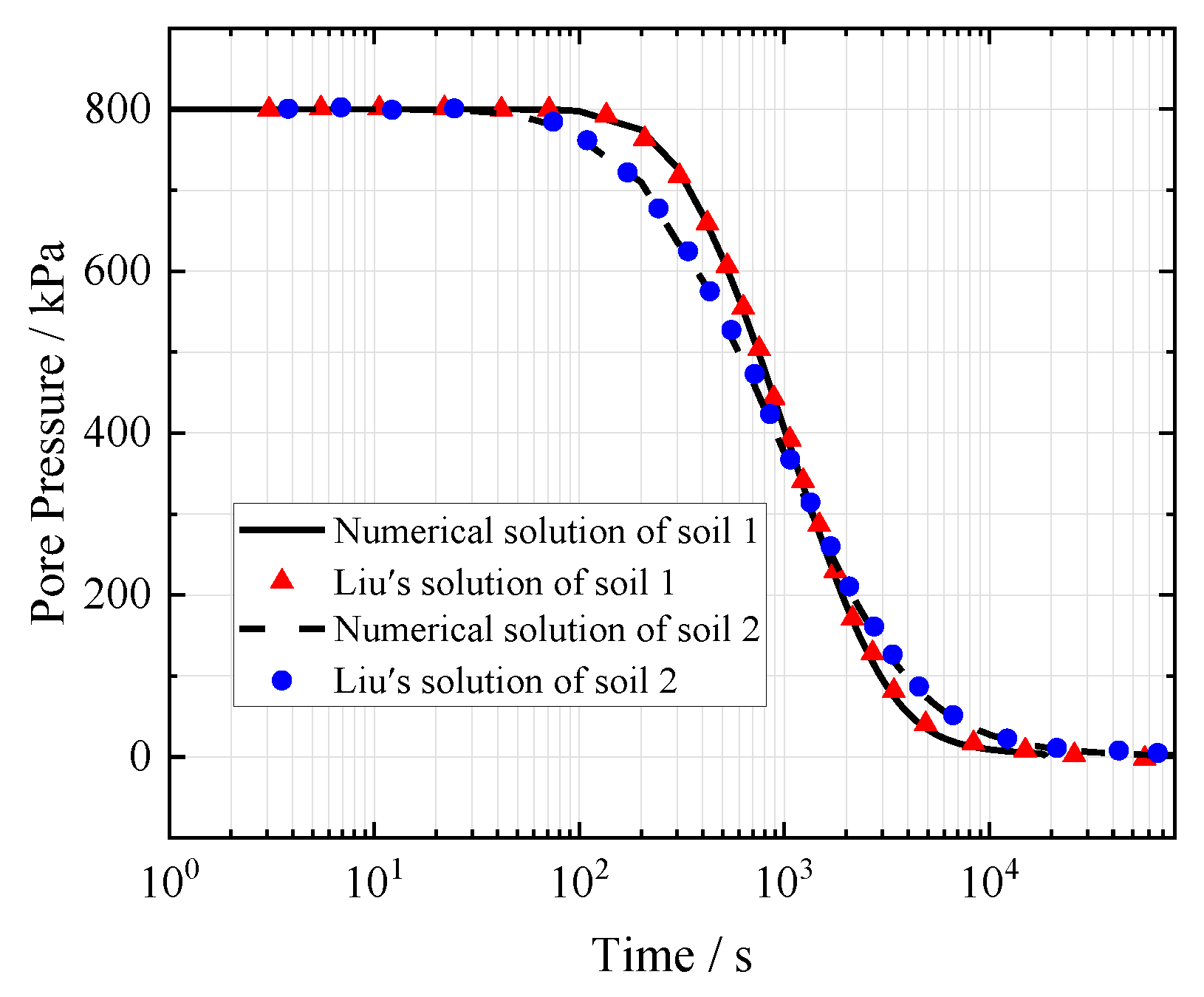

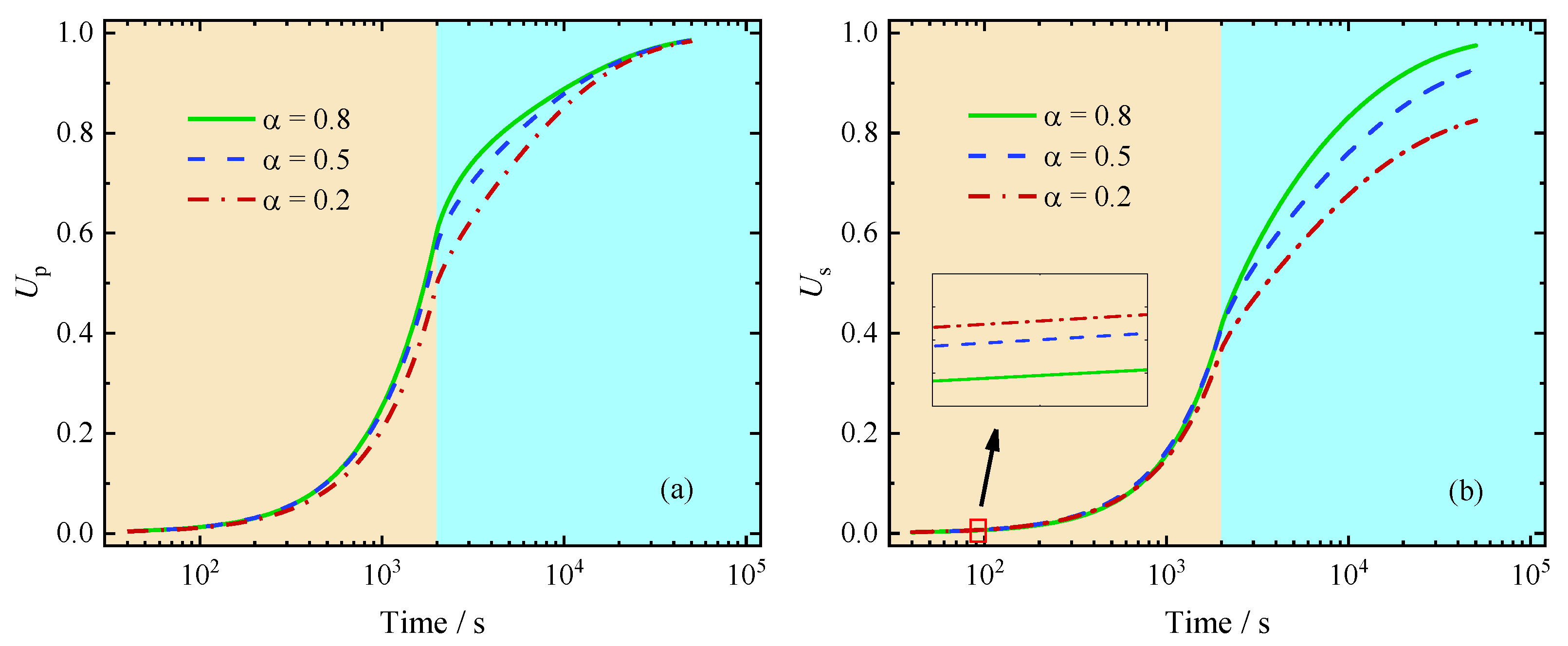
| Soil Number | h/m | k/(m/s) | α | E/(MPa) | F/(MPa·s) |
|---|---|---|---|---|---|
| 1 | 0.02 | 1 × 10−10 | 0.13 | 7.6 | 4560 |
| 2 | 0.02 | 4 × 10−11 | 0.35 | 17.0 | 51,000 |
| h/m | E0/(MPa) | E1/(MPa) | k/(m/s) | kβ/(m/s1−β) | η/(s) |
|---|---|---|---|---|---|
| 0.5 | 30 | 30 | 6 × 10−9 | 4.5 × 10−7 | 2000 |
| Time Factor t1/(s) | Numerical Up | Analytical Up |
|---|---|---|
| 1000 | 0.203949 | 0.203900 |
| 2000 | 0.288388 | 0.288352 |
| 3000 | 0.353064 | 0.353035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, T.; Yu, Y.; Zeng, T. Revisiting the Consolidation Model by Taking the Rheological Characteristic and Abnormal Diffusion Process into Account. Fractal Fract. 2025, 9, 233. https://doi.org/10.3390/fractalfract9040233
Feng T, Yu Y, Zeng T. Revisiting the Consolidation Model by Taking the Rheological Characteristic and Abnormal Diffusion Process into Account. Fractal and Fractional. 2025; 9(4):233. https://doi.org/10.3390/fractalfract9040233
Chicago/Turabian StyleFeng, Tao, Yongtang Yu, and Tao Zeng. 2025. "Revisiting the Consolidation Model by Taking the Rheological Characteristic and Abnormal Diffusion Process into Account" Fractal and Fractional 9, no. 4: 233. https://doi.org/10.3390/fractalfract9040233
APA StyleFeng, T., Yu, Y., & Zeng, T. (2025). Revisiting the Consolidation Model by Taking the Rheological Characteristic and Abnormal Diffusion Process into Account. Fractal and Fractional, 9(4), 233. https://doi.org/10.3390/fractalfract9040233






