A Study on the Mechanical Properties of Unbolted and Bolted Composite Rock Masses Under the Influence of Different Grain Sizes

Abstract

In order to explore the influence of grain size on the mechanical properties of unbolted and bolted composite rock masses, uniaxial compression tests were carried out on unbolted and bolted composite rock masses of different grain sizes. The characteristics of the variation in the strength, elastic modulus, Poisson’s ratio and energy parameters of composite rock masses with grain size were analyzed. The evolution process of crack propagation in the composite rock masses was studied, and the influence mechanism of rock grain size on the mechanical properties of the anchorage bearing structure of the rock surrounding the roadway was revealed. The results show that with an increase in the grain size, the peak strength and elastic modulus of a composite rock mass decrease gradually, and the post-peak residual strength, Poisson’s ratio and total input strain energy increase gradually. The evolution of crack propagation is from tensile cracking to tensile to shear mixed to shear cracking. Prestressed anchor bolts can effectively improve the peak strength and post-peak residual strength of composite rock masses and have inhibitory effects on crack propagation in the anchorage zone, such as weakening, deflection and crack arrest. Compared with an unbolted composite rock mass, the bearing capacity of a bolted composite rock mass is stronger, and its elastic modulus is significantly improved.

1. Introduction

With the gradual depletion of shallow mineral resources, mining operations are progressively extending to greater depths. Under the influence of high in situ stress and intense mining-induced disturbances in deep geological environments, roadways are increasingly susceptible to engineering challenges such as large, heterogeneous deformations and instability failures [1]. The excavation process disrupts the equilibrium of in situ stress, triggering the redistribution of the stress within the surrounding rock mass. When the concentrated stress exceeds the strength limit of the rock mass, localized failure occurs, resulting in the sequential development of a fractured zone near the excavation boundary and an intact zone in deeper regions. Rock bolting and grouting, as primary reinforcement methods, re-cement the fractured zone into an integrated structure that synergistically interacts with the intact zone to control the roadway convergence. The grain size distribution within the fractured zone critically governs the mechanical performance of these composite bearing structures, necessitating systematic experimental investigations into bolted and unbolted composite rock masses with varying grain sizes to advance the theoretical frameworks for deformation control.

Laboratory testing remains the most direct and reliable approach to characterizing rock mass mechanics. However, the in situ sampling of fractured rock masses—exhibiting weak cementation, low strength and high disturbance sensitivity and deformability—poses significant practical challenges in roadway environments. Consequently, simulation techniques using similar materials, including prefabricated fractures or reconstructed rock-like materials, are widely employed for experimental studies. Cheng et al. [2] demonstrated through uniaxial compression tests on fractured analogs that both the peak and residual strength decreased approximately linearly with an increasing length of the prefabricated fracture. Xu et al. [3] investigated the mechanical behavior of bolts in anchored soft rock with prefabricated fractures at varying dip angles, establishing a linear regression model for the axial strain, incorporating pull-out load and fracture inclination parameters. Chen et al. [4] revealed linear reductions in the compressive strength, elastic modulus, peak energy and impact energy index with fracture length in coal–rock composites. Zhang et al. [5] observed trans-layer crack propagation and renewed acoustic emission activity in fractured mudstone–sandstone composites upon reaching the lithology-specific strength limits. Özge Dinç Göğüş [6] identified the mineral composition as the dominant factor controlling the rock deformation mechanisms. Wang et al. [7] studied the crack evolution mechanisms of yellow sandstone of different grain sizes, finding that the fractal dimension of the macroscopic fractures on the post-failure rock surfaces exhibited a decreasing trend with an increasing particle size, indicating that grain size exerts certain control over the evolutionary process of macroscopic fractures. Wu et al. [8] conducted uniaxial compression tests on rocks containing prefabricated orthogonal intersecting fissures, revealing that fissure length had a minimal impact on the rock’s strength, while the angle between the fissures and the direction of loading constituted the primary factor influencing the rock’s strength.

While prefabricated fractures are commonly used to simulate damage, these artificial discontinuities tend to seal rapidly under a high ground pressure and seepage forces due to mud–water infilling. Researchers therefore prioritize reconstruction with similar materials to replicate the mechanical behavior of naturally cemented fractured rock masses. Li Yingjie and Pan et al. [9,10] employed analogous materials to simulate the failure patterns in fractured/soft rock tunnels, demonstrating that shear failure initiates at the sidewalls before propagating upward to generate tensile cracks in the roof strata. Elices et al. [11] reported an inverse correlation between the size of the coarse aggregate and concrete’s tensile strength. Cheng et al. [12] established a coupled relationship between the cumulative acoustic emission counts and the damage evolution in backfill-surrounding rock composites under loading. Jing et al. [13] utilized large-scale physical modeling to characterize the load-bearing mechanisms, the evolution of the displacement field and the fracture patterns in anchored structures during progressive excavation. Su et al. [14] quantified the crushing behavior of fractured roof rocks, deriving a mathematical relationship between the bulking coefficient and the block size under compaction stress. Zhou et al. [15] employed high-strength gypsum to fabricate specimens with prefabricated fissures and conducted uniaxial compression tests to investigate the effectiveness of prestressed bolts in achieving crack arrest. Their findings reveal that the post-peak strength resulted from the combined effects of a “dowel” anchoring mechanism (the shear resistance of the bolt) and an “axial compression” anchoring mechanism.

The existing research has predominantly focused on the intrinsic mechanical properties of fractured zone rock masses, providing foundational insights for roadway stability control. However, systematic investigations into composite systems combining fractured and intact zones—particularly regarding the effects of grain size on the mechanical response and crack propagation in bolted/unbolted configurations—remain notably scarce. To address this gap, the authors simulated the fractured roadway surrounding rock by embedding coal gangue grains of varying sizes into the cement mortar and installing rock bolts, creating composite specimens through integration with the intact analogs. Laboratory uniaxial compression tests were conducted to systematically analyze mechanical properties, crack evolution processes, and energy dissipation characteristics of both bolted and unbolted composite rock masses under different grain size conditions. This experimental approach elucidates the governing mechanisms by which rock block size influences the mechanical performance of anchored bearing structures, offering critical theoretical support for optimizing stability control strategies in deep underground roadways.

2. Preparation and Testing Protocol for Composite Rock Specimens

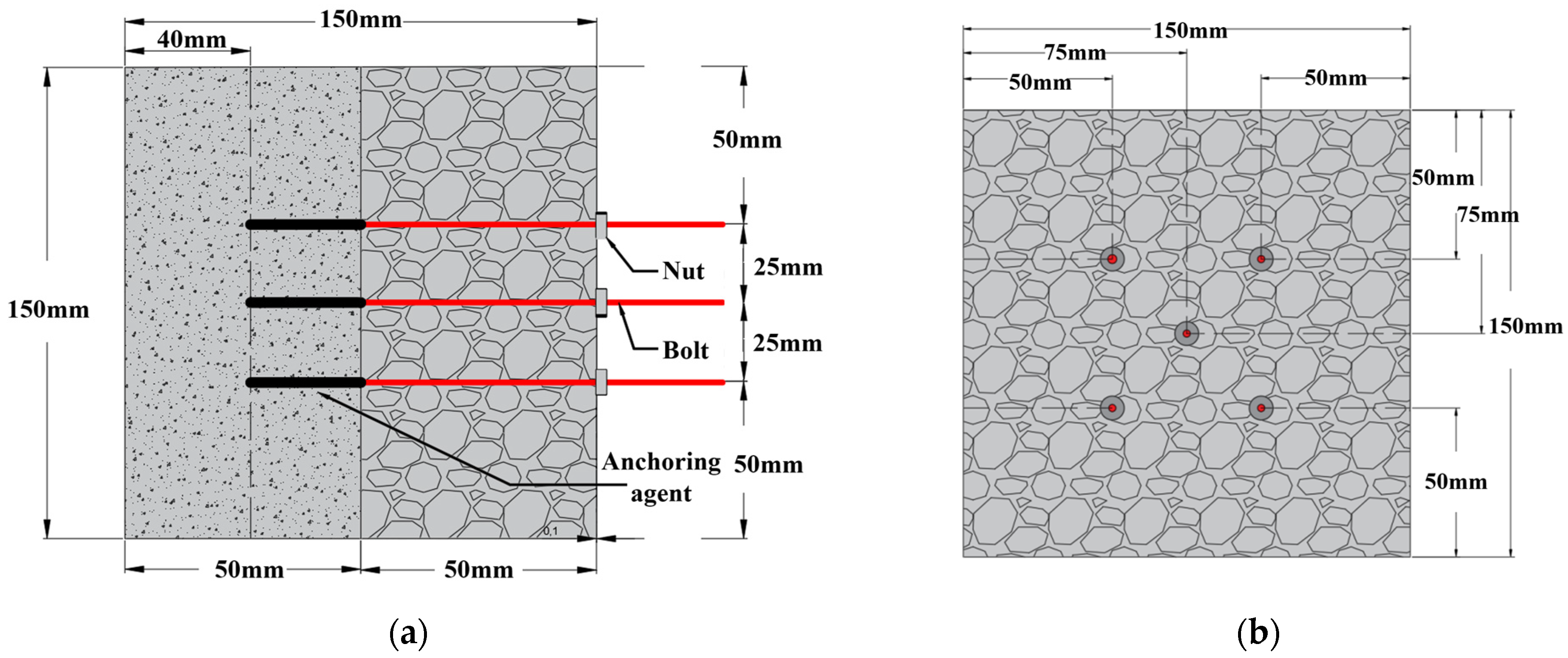
2.1. Preparation of Composite Rock Specimens

The mechanical testing utilized cubical rock-like specimens (composed of the cement, sand, and water) with dimensions of 150 mm × 150 mm × 150 mm. Both unbolted and bolted composite configurations were prepared. As shown in Figure 1, each composite specimen consisted of the fractured zone and the intact zone. The cementitious binder was formulated at a weight ratio of cement:sand:water = 1:5:2. For unbolted specimens, the fractured zone was simulated by embedding coal gangue grains into eight distinct size groups: 3–5 mm, 5–7 mm, 7–9 mm, 9–11 mm, 11–13 mm, 13–15 mm, 15–17 mm, and 17–19 mm (Figure 2).

The fabrication process initiated with the casting of the intact zone by pouring the binder into the molds to a height of 75 mm, followed by vibration compaction. Subsequently, 500 g of pre-screened coal gangue grains were homogeneously mixed with the binder and poured into the remaining mold space to form the fractured zone, which was then compacted and surface-leveled. Specimens were demolded after 24 h of initial curing and subjected to a 28-day standardized curing protocol. Final surface preparation involved the precision grinding of the specimen end faces to achieve surface non-parallelism below 0.02 mm, ensuring mechanical stability and testing accuracy.

The preparation of bolted specimens followed a procedure similar to that of unbolted specimens. The process began by pouring the cementitious binder into the mold to a depth of 40 mm. Five HRB400 rebars (Manufacturer: Shagang Group, Zhangjiagang City, Jiangsu Province, China) (6 mm in diameter) were then fixed at predetermined positions onto the slurry surface. Additional binder was poured until the mold was half-filled, followed by vibration compaction. After partial curing, the rebars were temporarily extracted, and anchoring agents were injected into the boreholes. The rebars were reinserted in an end-anchored configuration. Subsequently, 500 g of coal gangue grains (pre-screened to the designated size range) were thoroughly mixed with the binder and poured to fill the remaining mold space. Vibration compaction and surface leveling were performed, followed by the same post-processing steps as for unbolted specimens. Following curing completion, epoxy resin-based anchoring adhesive was selected as the grouting material. With an anchorage length of 8 cm, the specimens were fabricated with installed bolts, cured for 24 h, and subsequently subjected to a pre-tightening force of 0.5 kN applied via a torque wrench after complete hardening. The final specimens are illustrated in Figure 3.

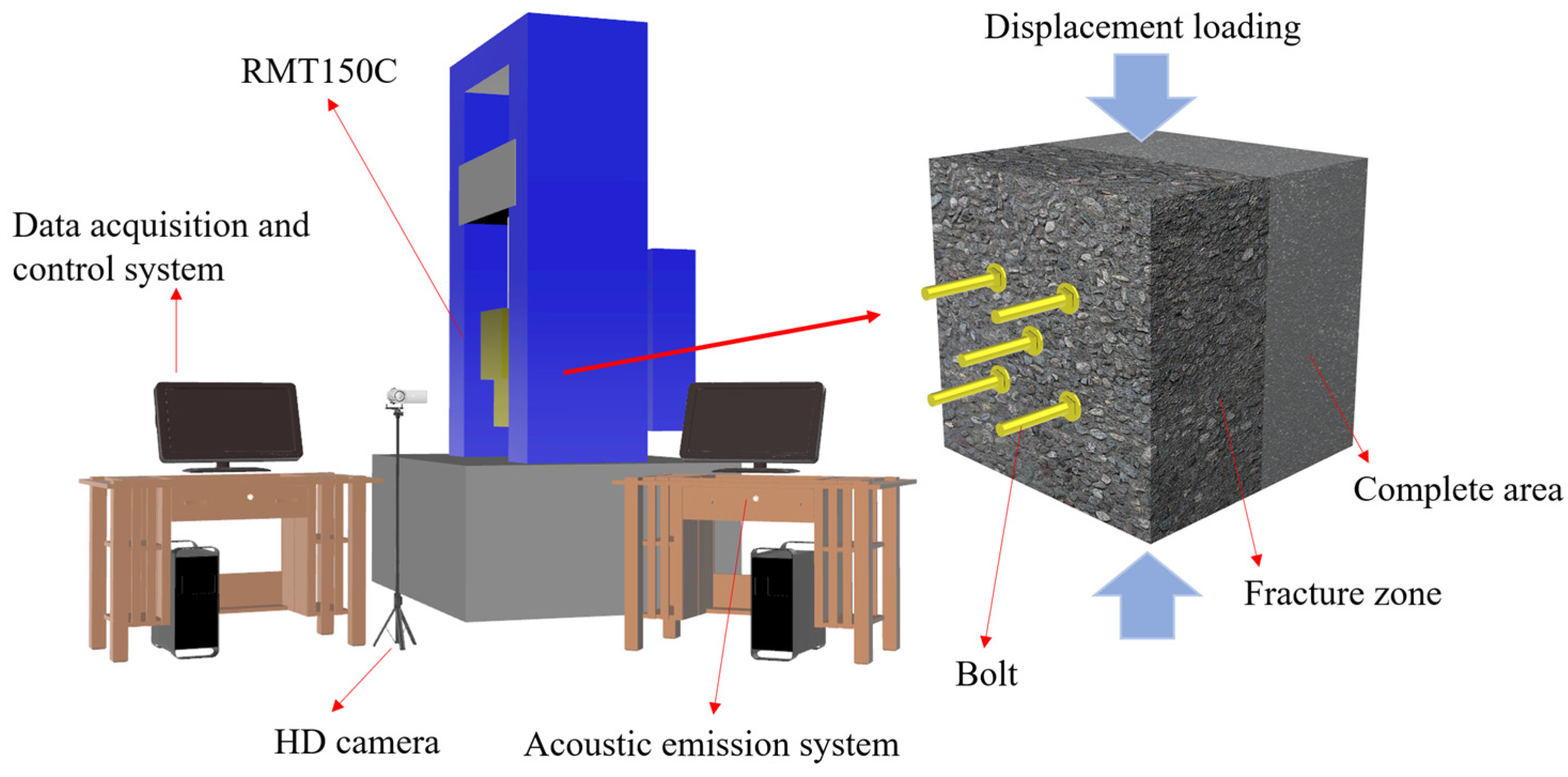
2.2. Test Platform and Test Process

The test was conducted on an RMT-150C electro-hydraulic servo testing machine (manufacturer: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, China) under uniaxial loading conditions (Figure 4), with a loading rate of 0.02 mm/s, the maximum displacement of 25 mm, and the maximum axial pressure of 1300 kN. Electrical resistance strain gauges (BX120-3AA, manufacturer: Beijing Yiyang Strain and Vibration Testing Technology Co., Ltd., Beijing, China) were affixed to the specimen surface to monitor strain. A PCI-2 32-channel acoustic emission monitoring system (manufacturer: Mistras Group, Princeton, NJ, USA) was employed to capture acoustic emission signals generated during specimen failure. The RMT-150C machine recorded the axial force and displacement in real time throughout the loading. The test was terminated when the displacement reached 25 mm, at which point the machine ceased vertical velocity application.

3. Analysis of Test Results of Composite Rock Mass

3.1. Mechanical Properties of Composite Rock Mass

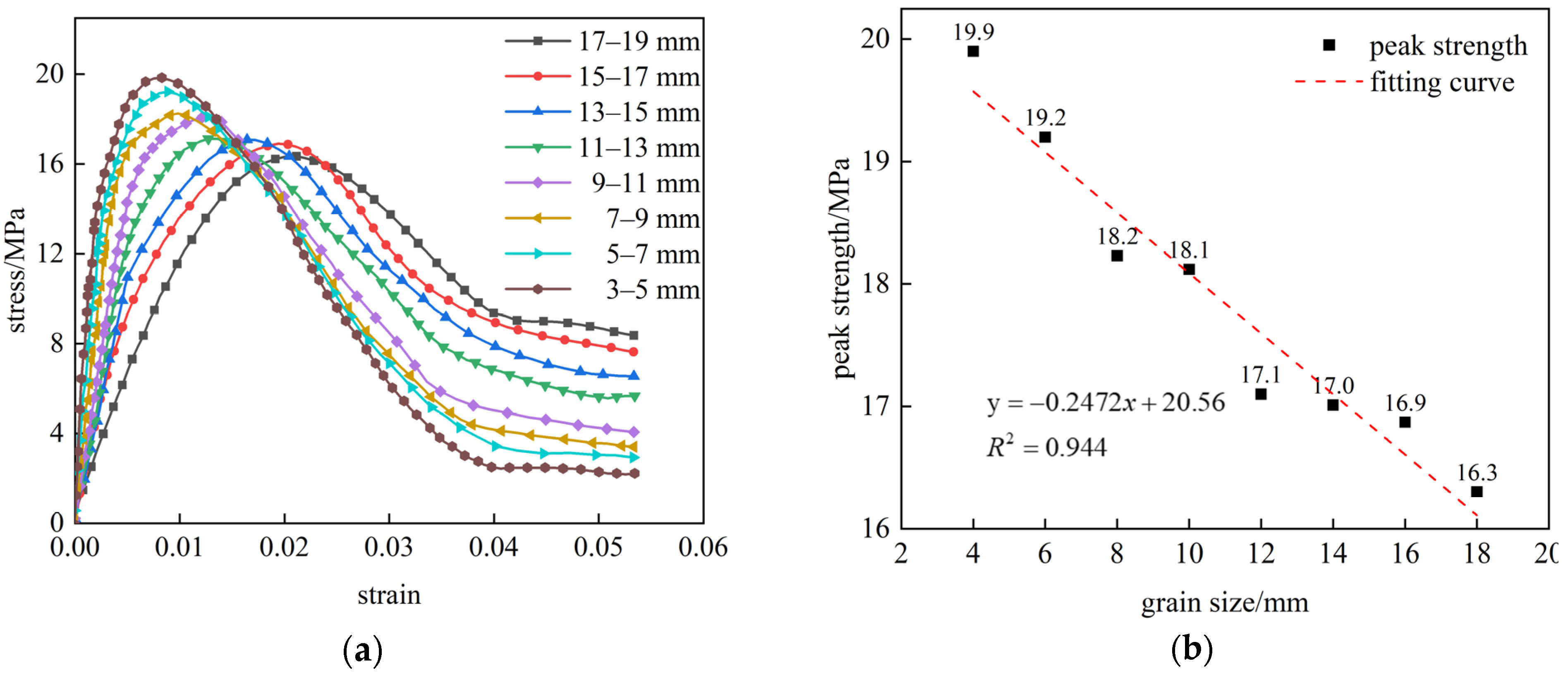
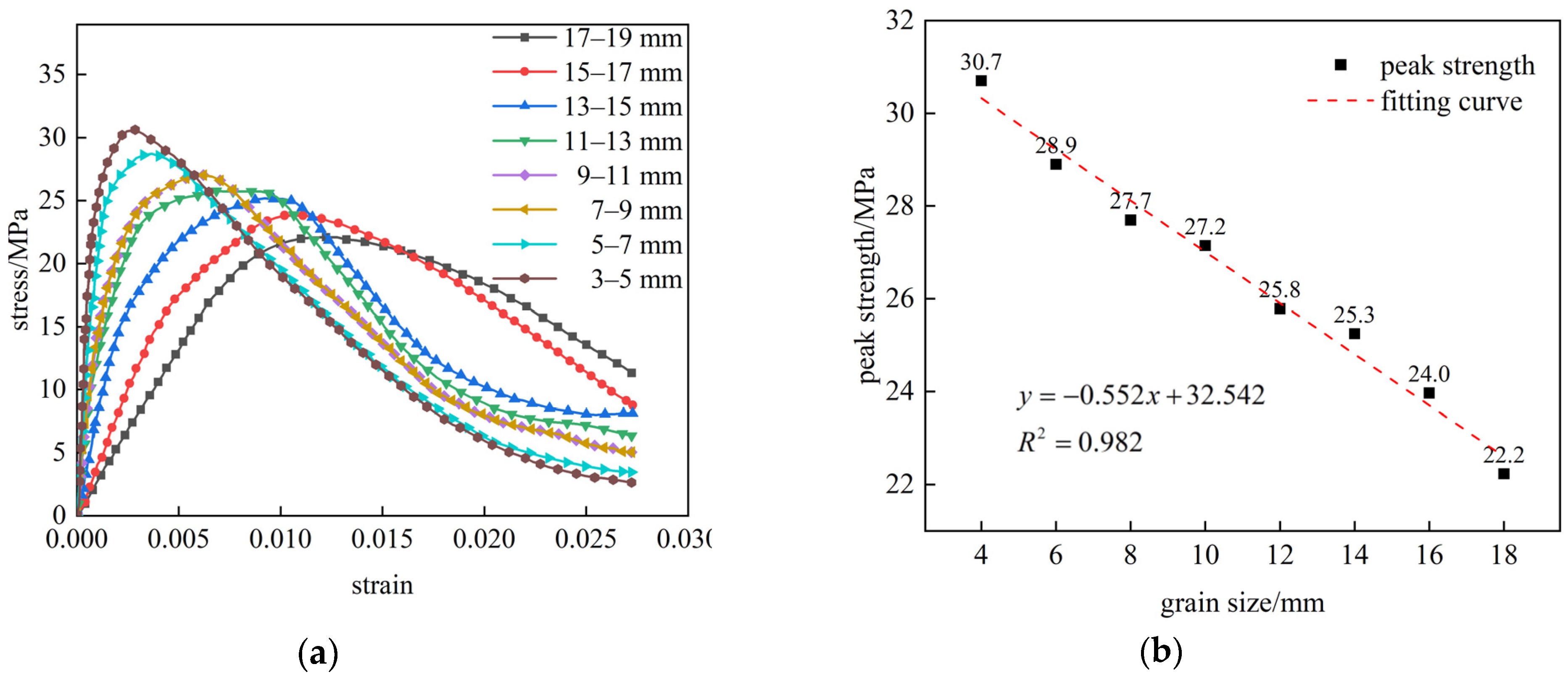
3.1.1. Stress–Strain Curve

Figure 5a shows the stress–strain curves of the unbolted composite rock specimens under different grain size conditions, and Figure 5b displays the peak strengths of the unbolted composite rock specimens under different grain size conditions. The analysis of Figure 5 reveals that the peak strengths of the unbolted composite rock specimens are concentrated in the range of 15–20 MPa. The peak strengths for grain sizes of 3–5 mm, 5–7 mm, 7–9 mm, 9–11 mm, 11–13 mm, 13–15 mm, 15–17 mm, and 17–19 mm are 19.90 MPa, 19.20 MPa, 18.23 MPa, 18.12 MPa, 17.10 MPa, 17.01 MPa, 16.87 MPa, and 16.30 MPa, respectively, indicating a gradual decrease in peak strength with increasing grain size. The analysis of Figure 5a shows that the post-peak strength decline rate of the unbolted composite rock specimens becomes slower as the grain size increases, with more pronounced plastic characteristics.

Figure 6a presents the stress–strain curves of the bolted composite rock specimens under different grain size conditions, and Figure 6b illustrates the peak strengths of the bolted composite rock specimens under different grain size conditions. The analysis of Figure 6 demonstrates that after the addition of rockbolts, the compressive strength of the composite rock specimens increases significantly, with the peak strengths ranging from 20 to 35 MPa. The peak strengths for the grain sizes of 3–5 mm, 5–7 mm, 7–9 mm, 9–11 mm, 11–13 mm, 13–15 mm, 15–17 mm, and 17–19 mm are 30.7 MPa, 28.90 MPa, 27.70 MPa, 27.15 MPa, 25.79 MPa, 25.25 MPa, 23.97 MPa, and 22.23 MPa, respectively, showing an approximately linear decreasing trend in peak strength with increasing grain size.

The comparative analysis of Figure 5 and Figure 6 indicates that the variation of the peak strength with the grain size follows a similar pattern for both the bolted and unbolted composite rock specimens. However, the bolted specimens exhibit significantly higher peak strengths compared to the unbolted specimens. For example, the peak strengths for the grain sizes of 3–5 mm, 9–11 mm, and 17–19 mm increase by 54%, 51%, and 36%, respectively, demonstrating a marked enhancement in the failure resistance of the bolted composite rock specimens. Additionally, the overall deformation of the bolted specimens is smaller than that of the unbolted specimens, and the plastic characteristics become more pronounced with increasing the grain size in the bolted specimens.

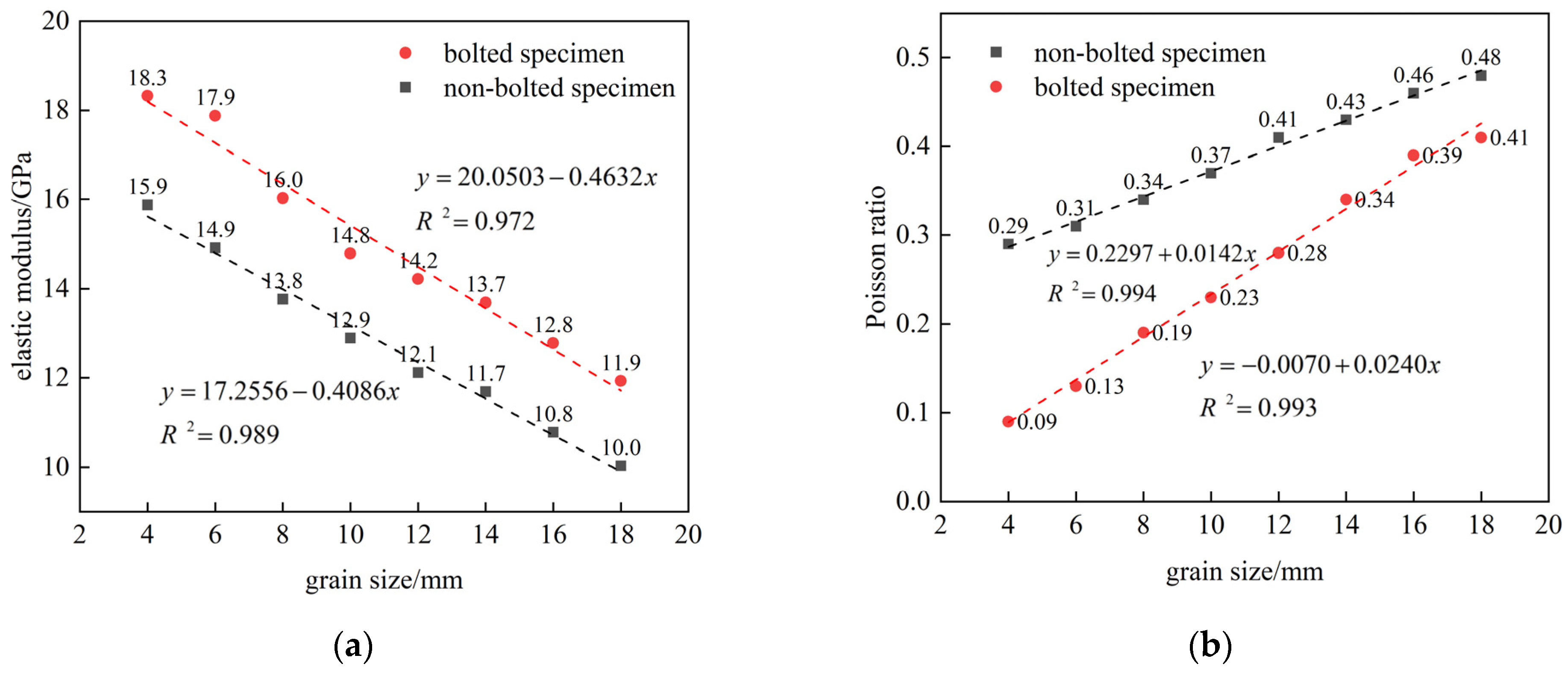
3.1.2. Elastic Modulus and Poisson’s Ratio

Figure 7a shows the elastic modulus of the unbolted and bolted composite rock specimens under different grain size conditions, and Figure 7b displays the Poisson’s ratio of the unbolted and bolted composite rock specimens under different grain size conditions. The analysis of Figure 7a reveals that the elastic modulus of both the unbolted and bolted composite rock specimens gradually decreases with increasing the grain size. Moreover, the elastic modulus of the bolted composite rock specimens is significantly higher compared to that of unbolted specimens. The analysis of Figure 7b indicates that the Poisson’s ratio of both the unbolted and bolted composite rock specimens gradually increases with increasing the grain size. However, the Poisson’s ratio of the bolted composite rock specimens is markedly reduced relative to that of the unbolted specimens.

3.2. Analysis of Crack Propagation in Composite Rock Mass

3.2.1. Crack Propagation of Unbolted Composite Rock Mass

The crack propagation in the composite rock specimens at different stages was recorded using a high-speed camera (pco.1200hs, manufacturer: Cooke Corporation, Eliot, ME, USA). SJ-01, SJ-02, SJ-03, SJ-04, and SJ-05 represent the unbolted composite rock specimens with the grain sizes of 7–9 mm, 9–11 mm, 11–13 mm, 13–15 mm, and 15–17 mm, respectively.

Table 1. Crack propagation of unbolted specimen.

Number	(a) Initial Cracks	(b) Peak Stress Stage	(c) End of Loading	(d) Side Failure of Specimen
SJ-01
SJ-02
SJ-03
SJ-04
SJ-05

details the crack propagation process of the unbolted composite rock specimens under uniaxial compression.

During the initial loading stage of the specimen SJ-01, a tensile crack (1) parallel to the loading direction initiated at the specimen edge and propagated toward both ends. As loading continued, U-shaped cracks (2,3) formed at the specimen ends. Although spalling occurred in regions (2,3), no significant structural damage was observed until the crack (1) fully penetrated the specimen, causing a loss of bearing capacity and unstable failure.

In the specimen SJ-02, a tensile crack (1) parallel to the loading direction first formed in the central region during initial loading. Additional tensile cracks parallel to the loading direction subsequently developed on both sides. The cracks (1,3) propagated to the specimen ends, resulting in structural fracture.

For the specimen SJ-03, a tensile crack (1) along the loading direction appeared on the left side during the initial loading, followed by a tensile crack (2) on the right side and a transverse crack (3) at the lower end. Continued loading caused spalling in region (3), and the crack (1) propagated through the specimen, leading to failure.

In the specimen SJ-04, cracks initiated at the upper-left (1) and lower bilateral regions (2,3) during the initial loading. The crack (1) rapidly propagated and caused surface spalling, while the cracks (2,3) extended along the loading direction until the specimen lost bearing capacity.

For the specimen SJ-05, a tensile crack (1) parallel to the loading direction formed on the right side during the initial loading and gradually extended toward both ends. When the crack (1) reached the ends, it deflected and propagated densely until failure.

Column (d) of Table 1 shows the side crack distribution of the unbolted specimens after loading. The smaller grain-sized specimens SJ-01 and SJ-02 exhibited tensile cracks parallel to the loading direction, while SJ-03 displayed mixed tensile-shear cracks. The specimens SJ-04 and SJ-05 showed cracks oriented at approximately 30° to the loading direction, dominated by shear cracks.

The analysis of crack propagation in the unbolted specimens reveals that tensile cracks parallel to the loading direction initiate during the initial loading stage, propagate to the specimen ends with continued loading, and ultimately cause tensile failure and a loss of bearing capacity.

3.2.2. Crack Propagation of Bolted Composite Rock Mass

Table 2. Crack propagation of bolted specimen.

Number	(a) Initial Cracks	(b) Peak Stress Stage	(c) End of Loading	(d) Side Failure of Specimen
LJ-01
LJ-02
LJ-03
LJ-04
LJ-05

presents the crack propagation process of the bolted composite rock specimens under uniaxial compression. LJ-01, LJ-02, LJ-03, LJ-04, and LJ-05 represent the bolted composite rock specimens with the grain sizes of 7–9 mm, 9–11 mm, 11–13 mm, 13–15 mm, and 15–17 mm, respectively.

During the initial loading stage of the specimen LJ-01, a tensile crack (1) parallel to the loading direction initiated between the rockbolts, and a fine crack (2) formed at the lower-right corner. As loading continued, the cracks (1,2) propagated toward the rockbolts and ceased extending upward. Both cracks then deflected, forming a crack (3) perpendicular to the loading direction. With further propagation of the cracks (1,2,3), a tensile crack (4) emerged at the intersection of the cracks (1,3) with the rockbolts and extended toward the upper end. The crack (1,4) propagated along the loading direction until reaching the specimen ends, causing failure.

For specimen LJ-02, fine cracks initiated on the left side and lower-right corner during the initial loading. Upon contacting a rockbolt, the crack (1) ceased propagating in its original direction and deflected toward the upper-left corner. Near the peak strength, a tensile crack (3) formed and propagated along the loading direction. The crack (3) stopped extending upon contacting the rockbolts, while the crack (2) caused spalling at the lower-right corner. The crack (1) eventually penetrated the specimen, leading to failure.

The crack propagation in the specimen LJ-03 was similar to that in LJ-01. During the initial loading, tensile cracks (1,2) parallel to the loading direction formed between the rockbolts, and an inverted V-shaped crack appeared at the lower-right corner. Upon contacting the rockbolts, the cracks (1,2) generated a perpendicular crack (4) that propagated and intersected between the two rockbolts. The cracks (1,2) did not reach the upper end but extended to the lower end, resulting in failure.

In the specimen LJ-04, a tensile crack (1) parallel to the loading direction initiated at the lower-right corner during the initial loading, propagating toward the ends with minor spalling. Near the peak strength, tensile cracks (2,3) parallel to the loading direction formed between the rockbolts. The crack (3) deflected toward the upper-left after contacting a rockbolt. The continuous propagation of the crack (3) through the specimen caused loss of bearing capacity.

For the specimen LJ-05, a tensile crack (2) parallel to the loading direction initiated at the lower-left corner during the initial loading and propagated toward the ends. Tensile cracks (1,3,4) initiated at the rockbolts and extended toward the ends. The cracks (4,5) merged into a main crack during propagation. Failure occurred as the cracks intersected and propagated further.

Column (d) of Table 2 shows the side crack distribution of the bolted specimens after loading. The smaller grain-sized specimens LJ-01 and LJ-02 exhibited tensile cracks parallel to the loading direction, while LJ-03 displayed mixed tensile-shear cracks. The specimens LJ-04 and LJ-05 showed cracks oriented at varying angles to the loading direction, dominated by shear cracks. As the grain size increased, shear cracks became more prominent, indicating a transition from tensile to shear crack failure modes.

Compared to the unbolted specimens, the bolted specimens exhibited distinct crack propagation behaviors.The prestressed rockbolts altered the stress state of the composite rock, forming a reinforced zone. The rockbolts suppressed crack propagation within this zone through weakening, deflection, and arrest effects. For example, cracks contacting the rockbolts were weakened (e.g., the crack 3 in LJ-02, the crack 1 in LJ-03), deflected (e.g., the crack 1 in LJ-02, the crack 3 in LJ-04), or arrested (e.g., the crack 3 in LJ-01, the crack 3 in LJ-05). However, the rockbolts could not prevent the formation of new cracks, as stress concentration near the bolt holes sometimes induced additional cracks (e.g., the crack 1 in LJ-05).

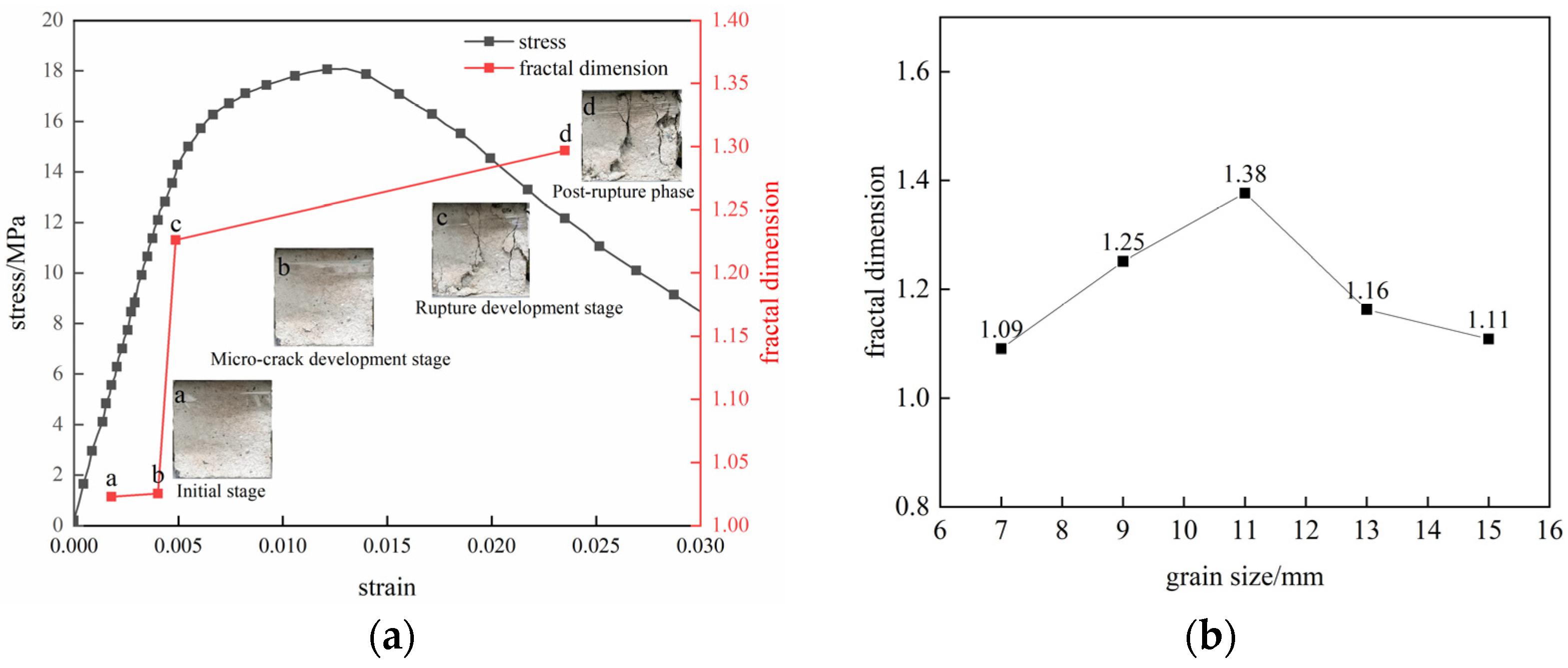
3.2.3. Study on Fractal Characteristics of Combined Rock Mass Fractures

The fractal dimension can characterize the relationship between the surface and crack structure evolution in specimens, correlating with the complexity, heterogeneity, surface roughness, and regularity of internal structures [16,17,18,19,20,21,22]. The fractal theory was applied to study the non-bolted composite rock masses. The definition of the fractal box-counting dimension is as follows: Let A be any non-empty bounded subset in Rⁿ. For any r > 0, let N_r(A) denote the minimum number of n-dimensional cubes with edge length r required to cover A. If there exists d such that r → 0,

$$N_r\left(A\right)=c/r^d$$

(1)

then d is termed the box-counting dimension of A, where N_r(A) is the minimum number of boxes with characteristic scale r covering the crack set A, and c is a proportionality constant.

$$\mathit{lg}{N}_r\left(A\right)=\mathit{lg}c-d\mathit{lg}r$$

(2)

$$d={\displaystyle \frac{\mathit{lg}c-\mathit{lg}{N}_r\left(A\right)}{\mathit{lg}r}}$$

(3)

In practical calculations, N_r(A) values were statistically determined for different r. A log-log plot of lg r (horizontal axis) versus lg N_r(A) (vertical axis) was generated. The absolute value of the slope of the fitted line through these points yielded the fractal box dimension of set A.

Using the fractal theory, the fractal dimensions of the overall cracks in different composite specimens were computed.

$$d={\displaystyle \frac{\mathit{lg}c-\mathit{lg}{N}_r\left(A_0\right)}{\mathit{lg}r}}$$

(4)

Here, A₀ represents the set of all surface cracks on the specimen. To ensure comparability, the characteristic scale r was maintained under identical transformation modes. For different crack types within the same specimen, the relative positions of cracks and the specimen were kept consistent. Surface cracks were first processed digitally (Figure 8), followed by a uniform fractal analysis of the binarized images.

The calculated fractal dimensions of the composite specimens are shown in Figure 9. Figure 9a presents the results for the non-bolted composite rock with 9–11 mm grain size. The fractal dimension remained low during the initial loading, slightly increased during the microcrack stable growth stage, and sharply rose in the unstable crack propagation stage as surface cracks densely developed. In the post-failure stage, the fractal dimension continued to increase, but the rate diminished compared to the transition from microcrack to the unstable stages, as crack widening dominated over new propagation.

Figure 9b illustrates the fractal dimension variations for the non-bolted composite rock with different grain sizes. The surface crack fractal dimensions ranged from 1.09 to 1.38, with higher values indicating greater structural complexity.

As a highly heterogeneous geological material [23], rock behavior manifests across the stages: pore–crack compaction, the elastic deformation with stable microcrack growth, the unstable crack propagation, and the post-failure. The fractal dimension evolution aligns closely with the crack propagation: higher damage levels correspond to larger fractal dimensions, quantitatively reflecting the crack development during rock failure.

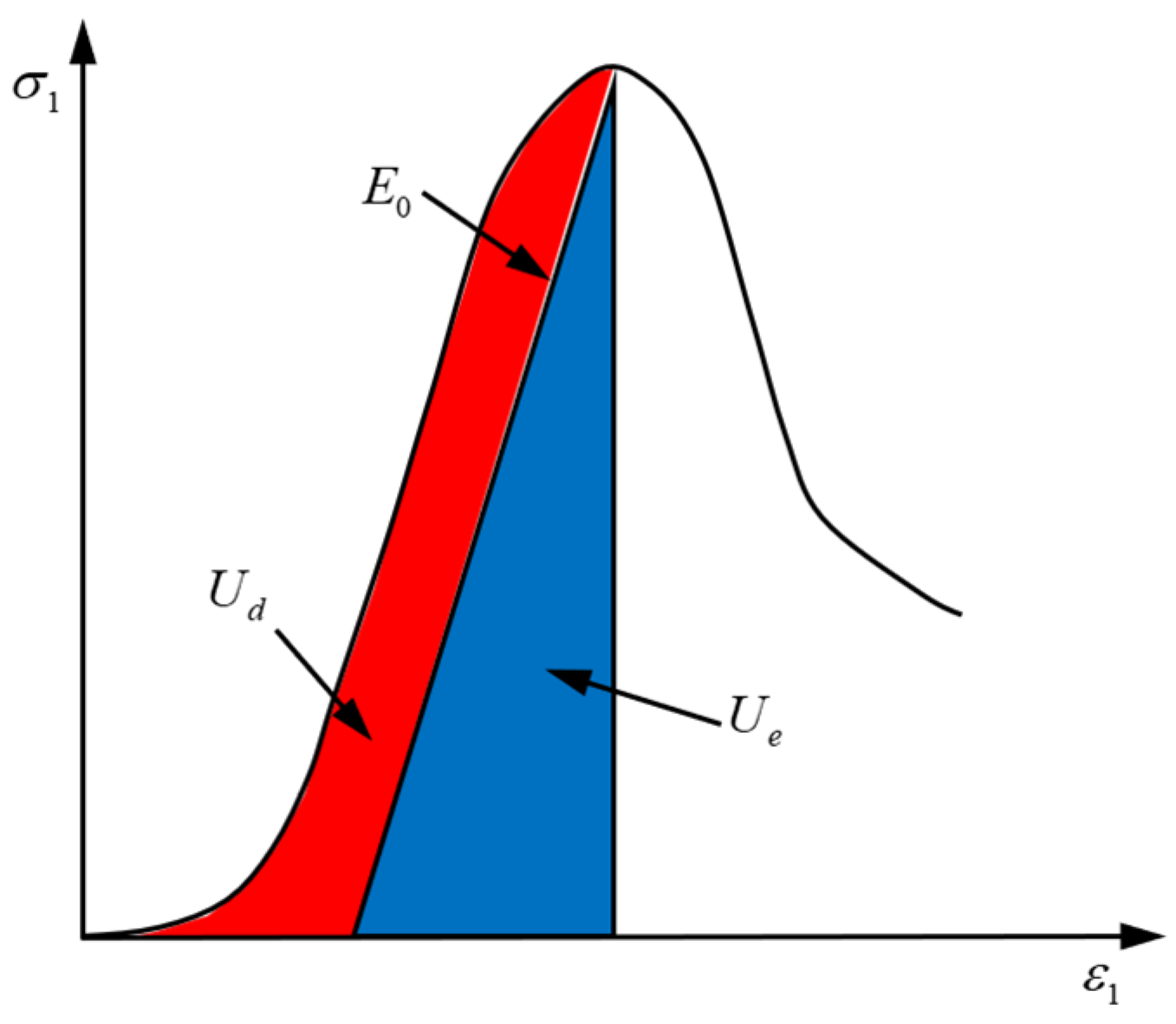
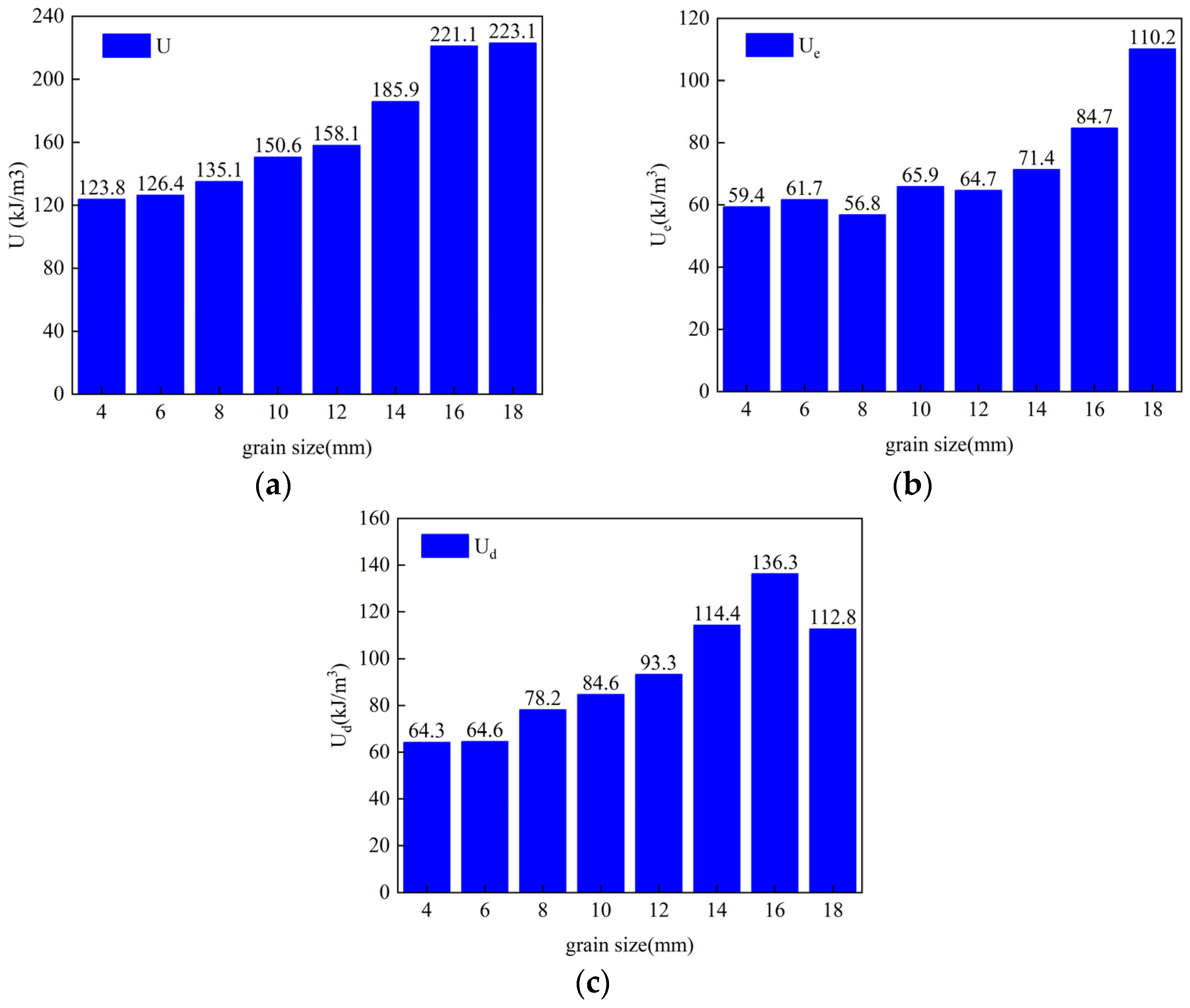
3.3. Energy Evolution of Combined Rock Mass

In analyzing the energy evolution of the composite rock masses, it is assumed that the experimental system is a closed system without heat exchange with the external environment. Under static loading conditions, ignoring the kinetic energy converted by rock ejection near the peak strength of the composite rock masses, the total input strain energy U generated by the axial stress under uniaxial compression is derived from the first law of thermodynamics,

$$U=U_d+U_e$$

(5)

where U_d is the dissipated strain energy and U_e is the releasable elastic strain energy.

As shown in Figure 10, the relationship between U_d and U_e in the stress–strain curve of composite rock masses under uniaxial compression is illustrated [24]. The area enclosed by the stress–strain curve and the unloading elastic modulus E_u (E_u can be approximated by E₀, the initial elastic modulus) represents U_d, which corresponds to energy dissipated by internal damage and plastic deformation. The shaded area denotes U_e, the elastic strain energy released after unloading. Thermodynamic theory indicates that energy dissipation is unidirectionally irreversible, while energy release is bidirectional and reversible under specific conditions.

Since no confining pressure exists in the uniaxial compression tests, only the axial stress contributes to work throughout the process. Thus, the strain energy components can be expressed as

$$U={\int }_0^{{\epsilon }_1}{\sigma }_{1}d{\epsilon }_1$$

(6)

$$U_e\approx {\displaystyle \frac{1}{2E_0}}{\sigma }_1^2$$

(7)

where σ₁ is the axial stress and E₀ is the initial elastic modulus.

Figure 11 displays the strain energy histogram for the non-bolted composite rock masses with varying grain sizes. By calculating the energy parameter variations for eight groups of gangue-like rock masses, it was found that the total input strain energy gradually increases with the grain size. The releasable strain energy shows negligible fluctuations at smaller grain sizes but exhibits significant increases at 15–17 mm and 17–19 mm. The dissipated strain energy generally rises with the grain size, except for a slight decrease in the 17–9 mm group. This is attributed to the declining compressive strength and increasing residual stress intensity of the non-bolted composite rock masses as the grain size grows. Under uniaxial compression, higher total energy input from the axial forces leads to increased conversion into other energy parameters.

Figure 12 presents the strain energy histogram for the bolted composite rock masses. After bolt reinforcement, the compressive strength increases, reducing the total work done by external forces compared to the non-bolted specimens. Consequently, all energy parameters decrease. However, under identical bolting conditions, larger grain sizes still weaken the bearing capacity, leading to gradual increases in the total input energy.

4. Discussion

The roadway sequentially exhibits the fractured and intact zones from the free surface into the deep surrounding rock. As primary support methods, rockbolts and grouting rebind the fractured zone into an integrated mass, forming a bearing structure with the intact zone to collectively control the roadway deformation, as shown in Figure 13. The grain size of the rock blocks within the fractured zone directly influences the mechanical performance of the bearing structure. Thus, this study pioneered the simulation of the roadway surrounding rock fracture zones with varying fragmentation states by incorporating coal gangue grains of different sizes into mortar. These were combined with intact specimens to form the composite rock masses, simulating the combined fractured and intact zones of roadway surrounding rock. Laboratory uniaxial compression tests were conducted to investigate the mechanical properties, the crack propagation processes, and the energy evolution of the both non-bolted and bolted composite rock masses under different grain size influences. The experimental investigation revealed the following:

(1)

For the grouted fractured zones with smaller rock block sizes, the bearing structure exhibits higher strength and greater pressure resistance. However, its post-failure residual strength is low, though still retaining some load-bearing capacity. Reduced friction and interlocking between the small blocks result in weaker overall bearing capacity, consistent with the large-deformation roadway behavior;

(2)

Compared to the small grains, the grouted structures with larger rock blocks show lower initial strength and pressure resistance. However, their post-failure residual strength is higher due to enhanced friction and interlocking between the larger blocks, improving the overall bearing capacity;

(3)

The prestressed rockbolts significantly enhance the mechanical performance of the bearing structure, suppressing the crack propagation within the anchored zone through weakening, deflection, and arrest effects.

The specimens in this experiment were fabricated using similar materials with good homogeneity, yet several experimental considerations require attention. First, during the bolt installation, while vertical alignment should be maintained, the anchor rod displacement inevitably occurs during the layered compaction process of specimen preparation. To simplify the influencing factors and emphasize the grain size effects, the interface stress conditions and the force chain transmission effects were not considered. Second, the confining pressure was disregarded during the uniaxial compression testing of composite rock mass specimens. Therefore, true triaxial tests on the composite rock masses will constitute the subsequent research direction.

5. Conclusions

This study employed laboratory experimental methods to simulate varying states of the roadway surrounding rock fracture zones by incorporating coal gangue grains of different sizes and rock bolts into mortar. These were combined with intact specimens to create fractured–intact composite rock masses. Mechanical testing was conducted, with uniaxial compression tests and crack propagation analysis yielding the following principal conclusions:

(1)

Both the non-bolted and bolted composite rock masses exhibited a gradual decrease in the peak strength with increasing grain size, while their post-peak residual strengths progressively increased. The prestressed rock bolts effectively enhanced both the peak and post-peak residual strengths of the composite rock masses. Compared to the bolted specimens, the non-bolted composite rock masses demonstrated a progressively slower decline rate in the post-peak strength stages as the grain size increased, accompanied by more pronounced plastic characteristics;

(2)

The elastic modulus of both non-bolted and bolted composite rock masses decreases with increasing grain size, while their Poisson’s ratio increases. Bolted composite rock masses exhibit significantly higher elastic moduli than non-bolted counterparts;

(3)

The crack propagation in the composite rock masses evolves through tensile cracks to tensile–shear mixed and shear cracks. With increasing particle size, the shear crack dominance becomes more pronounced. The prestressed bolts exhibit suppressive effects on the crack development within the anchored zones through mechanisms of weakening, deflection, and crack arrest. The variations in the fractal dimension align with the rock crack propagation processes, demonstrating that higher specimen damage levels correspond to greater fractal dimension values;

(4)

The total input energy for both the non-bolted and bolted composite rock masses increases with grain size. The bolted specimens demonstrate stronger bearing capacity, higher compressive strength, and reduced energy parameters compared to the non-bolted ones.