A Geometry-Dependent Void Closure Model Considering Void Deformation and Orientation Changes during Hot Metal Formation
Abstract
:1. Introduction
2. Description of the Meso-Scale Approach
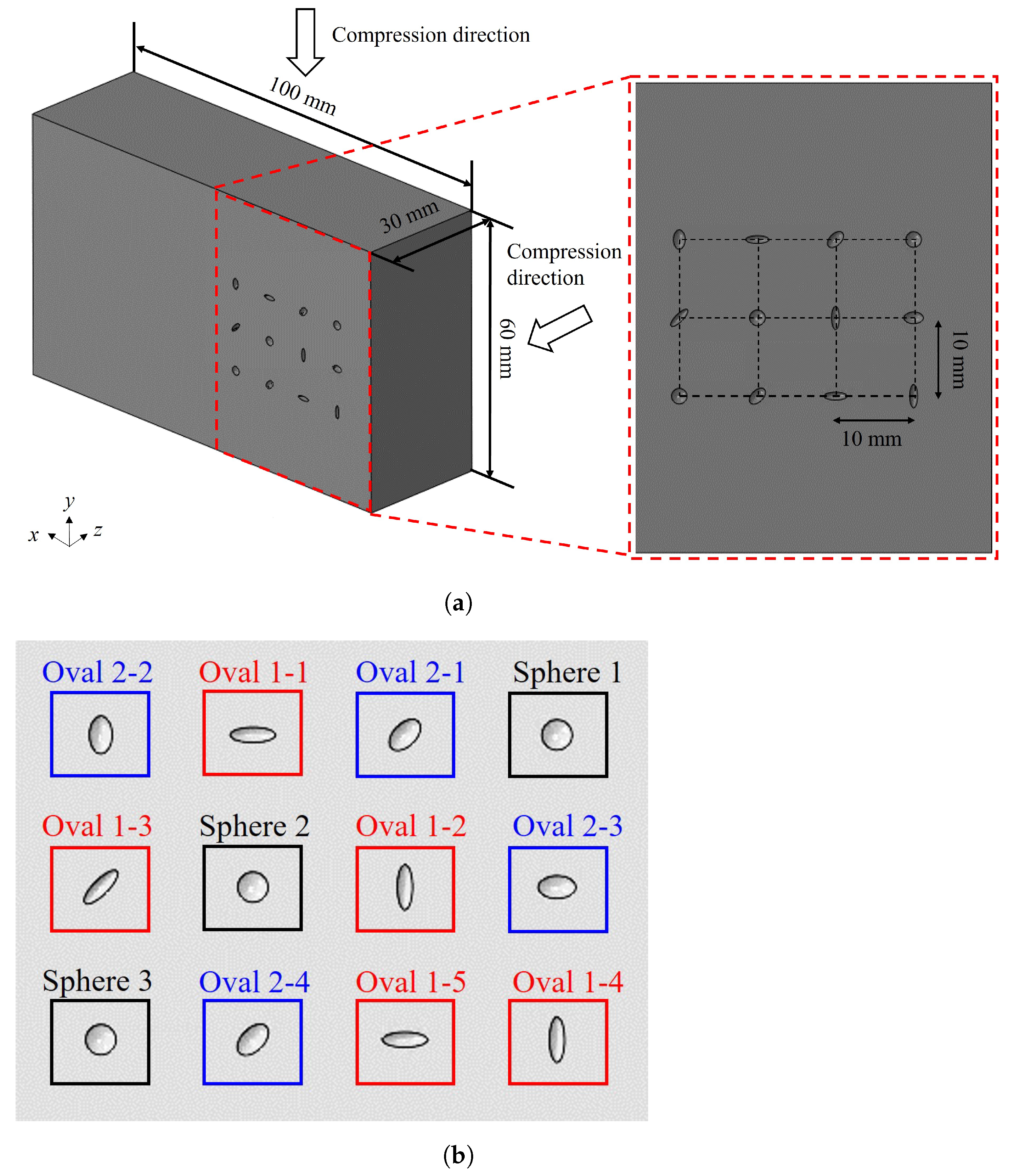
2.1. Representative Volume Element
2.2. Boundary Conditions
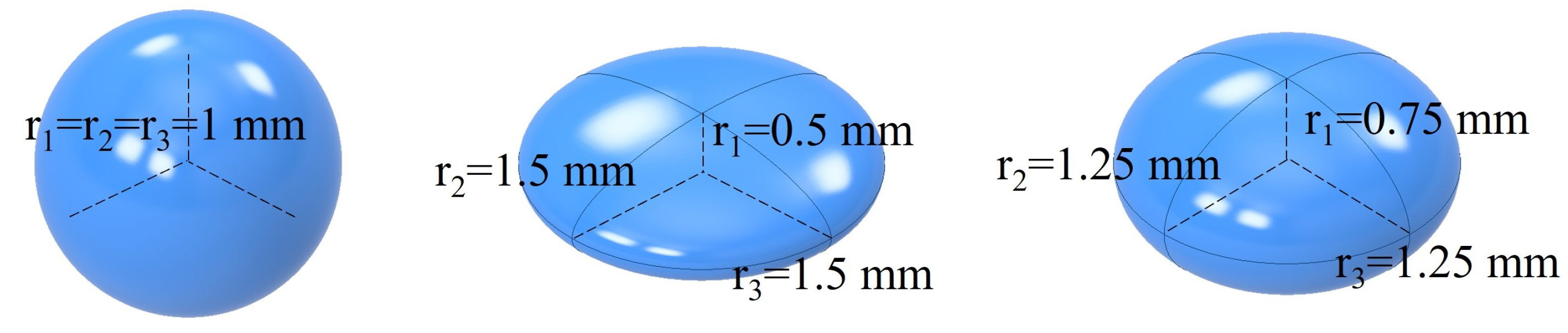
2.3. Equivalent Ellipsoid
3. Void Closure Model
4. Results and Discussion
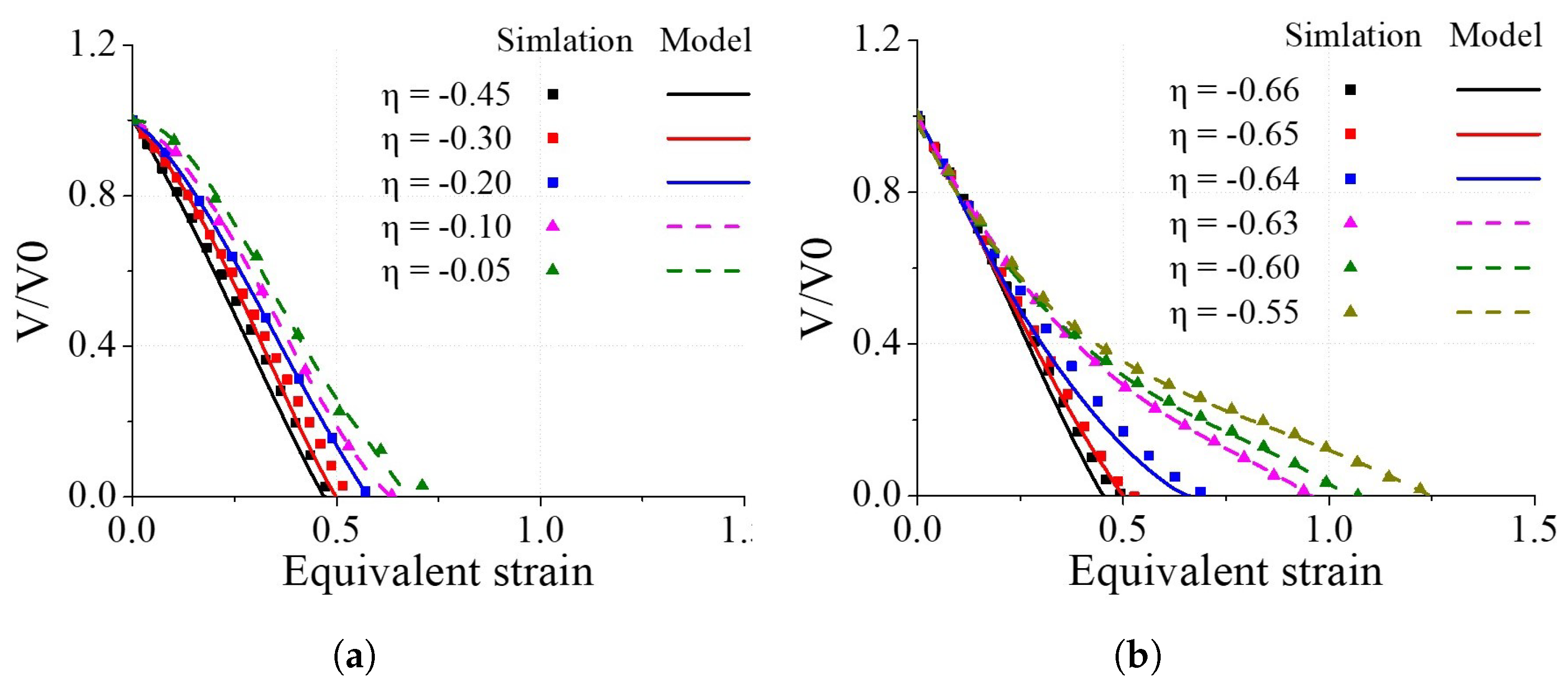
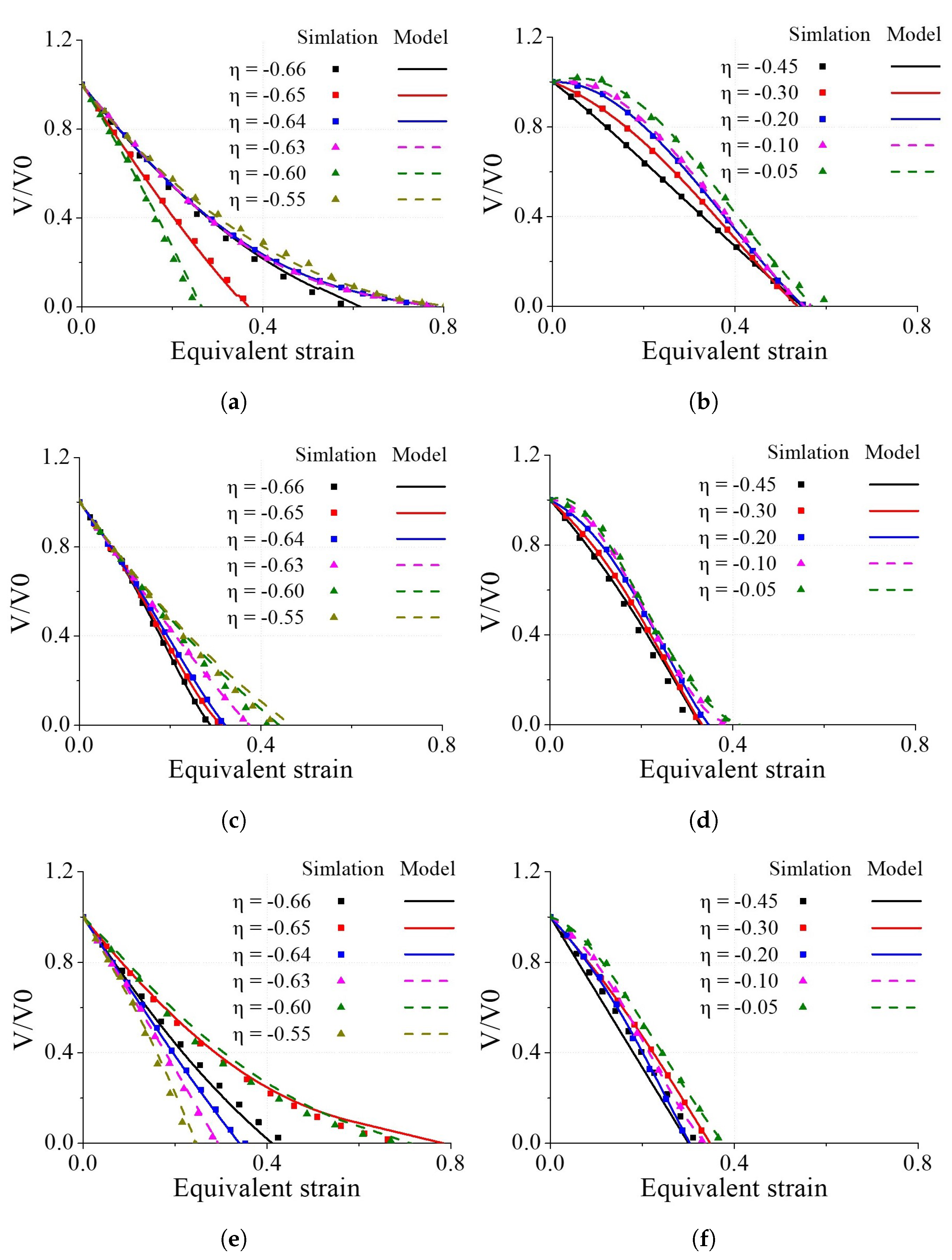
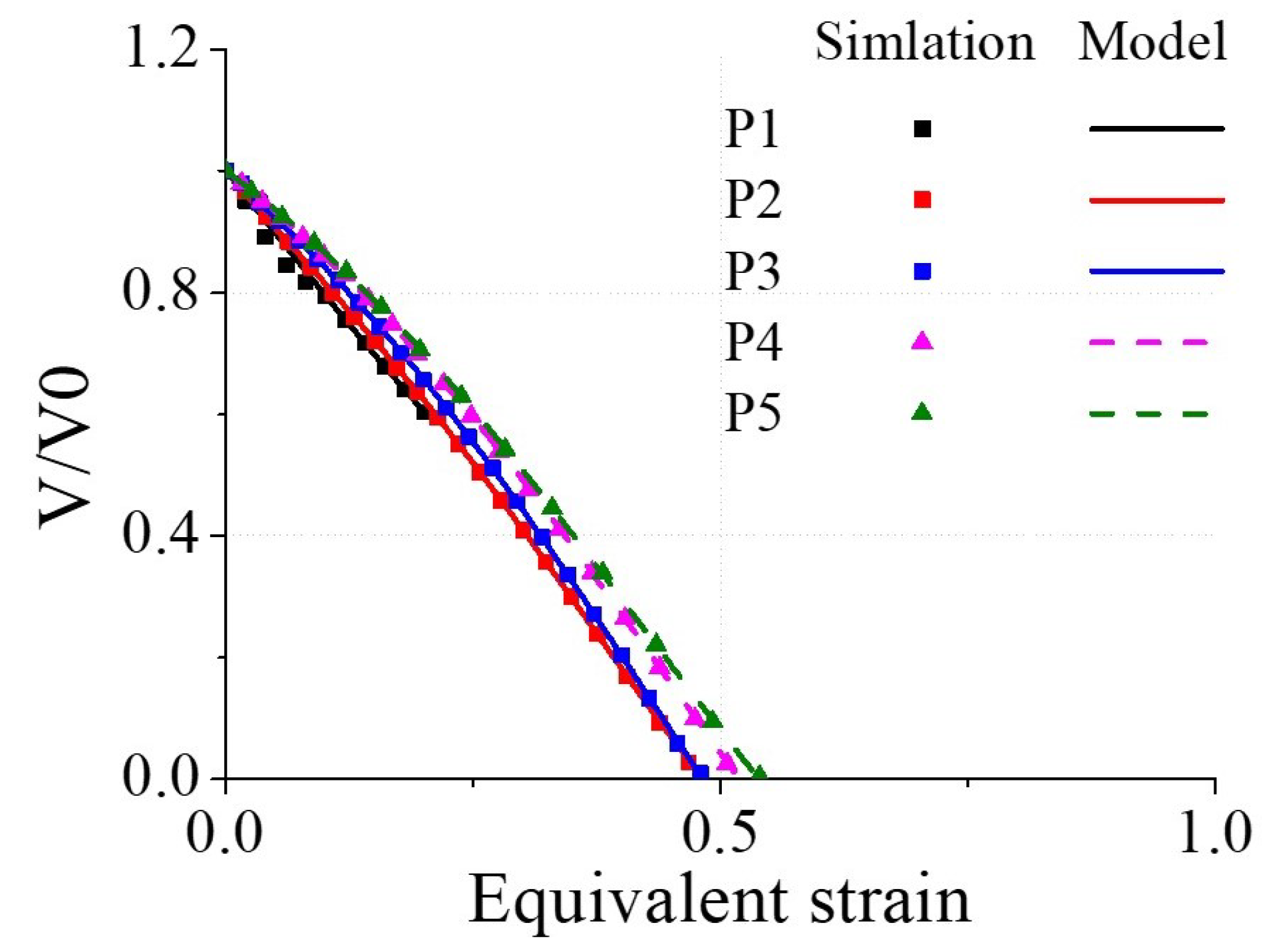
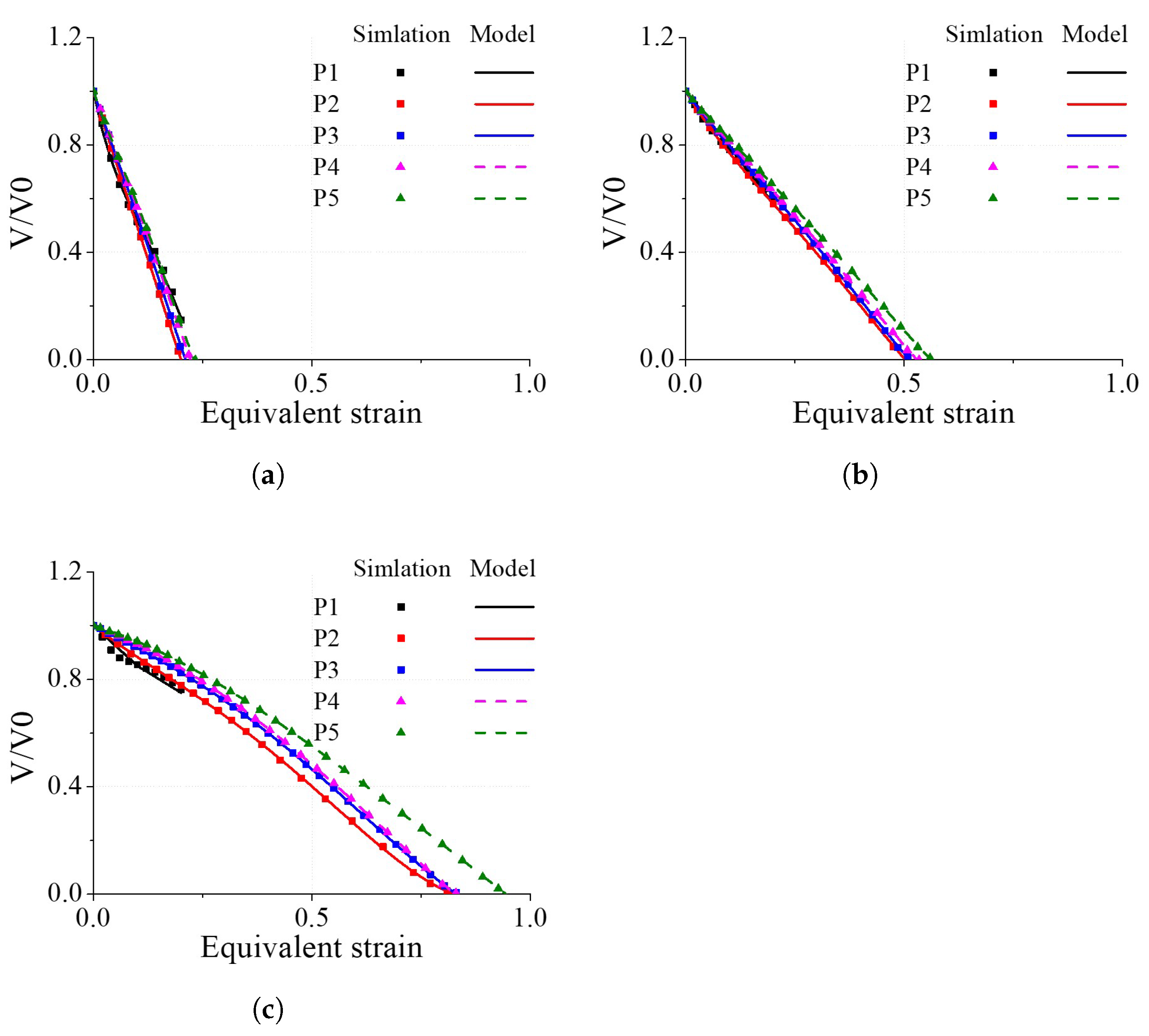
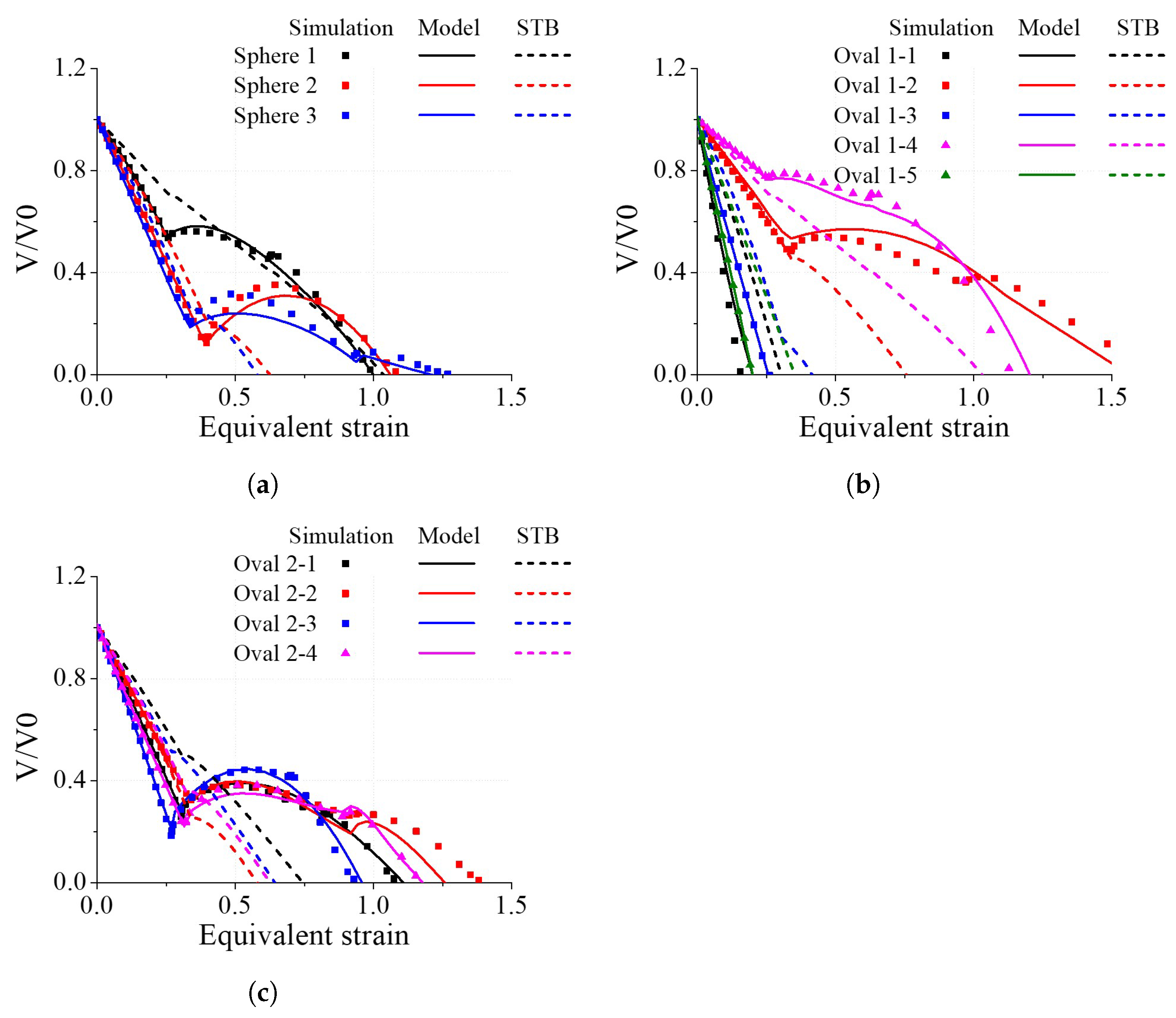
4.1. Void Closure Model Coefficients from RVE Analyses
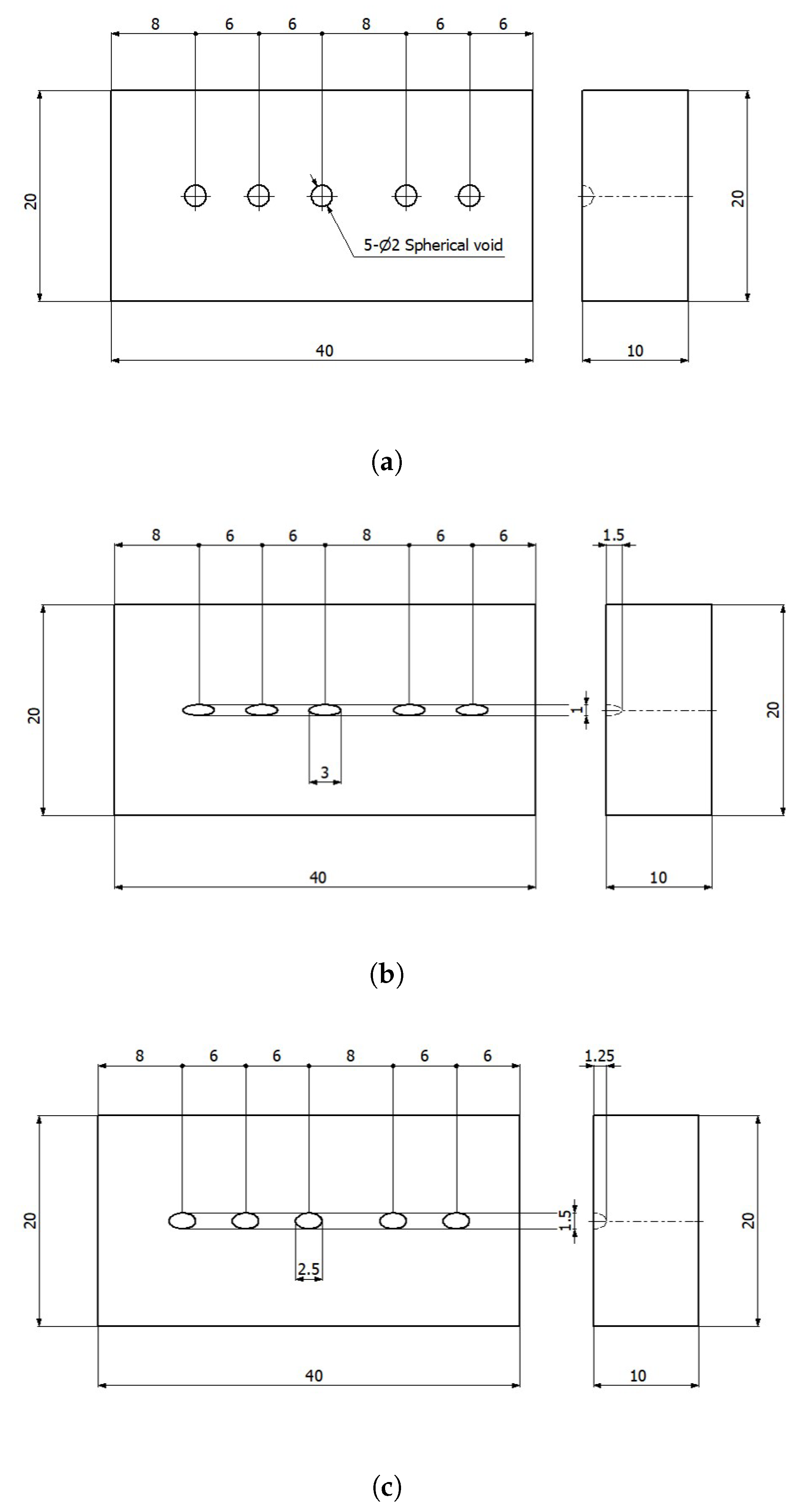
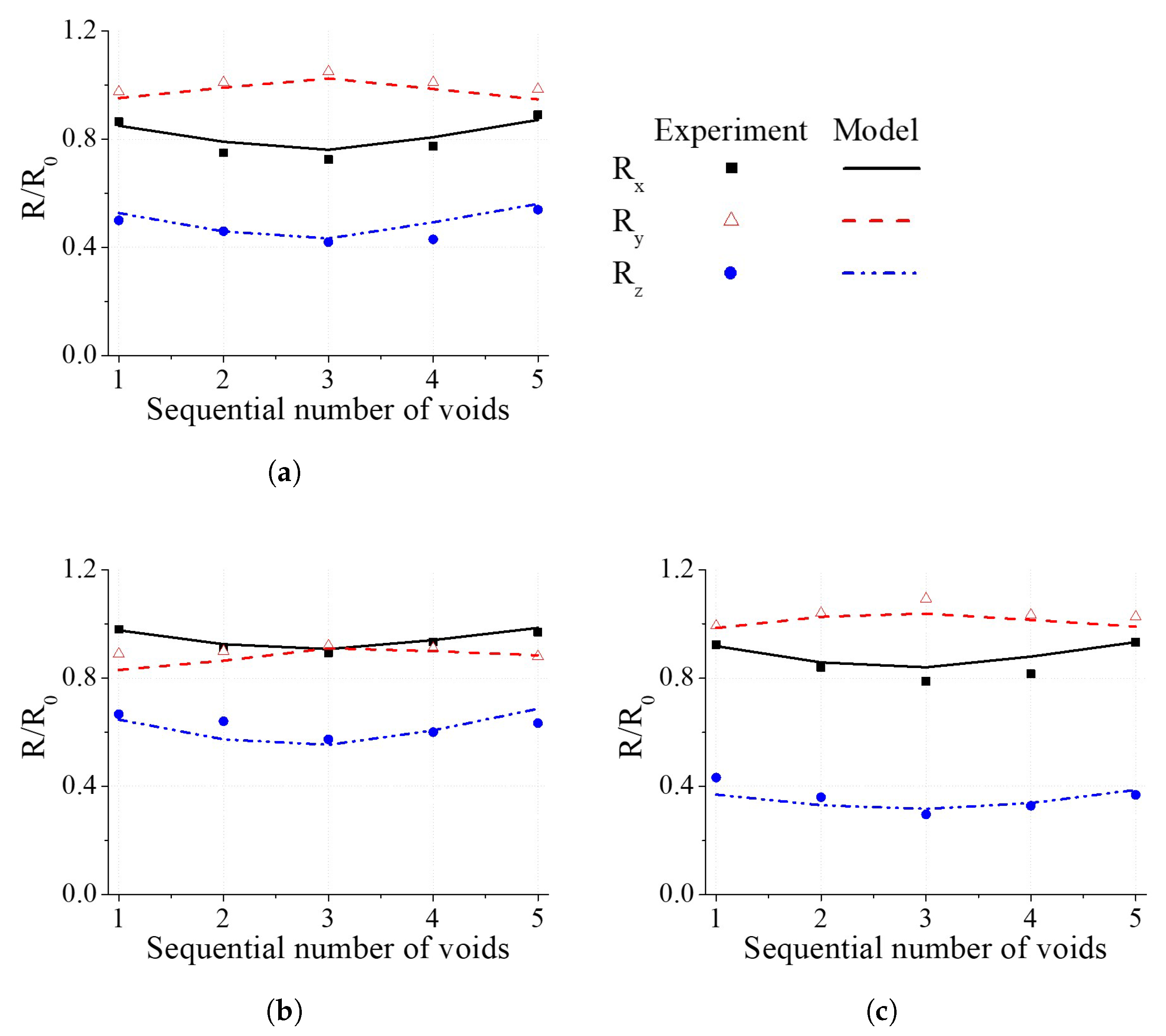
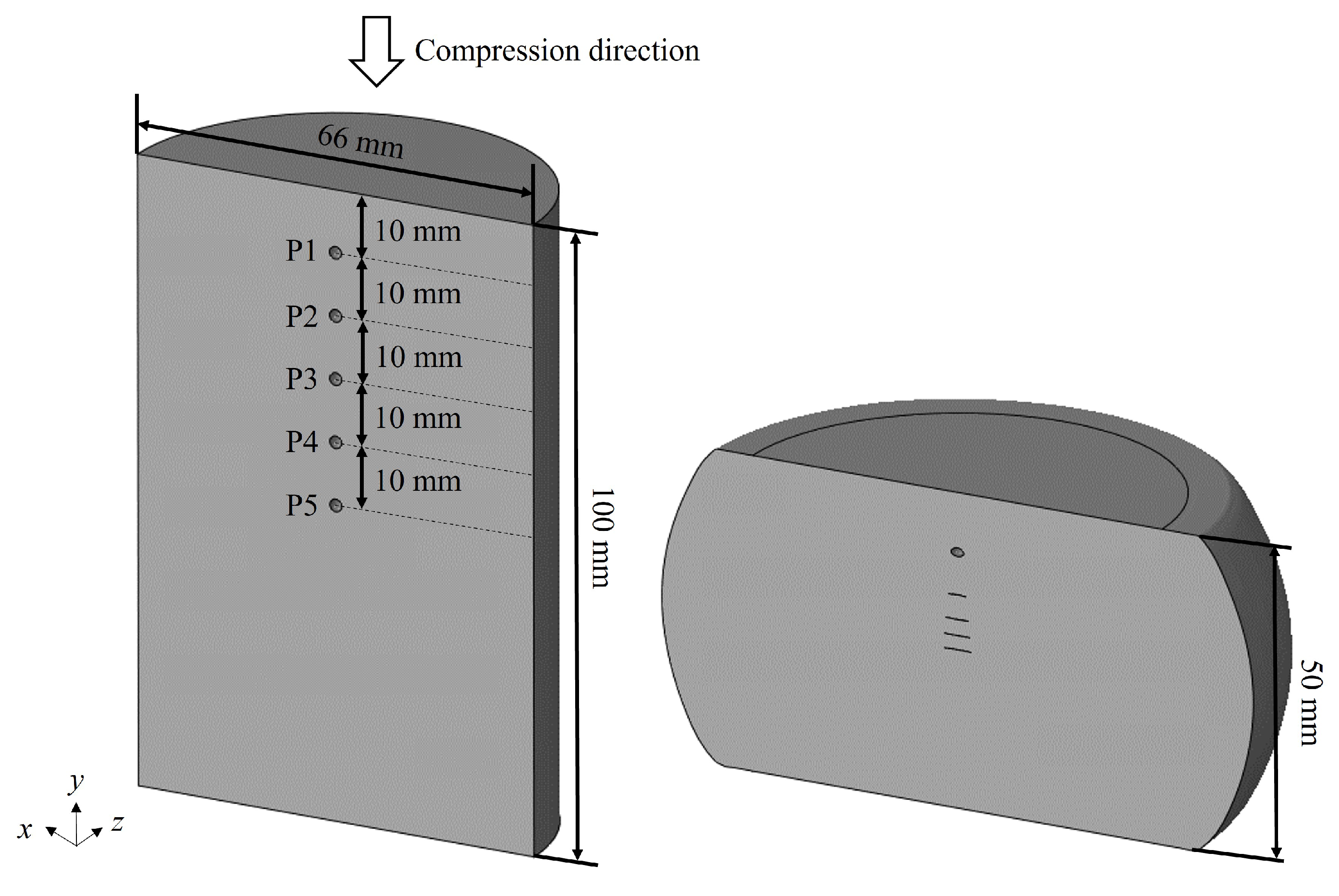
4.2. Experimental Verification of the Void Closure Model
4.3. Void Closure Behaviour in an Upsetting Process
4.4. Void Closure Behaviour in Multi-Stage Compression of a Rectangular Bar
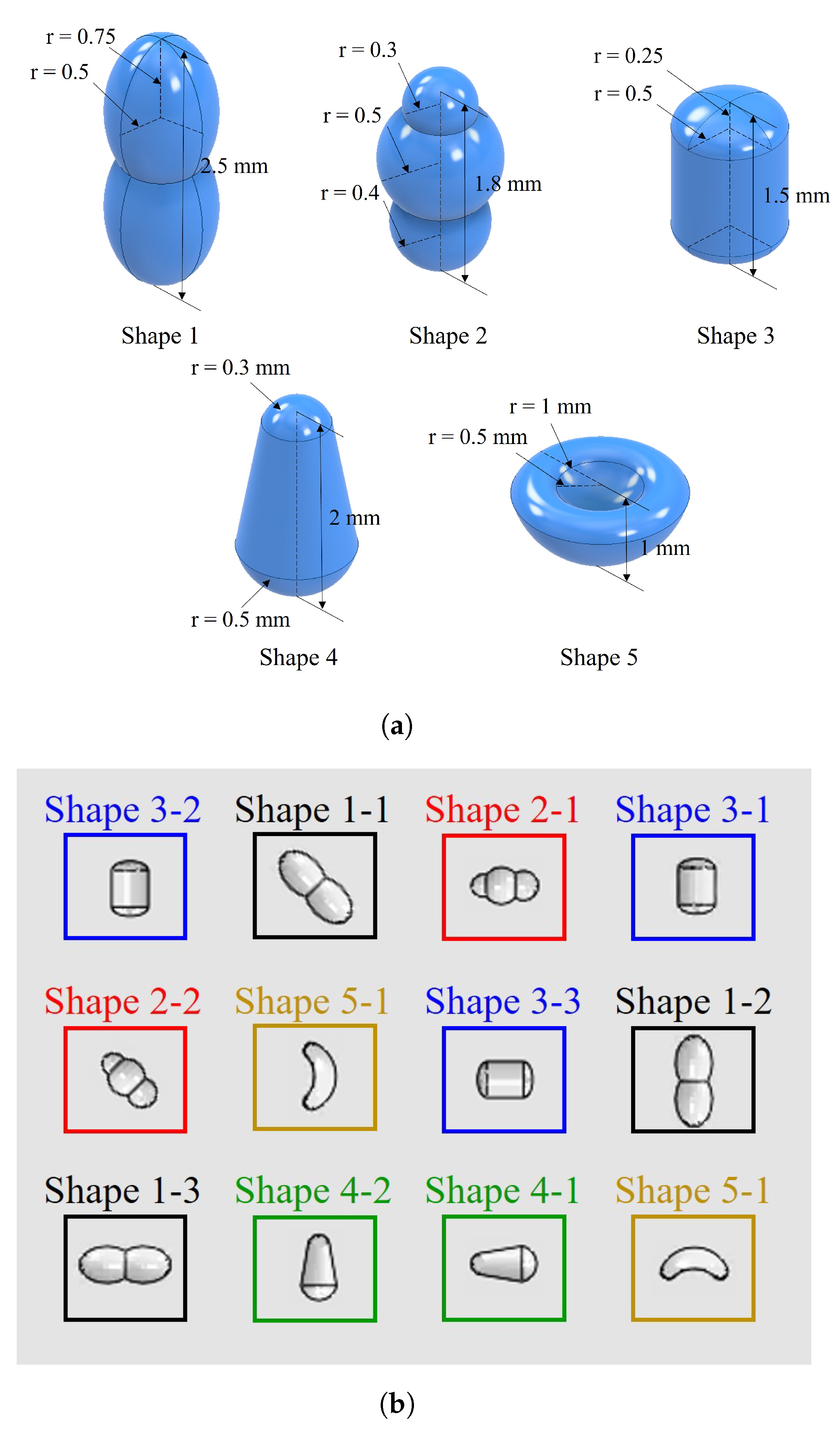
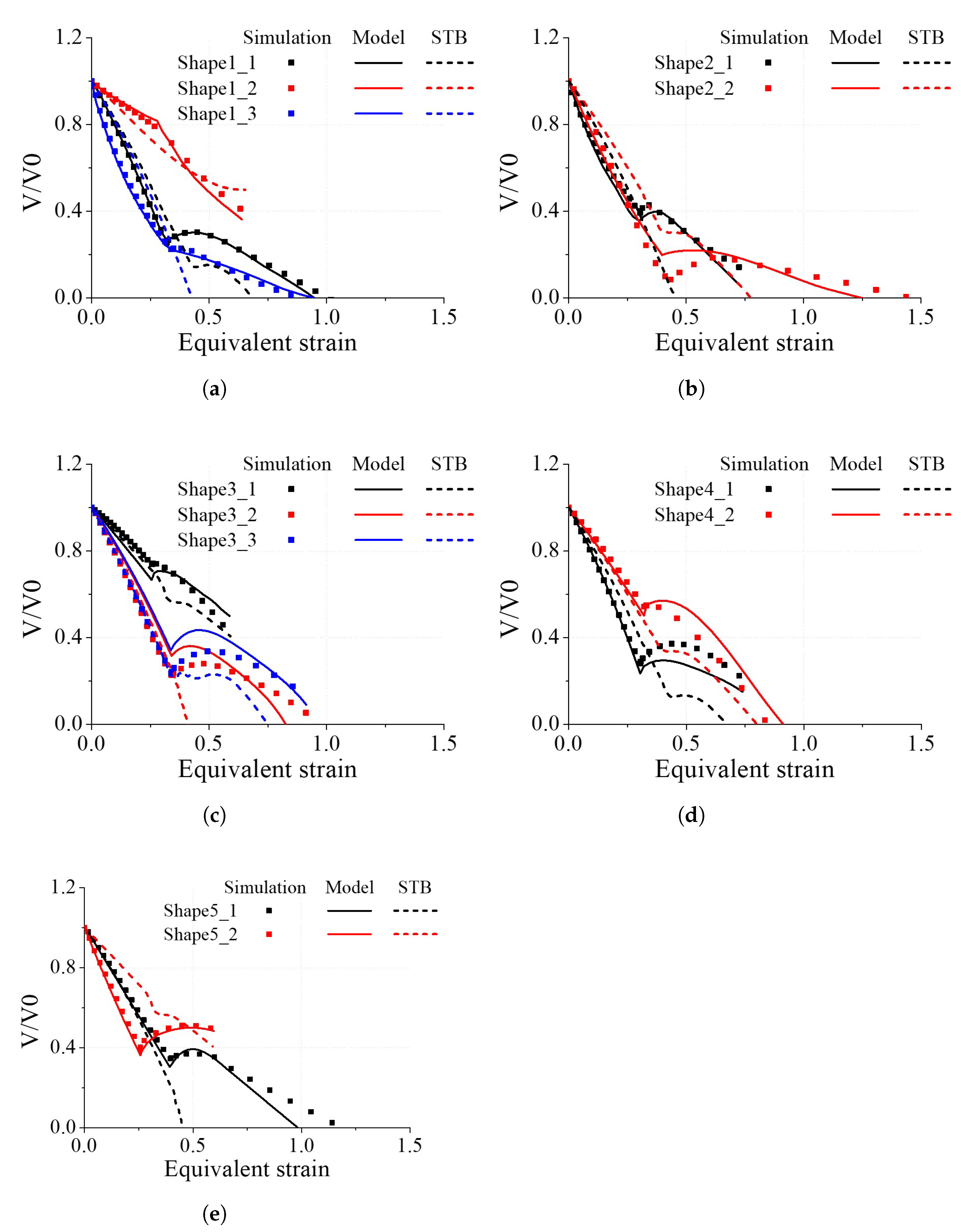
4.5. Void Closure Behaviour of Randomly Shaped Voids
4.6. Application to the Cogging Process
5. Conclusions
- Through RVE analysis, it was observed that void closure behaviour differed depending on the Lode angle when considering the same void shape and orientation. Additionally, in most cases, it was observed that voids tended to close more effectively as the triaxiality decreases.
- In some cases, there was a lack of significant correlation between the closure behaviour of the voids and the triaxiality. In these cases, it was observed that the compression displacement of the ellipsoidal voids had a more considerable influence compared to the triaxiality.
- It was observed that, when the compression amount was significant along the major axis of the void while minimal deformation occurred along the minor axis, an increase in the initial void volume was observed. Additionally, in the case of multi-stage compression of a rectangular bar, an increase in void volume was observed when the compression direction was changed.
- When the proposed void closure model was applied to the compression of cylindrical billets, forging of rectangular billets, and cogging processes, it successfully predicted the void volume changes during the processes. In particular, it was able to predict complex behaviours, such as an increase in void volume. Furthermore, the model was able to predict the void closure behaviour of voids with random shapes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Dudra, S.P.; Im, Y.T. Analysis of void closure in open-die forging. Int. J. Mach. Tools Manuf. 1990, 30, 65–75. [Google Scholar] [CrossRef]
- Wang, X.; Dong, X. A void evolution model accounting for stress triaxiality, Lode parameter and effective strain for hot metal forming. Int. J. Mech. Sci. 2020, 168, 105309. [Google Scholar] [CrossRef]
- Zhang, X.X.; Cui, Z.S.; Chen, W.; Li, Y. A criterion for void closure in large ingots during hot forging. J. Mater. Process. Technol. 2009, 209, 1950–1959. [Google Scholar] [CrossRef]
- Chen, J.; Chandrashekhara, K.; Mahimkar, C.; Lekakh, S.N.; Richards, V. Void closure prediction in cold rolling using finite element analysis and neural network. J. Mater. Process. Technol. 2011, 211, 245–255. [Google Scholar] [CrossRef]
- Saby, M.; Bernacki, M.; Roux, E.; Bouchard, P.O. Three-dimensional analysis of real void closure at the meso-scale during hot metal forming processes. Comput. Mater. Sci. 2013, 77, 194–201. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, R.; Liu, T.; Zhou, C.; Jia, L.J. Effect of initial void shape on void growth of structural steels based on micromechanical RVE models. J. Mater. Civ. Eng. 2022, 34, 04022010. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, R.; Liu, T.; Zhou, C.; Gu, T.; Chen, B.; Chen, Y.; Jia, L.J. Growth of random polyhedral void in structural steel based on micromechanical RVE simulations. Adv. Eng. Softw. 2023, 175, 103344. [Google Scholar] [CrossRef]
- Gravier, P.; Mas, F.; Barthelemy, A.; Boller, E.; Salvo, L.; Lhuissier, P. Pore closure in thick aluminum plate: From industrial hot rolling to individual pore observation. J. Mater. Process. Technol. 2022, 303, 117509. [Google Scholar] [CrossRef]
- Gravier, P.; Mas, F.; Barthelemy, A.; Boller, E.; Salvo, L.; Lhuissier, P. Mechanisms and kinetics of pore closure in thick aluminum plate. J. Mater. Process. Technol. 2022, 303, 117499. [Google Scholar] [CrossRef]
- Feng, C.; Cui, Z. A 3-D model for void evolution in viscous materials under large compressive deformation. Int. J. Plast. 2015, 74, 192–212. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, X.; Chen, H.; Ren, J. Void closure behavior during plastic deformation using the representative volume element model. Appl. Phys. A 2020, 126, 1–13. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, X.; Chen, H.; Ren, J. Void-closure behavior and a new void-evolution model for various stress states. Mater. Technol. 2021, 55, 105–113. [Google Scholar] [CrossRef]
- Tanaka, M.; Ono, S.I.; Tsuneno, M. A numerical analysis of void crushing during side compression of round bar by flat dies. J. Jpn. Soc. Technol. Plast. 1987, 28, 238–244. [Google Scholar]
- Saby, M. Understanding and Modeling of Void Closure Mechanisms in Hot Metal Forming Processes. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Paris, Paris, France, 2013. [Google Scholar]
- Saby, M.; Bernacki, M.; Bouchard, P.O. Understanding and modeling of void closure mechanisms in hot metal forming processes: A multiscale approach. Procedia Eng. 2014, 81, 137–142. [Google Scholar] [CrossRef]
- Chbihi, A.; Bouchard, P.O.; Bernacki, M.; Muñoz, D.P. Influence of Lode angle on modelling of void closure in hot metal forming processes. Finite Elem. Anal. Des. 2017, 126, 13–25. [Google Scholar] [CrossRef]
- Zhang, Q.; Niu, L.; Liang, Z.; Cao, M.; Zhou, T. A porosity closure model considering stress triaxiality ratio and Lode stress parameter. J. Mater. Process. Technol. 2020, 286, 116824. [Google Scholar] [CrossRef]
- Gouverneur, M.; Bailly, D.; Hirt, G. Investigation on the Influence of Shear on Void Closure in Open-Die Forging Processes. Steel Res. Int. 2022, 93, 2200327. [Google Scholar] [CrossRef]
- Niu, L.; Zhang, Q. A void closure model based on hydrostatic integration and the Lode parameter for additive manufacturing AlSi10Mg. J. Manuf. Process. 2022, 73, 235–247. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Tvergaard, V. Material failure by void growth to coalescence. Adv. Appl. Mech. 1989, 27, 83–151. [Google Scholar]
- Ragab, A. Application of an extended void growth model with strain hardening and void shape evolution to ductile fracture under axisymmetric tension. Eng. Fract. Mech. 2004, 71, 1515–1534. [Google Scholar] [CrossRef]
- Harris, N.; Shahriari, D.; Jahazi, M. Development of a fast converging material specific void closure model during ingot forging. J. Manuf. Process. 2017, 26, 131–141. [Google Scholar] [CrossRef]
- Saby, M.; Bouchard, P.O.; Bernacki, M. A geometry-dependent model for void closure in hot metal forming. Finite Elem. Anal. Des. 2015, 105, 63–78. [Google Scholar] [CrossRef]
- Park, J.; Han, B.; Kwon, H.; Kim, N. Numerical Simulation of Crack Condition in Forging Products of M50 Bearing Steel Based on Processing Map Theory. Metals 2023, 13, 921. [Google Scholar] [CrossRef]
- Vaz, M., Jr.; de Santi, N., Jr.; Verran, G.; de Souza Neto, E. Numerical and experimental assessment of ductile fracture in tensile and compressive-dominant processes. J. Mater. Process. Technol. 2006, 177, 300–303. [Google Scholar] [CrossRef]
- Chen, K.; Yang, Y.; Shao, G.; Liu, K. Strain function analysis method for void closure in the forging process of the large-sized steel ingot. Comput. Mater. Sci. 2012, 51, 72–77. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.; Oh, I.Y.; Han, S.W.; Kim, J.H.; VanTyne, C.J.; Moon, Y.H. Advanced disk-forging process in producing heavy defect-free disk using counteracting dies. Int. J. Mater. Form. 2021, 14, 281–291. [Google Scholar] [CrossRef]
- Kim, P.; Chun, M.; Yi, J.; Moon, Y. Pass schedule algorithms for hot open die forging. J. Mater. Process. Technol. 2002, 130, 516–523. [Google Scholar] [CrossRef]
- Choi, S.; Chun, M.; Van Tyne, C.; Moon, Y. Optimization of open die forging of round shapes using FEM analysis. J. Mater. Process. Technol. 2006, 172, 88–95. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Van Tyne, C.; Joo, B.; Moon, Y. Internal void closure during the forging of large cast ingots using a simulation approach. J. Mater. Process. Technol. 2011, 211, 1136–1145. [Google Scholar] [CrossRef]
- Hibbe, P.; Hirt, G. Analysis of the bond strength of voids closed by open-die forging. Int. J. Mater. Form. 2020, 13, 117–126. [Google Scholar] [CrossRef]
- Kim, N.; Ko, D.C.; VanTyne, C.J.; Han, S.W.; Abolhasani, D.; Moon, Y.H. Innovative square cogging to enhance void closure efficiency during forging of continuously cast round blooms. Int. J. Mater. Form. 2022, 15, 63. [Google Scholar] [CrossRef]






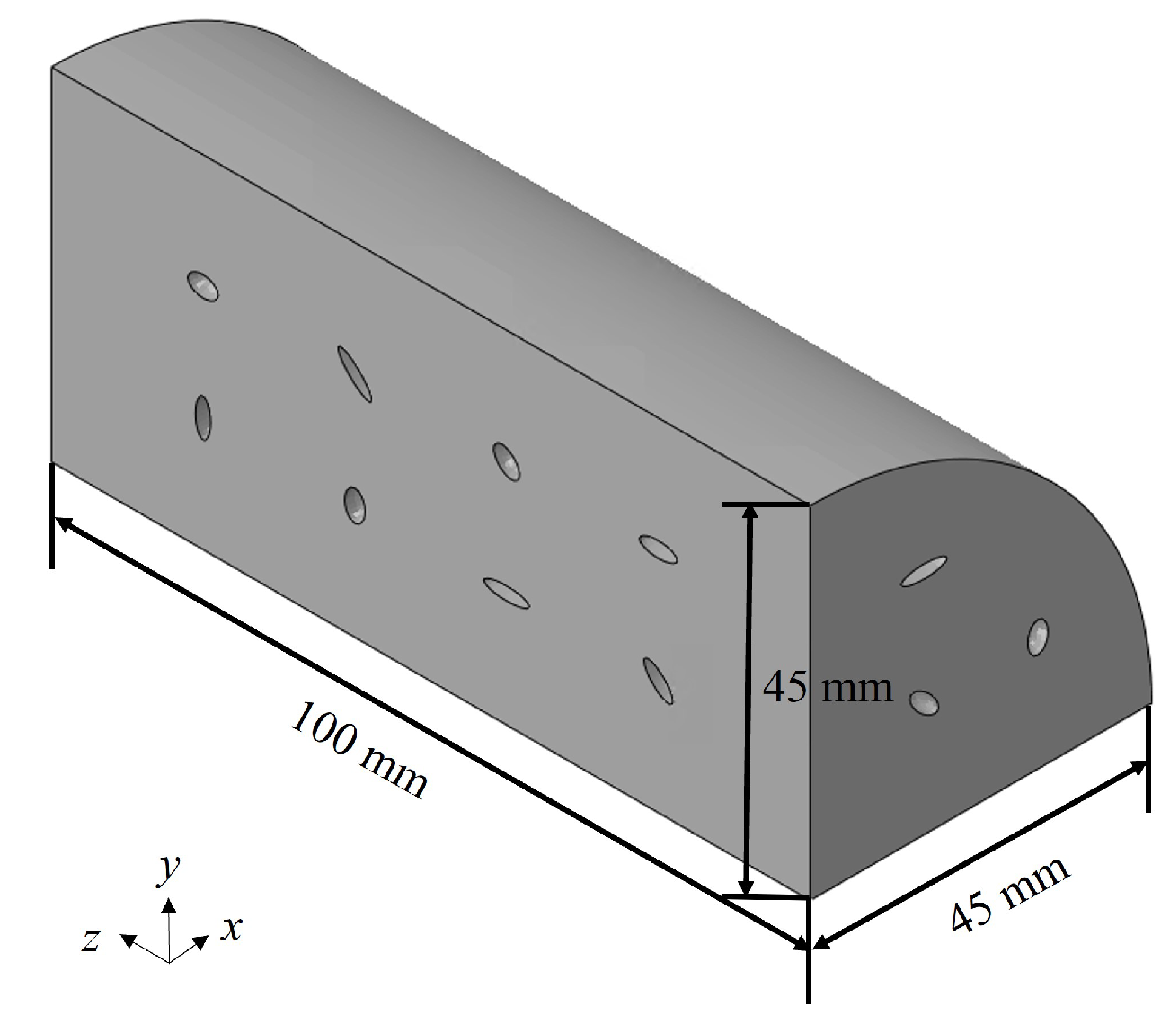
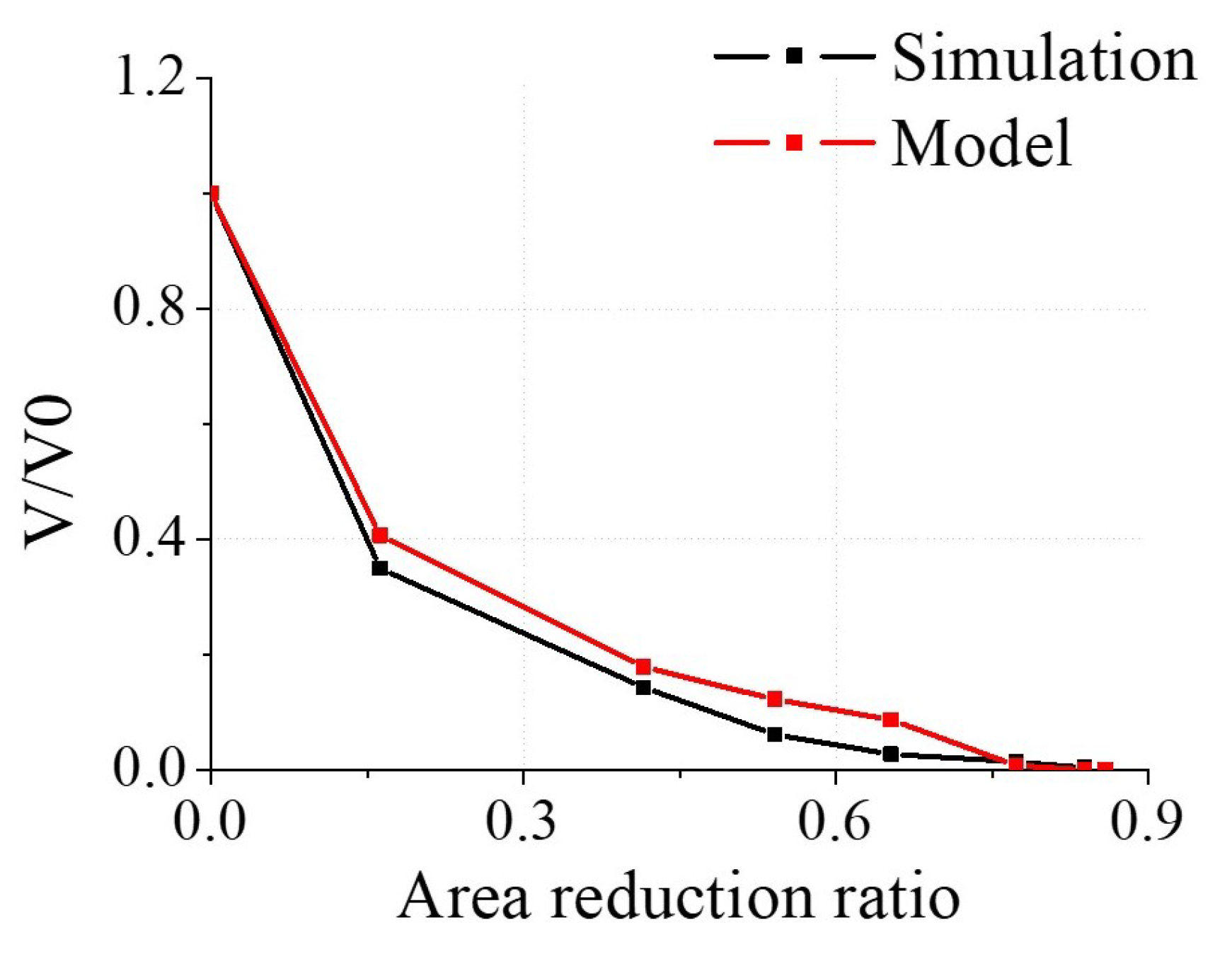
| Initial | Pass 1 | Pass 2 | Pass 3 | Pass 4 | Pass 5 | Pass 6 | Pass 7 | |
|---|---|---|---|---|---|---|---|---|
| Cross-section size [mm] | ∅90 | |||||||
| Angle of rotation [°] | - | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| Area reduction ratio | 0 | 0.16 | 0.42 | 0.54 | 0.65 | 0.77 | 0.84 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Park, J.; Kim, Y.; Kwon, H.; Kim, N. A Geometry-Dependent Void Closure Model Considering Void Deformation and Orientation Changes during Hot Metal Formation. J. Manuf. Mater. Process. 2023, 7, 117. https://doi.org/10.3390/jmmp7030117
Kim J, Park J, Kim Y, Kwon H, Kim N. A Geometry-Dependent Void Closure Model Considering Void Deformation and Orientation Changes during Hot Metal Formation. Journal of Manufacturing and Materials Processing. 2023; 7(3):117. https://doi.org/10.3390/jmmp7030117
Chicago/Turabian StyleKim, Jihyun, Joonhee Park, Yosep Kim, Hyukjoon Kwon, and Naksoo Kim. 2023. "A Geometry-Dependent Void Closure Model Considering Void Deformation and Orientation Changes during Hot Metal Formation" Journal of Manufacturing and Materials Processing 7, no. 3: 117. https://doi.org/10.3390/jmmp7030117
APA StyleKim, J., Park, J., Kim, Y., Kwon, H., & Kim, N. (2023). A Geometry-Dependent Void Closure Model Considering Void Deformation and Orientation Changes during Hot Metal Formation. Journal of Manufacturing and Materials Processing, 7(3), 117. https://doi.org/10.3390/jmmp7030117







