Fabrication of Novel Hybrid Al-SiC-ZrO2 Composites via Powder Metallurgy Route and Intelligent Modeling for Their Microhardness
Abstract
1. Introduction
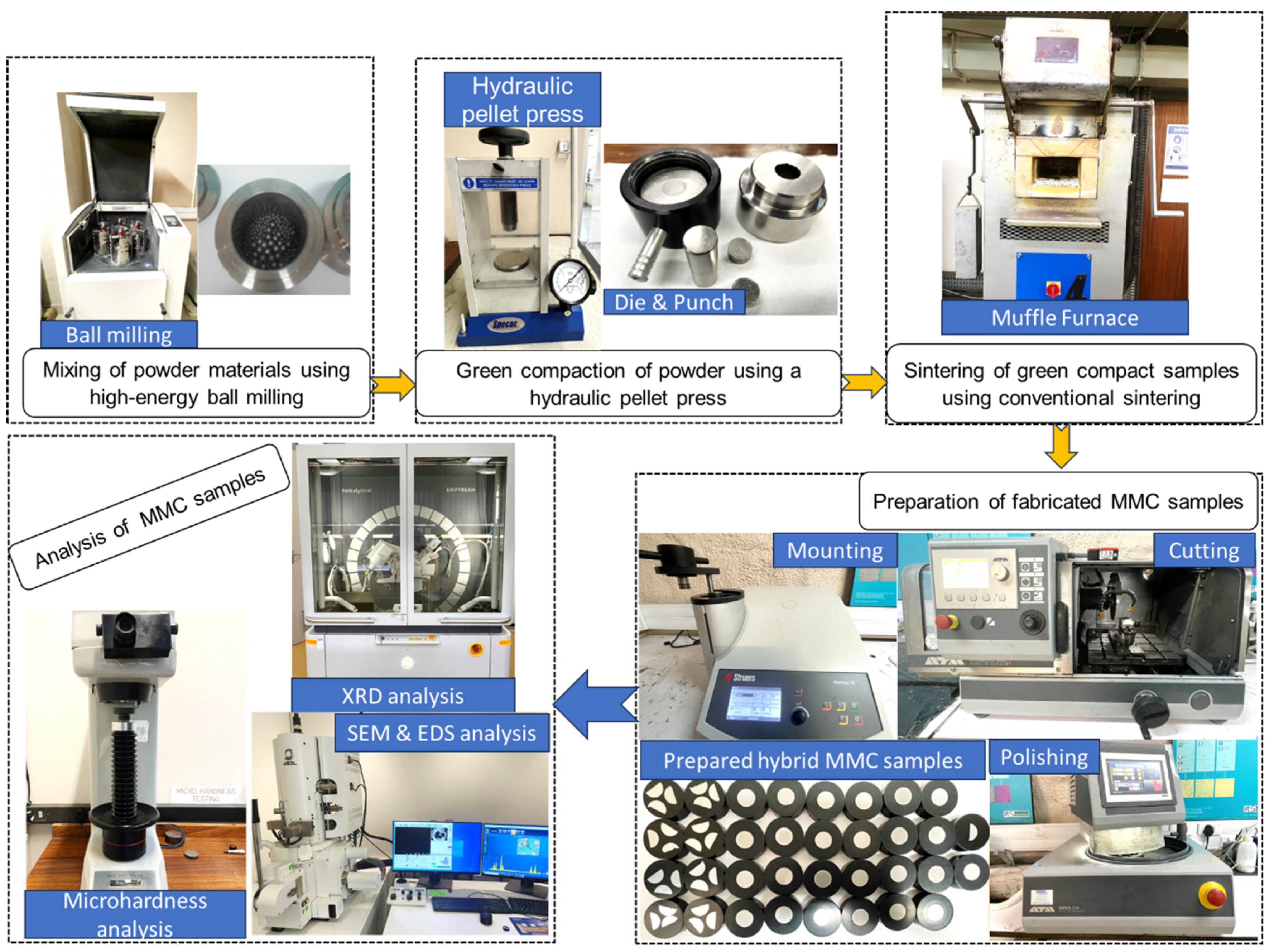
2. Materials and Methods
3. Results and Discussion
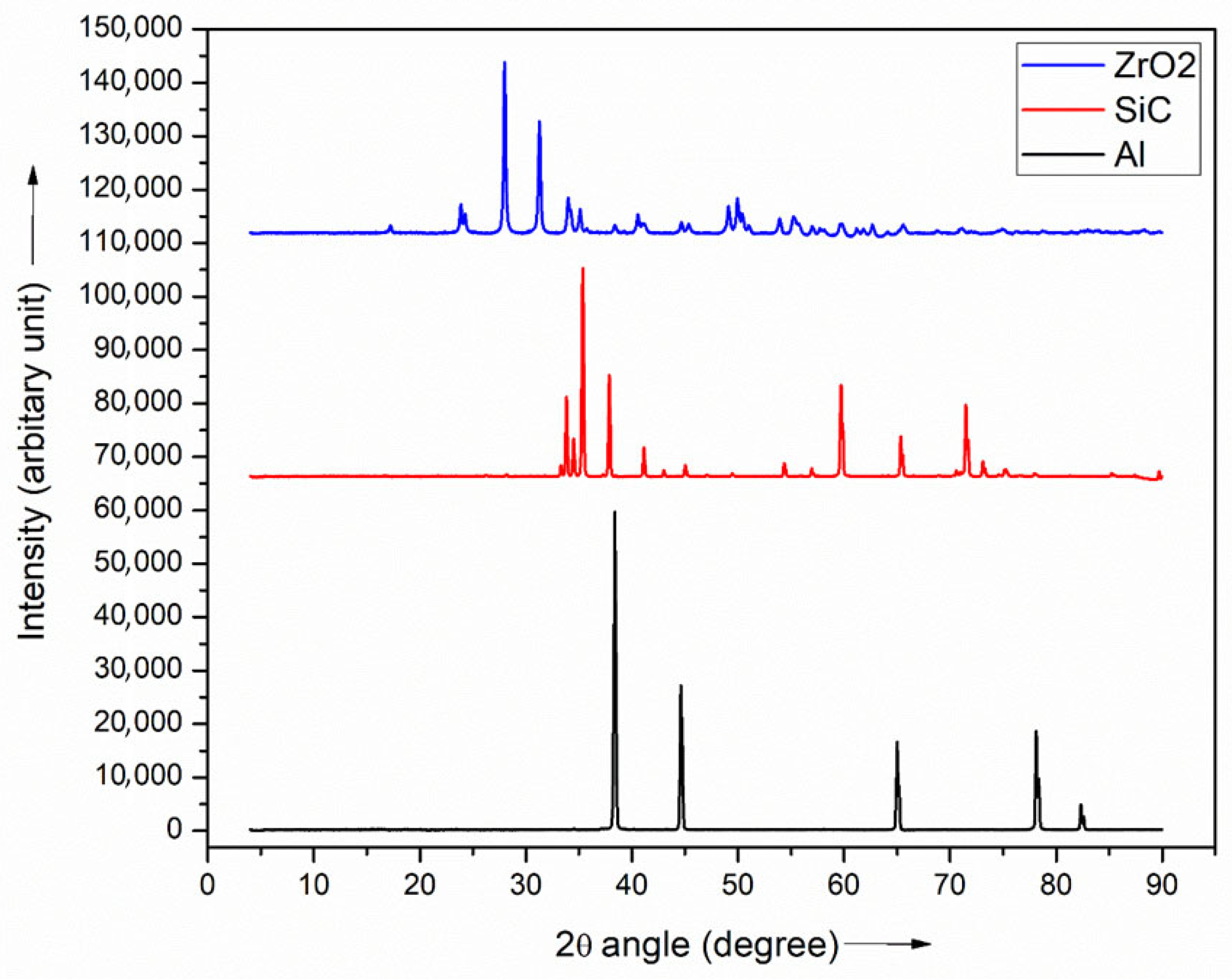
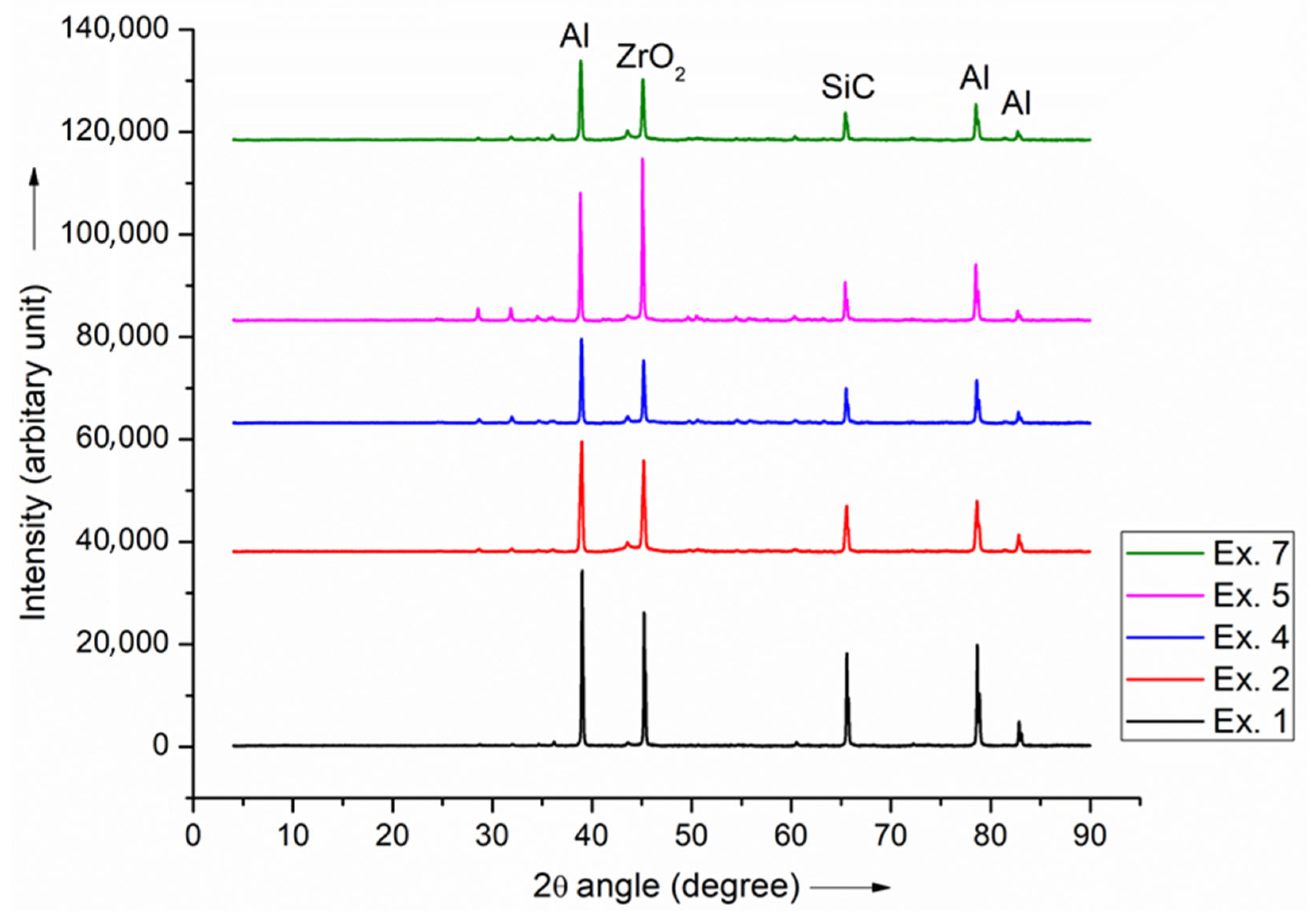
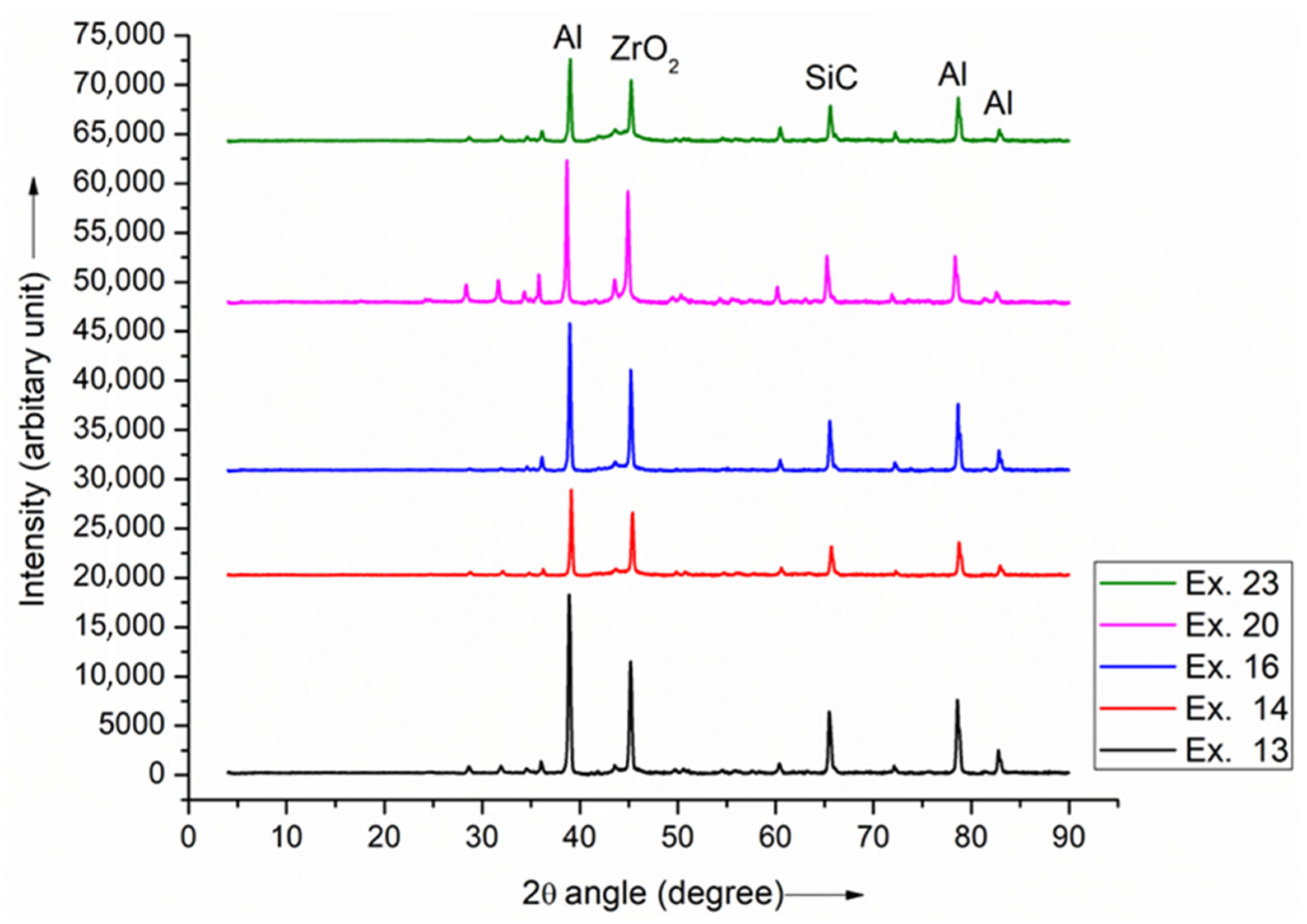
3.1. XRD Analysis
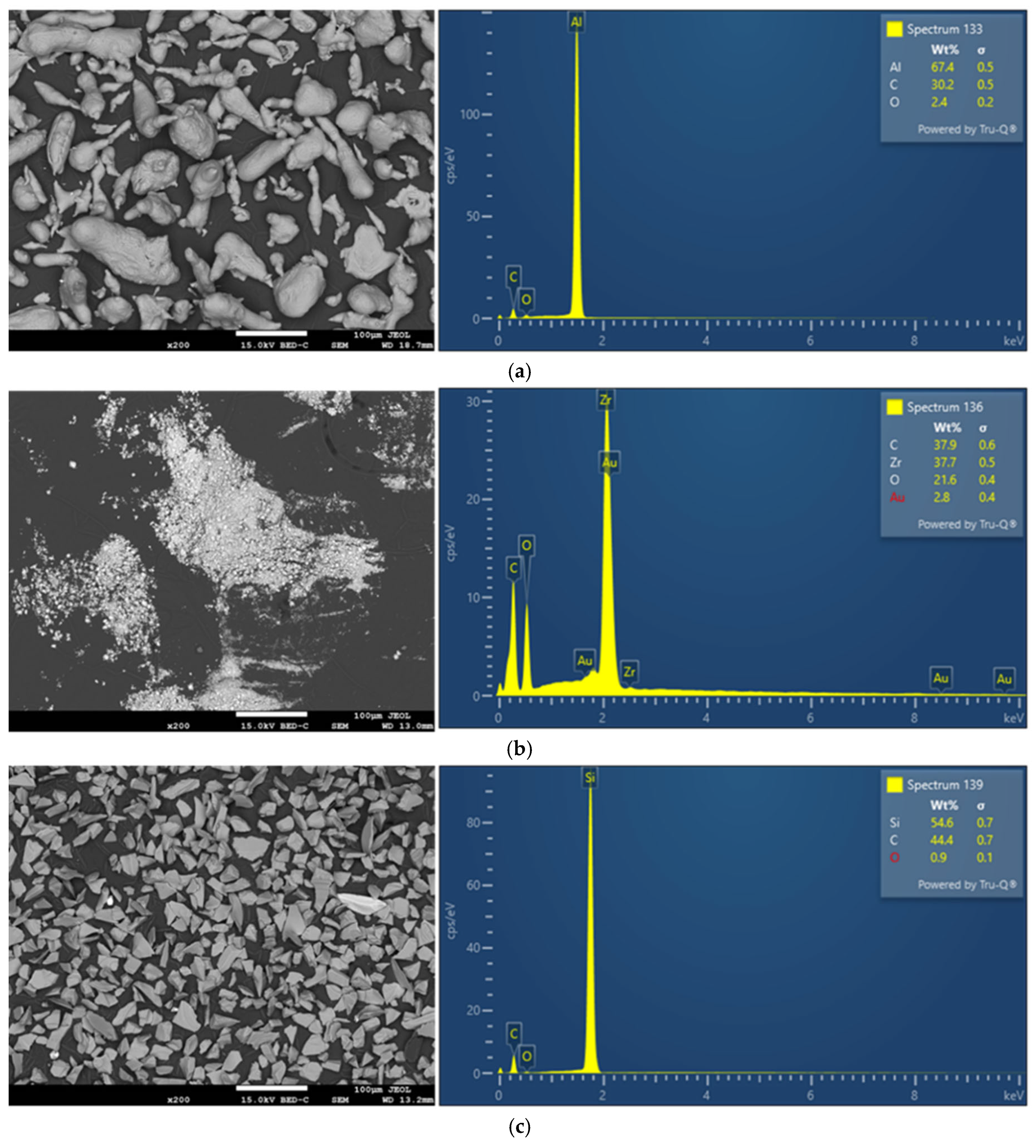
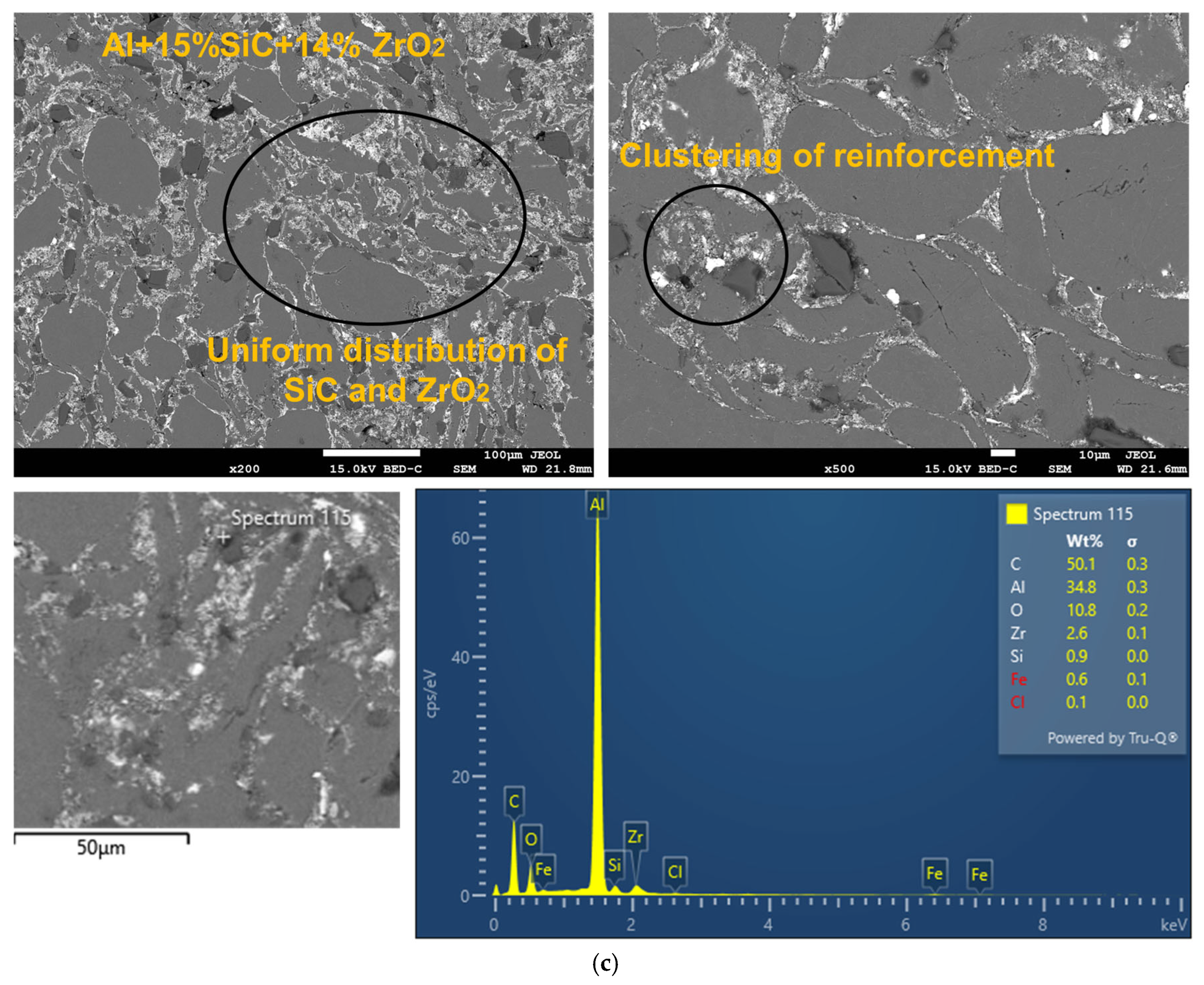
3.2. Morphological Analysis
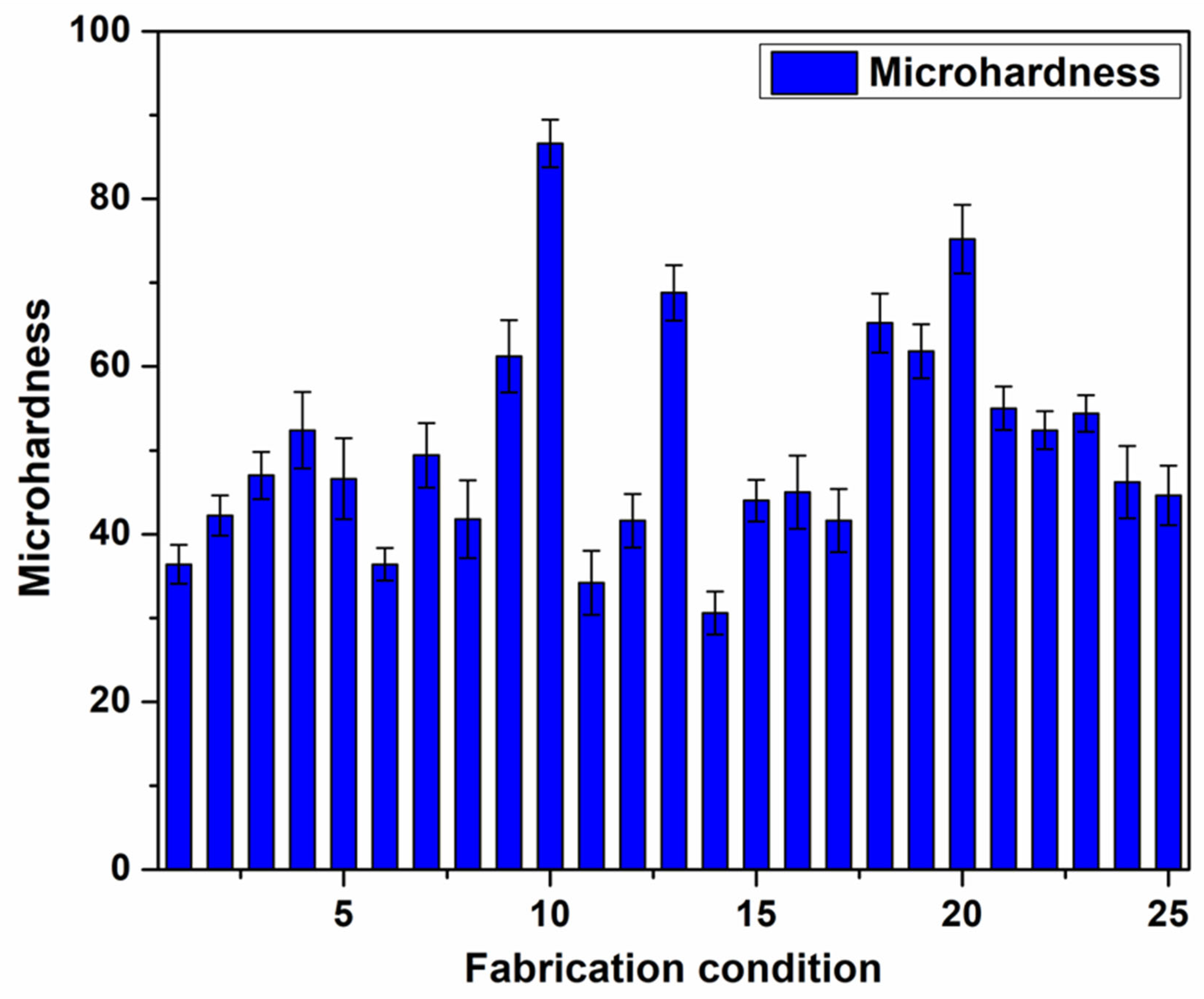
3.3. Microhardness Analysis
4. Modeling for Microhardness
4.1. Integrated Particle Swarm Optimization–Support Vector Machine (PSO-SVM)
4.2. Implementation and Evaluation of PSO-SVM Model
5. Conclusions
- The powder metallurgy route has been found effective good for the hybridization of Al-based MMCs with SiC and ZrO2 reinforcement elements.
- Optimal mixing and sintering of all composite samples have been achieved, as proved by XRD results that show peaks of Al, SiC, and ZrO2 particles for all the fabricated MMCs.
- No purities or other irreverent peaks are observed in the XRD pattern of any the fabricated composites, which confirms the good fabrication quality of MMC products with the proper distribution of SiC and ZrO2 reinforcement particles over the Al matrix material.
- Uniform spreading of both reinforcement elements SiC and ZrO2, in Al matrix has been observed.
- The appearance of Al, Si, C, Zr, and O in EDS spectra confirms the effectiveness of ball milling and sintering of composites for all fabrication conditions.
- The highest and lowest microhardness values of 86.6 HVN and 30.6 HVN, respectively, have been achieved.
- During the SEM investigation, fewer powder clusters, microcracks, and pores were identified, which have a direct impact on the microhardness values of the manufactured hybrid MMCs. Also, appropriate precautions were implemented during the PM route’s mixing, compaction, and sintering stages.
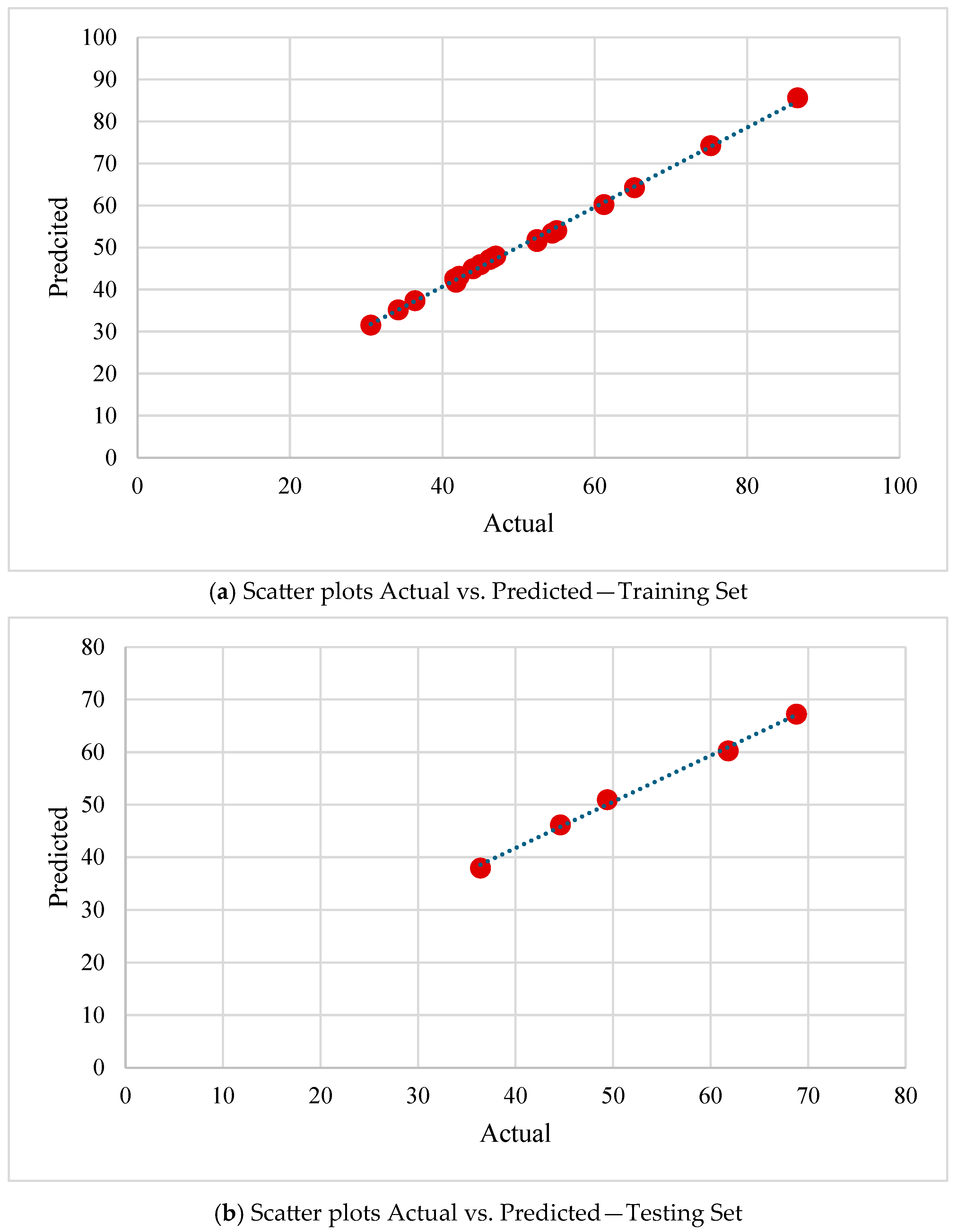
- The proposed PSO-SVM model demonstrates promising accuracy and reliability in predicting microhardness across both training and testing datasets, supported by high R2 values of 0.995 and 0.982, respectively. The model’s low error metrics in testing, including an RMSE of 1.557 and a MAPE of 3.141, confirm its effectiveness in capturing the complex, non-linear relationships inherent in powder metallurgy processes.
- By integrating PSO for hyperparameter tuning, the PSO-SVM model overcomes the limitations of traditional SVM. Its robust generalization capability, demonstrated by consistent performance across training and testing datasets, makes it a powerful tool for accurate predictions, even with limited data—ideal for small-sample scenarios in materials science research.
- While the RSM model offers a baseline with an R2 of 0.812, its higher MAE and MAPE, along with low adjusted and predicted R2 values, reveal its limitations in capturing non-linear patterns. This highlights the superior accuracy and robustness of the PSO-SVM model for modeling complex material behavior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, L.; Singh, B.; Saxena, K.K. Manufacturing techniques for metal matrix composites (MMC): An overview. Adv. Mater. Process. Technol. 2020, 6, 441–457. [Google Scholar] [CrossRef]
- Tian, X.; Huang, Y.; Zhang, L.; Zhao, F.; Chen, Y.; Liu, X. Preparation of AlN–SiC Bonded Al2O3–C Refractory and Its Properties Evolution after Oxidation. Ceram. Int. 2024, 50, 446–451. [Google Scholar] [CrossRef]
- Hashim, A.; Ibrahim, H.; Hadi, A. Fabrication of SiC–Al2O3 Nanoceramic Doped Organic Polymer for Flexible Nanoelectronics and Optical Applications. Silicon 2024, 16, 6575–6587. [Google Scholar] [CrossRef]
- Sarmah, P.; Patowari, P.K. Mechanical and tribological analysis of the fabricated Al 6063-based MMCs with SiC reinforcement particles. Silicon 2023, 15, 2781–2796. [Google Scholar] [CrossRef]
- Li, P.; Chen, T.; Qin, H. Effects of pressure on microstructure and mechanical properties of SiC/2024 Al-based composites fabricated by powder thixoforming. J. Mater. Sci. 2017, 52, 2045–2059. [Google Scholar] [CrossRef]
- Jenczyk, P.; Grzywacz, H.; Milczarek, M.; Jarzabek, D.M. Mechanical and tribological properties of co-electrodeposited particulate-reinforced metal matrix composites: A critical review with interfacial aspects. Materials 2021, 14, 3181. [Google Scholar] [CrossRef] [PubMed]
- Madhukar, M.P.; Selvaraj, N.; Rao, C.S.P. Manufacturing of aluminium nano hybrid composites: A state of review. Mater. Sci. Eng. 2016, 149, 12114. [Google Scholar] [CrossRef]
- Nagasai, B.P.; Srikanth, S.; Babu, J.R. Mechanical properties of AA 7075-nano ZrO2 reinforced matrix composites. In Advances in Applied Mechanical Engineering; Springer: Singapore, 2020; pp. 921–928. [Google Scholar]
- Tosun, G.; Kurt, M. The Porosity, Microstructure, and Hardness of Al-Mg Composites Reinforced with Microparticle SiC/Al2O3 Produced Using Powder Metallurgy. Compos. Part B Eng. 2019, 174, 106965. [Google Scholar] [CrossRef]
- Sankhla, A.M.; Patel, K.M.; Makhesana, M.A.; Giasin, K.; Pimenov, D.Y.; Wojciechowski, S.; Khanna, N. Effect of Mixing Method and Particle Size on Hardness and Compressive Strength of Aluminium-Based Metal Matrix Composite Prepared through Powder Metallurgy Route. J. Mater. Res. Technol. 2022, 18, 282–292. [Google Scholar] [CrossRef]
- Garg, P.; Jamwal, A.; Kumar, D.; Sadasivuni, K.K.; Hussain, M.C.; Gupta, P. Advance research progresses in aluminium matrix composites: Manufacturing & applications. J. Mater. Res. Tech. 2019, 8, 4924–4939. [Google Scholar]
- Chatterjee, A.; Sen, S.; Paul, S.; Roy, P.; Seikh, A.H.; Alnaser, I.A.; Das, K.; Sutradhar, G.; Ghosh, M. Fabrication and Characterization of SiC-reinforced Aluminium Matrix Composite for Brake Pad Applications. Metals 2023, 13, 584. [Google Scholar] [CrossRef]
- Marmol, G.; Ferreira, D.P.; Fangueiro, R. Automotive and construction applications of fiber reinforced composites. In Fiber Reinforced Composites: Constituents, Compatibility, Perspectives, and Applications Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2021; pp. 785–788. [Google Scholar]
- Zhou, M.Y.; Ren, L.B.; Fan, L.L.; Zhang, Y.W.X.; Lu, T.H.; Quan, G.F.; Gupta, M. Progress in research on hybrid metal matrix composites. J. Alloys Comp. 2020, 842, 155274. [Google Scholar] [CrossRef]
- Ravi Kumar, K.; Pridhar, T.; Sree Balaji, V.S. Mechanical properties and characterization of zirconium oxide (ZrO2) and coconut shell ash (CSA) reinforced aluminium (Al 6082) matrix hybrid composite. J. Alloys Compd. 2018, 765, 171–179. [Google Scholar] [CrossRef]
- Zare, R.; Sharifi, H.; Saeri, M.R. Investigating the effect of SiC particles on the physical and thermal properties of Al6061/SiC composite. J. Alloys Compd. 2019, 801, 520–528. [Google Scholar] [CrossRef]
- Kiran Kumar, G.K.; Bhavani Sankar, C. Mechanical behaviour of silicon carbide (SiC)/fly ash particles reinforced aluminium-7075 based metal matrix composite fabricated by stir casting method. IJSART 2019, 5, 527–534. [Google Scholar]
- Yadav, S.; Gangwar, S.; Yadav, P.C.; Pathak, V.K.; Sahu, S. Mechanical and Corrosion Behavior of SiC/Graphite/ZrO2 Hybrid Reinforced Aluminum-Based Composites for Marine Environment. Surf. Topogr. Metrol. Prop. 2021, 9, 045022. [Google Scholar] [CrossRef]
- Ghandvar, H.; Jabbar, M.A.; Petrů, M.; Bakar, T.A.A.; Ler, L.J.; Rahimian Koloor, S.S. Role of YSZ Particles on Microstructural, Wear, and Corrosion Behavior of Al-15%Mg2Si Hybrid Composite for Marine Applications. J. Mar. Sci. Eng. 2023, 11, 1050. [Google Scholar] [CrossRef]
- Dey, D.; Bhowmik, A.; Biswas, A. Effect of SiC content on mechanical and tribological properties of Al2024-SiC composites. Silicon 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Shamim, F.A.; Dvivedi, A.; Kumar, P. Fabrication and characterization of Al6063/SiC composites using electromagnetic stir casting process. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2022, 236, 187–193. [Google Scholar] [CrossRef]
- Maji, P.; Ghosh, S.K.; Nath, R.K.; Karmakar, R. Microstructural, mechanical and wear characteristics of aluminum matrix composites fabricated by friction stir processing. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 191. [Google Scholar] [CrossRef]
- Muralidharan, N.; Chockalingam, K.; Kalaiselvan, K.; Nithyavathy, N. Investigation of ZrO2 reinforced aluminium metal matrix composites by liquid metallurgy route. Adv. Mater. Proces. Tech. 2023, 9, 593–607. [Google Scholar] [CrossRef]
- Nataraja, M.; Balakumar, G.; Santhosh, N.; Rudra Naik, M. Characterization of Wear Rate of Al-12wt%Si Alloy-Based MMC Reinforced with ZrO2 Particulates. Mater. Res. Express 2024, 11, 036522. [Google Scholar] [CrossRef]
- Parveen, A.; Chauhan, N.R.; Suhaib, M. Influence of compaction pressure and Si3N4/ZrO2 reinforcement on the properties of aluminium hybrid composites. Adv. Mater. Process. Tech. 2022, 8, 2905–2917. [Google Scholar] [CrossRef]
- Nagasai, B.P.; Anusha, C.H.; Rajesh, A. Study on mechanical properties of Al-6061/ZrO2 reinforced metal matrix composites. Mater. Today Proc. 2021, 47, 4552–4557. [Google Scholar] [CrossRef]
- Gemeda, B.A.; Sinha, D.K.; Singh, G.K.; Alghtani, A.H.; Tirth, V.; Algahtani, A.; Mengesha, G.A.; Ahmed, G.M.S.; Hossain, N. Effect of sintering temperatures, reinforcement size on mechanical properties and fortification mechanisms on the particle size distribution of B4C, SiC, and ZrO2 in titanium metal matrix composites. Materials 2022, 15, 5525. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Abdelrazeq, M.W.; Mattli, M.R.; Yusuf, M.M.; Alashraf, A.; Matli, P.R.; Shakoor, R.A. Structural and mechanical properties of Al-SiC-ZrO2 nanocomposites fabricated by microwave sintering technique. Crystals 2020, 10, 904. [Google Scholar] [CrossRef]
- Ramesh, S.; Govindaraju, N.; Suryanarayan, C.P. Investigation on mechanical and fatigue behaviour of aluminium-based SiC/ZrO2 particle reinforced MMC. IOP Conf. Ser. Mater. Sci. Eng. 2018, 346, 012030. [Google Scholar] [CrossRef]
- Azad, M.; Ya, H.H.; Azeem, M.; Bin, P.; Sapuan, M.; Khan, R.; Arif, S.; Husain, A. Modelling and Optimisation of Hardness Be-haviour of Sintered Al/SiC Composites Using RSM and ANN: A Comparative Study. Integr. Med. Res. 2020, 9, 14036–14050. [Google Scholar] [CrossRef]
- Garg, A.; Lam, J.S.L.; Gao, L. Power consumption and tool life models for the production process. J. Clean. Prod. 2016, 131, 754–764. [Google Scholar] [CrossRef]
- Ipakchi, H.; Rezadoust, A.M.; Esfandeh, M. Modeling and Optimization of Electrospinning Conditions of PVB Nanofiber by RSM and PSO-LSSVM Models for Improved Interlaminar Fracture Toughness of Laminated Composites. J. Compos. Mater. 2019, 54, 363–378. [Google Scholar] [CrossRef]
- Khan, K.; Johari, M.A.M.; Amin, M.N.; Khan, M.I.; Iqbal, M. Optimization of Colloidal Nano-Silica Based Cementitious Mortar Composites Using RSM and ANN Approaches. Results Eng. 2023, 20, 101390. [Google Scholar] [CrossRef]
- Hamzat, A.K.; Salman, U.T.; Murad, M.S.; Altay, O.; Bahceci, E.; Asmatulu, E.; Bakir, M.; Asmatulu, R. Development of Robust Machine Learning Models for Predicting Flexural Strengths of Fiber-Reinforced Polymeric Composites. Hybrid Adv. 2025, 8, 100385. [Google Scholar] [CrossRef]
- Danish, M.; Gupta, M.K.; Irfan, S.A.; Ghazali, S.M.; Rathore, M.F.; Krolczyk, G.M.; Alsaady, A. Machine learning models for prediction and classification of tool wear in sustainable milling of additively manufactured 316 stainless steel. Results Eng. 2024, 22, 102015. [Google Scholar] [CrossRef]
- Xu, C.; Yao, S.; Wang, G.; Wang, Y.; Xu, J. A prediction model of drilling force in CFRP internal chip removal hole drilling based on support vector regression. Int. J. Adv. Manuf. Technol. 2021, 117, 1505–1516. [Google Scholar] [CrossRef]
- Zhao, M.; Xue, B.; Li, B.; Zhu, J.; Song, W. Ensemble learning with support vector machines algorithm for surface roughness prediction in longitudinal vibratory ultrasound-assisted grinding. Precis. Eng. 2024, 88, 382–400. [Google Scholar] [CrossRef]
- Acosta, S.M.; Oliveira, R.M.A.; Sant’anna, Â.M.O. Machine learning algorithms applied to intelligent tyre manufacturing. Int. J. Comput. Integr. Manuf. 2023, 37, 497–507. [Google Scholar] [CrossRef]
- Padmavathi, K.R.; Ramakrishnan, R.; Karthikeyan, L.; Tamizhselvan, S.; Chezhian Babu, S. Comparison of the mechanical properties of micro/nano SiC/TiO2 reinforced aluminium metal matrix composites. Mater. Today Proc. 2023, 72, 1996–2001. [Google Scholar] [CrossRef]
- ASTM E92-23; Standard Test Methods for Vickers Hardness and Knoop Hardness of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2023.
- Reddy, P.V.; Kumar, G.S.; Krishnudu, D.M.; Rao, H.R. Mechanical and wear performances of aluminium-based metal matrix composites: A review. J. Bio Tribo-Corro 2020, 6, 83. [Google Scholar] [CrossRef]
- Sekar, K.; Manohar, M.; Jayakumar, K. Mechanical and tribological properties of A356/Al2O3/MoS2 hybrid composites synthesized through combined stir and squeeze casting. In Advances in Materials and Metallurgy; Springer: Singapore, 2019; pp. 115–125. [Google Scholar]
- Kumar, R.; Anand, R.S. Bearing fault diagnosis using multiple feature selection algorithms with SVM. Prog. Artif. Intell. 2024, 13, 119–133. [Google Scholar] [CrossRef]
- Camposeco-Negrete, C.; de Dios Calderón-Nájera, J. Optimization of Energy Consumption and Surface Roughness in Slot Milling of AISI 6061 T6 Using the Response Surface Method. Int. J. Adv. Manuf. Technol. 2019, 103, 4063–4069. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| Speed of milling | 200 rpm |
| Ball-to-powder ratio | 10:1 |
| Process control agent | Stearic Acid |
| Material for ball | Stainless steel |
| Fabrication Parameter | Levels | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Wt.% of SiC | 3 | 7 | 11 | 15 | 19 |
| Wt.% of ZrO2 | 2 | 5 | 8 | 11 | 14 |
| Milling time (min) | 20 | 40 | 60 | 80 | 100 |
| Sintering temperature (°C) | 500 | 530 | 560 | 590 | 620 |
| Sintering time (min) | 80 | 90 | 100 | 110 | 120 |
| Expt. No. | Fabrication Parameters | Microhardness (VHN) | ||||
|---|---|---|---|---|---|---|
| Wt.% of SiC | Wt.% of ZrO2 | Sintering Temperature (°C) | Sintering Time (min) | Milling Time (min) | ||
| 1 | 3 | 2 | 500 | 80 | 20 | 36.4 ± 2.32 |
| 2 | 3 | 5 | 530 | 90 | 40 | 42.2 ± 2.14 |
| 3 | 3 | 8 | 560 | 100 | 60 | 47 ± 2.8 |
| 4 | 3 | 11 | 590 | 110 | 80 | 52.4 ± 4.58 |
| 5 | 3 | 14 | 620 | 120 | 100 | 46.6 ± 4.84 |
| 6 | 7 | 2 | 530 | 100 | 80 | 36.4 ± 1.95 |
| 7 | 7 | 5 | 560 | 110 | 100 | 49.4 ± 3.84 |
| 8 | 7 | 8 | 590 | 120 | 20 | 41.8 ± 4.64 |
| 9 | 7 | 11 | 620 | 80 | 40 | 61.2 ± 4.31 |
| 10 | 7 | 14 | 500 | 90 | 60 | 86.6 ± 2.85 |
| 11 | 11 | 2 | 560 | 120 | 40 | 34.2 ± 3.84 |
| 12 | 11 | 5 | 590 | 80 | 60 | 41.6 ± 3.19 |
| 13 | 11 | 8 | 620 | 90 | 80 | 68.8 ± 3.31 |
| 14 | 11 | 11 | 500 | 100 | 100 | 30.6 ± 2.55 |
| 15 | 11 | 14 | 530 | 110 | 20 | 44 ± 2.47 |
| 16 | 15 | 2 | 590 | 90 | 100 | 45 ± 4.38 |
| 17 | 15 | 5 | 620 | 100 | 20 | 41.6 ± 3.77 |
| 18 | 15 | 8 | 500 | 110 | 40 | 65.2 ± 3.52 |
| 19 | 15 | 11 | 530 | 120 | 60 | 61.8 ± 3.22 |
| 20 | 15 | 14 | 560 | 80 | 80 | 75.2 ± 4.12 |
| 21 | 19 | 2 | 620 | 110 | 60 | 55 ± 2.59 |
| 22 | 19 | 5 | 500 | 120 | 80 | 52.4 ± 2.28 |
| 23 | 19 | 8 | 530 | 80 | 100 | 54.4 ± 2.17 |
| 24 | 19 | 11 | 560 | 90 | 20 | 46.2 ± 4.31 |
| 25 | 19 | 14 | 590 | 100 | 40 | 44.6 ± 3.55 |
| Parameter | Value | Description |
|---|---|---|
| Swarm size | 30 | Number of particles |
| Iterations | 50 | Maximum number of optimization steps |
| Dimensions | 2 | Optimized parameters: C (BoxConstraint), γ (KernelScale) |
| Inertia weight (w) | 0.5 | Balances global and local search |
| Cognitive factor (c1) | 1 | Influence of personal best |
| Social factor (c2) | 1 | Influence of global best |
| C range | [1 × 10−6, 100] | Search range for SVM BoxConstraint |
| γ range | [1 × 10−6, 10] | Search range for SVM KernelScale |
| Objective function | RMSE | Evaluated on training set |
| Random seed | rng(42) | Ensures reproducible PSO initialization |
| Parameter | Value | Description |
|---|---|---|
| Kernel function | Gaussian (RBF) | Used for non-linear regression |
| Solver | SMO (sequential minimal optimization) | Optimization algorithm |
| C (BoxConstraint) | Best value from PSO, i.e., 97.6576 | Regularization parameter |
| γ (KernelScale) | Best value from PSO, i.e., 1.7525 | Gaussian kernel width |
| Standardization | Enabled | Features scaled to zero mean, unit variance |
| Evaluation metrics | R2, RMSE, MAE, MAPE | Used on both training and testing sets |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 15 | 3463.16 | 230.877 | 2.59 | 0.076 |
| Linear | 5 | 1641.92 | 328.385 | 3.68 | 0.043 * |
| 1 | 3.44 | 3.440 | 0.04 | 0.849 | |
| 1 | 54.19 | 54.195 | 0.61 | 0.456 | |
| 1 | 441.09 | 441.091 | 4.95 | 0.053 * | |
| 1 | 697.23 | 697.230 | 7.82 | 0.021 * | |
| 1 | 455.21 | 455.211 | 5.10 | 0.050 * | |
| 2-Way Interaction | 10 | 2276.44 | 227.644 | 2.55 | 0.087 |
| 1 | 243.90 | 243.901 | 2.73 | 0.133 | |
| 1 | 572.25 | 572.254 | 6.42 | 0.032 * | |
| 1 | 688.23 | 688.230 | 7.72 | 0.021 * | |
| 1 | 329.13 | 329.135 | 3.69 | 0.087 | |
| 1 | 383.72 | 383.716 | 4.30 | 0.068 | |
| 1 | 550.48 | 550.478 | 6.17 | 0.035 * | |
| 1 | 167.30 | 167.303 | 1.88 | 0.204 | |
| 1 | 520.43 | 520.426 | 5.84 | 0.039 * | |
| 1 | 602.48 | 602.475 | 6.76 | 0.029 * | |
| 1 | 334.83 | 334.827 | 3.75 | 0.085 | |
| Error | 9 | 802.63 | 89.181 | ||
| Total | 24 | 4265.79 | |||
| Model Summary | |||||
| R-sq | R-sq(adj) | R-sq(pred) | |||
| 0.812 | 0.498 | 0.000 | |||
| Model | Statistical Metrics | ||||
|---|---|---|---|---|---|
| R2 | RSME | MAE | MAPE | ||
| PSO-SVM | Training | 0.995 | 0.920 | 0.894 | 1.895 |
| Testing | 0.982 | 1.557 | 1.557 | 3.141 | |
| RSM | Overall | 0.812 | 5.665 | 4.410 | 9.838 |
| t-Test t-Statistic | t-Test p-Value | F-Test F-Statistic | F-Test p-Value | Pearson Correlation (r) |
|---|---|---|---|---|
| −0.900 | 0.377 | 1.135 | 0.379 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarmah, P.; Pawanr, S.; Gupta, K. Fabrication of Novel Hybrid Al-SiC-ZrO2 Composites via Powder Metallurgy Route and Intelligent Modeling for Their Microhardness. Ceramics 2025, 8, 91. https://doi.org/10.3390/ceramics8030091
Sarmah P, Pawanr S, Gupta K. Fabrication of Novel Hybrid Al-SiC-ZrO2 Composites via Powder Metallurgy Route and Intelligent Modeling for Their Microhardness. Ceramics. 2025; 8(3):91. https://doi.org/10.3390/ceramics8030091
Chicago/Turabian StyleSarmah, Pallab, Shailendra Pawanr, and Kapil Gupta. 2025. "Fabrication of Novel Hybrid Al-SiC-ZrO2 Composites via Powder Metallurgy Route and Intelligent Modeling for Their Microhardness" Ceramics 8, no. 3: 91. https://doi.org/10.3390/ceramics8030091
APA StyleSarmah, P., Pawanr, S., & Gupta, K. (2025). Fabrication of Novel Hybrid Al-SiC-ZrO2 Composites via Powder Metallurgy Route and Intelligent Modeling for Their Microhardness. Ceramics, 8(3), 91. https://doi.org/10.3390/ceramics8030091






