Lyapunov-Based Pitch Control for Electric Vehicles Using In-Wheel Motors
Abstract
1. Introduction
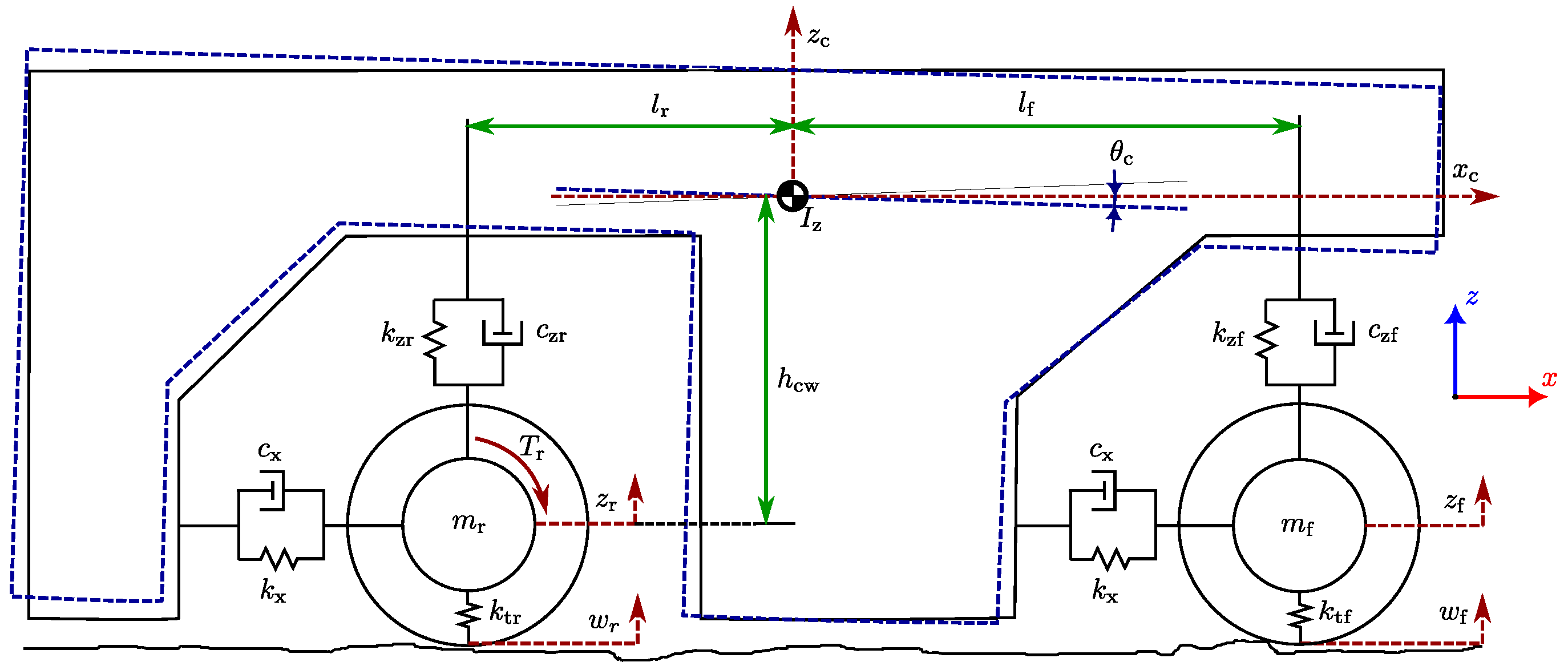
2. Vertical, Pitch, and Longitudinal Vehicle Dynamics
2.1. Suspension Forces
2.2. Vertical Dynamics
2.3. Longitudinal Dynamics
2.4. Pitch Dynamics
2.5. In-Wheel Motor
2.6. Road Roughness
3. Pitch Rate Attenuation Control
3.1. Road Profile Estimation
3.2. Numerical Implementation
4. Results
- Urban test. Vehicle traveling through an ISO B road profile at .
- Highway test. Vehicle traveling through an ISO A road profile at .
- Bump test. Vehicle traveling through a speed bump obstacle at .
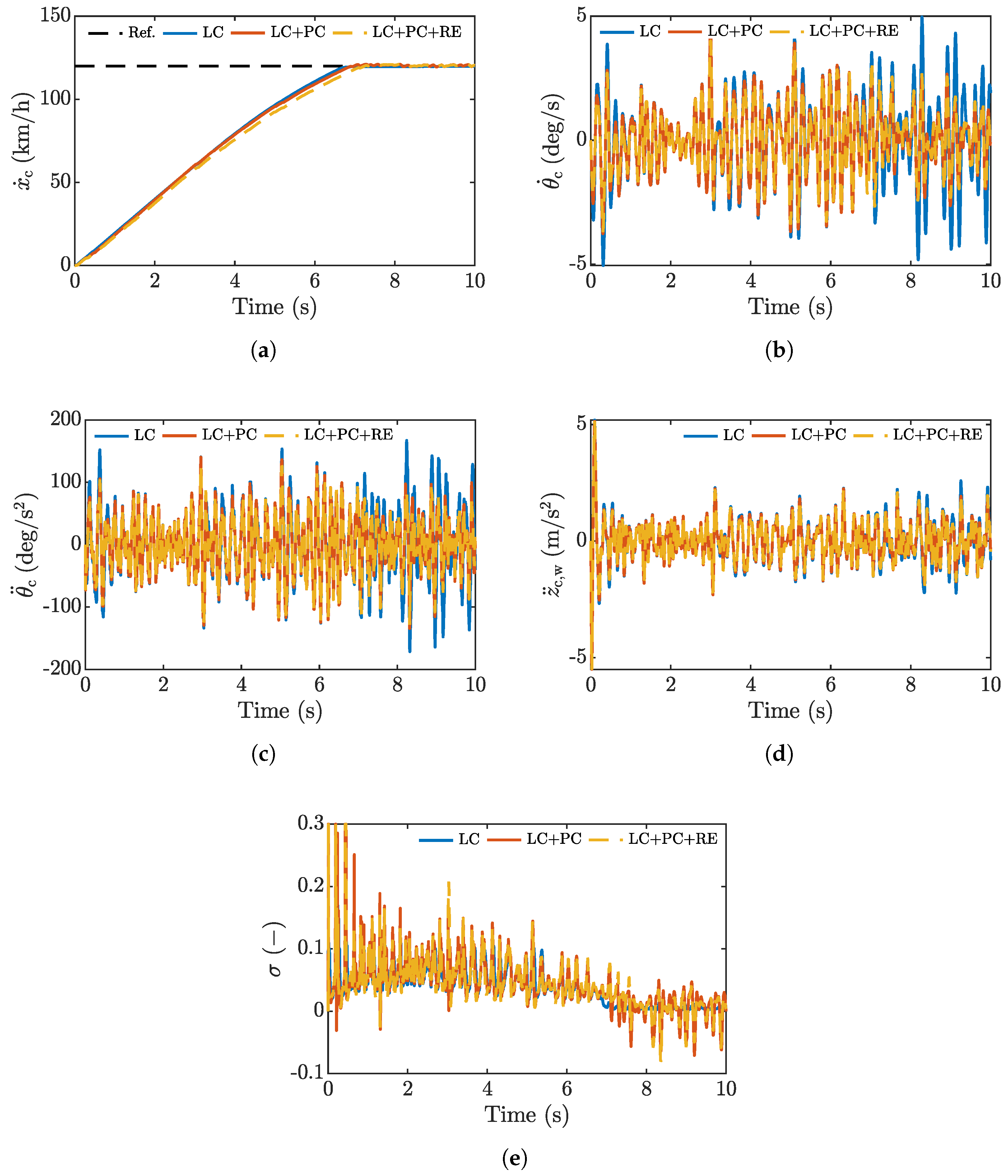
4.1. Urban Test
4.2. Highway Test
4.3. Bump Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| Longitudinal damping coefficient | |
| Suspension damping coefficient | |
| Changing longitudinal distance between wheel center and vehicle CoG | |
| Changing vertical distance between wheel center and vehicle CoG | |
| Rolling resistance zero-degree polynomial coefficient | |
| Rolling resistance second-degree polynomial coefficient | |
| Road roughness cut-off frequency | |
| Rolling resistant coefficient function | |
| g | Gravity acceleration |
| Height from vehicle CoG to the wheel center | |
| i | Axle index (f–front,r–rear) |
| Tire stiffness | |
| Longitudinal stiffness coefficient | |
| Suspension spring stiffness | |
| Semi-wheelbase distance | |
| Sprung mass | |
| Corner sprung mass | |
| Sprung mass | |
| Unsprung mass | |
| White noise signal | |
| r | Pitch rate error |
| sign coefficient | |
| Settling time | |
| Road profile | |
| Estimated road profile | |
| Longitudinal displacement of sprung mass | |
| Longitudinal displacement of unsprung mass | |
| Sprung mass longitudinal velocity reference | |
| Observation vector | |
| Vertical displacement of the sprung mass CoG | |
| Vertical displacement of the unsprung mass | |
| Corner vertical displacement | |
| Weighted sprung mass vertical acceleration | |
| Vehicle frontal area | |
| Kalman filter state matrix | |
| Tire stiffness factor | |
| Aerodynamic drag coefficient | |
| Tire shape factor | |
| Tire peak factor | |
| Tire curvature factor | |
| Aerodynamic drag force | |
| Longitudinal dissipative contribution suspension force | |
| Longitudinal elastic contribution to the suspension force | |
| Vertical shock absorber suspension force | |
| Vertical spring suspension force | |
| Wheel rolling resistance force | |
| Tire longitudinal force | |
| Goodness of fit | |
| Road roughness index | |
| Kalman filter observation matrix | |
| I | Identity matrix |
| Pitch moment of inertia | |
| Kalman gain matrix | |
| Model noise covariance matrix | |
| Measurement noise covariance matrix | |
| Laden rear wheel radius | |
| Tire longitudinal force offset | |
| Longitudinal torque command | |
| Rear in-wheel motor torque | |
| Motor torque reference | |
| Saturated motor torque reference | |
| Pitch rate control command | |
| V | Lyapunov function |
| Road inclination angle | |
| Sprung mass longitudinal velocity error | |
| Lyapunov control gain | |
| Air density | |
| Pitch angle at vehicle CoG | |
| Kalman filter state vector | |
| Tire slip ratio | |
| Motor output filtering time constant | |
| Rear axle angular velocity | |
| Acronyms | |
| CoG | Center of gravity |
| IWM | In-wheel motor |
| ISO | International Organization for Standardization |
| LC | Longitudinal control |
| MPC | Model predictive control |
| PC | Pitch control |
| PI | Proportional–integral control |
| RE | Road profile estimator |
| RMS | Root mean square |
References
- Deepak, K.; Frikha, M.A.; Benômar, Y.; El Baghdadi, M.; Hegazy, O. In-Wheel Motor Drive Systems for Electric Vehicles: State of the Art, Challenges, and Future Trends. Energies 2023, 16, 3121. [Google Scholar] [CrossRef]
- Szewczyk, P.; Łebkowski, A. Studies on Energy Consumption of Electric Light Commercial Vehicle Powered by In-Wheel Drive Modules. Energies 2021, 14, 7524. [Google Scholar] [CrossRef]
- Gobbi, M.; Sattar, A.; Palazzetti, R.; Mastinu, G. Traction motors for electric vehicles: Maximization of mechanical efficiency—A review. Appl. Energy 2024, 357, 122496. [Google Scholar] [CrossRef]
- Fujimoto, H.; Sato, S. Pitching control method based on quick torque response for electric vehicle. In Proceedings of the 2010 International Power Electronics Conference-ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 801–806. [Google Scholar]
- Kopylov, S.; Ambrož, M.; Petan, Ž.; Kunc, R.; Zheng, S.; Hou, Z. Vehicle pitch dynamics control using in-wheel motors. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 239, 1733–1744. [Google Scholar] [CrossRef]
- Ryu, K.; Kim, B.; Yoo, J.; Kim, J.; Bang, J.S.; Back, J. Robust Torque Vectoring with Desired Cornering Stiffness for In-Wheel Motor Vehicles. IEEE Access 2023, 11, 133021–133033. [Google Scholar] [CrossRef]
- Puma-Araujo, S.D.; Galluzzi, R.; Sánchez-Sánchez, X.; Ramirez-Mendoza, R.A. Study of Viscoelastic Rubber Mounts on Vehicle Suspensions with In-Wheel Electric Motors. Materials 2021, 14, 3356. [Google Scholar] [CrossRef]
- Zhiqiang, G.; Wei, W.; Shihua, Y. Longitudinal-vertical dynamics of wheeled vehicle under off-road conditions. Veh. Syst. Dyn. 2022, 60, 470–490. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, J.; Zhao, H.; Lu, C.; Chen, H. MPC-Based Slip Ratio Control for Electric Vehicle Considering Road Roughness. IEEE Access 2019, 7, 52405–52413. [Google Scholar] [CrossRef]
- Feng, J.; Liang, J.; Lu, Y.; Zhuang, W.; Pi, D.; Yin, G.; Xu, L.; Peng, P.; Zhou, C. An Integrated Control Framework for Torque Vectoring and Active Suspension System. Chin. J. Mech. Eng. 2024, 37, 10. [Google Scholar] [CrossRef]
- Li, Q.; Ma, C.; Zhang, N.; Guo, Y.; Degano, M.; Gerada, C.; Zhou, S.; An, Y. Analysis of longitudinal-vertical coupling vibration of four hub motors driven electric vehicle under unsteady condition. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Xu, W.; Chen, H.; Zhao, H.; Ren, B. Torque optimization control for electric vehicles with four in-wheel motors equipped with regenerative braking system. Mechatronics 2019, 57, 95–108. [Google Scholar] [CrossRef]
- Vidal, V.; Stano, P.; Tavolo, G.; Dhaens, M.; Tavernini, D.; Gruber, P.; Sorniotti, A. On Pre-Emptive In-Wheel Motor Control for Reducing the Longitudinal Acceleration Oscillations Caused by Road Irregularities. IEEE Trans. Veh. Technol. 2022, 71, 9322–9337. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Y.; Lin, F.; Zhang, C.; Deng, H. Integrated control for distributed in-wheel motor drive electric vehicle based on states estimation and nonlinear MPC. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 893–906. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, K.K.K. Model Predictive Control for Energy-Efficient Yaw-Stabilizing Torque Vectoring in Electric Vehicles with Four In-Wheel Motors. IEEE Access 2023, 11, 37665–37680. [Google Scholar] [CrossRef]
- Castellanos Molina, L.M.; Manca, R.; Hegde, S.; Amati, N.; Tonoli, A. Predictive handling limits monitoring and agility improvement with torque vectoring on a rear in-wheel drive electric vehicle. Veh. Syst. Dyn. 2023, 62, 2185–2209. [Google Scholar] [CrossRef]
- Asperti, M.; Vignati, M.; Sabbioni, E. Torque Vectoring Control as an Energy-Efficient Alternative to Vehicle Suspensions Tuning. Energies 2024, 17, 2903. [Google Scholar] [CrossRef]
- Hou, R.; Zhai, L.; Sun, T.; Hou, Y.; Hu, G. Steering stability control of a four in-wheel motor drive electric vehicle on a road with varying adhesion coefficient. IEEE Access 2019, 7, 32617–32627. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.; Sun, D. Torque distribution algorithm for stability control of electric vehicle driven by four in-wheel motors under emergency conditions. IEEE Access 2019, 7, 104737–104748. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, S.; Zhao, Y.; Gao, Z.; Li, C. Optimized handling stability control strategy for a four in-wheel motor independent-drive electric vehicle. IEEE Access 2019, 7, 17017–17032. [Google Scholar] [CrossRef]
- Xu, W.; Chen, H.; Wang, J.; Zhao, H. Velocity optimization for braking energy management of in-wheel motor electric vehicles. IEEE Access 2019, 7, 66410–66422. [Google Scholar] [CrossRef]
- Yim, S. Integrated chassis control with four-wheel independent steering under constraint on front slip angles. IEEE Access 2021, 9, 10338–10347. [Google Scholar] [CrossRef]
- Chae, M.; Hyun, Y.; Yi, K.; Nam, K. Dynamic handling characteristics control of an in-wheel-motor driven electric vehicle based on multiple sliding mode control approach. IEEE Access 2019, 7, 132448–132458. [Google Scholar] [CrossRef]
- Yu, Z.; Hou, Y.; Leng, B.; Xiong, L.; Li, Y. Disturbance compensation and torque coordinated control of four in-wheel motor independent-drive electric vehicles. IEEE Access 2020, 8, 119758–119767. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Path tracking control with four-wheel independent steering, driving and braking systems for autonomous electric vehicles. IEEE Access 2022, 10, 74733–74746. [Google Scholar] [CrossRef]
- Lin, C.; Liang, S.; Chen, J.; Gao, X. A multi-objective optimal torque distribution strategy for four in-wheel-motor drive electric vehicles. IEEE Access 2019, 7, 64627–64640. [Google Scholar] [CrossRef]
- Tian, J.; Ding, J.; Zhang, C.; Luo, S. Four-wheel differential steering control of IWM driven evs. IEEE Access 2020, 8, 152963–152974. [Google Scholar] [CrossRef]
- Ricciardi, V.; Ivanov, V.; Dhaens, M.; Vandersmissen, B.; Geraerts, M.; Savitski, D.; Augsburg, K. Ride Blending Control for Electric Vehicles. World Electr. Veh. J. 2019, 10, 36. [Google Scholar] [CrossRef]
- Kanchwala, H.; Wideberg, J. Pitch reduction and traction enhancement of an EV by real-time brake biasing and in-wheel motor torque control. Int. J. Veh. Syst. Model. Test. 2016, 11, 165–192. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, L.; Yu, Z.; Yang, X.; Hou, Y.; Leng, B. Model-Based Pitch Control for Distributed Drive Electric Vehicle; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Bunlapyanan, C.; Chantranuwathana, S.; Phanomchoeng, G. Analytical Investigation of Vertical Force Control in In-Wheel Motors for Enhanced Ride Comfort. Appl. Sci. 2024, 14, 6582. [Google Scholar] [CrossRef]
- Kurz, C.; Stangenberg, L.; Gauterin, F. A Generic Approach to Modeling Vehicle Pitch Dynamics on a Vehicle Test Bench. IEEE Open J. Veh. Technol. 2023, 4, 739–748. [Google Scholar] [CrossRef]
- ISO 8608:2016; Mechanical Vibration–Road Surface Profiles–Reporting of Measured Data. International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- Luo, Y.; Tan, D. Study on the dynamics of the in-wheel motor system. IEEE Trans. Veh. Technol. 2012, 61, 3510–3518. [Google Scholar]
- Cespi, R.; Galluzzi, R. Model–Based Actuated Vertical Control of Ground Vehicles with Non-Negligible Roll Dynamics. In Proceedings of the 2022 International Symposium on Electromobility (ISEM), Puebla, Mexico, 17–19 October 2022; pp. 1–6. [Google Scholar]
- Doumiati, M.; Victorino, A.; Charara, A.; Lechner, D. Estimation of road profile for vehicle dynamics motion: Experimental validation. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 5237–5242, ISSN 2378-5861. [Google Scholar] [CrossRef]
- Lewis, F.L.; Xie, L.; Popa, D. Optimal and Robust Estimation: With an Introduction to Stochastic Control Theory; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier Ltd.: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- ISO 2631:1997(E); Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements. International Organization for Standardization (ISO): Geneva, Switzerland, 1997.





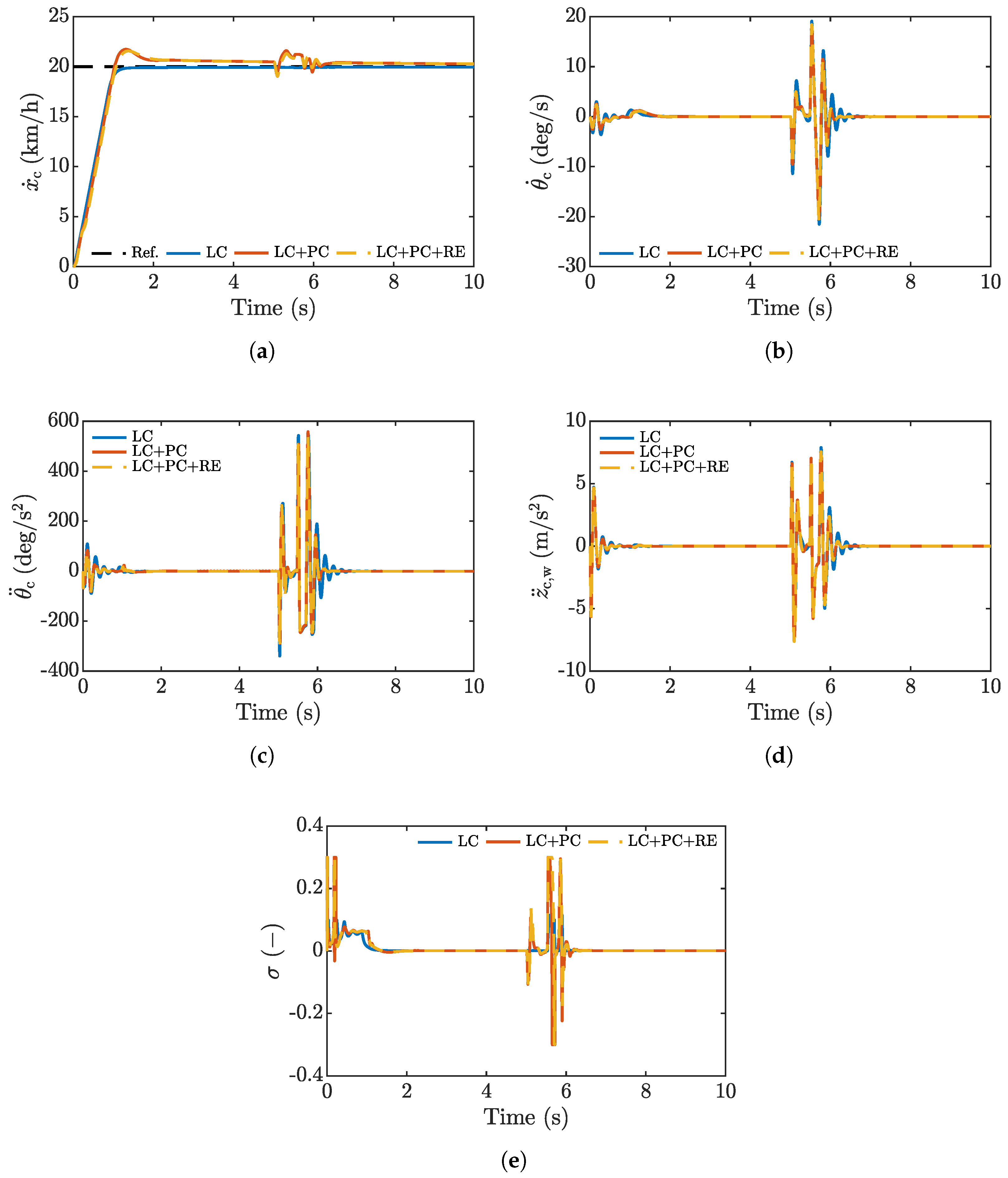
| Description | Symbol | Value | Units |
|---|---|---|---|
| Sprung mass | 715 | ||
| Distance from vehicle CoG to wheel | |||
| Front wheel distance to vehicle CoG | |||
| Rear wheel distance to vehicle CoG | |||
| Pitch inertia | |||
| Longitudinal spring stiffness | |||
| Longitudinal damping coefficient | |||
| Front unsprung mass | |||
| Front spring stiffness | |||
| Front damping coefficient | |||
| Rear unsprung mass | |||
| Rear spring stiffness | |||
| Rear damping coefficient | |||
| Laden wheel radius | |||
| Wheel spring stiffness | , | ||
| Torque control time constant | |||
| Mass density of the air | |||
| Frontal area of the vehicle | |||
| Drag coefficient | − | ||
| Gravitational acceleration | |||
| Rolling resistance coeff. (zero degree) | − | ||
| Rolling resistance coeff. (second degree) | |||
| Tire nominal stiffness factor | − | ||
| Tire nominal shape factor | − | ||
| Tire nominal peak factor | 8164 | ||
| Tire nominal curvature factor | − | ||
| Tire nominal longitudinal force offset | 0 |
| Control Type | (km/h) | (deg/s) | (deg/s2) | (m/s2) | (Nm) | (−) |
|---|---|---|---|---|---|---|
| LC | ||||||
| LC+PC | +1.15% | −41.26% | −36.95% | −6.93% | +40.88% | +60.7% |
| LC+PC+RE | +1.15% | −41.26% | −36.51% | −6.93% | +30.58% | +42.86% |
| Control Type | (km/h) | (deg/s) | (deg/s2) | (m/s2) | (Nm) | (−) |
|---|---|---|---|---|---|---|
| LC | ||||||
| LC+PC | +0.49% | −20.81% | −16.66% | −6.45% | +5.62% | +9.26% |
| LC+PC+RE | +0.54% | −24.85% | −20.53% | −7.53% | +3.20% | 3.70% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valdivieso-Soto, A.; Galluzzi, R.; Tramacere, E.; Cespi, R.; Castellanos Molina, L.M. Lyapunov-Based Pitch Control for Electric Vehicles Using In-Wheel Motors. Vehicles 2025, 7, 37. https://doi.org/10.3390/vehicles7020037
Valdivieso-Soto A, Galluzzi R, Tramacere E, Cespi R, Castellanos Molina LM. Lyapunov-Based Pitch Control for Electric Vehicles Using In-Wheel Motors. Vehicles. 2025; 7(2):37. https://doi.org/10.3390/vehicles7020037
Chicago/Turabian StyleValdivieso-Soto, Andrew, Renato Galluzzi, Eugenio Tramacere, Riccardo Cespi, and Luis M. Castellanos Molina. 2025. "Lyapunov-Based Pitch Control for Electric Vehicles Using In-Wheel Motors" Vehicles 7, no. 2: 37. https://doi.org/10.3390/vehicles7020037
APA StyleValdivieso-Soto, A., Galluzzi, R., Tramacere, E., Cespi, R., & Castellanos Molina, L. M. (2025). Lyapunov-Based Pitch Control for Electric Vehicles Using In-Wheel Motors. Vehicles, 7(2), 37. https://doi.org/10.3390/vehicles7020037







