Dynamic Differencing-Based Hybrid Network for Improved 3D Skeleton-Based Motion Prediction
Abstract
1. Introduction
- We propose Dynamic Differencing-based Hybrid Networks (2DHnet), providing a more holistic representation of human motion, encompassing both static skeletal structure and dynamic motion changes, and enabling effective human motion prediction.
- In 2DHnet, we develop the Attention-based Spatial–Temporal Dependencies Extractor (AST-DE), which includes two main components: (1) Temporal-wise Attention, to capture features from historical information in the time dimension; and (2) Spatial-wise Feature Extractor, to capture spatial features between human joints.
- In 2DHnet, we develop the Dynamic Differential Dependencies Extractor (2D-DE), which leverages multiple differential operations on 3D skeleton data to extract rich dynamic features, enabling 2DHnet to more accurately capture dynamic information such as velocity and acceleration, which enhances prediction accuracy.
- We conduct experiments to quantitatively and qualitatively verify that our proposed 2DHnet consistently outperforms existing methods, by , of MPJPE on average on the Human3.6M and 3DPW datasets, respectively.
2. Related Work
2.1. Three-Dimensional Skeleton-Based Human Motion Prediction
2.2. MLP-Based Feature Modeling
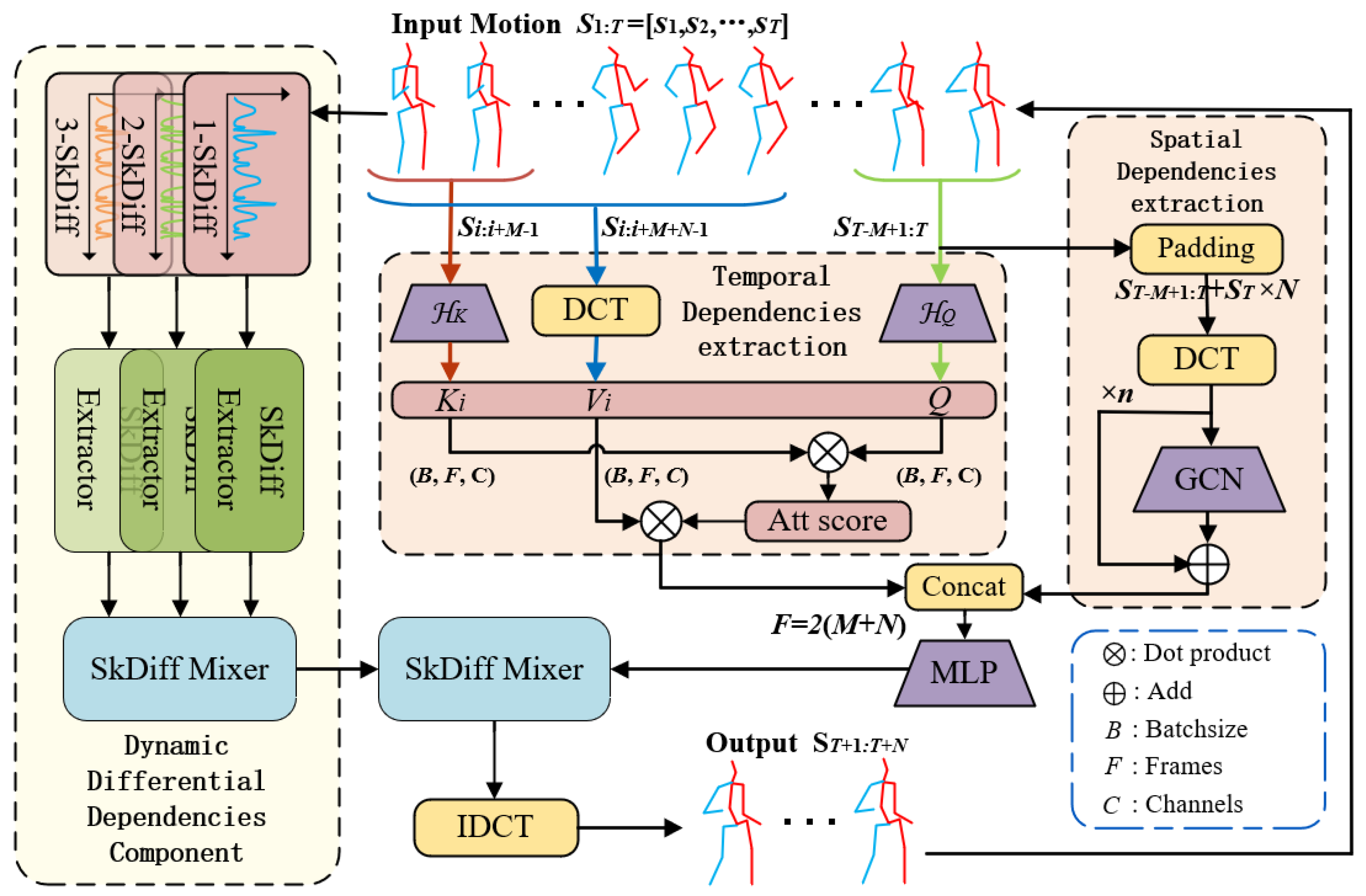
3. Method
3.1. Overall Architecture
3.2. Attention-Based Spatial–Temporal Dependencies Extractor (AST-DE)
3.2.1. Temporal-Wise Attention
3.2.2. Spatial-Wise Feature Extractor
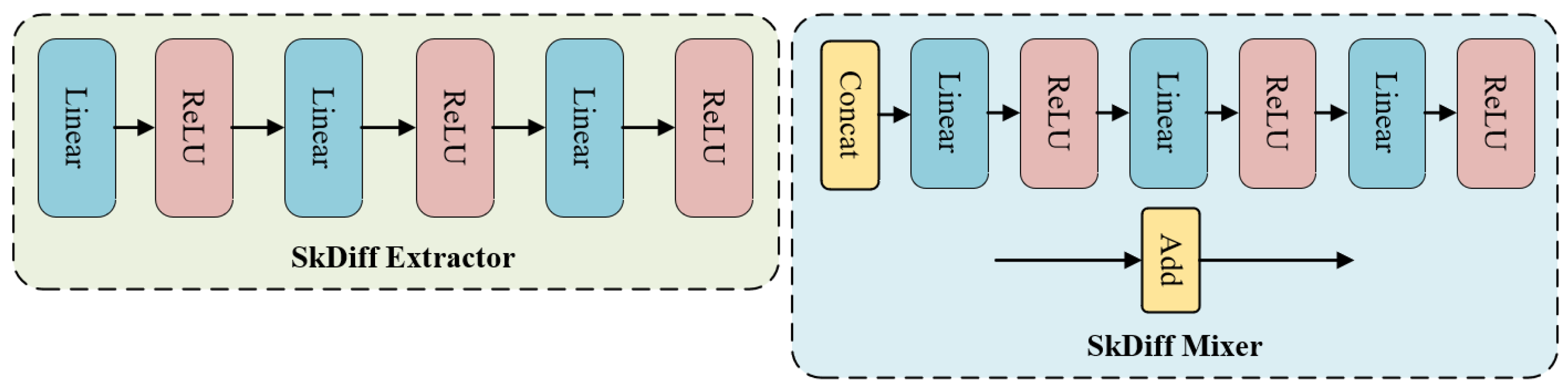
3.3. Principle of SkDiff
3.4. Loss
4. Experimental Results and Datasets
4.1. Datasets
4.1.1. Human3.6M
4.1.2. 3DPW
4.2. Experimental Metric
4.3. Experimental Settings
4.4. Comparison with State-of-the-Art Methods
4.4.1. Results on Human3.6M
4.4.2. Results on 3DPW
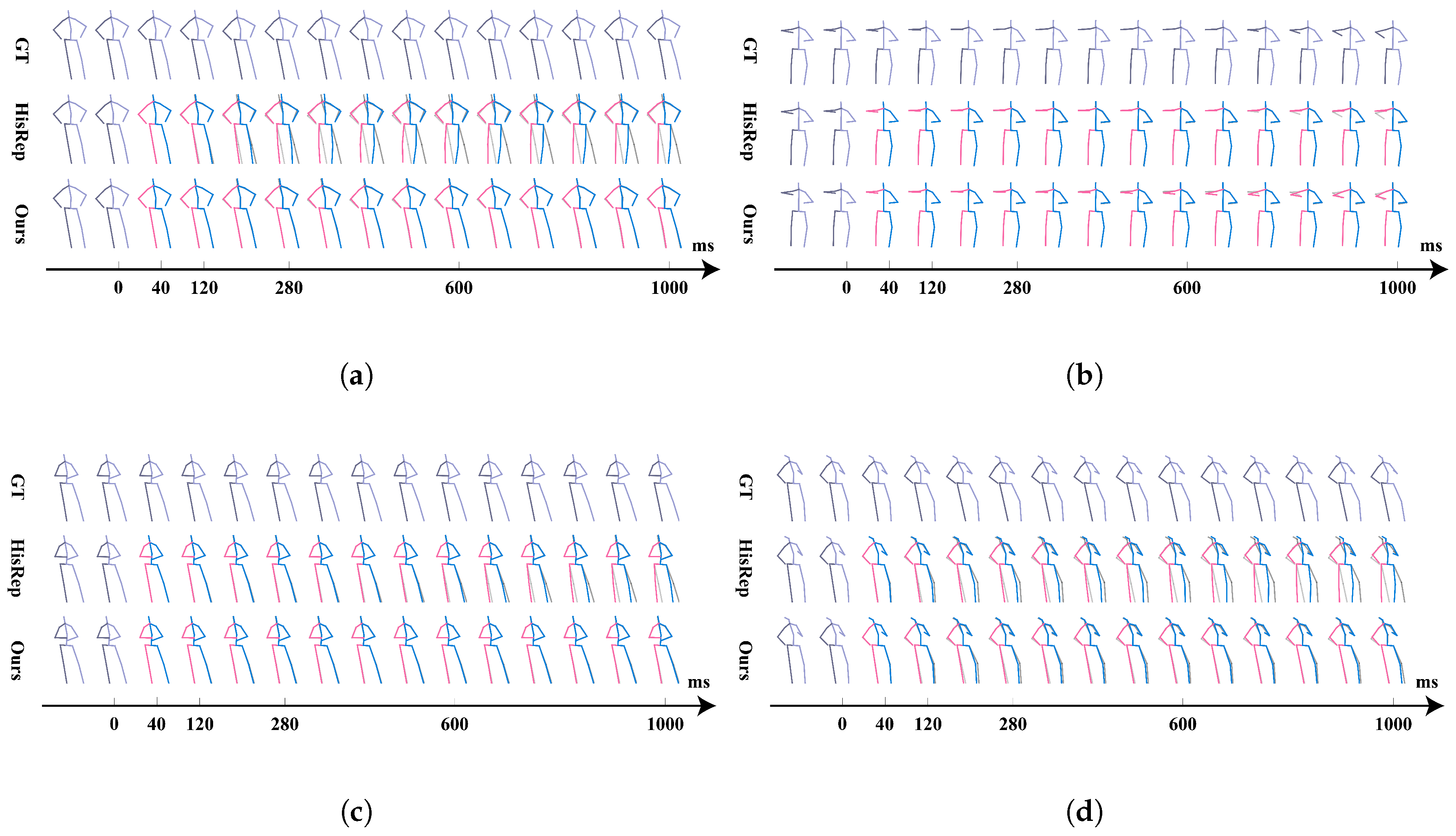
4.5. Visualization Analysis
4.6. Ablation Study
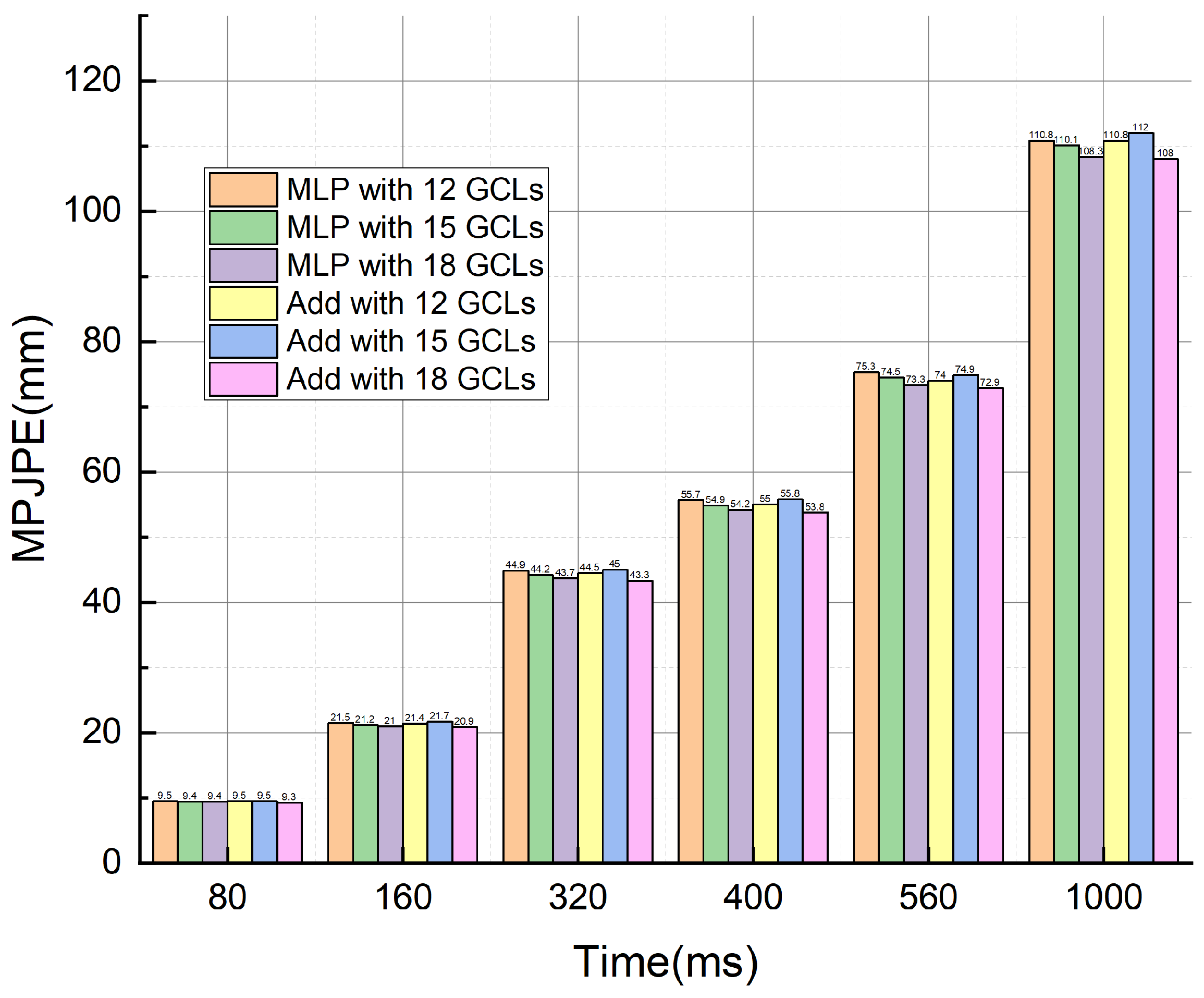
4.6.1. Effect of the Number of GCLs in AST-DE
4.6.2. Effect of Different Configurations
- Enabling only the AST-DE significantly improves model performance, particularly across various time horizons. This suggests that the AST-DE effectively captures the correlation between temporal sequence attention features and spatial graphical features.
- When the AST-DE is absent and the model relies solely on the 2D-DE for prediction, the performance deteriorates markedly. This indicates that the differential information alone causes a loss of skeletal data and fails to model complete and effective motion semantics.
- Integrating the 2D-DE with the AST-DE enhances the model’s long-term prediction capabilities. As noted earlier, our approach is effective in correcting long-term errors using the 2D-DE. As shown in Table 4, the combined model outperforms the models using a single component, reducing MPJPE by 1.4 at 1000 ms.
4.6.3. Effect of the Number of MLP Channels in SKDiff Block
4.6.4. Effect of the Number of Channels in SkDiff Extractor and SkDiff Mixer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghafir, I.; Prenosil, V.; Svoboda, J.; Hammoudeh, M. A survey on network security monitoring systems. In Proceedings of the 2016 IEEE 4th International Conference on Future Internet of Things and Cloud Workshops (FiCloudW), Vienna, Austria, 22–24 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 77–82. [Google Scholar]
- MacKenzie, I.S. Human-Computer Interaction: An Empirical Research Perspective; Morgan Kaufmann: Cambridge, MA, USA, 2012. [Google Scholar]
- Weinland, D.; Ronfard, R.; Boyer, E. A survey of vision-based methods for action representation, segmentation and recognition. Comput. Vis. Image Underst. 2011, 115, 224–241. [Google Scholar] [CrossRef]
- Wang, J.M.; Fleet, D.J.; Hertzmann, A. Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 283–298. [Google Scholar] [CrossRef] [PubMed]
- Brand, M.; Hertzmann, A. Style machines. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 183–192. [Google Scholar]
- Zhong, J.; Cao, W. Geometric algebra-based multiscale encoder-decoder networks for 3D motion prediction. Appl. Intell. 2023, 53, 26967–26987. [Google Scholar] [CrossRef]
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent Network Models for Human Dynamics. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4346–4354. [Google Scholar]
- Jain, A.; Zamir, A.R.; Savarese, S.; Saxena, A. Structural-rnn: Deep learning on spatio-temporal graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5308–5317. [Google Scholar]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2891–2900. [Google Scholar]
- Shi, J.; Zhong, J.; Cao, W. Multi-semantics Aggregation Network based on the Dynamic-attention Mechanism for 3D Human Motion Prediction. IEEE Trans. Multimed. 2023, 26, 5194–5206. [Google Scholar] [CrossRef]
- Li, M.; Chen, S.; Zhao, Y.; Zhang, Y.; Wang, Y.; Tian, Q. Dynamic multiscale graph neural networks for 3d skeleton based human motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 214–223. [Google Scholar]
- Mao, W.; Liu, M.; Salzmann, M.; Li, H. Learning Trajectory Dependencies for Human Motion Prediction. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Los Alamitos, CA, USA, 27 October–2 November 2019; pp. 9488–9496. [Google Scholar]
- Wei, M.; Miaomiao, L.; Mathieu, S. History Repeats Itself: Human Motion Prediction via Motion Attention. In Proceedings of the Europe Conference on Computer Vision ECCV, Online, 23–28 August 2020. [Google Scholar]
- Gu, B.; Tang, J.; Ding, R.; Liu, X.; Yin, J.; Zhang, Z. April-GCN: Adjacency Position-velocity Relationship Interaction Learning GCN for Human motion prediction. Knowl.-Based Syst. 2024, 292, 111613. [Google Scholar] [CrossRef]
- Zhong, J.; Cao, W. Geometric algebra-based multiview interaction networks for 3D human motion prediction. Pattern Recognit. 2023, 138, 109427. [Google Scholar] [CrossRef]
- Cao, W.; Li, S.; Zhong, J. A dual attention model based on probabilistically mask for 3D human motion prediction. Neurocomputing 2022, 493, 106–118. [Google Scholar] [CrossRef]
- Du, X.; Wang, Y.; Li, Z.; Yan, S.; Liu, M. TFAN: Twin-Flow Axis Normalization for Human Motion Prediction. IEEE Signal Process. Lett. 2024, 31, 486–490. [Google Scholar] [CrossRef]
- Xu, C.; Tan, R.T.; Tan, Y.; Chen, S.; Wang, Y.G.; Wang, X.; Wang, Y. Eqmotion: Equivariant multi-agent motion prediction with invariant interaction reasoning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1410–1420. [Google Scholar]
- Guo, W.; Du, Y.; Shen, X.; Lepetit, V.; Alameda-Pineda, X.; Moreno-Noguer, F. Back to mlp: A simple baseline for human motion prediction. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 4809–4819. [Google Scholar]
- Li, C.; Zhang, Z.; Lee, W.S.; Lee, G.H. Convolutional Sequence to Sequence Model for Human Dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Li, S.; Li, W.; Cook, C.; Zhu, C.; Gao, Y. Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Liu, J.; Wang, G.; Duan, L.Y.; Abdiyeva, K.; Kot, A.C. Skeleton-Based Human Action Recognition with Global Context-Aware Attention LSTM Networks. IEEE Trans. Image Process. 2018, 27, 1586–1599. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Wang, J.; Hu, J.F. Predicting human poses via recurrent attention network. Vis. Intell. 2023, 1, 18. [Google Scholar] [CrossRef]
- Zhong, C.; Hu, L.; Zhang, Z.; Ye, Y.; Xia, S. Spatial-Temporal Gating-Adjacency GCN for Human Motion Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- He, Z.; Zhang, L.; Wang, H. An initial prediction and fine-tuning model based on improving GCN for 3D human motion prediction. Front. Comput. Neurosci. 2023, 17, 1145209. [Google Scholar]
- Fu, J.; Yang, F.; Dang, Y.; Liu, X.; Yin, J. Learning Constrained Dynamic Correlations in Spatiotemporal Graphs for Motion Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 14273–14287. [Google Scholar] [CrossRef] [PubMed]
- Martínez-González, A.; Villamizar, M.; Odobez, J.M. Pose Transformers (POTR): Human Motion Prediction with Non-Autoregressive Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Mi, L.; Ding, R.; Zhang, X. Skeleton-based human motion prediction via spatio and position encoding transformer network. In Proceedings of the International Conference on Artificial Intelligence, Virtual Reality, and Visualization (AIVRV 2022), Chongqing, China, 2–4 September 2022; SPIE: Bellingham, WA, USA, 2023; Volume 12588, pp. 186–191. [Google Scholar]
- Zhao, M.; Tang, H.; Xie, P.; Dai, S.; Sebe, N.; Wang, W. Bidirectional transformer gan for long-term human motion prediction. ACM Trans. Multimed. Comput. Commun. Appl. 2023, 19, 163. [Google Scholar] [CrossRef]
- Meneses, M.; Matos, L.; Prado, B.; Carvalho, A.; Macedo, H. SmartSORT: An MLP-based method for tracking multiple objects in real-time. J. -Real-Time Image Process. 2021, 18, 913–921. [Google Scholar] [CrossRef]
- Cao, G.; Huang, W.; Lan, X.; Zhang, J.; Jiang, D.; Wang, Y. MLP-DINO: Category Modeling and Query Graphing with Deep MLP for Object Detection. In Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI-24), Jeju, Republic of Korea, 3–9 August 2024. [Google Scholar]
- Chen, S.; Xie, E.; Ge, C.; Chen, R.; Liang, D.; Luo, P. Cyclemlp: A mlp-like architecture for dense visual predictions. IEEE Trans. Pattern Anal. Mach. Intell. 2021. Volume abs/2107.10224. Available online: https://arxiv.org/abs/2107.10224 (accessed on 6 December 2024).
- Boughrara, H.; Chtourou, M.; Amar, C.B. MLP neural network based face recognition system using constructive training algorithm. In Proceedings of the International Conference on Multimedia Computing & Systems, Tangiers, Morocco, 10–12 May 2012. [Google Scholar]
- Shahreza, H.O.; Hahn, V.K.; Marcel, S. MLP-Hash: Protecting Face Templates via Hashing of Randomized Multi-Layer Perceptron. arXiv 2022, arXiv:2204.11054. [Google Scholar]
- Bouazizi, A.; Holzbock, A.; Kressel, U.; Dietmayer, K.; Belagiannis, V. MotionMixer: MLP-based 3D Human Body Pose Forecasting. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22. International Joint Conferences on Artificial Intelligence Organization, Vienna, Austria, 23–29 July 2022; pp. 791–798. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3. 6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering accurate 3d human pose in the wild using imus and a moving camera. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 601–617. [Google Scholar]
- Dang, L.; Nie, Y.; Long, C.; Zhang, Q.; Li, G. Msr-gcn: Multi-scale residual graph convolution networks for human motion prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 11467–11476. [Google Scholar]
- Ma, T.; Nie, Y.; Long, C.; Zhang, Q.; Li, G. Progressively generating better initial guesses towards next stages for high-quality human motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6437–6446. [Google Scholar]
- Li, M.; Chen, S.; Zhang, Z.; Xie, L.; Tian, Q.; Zhang, Y. Skeleton-parted graph scattering networks for 3d human motion prediction. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 18–36. [Google Scholar]
- Tang, J.; Zhang, J.; Ding, R.; Gu, B.; Yin, J. Collaborative multi-dynamic pattern modeling for human motion prediction. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 3689–3700. [Google Scholar] [CrossRef]

| Motion | Walking | Eating | Smoking | Discussion | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Milliseconds | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 |
| PGBIG [40] | 10.2 | 19.8 | 34.5 | 40.3 | 7.0 | 15.1 | 30.6 | 38.1 | 6.6 | 14.1 | 28.2 | 34.7 | 10.0 | 23.8 | 53.6 | 66.7 |
| SPGSN [41] | 10.1 | 19.4 | 34.8 | 41.5 | 7.1 | 14.9 | 30.5 | 37.9 | 6.7 | 13.8 | 28.0 | 34.6 | 10.4 | 23.8 | 53.6 | 67.1 |
| EqMotion [18] | 9.2 | 18.2 | 34.2 | 41.4 | 6.6 | 14.2 | 30.0 | 37.7 | 6.2 | 12.8 | 26.7 | 33.6 | 9.1 | 22.0 | 51.8 | 65.3 |
| SIMLPE [19] | 9.9 | - | - | 39.6 | 5.9 | - | - | 36.1 | 6.5 | - | - | 36.3 | 9.4 | - | - | 64.3 |
| TFAN [17] | 10.0 | 19.9 | 36.5 | 43.1 | 5.9 | 13.6 | 28.4 | 35.9 | 6.6 | 14.3 | 29.8 | 36.8 | 9.1 | 21.9 | 50.0 | 63.4 |
| April-GCN [14] | 9.2 | 18.7 | 34.4 | 41.1 | 6.2 | 14.1 | 30.0 | 37.7 | 5.8 | 13.1 | 27.0 | 33.7 | 8.9 | 22.6 | 52.8 | 65.8 |
| Ours | 9.5 | 18.9 | 33.0 | 38.1 | 5.7 | 13.3 | 27.9 | 35.2 | 5.9 | 12.3 | 23.9 | 30.1 | 8.2 | 17.7 | 34.1 | 43.4 |
| Motion | Directions | Greeting | Phoning | Posing | ||||||||||||
| Milliseconds | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 |
| PGBIG [40] | 7.2 | 17.6 | 40.9 | 51.5 | 15.2 | 34.1 | 71.6 | 87.1 | 8.3 | 18.3 | 38.7 | 48.4 | 10.7 | 25.7 | 60.0 | 76.6 |
| SPGSN [41] | 7.4 | 17.2 | 39.8 | 50.3 | 14.6 | 32.6 | 70.6 | 86.4 | 8.7 | 18.3 | 38.7 | 48.5 | 10.7 | 25.3 | 59.9 | 76.5 |
| EqMotion [18] | 6.6 | 15.8 | 39.0 | 50.0 | 12.7 | 30.0 | 69.1 | 86.3 | 7.7 | 17.3 | 38.2 | 48.4 | 9.3 | 23.7 | 59.6 | 77.5 |
| SIMLPE [19] | 6.5 | - | - | 55.8 | 12.4 | - | - | 77.3 | 8.1 | - | - | 48.6 | 8.8 | - | - | 73.8 |
| TFAN [17] | 6.5 | 17.1 | 43.1 | 54.9 | 12.3 | 28.4 | 62.4 | 76.9 | 7.9 | 17.5 | 38.3 | 48.3 | 8.6 | 22.1 | 55.4 | 72.0 |
| April-GCN [14] | 6.2 | 16.4 | 40.1 | 50.8 | 13.0 | 32.0 | 71.7 | 87.8 | 7.4 | 17.3 | 38.0 | 47.8 | 9.0 | 23.7 | 59.5 | 77.0 |
| Ours | 6.6 | 17.8 | 43.6 | 55.5 | 12.3 | 29.2 | 62.9 | 77.8 | 7.8 | 17.9 | 38.4 | 48.2 | 7.3 | 16.9 | 34.7 | 45.5 |
| Motion | Purchases | Sitting | Sitting Down | Taking Photo | ||||||||||||
| Milliseconds | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 |
| PGBIG [40] | 12.5 | 28.7 | 60.1 | 73.3 | 8.8 | 19.2 | 42.4 | 53.8 | 13.9 | 27.9 | 57.4 | 71.5 | 8.4 | 18.9 | 42.0 | 53.3 |
| SPGSN [41] | 12.8 | 28.6 | 61.0 | 74.4 | 9.3 | 19.4 | 42.3 | 53.6 | 14.2 | 27.7 | 56.8 | 70.7 | 8.8 | 18.9 | 41.5 | 52.7 |
| EqMotion [18] | 11.3 | 26.6 | 59.8 | 74.1 | 8.3 | 18.1 | 41.1 | 53.0 | 13.2 | 26.3 | 56.0 | 70.4 | 8.1 | 17.8 | 41.0 | 52.7 |
| SIMLPE [19] | 11.7 | - | - | 72.4 | 8.6 | - | - | 55.2 | 13.6 | - | - | 70.8 | 7.8 | - | - | 50.8 |
| TFAN [17] | 11.7 | 27.6 | 59.0 | 73.1 | 8.7 | 19.2 | 42.8 | 54.4 | 13.6 | 29.1 | 57.5 | 70.3 | 7.7 | 17.5 | 39.7 | 50.5 |
| April-GCN [14] | 11.0 | 26.8 | 59.2 | 73.0 | 8.0 | 18.1 | 41.7 | 53.3 | 13.0 | 26.7 | 56.5 | 70.8 | 7.8 | 18.0 | 41.5 | 52.9 |
| Ours | 12.1 | 29.0 | 61.5 | 76.1 | 8.4 | 19.0 | 42.3 | 53.7 | 14.0 | 30.2 | 59.3 | 72.2 | 7.8 | 17.9 | 40.3 | 51.4 |
| Motion | Waiting | Walking Dog | Walking Together | Average | ||||||||||||
| Milliseconds | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 | 80 | 160 | 320 | 400 |
| PGBIG [40] | 8.9 | 20.1 | 43.6 | 54.3 | 18.8 | 39.3 | 73.7 | 86.4 | 8.7 | 18.6 | 34.4 | 41.0 | 10.3 | 22.7 | 47.4 | 58.5 |
| SPGSN [41] | 9.2 | 19.8 | 43.1 | 54.1 | - | - | - | - | 8.9 | 18.2 | 33.8 | 40.9 | 10.4 | 22.3 | 47.1 | 58.3 |
| EqMotion [18] | 7.9 | 17.9 | 41.5 | 53.1 | 16.6 | 35.9 | 72.0 | 85.7 | 8.1 | 17.1 | 32.4 | 39.2 | 9.4 | 20.9 | 46.2 | 57.9 |
| SIMLPE [19] | 7.8 | - | - | 53.2 | 18.2 | - | - | 83.6 | 8.4 | - | - | 41.2 | 9.6 | - | - | 57.3 |
| TFAN [17] | 7.6 | 17.6 | 40.8 | 51.7 | 18.0 | 38.1 | 71.0 | 84.0 | 8.4 | 18.0 | 35.7 | 43.7 | 9.5 | 21.5 | 46.0 | 57.3 |
| April-GCN [14] | 7.7 | 18.4 | 41.6 | 52.3 | 16.7 | 37.0 | 71.3 | 84.0 | 8.0 | 17.6 | 33.2 | 40.0 | 9.2 | 21.4 | 46.6 | 57.8 |
| Ours | 7.6 | 18.4 | 42.1 | 53.5 | 18.3 | 38.8 | 72.7 | 85.7 | 7.9 | 17.0 | 33.0 | 40.0 | 9.3 | 20.1 | 43.3 | 53.8 |
| Motion | Walking | Eating | Smoking | Discussion | Directions | Greeting | Phoning | Posing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Milliseconds | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 |
| PGBIG [40] | 48.1 | 56.4 | 51.1 | 76.0 | 46.5 | 69.5 | 87.1 | 118.2 | 69.3 | 100.4 | 110.2 | 143.5 | 65.9 | 102.7 | 106.1 | 164.8 |
| SPGSN [41] | 46.9 | 53.6 | 49.8 | 73.4 | 46.7 | 68.6 | - | - | 70.1 | 100.5 | - | - | 66.7 | 102.5 | - | - |
| EqMotion [18] | 50.7 | 58.8 | 50.7 | 76.2 | 45.4 | 67.3 | 87.1 | 116.8 | 69.8 | 101.2 | 111.6 | 144.2 | 65.8 | 102.3 | 111.2 | 169.6 |
| SIMLPE [19] | 46.8 | 55.7 | 49.6 | 74.5 | 47.2 | 69.3 | 85.7 | 116.3 | 73.1 | 106.7 | 99.8 | 137.5 | 66.3 | 103.3 | 103.4 | 168.7 |
| TFAN [17] | 53.0 | 64.4 | 49.5 | 76.7 | 48.6 | 72.4 | 84.7 | 116.3 | 72.4 | 107.2 | 100.9 | 138.5 | 66.7 | 105.5 | 102.1 | 166.8 |
| April-GCN [14] | 49.4 | 54.8 | 50.6 | 74.6 | 46.5 | 68.8 | 88.0 | 117.7 | 70.3 | 100.0 | 111.0 | 142.6 | 65.5 | 100.3 | 109.7 | 166.4 |
| Ours | 46.8 | 60.7 | 48.8 | 74.0 | 42.3 | 65.5 | 66.6 | 106.2 | 73.3 | 104.5 | 103.0 | 140.9 | 66.1 | 104.5 | 72.4 | 137.8 |
| Motion | Purchases | Sitting | Sitting Down | Taking Photo | Waiting | Walking Dog | Walking Together | Average | ||||||||
| Milliseconds | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 | 560 | 1000 |
| PGBIG [40] | 95.3 | 133.3 | 74.4 | 116.1 | 96.7 | 147.8 | 74.3 | 118.6 | 72.2 | 103.4 | 104.7 | 139.8 | 51.9 | 64.3 | 76.9 | 110.3 |
| SPGSN [41] | - | - | 75.0 | 116.2 | - | - | 75.6 | 118.2 | 73.5 | 103.6 | - | - | - | - | 77.4 | 109.6 |
| EqMotion [18] | 97.4 | 136.9 | 74.2 | 116.0 | 96.9 | 148.9 | 77.7 | 122.4 | 73.5 | 105.8 | 104.4 | 142.1 | 50.4 | 62.0 | 77.8 | 111.4 |
| SIMLPE [19] | 93.8 | 132.5 | 75.4 | 114.1 | 95.7 | 142.4 | 71.0 | 112.8 | 71.6 | 104.6 | 105.6 | 141.2 | 50.8 | 61.5 | 75.7 | 109.4 |
| TFAN [17] | 96.1 | 136.1 | 75.4 | 114.0 | 95.2 | 141.8 | 71.2 | 113.9 | 70.4 | 105.0 | 107.1 | 146.5 | 55.2 | 70.3 | 76.5 | 111.7 |
| April-GCN [14] | 96.8 | 135.4 | 75.4 | 117.2 | 98.7 | 149.3 | 75.9 | 119.1 | 72.3 | 103.6 | 103.2 | 137.1 | 50.5 | 61.1 | 77.6 | 109.9 |
| Ours | 98.6 | 136.9 | 74.5 | 115.2 | 96.9 | 143.3 | 72.7 | 115.2 | 72.9 | 105.7 | 108.2 | 143.9 | 51.0 | 65.5 | 72.9 | 108.0 |
| Milliseconds | 200 | 400 | 600 | 800 | 1000 |
|---|---|---|---|---|---|
| DMGNN [11] | 37.3 | 67.8 | 94.5 | 109.7 | 123.6 |
| LTD [12] | 35.6 | 67.8 | 90.6 | 106.9 | 117.8 |
| MSR [39] | 37.8 | 71.3 | 93.9 | 110.8 | 121.5 |
| PGBIG [40] | 35.3 | 67.8 | 89.6 | 102.6 | 109.4 |
| DPnet [42] | 29.3 | 58.3 | 79.8 | 94.4 | 104.1 |
| April-GCN [14] | 30.4 | 61.8 | 88.0 | 98.2 | 105.4 |
| Ours | 26.2 | 44.7 | 59.5 | 66.9 | 71.2 |
| TSAtt | Depth | Padding | Mixer | 80 ms | 160 ms | 320 ms | 400 ms | 560 ms | 1000 ms |
|---|---|---|---|---|---|---|---|---|---|
| ✓ | - | - | - | 9.3 | 20.9 | 43.6 | 54.1 | 73.6 | 109.7 |
| 1 | Last | MLP | 362.2 | 363.1 | 367.1 | 369.3 | 550.2 | 695.1 | |
| ✓ | 1 | Last | MLP | 9.4 | 21.0 | 43.7 | 54.2 | 73.3 | 108.3 |
| ✓ | 2 | Last | MLP | 9.7 | 21.8 | 45.4 | 56.1 | 75.4 | 111.0 |
| ✓ | 3 | Last | MLP | 9.4 | 21.2 | 44.1 | 54.5 | 73.4 | 108.1 |
| ✓ | 1 | First | MLP | 9.7 | 21.4 | 44.2 | 54.7 | 74.1 | 109.5 |
| ✓ | 2 | First | MLP | 9.5 | 21.4 | 44.3 | 55.0 | 74.3 | 109.8 |
| ✓ | 3 | First | MLP | 9.6 | 21.4 | 44.7 | 55.4 | 74.7 | 109.6 |
| ✓ | 1 | Last | Add | 9.3 | 20.9 | 43.3 | 53.8 | 72.9 | 108.0 |
| ✓ | 2 | Last | Add | 9.6 | 21.6 | 44.8 | 55.3 | 74.3 | 110.5 |
| ✓ | 3 | Last | Add | 9.5 | 21.5 | 44.3 | 54.8 | 73.7 | 109.7 |
| ✓ | 1 | First | Add | 9.6 | 21.6 | 44.5 | 55.0 | 73.9 | 110.1 |
| ✓ | 2 | First | Add | 9.5 | 21.5 | 44.4 | 55.0 | 74.3 | 111.1 |
| ✓ | 3 | First | Add | 9.4 | 21.2 | 43.7 | 53.9 | 72.8 | 107.2 |
| Number of Channels | 80 ms | 160 ms | 320 ms | 400 ms | 560 ms | 1000 ms |
|---|---|---|---|---|---|---|
| 128 | 9.3 | 20.9 | 43.3 | 53.8 | 72.9 | 108.0 |
| 256 | 9.5 | 21.4 | 44.1 | 54.5 | 73.4 | 109.6 |
| 512 | 9.6 | 21.6 | 44.7 | 55.4 | 74.6 | 110.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, R.; Lu, C.; Zhong, J. Dynamic Differencing-Based Hybrid Network for Improved 3D Skeleton-Based Motion Prediction. AI 2024, 5, 2897-2913. https://doi.org/10.3390/ai5040139
Ji R, Lu C, Zhong J. Dynamic Differencing-Based Hybrid Network for Improved 3D Skeleton-Based Motion Prediction. AI. 2024; 5(4):2897-2913. https://doi.org/10.3390/ai5040139
Chicago/Turabian StyleJi, Ruiya, Chengjie Lu, and Jianqi Zhong. 2024. "Dynamic Differencing-Based Hybrid Network for Improved 3D Skeleton-Based Motion Prediction" AI 5, no. 4: 2897-2913. https://doi.org/10.3390/ai5040139
APA StyleJi, R., Lu, C., & Zhong, J. (2024). Dynamic Differencing-Based Hybrid Network for Improved 3D Skeleton-Based Motion Prediction. AI, 5(4), 2897-2913. https://doi.org/10.3390/ai5040139






