Aberrometric, Geometrical, and Biomechanical Characterization of Sound-Induced Vibrational Modes of the Living Human Cornea
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Experimental Measurements
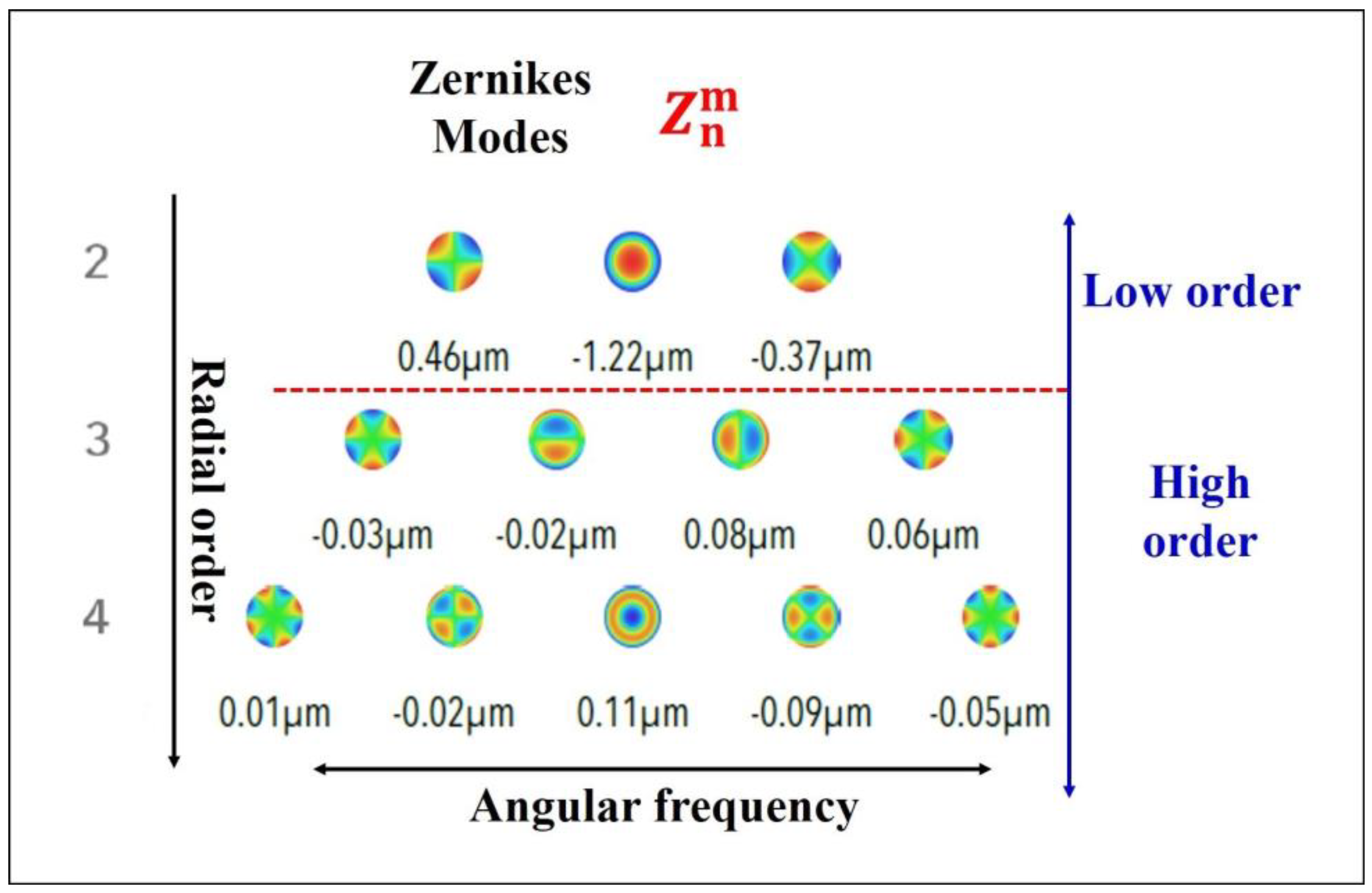
2.3. Wavefront Analysis
2.4. Corneal Surface Reconstruction
2.5. Biomechanical Model
2.6. Statistical Analysis and Image Reconstruction Processing
3. Results
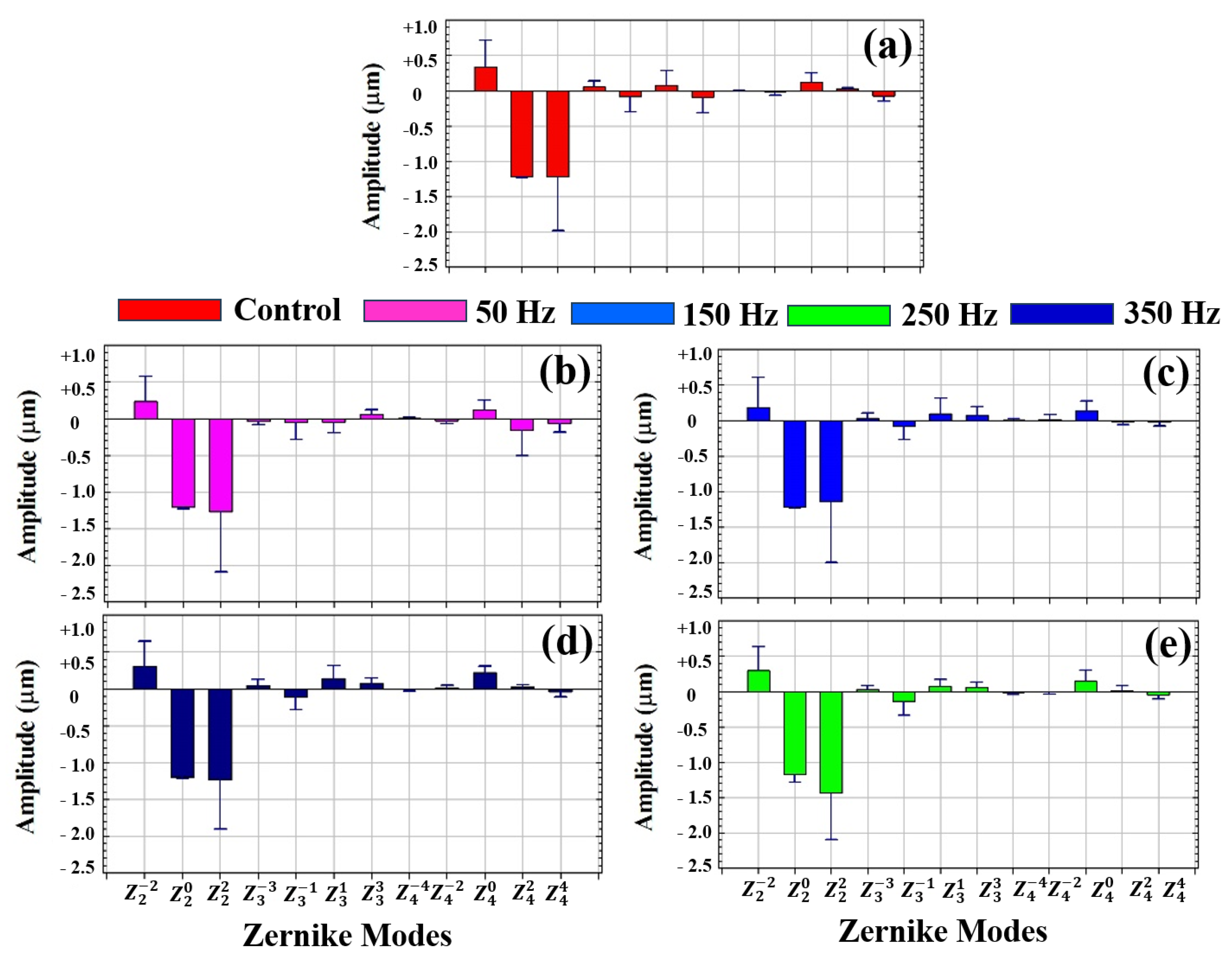
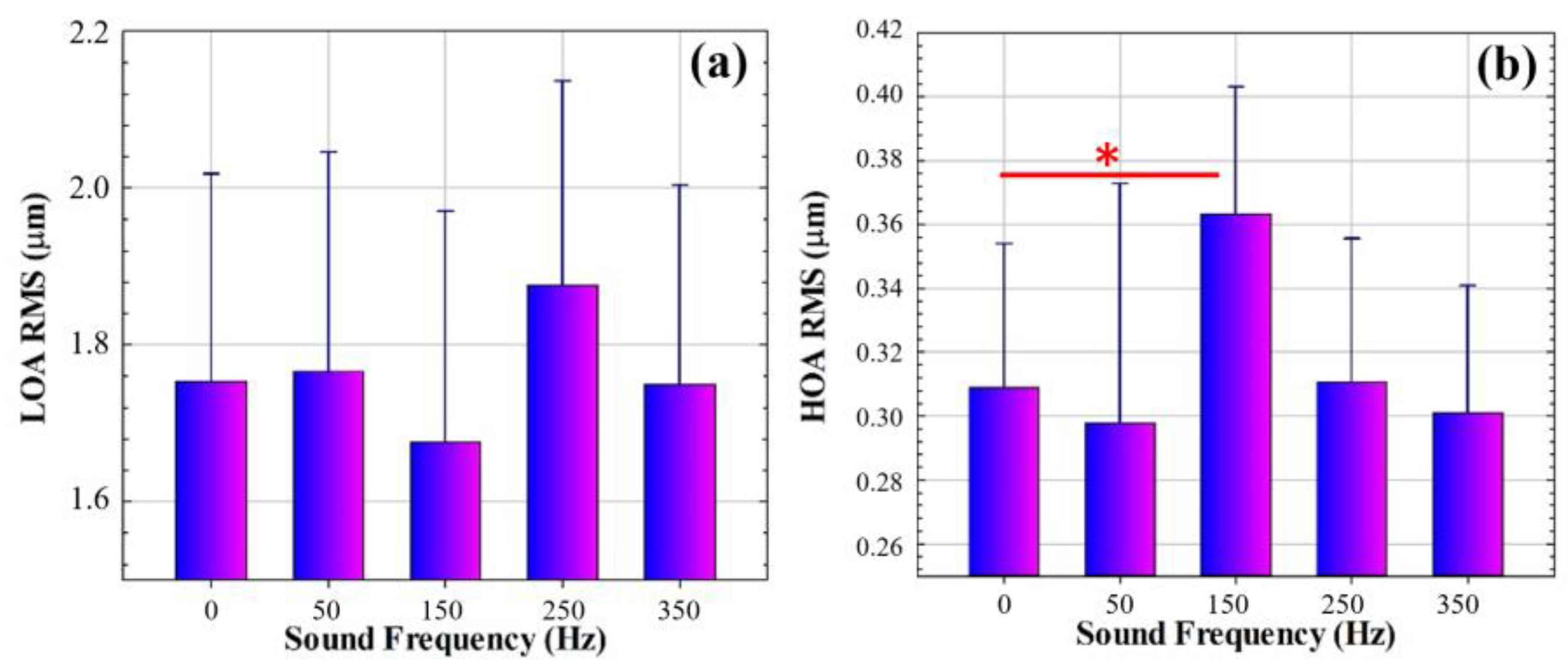
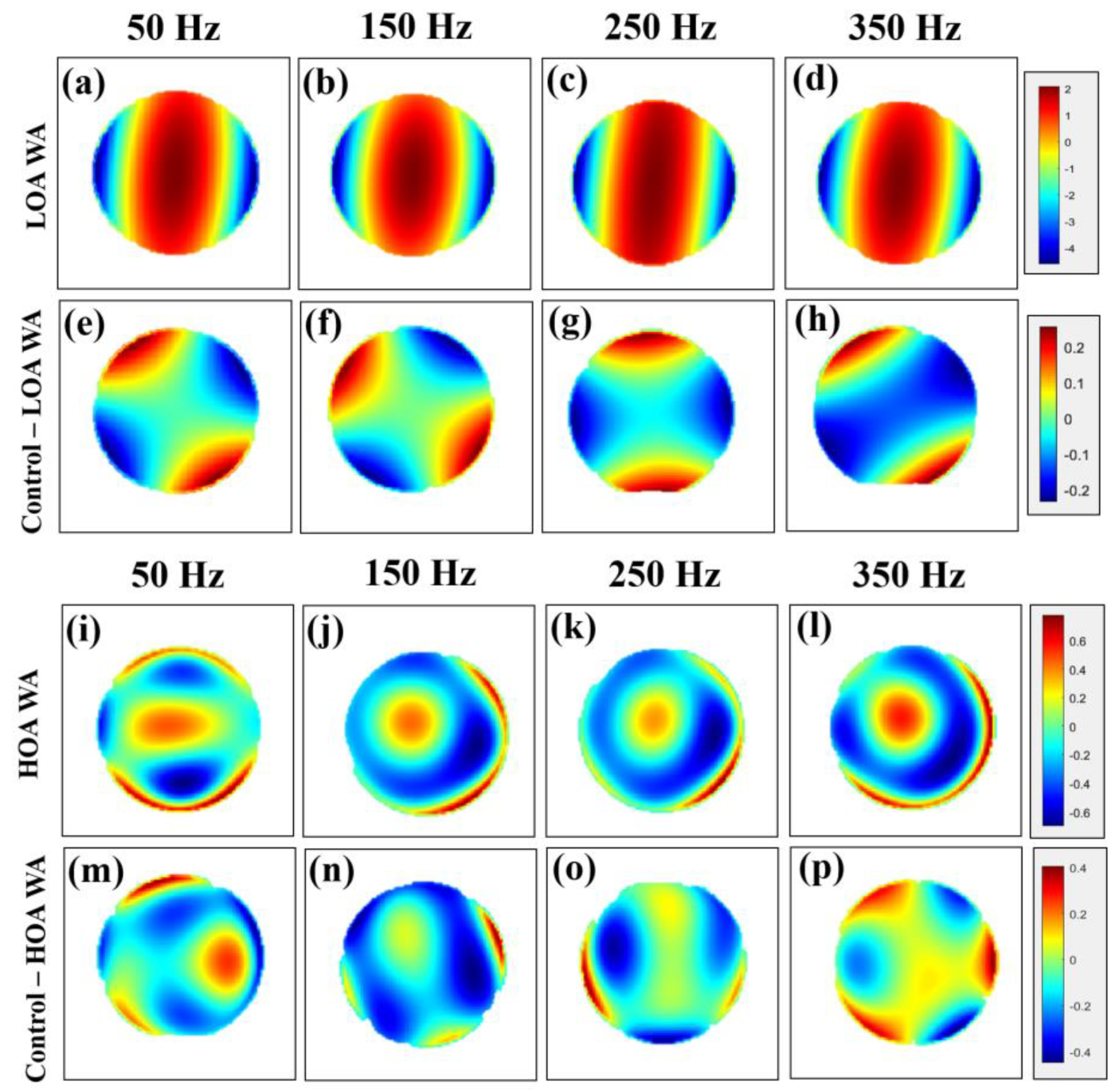
3.1. Wavefront Aberrometry
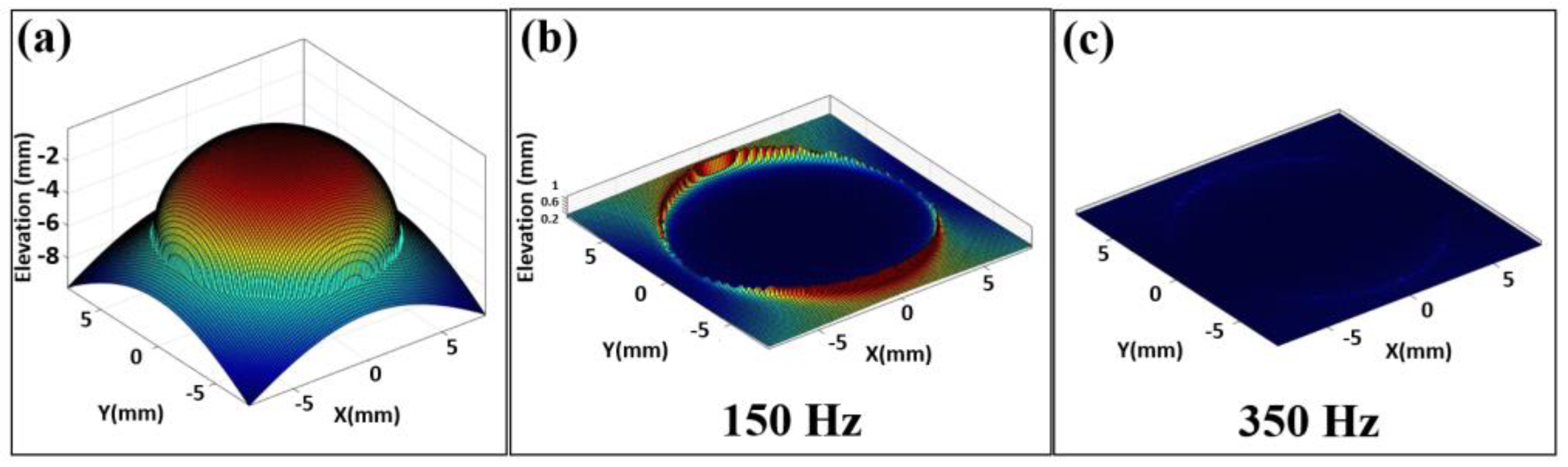
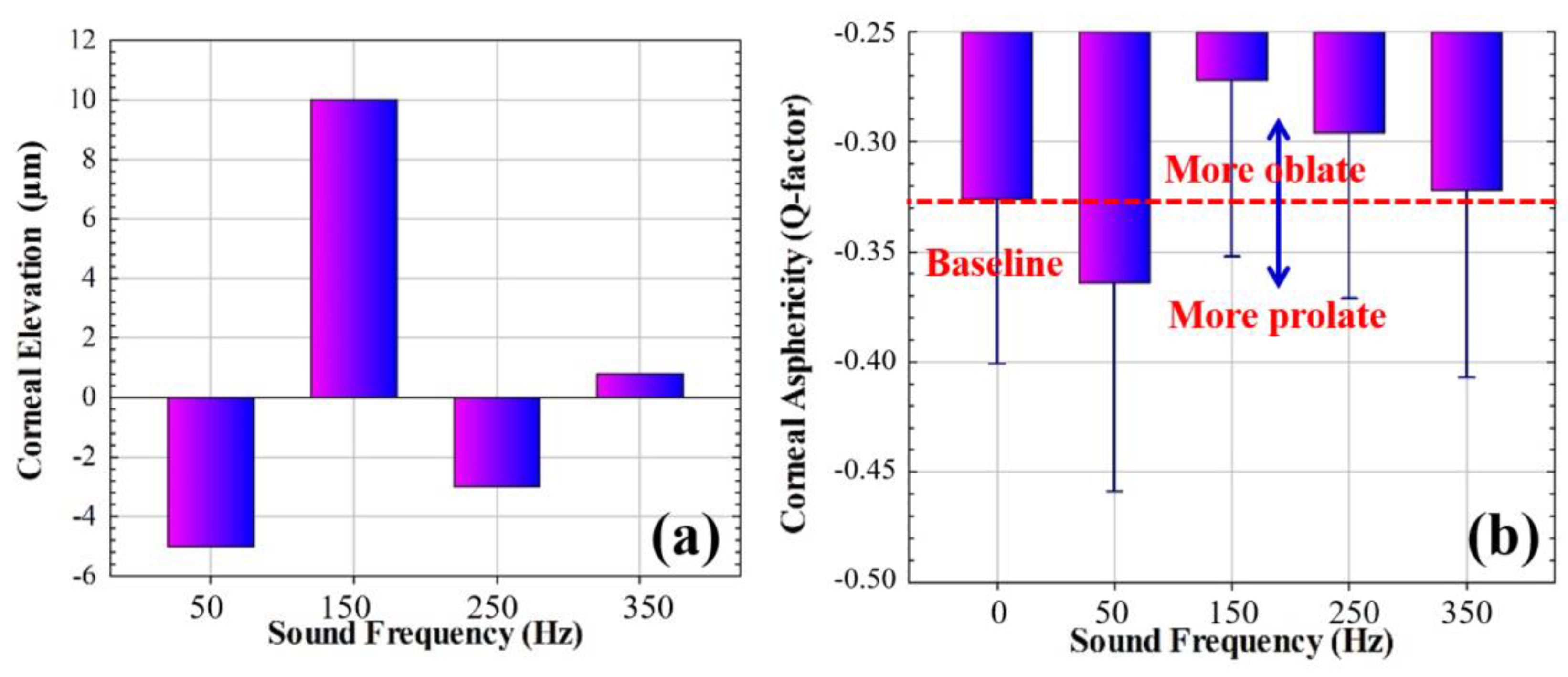
3.2. Corneal Geometry
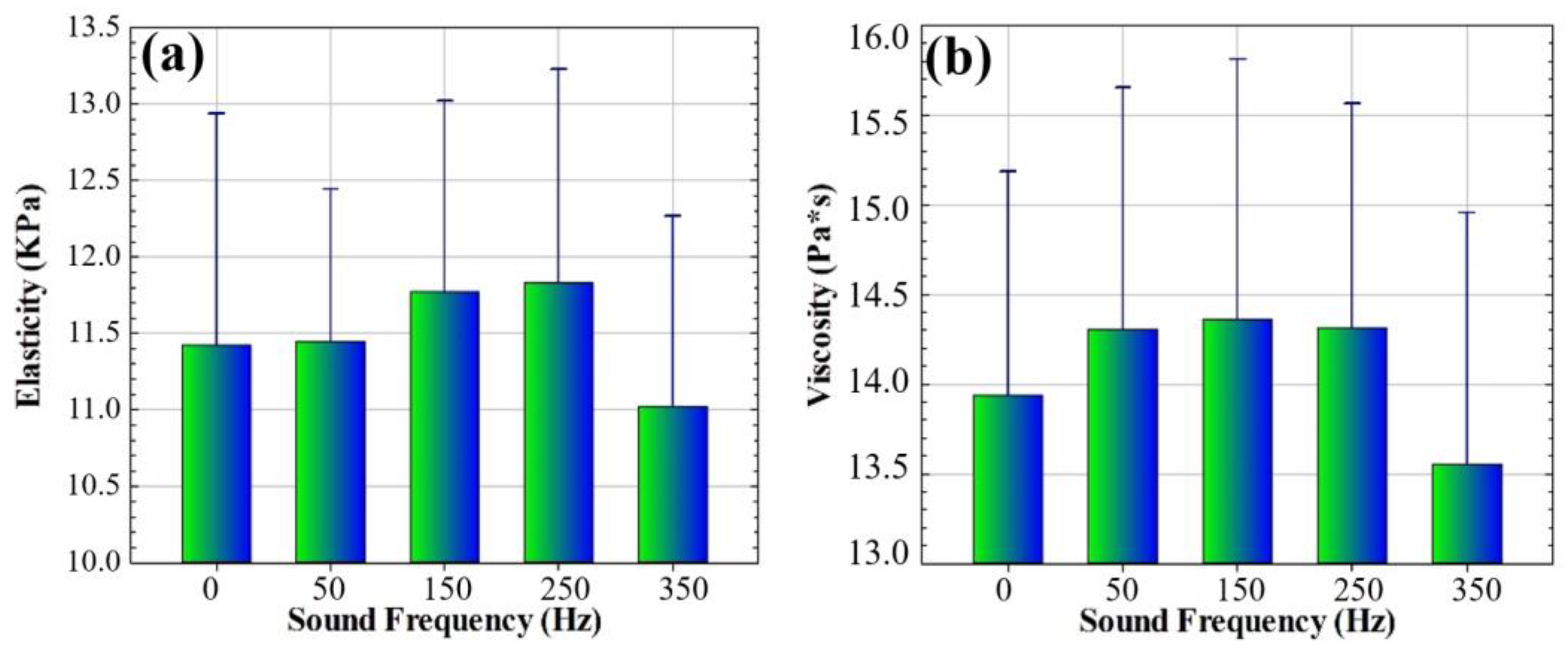
3.3. Biomechanical Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marinescu, M.; Dascalescu, D.; Constantin, M.; Coviltir, V.; Burcel, M.; Darabus, D.; Ciuluvica, R.; Stanila, D.; Potop, V.; Alexandrescu, C. Corneal Biomechanics—An Emerging Ocular Property with a Significant Impact. Maedica 2022, 17, 925–930. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, A.S.; Staberg, L.G.; Schlegel, W.A. Viscoelastic properties of human cornea. Exp. Mech. 1973, 13, 497–503. [Google Scholar] [CrossRef]
- Espana, E.M.; Birk, D.E. Composition, structure and function of the corneal stroma. Exp. Eye Res. 2020, 198, 108137. [Google Scholar] [CrossRef]
- Hatami-Marbini, H.; Etebu, E. Hydration dependent biomechanical properties of the corneal stroma. Exp. Eye Res. 2013, 116, 47–54. [Google Scholar] [CrossRef]
- Schweitzer, C.; Korobelnik, J.F.; Boniol, M.; Cougnard-Gregoire, A.; Le Goff, M.; Malet, F.; Rougier, M.B.; Delyfer, M.N.; Dartigues, J.F.; Delcourt, C. Associations of biomechanical properties of the cornea with environmental and metabolic factors in an elderly population: The ALIENOR study. Investig. Ophthalmol. Vis. Sci. 2016, 57, 2003–2011. [Google Scholar] [CrossRef]
- Kamiya, K.; Shimizu, K.; Ohmoto, F. Effect of aging on corneal biomechanical parameters using the ocular response analyzer. J. Refract. Surg. 2009, 25, 888–893. [Google Scholar] [CrossRef] [PubMed]
- David, R.; Zangwill, L.; Briscoe, D.; Dagan, M.; Yagev, R.; Yassur, Y. Diurnal intraocular pressure variations: An analysis of 690 diurnal curves. Br. J. Ophthalmol. 1992, 76, 280–283. [Google Scholar] [CrossRef] [PubMed]
- Marcellán, M.C.; Remón, L.; Ávila, F.J. Corneal hysteresis and intraocular pressure are altered in silicone-hydrogel soft contact lenses wearers. Int. Ophthalmol. 2022, 42, 2801–2809. [Google Scholar] [CrossRef] [PubMed]
- Bao, F.; Lopes, B.T.; Zheng, X.; Ji, Y.; Wang, J.; Elsheikh, A. Corneal Biomechanics Losses Caused by Refractive Surgery. Curr. Eye Res. 2023, 48, 137–143. [Google Scholar] [CrossRef]
- Esporcatte, L.P.G.; Salomão, M.Q.; Lopes, B.T.; Sena, N.; Ferreira, É.; Filho, J.B.R.; Machado, A.P.; Ambrósio, P., Jr. Biomechanics in keratoconus diagnosis. Curr. Eye Res. 2023, 48, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Elhusseiny, A.M.; Scarcelli, G.; Saeedi, O.J. Corneal Biomechanical Measures for Glaucoma: A Clinical Approach. Bioengineering 2023, 10, 1108. [Google Scholar] [CrossRef] [PubMed]
- Salomão, M.Q.; Hofling-Lima, A.L.; Gomes Esporcatte, L.P.; Lopes, B.; Vinciguerra, R.; Vinciguerra, P.; Bühren, J.; Sena, N., Jr.; Luz Hilgert, G.S.; Ambrósio, R., Jr. The Role of Corneal Biomechanics for the Evaluation of Ectasia Patients. Int. J. Environ. Res. Public Health 2020, 17, 2113. [Google Scholar] [CrossRef] [PubMed]
- Esporcatte, L.P.G.; Salomão, M.Q.; Junior, N.S.; Machado, A.P.; Ferreira, É.; Loureiro, T.; Junior, R.A. Corneal biomechanics for corneal ectasia: Update. Saudi J. Ophthalmol. 2022, 36, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Lau, W.; Pye, D. A clinical description of Ocular Response Analyzer measurements. Investig. Ophthalmol. Vis. Sci. 2011, 52, 2911–2916. [Google Scholar] [CrossRef] [PubMed]
- Luce, D.A. Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J. Cataract Refract. Surg. 2005, 31, 156–162. [Google Scholar] [CrossRef] [PubMed]
- Zimprich, L.; Diedrich, J.; Bleeker, A.; Schweitzer, J.A. Corneal Hysteresis as a Biomarker of Glaucoma: Current Insights. Clin. Ophthalmol. 2020, 14, 2255–2264. [Google Scholar] [CrossRef]
- Sit, A.J.; Chen, T.C.; Takusagawa, H.L.; Rosdahl, J.A.; Hoguet, A.; Chopra, V.; Richter, G.M.; Ou, Y.; Kim, S.J.; WuDunn, D. Corneal Hysteresis for the Diagnosis of Glaucoma and Assessment of Progression Risk: A Report by the American Academy of Ophthalmology. Ophthalmology 2023, 130, 433–442. [Google Scholar] [CrossRef] [PubMed]
- del Buey, M.A.; Cristóbal, J.A.; Ascaso, F.J.; Lavilla, L.; Lanchares, E. Biomechanical properties of the cornea in Fuchs’ corneal dystrophy. Investig. Ophthalmol. Vis. Sci. 2009, 50, 3199–3202. [Google Scholar] [CrossRef]
- Ortiz, D.; Piñero, D.; Shabayek, M.H.; Arnalich-Montiel, F.; Alió, J.L. Corneal biomechanical properties in normal, post-laser in situ keratomileusis, and keratoconic eyes. J. Cataract Refract. Surg. 2007, 33, 1371–1375. [Google Scholar] [CrossRef]
- Lopes, B.T.; Roberts, C.J.; Elsheikh, A.; Vinciguerra, R.; Vinciguerra, P.; Reisdorf, S.; Berger, S.; Koprowski, R.; Ambrósio, R., Jr. Repeatability and Reproducibility of Intraocular Pressure and Dynamic Corneal Response Parameters Assessed by the Corvis ST. J. Ophthalmol. 2017, 2017, 8515742. [Google Scholar] [CrossRef] [PubMed]
- Borderie, V.; Beauruel, J.; Cuyaubère, R.; Georgeon, C.; Memmi, B.; Sandali, O. Comprehensive Assessment of Corvis ST Biomechanical Indices in Normal and Keratoconus Corneas with Reference to Corneal Enantiomorphism. J. Clin. Med. 2023, 12, 690. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, J.; Jiang, J.; Zhang, X.; Ran, Z.; Jiang, F.; Zheng, X.; Wang, J.; Elsheikh, A.; Bao, F. Evaluation of changes in corneal biomechanics after orthokeratology using Corvis ST. Contact Lens Anterior Eye 2024, 47, 102100. [Google Scholar] [CrossRef]
- Long, Q.; Wang, J.; Yang, X.; Jin, Y.; Ai, F.; Li, Y. Assessment of Corneal Biomechanical Properties by CorVis ST in Patients with Dry Eye and in Healthy Subjects. J. Ophthalmol. 2015, 2015, 380624. [Google Scholar] [CrossRef]
- Wang, X.; McAlinden, C.; Zhang, H.; Yan, J.; Wang, D.; Wei, W.; Mi, S. Assessment of corneal biomechanics, tonometry and pachymetry with the Corvis ST in myopia. Sci. Rep. 2021, 11, 3041. [Google Scholar] [CrossRef]
- Glass, D.H.; Roberts, C.J.; Litsky, A.S.; Weber, P.A. A Viscoelastic Biomechanical Model of the Cornea Describing the Effect of Viscosity and Elasticity on Hysteresis. Investig. Ophthalmol. Vis. Sci. 2008, 49, 3919–3926. [Google Scholar] [CrossRef] [PubMed]
- Ávila, F.J.; del Barco, Ó.; Marcellán, M.C.; Remón, L. A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea. Photonics 2024, 11, 524. [Google Scholar] [CrossRef]
- Kwon, S.J.; Jeong, M.K. Advances in ultrasound elasticity imaging. Biomed. Eng. Lett. 2017, 7, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Aglyamov, S.R.; Larin, K.V.; Twa, M.D. In Vivo Human Corneal Shear-wave Optical Coherence Elastography. Optom. Vis. Sci. 2021, 98, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Ramier, A.; Tavakol, B.; Yun, S.H. Measuring mechanical wave speed, dispersion, and viscoelastic modulus of the cornea using optical coherence elastography. Opt. Express 2019, 27, 16635–16649. [Google Scholar] [CrossRef]
- Han, Z.; Li, J.; Singh, M.; Aglyamov, S.R.; Wu, C.; Liu, C.H.; Larin, K.V. Analysis of the effects of curvature and thickness on elastic wave velocity in cornea-like structures by finite element modeling and optical coherence elastography. Appl. Phys. Lett. 2015, 106, 233702. [Google Scholar] [CrossRef] [PubMed]
- Larin, K.V. Investigating Elastic Anisotropy of the Porcine Cornea as a Function of Intraocular Pressure With Optical Coherence Elastography. J. Refract. Surg. 2016, 32, 562–567. [Google Scholar]
- Lan, G.; Gu, B.; Larin, K.V.; Twa, M.D. Clinical Corneal Optical Coherence Elastography Measurement Precision: Effect of Heartbeat and Respiration. Transl. Vis. Sci. Technol. 2020, 9, 3. [Google Scholar] [CrossRef]
- Ávila, F.J.; Marcellán, M.C.; Remón, L. In Vivo Biomechanical Response of the Human Cornea to Acoustic Waves. Optics 2023, 4, 584–594. [Google Scholar] [CrossRef]
- Thibos, L.N.; Applegate, R.A.; Schwiegerling, J.T.; Webb, R. Standards for reporting the optical aberrations of eyes. J. Refract. Surg. 2002, 18, S652–S660. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Martínez, I.; González-Méijome, J.M.; Faria-Ribeiro, M. Linear fitting of biconic surfaces for corneal modeling. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2024, 41, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Crespo, M.A.; Jimenez, H.J.; Deshmukh, T.; Pulido, J.S.; Saad, A.S.; Silver, F.H.; Benedetto, D.A.; Rapuano, C.J.; Syed, Z.A. In Vivo Determination of the Human Corneal Elastic Modulus Using Vibrational Optical Coherence Tomography. Transl. Vis. Sci. Technol. 2022, 11, 11. [Google Scholar] [CrossRef]
- Silver, F.H.; Benedetto, D.A.; Rapuano, C.J.; Syed, Z.A. Identification of the Vibrational Optical Coherence Tomography Corneal Cellular Peak. Transl. Vis. Sci. Technol. 2023, 12, 11. [Google Scholar]
- Akca, B.I.; Chang, E.W.; Kling, S.; Ramier, A.; Scarcelli, G.; Marcos, S.; Yun, S.H. Observation of sound-induced corneal vibrational modes by optical coherence tomography. Biomed. Opt. Express 2015, 6, 3313–3319. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Aglyamov, S.; Larin, K.V.; Twa, M.D. In vivo human corneal natural frequency quantification using dynamic optical coherence elastography: Repeatability and reproducibility. J. Biomech. 2021, 121, 110427. [Google Scholar] [CrossRef]
- Lan, G.; Larin, K.V.; Aglyamov, S.; Twa, M.D. Characterization of natural frequencies from nanoscale tissue oscillations using dynamic optical coherence elastography. Biomed. Opt. Express 2020, 11, 3301–3318. [Google Scholar] [CrossRef] [PubMed]
- McAuley, R.; Nolan, A.; Curatolo, A.; Alexandrov, S.; Zvietcovich, F.; Varea Bejar, A.; Marcos, S.; Leahy, M.; Birkenfeld, J.S. Co-axial acoustic-based optical coherence vibrometry probe for the quantification of resonance frequency modes in ocular tissue. Sci. Rep. 2022, 12, 18834. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Shi, Q.; Wang, Y.; Ma, G.; Cai, J.; Feng, J.; Huang, Y.; Gu, B.; An, L.; Xu, J.; et al. Spatial Assessment of Heterogeneous Tissue Natural Frequency Using Micro-Force Optical Coherence Elastography. Front. Bioeng. Biotechnol. 2022, 10, 851094. [Google Scholar] [CrossRef] [PubMed]
- Koprowski, R.; Ambrósio, R., Jr. Quantitative assessment of corneal vibrations during intraocular pressure measurement with the air-puff method in patients with keratoconus. Comput. Biol. Med. 2015, 66, 170–178. [Google Scholar] [CrossRef] [PubMed]

| Demographic Information (N = 5) | |
|---|---|
| Male/female | 2/5 |
| Age (mean ± std) | 35 ± 10 |
| Ethnicity | Caucasian |
| Ophthalmic History | Not found |
| Medical History | Not found |
| IOP (mean ± std) | 15.32 ± 2.94 mmHg |
| Parameter | Information | Instrument |
|---|---|---|
| Zernike coefficients (mode number) [µm] | Corneal wavefront aberrometry | Galilei G2 |
| Pupil aperture [mm] | Area of the wavefront measurement | Galilei G2 |
| Q-factor | Corneal asphericity | Galilei G2 |
| Flat R1 [mm] | Flat corneal radius | Galilei G2 |
| Steep R2 [mm] | Steep corneal radius | Galilei G2 |
| CH [mmHg] | Corneal hysteresis | ORA |
| CRF [mmHg] | Corneal resistant factor | ORA |
| IOP [mmHg] | Intraocular pressure | ORA |
| 50 Hz | 150 Hz | 250 Hz | 350 Hz | |
| Wavefront | ||||
| LOA | ↑ 0.70% | ↓ 5.10% | ↑ 11.98% | ↓ 6.70% |
| HOA | ↓ 3.62% | ↑ 21.92% | ↓ 14.43% | ↓ 3.15% |
| Corneal geometry | ||||
| Q value | ↑ 11.66% | ↓ 16.56% | ↓ 9.20% | ↓ 1.23% |
| Biomechanics | ||||
| Elasticity | ↑ 0.18% | ↑ 3.05% | ↑ 3.56% | ↓3.53% |
| Viscosity | ↑ 2.65% | ↑ 3.05% | ↑ 2.71% | ↓ 2.74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ávila, F.J.; Barco, Ó.d.; Marcellán, M.C.; Remón, L. Aberrometric, Geometrical, and Biomechanical Characterization of Sound-Induced Vibrational Modes of the Living Human Cornea. Optics 2025, 6, 5. https://doi.org/10.3390/opt6010005
Ávila FJ, Barco Ód, Marcellán MC, Remón L. Aberrometric, Geometrical, and Biomechanical Characterization of Sound-Induced Vibrational Modes of the Living Human Cornea. Optics. 2025; 6(1):5. https://doi.org/10.3390/opt6010005
Chicago/Turabian StyleÁvila, Francisco J., Óscar del Barco, Maria Concepción Marcellán, and Laura Remón. 2025. "Aberrometric, Geometrical, and Biomechanical Characterization of Sound-Induced Vibrational Modes of the Living Human Cornea" Optics 6, no. 1: 5. https://doi.org/10.3390/opt6010005
APA StyleÁvila, F. J., Barco, Ó. d., Marcellán, M. C., & Remón, L. (2025). Aberrometric, Geometrical, and Biomechanical Characterization of Sound-Induced Vibrational Modes of the Living Human Cornea. Optics, 6(1), 5. https://doi.org/10.3390/opt6010005







