A New Approach to Designing Multi-Element Planar Solar Concentrators: Geometry Optimization for High Angular Selectivity and Efficient Solar Energy Collection

Abstract

This paper introduces a novel approach to the design of multi-element planar solar concentrators, aimed at optimizing solar energy harvesting systems. The proposed methodology is based on the integration of identical unit cells, strategically arranged to enhance solar radiation capture efficiency and achieve high angular selectivity. Mathematical modeling of the operational principles of the unit cells forms the foundation for determining production parameters and streamlining the concentrator assembly process. Particular emphasis is placed on analyzing key performance metrics, such as solar radiation concentration and optical efficiency, thereby advancing the understanding of the relationship between design parameters and energy output. The study employs MATLAB R2022b and ZemaxOpticStudio 13 software to model the solar concentrator, identifying the optimal cell configuration to achieve a geometric concentration ratio of 3.45, with angular selectivity ranging from 23° to 90°. This research contributes significantly to the field of solar concentrator technology, offering a pathway for more efficient utilization of renewable energy sources and improved adaptability to diverse operating conditions.

1. Introduction

Solar radiation, as the most abundant and widely available natural energy source, possesses the potential to meet global electricity demand. However, the relatively low energy density of solar radiation reaching the Earth’s surface necessitates the use of extensive areas of photovoltaic (PV) converters for efficient energy conversion. These converters are typically composed of silicon wafers with specific electronic structures, such as p-n junctions, heterojunctions, etc. [1]. Unfortunately, the substantial quantities of semiconductor materials required, coupled with the associated manufacturing processes, pose significant limitations to the widespread adoption of solar panels. Consequently, a promising approach to enhancing the deployment of photovoltaic technologies lies in reducing the area of photosensitive elements. This can be achieved by increasing the energy density of incident solar radiation through the use of solar concentration techniques [2].

Solar concentrators are highly efficient devices that convert low-density solar energy into a concentrated radiation flux. Currently, a wide variety of solar concentrator configurations exist, predominantly based on traditional optical systems such as lenticular [3], mirror [4], and planar (Fresnel) optics [5,6].

Table 1. The main types of solar concentrator base elements and their typical characteristics.

Type	Operation Mechanism	GCR (arb. Units)	AA (°)
Flat reflector	Reflective coating	2	1
V-trough	Reflective coating	2	20
Parabolic dish/trough	Reflective coating	70	0.26
Linear Fresnel reflector	Reflective coating	6–15	1
Light funnel/ homogenizer	Refractive and Total internal reflection (TIR)	1.5	20
Compound parabolic concentrator	Refractive and TIR	4	20
Fresnel lens	Refractive	1000	1.3
Wedge prism	Refractive and TIR or reflective coating	3.77	50
Wedge prism with planar waveguide	Refractive and TIR or reflective coating	–	45

presents the primary types of basic elements used in solar concentrators, their operational mechanisms, and typical values of key characteristics, including the geometric concentration ratio (GCR) and acceptance angle (AA).

The first four rows of Table 1 describe basic elements based on reflective surfaces. These elements exhibit high reflection and are achromatic across the entire solar radiation spectrum, making them suitable as primary components in multicomponent systems. However, their complex manufacturing processes and susceptibility to contamination in outdoor environments significantly reduce their operational efficiency. The subsequent rows of Table 1 summarize volumetric elements that operate on the principles of refraction and total internal reflection. With the exception of Fresnel lenses, achieving high GCRs with these elements often requires a substantial amount of optical material, which increases the mass and dimensions of the concentrator. Consequently, such elements are typically employed as secondary components in more complex multicomponent systems [7]. It is important to note that concentrator configurations are not limited to the shapes listed in Table 1; they can be significantly more complex, combining multiple simple shapes [8] or utilizing materials with varying refractive indices [9].

For solar concentrators to be viable in photovoltaic applications, they must be compact and fabricated from cost-effective materials, such as PMMA or PC plastics [10,11]. Unlike traditional silicon photovoltaic panels, which pose disposal challenges at the end of their lifecycle, plastics can be efficiently recycled or reprocessed for further use. This advantage has led to the limited adoption of concentrators based on lenticular systems or metal parabolic mirrors [12], which are often bulky and prone to issues such as high wind resistance, dust accumulation, and snow buildup. Planar solar concentrators, on the other hand, offer a compact and thin design, avoiding these drawbacks [5]. However, systems like Fresnel lenses [13] are constrained by their aperture size, limiting their ability to collect energy from large areas. Additionally, at larger apertures, Fresnel lenses exhibit a significant back segment, increasing the overall thickness of the system. Their narrow acceptance angle further limits their practical application. Figure 1 provides schematic illustrations of these elements for clarity.

An optimal approach to designing compact solar concentrators involves planar schemes based on optical waveguide principles [38]. Despite their compactness, these systems face challenges in efficiently coupling radiation into the planar waveguide. Current methods for radiation injection include: (i) reflective and refractive elements, which complicate the system; (ii) luminescent materials, which drastically reduce efficiency; and (iii) diffraction gratings, which exhibit strong spectral selectivity. These limitations highlight the need for alternative solutions in the development of planar solar concentrators.

In this paper, we propose a novel approach to the design of multi-element planar solar concentrators with variable geometry and high AA to the angle of incident solar radiation. By combining identical, easily manufacturable elementary cells and arranging them in a specific configuration, we achieve efficient solar energy collection. The number of elementary cells can be adjusted to tailor the radiation concentration area to specific requirements. The study begins with a mathematical analysis of a single unit cell to determine optimal manufacturing parameters, followed by the assembly of a solar concentrator from these cells. Key parameters such as GCR, optical efficiency, and AA are analyzed and presented, providing a comprehensive understanding of the proposed concentrator’s performance. This work contributes to advancing solar concentrator technology, offering a pathway for more efficient and adaptable renewable energy systems.

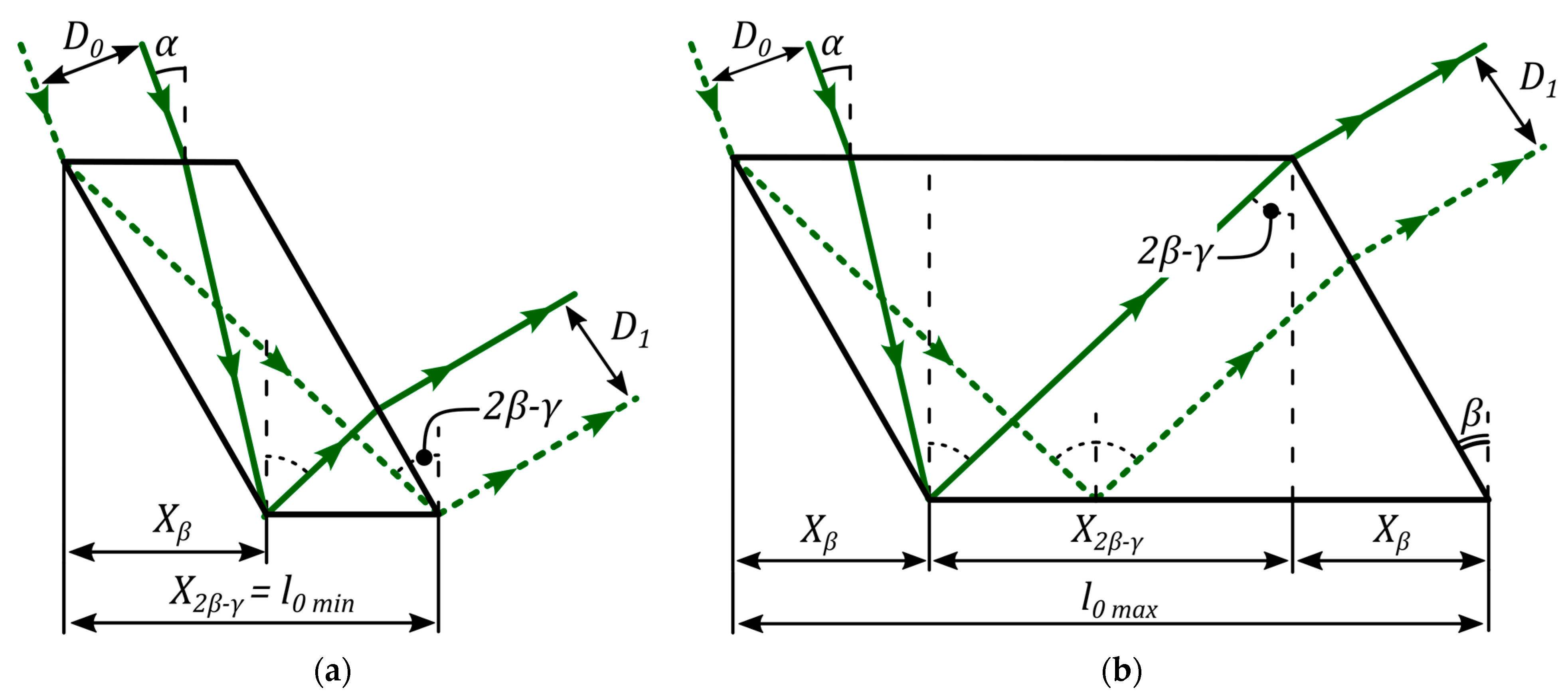
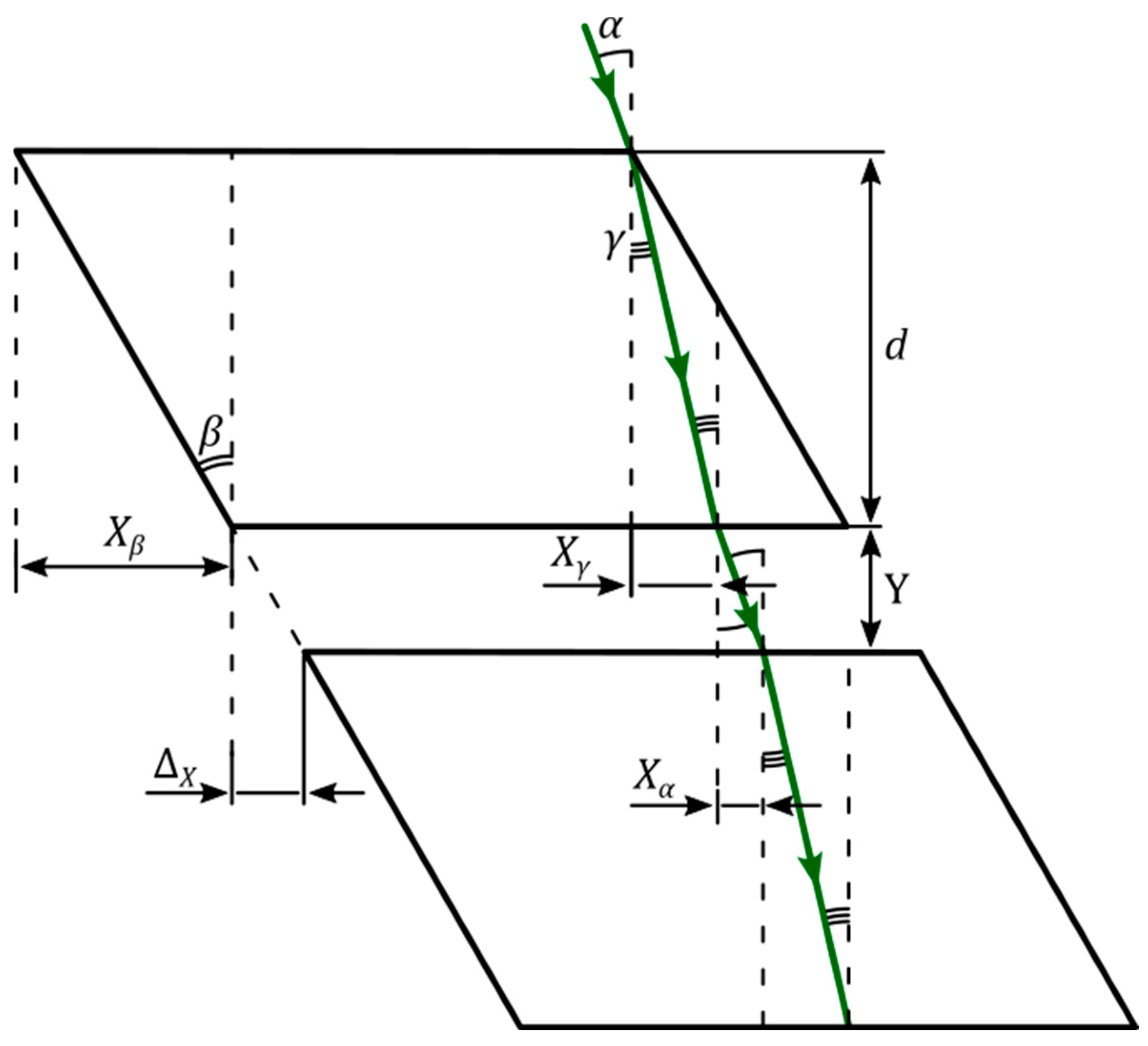
2. Theoretical Model of Unit Cells

A planar solar concentrator designed for operation in a medium with a refractive index of $n_0\left(\lambda \right)=1$ consists of an array of identical plane-parallel plates. These plates feature mutually parallel inclined surfaces oriented at an angle $\beta$ relative to the normal of their receiving surfaces. Each plate has a thickness $d$ and a length $l_0$, as illustrated in Figure 2.

The operational principle of a solar concentrator unit cell can be described through the following three key steps:

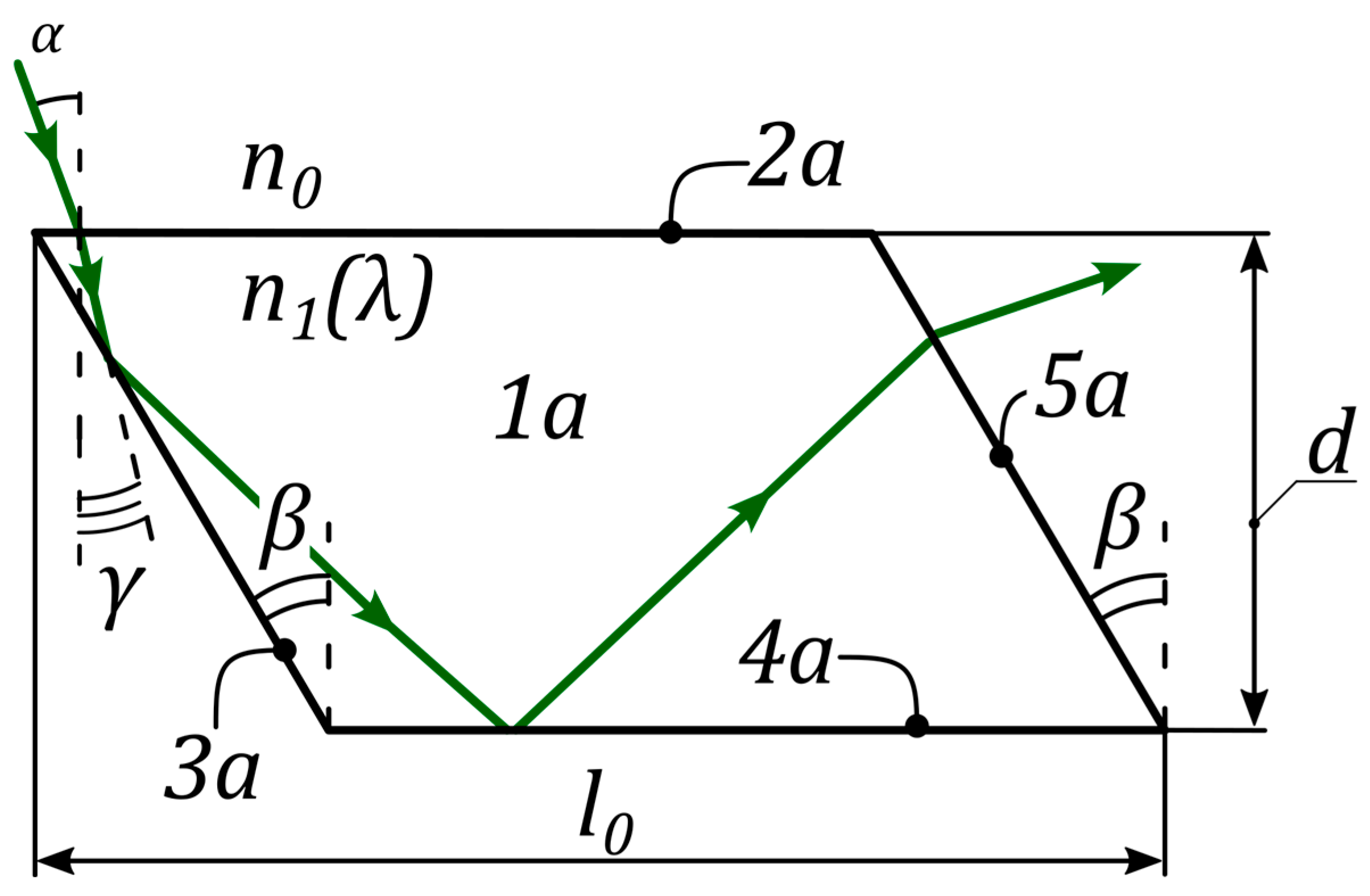
• Refraction at the Receiving Surface: Electromagnetic waves emitted by the Sun strike the receiving surface (2a) of the plates (1a) at an angle $\alpha$. Upon entering the material, the waves are refracted according to Snell’s law due to the difference in refractive indices between the external medium $n_0\left(\lambda \right)$ and the material of the concentrator cell $n_1\left(\lambda \right)$, where $n_1\left(\lambda \right)$ represents the refractive index of the cell material.
• Propagation and First Reflection: As illustrated in Figure 2, the refracted electromagnetic wave propagates at an angle $\gamma$ toward the nearest end surface (3a) of the corresponding plate (1a). At this surface, the wave undergoes TIR, adhering to the principles of geometric optics.
• Subsequent Reflections and Propagation: Following the first reflection, the electromagnetic wave travels along the plate (1a) toward the surface (4a), where it is again reflected via TIR. This reflection directs the wave toward the opposite end surface (5a), ensuring its continued propagation within the cell.

For the solar concentrator to function effectively, it is essential to achieve the confinement of solar radiation within the cell through TIR at both the left and bottom faces. The critical parameter governing the fulfillment of these conditions is the angle of radiation propagation $\gamma$ inside the cell, which is determined by Snell’s law:

$$\gamma =\arcsin ({\displaystyle \frac{n_0\left(\lambda \right)}{n_1\left(\lambda \right)}}\cdot \sin \alpha ),$$

(1)

where $\alpha$ is the angle of incidence of radiation on the front face of the cell, and $\gamma$ is the angle of propagation inside the cell. This angle is pivotal, as it dictates whether the conditions for TIR are met, ensuring efficient radiation propagation within the concentrator.

To optimize the design parameters of the planar solar concentrator, mathematical modeling was conducted using MATLAB software. Figure 3 provides a graphical representation of the relationship between the propagation angle $\gamma$, the refractive index of the cell material $n_1$, and the angle of incidence $\alpha$. This relationship is critical, as it directly influences the fulfillment of TIR conditions, which are essential for the effective operation of the concentrator cell.

Next, we derive the angle of inclination $\beta$ of the side surfaces as a function of the angle of incidence $\alpha$ and the refractive index $n_1\left(\lambda \right)$ of the cell material. For the ray incident on the left side face to undergo TIR, the angle $\gamma$ must satisfy two conditions: (i) $\gamma$ must be less than the prism angle $\beta$, as otherwise the ray will not reach the left face, and (ii) the angle of incidence on the left face must exceed the critical angle for TIR. These conditions yield the first set of constraints:

$$\left\{\begin{array}{c}90-\beta +\gamma \ge \arcsin \left({\displaystyle \frac{n_0\left(\lambda \right)}{n_1\left(\lambda \right)}}\right)\\ \beta \ge \gamma \end{array}\right..$$

(2)

The second condition for ray propagation within the cell requires TIR to occur at the bottom edge. This imposes the following double inequality on the angles:

$$\arcsin \left({\displaystyle \frac{n_0\left(\lambda \right)}{n_1\left(\lambda \right)}}\right)\le 2\beta +\gamma \le 90.$$

(3)

Finally, to ensure that the radiation exits the unit cell without undergoing TIR at the right (exit) face, the following constraints must be satisfied:

$$\left\{\begin{array}{c}3\beta -\gamma -90\le \arcsin \left({\displaystyle \frac{n_0\left(\lambda \right)}{n_1\left(\lambda \right)}}\right)\\ \beta \ge 90-2\beta +\gamma \end{array}\right..$$

(4)

Combining these conditions, the permissible range for the angle $\beta$ is determined by the final relation:

$$\left\{\begin{array}{c}\beta \le {\displaystyle \frac{90+\gamma +{\alpha }_{ex}}{3}}\\ \beta \ge \gamma \end{array},\right.$$

(5)

where ${\alpha }_{ex}=\arcsin \left({\displaystyle \frac{n_0\left(\lambda \right)}{n_1\left(\lambda \right)}}\right)$. The solution region for these constraints is illustrated in Figure 4, where the abscissa represents the angle $\beta$ (inclination of the side faces), and the ordinate represents the angle $\alpha$ (angle of incidence on the input face). The intensity map highlights the solution regions for different ranges of the cell’s refractive index $n_1\left(\lambda \right)$.

Analysis of the obtained solution region reveals that an inclination angle of the side face $\beta =43°$ enables the solar concentrator cell to operate effectively across the entire range of incident radiation angles, $0<\alpha <90°$. This condition, however, is only satisfied when the cell is fabricated from a material with a refractive index $n_1\left(\lambda \right)$ within the range of 1.47 to 1.61.

Subsequently, based on the selected parameters, the GCR was calculated for a single solar concentrator cell with side faces inclined at $\beta =43°$, independent of the intrinsic length-to-thickness ratio of the cell. The ray-tracing diagram required for this calculation is illustrated in Figure 5. The GCR is defined as the ratio of the maximum beam diameter $D_0$ incident on the entrance face of the cell to the beam diameter $D_1$ propagating within the cell.

The aperture of the beam incident on the element, which, after refraction, fully illuminates the side face, is denoted as $D_0$. Since the beam strikes the receiving face at an angle $\alpha$, the relationship between $D_0$ and its projection $x_0$ on the input face is given by

$$D_0=x_0\cos \alpha ,$$

(6)

where $x_0$ represents the projection of $D_0$ onto the input face. The projection $x_0$ can be expressed as follows:

$$x_0=X_{\beta }-X_{\gamma },$$

(7)

where $X_{\beta }$ is the projection of the side face onto the horizontal plane, and $X_{\gamma }$ is the projection of the path traveled by the ray propagating inside the cell at an angle $\gamma$ to the vertical. Consequently, the value of $D_0$ is determined by

$$D_0=d·\left(\tan \beta -\tan \gamma \right)·\cos \alpha ,$$

(8)

where $d$ is the thickness of the cell.

The aperture of the beam $D_1$ at the exit from the cell corresponds to the projection of the aperture onto the horizontal axis. This projection is defined as the difference in the optical paths of the dashed and solid beams in the horizontal plane (see Figure 5b). Thus, $D_1$ can be calculated as follows:

$$D_1=d·\left(\tan \left(2\beta -\gamma \right)-\tan \beta \right)·\cos \left(2\beta +\gamma \right).$$

(9)

The final expression for the GCR, which depends on the prism angle $\beta$ and the angle of incidence $\alpha$, is given by

$$GCR={\displaystyle \frac{\left(\tan \beta -\tan \gamma \right)·\cos \alpha }{\left(\tan (2\beta -\gamma )-\tan \beta \right)·\cos (2\beta -\gamma )}}.$$

(10)

Figure 6 provides a graphical interpretation of this relationship for a fixed $\beta =43°$. It is evident that, across the entire range of incident angles, the GCR remains below 1 and decreases as the angle of incidence $\alpha$ increases.

The next parameter calculated for the solar concentrator cell is the minimum and maximum cell length. Referring again to Figure 5, which illustrates two boundary cases of ray propagation within the cell, the minimum cell length $l_{0min}$ is determined by the dashed ray striking the leftmost point of the entrance face, while the maximum cell length $l_{0max}$ is defined by the solid ray. In the former case, the optical path length between refraction and reflection is treated as infinitesimal, whereas in the latter case, the path length between refraction and reflection from the side and bottom edges is considered infinitesimal. The minimum length corresponds to the intersection of the dashed ray with the bottom edge, while the maximum length corresponds to the intersection of the solid ray with the top edge.

For convenience, the cell length $l_0$ is normalized by its thickness $d$. The relationship between these parameters, as a function of $\beta$ and $\gamma$, is described by the inequality:

$$\left\{\begin{array}{c}{\displaystyle \frac{l_{0min}}{d}}\ge \tan \left(2\beta -\gamma \right)\\ {\displaystyle \frac{l_{0max}}{d}}\le 2·\tan \beta +\tan \left(2\beta -\gamma \right)\end{array}.\right.$$

(11)

Figure 7 presents a graphical illustration of the solution region for this relationship, while Figure 8 shows a cross-section of the two-dimensional distributions from Figure 7 for $\beta =43°$. As previously established, this angle of inclination ensures maximum AA ($0°<\alpha <90°$) when the cell is made of a material with a refractive index $n_1\left(\lambda \right)$ in the range of 1.47 to 1.61. The functions describing ${\displaystyle \frac{l_{0max}}{d}}$ and ${\displaystyle \frac{l_{0min}}{d}}$ define the permissible limits for the cell length $l_0$.

Analysis of Figure 8 reveals that no single cell length $l_0$ can achieve AA across the entire range from 0° to 90°. As the angle of incidence $\alpha$ decreases, the acceptable region for $l_0$ narrows, further constraining the cell’s operational conditions. To maximize the effective length while minimizing the thickness of both the unit cell and the overall concentrator, the minimum value of ${\displaystyle \frac{l_{0max}}{d}}$ was selected as the optimal length. This minimum value, denoted by a horizontal line in Figure 8, is ${\mathrm{m}\mathrm{i}\mathrm{n}(l}_{0max})=2.81$. By determining the intersection of this line with the function describing ${\displaystyle \frac{l_{0min}}{d}}$, the AA of the cell was established as $24°\le \alpha <90°$, with ${\displaystyle \frac{l_0}{d}}=2.81$.

In summary, the unit cell of the planar solar concentrator, as illustrated in Figure 2, is a plane-parallel plate with mutually parallel end surfaces inclined at $\beta =43°$. The cell should have a length-to-thickness ratio ${\displaystyle \frac{l_0}{d}}=2.81$ and be fabricated from a material with a refractive index $n_1\left(\lambda \right)$ between 1.47 and 1.61. Under these conditions, the cell exhibits AA in the range $24°\le \alpha <90°$ and achieves an average GCR of 0.59.

3. Theoretical Model of Solar Concentrator

After determining the fundamental parameters of a single cell, the design of the entire planar solar concentrator was developed. The concentrator comprises an array of identical plane-parallel plates with mutually parallel inclined surfaces, oriented at an angle $\beta =43°$ relative to the normal of the receiving surfaces. Each plate has a maximum length-to-thickness ratio of ${\displaystyle \frac{l_0}{d}}=2.81$, as illustrated in Figure 9.

The operational principle of the planar solar concentrator can be described through the following eight steps:

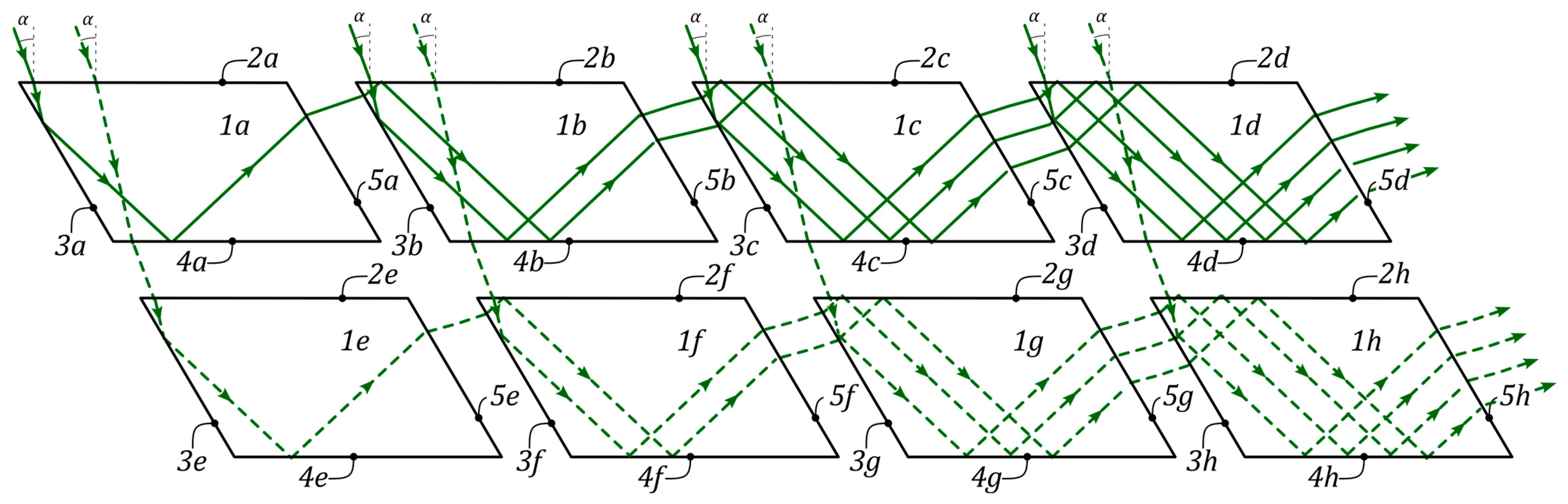
• Wave Propagation Between Cells: As depicted in Figure 9, an electromagnetic wave exits the first plate (1a) and propagates through the air to the adjacent cell (1b) in the row.
• Refraction at the Next Cell: The wave enters the end surface (3b) of the plate (1b) and is refracted due to the difference in refractive indices $n_0\left(\lambda \right)$ and $n_1\left(\lambda \right)$.
• Reflection Within the Cell: The wave propagates along plate (1b) toward the receiving surface (2b), where it undergoes TIR toward the opposite surface (4b).
• Second Reflection and Propagation: The wave is reflected again from the surface (4b) via TIR and propagates toward the end surface (5b).
• Repetition Across Cells: The wave exits plate (1b), and the process repeats for each subsequent cell in the row. The propagation concludes at the exit of the final cell, after which the wave travels to the radiation receiver (not shown in Figure 9).
• Waves Incident on Intermediate Cells: If waves strike the receiving surfaces (2a or 2b) of plates (1a and 1b) that are not at the row’s beginning, the process described above repeats for each respective cell.
• Waves Missing End Surfaces: Waves that strike the receiving surfaces (2a and 2d) but, due to refraction, miss the end surfaces (3a and 3d) exit through surfaces (4a and 4d) and propagate to the next row of plates (1e and 1h). The process repeats for each cell in the new row.
• Waves Passing Through Multiple Rows: Waves that do not strike the end surfaces of any plate pass through the rows until they reach the last row, where they finally interact with the end surfaces, repeating the described process.

Optimization of Cell Arrangement

The planar solar concentrator, as shown in Figure 10, can consist of 2 to $N_y$ rows of unit cells spaced $Y$ apart. Each row is horizontally offset by $\mathsf{\Delta }x$, with all side faces lying in the same plane. The maximum number of rows $N_y$ is determined by ensuring that all rays incident on the first row’s receiving surfaces strike the left side edge of the last row.

For a single electromagnetic wave, the wave shifts horizontally by $X_{\gamma }=d·\tan \gamma$ after refraction on the receiving surface (2a). Upon exiting the cell, the wave’s propagation angle remains unchanged, resulting in an additional shift of $X_{\alpha }=Y·\tan \alpha$ over the distance $Y$ between rows. The lateral displacement of each row’s side surface is given by

$$X_{\beta }+X_{\mathsf{\Delta }}=\left(d+Y\right)·\tan \beta ,$$

(12)

except for the first row, which only contributes

$$X_{\beta }=d·\tan \beta .$$

(13)

The criterion for determining $N_y$ is that the lateral displacement of the side faces must exceed the wave’s horizontal shift. This leads to the following inequality:

$${\displaystyle \frac{N_y}{d}}={\displaystyle \frac{\tan \left(2\beta -\gamma \right)+\tan \gamma }{(\tan \beta -\tan \gamma )-Y(\tan \beta -\tan \alpha )}},$$

(14)

where $Y={\displaystyle \frac{d}{n}}$, and $n$ is a natural number between 1 and 10. Values of $n<1$ increase the concentrator’s size, while $n>10$ complicates assembly and alignment.

Figure 11 shows the result of modeling the number of rows $N_y$ in a planar solar concentrator depending on the angle of incidence of radiation on the receiving surface of the cell and depending on the refractive index of the material from which the cell is made. The figure shows that in the region of small angles of incidence, there is an increase in the number of rows to capture all the radiation. This value can reach up to 14 rows. It was previously found that the optimum AA of the cell is in the range of $24°$ to $90°$ (the right border of the region is not included), and in this region, the maximum number of rows is already 7. This result was achieved with $\beta =43°$ and a cell gap value $Y={\displaystyle \frac{d}{10}}$.

Figure 11 shows the modeled number of rows $N_y$ as a function of the incident angle $\alpha$ and the cell’s refractive index $n_1\left(\lambda \right)$. For small angles of incidence, up to 14 rows may be required to capture all radiation. However, within the optimal AA range of $24°\le \alpha <90°$, the maximum number of rows is 7, achieved with $\beta =43°$ and $Y={\displaystyle \frac{d}{10}}$.

GCR Calculation

For a concentrator with $N_y=7$ rows and one cell per row, the GCR is the ratio of the receiving face area of the first cell to the total side face area of all cells. The receiving face area is

$$D_{0big}=X_{\beta }+X_{2\beta -\gamma },$$

(15)

where $X_{\beta }=d·\tan \beta$, and $X_{2\beta -\gamma }=d·\tan (2\beta -\gamma )$. The side face area is

$$D_{1big}={\displaystyle \frac{d+N_y·(d+Y)}{\cos \beta }},$$

(16)

where $Y={\displaystyle \frac{d}{n}}$. The GCR is

$$GCR={\displaystyle \frac{\cos \beta ·(d·\tan \beta +d·\tan (2\beta -\gamma ))}{d+N_y·(d+Y)}}.$$

(17)

For $n=10$, this simplifies to

$$GCR={\displaystyle \frac{\cos \beta ·(\tan \beta +\tan (2\beta -\gamma ))}{1+1.1·N_y}}.$$

(18)

Figure 12 shows the GCR distribution for this configuration. The GCR remains below 1, with an average value of 0.21 within the optimal AA range.

Gap Between Cells in a Row

The permissible gap $∆X$ between cells in a row was calculated by considering the propagation of boundary electromagnetic waves, as shown in Figure 13. The gap must ensure that the outermost ray from the first cell’s side edge strikes the neighboring cell’s side edge:

$$0<{\displaystyle \frac{∆X}{d}}\le 0.12.$$

(19)

Maximum Number of Cells per Row

Using Zemax OpticStudio, a full 3D model of the concentrator was created, and ray tracing was performed for the AM0 solar spectrum (280–4000 nm) at incident angles from 24° to 90°. The optimal number of cells per row was found to be $N_x=15$.

Final GCR Calculation

The final GCR for the entire concentrator, optimized for $N_x=15$ and $N_y=7$, is

$$GCR={\displaystyle \frac{\cos \beta ·\left(\tan \beta +\tan \left(2\beta -\gamma \right)+N_x(0.12+\tan \beta +\tan \left(2\beta -\gamma \right))\right)}{1+{1.1·N}_y}}$$

(20)

Figure 14 shows the GCR distribution for this configuration. The GCR exceeds 1, with an average value of 3.45 within the optimal AA range. This demonstrates the concentrator’s ability to efficiently capture and concentrate solar radiation.

4. Discussion

The results of the proposed planar solar concentrator are compared with existing solar energy harvesting devices in Figure 15, which presents a histogram of the GCR and AA for various methods. The comparison highlights the unique advantages and trade-offs of the proposed design relative to established technologies. Below is a detailed analysis of the key findings:

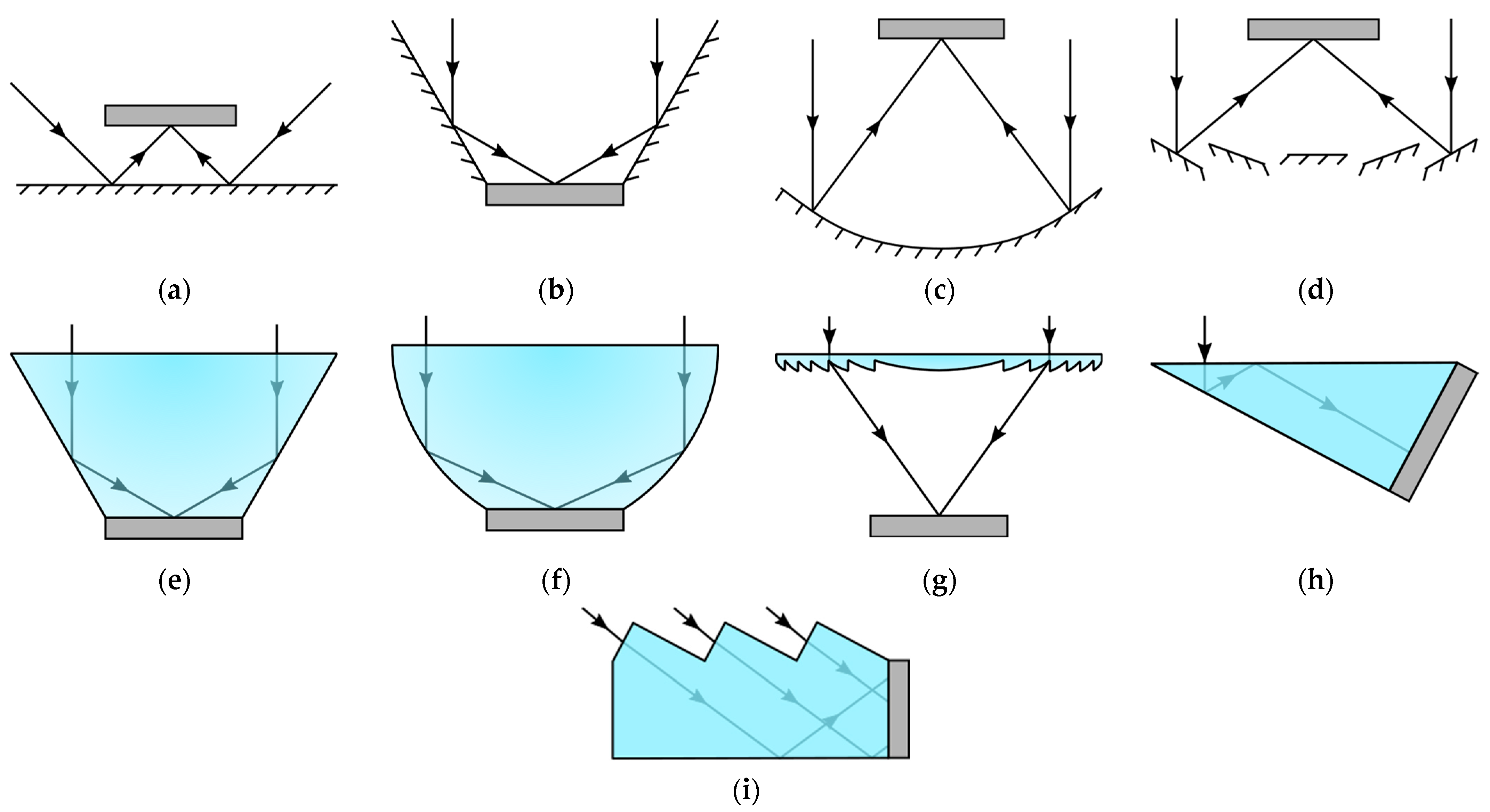
• Light Funnel/Homogenizer (Method 1): This method achieves a GCR of 1.5 with an AA range of 0° to 20° [3]. While it offers moderate concentration, its limited angular range restricts its applicability in environments with varying solar angles.
• Flat Mold (Method 2): With a GCR of 2 and an AA of 0° to 1° [4], this method provides higher concentration but is highly sensitive to alignment, making it impractical for most real-world applications.
• V-Shaped Trough (Method 3): This design achieves a GCR of 2 and an AA of 0° to 20° [5]. Although it offers a wider angular range than Method 2, its concentration efficiency remains relatively low.
• Wedge Prism (Method 4): This method achieves a higher GCR of 3.77 with an AA of 0° to 50° [6]. Its broader angular range makes it more versatile, but its concentration efficiency is still limited compared to more advanced designs.
• Compound Parabolic Concentrator (Method 5): With a GCR of 4 and an AA of 0° to 20° [8], this method offers improved concentration but remains constrained by its narrow angular range.
• Linear Fresnel Reflector (Method 6): This design achieves a GCR ranging from 6 to 15, with an AA of 0° to 1° [10]. While it provides high concentration, its extreme sensitivity to alignment limits its practicality.
• Parabolic Shape (Method 7): This method achieves a GCR of 70 with an AA of 0° to 0.26° [12]. Although it offers exceptional concentration, its extremely narrow angular range makes it unsuitable for applications requiring flexibility in solar tracking.
• Fresnel Lens (Method 8): With a GCR of 1000 and an AA of 0° to 1.3° [13], this method provides the highest concentration among the compared technologies. However, its narrow angular range and complexity in manufacturing and alignment pose significant challenges.
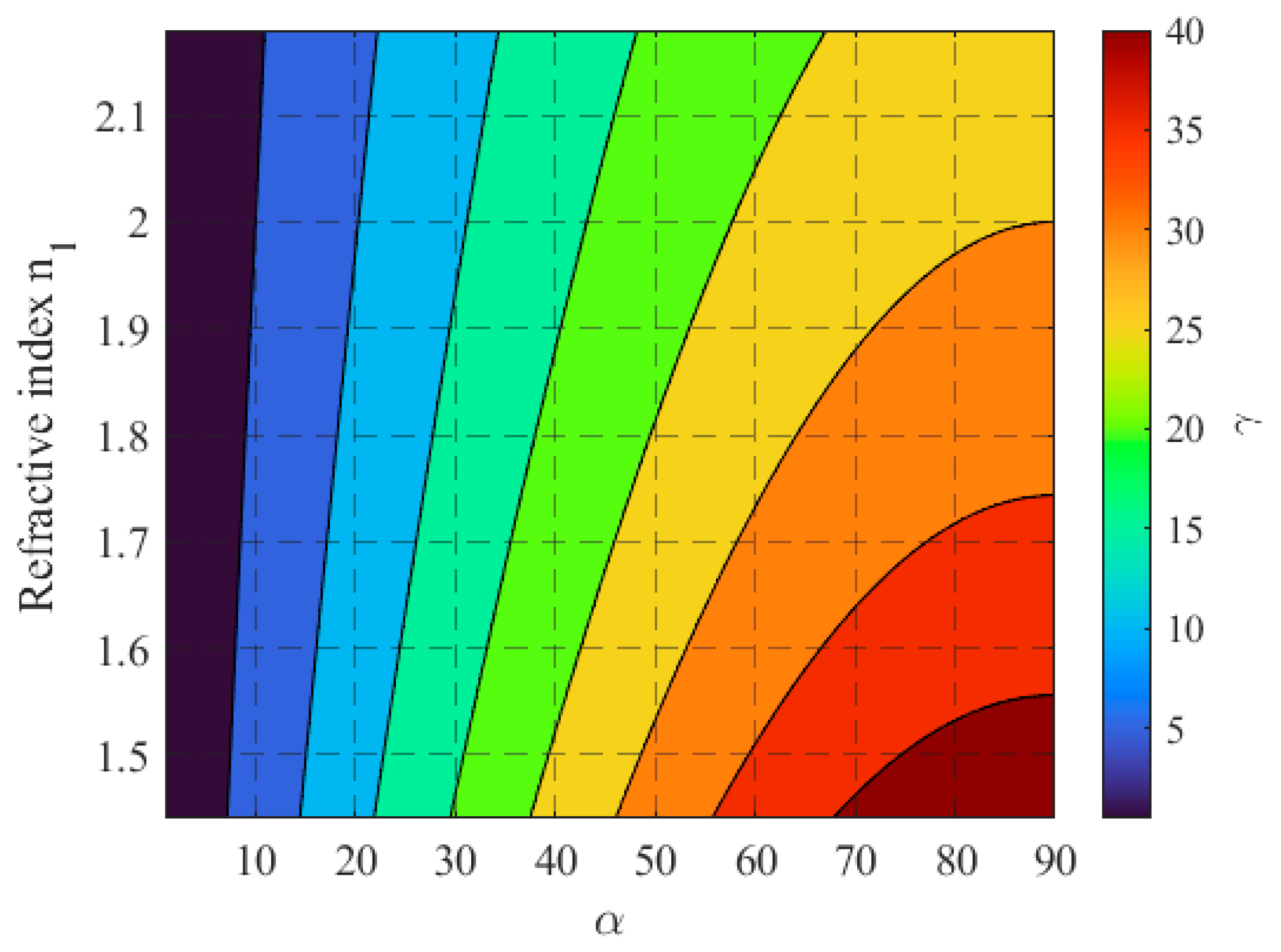
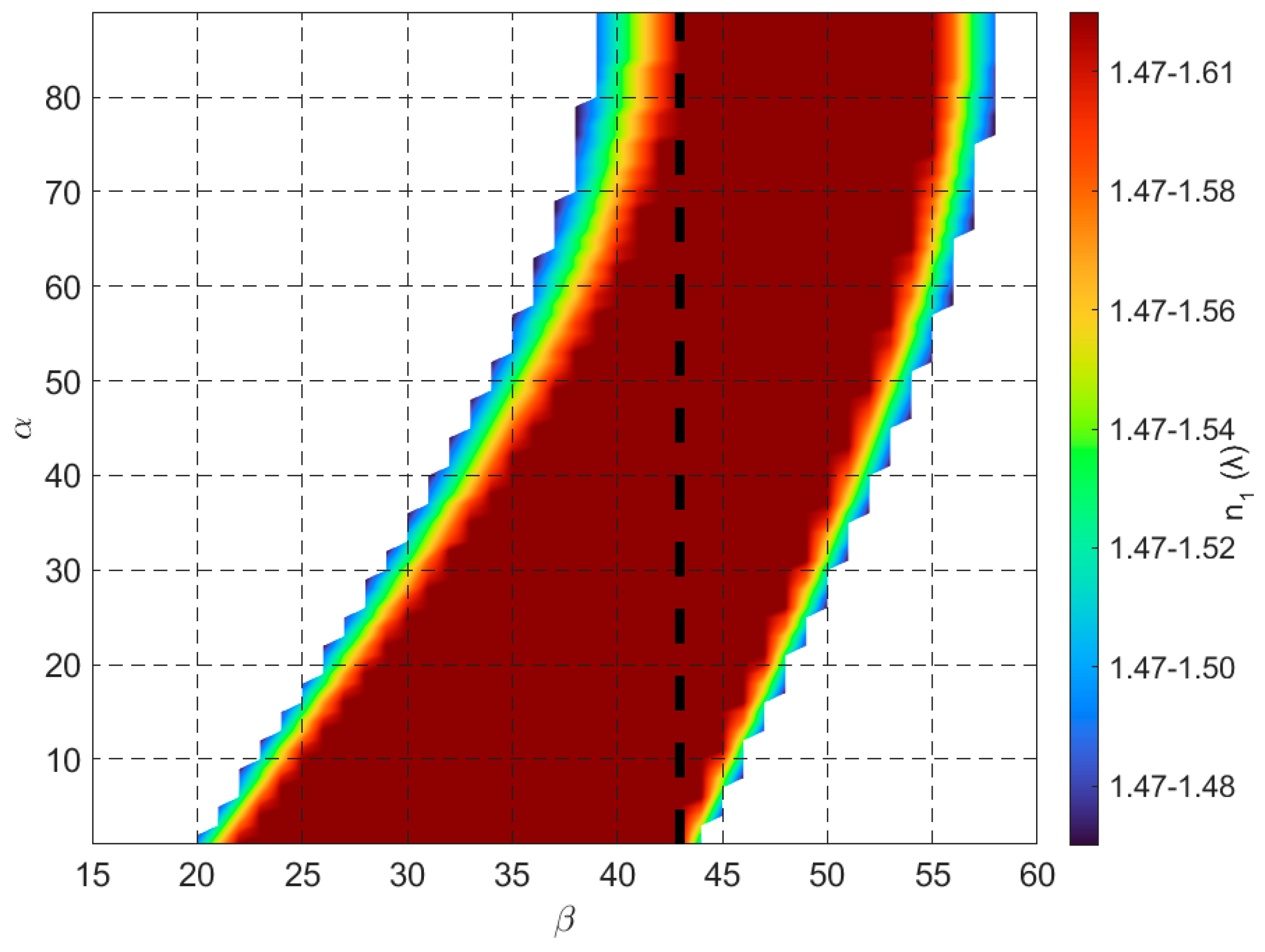
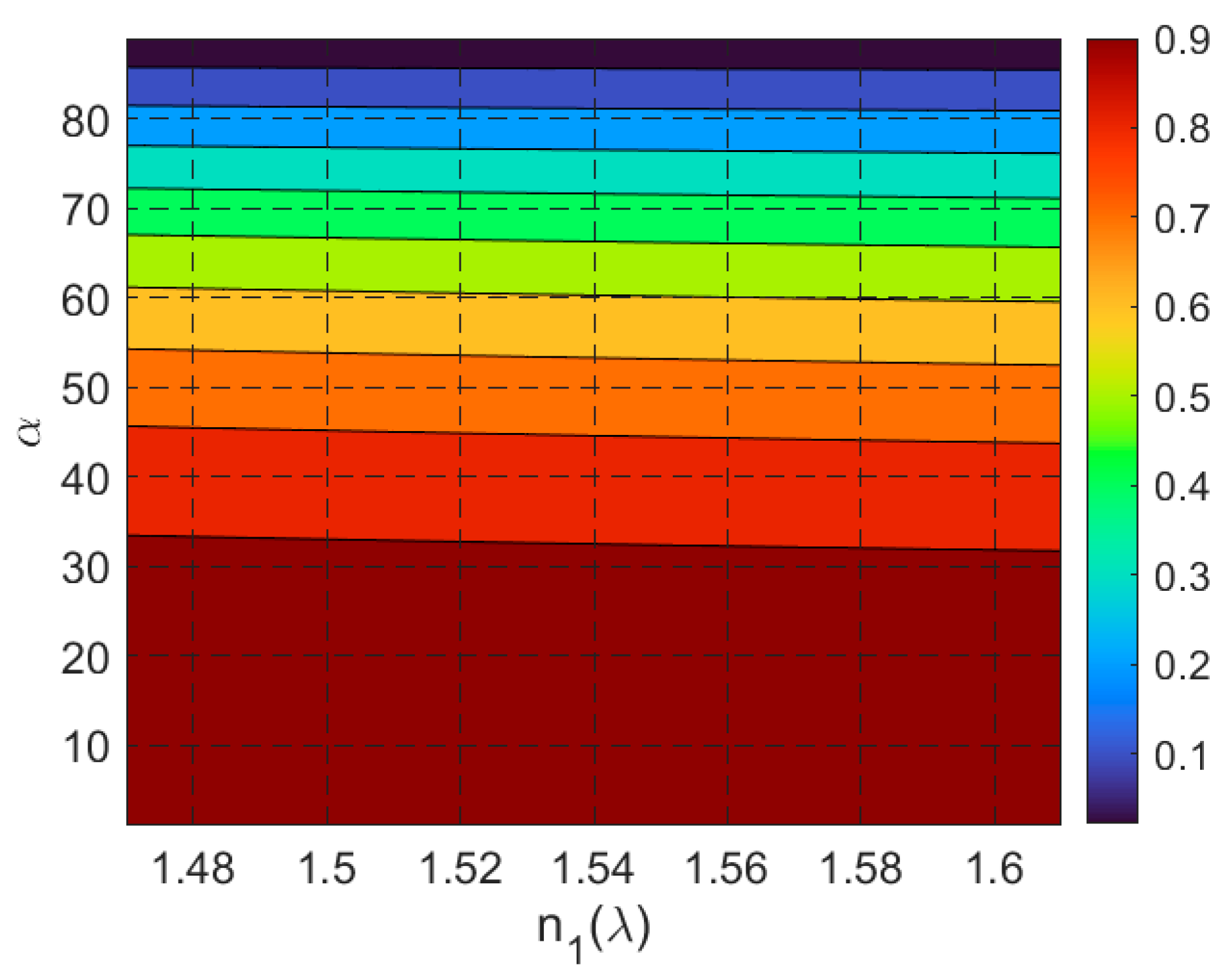
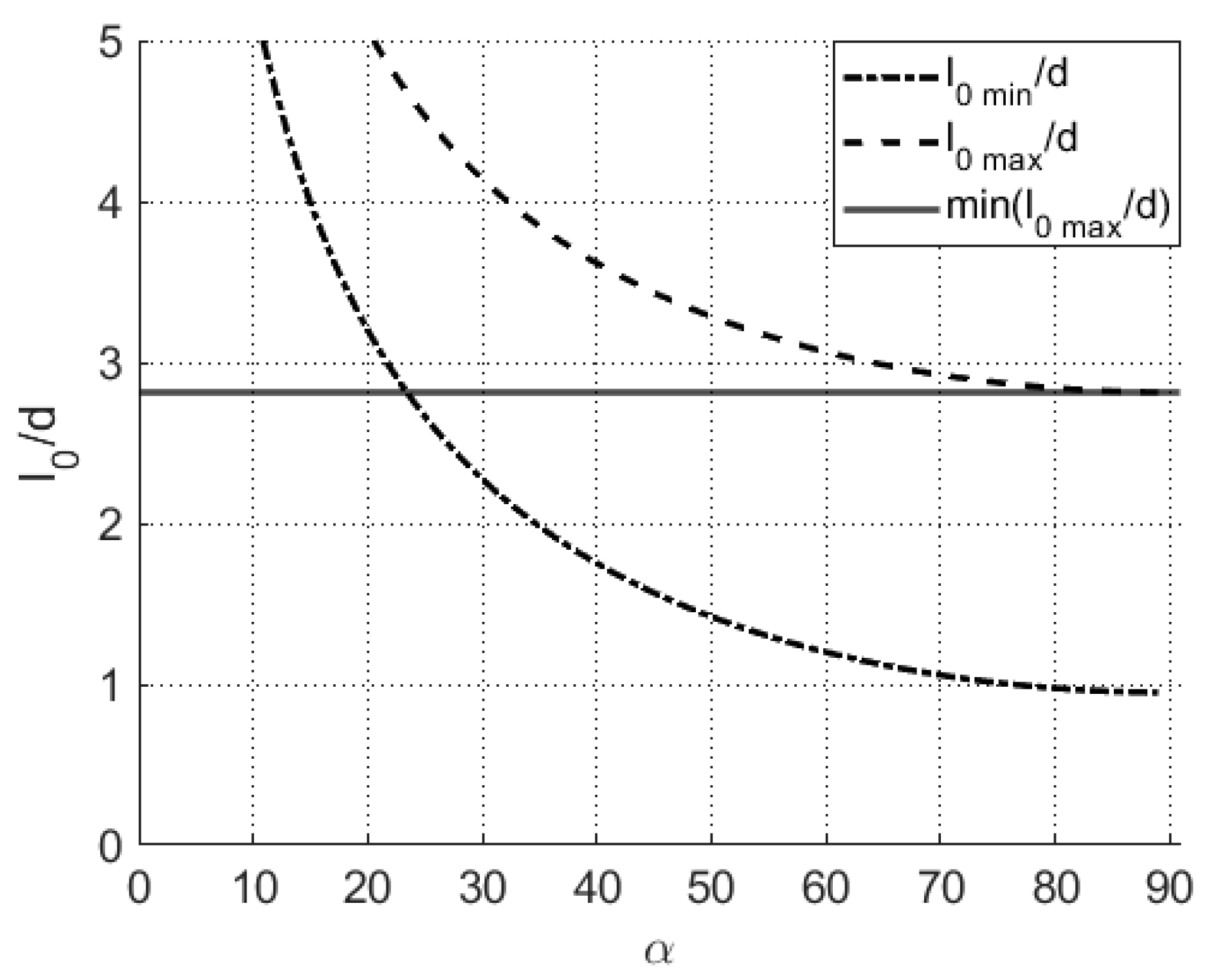
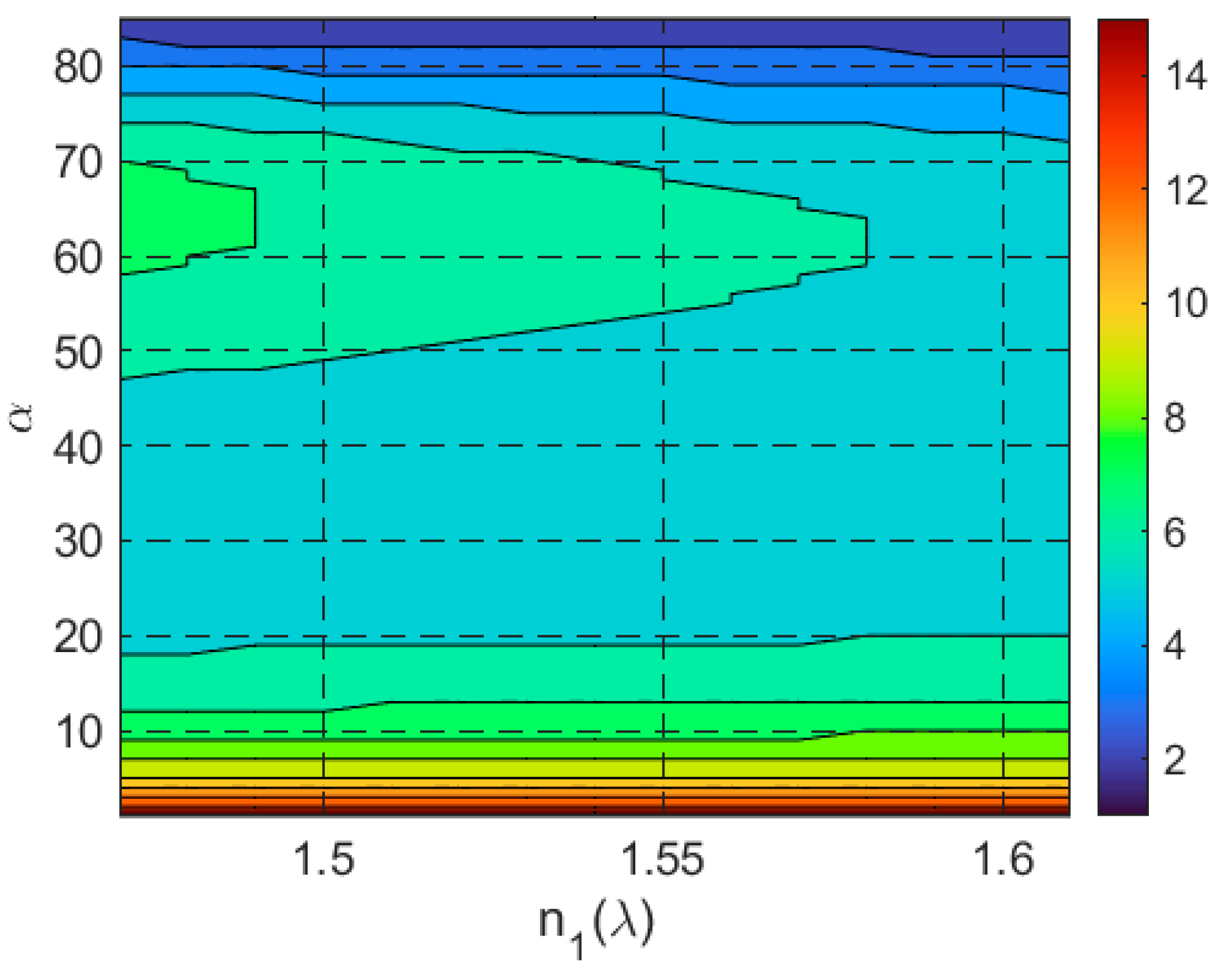
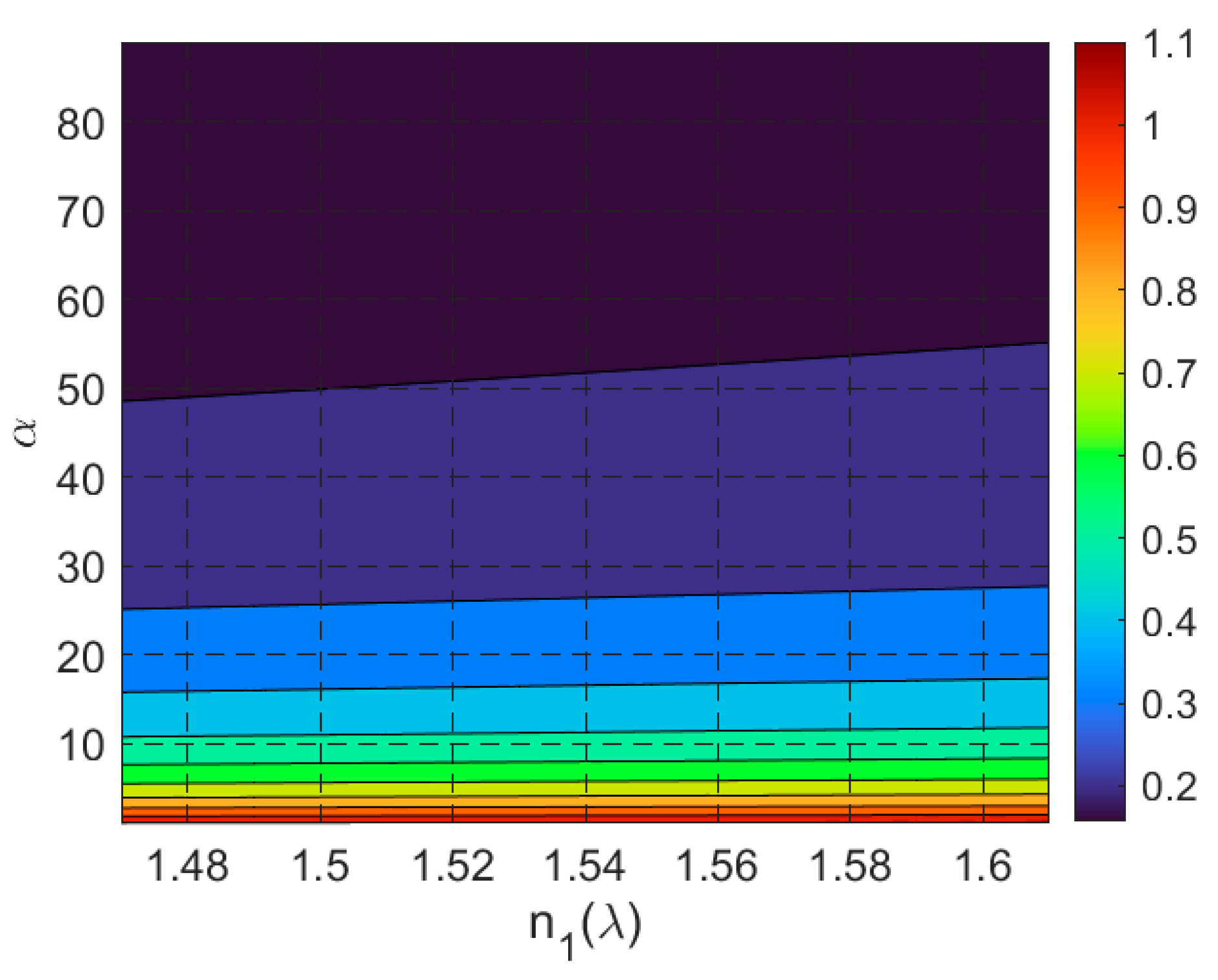
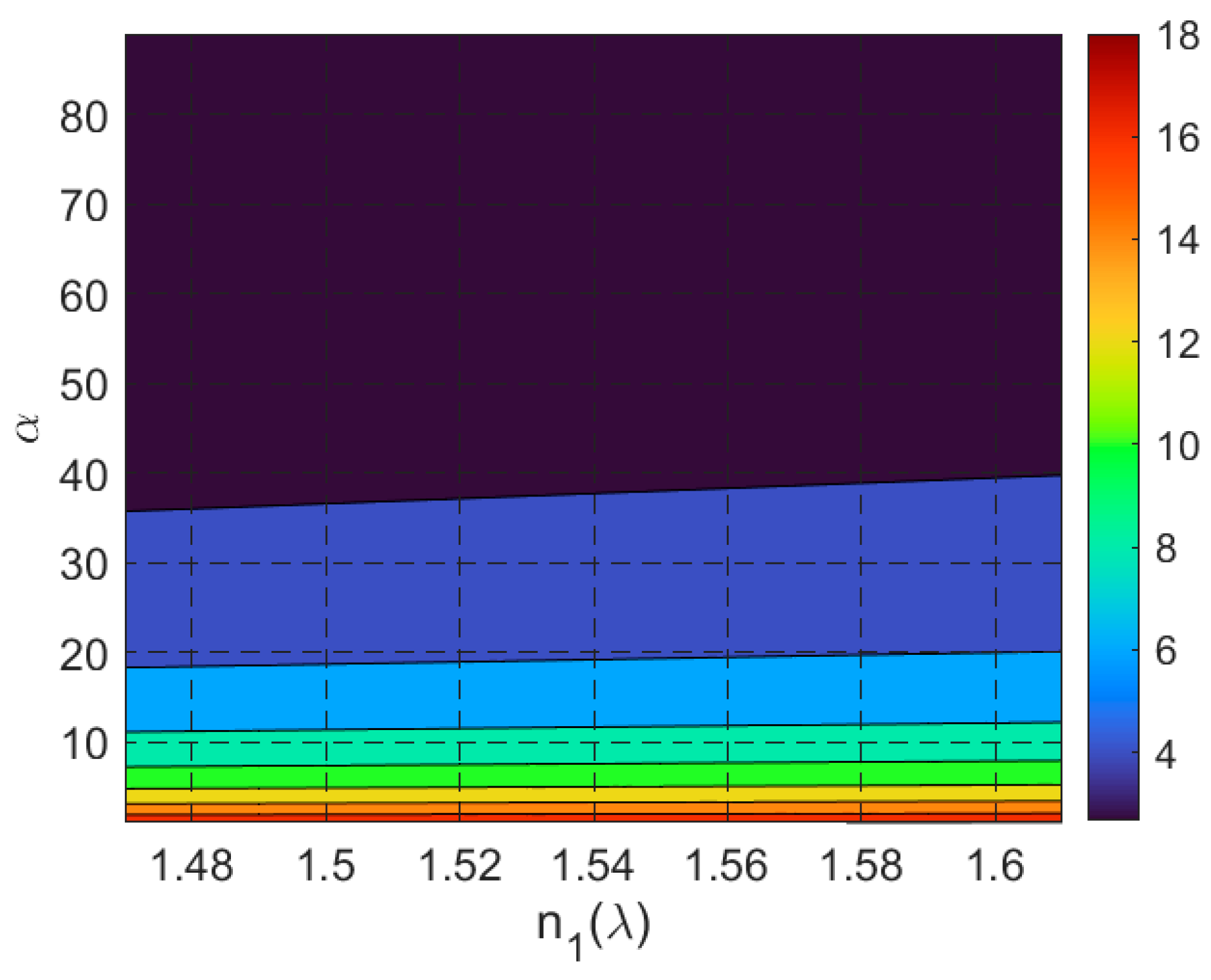
• Proposed Planar Solar Concentrator: The proposed design achieves a GCR of 3.45 with an AA of 23° to 90° (excluding boundaries). This represents a significant improvement in angular range compared to most existing methods, making it highly adaptable to varying solar angles without requiring precise alignment. While its GCR is lower than that of parabolic or Fresnel lens-based systems, its broad AA and simplicity in design and assembly make it a promising solution for practical applications, particularly in environments where solar tracking is impractical or cost-prohibitive.

Key Advantages of the Proposed Design

• wide range of incident angles (23° to 90°), making it suitable for stationary installations and regions with significant seasonal variations in solar elevation.
• Simplified Design and Assembly: The use of identical plane-parallel plates with a fixed inclination angle ($\beta =43°$) and a length-to-thickness ratio of ${\displaystyle \frac{l_0}{d}}=2.81$ simplifies manufacturing and assembly processes.
• Material Efficiency: The design minimizes the use of optical materials, reducing both cost and weight while maintaining performance.
• Scalability: The modular nature of the design allows for easy scaling by adjusting the number of rows ($N_y$) and cells per row ($N_x$).

Figure 15. Comparative analysis of the obtained simulation results of the planar solar concentrator concept with the existing different analogues: (a) GCR and (b) AA.

Figure 15. Comparative analysis of the obtained simulation results of the planar solar concentrator concept with the existing different analogues: (a) GCR and (b) AA.

5. Conclusions

This paper presents a comprehensive calculation and modeling study conducted using MATLAB software, grounded in the principles of geometrical optics. The study culminates in the development of a novel planar solar concentrator designed for operation in a medium with a refractive index of $n_0=1$. The concentrator comprises at least one row of unit cells, each of which is an identical plane-parallel plate with mutually parallel end surfaces inclined at an angle $\beta =43°$ relative to the normal of the receiving surfaces. The material used for the concentrator cells has a refractive index $n_1\left(\lambda \right)$ within the range of 1.47 to 1.61 and is optically transparent across the wavelength range λ of 0.3 to 2.5 μm.

The cells are spaced at a distance $X$ from one another, with the length $l_0$ and thickness $d$ of each plate, as well as the spacing $X$, selected based on the following conditions: ${\displaystyle \frac{l_0}{d}}=2.81$ and $0<{\displaystyle \frac{∆X}{d}}\le 0.12$. These parameters ensure optimal performance and alignment of the concentrator cells.

To validate the proposed design, the configuration of the planar solar concentrator was thoroughly investigated using the commercial ray-tracing software Zemax OpticStudio. A total of 10⁶ rays across the entire AM0 solar spectrum (280–4000 nm) were traced to evaluate the system’s performance. The results confirmed that the optimal configuration consists of $N_x=15$ cells per row and $N_y=7$ rows, with the distance between rows $Y={\displaystyle \frac{d}{n}}$, where n is a natural number between 1 and 10. The value of n can be adjusted based on specific design requirements and constraints.

The GCR of the developed concentrator was determined to be GCR = 3.45, with an AA range of 23° to 90° (excluding boundaries). This combination of moderate concentration efficiency and broad AA makes the proposed design highly adaptable to varying solar angles, offering a practical and efficient solution for solar energy harvesting applications. The findings of this study contribute to the advancement of planar solar concentrator technology, providing a scalable and cost-effective approach to renewable energy systems.