Micromechanical Estimates Compared to FE-Based Methods for Modelling the Behaviour of Micro-Cracked Viscoelastic Materials
Abstract
1. Introduction
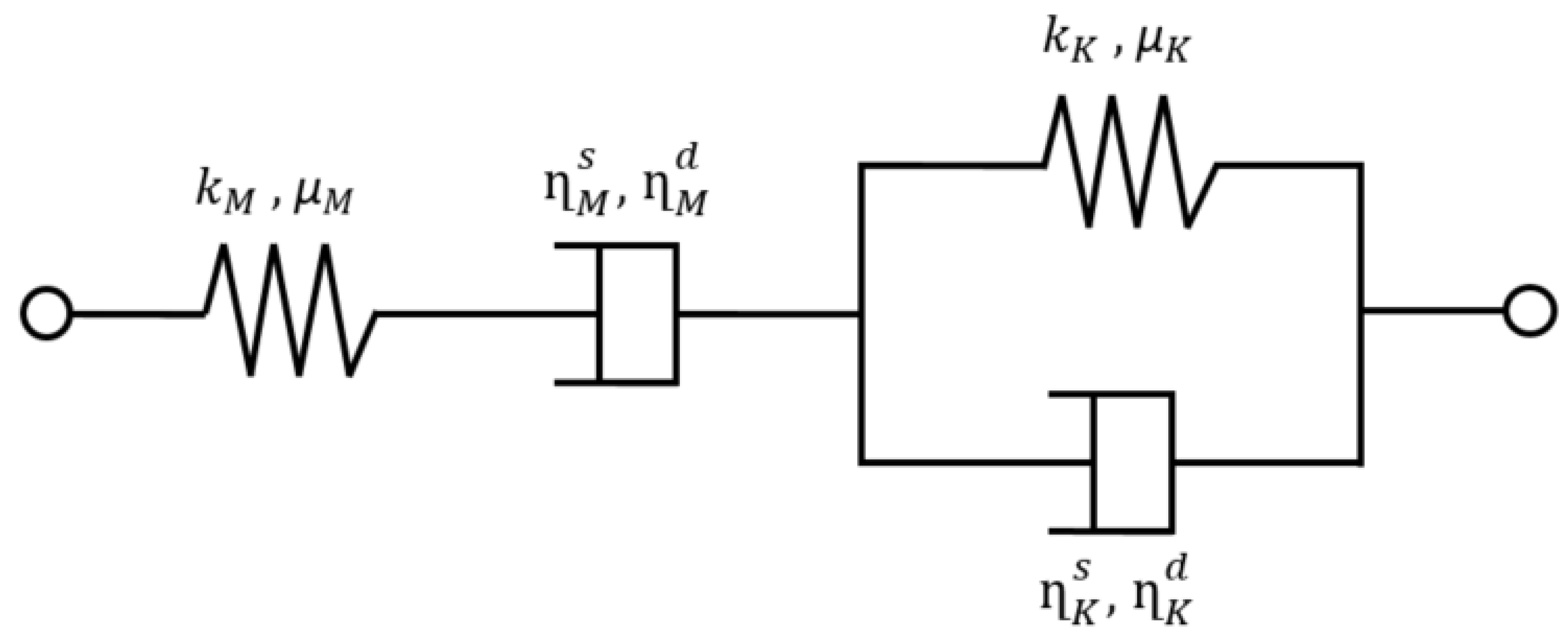
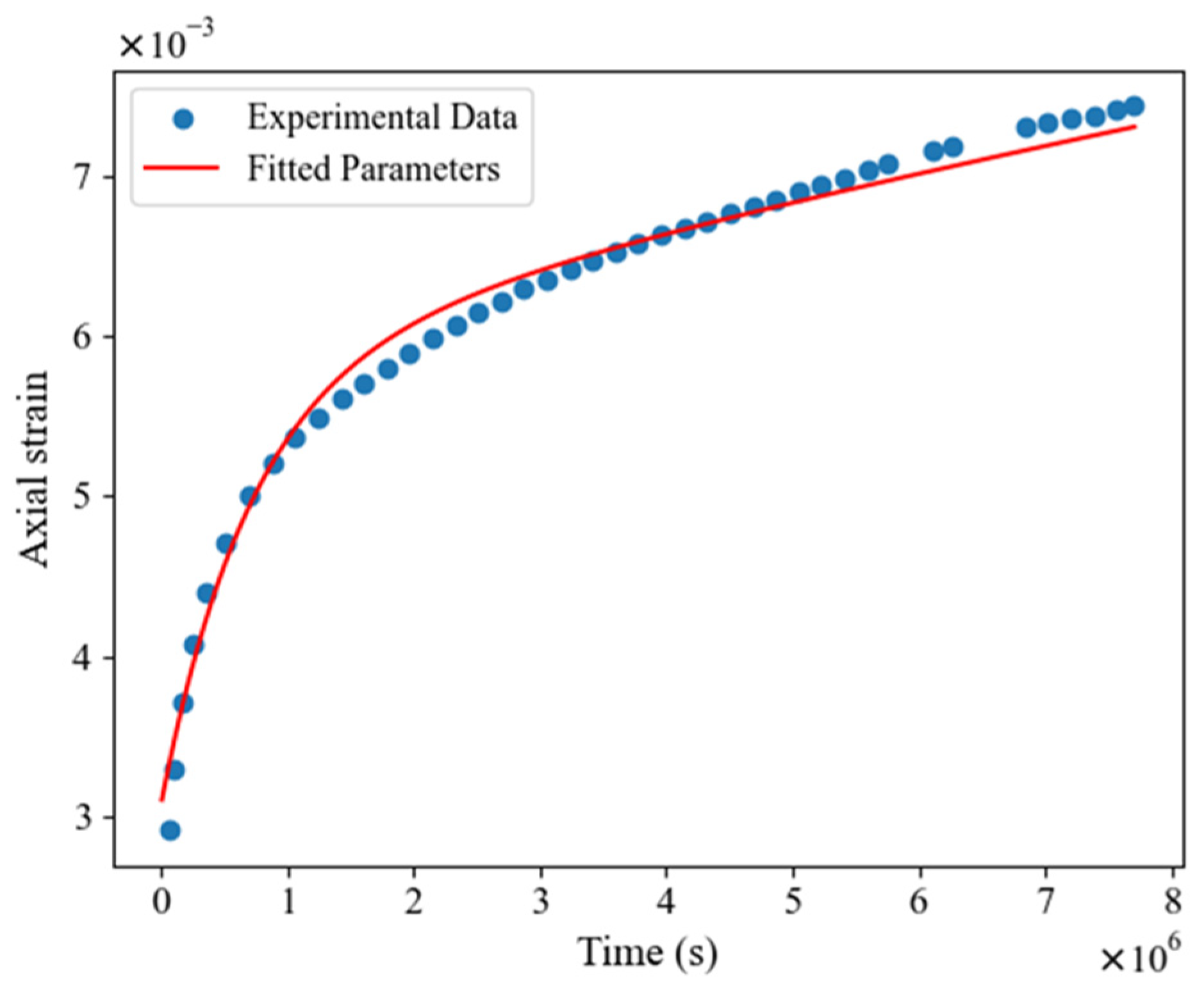
2. Viscoelastic Burgers Model
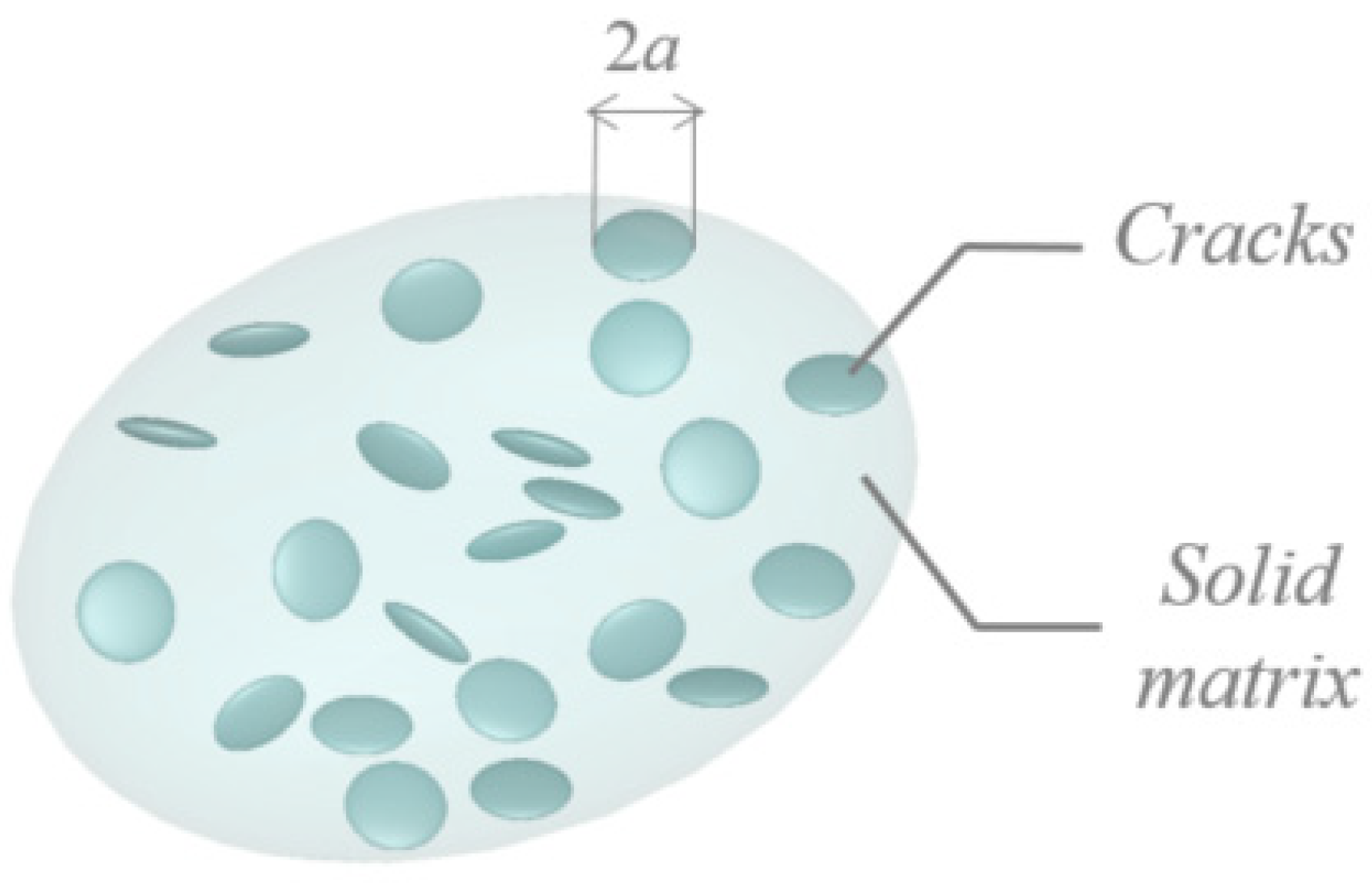
3. Representation of Cracking in a Viscoelastic Material
3.1. Isotropic Crack Distribution
3.2. Parallel Crack Distribution
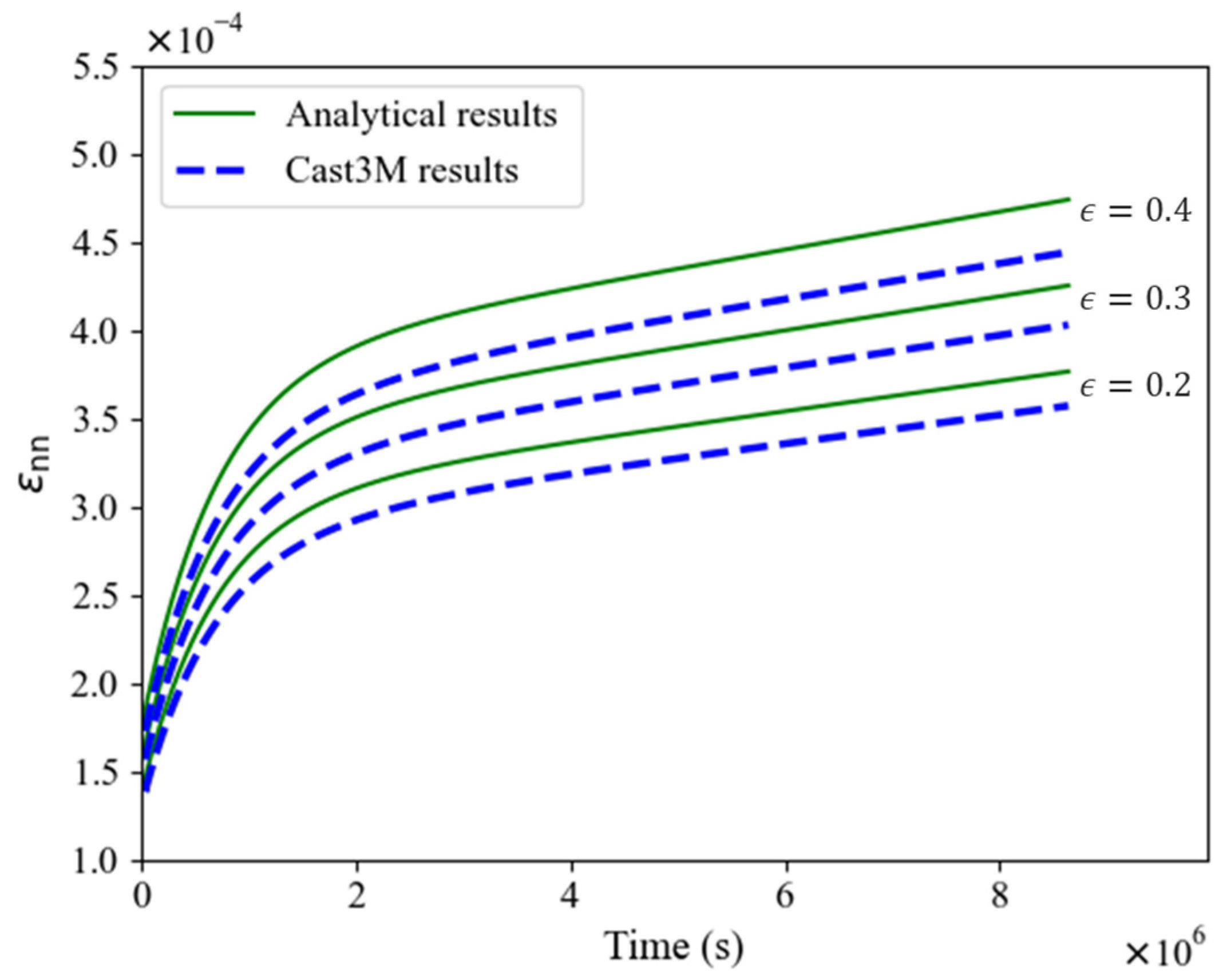
4. Numerical Simulations
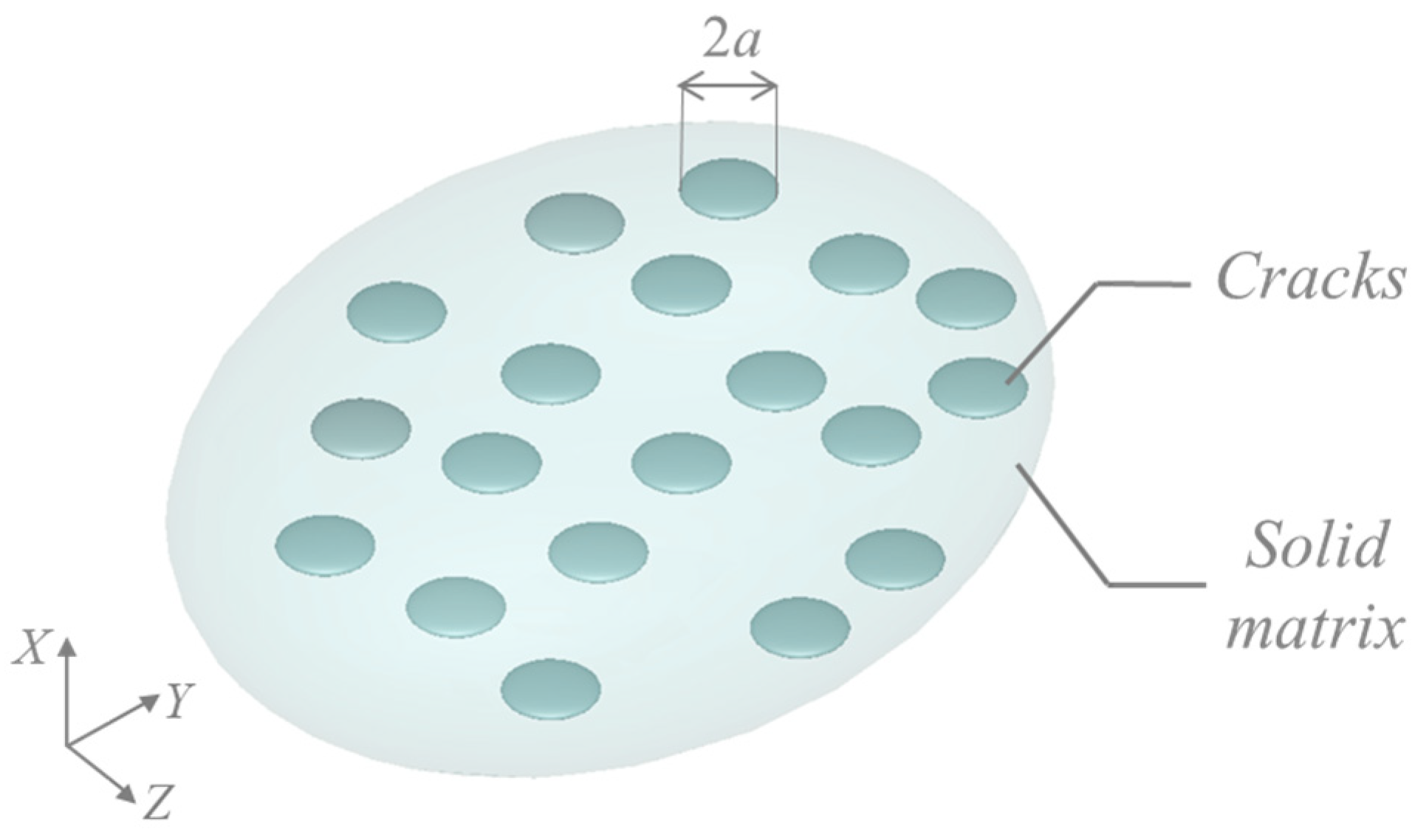
4.1. Three-Dimensional Microstructures and Meshes
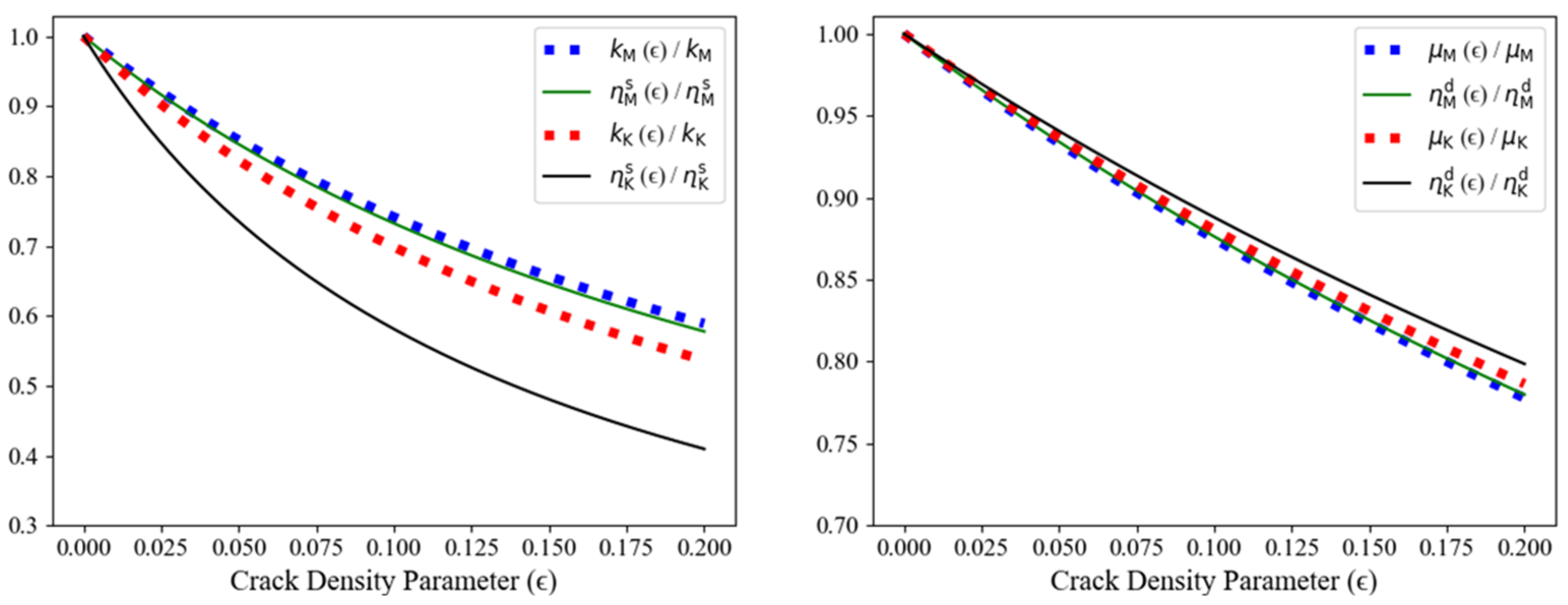
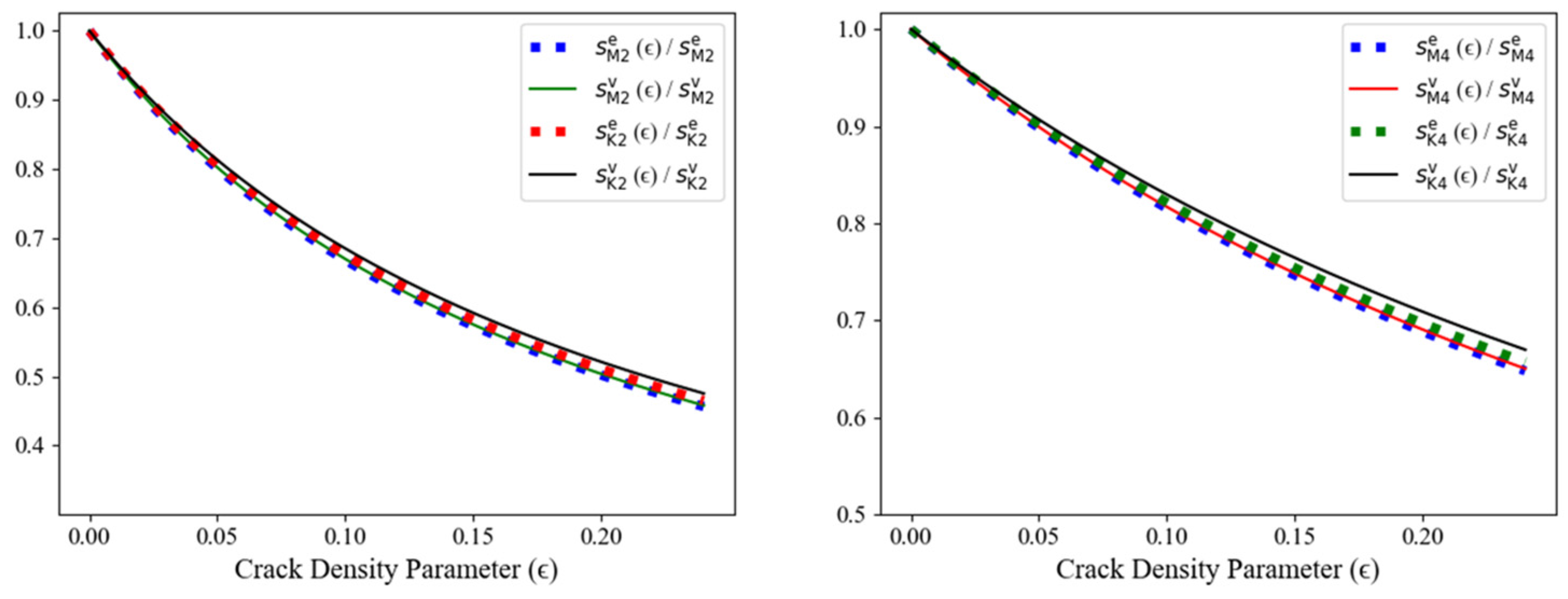
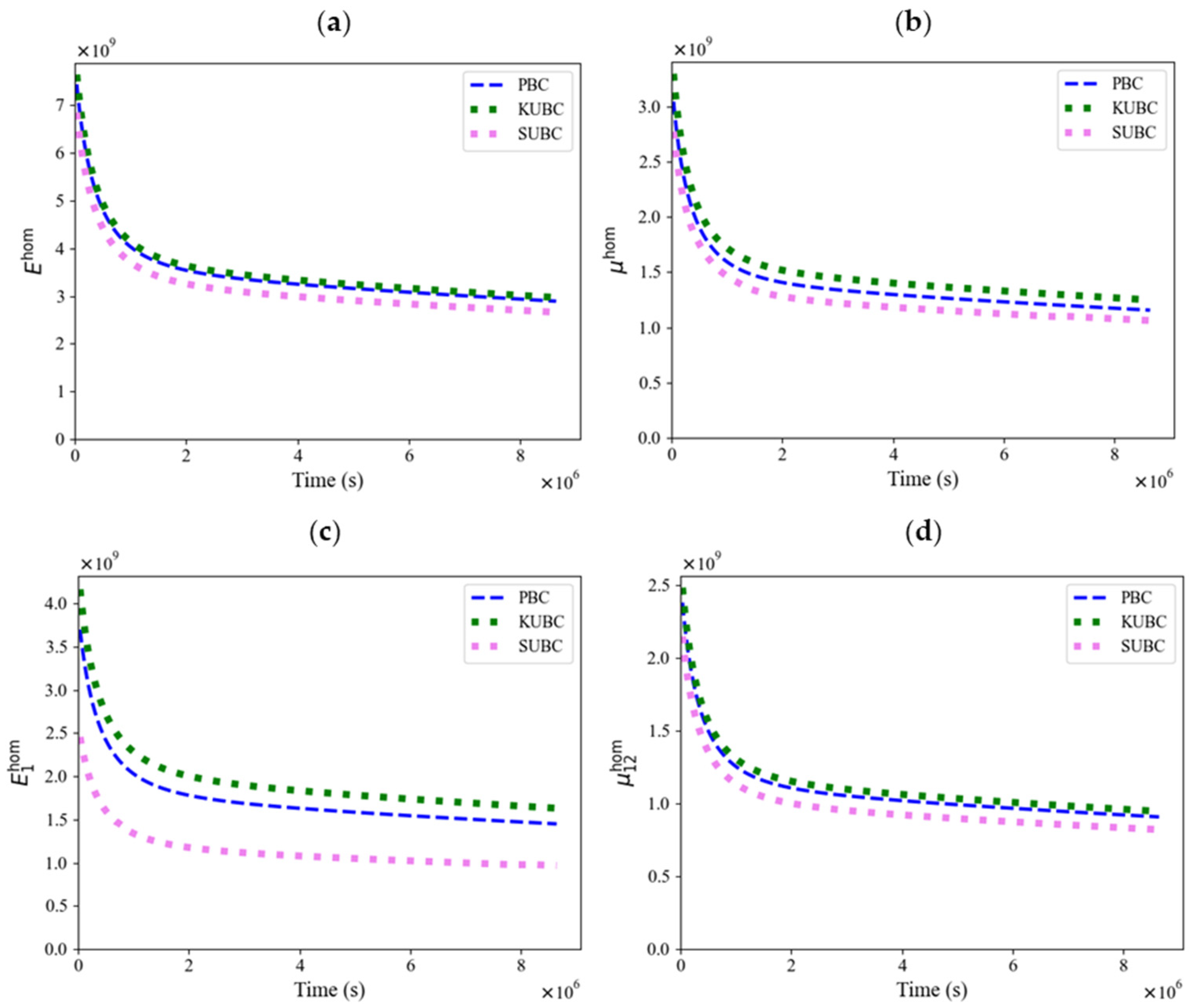
4.2. Transversely Isotropic Case Results
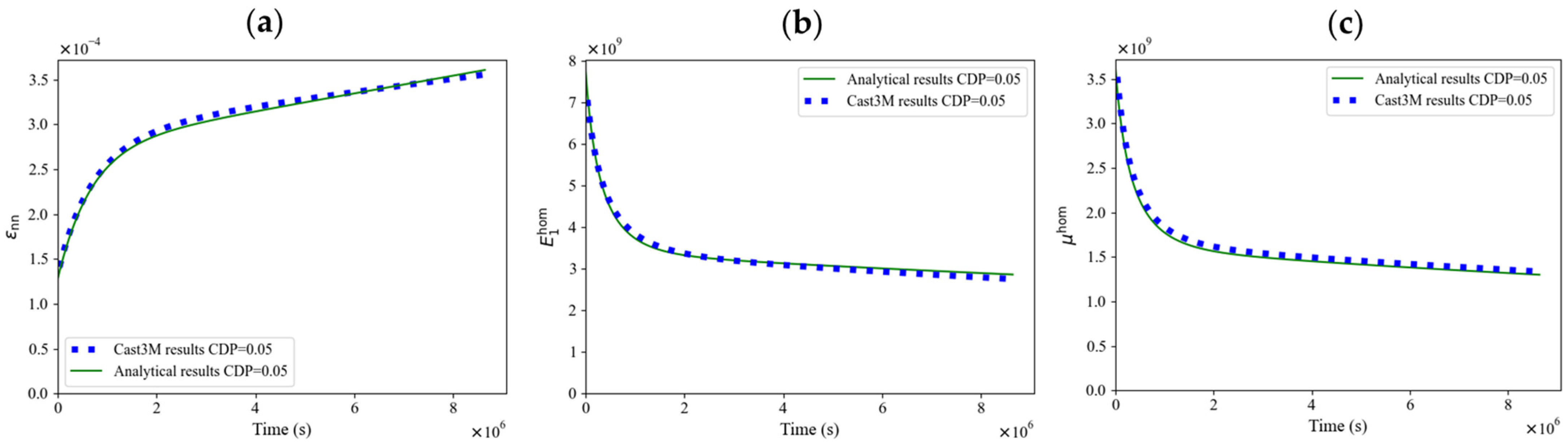
4.3. Isotropic Case Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andra Dossier d’options de Sûreté—Partie Exploitation (DOS-EXPL), Technical Report, 2016.
- De La Vaissière, R.; Armand, G.; Talandier, J. Gas and water flow in an excavation-induced fracture network around an underground drift: A case study for a radioactive waste repository in clay rock. J. Hydrol. 2015, 521, 141–156. [Google Scholar] [CrossRef]
- Armand, G.; Leveau, F.; Nussbaum, C.; de La Vaissiere, R.; Noiret, A.; Jaeggi, D.; Landrein, P.; Righini, C. Geometry and Properties of the Excavation-Induced Fractures at the Meuse/Haute-Marne URL Drifts. Rock Mech. Rock Eng. 2014, 47, 21–41. [Google Scholar] [CrossRef]
- Rahal, S.; Sellier, A.; Casaux-Ginestet, G. Poromechanical consolidation and basic creep interactions around tunnel excavation. Int. J. Rock Mech. Min. Sci. 2017, 94, 55–63. [Google Scholar] [CrossRef]
- Andra Dossier d’options de Sûreté—Partie Après Fermeture (DOS-AF), Technical Report, 2016.
- Nguyen, S.T.; Dormieux, L.; Pape, Y.L.; Sanahuja, J. A Burger Model for the Effective Behavior of a Microcracked Viscoelastic Solid. Int. J. Damage Mech. 2011, 20, 1116–1129. [Google Scholar] [CrossRef]
- Bluthé, J.; Bary, B.; Lemarchand, E. Contribution of FE and FFT-based methods to the determination of the effective elastic and conduction properties of composite media with flat inclusions and infinite contrast. Int. J. Solids Struct. 2021, 216, 108–122. [Google Scholar] [CrossRef]
- Marigo, J.-J.; Maurini, C.; Pham, K. An overview of the modelling of fracture by gradient damage models. Meccanica 2016, 51, 3107–3128. [Google Scholar] [CrossRef]
- Cao, Y.J.; Shen, W.Q.; Shao, J.F.; Wang, W. A novel FFT-based phase field model for damage and cracking behavior of heterogeneous materials. Int. J. Plast. 2020, 133, 102786. [Google Scholar] [CrossRef]
- Dormieux, L.; Kondo, D. Stress-based estimates and bounds of effective elastic properties: The case of cracked media with unilateral effects. Comput. Mater. Sci. 2009, 46, 173–179. [Google Scholar] [CrossRef]
- Tsitova, A.; Bernachy-Barbe, F.; Bary, B.; Hild, F. Experimental and numerical analyses of the interaction of creep with mesoscale damage in cementitious materials. Mech. Mater. 2023, 184, 104715. [Google Scholar] [CrossRef]
- Mazars, J. A description of micro- and macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Dormieux, L.; Kondo, D.; Ulm, F.-J. A micromechanical analysis of damage propagation in fluid-saturated cracked media. C. R. Méc. 2006, 334, 440–446. [Google Scholar] [CrossRef]
- Castañeda, P.P.; Willis, J.R. The effect of spatial distribution on the effective behavior of composite materials and cracked media. J. Mech. Phys. Solids 1995, 43, 1919–1951. [Google Scholar] [CrossRef]
- Hershey, A.V. The Elasticity of an Isotropic Aggregate of Anisotropic Cubic Crystals. J. Appl. Mech. 2021, 21, 236–240. [Google Scholar] [CrossRef]
- Hashin, Z. The differential scheme and its application to cracked materials. J. Mech. Phys. Solids 1988, 36, 719–734. [Google Scholar] [CrossRef]
- Budiansky, B.; O’connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Shao, J.F.; Rudnicki, J.W. A microcrack-based continuous damage model for brittle geomaterials. Mech. Mater. 2000, 32, 607–619. [Google Scholar] [CrossRef]
- Bluthé, J.; Bary, B.; Lemarchand, E. Closure of parallel cracks: Micromechanical estimates versus finite element computations. Eur. J. Mech. A/Solids 2020, 81, 103952. [Google Scholar] [CrossRef]
- Ricaud, J.-M.; Masson, R. Effective properties of linear viscoelastic heterogeneous media: Internal variables formulation and extension to ageing behaviours. Int. J. Solids Struct. 2009, 46, 1599–1606. [Google Scholar] [CrossRef]
- Beurthey, S.; Zaoui, A. Structural morphology and relaxation spectra of viscoelastic heterogeneous materials. Eur. J. Mech. A/Solids 2000, 19, 1–16. [Google Scholar] [CrossRef]
- Schapery, R. A Simple Collocation Method for Fitting Viscoelastic Models to Experimental Data; Graduate Aeronautical Laboratory, California Institute of Technology: Pasadena, CA, USA, 1962. [Google Scholar]
- Ferreira, L.P.; Lopes, P.C.F.; Leiderman, R.; Aragão, F.T.S.; Pereira, A.M.B. An image-based numerical homogenization strategy for the characterization of viscoelastic composites. Int. J. Solids Struct. 2023, 267, 112142. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Dormieux, L.; Kondo, D. Approche micromécanique du couplage perméabilité–endommagement. C. R. Méc. 2004, 332, 135–140. [Google Scholar] [CrossRef]
- Nguyen, S.T. Propagation de Fissures et Endommagement par Microfissures des Matériaux Viscoélastiques Linéaires non Vieillissants. Ph.D. Thesis, Université Paris-Est, Créteil, France, 2010. Available online: https://pastel.hal.science/tel-00598511 (accessed on 10 May 2022).
- Cuvilliez, S.; Djouadi, I.; Raude, S.; Fernandes, R. An elastoviscoplastic constitutive model for geomaterials: Application to hydromechanical modelling of claystone response to drift excavation. Comput. Geotech. 2017, 85, 321–340. [Google Scholar] [CrossRef]
- Mánica, M.; Gens, A.; Vaunat, J.; Ruiz, D.F. A time-dependent anisotropic model for argillaceous rocks. Application to an underground excavation in Callovo-Oxfordian claystone. Comput. Geotech. 2017, 85, 341–350. [Google Scholar] [CrossRef]
- Zhang, C.; Rothfuchs, T. Experimental study of the hydro-mechanical behaviour of the Callovo-Oxfordian argillite. Appl. Clay Sci. 2004, 26, 325–336. [Google Scholar] [CrossRef]
- Armand, G.; Conil, N.; Talandier, J.; Seyedi, D.M. Fundamental aspects of the hydromechanical behaviour of Callovo-Oxfordian claystone: From experimental studies to model calibration and validation. Comput. Geotech. 2017, 85, 277–286. [Google Scholar] [CrossRef]
- Nguyen, S.T. Generalized Kelvin model for micro-cracked viscoelastic materials. Eng. Fract. Mech. 2014, 127, 226–234. [Google Scholar] [CrossRef]
- Nguyen, S.T.; Vu, M.; Vu, N.; Thi Thu Nga, N.; Gasser, A.; Rekik, A. Generalized Maxwell model for micro-cracked viscoelastic materials. Int. J. Damage Mech. 2015, 26, 697–710. [Google Scholar] [CrossRef]
- March, N.G.; Gunasegaram, D.R.; Murphy, A.B. Evaluation of computational homogenization methods for the prediction of mechanical properties of additively manufactured metal parts. Addit. Manuf. 2023, 64, 103415. [Google Scholar] [CrossRef]
- Walpole, L.J. Elastic Behavior of Composite Materials: Theoretical Foundations. In Advances in Applied Mechanics; Yih, C.-S., Ed.; Elsevier: Amsterdam, The Netherlands, 1981; Volume 21, pp. 169–242. [Google Scholar]
- Bluthe, J. Modélisation Couplée et Simulation Numérique des Phénomènes de Colmatage des Argilites. Ph.D. Thesis, Paris Est, Créteil, France, 2019. Available online: http://www.theses.fr/2019PESC1027 (accessed on 27 November 2021).
- Helfer, T.; Michel, B.; Proix, J.-M.; Salvo, M.; Sercombe, J.; Casella, M. Introducing the open-source mfront code generator: Application to mechanical behaviours and material knowledge management within the PLEIADES fuel element modelling platform. Comput. Math. Appl. 2015, 70, 994. [Google Scholar] [CrossRef]
- Bary, B.; Bourcier, C.; Helfer, T. Analytical and 3D numerical analysis of the thermoviscoelastic behavior of concrete-like materials including interfaces. Adv. Eng. Softw. 2017, 112, 16–30. [Google Scholar] [CrossRef]
- Honório, T.; Bary, B.; Benboudjema, F. Multiscale estimation of ageing viscoelastic properties of cement-based materials: A combined analytical and numerical approach to estimate the behaviour at early age. Cem. Concr. Res. 2016, 85, 137–155. [Google Scholar] [CrossRef]
- Charpin, L.; Ehrlacher, A. Estimating the poroelastic properties of cracked materials. Acta Mech. 2014, 225, 2501–2519. [Google Scholar] [CrossRef]
- Vasylevskyi, K.; Drach, B.; Tsukrov, I. On micromechanical modeling of orthotropic solids with parallel cracks. Int. J. Solids Struct. 2018, 144–145, 46–58. [Google Scholar] [CrossRef]
- Hannay, J.H.; Nye, J.F. Fibonacci numerical integration on a sphere. J. Phys. A Math. Gen. 2004, 37, 11591. [Google Scholar] [CrossRef]







| Parts | ||||
|---|---|---|---|---|
| Maxwell | 6.872 | 3.870 | ||
| Kelvin | 7.308 | 3.099 |
| Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | |
|---|---|---|---|---|
| Number of mesh elements | 0.614 M | 1.115 M | 1.602 M | 2.55 M |
| 2.9877 (2.45%) | 2.8543 (1.78%) | 2.8941 (0.41%) | ||
| 1.2299 (4.39%) | 1.2066 (2.41%) | 1.1578 (1.71%) |
| Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | |
|---|---|---|---|---|
| Number of mesh elements | 0.675 M | 0.919 M | 1.88 M | 2.88 M |
| 1.3627 (6.71%) | 1.4053 (3.79%) | 1.4493 (0.78%) | ||
| 0.8918 (2.27%) | 0.9054 (0.77%) | 0.9089 (0.38%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou Chakra, S.; Bary, B.; Lemarchand, E.; Bourcier, C.; Granet, S.; Talandier, J. Micromechanical Estimates Compared to FE-Based Methods for Modelling the Behaviour of Micro-Cracked Viscoelastic Materials. Modelling 2024, 5, 625-641. https://doi.org/10.3390/modelling5020033
Abou Chakra S, Bary B, Lemarchand E, Bourcier C, Granet S, Talandier J. Micromechanical Estimates Compared to FE-Based Methods for Modelling the Behaviour of Micro-Cracked Viscoelastic Materials. Modelling. 2024; 5(2):625-641. https://doi.org/10.3390/modelling5020033
Chicago/Turabian StyleAbou Chakra, Sarah, Benoît Bary, Eric Lemarchand, Christophe Bourcier, Sylvie Granet, and Jean Talandier. 2024. "Micromechanical Estimates Compared to FE-Based Methods for Modelling the Behaviour of Micro-Cracked Viscoelastic Materials" Modelling 5, no. 2: 625-641. https://doi.org/10.3390/modelling5020033
APA StyleAbou Chakra, S., Bary, B., Lemarchand, E., Bourcier, C., Granet, S., & Talandier, J. (2024). Micromechanical Estimates Compared to FE-Based Methods for Modelling the Behaviour of Micro-Cracked Viscoelastic Materials. Modelling, 5(2), 625-641. https://doi.org/10.3390/modelling5020033







