Cartesian Aerial Manipulator with Compliant Arm
Abstract
:1. Introduction
1.1. Aerial Manipulation
1.2. Positioning Accuracy
1.3. Contribution of This Work
2. System Description
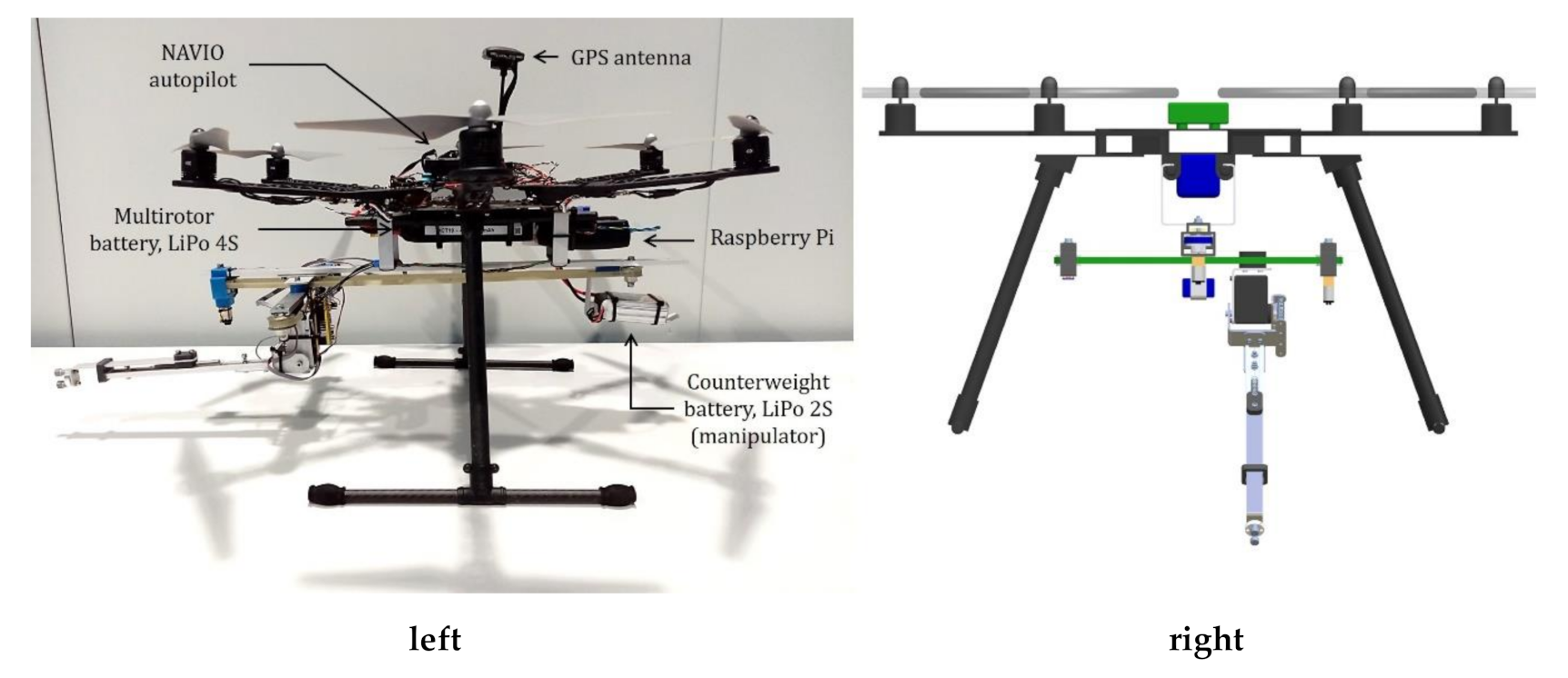
2.1. Motivation
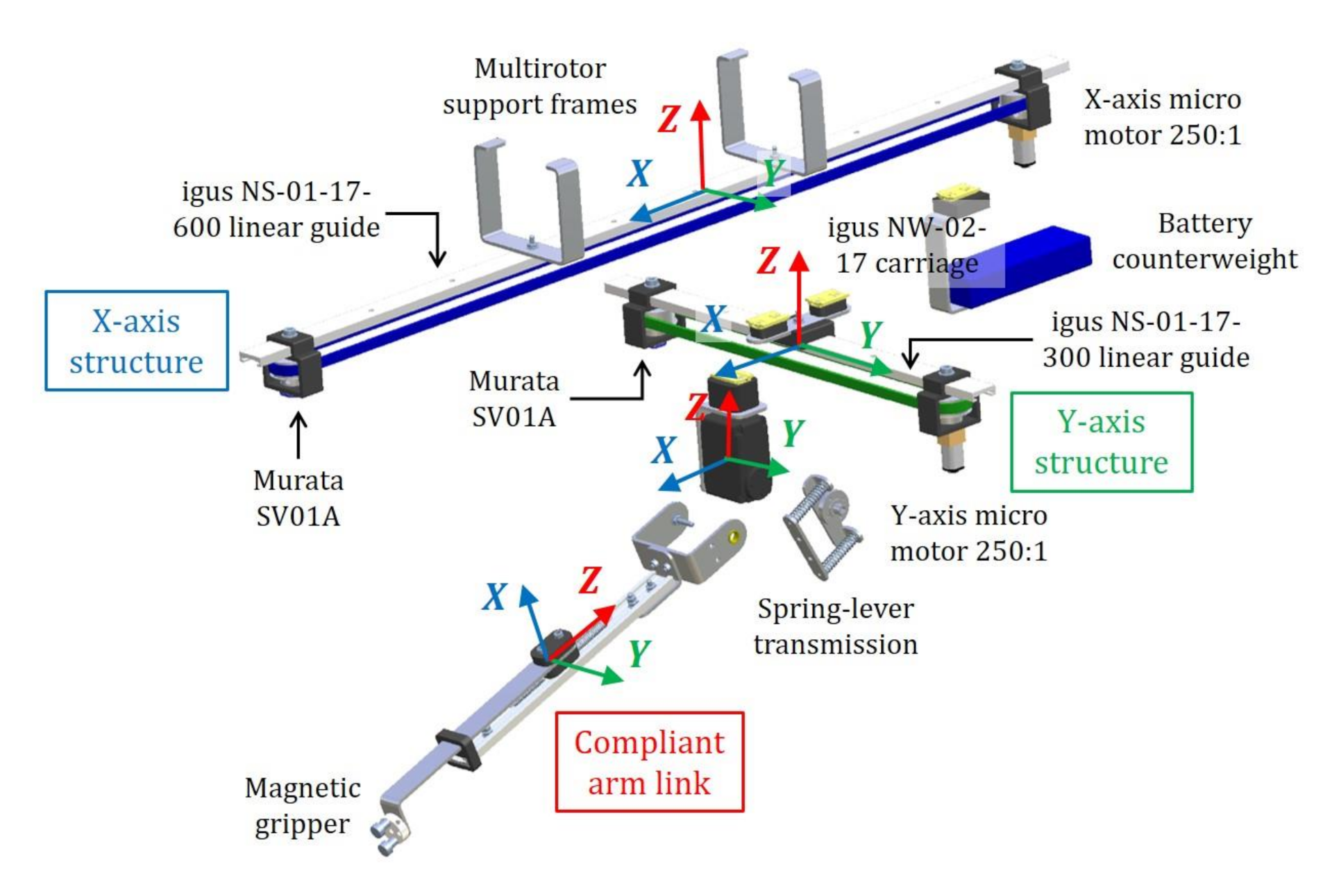
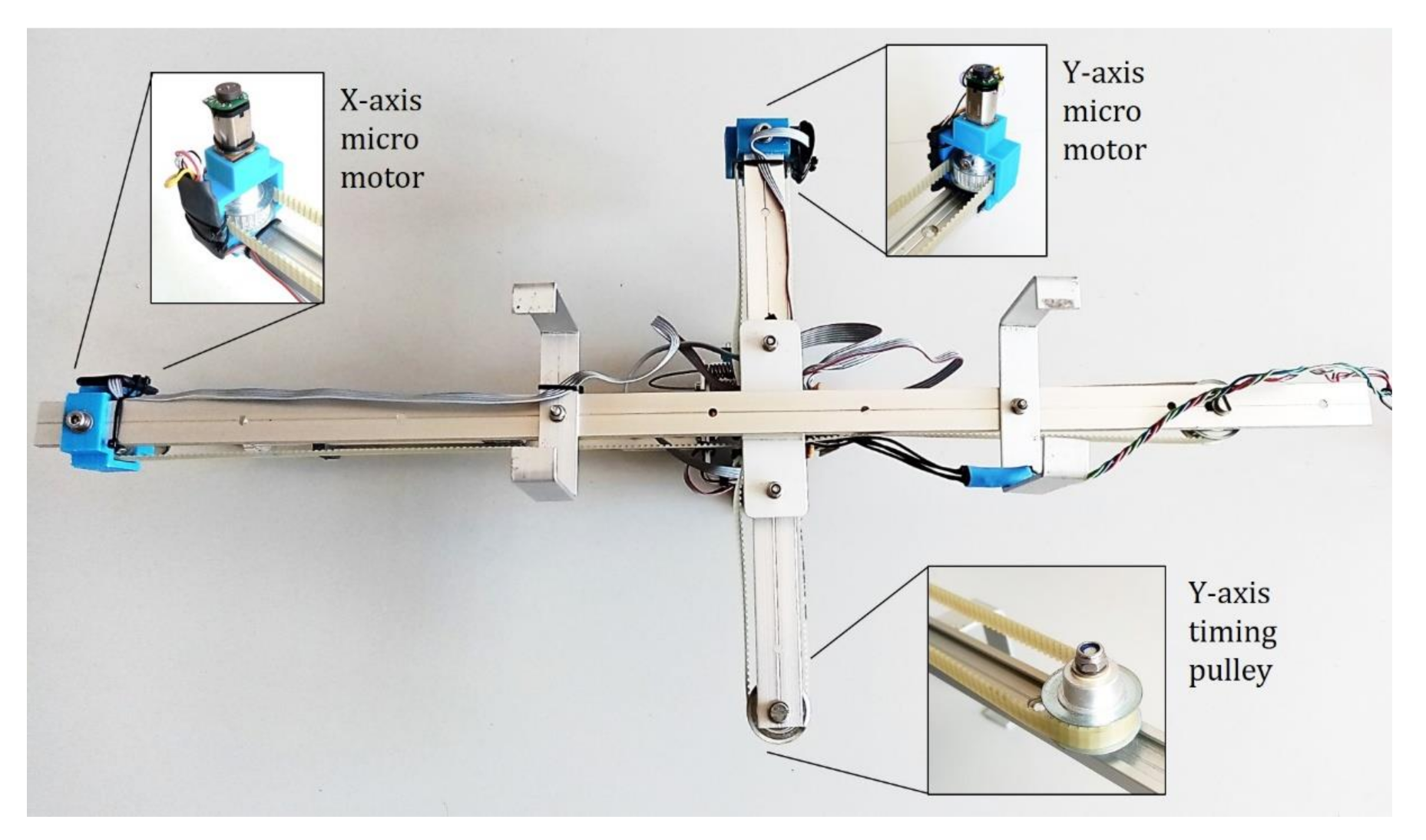
2.2. Mechanical Design
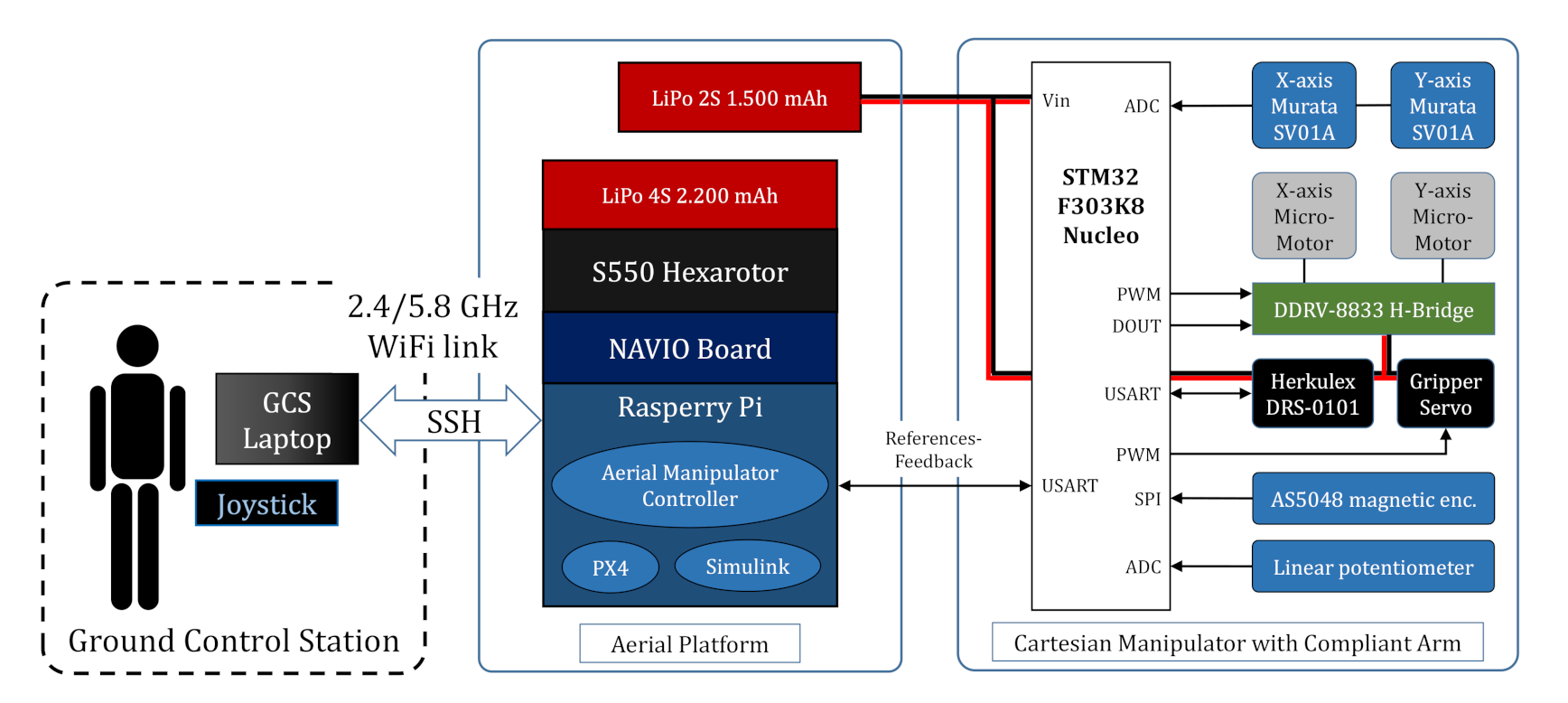
2.3. Hardware Architecture
- The two potentiometers used to estimate the displacement of the linear base.
- The magnetic encoder attached to the servo that measures the joint deflection.
- The linear potentiometer in the link used to estimate the pushing/pulling force.
3. Modelling
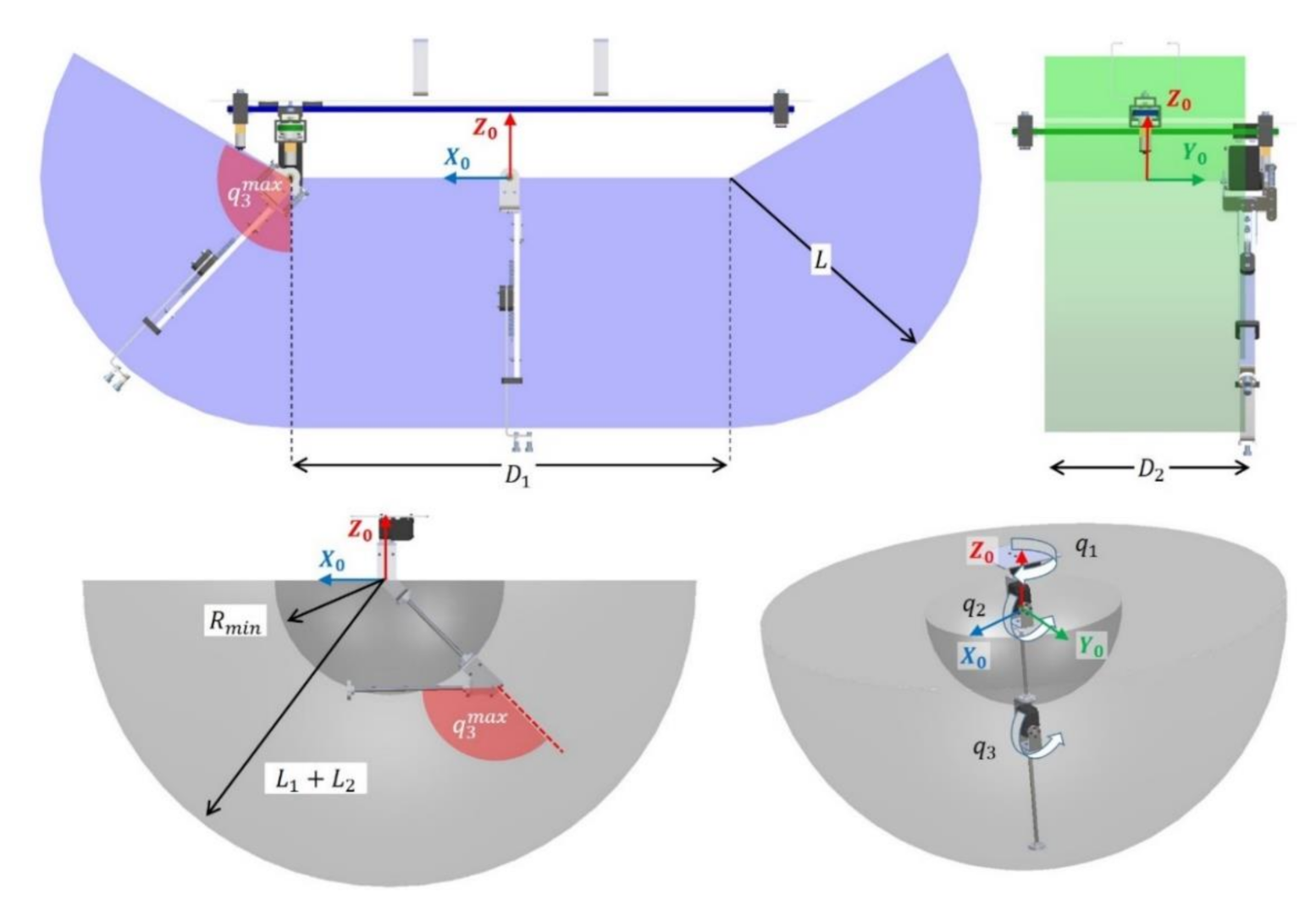
3.1. Kinematic Model
3.2. Positioning Accuracy and Workspace
3.3. Dynamic Model
4. Estimation and Control
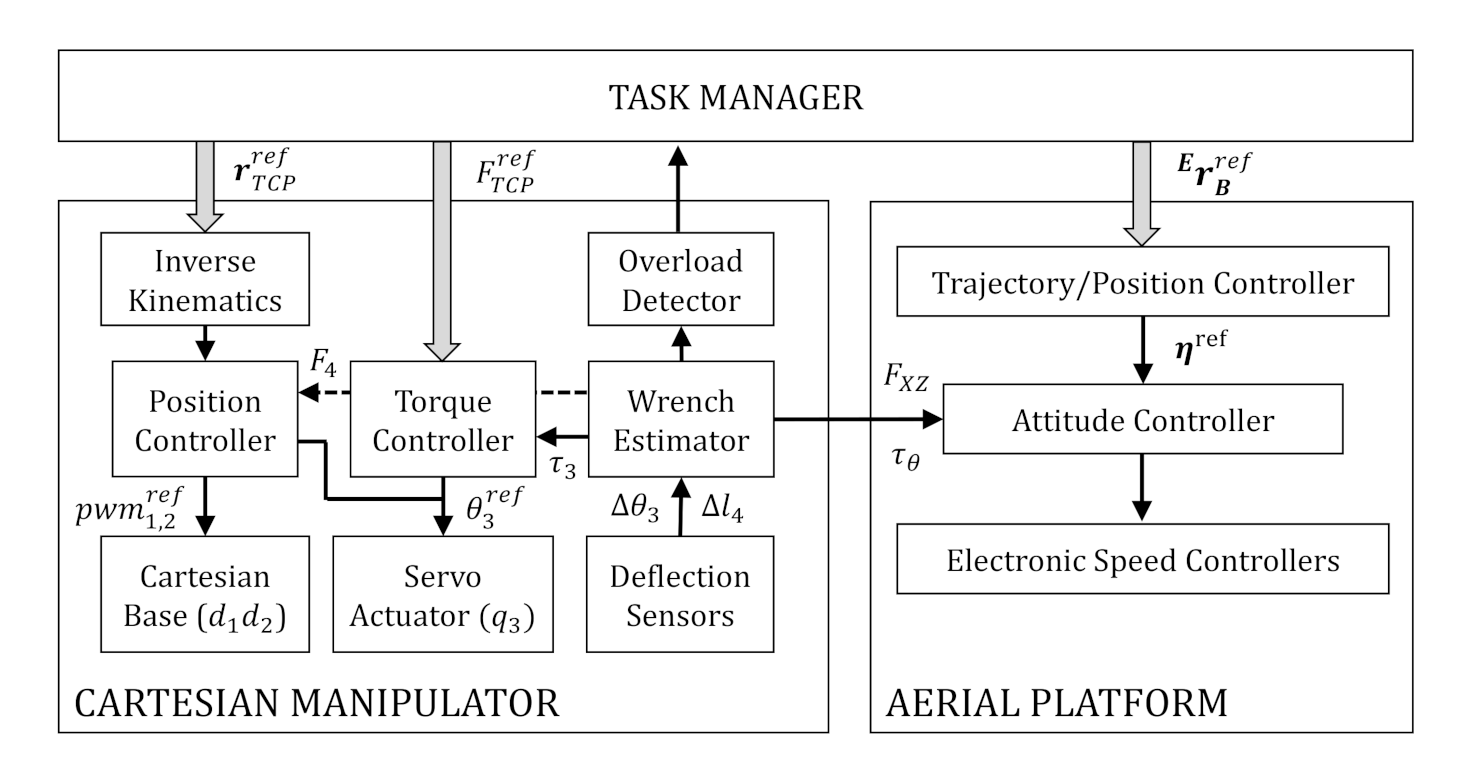
4.1. Cartesian Base Control
4.2. Force-Torque Estimation with Compliant Arm
4.3. Cartesian Aerial Manipulator Control Scheme
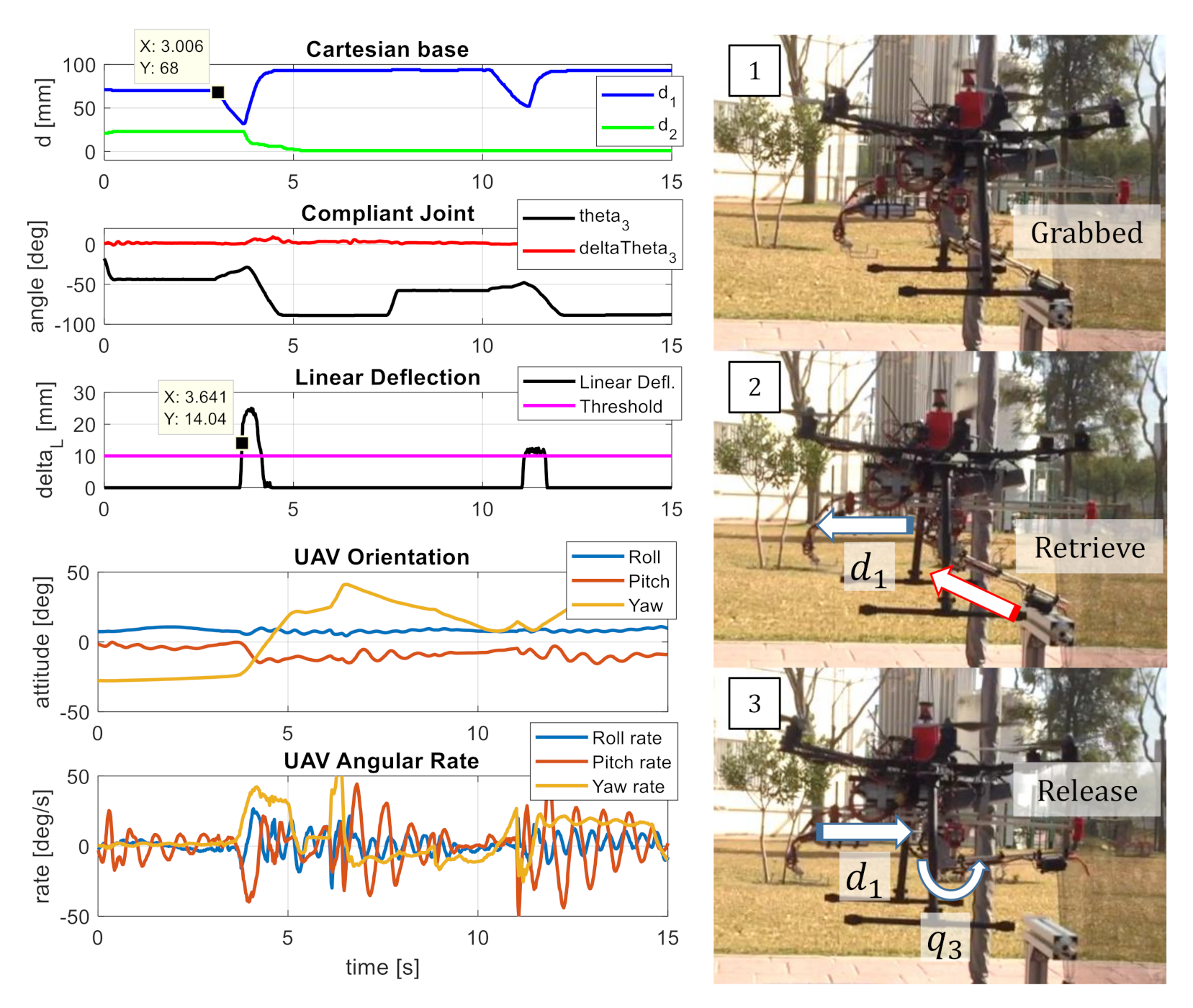
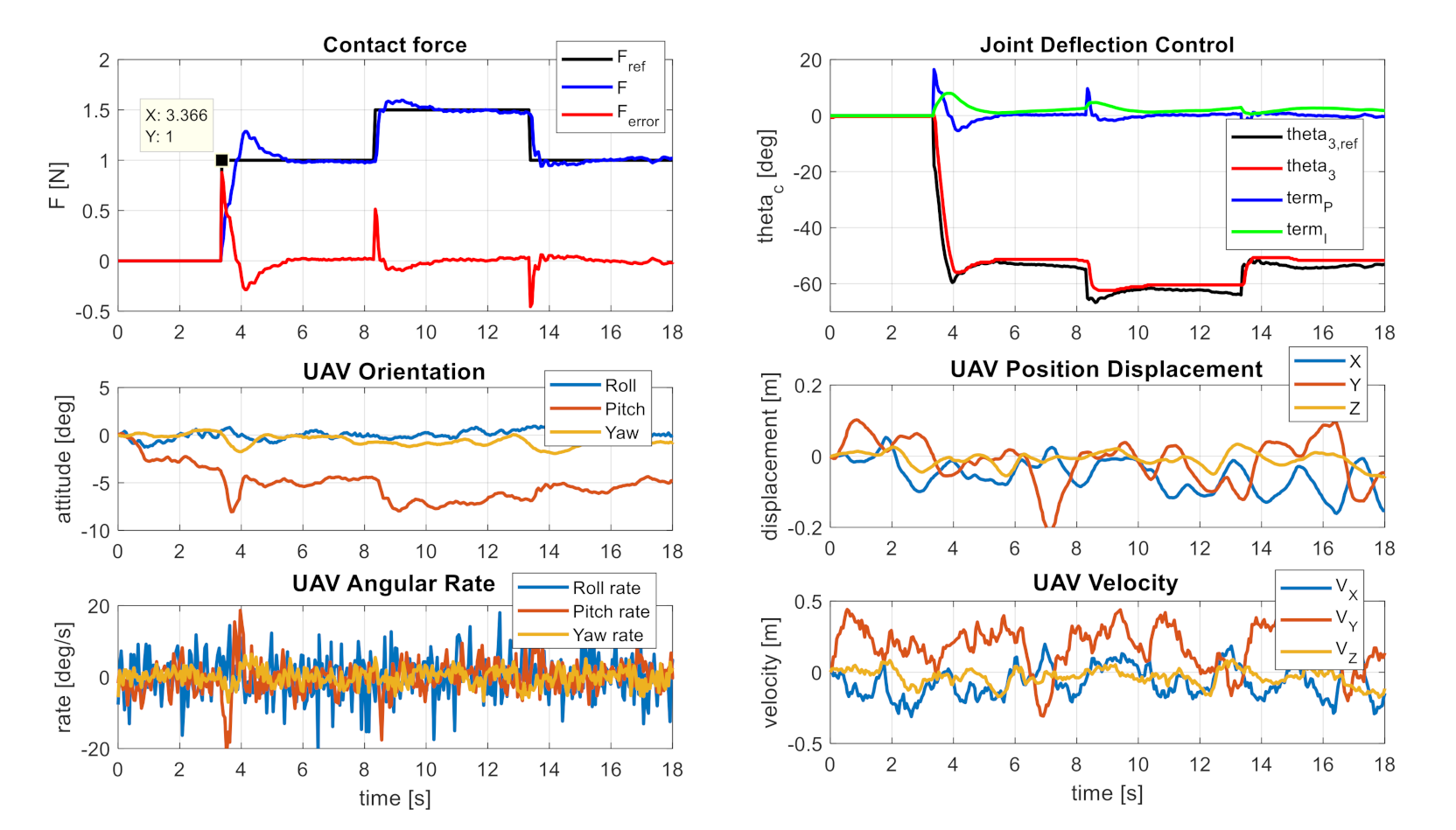
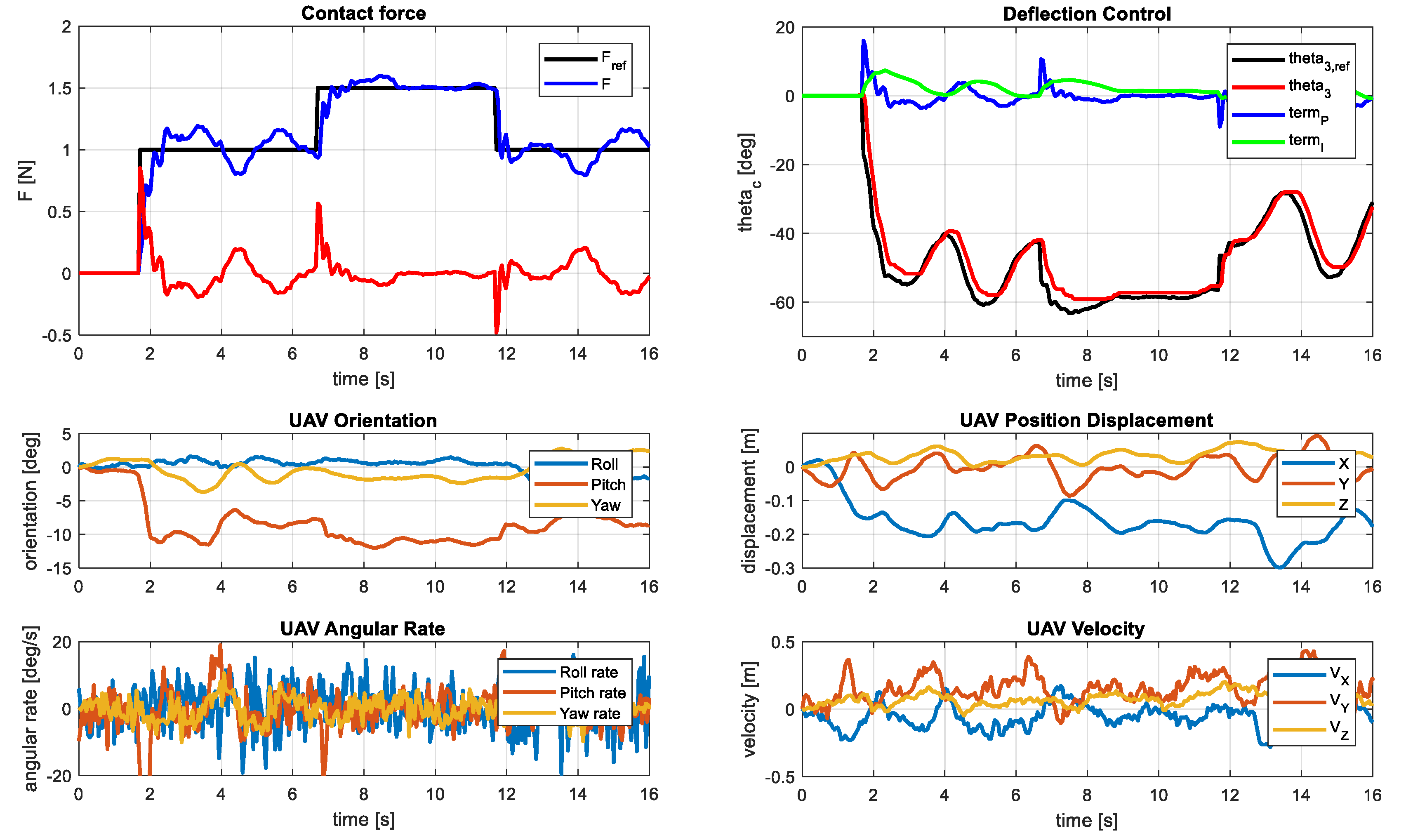
5. Experimental Results
5.1. Cartesian Base Control
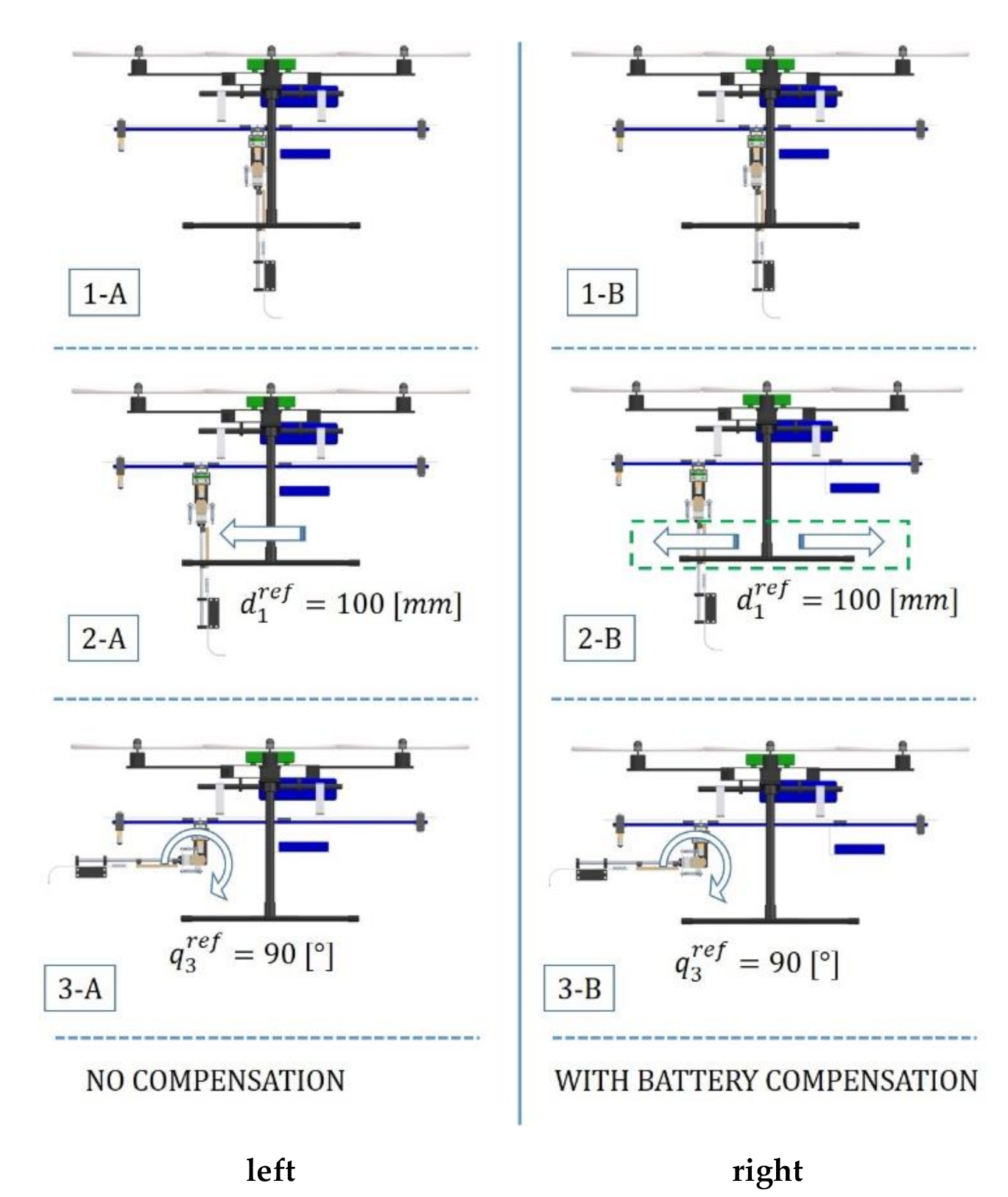
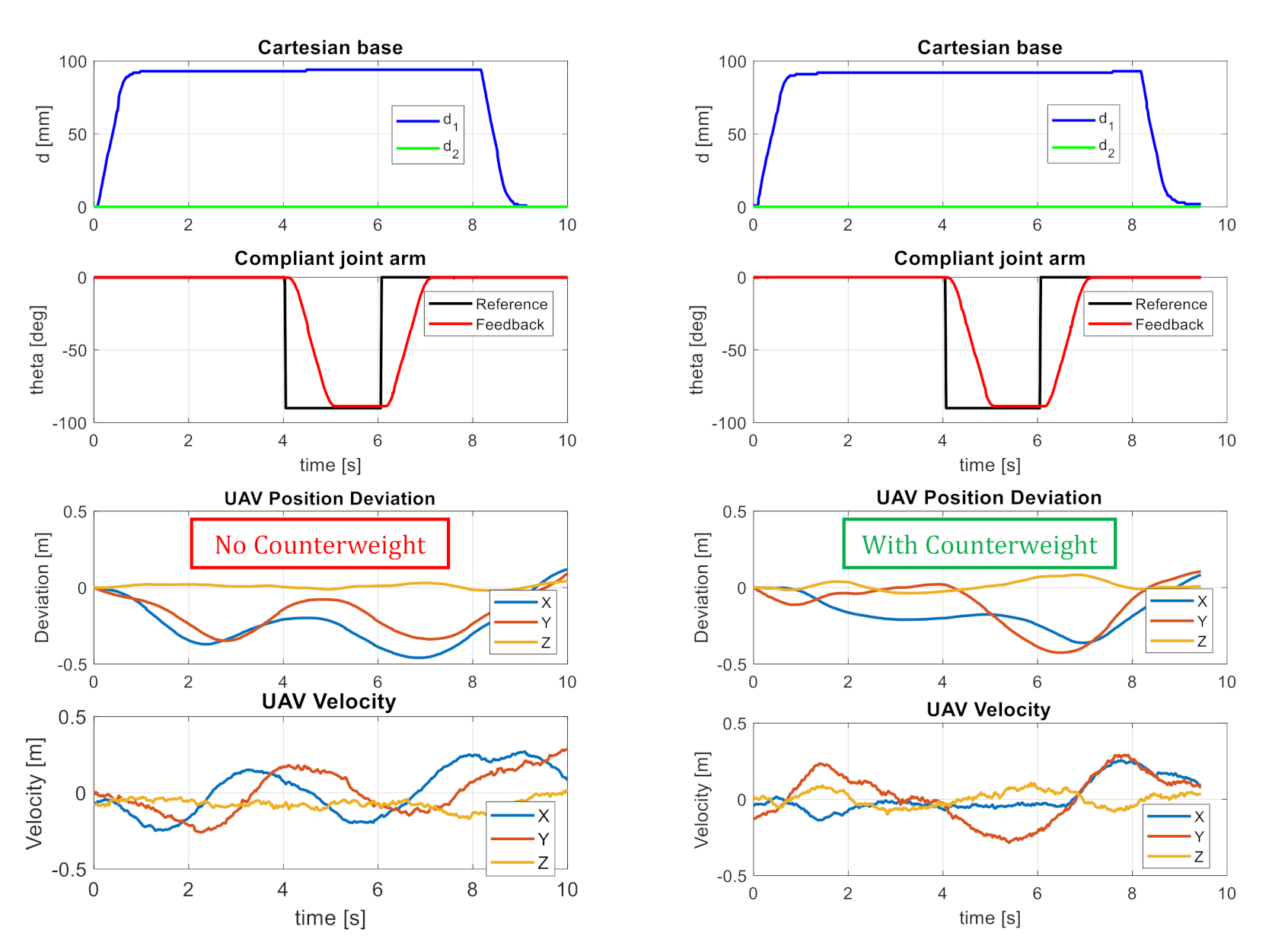
5.2. Compensation of Mass Displacement
5.3. Monitoring Linear Deflection in Grabbing Conditions
5.4. Contact Force Control
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- The AERIAL-CORE Project. Available online: https://aerial-core.eu/ (accessed on 28 December 2020).
- Suarez, A.; Real, F.; Vega, V.M.; Heredia, G.; Rodriguez-Castano, A.; Ollero, A. Compliant Bimanual Aerial Manipulation: Standard and Long Reach Configurations. IEEE Access 2020, 8, 88844–88865. [Google Scholar] [CrossRef]
- Trujillo, M.A.; Dios, J.R.M.-D.; Martín, C.; Viguria, A.; Ollero, A. Novel Aerial Manipulator for Accurate and Robust Industrial NDT Contact Inspection: A New Tool for the Oil and Gas Inspection Industry. Sensors 2019, 19, 1305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ollero, A.; Cortés, J.; Santamaria-Navarro, Àngel; Trujillo, M.A.; Balachandran, R.; Andrade-Cetto, J.; Rodriguez, A.; Heredia, G.; Franchi, A.; Antonelli, G.; et al. The AEROARMS Project: Aerial Robots with Advanced Manipulation Capabilities for Inspection and Maintenance. IEEE Robot. Autom. Mag. 2018, 25, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, T.; Yasui, S.; Fujihara, M.; Ohara, K.; Ashizawa, S.; Ichikawa, A.; Okino, A.; Oomichi, T.; Fukuda, T. Wall contact by octo-rotor UAV with one DoF manipulator for bridge inspection. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5122–5127. [Google Scholar]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Forte, F.; Keemink, A.Q.L.; Stramigioli, S.; Carloni, R.; Marconi, L. Developing an Aerial Manipulator Prototype: Physical Interaction with the Environment. IEEE Robot. Autom. Mag. 2014, 21, 41–50. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Design of an Anthropomorphic, Compliant, and Lightweight Dual Arm for Aerial Manipulation. IEEE Access 2018, 6, 29173–29189. [Google Scholar] [CrossRef]
- Seo, H.; Kim, S.; Kim, H.J. Aerial grasping of cylindrical object using visual servoing based on stochastic model predictive control. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6362–6368. [Google Scholar]
- Chen, H.; Quan, F.; Fang, L.; Zhang, S. Aerial Grasping with a Lightweight Manipulator Based on Multi-Objective Optimization and Visual Compensation. Sensors 2019, 19, 4253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Valve turning using a dual-arm aerial manipulator. In Proceedings of the 2014 International Conference on Un-manned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 836–841. [Google Scholar]
- Hamaza, S.; Georgilas, I.; Fernandez, M.; Sanchez-Cuevas, P.J.; Richardson, T.; Heredia, G.; Ollero, A. Sensor Installation and Retrieval Operations Using an Unmanned Aerial Manipulator. IEEE Robot. Autom. Lett. 2019, 4, 2793–2800. [Google Scholar] [CrossRef] [Green Version]
- Wopereis, H.W.; Hoekstra, J.J.; Post, T.H.; Folkertsma, G.A.; Stramigioli, S.; Fumagalli, M. Application of substantial and sustained force to vertical surfaces using a quadrotor. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2704–2709. [Google Scholar]
- Tognon, M.; Chavez, H.A.T.; Gasparin, E.; Sable, Q.; Bicego, D.; Mallet, A.; Lany, M.; Santi, G.; Revaz, B.; Cortés, J.; et al. A Truly-Redundant Aerial Manipulator System with Application to Push-and-Slide Inspection in Industrial Plants. IEEE Robot. Autom. Lett. 2019, 4, 1846–1851. [Google Scholar] [CrossRef] [Green Version]
- Chermprayong, P.; Zhang, K.; Xiao, F.; Kovac, M. An Integrated Delta Manipulator for Aerial Repair: A New Aerial Robotic System. IEEE Robot. Autom. Mag. 2019, 26, 54–66. [Google Scholar] [CrossRef]
- Shimahara, S.; Leewiwatwong, S.; Ladig, R.; Shimonomura, K. Aerial torsional manipulation employing multi-rotor flying robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1595–1600. [Google Scholar]
- Nguyen, H.N.; Park, S.; Lee, D. Aerial tool operation system using quadrotors as rotating thrust generators. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015. [Google Scholar]
- Bellicoso, C.D.; Buonocore, L.R.; Lippiello, V.; Siciliano, B. Design, modeling and control of a 5-DoF light-weight robot arm for aerial manipulation. In Proceedings of the 2015 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; pp. 853–858. [Google Scholar]
- Cano, R.; Pérez, C.; Pruano, F.; Ollero, A.; Heredia, G. Mechanical design of a 6-DOF aerial manipulator for assembling structures using UAVs. In Proceedings of the 2nd RED-UAS 2013 Workshop on Research, Education and Development of Unmanned Aerial Systems, Compiegne, France, 20–22 November 2013. [Google Scholar]
- Suarez, A.; Heredia, G.; Ollero, A. Lightweight compliant arm with compliant finger for aerial manipulation and inspection. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4449–4454. [Google Scholar]
- Yuksel, B.; Mahboubi, S.; Secchi, C.; Bulthoff, H.H.; Franchi, A. Design, identification and experimental testing of a light-weight flexible-joint arm for aerial physical interaction. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 870–876. [Google Scholar]
- Miyazaki, R.; Paul, H.; Kominami, T.; Shimonomura, K. Wire-Suspended Device Control Based on Wireless Communication with Multirotor for Long Reach-Aerial Manipulation. IEEE Access 2020, 8, 172096–172104. [Google Scholar] [CrossRef]
- Paul, H.; Miyazaki, R.; Ladig, R.; Shimonomura, K. Landing of a Multirotor Aerial Vehicle on an Uneven Surface Using Multiple On-board Manipulators. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, China, 4–8 November 2019; pp. 1926–1933. [Google Scholar]
- Bartelds, T.; Capra, A.; Hamaza, S.; Stramigioli, S.; Fumagalli, M. Compliant Aerial Manipulators: Toward a New Generation of Aerial Robotic Workers. IEEE Robot. Autom. Lett. 2016, 1, 477–483. [Google Scholar] [CrossRef] [Green Version]
- Cataldi, E.; Muscio, G.; Trujillo, M.A.; Rodriguez, Y.; Pierri, F.; Antonelli, G.; Caccavale, F.; Viguria, A.; Chiaverini, S.; Ollero, A. Impedance Control of an aerial-manipulator: Preliminary results. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 3848–3853. [Google Scholar]
- Ruggiero, F.; Cacace, J.; Sadeghian, H.; Lippiello, V. Impedance control of VToL UAVs with a momentum-based external generalized forces estimator. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 2093–2099. [Google Scholar]
- Suarez, A.; Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms. Appl. Sci. 2020, 10, 8927. [Google Scholar] [CrossRef]
- Tomic, T.; Haddadin, S. A unified framework for external wrench estimation, interaction control and collision reflexes for flying robots. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4197–4204. [Google Scholar]
- Garcia-Cruz, X.; Sergiyenko, O.; Tyrsa, V.; López, M.R.; Hernández-Balbuena, D.; Rodriguez-Quiñonez, J.; Basaca-Preciado, L.; Mercorelli, P.; Quiñonez, J.C.R. Optimization of 3D laser scanning speed by use of combined variable step. Opt. Lasers Eng. 2014, 54, 141–151. [Google Scholar] [CrossRef]
- Lindner, L.; Sergiyenko, O.; Rivas-Lopez, M.; Ivanov, M.; Quiñonez, J.C.R.; Hernandez-Balbuena, D.; Fuentes, W.F.; Tyrsa, V.; Muerrieta-Rico, F.N.; Mercorelli, P. Machine vision system errors for unmanned aerial vehicle navigation. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, Scotland, 19–21 June 2017; pp. 1615–1620. [Google Scholar]
- Ruggiero, F.; Trujillo, M.A.; Cano, R.; Ascorbe, H.; Viguria, A.; Perez, C.; Lippiello, V.; Ollero, A.; Siciliano, B. A multilayer control for multirotor UAVs equipped with a servo robot arm. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4014–4020. [Google Scholar]
- Lippiello, V.; Cacace, J.; Santamaria-Navarro, A.; Andrade-Cetto, J.; Trujillo, M.A.; Esteves, Y.R.; Viguria, A. Hybrid Visual Servoing With Hierarchical Task Composition for Aerial Manipulation. IEEE Robot. Autom. Lett. 2016, 1, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Rajappa, S.; Ryll, M.; Bulthoff, H.H.; Franchi, A. Modeling, control and design optimization for a fully-actuated hexa-rotor aerial vehicle with tilted propellers. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4006–4013. [Google Scholar]
- Ryll, M.; Bicego, D.; Franchi, A. Modeling and control of FAST-Hex: A fully-actuated by synchronized-tilting hexa-rotor. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1689–1694. [Google Scholar]
- Ryll, M.; Muscio, G.; Pierri, F.; Cataldi, E.; Antonelli, G.; Caccavale, F.; Bicego, D.; Franchi, A. 6D interaction control with aerial robots: The flying end-effector paradigm. Int. J. Robot. Res. 2019, 38, 1045–1062. [Google Scholar] [CrossRef] [Green Version]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfandler, P.; Angst, U.; Siegwart, R.; Nieto, J. An omni-directional aerial manipulation platform for contact-based inspection. In Proceedings of the Robotics: Science and Systems, Breisgau, Germany, 22–26 June 2019. [Google Scholar]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar]
- Lippiello, V.; Ruggiero, F. Cartesian Impedance Control of a UAV with a Robotic Arm. In Proceedings of the IFAC Proceedings Volumes, Dubrovnik, Croatia, 5–7 September 2012; Volume 45, pp. 704–709. [Google Scholar]





| Cartesian Manipulator | Compliant Joint Arm | ||
|---|---|---|---|
| Actuator features | Stall torque: 0.3 Nm Mass: 10 g, 120 RPM | Actuator features | Stall torque: 1.17 Nm Stiffness: 1.4 Nm/rad |
| Linear range | X–axis: 500 mm | Rotation range | ± 120° |
| Y–axis: 250 mm | Joint deflection | 30° | |
| Max. speed | 100 mm/s | Link length | 250 mm |
| Total mass | 0.85 kg (including battery–2S LiPo, 1500 mAh) | ||
| Structure | Mass [kg] | Ixx [kg·m2] | Iyy [kg·m2] | Izz [kg·m2] |
|---|---|---|---|---|
| Hexa-rotor | 1.27 | 1.9 × 10−2 | 1.8 × 10−2 | 3.0 × 10−2 |
| X–axis | 0.2 | 7.9 × 10−5 | 6.8 × 10−3 | 6.8 × 10−3 |
| Y–axis | 0.14 | 1.0 × 10−3 | 2.1 × 10−5 | 1.0 × 10−3 |
| Servo | 0.08 | 3.4 × 10−5 | 3.0 × 10−5 | 1.0 × 10−5 |
| Link | 0.09 | 6.0 × 10−4 | 6.0 × 10−4 | 1.1 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suarez, A.; Perez, M.; Heredia, G.; Ollero, A. Cartesian Aerial Manipulator with Compliant Arm. Appl. Sci. 2021, 11, 1001. https://doi.org/10.3390/app11031001
Suarez A, Perez M, Heredia G, Ollero A. Cartesian Aerial Manipulator with Compliant Arm. Applied Sciences. 2021; 11(3):1001. https://doi.org/10.3390/app11031001
Chicago/Turabian StyleSuarez, Alejandro, Manuel Perez, Guillermo Heredia, and Anibal Ollero. 2021. "Cartesian Aerial Manipulator with Compliant Arm" Applied Sciences 11, no. 3: 1001. https://doi.org/10.3390/app11031001
APA StyleSuarez, A., Perez, M., Heredia, G., & Ollero, A. (2021). Cartesian Aerial Manipulator with Compliant Arm. Applied Sciences, 11(3), 1001. https://doi.org/10.3390/app11031001






