Study of the Reaction 2-(p-Nitrophenyl)ethyl Bromide + OH− in Dimeric Micellar Solutions
Abstract
:1. Introduction
2. Results and Discussion
2.1. Characteristics of the Dimeric Micellar Reaction Media
| Surfactant | 103 × cmc/M a | α a | C*/M a | 103 × cmc/M b (NaOH 5 × 10−3 M) |
|---|---|---|---|---|
| 12-2-12,2Br- | 0.95 | 0.17 | 0.016 | 0.39 |
| 12-3-12,2Br- | 0.99 | 0.22 | 0.036 | 0.37 |
| 12-4-12,2Br- | 1.1 | 0.25 | 0.025 | 0.44 |
| 12-5-12,2Br- | 1.1 | 0.28 | 0.029 | 0.37 |
| 12-6-12,2Br- | 0.99 | 0.31 | 0.028 | 0.39 |
| 12-8-12,2Br- | 0.88 | 0.40 | 0.031 | 0.26 |
| 12-10-12,2Br- | 0.59 | 0.45 | 0.028 | 0.20 |
| 12-12-12,2Br- | 0.36 | 0.45 | 0.023 | 0.17 |

2.2. Kinetic Results


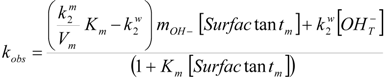
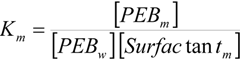
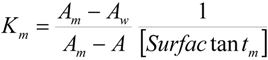

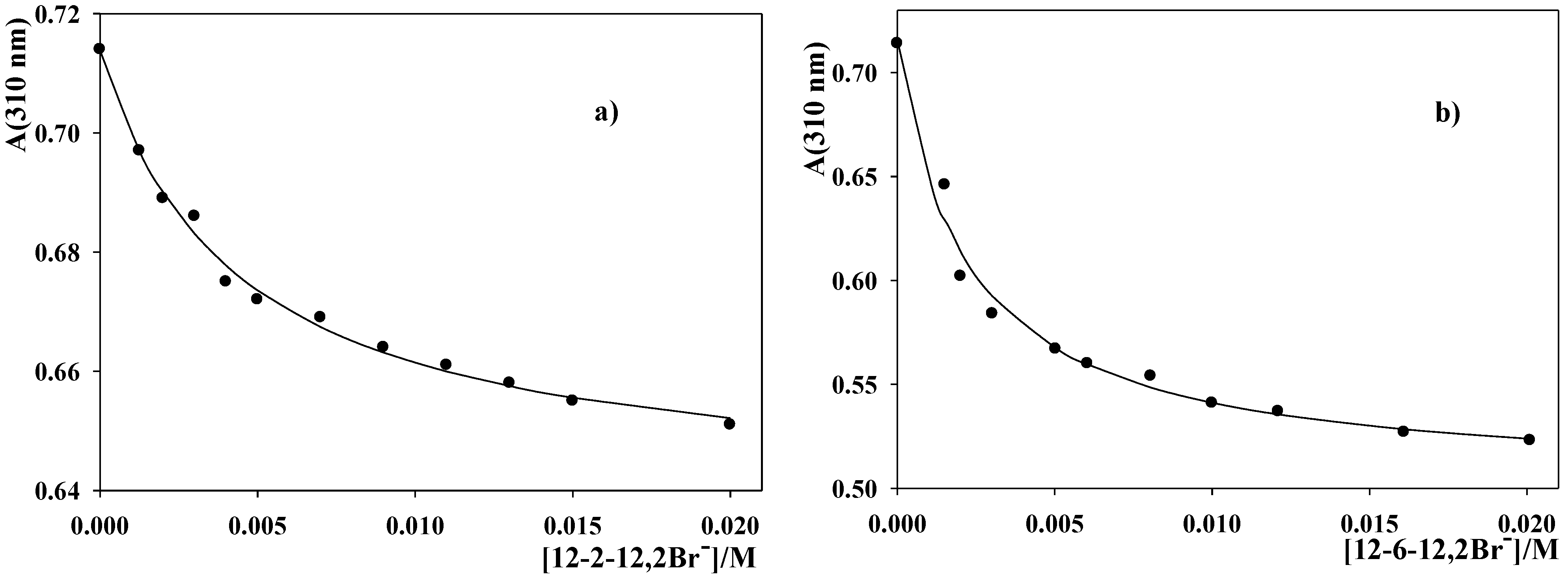
| Surfactant | 102 × k2m = (k2m/Vm)/s−1 | Km/M−1 |
|---|---|---|
| 12-2-12,2Br− | 1.3 ± 0.3 | 240 ± 70 (190 ± 20) |
| 12-3-12,2Br− | 1.3 ± 0.1 | 280 ± 40 (250 ± 30) |
| 12-4-12,2Br− | 1.9 ± 0.1 | 380 ± 50 (330 ± 30) |
| 12-5-12,2Br− | 2.2 ± 0.2 | 310 ± 50 (270 ± 30) |
| 12-6-12,2Br− | 1.7 ± 0.1 | 350 ± 50 (310 ± 30) |
| 12-8-12,2Br− | 1.7 ± 0.1 | 320 ± 40 (300 ± 40) |
| 12-10-12,2Br− | 1.9 ± 0.1 | 270 ± 50 (280 ± 30) |
| 12-12-12,2Br− | 2.2 ± 0.1 | 300 ± 50 (340 ± 30) |

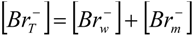


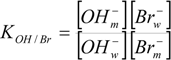
3. Experimental
3.1. Materials
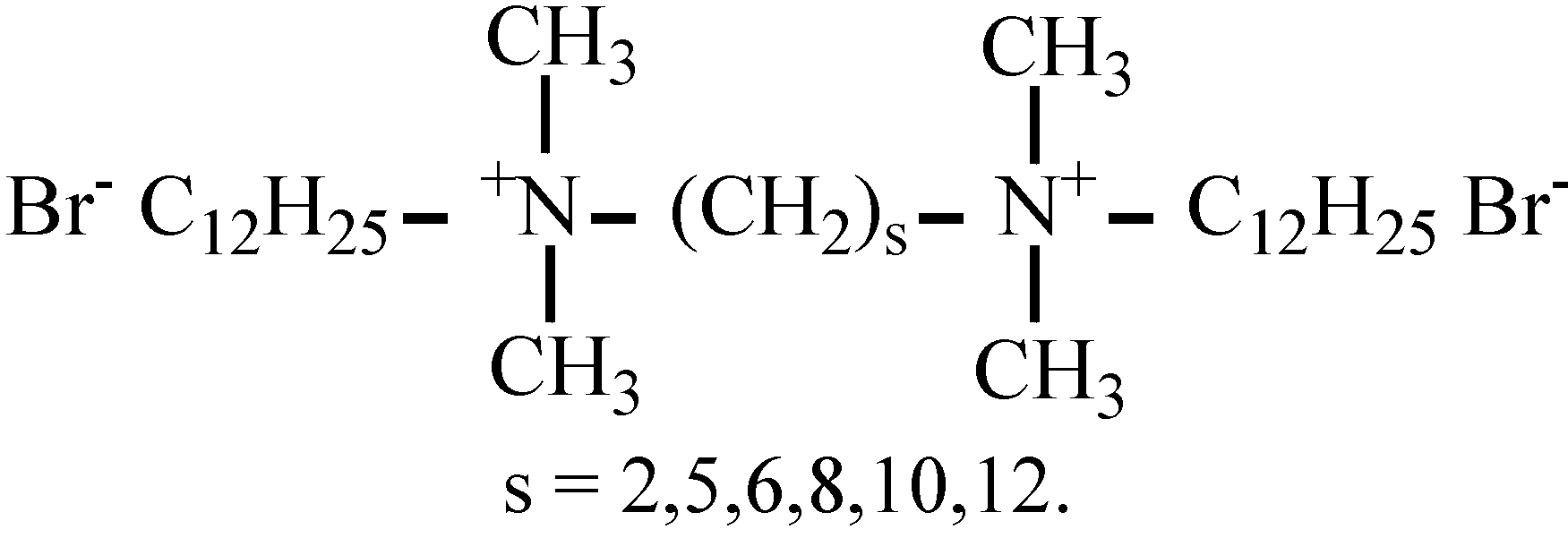
3.2. Steady-State Fluorescence Measurements
3.3. Kinetics
4. Conclusions
- - The equilibrium ion-exchange constant KOH/Br for the competition between the bromide and the hydroxide ions for the positively charged surface of the dimeric micelles is similar to those for conventional alkyltrimethylammonium bromide micelles.
- - KOH/Br does not substantially change when the morphological transition from spherical to elongated micelles happens.
- - The equilibrium binding constant of 2-(p-nitrophenyl)ethyl bromide molecules to the dimeric micelles is similar for all the dimeric micellar solutions. They are also similar to those found for conventional alkyltrimethylammonium bromide surfactants.
- - Dimeric micelles accelerate the reaction more than two orders of magnitude as compared to pure water.
Acknowledgements
References and Notes
- Evans, D.F.; Wenneström, H. The Colloidal Domain: Where Physics, Chemistry and Biology Meets; VCH: New York, NY, USA, 1994. [Google Scholar]
- da Rocha Pereira, R.; Zanette, D.; Nome, F. Application of the pseudophase-ion exchange model to microemulsions of anionic detergents. J. Phys. Chem. 1990, 94, 356–361. [Google Scholar] [CrossRef]
- Romsted, L.S. A general kinetic theory of rate enhancements for reactions between organic substrates and hydrophilic ions in micellar solutions. In Micellization, Solubilization and Microemulsion; Mittal, K.L., Ed.; Plenum: New York, NY, USA, 1977; Volume 2, p. 489. [Google Scholar]
- Bunton, C.A.; Nome, F.; Quina, F.H.; Romsted, L.S. Ion binding and reactivity at charged aqueous interfaces. Acc. Chem. Res. 1991, 24, 357–364. [Google Scholar] [CrossRef]
- Bunton, C.A.; Yao, J.; Romsted, L.S. Micellar catalysis, a useful misnomer. Curr. Opin. Colloid Interface Sci. 1997, 2, 622–628. [Google Scholar] [CrossRef]
- Savelli, G.; Germani, R.; Brinchi, L. Reactivity control by aqueous amphiphilic self-assembling systems. In Reactions and Synthesis in Surfactant System; Texter, J., Ed.; Dekker: New York, NY, USA, 2001; Volume 100, p. 175. [Google Scholar]
- Quina, F.H.; Politi, M.J.; Cuccovia, I.M.; Martins-Franchetti, S.M.; Chaimovich, H. Alkaline hydrolysis in micellar sodium dodecyl sulfate: The binding of –OH to anionic micelles. In Solution Behavior of Surfactants: Theoretical and Applied Aspect; Mittal, K.L.E., Fendler, J., Eds.; Plenum Pres: New York, NY, USA, 1982; Volume 2, p. 1125. [Google Scholar]
- Menger, F.M.; Keiper, J.N. Gemini surfactants. Angew. Chem. Int. Ed. 2000, 39, 1906–1920. [Google Scholar] [CrossRef]
- Zana, R. Dimeric and oligomeric surfactants. Behavior at interfaces and in aqueous solutions: A review. Adv. Colloid Interface Sci. 2002, 97, 205–253. [Google Scholar] [CrossRef]
- Zana, R.; Xia, J. Synthesis, Interfacial and Solution-Phase Behavior and Applications; M. Dekker Inc.: New York, NY, USA, 2004. [Google Scholar]
- Graciani, M.M.; Rodríguez, A.; Martín, V.I.; Moyá, M.L. Concentration and medium micellar kinetic effects caused by morphological transitions. Langmuir 2010, 26, 18659–18668. [Google Scholar]
- Wilk, K.A.; Burczyk, B. Micellar effects upon the reaction of hydroxide ions with 2-phenylethyl derivatives. J. Phys. Chem. 1989, 93, 8219–8223. [Google Scholar]
- Brinchi, L.; Germani, R.; Savelli, G.; Bunton, C.A. Elimination in sulfobetaine micelles. Effect of head group bulk. J. Phys. Org. Chem. 1999, 12, 890–894. [Google Scholar]
- Rodríguez, A.; Muñoz, M.; Graciani, M.M.; Moyá, M.L. Kinetic micellar effects in tetradecyltrimethylammonium bromide-pentanol micellar solutions. J. Colloid Interface Sci. 2002, 248, 455–461. [Google Scholar] [CrossRef]
- Quina, F.H.; Chaimovich, H. Ion Exchange in micellar solutions. 1. Conceptual framework for ion exchange in micellar solutions. J. Phys. Chem. 1979, 83, 1844–1850. [Google Scholar] [CrossRef]
- Bertoncini, C.R.A.; Nome, F.; Cerichelli, G.; Bunton, C.A. Effects of 1-butanol upon SN2 reactions in cationic micelles. A quantitative treatment. J. Phys. Chem. 1990, 94, 5875–5878. [Google Scholar] [CrossRef]
- Sepúlveda, L. Absorbances of solutions of cationic micelles and organic anions. J. Colloid Interface Sci. 1974, 46, 372–379. [Google Scholar] [CrossRef]
- Wilk, K.A. Salt effects on basic dehydrobromination reactions in nonfunctional micelles. J. Phys. Chem. 1989, 93, 7432–7435. [Google Scholar] [CrossRef]
- Wilk, K.A. Influence of N-hexadecyl-N,N,N-trimethyalmmonium nitrate on the dehydrobromination reaction of para-phenylethyl derivatives. Int. J. Chem. Kinet. 1990, 22, 253–259. [Google Scholar] [CrossRef]
- Wilk, K.A. Dehydrobromination reactions of para-substituted 2-phenylethyl derivatives in functional micelles. J. Phys. Chem. 1991, 95, 3405–3415. [Google Scholar] [CrossRef]
- Novaki, L.P.; El Seoud, O. Solvatochromism in aqueous micellar solutions: Effects of the molecular structures of solvatochromic probes and surfactants. Phys. Chem. Chem. Phys. 1999, 1, 1957–1964. [Google Scholar]
- Kuwamoto, K.; Asakawa, T.; Ohta, A.; Miyagishi, S. Degree of micelle ionization and micellar growth for Gemini surfactants detected by 6-methoxy N-(3-sulfopropylquinolinium) fluorescence quenching. Langmuir 2005, 21, 7691–7695. [Google Scholar] [CrossRef]
- Asakawa, T.; Kitano, H.; Ohta, A.; Miyagishi, S. Convenient estimation for counterion dissociation of cationic micelles using chloride-sensitive fluorescent probe. J. Colloid Interface Sci. 2001, 242, 284–287. [Google Scholar] [CrossRef]
- Graciani, M.M.; Rodríguez, A.; Moyá, M.L. Study of the reaction metil 4-nitrobenzenesulfonate and bromide ions in mixed single-chain-gemini mixed micellar solutions: Kinetic evidence for morphological transitions. J. Colloid Interface Sci. 2008, 328, 324–330. [Google Scholar] [CrossRef]
- Gerakis, A.M.; Koupparis, M.A. Physicochemical studies of the cetyltrimethylammonium bromide by using a bromide selective electrode. Talanta 1994, 41, 765–773. [Google Scholar] [CrossRef]
- Danino, D.; Talmon, Y.; Levy, H.; Beinert, G.; Zana, R. Branched threadlike micelles in an aqueous solution of a trimeric surfactant. Science 1995, 269, 1420–1421. [Google Scholar]
- Rodríguez, A.; Graciani, M.M.; Cordobés, F.; Moyá, M.L. Water-ethylene glycol cationic dimeric micellar solutions: Aggregation, micellar growth and characteristics as reaction media. J. Phys. Chem. B 2009, 113, 7767–7769. [Google Scholar]
- Oda, R.; Panizza, P.; Schmitz, M.; Lequeux, F. Direct evidence of the shear-induced structure of wormlike micelles: Gemini surfactant 12-2-12. Langmuir 1997, 13, 6407–6412. [Google Scholar] [CrossRef]
- Berheim-Groswasser, A.; Zana, R.; Talmon, Y. Sphere-to-cylinder transitions in aqueous micellar solutions of a dimeric (gemini) surfactant. J. Phys. Chem. B 2000, 104, 4005–4009. [Google Scholar] [CrossRef]
- Wetting, S.S.; Verral, R.E. Thermodynamic studies of aqueos m-s-m gemini surfactant systems. J. Colloid Interface Sci. 2001, 235, 310–316. [Google Scholar] [CrossRef]
- Kalyanasundaram, K.; Thomas, J.K. Environmental effects on vibronic band intensities in pyrene monomer fluorescence and their application in studies of micellar systems. J. Am. Chem. Soc. 1977, 99, 2039–2044. [Google Scholar] [CrossRef]
- Menger, F.M.; Keiper, J.S.; Mbadugha, B.N.A.; Caran, K.L.; Romsted, L.S. Interfacial composition of Gemini surfactant micelles determined by chemical trapping. Langmuir 2000, 16, 9095–9098. [Google Scholar] [CrossRef]
- Zana, R. Microviscosity of aqueous surfactant micelles. Effects of various parameters. J. Phys. Chem. B 1999, 103, 9117–9125. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Graciani, M.d.M.; Rodríguez, A.; Martín, V.I.; Moyá, M.L. Study of the Reaction 2-(p-Nitrophenyl)ethyl Bromide + OH− in Dimeric Micellar Solutions. Molecules 2011, 16, 9467-9479. https://doi.org/10.3390/molecules16119467
Graciani MdM, Rodríguez A, Martín VI, Moyá ML. Study of the Reaction 2-(p-Nitrophenyl)ethyl Bromide + OH− in Dimeric Micellar Solutions. Molecules. 2011; 16(11):9467-9479. https://doi.org/10.3390/molecules16119467
Chicago/Turabian StyleGraciani, María del Mar, Amalia Rodríguez, Victoria I. Martín, and María Luisa Moyá. 2011. "Study of the Reaction 2-(p-Nitrophenyl)ethyl Bromide + OH− in Dimeric Micellar Solutions" Molecules 16, no. 11: 9467-9479. https://doi.org/10.3390/molecules16119467
APA StyleGraciani, M. d. M., Rodríguez, A., Martín, V. I., & Moyá, M. L. (2011). Study of the Reaction 2-(p-Nitrophenyl)ethyl Bromide + OH− in Dimeric Micellar Solutions. Molecules, 16(11), 9467-9479. https://doi.org/10.3390/molecules16119467




