Accelerating a Geometrical Approximated PCA Algorithm Using AVX2 and CUDA
Abstract
:1. Introduction
- Plotting and visualizing data and potential structures in the data in lower dimensions;
- Applying stochastic models;
- Solving the “curse of dimensionality”;
- Facilitating the prediction and classification of the new data sets (i.e., query data sets with unknown class labels).
- We introduce four implementations of the gaPCA algorithm: three targeting multi-core CPUs developed in Matlab, Python and C++ and a GPU-accelerated CUDA implementation;
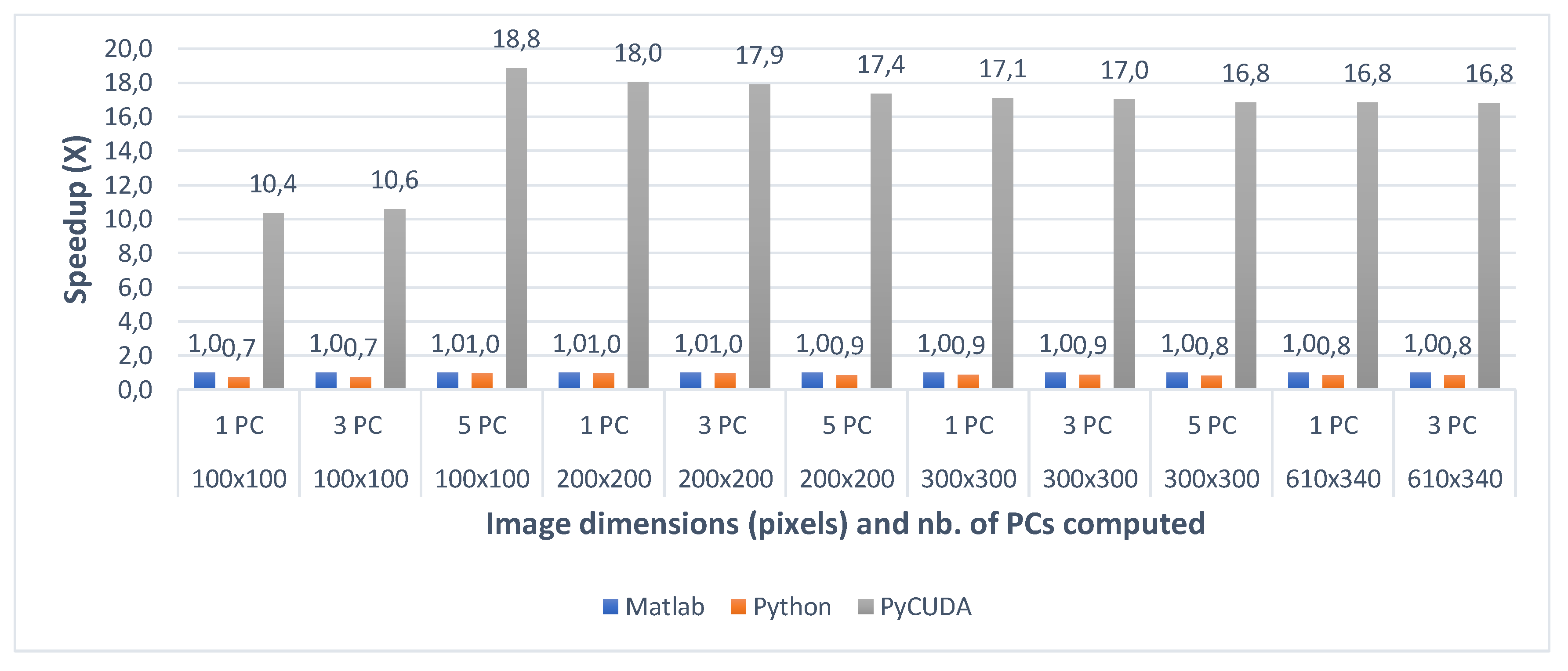
- A comparative assessment of the execution times of the Matlab, Python and PyCUDA multi-core implementations. Our experiments showed that our multi-core PyCUDA implementation is up to 18.84× faster than its Matlab equivalent;
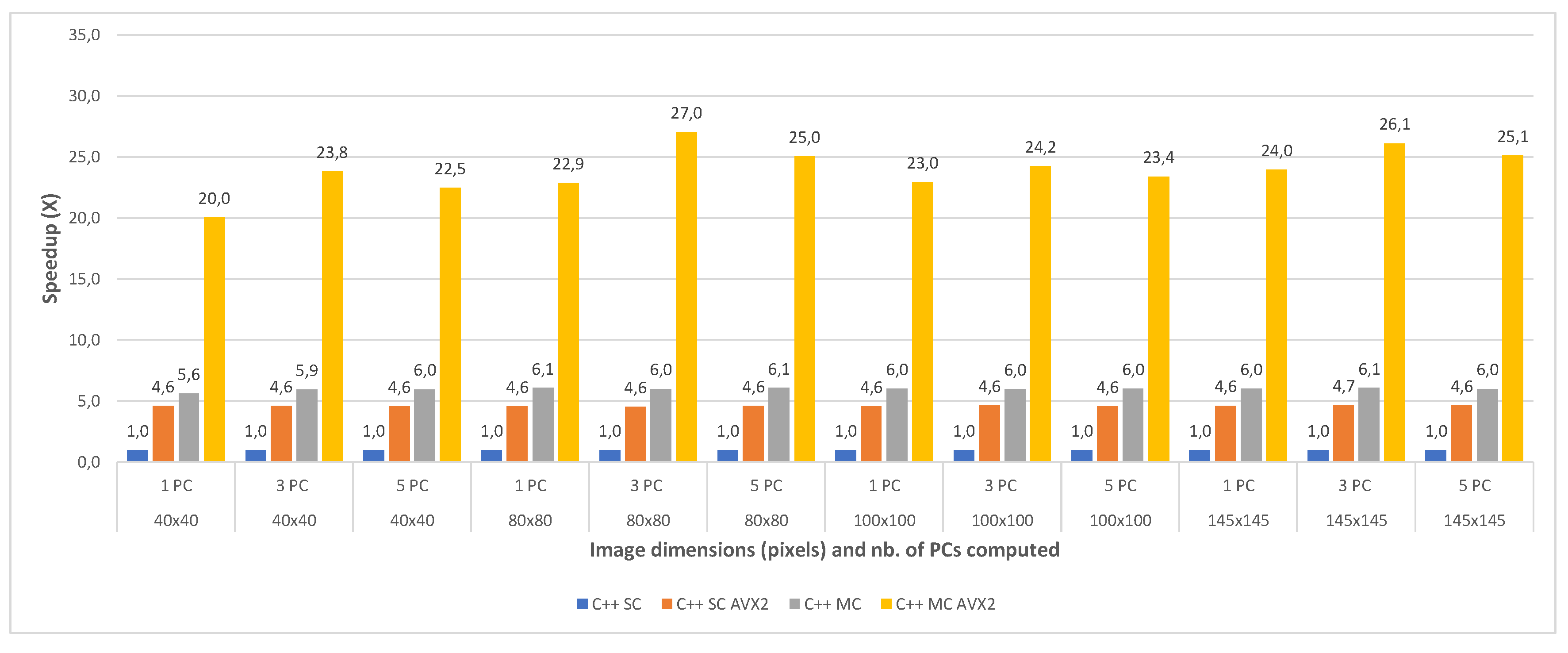
- A comparative assessment of the execution times of the C++ single-core, C++ multi-core, C++ single-core Advanced Vector eXtensions (AVX2) and C++ multi-core AVX2 implementations. The multi-core C++ AVX2 implementation proved to be up to 27.04× faster than the C++ single core one;
- Evaluation of the GPU accelerated CUDA implementation compared to the other implementations. Our experiments show that our CUDA Linux GPU implementation is the fastest, with speed ups up to 29.44× compared to the C++ single core baseline;
- Energy consumption analysis.
2. Background and Related Work
2.1. Projection Pursuit Algorithms
2.2. Parallel Implementations of PP Algorithms
3. Experimental Setup
3.1. Hardware
3.2. Software
- Matlab R2019b with Matlab Parallel Computing Toolbox
- Python 3.6.8
- NVIDIA CUDA toolkit release 10.1, V10.1.243
- PyCUDA version 2019.1.2
- gcc version 7.4.0
3.3. Datasets
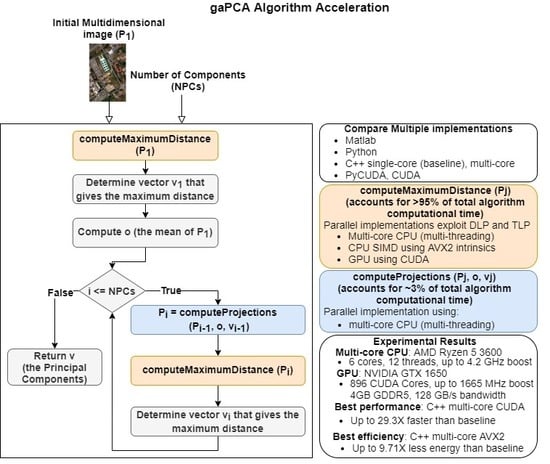
4. The gaPCA Algorithm
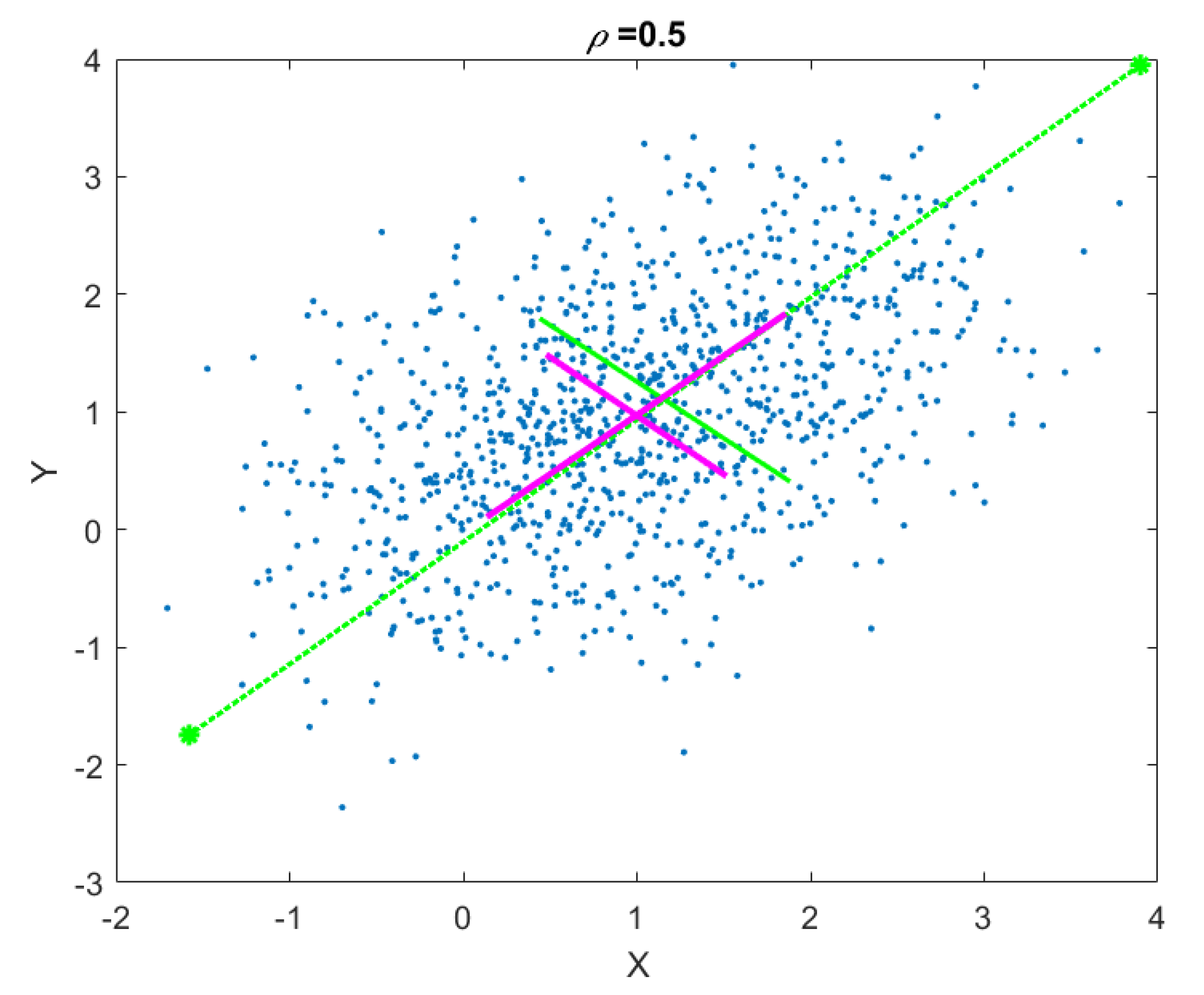
4.1. Description of the gaPCA Algorithm
4.2. gaPCA in Land Classification Applications
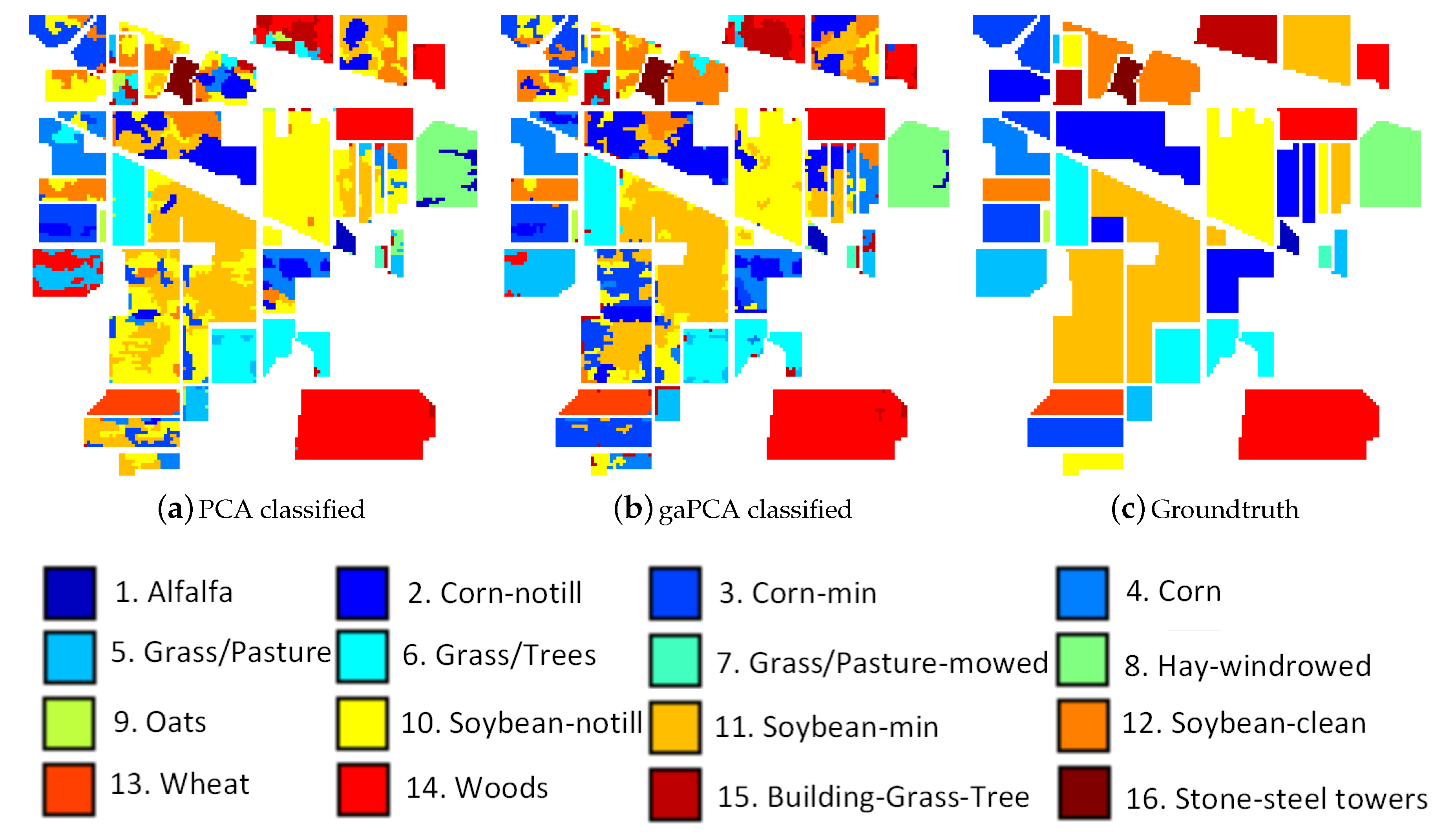
4.2.1. Indian Pines Dataset
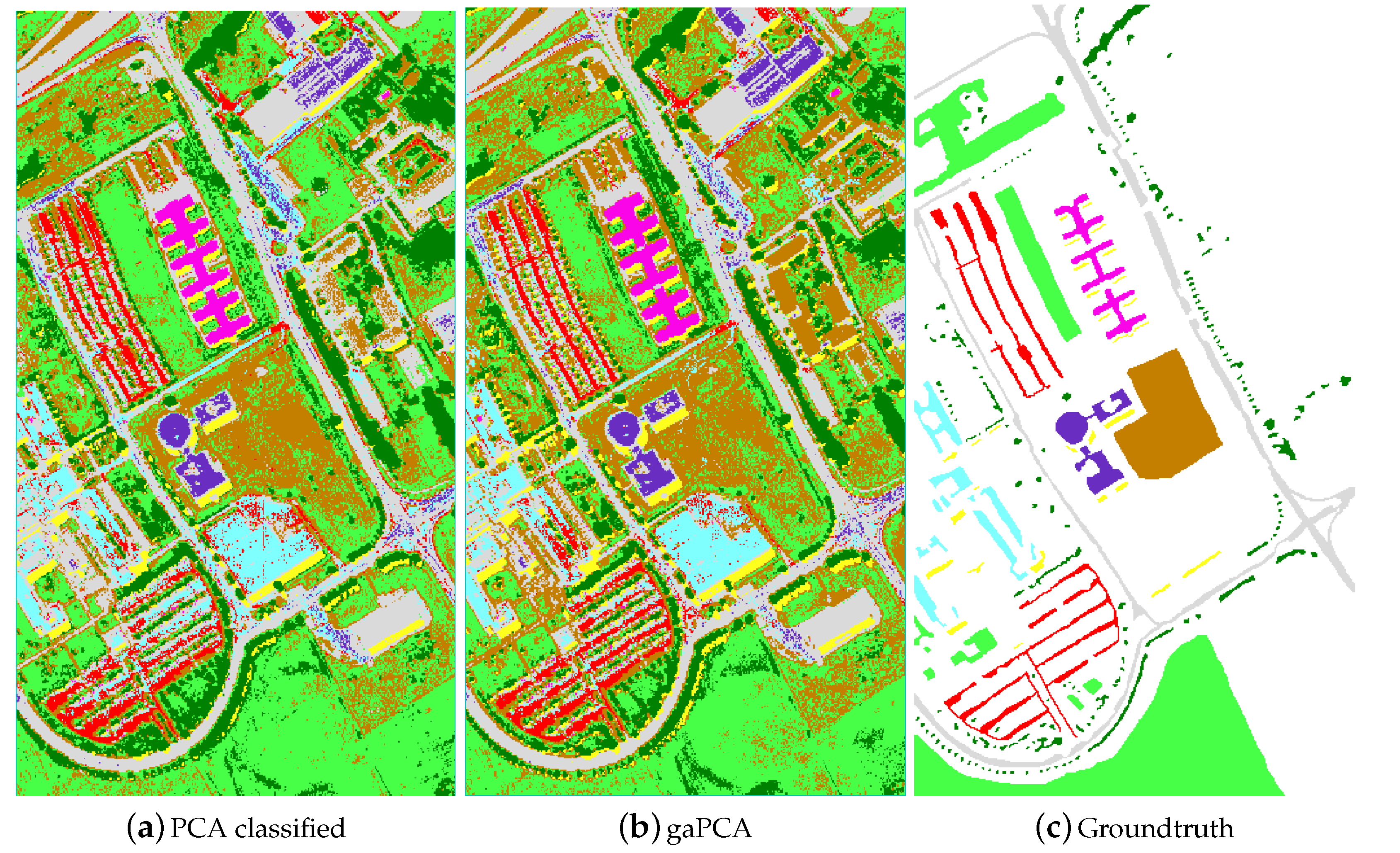
4.2.2. Pavia University Dataset
5. Parallelization of the gaPCA Algorithm
5.1. Matlab, Python and PyCUDA Implementations
CUDA Implementation
5.2. C++ Implementations
6. Results and Discussion
6.1. Execution Time Performance
6.1.1. Matlab vs. Python and PyCUDA
6.1.2. C++ Single Core vs. Multicore
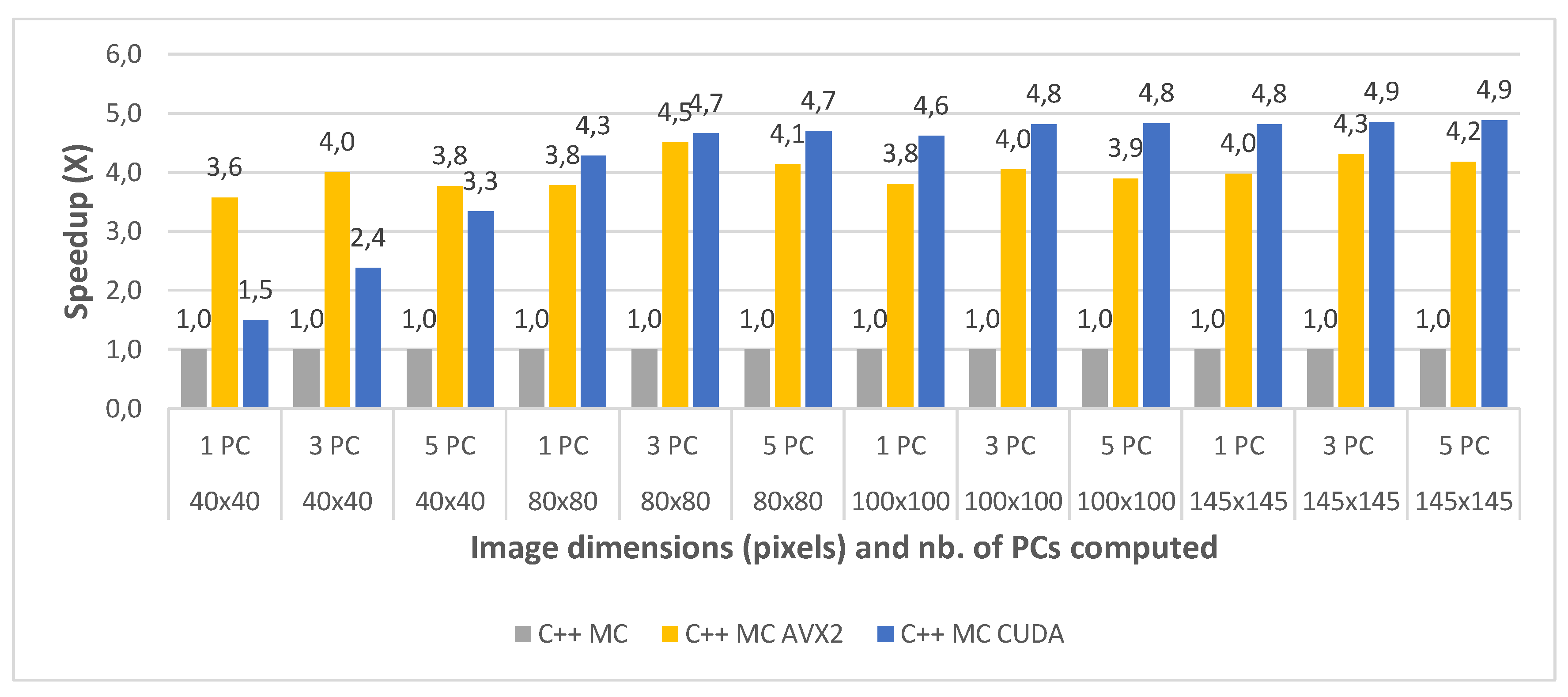
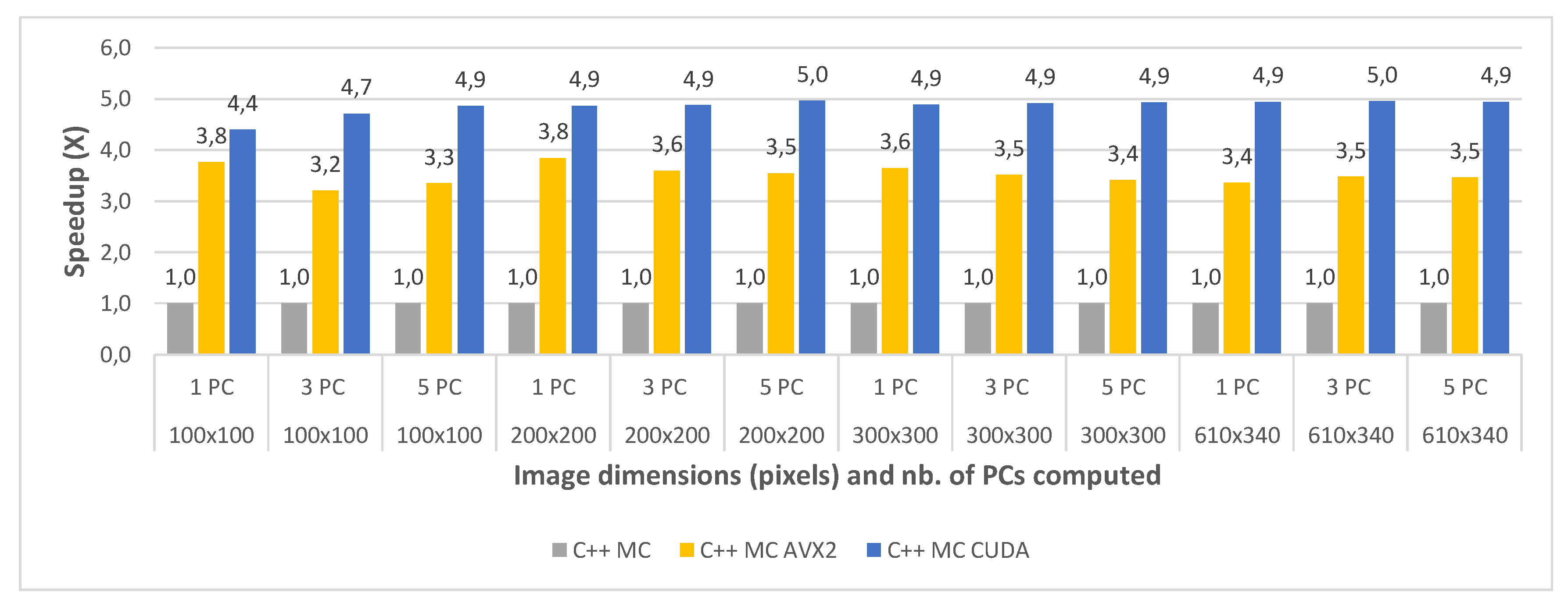
6.1.3. C++ Multi Core vs. CUDA
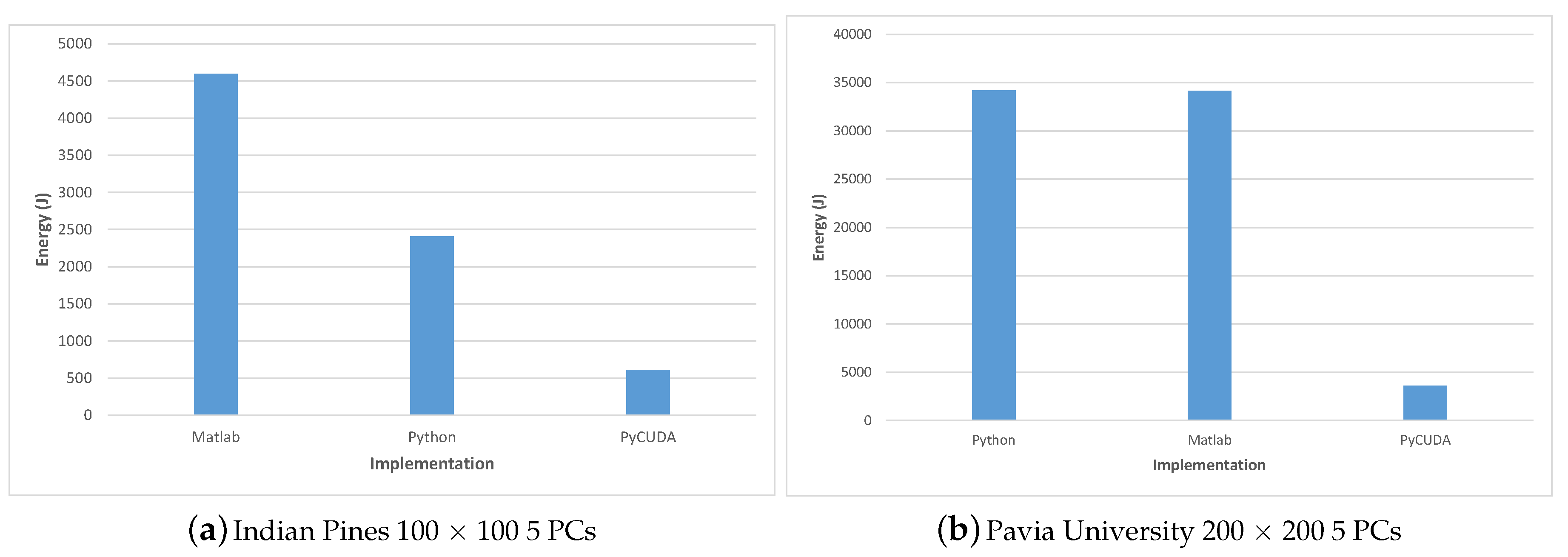
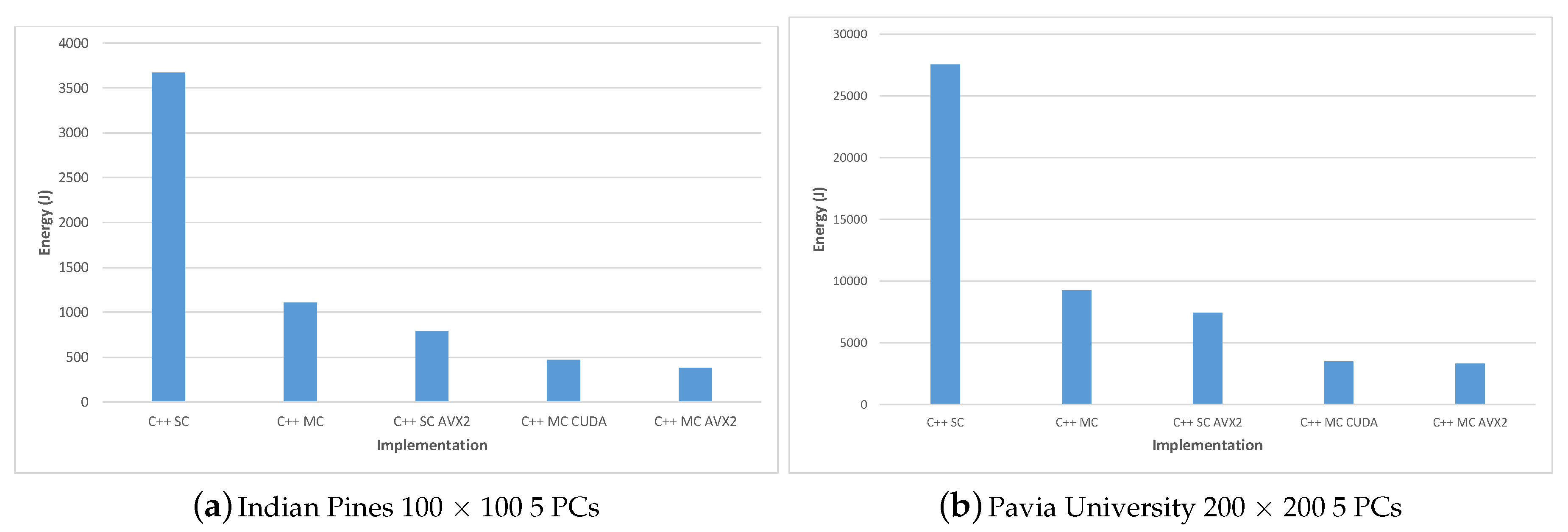
6.2. Energy Efficiency
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Code Listings for gaPCA Parallel Implementations
References
- Ali, A.; Qadir, J.; ur Rasool, R.; Sathiaseelan, A.; Zwitter, A.; Crowcroft, J. Big Data for Development: Applications and Techniques. Big Data Anal. 2016, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 2011. [Google Scholar]
- ESA: AVIRIS (Airborne Visible/Infrared Imaging Spectrometer). Available online: https://earth.esa.int/web/eoportal/airborne-sensors/aviris (accessed on 10 July 2019).
- Sorzano, C.O.S.; Vargas, J.; Montano, A.P. A Survey of Dimensionality Reduction Techniques. arXiv 2014, arXiv:1403.2877. [Google Scholar]
- van der Maaten, L.; Postma, E.O.; van den Herik, J. Dimensionality Reduction: A Comparative Review; BibSonomy: Wurzburg, Germany, 2009. [Google Scholar]
- Barcaru, A. Supervised Projection Pursuit—A Dimensionality Reduction Technique Optimized for Probabilistic Classification. Chemom. Intell. Lab. Syst. 2019, 194, 103867. [Google Scholar] [CrossRef]
- Friedman, J.H.; Tukey, J.W. A Projection Pursuit Algorithm for Exploratory Data Analysis. IEEE Trans. Comput. 1974, 100, 881–890. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.I. Hyperspectral Data Processing: Algorithm Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lindholm, E.; Nickolls, J.; Oberman, S.; Montrym, J. NVIDIA Tesla: A Unified Graphics and Computing Architecture. IEEE Micro 2008, 28, 39–55. [Google Scholar] [CrossRef]
- Zhang, W.; Du, X.; Huang, A.; Yin, H. Analysis and Comprehensive Evaluation of Water Use Efficiency in China. Water 2019, 11, 2620. [Google Scholar] [CrossRef] [Green Version]
- Meehan, S.W.; Orlova, D.Y.; Moore, W.A.; Parks, D.R.; Meehan, C.; Walther, G.; Herzenberg, L.A. Fully Automated (Unsupervised) Identification, Matching, Display and Quantitation of Subsets (Clusters) by Exhaustive Projection Pursuit Methods. U.S. Patent App. 16/401,067, 28 November 2019. [Google Scholar]
- Lee, Y.D.; Cook, D.; Park, J.W.; Lee, E.K. PPtree: Projection pursuit classification tree. Electron. J. Stat. 2013, 7, 1369–1386. [Google Scholar] [CrossRef]
- Lee, E.K.; Cook, D.; Klinke, S.; Lumley, T. Projection pursuit for exploratory supervised classification. J. Comput. Graph. Stat. 2005, 14, 831–846. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wan, J.; Gao, X. Toward the Health Measure for Open Source Software Ecosystem Via Projection Pursuit and Real-Coded Accelerated Genetic. IEEE Access 2019, 7, 87396–87409. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, X. Projection pursuit flood disaster classification assessment method based on multi-swarm cooperative particle swarm optimization. J. Water Resour. Prot. 2011, 3, 415. [Google Scholar] [CrossRef] [Green Version]
- YU, G.R.; YE, H.; XIA, Z.Q.; Zhao, X.Y. Improvement of Projection Pursuit Classification Model and Its Application in Evaluating Water Quality. J. Sichuan Univ. 2008, 6. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, H.; Li, S.; Yao, X.; Liu, M. Prediction of binding affinities to β1 isoform of human thyroid hormone receptor by genetic algorithm and projection pursuit regression. Bioorganic Med. Chem. Lett. 2007, 17, 2474–2482. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, H.; Yao, X.; Liu, M. Prediction of ozone tropospheric degradation rate constants by projection pursuit regression. Anal. Chim. Acta 2007, 589, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Aladjem, M. Projection pursuit mixture density estimation. IEEE Trans. Signal Process. 2005, 53, 4376–4383. [Google Scholar] [CrossRef]
- Touboul, J. Projection pursuit through relative entropy minimization. Commun. Stat. Simul. Comput. 2011, 40, 854–878. [Google Scholar] [CrossRef] [Green Version]
- Bali, J.L.; Boente, G.; Tyler, D.E.; Wang, J.L. Robust functional principal components: A projection-pursuit approach. Ann. Stat. 2011, 39, 2852–2882. [Google Scholar] [CrossRef] [Green Version]
- Loperfido, N. Skewness-based projection pursuit: A computational approach. Comput. Stat. Data Anal. 2018, 120, 42–57. [Google Scholar] [CrossRef]
- Choulakian, V. L1-norm projection pursuit principal component analysis. Comput. Stat. Data Anal. 2006, 50, 1441–1451. [Google Scholar] [CrossRef]
- Jimenez, L.O.; Landgrebe, D. Projection pursuit for high dimensional feature reduction: Parallel and sequential approaches. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 1, pp. 148–150. [Google Scholar]
- Peña, D.; Prieto, F.J.; Viladomat, J. Eigenvectors of a kurtosis matrix as interesting directions to reveal cluster structure. J. Multivar. Anal. 2010, 101, 1995–2007. [Google Scholar] [CrossRef] [Green Version]
- Croux, C.; Ruiz-Gazen, A. High breakdown estimators for principal components: The projection-pursuit approach revisited. J. Multivar. Anal. 2005, 95, 206–226. [Google Scholar] [CrossRef] [Green Version]
- Grochowski, M.; Duch, W. Projection pursuit constructive neural networks based on quality of projected clusters. In Proceedings of the International Conference on Artificial Neural Networks, Prague, Czech Republic, 3–6 September 2008; pp. 754–762. [Google Scholar]
- Grochowski, M.; Duch, W. Fast projection pursuit based on quality of projected clusters. In Proceedings of the International Conference on Adaptive and Natural Computing Algorithms, Ljubljana, Slovenia, 14–16 April 2011; pp. 89–97. [Google Scholar]
- Hui, G.; Lindsay, B.G. Projection pursuit via white noise matrices. Sankhya B 2010, 72, 123–153. [Google Scholar] [CrossRef]
- Kwatra, V.; Han, M. Fast Covariance Computation and Dimensionality Reduction for Sub-window Features in Images. In Proceedings of the 11th European Conference on Computer Vision: Part II, Crete, Greece, 5–11 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 156–169. [Google Scholar]
- Funatsu, N.; Kuroki, Y. Fast Parallel Processing using GPU in Computing L1-PCA Bases. In Proceedings of the TENCON 2010–2010 IEEE Region 10 Conference, Fukuoka, Japan, 21–24 November 2010; pp. 2087–2090. [Google Scholar]
- Jošth, R.; Antikainen, J.; Havel, J.; Herout, A.; Zemčík, P.; Hauta-Kasari, M. Real-time PCA calculation for spectral imaging (using SIMD and GP-GPU). J. Real Time Image Process. 2012, 7, 95–103. [Google Scholar] [CrossRef]
- Andrecut, M. Parallel GPU implementation of iterative PCA algorithms. J. Comput. Biol. 2009, 16, 1593–1599. [Google Scholar] [CrossRef] [Green Version]
- Melikyan, V.S.; Osipyan, H. Modified fast PCA algorithm on GPU architecture. In Proceedings of the IEEE East-West Design & Test Symposium (EWDTS 2014), Kiev, Ukraine, 26–29 September 2014; pp. 1–4. [Google Scholar]
- Antikainen, J.; Hauta-Kasari, M.; Jaaskelainen, T.; Parkkinen, J. Fast Non-Iterative PCA computation for spectral image analysis using GPU. In Proceedings of the Conference on Colour in Graphics, Imaging, and Vision. Society for Imaging Science and Technology, Joensuu, Finland, 14–17 June 2010; Volume 2010, pp. 554–559. [Google Scholar]
- Lazcano, R.; Madroñal, D.; Fabelo, H.; Ortega, S.; Salvador, R.; Callicó, G.M.; Juárez, E.; Sanz, C. Parallel implementation of an iterative PCA algorithm for hyperspectral images on a manycore platform. In Proceedings of the 2017 Conference on Design and Architectures for Signal and Image Processing (DASIP), Dresden, Germany, 27–29 September 2017; pp. 1–6. [Google Scholar]
- Lazcano, R.; Madroñal, D.; Fabelo, H.; Ortega, S.; Salvador, R.; Callico, G.; Juarez, E.; Sanz, C. Adaptation of an iterative PCA to a manycore architecture for hyperspectral image processing. J. Signal Process. Syst. 2019, 91, 759–771. [Google Scholar] [CrossRef]
- Martel, E.; Lazcano, R.; López, J.; Madroñal, D.; Salvador, R.; López, S.; Juarez, E.; Guerra, R.; Sanz, C.; Sarmiento, R. Implementation of the Principal Component Analysis onto High-Performance Computer facilities for hyperspectral dimensionality reduction: Results and comparisons. Remote Sens. 2018, 10, 864. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, D.; Gonzalez, C.; Mozos, D.; Lopez, S. FPGA implementation of the Principal Component Analysis algorithm for dimensionality reduction of hyperspectral images. J. Real Time Image Process. 2016. [Google Scholar] [CrossRef]
- Du, H.; Qi, H. An FPGA implementation of parallel ICA for dimensionality reduction in hyperspectral images. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 5, pp. 3257–3260. [Google Scholar]
- Mansoori, M.A.; Casu, M.R. Efficient FPGA Implementation of PCA Algorithm for Large Data using High Level Synthesis. In Proceedings of the 2019 15th Conference on Ph. D Research in Microelectronics and Electronics (PRIME), Lausanne, Switzerland, 15–18 July 2019; pp. 65–68. [Google Scholar]
- Wu, Z.; Li, Y.; Plaza, A.; Li, J.; Xiao, F.; Wei, Z. Parallel and distributed dimensionality reduction of hyperspectral data on cloud computing architectures. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 9, 2270–2278. [Google Scholar] [CrossRef]
- AMD Ryzen 5 3600 Processor Specifications. Available online: https://www.amd.com/en/products/cpu/amd-ryzen-5-3600 (accessed on 17 September 2019).
- GeForce GTX 1650. Available online: https://www.nvidia.com/ro-ro/geforce/graphics-cards/gtx-1650/ (accessed on 17 September 2019).
- Peaktech. Available online: https://www.peaktech.de/productdetail/kategorie/digital-leistungszangenmessgeraet/produkt/peaktech-1660.html/ (accessed on 24 January 2020).
- Pavia University Hyperspectral Remote Sensing Scene. Available online: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Pavia_University (accessed on 7 August 2019).
- Indian Pines Hyperspectral Remote Sensing Scene. Available online: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Indian_Pines (accessed on 7 August 2019).
- Machidon, A.L.; Ciobanu, C.B.; Machidon, O.M.; Ogrutan, P.L. On Parallelizing Geometrical PCA Approximation. In Proceedings of the 2019 18th RoEduNet Conference: Networking in Education and Research (RoEduNet), Galați, Romania, 10–12 October 2019; pp. 1–6. [Google Scholar]
- Härdle, W.; Klinke, S.; Turlach, B.A. XploRe: An Interactive Statistical Computing Environment; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dayal, M. A New Algorithm for Exploratory Projection Pursuit. arXiv 2018, arXiv:1112.4321. [Google Scholar]
- Ifarraguerri, A.; Chang, C.I. Unsupervised hyperspectral image analysis with projection pursuit. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2529–2538. [Google Scholar]
- Machidon, A.; Coliban, R.; Machidon, O.; Ivanovici, M. Maximum Distance-based PCA Approximation for Hyperspectral Image Analysis and Visualization. In Proceedings of the 2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, Greece, 4–6 July 2018. [Google Scholar] [CrossRef]
- Machidon, A.L.; Machidon, O.M.; Ogrutan, P.L. Face Recognition Using Eigenfaces, Geometrical PCA Approximation and Neural Networks. In Proceedings of the 2019 42nd International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 3–5 July 2019; pp. 80–83. [Google Scholar] [CrossRef]
- Machidon, A.L.; Del Frate, F.; Picchiani, M.; Machidon, O.M.; Ogrutan, P.L. Geometrical Approximated Principal Component Analysis for Hyperspectral Image Analysis. Remote Sens. 2020, 12, 1698. [Google Scholar] [CrossRef]
- ENVI Image Analysis Software. Available online: https://www.harrisgeospatial.com/Software-Technology/ENVI (accessed on 24 April 2020).
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef] [PubMed]
- PyCUDA. Available online: https://mathema.tician.de/software/pycuda/ (accessed on 19 August 2019).
- Python. Available online: https://www.python.org/ (accessed on 1 August 2019).
- Numba. Available online: https://numba.pydata.org/ (accessed on 1 August 2019).
- LLVM. Available online: https://llvm.org/ (accessed on 22 January 2019).
- OpenMP. Available online: https://www.openmp.org/ (accessed on 19 December 2019).
- Peleg, A.; Weiser, U. MMX technology extension to the Intel architecture. IEEE Micro 1996, 16, 42–50. [Google Scholar] [CrossRef]
- Raman, S.K.; Pentkovski, V.; Keshava, J. Implementing streaming SIMD extensions on the Pentium III processor. IEEE Micro 2000, 20, 47–57. [Google Scholar] [CrossRef]
- Lomont, C. Introduction to intel advanced vector extensions. Intel White Pap. 2011, 23. [Google Scholar]
- avx2. Available online: https://software.intel.com/en-us/cpp-compiler-developer-guide-and-reference-overview-intrinsics-for-intel-advanced-vector-extensions-2-intel-avx2-instructions/ (accessed on 22 January 2019).
- Kukunas, J. Power and Performance: Software Analysis and Optimization; Morgan Kaufmann: San Francisco, CA, USA, 2015. [Google Scholar]
- Luo, Y.; John, L.K.; Eeckhout, L. Self-monitored adaptive cache warm-up for microprocessor simulation. In Proceedings of the 16th Symposium on Computer Architecture and High Performance Computing, Foz Do Iguacu, Brazil, 27–29 October 2004; pp. 10–17. [Google Scholar] [CrossRef]


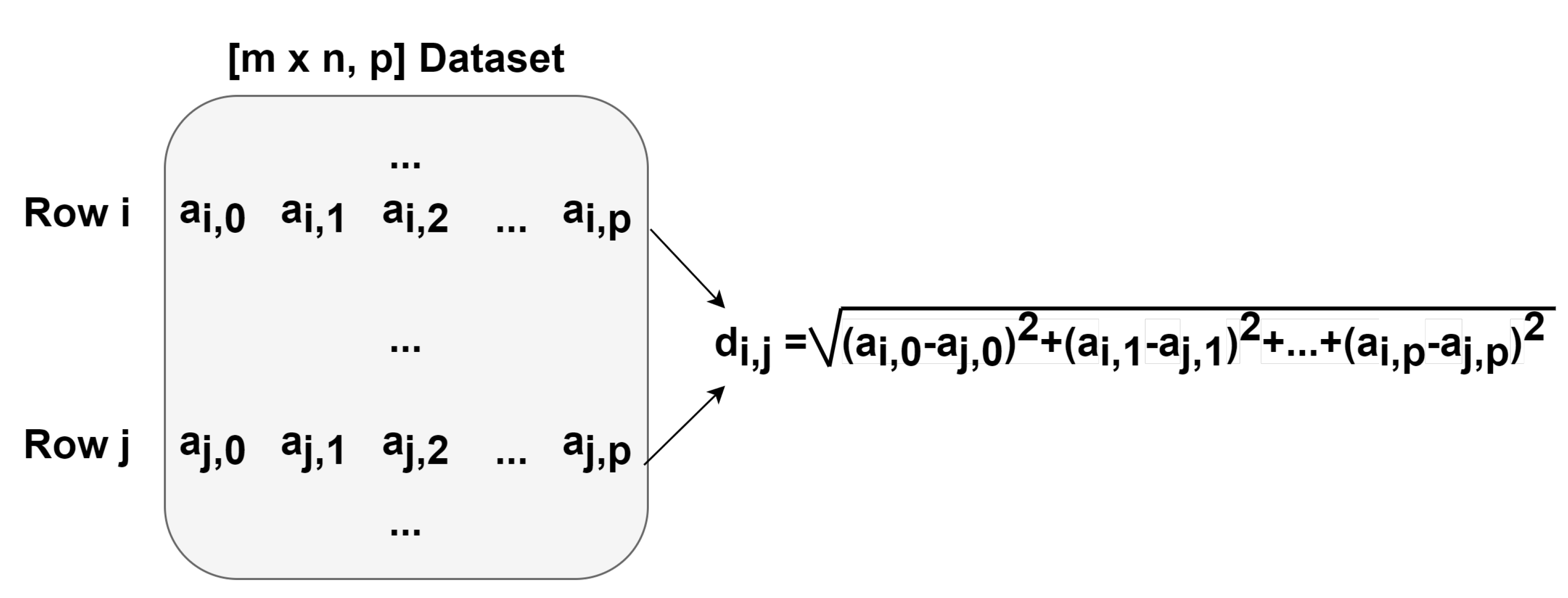
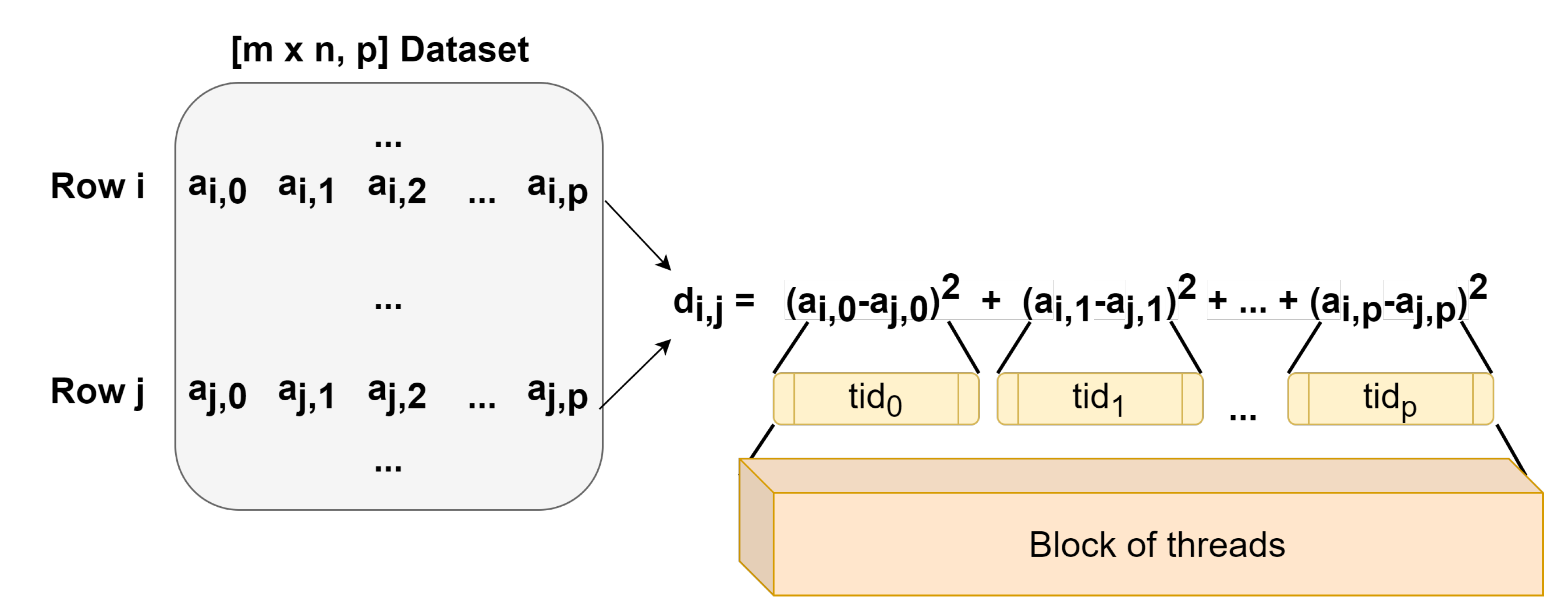



| Proccesor | AMD Ryzen 5 3600 |
|---|---|
| Cores | 6 |
| Threads | 12 |
| Base Clock | 3.6 GHz |
| Maximum Boost Clock | 4.2 GHz |
| Memory | 384KB L1, 3MB L2, 32MB L3 |
| GPU | GeForce GTX 1650 |
|---|---|
| CUDA Cores | 896 |
| Processor Base Clock | 1485 MHz |
| Processor Max Boost Clock | 1665 MHz |
| Memory | 4GB GDDR5 |
| Memory Bandwidth | 128 GB/s |
| Class | Training Pixels | PCA ML | gaPCA ML | PCA SVM | gaPCA SVM |
|---|---|---|---|---|---|
| Alfalfa | 32 | 98.7 | 80.5 | 18.2 | 18.2 |
| Corn notill | 1145 | 30.6 | 47.6 | 65.2 | 69.3 |
| Corn mintill | 595 | 51.6 | 69.2 | 34.9 | 46.1 |
| Corn | 167 | 84.9 | 100 | 31.4 | 37.7 |
| Grass pasture | 328 | 55.7 | 80.5 | 64.6 | 71.9 |
| Grass trees | 463 | 96.1 | 90.6 | 91.2 | 92.5 |
| Grass pasture mowed | 19 | 68.3 | 71.7 | 60 | 60 |
| Hay windrowed | 528 | 88.5 | 96.7 | 99.5 | 99.6 |
| Oats | 20 | 100 | 96.9 | 15.6 | 6.3 |
| Soybean notill | 681 | 83.7 | 77.1 | 40.9 | 56.1 |
| Soybean mintill | 1831 | 46.6 | 47.7 | 79.4 | 78.3 |
| Soybean clean | 457 | 36.9 | 77.7 | 11.8 | 36.1 |
| Wheat | 150 | 97.2 | 97 | 91.1 | 93.1 |
| Woods | 884 | 98.7 | 96.9 | 97.3 | 97.3 |
| Buildings Drives | 263 | 33.7 | 61.4 | 45.5 | 52.1 |
| Stone Steel Towers | 103 | 100 | 100 | 95.5 | 97.2 |
| zML = 25.1 (signif = yes) | OA(%) | 62.1 | 70.2 | 67.2 | 72.1 |
| zSVM = 24.8 (signif = yes) | Kappa | 0.57 | 0.67 | 0.62 | 0.68 |
| Class | Training Pixels | PCA ML | gaPCA ML | PCA SVM | gaPCA SVM |
|---|---|---|---|---|---|
| Asphalt (grey) | 1766 | 60.5 | 61.5 | 67.2 | 78.3 |
| Meadows (light green) | 2535 | 68.3 | 80 | 65 | 86.9 |
| Gravel (cyan) | 923 | 100 | 100 | 33.3 | 40 |
| Trees (dark green) | 599 | 88.2 | 89.7 | 100 | 67.7 |
| Metal sheets (magenta) | 872 | 100 | 100 | 100 | 100 |
| Bare soil (brown) | 1579 | 77.8 | 79.4 | 53.2 | 68.3 |
| Bitumen (purple) | 565 | 89.7 | 89.7 | 89.7 | 55.2 |
| Bricks (red) | 1474 | 68.3 | 72 | 81.7 | 86.6 |
| Shadows (yellow) | 876 | 100 | 100 | 100 | 100 |
| zML = 4.87 (signif = yes) | OA(%) | 72.2 | 78 | 69 | 78 |
| zSVM = 5.97 (signif = yes) | Kappa | 0.65 | 0.72 | 0.61 | 0.72 |
| Class | True | False |
|---|---|---|
| Asphalt (PCA) | 60.5 Asphalt | 29.5 Bitumen |
| Asphalt (gaPCA) | 61.5 Asphalt | 21.8 Bitumen |
| Meadows (PCA) | 68.3 Meadows | 25.8 Bare soil |
| Meadows (gaPCA) | 80 Meadows | 17.6 Bare soil |
| Bricks (PCA) | 68.3 Bricks | 25.6 Gravel |
| Bricks (gaPCA) | 72 Bricks | 24.3 Gravel |
| Crop Size | No. of PCs | Matlab | Python | PyCUDA |
|---|---|---|---|---|
| 40 × 40 | 1 | 0.275 | 1.260 | 0.153 |
| 40 × 40 | 3 | 0.832 | 2.802 | 0.449 |
| 40 × 40 | 5 | 1.448 | 3.519 | 0.756 |
| 80 × 80 | 1 | 8.326 | 6.797 | 0.769 |
| 80 × 80 | 3 | 24.678 | 18.265 | 2.319 |
| 80 × 80 | 5 | 40.990 | 29.333 | 3.884 |
| 100 × 100 | 1 | 22.090 | 14.531 | 1.592 |
| 100 × 100 | 3 | 66.377 | 41.929 | 4.843 |
| 100 × 100 | 5 | 110.449 | 68.647 | 8.004 |
| 145 × 145 | 1 | 104.134 | 64.498 | 5.843 |
| 145 × 145 | 3 | 313.070 | 181.152 | 18.036 |
| 145 × 145 | 5 | 521.057 | 298.212 | 30.137 |
| Crop Size | No. of PCs | Matlab | Python | PyCUDA |
|---|---|---|---|---|
| 100 × 100 | 1 | 9.507 | 13.476 | 0.866 |
| 100 × 100 | 3 | 28.439 | 39.126 | 2.745 |
| 100 × 100 | 5 | 47.580 | 64.131 | 4.497 |
| 200 × 200 | 1 | 195.801 | 204.855 | 10.391 |
| 200 × 200 | 3 | 575.083 | 601.477 | 31.884 |
| 200 × 200 | 5 | 957.494 | 992.193 | 53.496 |
| 300 × 300 | 1 | 883.342 | 1027.397 | 50.905 |
| 300 × 300 | 3 | 2653.649 | 3036.512 | 155.068 |
| 300 × 300 | 5 | 4432.107 | 5030.831 | 260.203 |
| 610 × 340 | 1 | 4501.181 | 5453.752 | 267.402 |
| 610 × 340 | 3 | 13,588.632 | 16,035.242 | 806.866 |
| 610 × 340 | 5 | 22,675.191 | 26,702.160 | 1347.312 |
| Crop Size | No. of PCs | C++ SC | C++ SC AVX2 | C++ MC | C++ MC AVX2 |
|---|---|---|---|---|---|
| 40 × 40 | 1 | 0.947 | 0.206 | 0.169 | 0.047 |
| 40 × 40 | 3 | 2.858 | 0.620 | 0.480 | 0.120 |
| 40 × 40 | 5 | 4.749 | 1.035 | 0.796 | 0.211 |
| 80 × 80 | 1 | 15.147 | 3.317 | 2.502 | 0.663 |
| 80 × 80 | 3 | 45.274 | 9.942 | 7.534 | 1.674 |
| 80 × 80 | 5 | 75.451 | 16.389 | 12.457 | 3.012 |
| 100 × 100 | 1 | 36.834 | 8.070 | 6.108 | 1.605 |
| 100 × 100 | 3 | 110.570 | 23.834 | 18.452 | 4.560 |
| 100 × 100 | 5 | 184.189 | 40.409 | 30.627 | 7.871 |
| 145 × 145 | 1 | 162.853 | 35.185 | 27.017 | 6.797 |
| 145 × 145 | 3 | 491.379 | 105.084 | 81.027 | 18.816 |
| 145 × 145 | 5 | 814.208 | 175.127 | 135.510 | 32.400 |
| Crop Size | No. of PCs | C++ SC | C++ SC AVX2 | C++ MC | C++ MC AVX2 |
|---|---|---|---|---|---|
| 100 × 100 | 1 | 18.373 | 4.63084 | 3.030 | 0.805 |
| 100 × 100 | 3 | 55.185 | 13.9219 | 9.025 | 2.814 |
| 100 × 100 | 5 | 91.666 | 23.1688 | 15.277 | 4.565 |
| 200 × 200 | 1 | 293.311 | 74.8406 | 48.650 | 12.652 |
| 200 × 200 | 3 | 880.324 | 222.279 | 144.703 | 40.199 |
| 200 × 200 | 5 | 1472.080 | 371.005 | 243.616 | 68.642 |
| 300 × 300 | 1 | 1488.370 | 387.629 | 247.666 | 67.894 |
| 300 × 300 | 3 | 4489.640 | 1165.61 | 741.890 | 211.110 |
| 300 × 300 | 5 | 7438.200 | 1933.44 | 1240.140 | 363.606 |
| 610 × 340 | 1 | 7956.360 | 2053.12 | 1322.530 | 393.734 |
| 610 × 340 | 3 | 23,962.794 | 6202.35 | 3975.840 | 1144.730 |
| 610 × 340 | 5 | 40,190.385 | 10,408.8 | 6605.060 | 1905.980 |
| Crop Size | No. of PCs | C++ MC | C++ MC AVX2 | C++ MC CUDA |
|---|---|---|---|---|
| 40 × 40 | 1 | 0.169 | 0.047 | 0.113 |
| 40 × 40 | 3 | 0.480 | 0.120 | 0.202 |
| 40 × 40 | 5 | 0.796 | 0.211 | 0.239 |
| 80 × 80 | 1 | 2.502 | 0.663 | 0.585 |
| 80 × 80 | 3 | 7.534 | 1.674 | 1.619 |
| 80 × 80 | 5 | 12.457 | 3.012 | 2.654 |
| 100 × 100 | 1 | 6.108 | 1.605 | 1.324 |
| 100 × 100 | 3 | 18.452 | 4.560 | 3.835 |
| 100 × 100 | 5 | 30.627 | 7.871 | 6.343 |
| 145 × 145 | 1 | 27.017 | 6.797 | 5.609 |
| 145 × 145 | 3 | 81.027 | 18.816 | 16.690 |
| 145 × 145 | 5 | 135.510 | 32.400 | 27.770 |
| Crop Size | No. of PCs | C++ MC | C++ MC AVX2 | C++ MC CUDA |
|---|---|---|---|---|
| 100 × 100 | 1 | 3.030 | 0.805 | 0.689 |
| 100 × 100 | 3 | 9.025 | 2.814 | 1.916 |
| 100 × 100 | 5 | 15.277 | 4.565 | 3.143 |
| 200 × 200 | 1 | 48.650 | 12.652 | 9.989 |
| 200 × 200 | 3 | 144.703 | 40.199 | 29.699 |
| 200 × 200 | 5 | 243.616 | 68.642 | 49.068 |
| 300 × 300 | 1 | 247.666 | 67.894 | 50.700 |
| 300 × 300 | 3 | 741.890 | 211.110 | 151.082 |
| 300 × 300 | 5 | 1240.140 | 363.606 | 251.730 |
| 610 × 340 | 1 | 1322.530 | 393.734 | 267.495 |
| 610 × 340 | 3 | 3975.840 | 1144.730 | 801.950 |
| 610 × 340 | 5 | 6605.060 | 1905.980 | 1336.010 |
| Dataset | Size | No. of PCs | Implementation | Energy (J) | Time (s) |
|---|---|---|---|---|---|
| Indian | 100 × 100 | 5 | Matlab | 4595.29 | 110.449 |
| Python | 2409.06 | 68.647 | |||
| PyCUDA | 609.23 | 8.004 | |||
| Pavia U | 200 × 200 | 5 | Matlab | 34,139.77 | 957.494 |
| Python | 34,192.04 | 992.193 | |||
| PyCUDA | 3589.8 | 53.496 |
| Dataset | Size | No. of PCs | Implementation | Energy (J) | Time (s) |
|---|---|---|---|---|---|
| Indian | 100 × 100 | 5 | C++ SC | 3672 | 184.189 |
| C++ MC | 1108.75 | 30.627 | |||
| C++ SC AVX2 | 792 | 40.409 | |||
| C++ MC CUDA | 471.43 | 6.343 | |||
| C++ MC AVX2 | 378 | 7.871 | |||
| Pavia U | 200 × 200 | 5 | C++ SC | 27,512.87 | 1472.080 |
| C++ MC | 9242.40 | 243.616 | |||
| C++ SC AVX2 | 7431.87 | 371.005 | |||
| C++ MC CUDA | 3491.43 | 49.068 | |||
| C++ MC AVX2 | 3328.63 | 68.642 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machidon, A.L.; Machidon, O.M.; Ciobanu, C.B.; Ogrutan, P.L. Accelerating a Geometrical Approximated PCA Algorithm Using AVX2 and CUDA. Remote Sens. 2020, 12, 1918. https://doi.org/10.3390/rs12121918
Machidon AL, Machidon OM, Ciobanu CB, Ogrutan PL. Accelerating a Geometrical Approximated PCA Algorithm Using AVX2 and CUDA. Remote Sensing. 2020; 12(12):1918. https://doi.org/10.3390/rs12121918
Chicago/Turabian StyleMachidon, Alina L., Octavian M. Machidon, Cătălin B. Ciobanu, and Petre L. Ogrutan. 2020. "Accelerating a Geometrical Approximated PCA Algorithm Using AVX2 and CUDA" Remote Sensing 12, no. 12: 1918. https://doi.org/10.3390/rs12121918