Numerical Calculation and 3-D Imaging of the Arrhenius Temperature Integral
Abstract
:1. Introduction
2. Theory
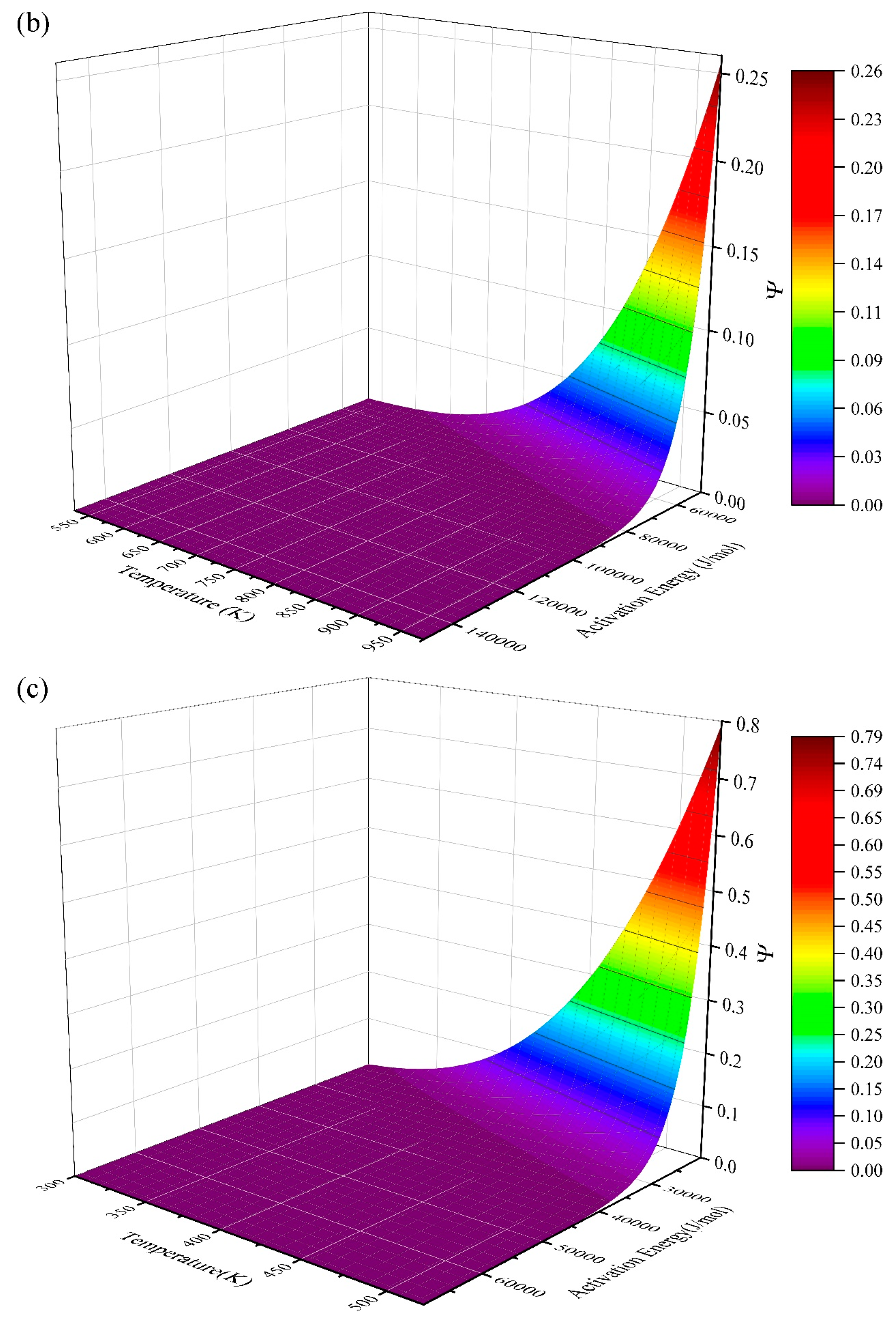
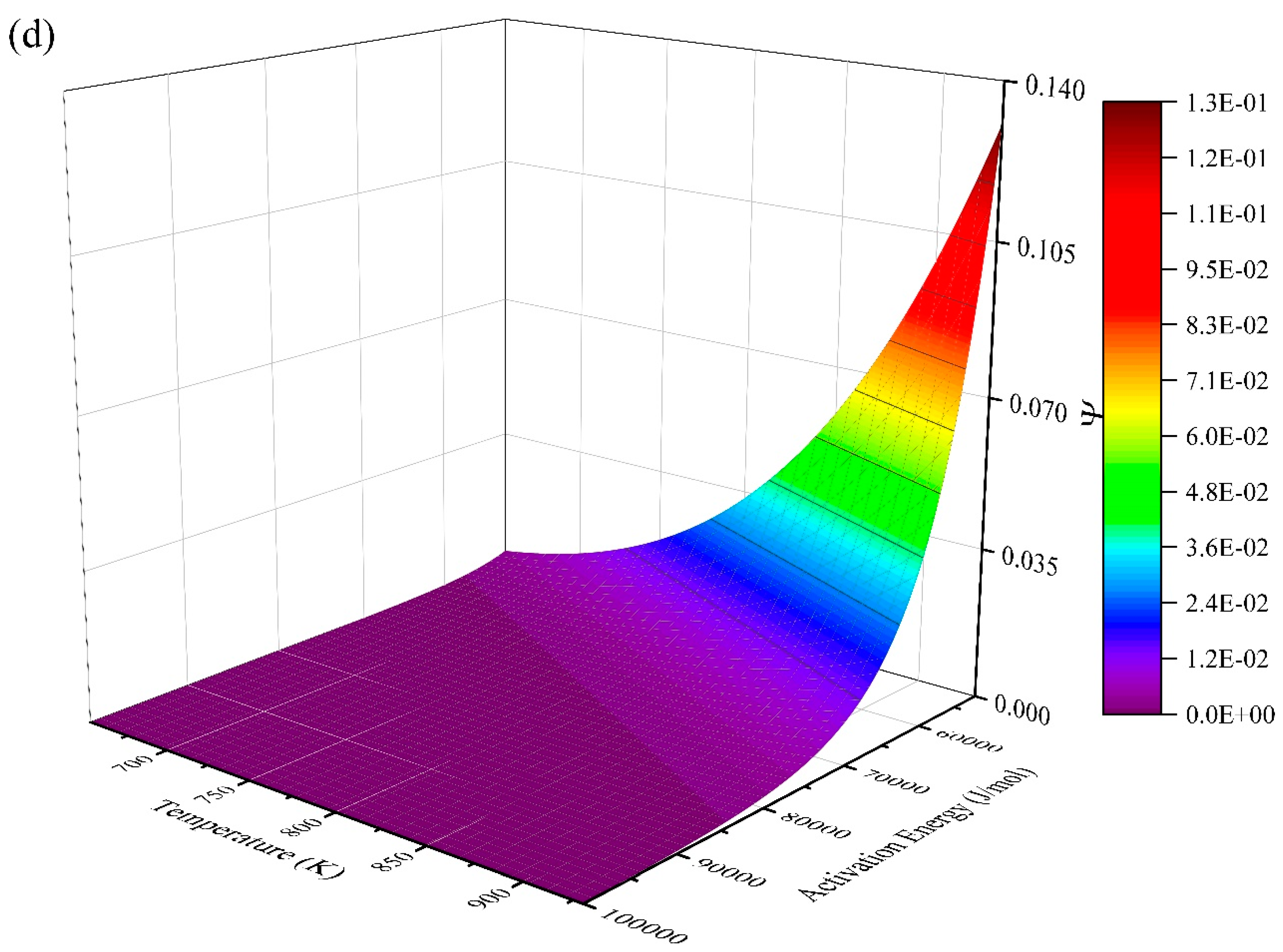
3. Error Analysis
4. Results and Discussion
5. Conclusions
6. Resource Codes
7. Standard Integral Values
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gautam, R.; Vinu, R. Unraveling the interactions in fast co-pyrolysis of microalgae model compounds via pyrolysis-GC/MS and pyrolysis-FTIR techniques. React. Chem. Eng. 2019, 4, 278–297. [Google Scholar] [CrossRef]
- Nestler, F.; Müller, V.P.; Ouda, M.; Hadrich, M.J.; Schaadt, A.; Bajohr, S.; Kolb, T. A novel approach for kinetic measurements in exothermic fixed bed reactors: Advancements in non-isothermal bed conditions demonstrated for methanol synthesis. React. Chem. Eng. 2021, 6, 1092–1107. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Xue, Z. Oxidation Kinetics of Vanadium Slag Roasting in the Presence of Calcium Oxide. Miner. Process. Extr. Metall. Rev. 2017, 38, 265–273. [Google Scholar] [CrossRef]
- Wang, H.H.; Li, G.Q.; Yang, J.; Ma, J.; Khan, B.S. The behavior of phosphorus during reduction and carburization of high-phosphorus oolitic hematite with H2 and CH4. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2016, 47, 2571–2581. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Liu, F.; Song, S.J. An extended analytical model for solid-state phase transformation upon continuous heating and cooling processes: Application in γ/α transformation. Acta Mater. 2012, 60, 3815–3829. [Google Scholar] [CrossRef]
- Fermoso, J.; Gil, M.V.; Pevida, C.; Pis, J.J.; Rubiera, F. Kinetic models comparison for non-isothermal steam gasification of coal–biomass blend chars. Chem. Eng. J. 2010, 161, 276–284. [Google Scholar] [CrossRef]
- Tai, H.-C.; Li, G.-C.; Huang, S.-J.; Jhu, C.-R.; Chung, J.-H.; Wang, B.Y.; Hsu, C.-S.; Brandmair, B.; Chung, D.-T.; Chen, H.M.; et al. Chemical distinctions between Stradivari’s maple and modern tonewood. Proc. Natl. Acad. Sci. USA 2017, 114, 27–32. [Google Scholar] [CrossRef]
- Aghili, A. Representation and evaluation of the Arrhenius and general temperature integrals by special functions. Thermochim. Acta 2021, 705, 179034. [Google Scholar] [CrossRef]
- Zhang, W.; Li, K.; Dong, J.H.; Li, C.Z.; Liu, A.H.; Zhang, J.H.; Xue, Z.L. Kinetic triplet from low-temperature carburization and carbon deposition reactions. J. Iron Steel Res. Int. 2022, 29, 1545–1558. [Google Scholar] [CrossRef]
- Li, K.; Zhang, W.; Fu, M.; Li, C.; Xue, Z. Discussion on Criterion of Determination of the Kinetic Parameters of the Linear Heating Reactions. Minerals 2022, 12, 81. [Google Scholar] [CrossRef]
- Li, K.; Gan, C.; Zhang, W.; Li, C.; Li, G. Validity of isothermal kinetic prediction by advanced isoconversional method. Chem. Phys. 2023, 567, 111801. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J.P. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Doyle, C.D. Series approximation to the equation of thermogravimetric data. Nature 1965, 207, 290–291. [Google Scholar] [CrossRef]
- Reich, L.; Levi, D. Thermal stability indices for polymeric materials based on energy considerations. Die Makromol. Chemie. 1963, 66, 102–113. [Google Scholar] [CrossRef]
- Doyle, C.D. Integral methods of kinetic analysis of thermogravimetric data. Macromol. Chem. Phys. 1964, 80, 220–224. [Google Scholar] [CrossRef]
- Zsakó, J. Kinetic analysis of thermogravimetric data, VI—Some problems of deriving kinetic parameters from TG curves. J. Therm. Anal. Calorim. 1973, 5, 239–251. [Google Scholar] [CrossRef]
- Órfão, J.J.M. Review and evaluation of the approximations to the temperature integral. AIChE J. 2007, 53, 2905–2915. [Google Scholar] [CrossRef]
- Neglur, R.; Grooff, D.; Hosten, E.; Aucamp, M.; Liebenberg, W. Approximation-based integral versus differential isoconversional approaches to the evaluation of kinetic parameters from thermogravimetry: Kinetic analysis of the dehydration of a pharmaceutical hydrate. J. Therm. Anal. Calorim. 2016, 123, 2599–2610. [Google Scholar] [CrossRef]
- Han, J.; Liu, D.; Qin, L.; Chen, W.; Xing, F. A modified temperature integral approximation formula and its application in pyrolysis kinetic parameters of waste tire. Energy Sources Part A Recover. Util. Environ. Eff. 2018, 40, 220–226. [Google Scholar] [CrossRef]
- Lin, Y.; Tian, Y.; Xia, Y.; Fang, S.; Liao, Y.; Yu, Z.; Ma, X. General distributed activation energy model (G-DAEM) on co-pyrolysis kinetics of bagasse and sewage sludge. Bioresour. Technol. 2019, 273, 545–555. [Google Scholar] [CrossRef]
- Senum, G.I.; Yang, R.T. Rational approximations of the integral of the Arrhenius function. J. Therm. Anal. Calorim. 1977, 11, 445–447. [Google Scholar] [CrossRef]
- Zsakó, J. Kinetic analysis of thermogravimetric data—XIV. Three integral methods and their computer programs. J. Therm. Anal. Calorim. 1980, 19, 333–345. [Google Scholar] [CrossRef]
- Serra, R.; Nomen, R.; Sempere, J. The Non-Parametric Kinetics A New Method for the Kinetic Study of Thermoanalytical Data. J. Therm. Anal. Calorim. 1998, 52, 933–943. [Google Scholar] [CrossRef]
- Rao, V.K.; Bardon, M.F. Integral of the boltzmann factor-A new approximation. J. Therm. Anal. 1996, 46, 323–326. [Google Scholar] [CrossRef]
- Flynn, J.H. The ‘Temperature Integral’—Its use and abuse. Thermochim. Acta 1997, 300, 83–92. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Tang, W.; Liu, Y.; Zhang, H.; Wang, C. New approximate formula for Arrhenius temperature integral. Thermochim. Acta 2003, 408, 39–43. [Google Scholar] [CrossRef]
- Capela, J.M.V.; Capela, M.V.; Ribeiro, C.A. Approximations for the generalized temperature integral: A method based on quadrature rules. J. Therm. Anal. Calorim. 2009, 97, 521–524. [Google Scholar] [CrossRef]
- Budrugeac, P. Applicability of some approximations of the temperature integral used for heating processes to processes taking place on cooling. J. Therm. Anal. Calorim. 2016, 124, 479–485. [Google Scholar] [CrossRef]
- Chen, H.X.; Liu, N.A. Approximations for the temperature integral. J. Therm. Anal. Calorim. 2008, 92, 573–578. [Google Scholar] [CrossRef]
- Chu, W. Derivative inverse series relations and lagrange expansion formula. Int. J. Number Theory 2013, 9, 1001–1013. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Gorbachev, V.M. A solution of the exponential integral in the non-isothermal kinetics for linear heating. J. Therm. Anal. Calorim. 1975, 8, 349–350. [Google Scholar] [CrossRef]
- Pérez-Maqueda, L.A.; Criado, J.M. The Accuracy of Senum and Yang’s Approximations to the Arrhenius Integral. J. Therm. Anal. Calorim. 2000, 60, 909–915. [Google Scholar] [CrossRef]
- Urbanovici, E.; Segal, E. Some problems concerning the temperature integral in non-isothermal kinetics: Part I. Generalities and some simple applications. Thermochim. Acta 1990, 168, 71–87. [Google Scholar] [CrossRef]
- Chen, H.; Liu, N. New procedure for derivation of approximations for temperature integral. AIChE J. 2006, 52, 4181–4185. [Google Scholar] [CrossRef]
- Ji, L.Q. New rational fraction approximating formulas for the temperature integral. J. Therm. Anal. Calorim. 2008, 91, 885–889. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britian? Statistical self-similarity and fractal dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
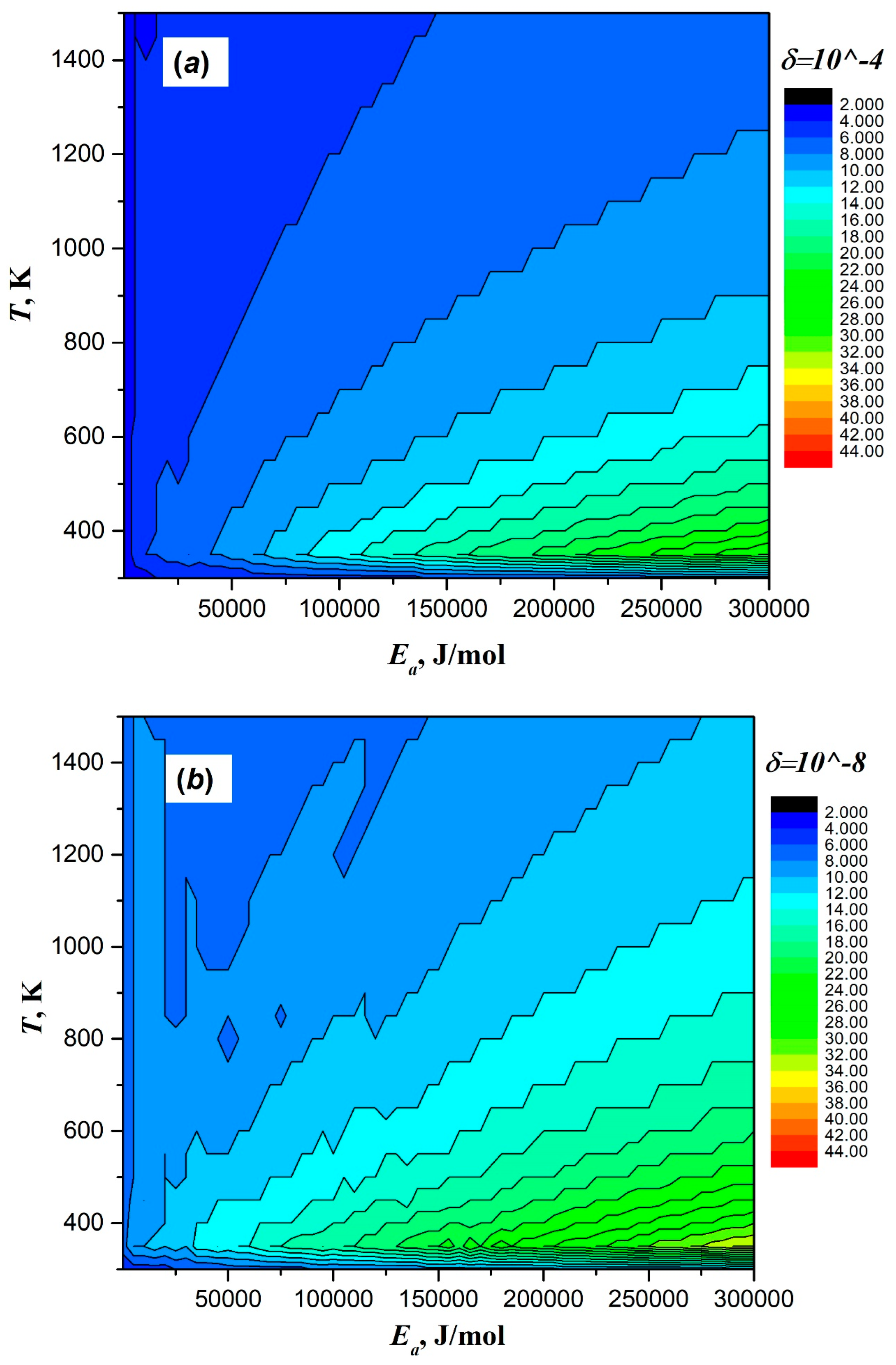
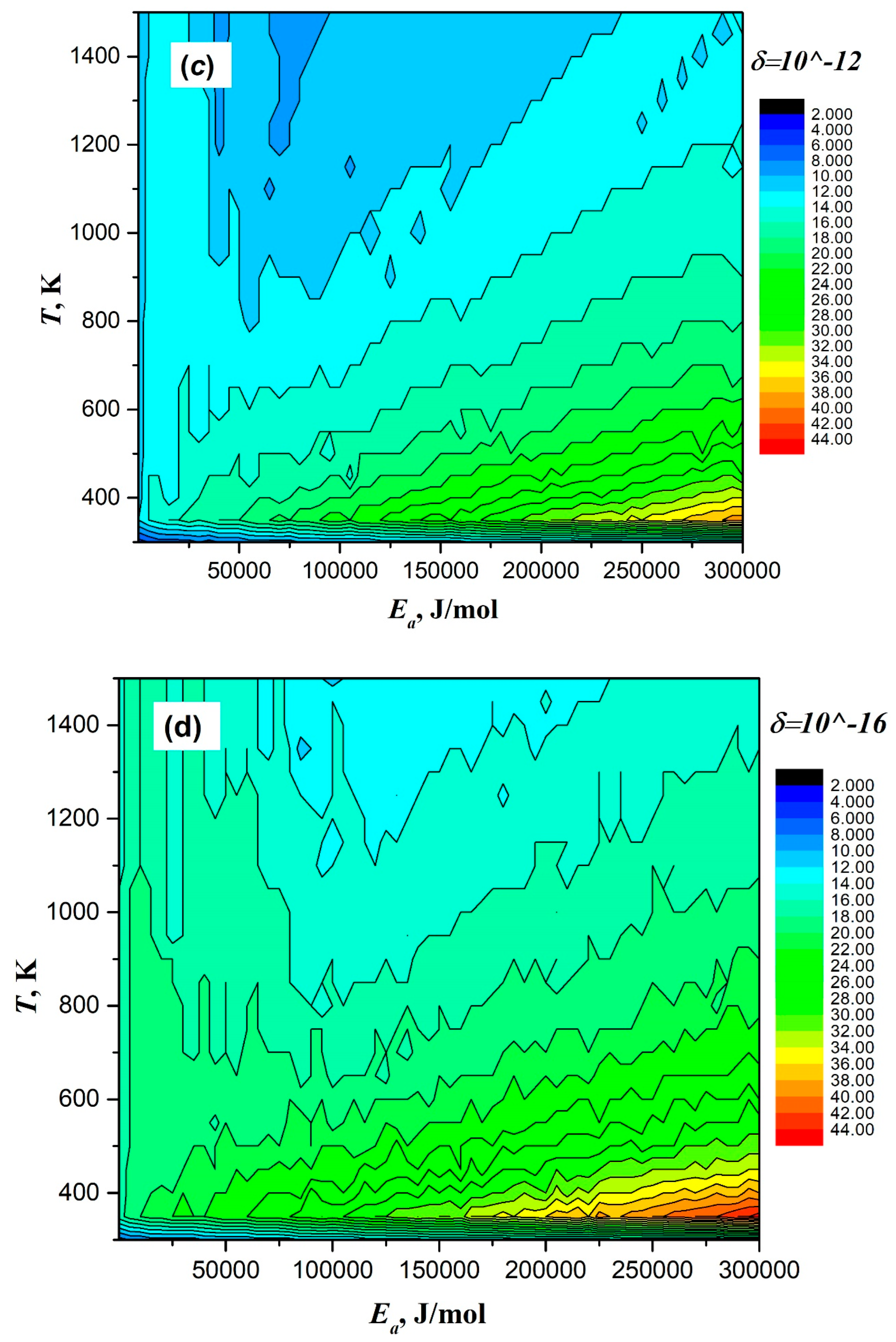

| Taylor Order n | Ea = 2 J/mol | Ea = 200 J/mol | Ea = 20,000 J/mol | Ea = 200,000 J/mol | ||||
|---|---|---|---|---|---|---|---|---|
| T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | |
| 1 | 301.82115578 | 901.64929838 | 284.65221331 | 867.71805582 | 1.47187736 | 41.45574855 | 1.11339239 × 10−17 | 6.64568260 × 10−8 |
| 2 | 301.83262904 | 901.66613166 | 285.72844879 | 869.31399874 | 1.84315996 | 44.66857854 | 2.03501118 × 10−17 | 9.66472837 × 10−8 |
| 3 | 301.83160096 | 901.66487181 | 285.63545060 | 869.19891467 | 1.88712698 | 44.76038220 | 3.15684847 × 10−17 | 1.05477139 × 10−7 |
| 4 | 301.83170869 | 901.66499125 | 285.64482423 | 869.20938372 | 1.88871043 | 44.75981330 | 4.17892561 × 10−17 | 1.07227989 × 10−7 |
| 5 | 301.83169624 | 901.66497815 | 285.64378407 | 869.20828368 | 1.88857776 | 44.75969041 | 4.88644170 × 10−17 | 1.07474026 × 10−7 |
| δ | 4.12482 × 10−8 | 1.5 × 10−8 | 3.6 × 10−6 | 1.3 × 10−6 | 7 × 10−5 | 2.7 × 10−6 | 0.144792 | 0.002289 |
| 6 | 301.83169778 | 901.66497973 | 285.64390756 | 869.20841067 | 1.88857039 | 44.75968614 | 5.27169484 × 10−17 | 1.07498862 × 10−7 |
| 7 | 301.83169758 | 901.66497953 | 285.64389214 | 869.20839504 | 1.88857151 | 44.75968706 | 5.44047391 × 10−17 | 1.07500633 × 10−7 |
| 8 | 301.83169761 | 901.66497955 | 285.64389414 | 869.20839705 | 1.88857153 | 44.75968709 | 5.50078992 × 10−17 | 1.07500716 × 10−7 |
| 9 | 301.83169761 | 901.66497955 | 285.64389388 | 869.20839679 | 1.88857152 | 44.75968708 | 5.51849690 × 10−17 | 1.07500718 × 10−7 |
| 10 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52277114 × 10−17 | 1.07500718 × 10−7 |
| δ | 0 | 0 | 1.05 × 10−10 | 3.45 × 10−11 | 0 | 0 | 0.000774 | 0 |
| 11 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52361451 × 10−17 | 1.07500718 × 10−7 |
| 12 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52374846 × 10−17 | 1.07500718 × 10−7 |
| 13 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376503 × 10−17 | 1.07500718 × 10−7 |
| 14 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376652 × 10−17 | 1.07500718 × 10−7 |
| 15 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| δ | 0 | 0 | 0 | 0 | 0 | 0 | 1.45 × 10−8 | 0 |
| 16 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| 17 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| 18 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| 19 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| 20 | 301.83169761 | 901.66497955 | 285.64389391 | 869.20839682 | 1.88857152 | 44.75968708 | 5.52376660 × 10−17 | 1.07500718 × 10−7 |
| δ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Quadrature Node m | Ea = 2 J/mol | Ea = 200 J/mol | Ea = 20,000 J/mol | Ea = 200,000 J/mol | ||||
|---|---|---|---|---|---|---|---|---|
| T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | T = 600 K | T = 1200 K | |
| 1 × 102 | 304.84987233 | 910.68041913 | 288.48730649 | 877.78754503 | 1.91652897 | 45.37009283 | 6.12793756 × 10−17 | 1.16596876 × 10−7 |
| 1 × 103 | 302.13351522 | 902.56652506 | 285.92824787 | 870.06645411 | 1.89135955 | 44.82059549 | 5.58241547 × 10−17 | 1.08390284 × 10−7 |
| δ | −0.008990585 | −0.00899 | −0.00895 | −0.00887 | −0.01331 | −0.01226 | −0.09772 | −0.07571 |
| 1 × 104 | 301.86187937 | 901.75513412 | 285.67232943 | 869.29420397 | 1.88885024 | 44.76577660 | 5.52961379 × 10−17 | 1.07589474 × 10−7 |
| δ | −0.000899059 | −0.0009 | −0.0009 | −0.00089 | −0.00133 | −0.00122 | −0.00946 | −0.00739 |
| 1 × 105 | 301.83471578 | 901.67399501 | 285.64673746 | 869.21697755 | 1.88859939 | 44.76029602 | 5.52435114 × 10−17 | 1.07509592 × 10−7 |
| δ | −8.99949 × 10−5 | −9 × 10−5 | −9 × 10−5 | −8.9 × 10−5 | −0.00013 | −0.00012 | −0.00095 | −0.00074 |
| 1 × 106 | 301.83199942 | 901.66588110 | 285.64417826 | 869.20925489 | 1.88857430 | 44.75974797 | 5.52382505 × 10−17 | 1.07501606 × 10−7 |
| δ | −8.99949 × 10−6 | −9 × 10−6 | −9 × 10−6 | −8.9 × 10−6 | −1.3 × 10−5 | −1.2 × 10−5 | −9.5 × 10−5 | −7.4 × 10−5 |
| Model | Approximation | P(x) |
|---|---|---|
| D | Doyle [32] | |
| CR | Coats and Redfern [12] | |
| G1 | Gorbachev (1st degree) [33] | |
| SY4 | Senum and Yang (4th degree) [21] | |
| PC8 | Perez-Maqueda and Criado (8th degree) [34] | |
| US4 | Urbanovici and Segal IV [35] | |
| CL | Chen and Liu [36] | |
| O3 | Órfão III [17] | |
| J3 | Ji III [37] |
| X = Ea/(RT) (T = 600 K) | MTALAB | Present Solution (n = 10) | Numerical Quadrature | D | CR | G1 | SY4 | PC8 | US4 | CL | O3 | J3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7.8106 × 101 | 7.8106 × 101 | 8.9108 × 101 | 6.6486 × 10−1 | −2.2086 × 102 | 6.3661 × 101 | 7.7575 × 101 | 7.8076 × 101 | 7.6156 × 101 | 9.8401 × 101 | 7.8106 × 101 | 7.8362 × 101 |
| 2 | 2.1597 × 101 | 2.1597 × 101 | 2.2517 × 101 | 6.2429 × 10−1 | −6.6416 × 101 | 1.9419 × 101 | 2.1575 × 101 | 2.1597 × 101 | 2.1429 × 101 | 2.8311 × 101 | 2.1597 × 101 | 2.1601 × 101 |
| 4 | 1.9093 × 100 | 1.9093 × 100 | 1.9187 × 100 | 1.7034 × 10−1 | 1.3648 × 100 | 1.8221 × 100 | 1.9092 × 100 | 1.9093 × 100 | 1.9059 × 100 | 2.5173 × 100 | 1.9093 × 100 | 1.9094 × 100 |
| 6 | 1.9083 × 10−1 | 1.9083 × 10−1 | 1.9096 × 10−1 | 3.1556 × 10−2 | 1.6513 × 10−1 | 1.8579 × 10−1 | 1.9083 × 10−1 | 1.9083 × 10−1 | 1.9071 × 10−1 | 2.4537 × 10−1 | 1.9083 × 10−1 | 1.9083 × 10−1 |
| 8 | 2.0481 × 10−2 | 2.0481 × 10−2 | 2.0490 × 10−2 | 5.1394 × 10−3 | 1.8868 × 10−2 | 2.0126 × 10−2 | 2.0481 × 10−2 | 2.0481 × 10−2 | 2.0475 × 10−2 | 2.5632 × 10−2 | 2.0481 × 10−2 | 2.0481 × 10−2 |
| 10 | 2.2981 × 10−3 | 2.2981 × 10−3 | 2.2982 × 10−3 | 7.8368 × 10−4 | 2.1792 × 10−3 | 2.2700 × 10−3 | 2.2981 × 10−3 | 2.2981 × 10−3 | 2.2978 × 10−3 | 2.8087 × 10−3 | 2.2981 × 10−3 | 2.2981 × 10−3 |
| 12 | 2.6575 × 10−4 | 2.6575 × 10−4 | 2.6576 × 10−4 | 1.1470 × 10−4 | 2.5601 × 10−4 | 2.6332 × 10−4 | 2.6575 × 10−4 | 2.6575 × 10−4 | 2.6572 × 10−4 | 3.1836 × 10−4 | 2.6575 × 10−4 | 2.6575 × 10−4 |
| 14 | 3.1404 × 10−5 | 3.1404 × 10−5 | 3.1402 × 10−5 | 1.6322 × 10−5 | 3.0546 × 10−5 | 3.1182 × 10−5 | 3.1404 × 10−5 | 3.1404 × 10−5 | 3.1402 × 10−5 | 3.6997 × 10−5 | 3.1404 × 10−5 | 3.1404 × 10−5 |
| 16 | 3.7724 × 10−6 | 3.7724 × 10−6 | 3.7724 × 10−6 | 2.2751 × 10−6 | 3.6926 × 10−6 | 3.7512 × 10−6 | 3.7724 × 10−6 | 3.7724 × 10−6 | 3.7723 × 10−6 | 4.3821 × 10−6 | 3.7724 × 10−6 | 3.7724 × 10−6 |
| 18 | 4.5901 × 10−7 | 4.5901 × 10−7 | 4.5900 × 10−7 | 3.1218 × 10−7 | 4.5126 × 10−7 | 4.5690 × 10−7 | 4.5901 × 10−7 | 4.5901 × 10−7 | 4.5900 × 10−7 | 5.2684 × 10−7 | 4.5901 × 10−7 | 4.5901 × 10−7 |
| 20 | 5.6429 × 10−8 | 5.6429 × 10−8 | 5.6430 × 10−8 | 4.2306 × 10−8 | 5.5651 × 10−8 | 5.6213 × 10−8 | 5.6429 × 10−8 | 5.6429 × 10−8 | 5.6428 × 10−8 | 6.4106 × 10−8 | 5.6429 × 10−8 | 5.6429 × 10−8 |
| T/K | Ea = 2 J/mol | Ea = 20,002 J/mol | Ea = 40,002 J/mol | Ea = 60,002 J/mol | Ea = 80,002 J/mol | Ea = 100,002 J/mol | Ea = 120,002 J/mol | Ea = 140,002 J/mol | Ea = 160,002 J/mol | Ea = 180,002 J/mol | Ea = 200,002 J/mol |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 300 | 1.9984 × 100 | 6.4068 × 10−4 | 2.0545 × 10−7 | 6.5897 × 10−11 | 2.1142 × 10−14 | 6.7844 × 10−18 | 2.1777 × 10−21 | 6.9916 × 10−25 | 2.2453 × 10−28 | 7.2121 × 10−32 | 2.3172 × 10−35 |
| 318 | 1.9984 × 101 | 8.1688 × 10−3 | 3.4100 × 10−6 | 1.4524 × 10−9 | 6.3035 × 10−13 | 2.7834 × 10−16 | 1.2483 × 10−19 | 5.6766 × 10−23 | 2.6130 × 10−26 | 1.2157 × 10−29 | 5.7090 × 10−33 |
| 336 | 3.7971 × 101 | 1.9709 × 10−2 | 1.0915 × 10−5 | 6.3972 × 10−9 | 3.9296 × 10−12 | 2.5059 × 10−15 | 1.6455 × 10−18 | 1.1055 × 10−21 | 7.5617 × 10−25 | 5.2465 × 10−28 | 3.6823 × 10−31 |
| 354 | 5.5959 × 101 | 3.6632 × 10−2 | 2.7010 × 10−5 | 2.1870 × 10−8 | 1.8958 × 10−11 | 1.7247 × 10−14 | 1.6239 × 10−17 | 1.5678 × 10−20 | 1.5425 × 10−23 | 1.5400 × 10−26 | 1.5556 × 10−29 |
| 372 | 7.3947 × 101 | 6.0526 × 10−2 | 5.9036 × 10−5 | 6.5170 × 10−8 | 7.8001 × 10−11 | 9.8417 × 10−14 | 1.2870 × 10−16 | 1.7265 × 10−19 | 2.3604 × 10−22 | 3.2746 × 10−25 | 4.5961 × 10−28 |
| 390 | 9.1935 × 101 | 9.3187 × 10−2 | 1.1877 × 10−4 | 1.7523 × 10−7 | 2.8220 × 10−10 | 4.7989 × 10−13 | 8.4604 × 10−16 | 1.5301 × 10−18 | 2.8199 × 10−21 | 5.2736 × 10−24 | 9.9776 × 10−27 |
| 408 | 1.0992 × 1002 | 1.3659 × 10−1 | 2.2414 × 10−4 | 4.3258 × 10−7 | 9.1447 × 10−10 | 2.0423 × 10−12 | 4.7284 × 10−15 | 1.1229 × 10−17 | 2.7174 × 10−20 | 6.6724 × 10−23 | 1.6574 × 10−25 |
| 426 | 1.2791 × 1002 | 1.9288 × 10−1 | 4.0116 × 10−4 | 9.9213 × 10−7 | 2.6921 × 10−9 | 7.7171 × 10−12 | 2.2931 × 10−14 | 6.9882 × 10−17 | 2.1700 × 10−19 | 6.8371 × 10−22 | 2.1792 × 10−24 |
| 444 | 1.4590 × 1002 | 2.6432 × 10−1 | 6.8611 × 10−4 | 2.1336 × 10−6 | 7.2838 × 10−9 | 2.6265 × 10−11 | 9.8160 × 10−14 | 3.7621 × 10−16 | 1.4691 × 10−18 | 5.8205 × 10−21 | 2.3327 × 10−23 |
| 462 | 1.6389 × 1002 | 3.5330 × 10−1 | 1.1278 × 10−3 | 4.3345 × 10−6 | 1.8290 × 10−8 | 8.1498 × 10−11 | 3.7631 × 10−13 | 1.7817 × 10−15 | 8.5949 × 10−18 | 4.2063 × 10−20 | 2.0823 × 10−22 |
| 480 | 1.8189 × 1002 | 4.6228 × 10−1 | 1.7901 × 10−3 | 8.3718 × 10−6 | 4.2978 × 10−8 | 2.3293 × 10−10 | 1.3079 × 10−12 | 7.5303 × 10−15 | 4.4167 × 10−17 | 2.6281 × 10−19 | 1.5817 × 10−21 |
| 498 | 1.9988 × 1002 | 5.9379 × 10−1 | 2.7540 × 10−3 | 1.5456 × 10−5 | 9.5179 × 10−8 | 6.1862 × 10−10 | 4.1652 × 10−12 | 2.8751 × 10−14 | 2.0216 × 10−16 | 1.4420 × 10−18 | 1.0404 × 10−20 |
| 516 | 2.1787 × 1002 | 7.5038 × 10−1 | 4.1200 × 10−3 | 2.7401 × 10−5 | 1.9987 × 10−7 | 1.5384 × 10−9 | 1.2263 × 10−11 | 1.0021 × 10−13 | 8.3418 × 10−16 | 7.0436 × 10−18 | 6.0155 × 10−20 |
| 534 | 2.3586 × 1002 | 9.3461 × 10−1 | 6.0104 × 10−3 | 4.6837 × 10−5 | 4.0012 × 10−7 | 3.6055 × 10−9 | 3.3646 × 10−11 | 3.2183 × 10−13 | 3.1354 × 10−15 | 3.0985 × 10−17 | 3.0969 × 10−19 |
| 552 | 2.5385 × 1002 | 1.1490 × 100 | 8.5707 × 10−3 | 7.7461 × 10−5 | 7.6707 × 10−7 | 8.0102 × 10−9 | 8.6610 × 10−11 | 9.5978 × 10−13 | 1.0833 × 10−14 | 1.2401 × 10−16 | 1.4358 × 10−18 |
| 570 | 2.7184 × 1002 | 1.3962 × 100 | 1.1972 × 10−2 | 1.2433 × 10−4 | 1.4140 × 10−6 | 1.6953 × 10−8 | 2.1043 × 10−10 | 2.6767 × 10−12 | 3.4675 × 10−14 | 4.5560 × 10−16 | 6.0542 × 10−18 |
| 588 | 2.8984 × 1002 | 1.6786 × 100 | 1.6410 × 10−2 | 1.9419 × 10−4 | 2.5151 × 10−6 | 3.4332 × 10−8 | 4.8509 × 10−10 | 7.0233 × 10−12 | 1.0355 × 10−13 | 1.5485 × 10−15 | 2.3418 × 10−17 |
| 606 | 3.0783 × 1002 | 1.9987 × 100 | 2.2112 × 10−2 | 2.9587 × 10−4 | 4.3305 × 10−6 | 6.6785 × 10−8 | 1.0659 × 10−9 | 1.7432 × 10−11 | 2.9029 × 10−13 | 4.9027 × 10−15 | 8.3734 × 10−17 |
| 624 | 3.2582 × 1002 | 2.3588 × 100 | 2.9328 × 10−2 | 4.4062 × 10−4 | 7.2372 × 10−6 | 1.2522 × 10−7 | 2.2419 × 10−9 | 4.1121 × 10−11 | 7.6803 × 10−13 | 1.4547 × 10−14 | 2.7864 × 10−16 |
| 642 | 3.4382 × 1002 | 2.7613 × 100 | 3.8340 × 10−2 | 6.4261 × 10−4 | 1.1769 × 10−5 | 2.2698 × 10−7 | 4.5293 × 10−9 | 9.2588 × 10−11 | 1.9271 × 10−12 | 4.0673 × 10−14 | 8.6810 × 10−16 |
| 660 | 3.6181 × 1002 | 3.2084 × 100 | 4.9459 × 10−2 | 9.1936 × 10−4 | 1.8663 × 10−5 | 3.9888 × 10−7 | 8.8190 × 10−9 | 1.9973 × 10−10 | 4.6052 × 10−12 | 1.0768 × 10−13 | 2.5458 × 10−15 |
| 678 | 3.7980 × 1002 | 3.7022 × 100 | 6.3022 × 10−2 | 1.2921 × 10−3 | 2.8918 × 10−5 | 6.8119 × 10−7 | 1.6597 × 10−8 | 4.1417 × 10−10 | 1.0522 × 10−11 | 2.7106 × 10−13 | 7.0607 × 10−15 |
| 696 | 3.9780 × 1002 | 4.2448 × 100 | 7.9394 × 10−2 | 1.7866 × 10−3 | 4.3858 × 10−5 | 1.1330 × 10−6 | 3.0267 × 10−8 | 8.2811 × 10−10 | 2.3065 × 10−11 | 6.5139 × 10−13 | 1.8601 × 10−14 |
| 714 | 4.1579 × 1002 | 4.8382 × 100 | 9.8971 × 10−2 | 2.4329 × 10−3 | 6.5210 × 10−5 | 1.8388 × 10−6 | 5.3615 × 10−8 | 1.6009 × 10−9 | 4.8659 × 10−11 | 1.4995 × 10−12 | 4.6725 × 10−14 |
| 732 | 4.3378 × 1002 | 5.4841 × 100 | 1.2217 × 10−1 | 3.2666 × 10−3 | 9.5191 × 10−5 | 2.9175 × 10−6 | 9.2446 × 10−8 | 2.9995 × 10−9 | 9.9066 × 10−11 | 3.3172 × 10−12 | 1.1231 × 10−13 |
| 750 | 4.5178 × 1002 | 6.1844 × 100 | 1.4944 × 10−1 | 4.3290 × 10−3 | 1.3660 × 10−4 | 4.5323 × 10−6 | 1.5545 × 10−7 | 5.4593 × 10−9 | 1.9514 × 10−10 | 7.0716 × 10−12 | 2.5910 × 10−13 |
| 768 | 4.6977 × 1002 | 6.9407 × 100 | 1.8124 × 10−1 | 5.6671 × 10−3 | 1.9292 × 10−4 | 6.9041 × 10−6 | 2.5538 × 10−7 | 9.6713 × 10−9 | 3.7276 × 10−10 | 1.4565 × 10−11 | 5.7539 × 10−13 |
| 786 | 4.8777 × 1002 | 7.7547 × 100 | 2.1808 × 10−1 | 7.3347 × 10−3 | 2.6845 × 10−4 | 1.0326 × 10−5 | 4.1051 × 10−7 | 1.6707 × 10−8 | 6.9194 × 10−10 | 2.9052 × 10−11 | 1.2332 × 10−12 |
| 804 | 5.0576 × 1002 | 8.6277 × 100 | 2.6045 × 10−1 | 9.3922 × 10−3 | 3.6840 × 10−4 | 1.5183 × 10−5 | 6.4661 × 10−7 | 2.8188 × 10−8 | 1.2505 × 10−9 | 5.6239 × 10−11 | 2.5568 × 10−12 |
| 822 | 5.2376 × 1002 | 9.5613 × 100 | 3.0890 × 10−1 | 1.1908 × 10−2 | 4.9903 × 10−4 | 2.1970 × 10−5 | 9.9934 × 10−7 | 4.6526 × 10−8 | 2.2043 × 10−9 | 1.0586 × 10−10 | 5.1393 × 10−12 |
| 840 | 5.4175 × 1002 | 1.0557 × 101 | 3.6398 × 10−1 | 1.4956 × 10−2 | 6.6780 × 10−4 | 3.1317 × 10−5 | 1.5172 × 10−6 | 7.5228 × 10−8 | 3.7955 × 10−9 | 1.9410 × 10−10 | 1.0035 × 10−11 |
| 858 | 5.5975 × 1002 | 1.1615 × 101 | 4.2624 × 10−1 | 1.8620 × 10−2 | 8.8349 × 10−4 | 4.4018 × 10−5 | 2.2653 × 10−6 | 1.1931 × 10−7 | 6.3933 × 10−9 | 3.4725 × 10−10 | 1.9066 × 10−11 |
| 876 | 5.7774 × 1002 | 1.2737 × 101 | 4.9628 × 10−1 | 2.2991 × 10−2 | 1.1564 × 10−3 | 6.1058 × 10−5 | 3.3297 × 10−6 | 1.8581 × 10−7 | 1.0549 × 10−8 | 6.0707 × 10−10 | 3.5313 × 10−11 |
| 894 | 5.9574 × 1002 | 1.3925 × 101 | 5.7468 × 10−1 | 2.8168 × 10−2 | 1.4983 × 10−3 | 8.3647 × 10−5 | 4.8224 × 10−6 | 2.8447 × 10−7 | 1.7073 × 10−8 | 1.0385 × 10−9 | 6.3849 × 10−11 |
| 912 | 6.1373 × 1002 | 1.5179 × 101 | 6.6205 × 10−1 | 3.4258 × 10−2 | 1.9229 × 10−3 | 1.1326 × 10−4 | 6.8879 × 10−6 | 4.2858 × 10−7 | 2.7130 × 10−8 | 1.7405 × 10−9 | 1.1286 × 10−10 |
| 930 | 6.3173 × 1002 | 1.6500 × 101 | 7.5901 × 10−1 | 4.1377 × 10−2 | 2.4458 × 10−3 | 1.5167 × 10−4 | 9.7100 × 10−6 | 6.3598 × 10−7 | 4.2375 × 10−8 | 2.8613 × 10−9 | 1.9529 × 10−10 |
| 948 | 6.4972 × 1002 | 1.7888 × 101 | 8.6618 × 10−1 | 4.9650 × 10−2 | 3.0845 × 10−3 | 2.0100 × 10−4 | 1.3520 × 10−5 | 9.3033 × 10−7 | 6.5120 × 10−8 | 4.6192 × 10−9 | 3.3118 × 10−10 |
| 966 | 6.6772 × 1002 | 1.9345 × 101 | 9.8419 × 10−1 | 5.9209 × 10−2 | 3.8590 × 10−3 | 2.6375 × 10−4 | 1.8606 × 10−5 | 1.3426 × 10−6 | 9.8548 × 10−8 | 7.3300 × 10−9 | 5.5104 × 10−10 |
| 984 | 6.8571 × 1002 | 2.0872 × 101 | 1.1137 × 100 | 7.0196 × 10−2 | 4.7913 × 10−3 | 3.4288 × 10−4 | 2.5324 × 10−5 | 1.9130 × 10−6 | 1.4698 × 10−7 | 1.1444 × 10−8 | 9.0052 × 10−10 |
| 1002 | 7.0371 × 1002 | 2.2468 × 101 | 1.2553 × 100 | 8.2759 × 10−2 | 5.9062 × 10−3 | 4.4183 × 10−4 | 3.4108 × 10−5 | 2.6929 × 10−6 | 2.1623 × 10−7 | 1.7594 × 10−8 | 1.4468 × 10−9 |
| 1020 | 7.2170 × 1002 | 2.4134 × 101 | 1.4096 × 100 | 9.7058 × 10−2 | 7.2309 × 10−3 | 5.6459 × 10−4 | 4.5484 × 10−5 | 3.7473 × 10−6 | 3.1398 × 10−7 | 2.6657 × 10−8 | 2.2872 × 10−9 |
| 1038 | 7.3970 × 1002 | 2.5872 × 101 | 1.5774 × 100 | 1.1326 × 10−1 | 8.7955 × 10−3 | 7.1572 × 10−4 | 6.0085 × 10−5 | 5.1581 × 10−6 | 4.5032 × 10−7 | 3.9834 × 10−8 | 3.5609 × 10−9 |
| 1056 | 7.5770 × 1002 | 2.7680 × 101 | 1.7592 × 100 | 1.3153 × 10−1 | 1.0633 × 10−2 | 9.0047 × 10−4 | 7.8665 × 10−5 | 7.0268 × 10−6 | 6.3830 × 10−7 | 5.8746 × 10−8 | 5.4638 × 10−9 |
| 1074 | 7.7569 × 1002 | 2.9561 × 101 | 1.9556 × 100 | 1.5206 × 10−1 | 1.2779 × 10−2 | 1.1248 × 10−3 | 1.0212 × 10−4 | 9.4789 × 10−6 | 8.9471 × 10−7 | 8.5562 × 10−8 | 8.2686 × 10−9 |
| 1092 | 7.9369 × 1002 | 3.1513 × 101 | 2.1674 × 100 | 1.7504 × 10−1 | 1.5272 × 10−2 | 1.3954 × 10−3 | 1.3149 × 10−4 | 1.2667 × 10−5 | 1.2409 × 10−6 | 1.2315 × 10−7 | 1.2350 × 10−8 |
| 1110 | 8.1168 × 1002 | 3.3537 × 101 | 2.3952 × 100 | 2.0067 × 10−1 | 1.8156 × 10−2 | 1.7199 × 10−3 | 1.6801 × 10−4 | 1.6778 × 10−5 | 1.7036 × 10−6 | 1.7524 × 10−7 | 1.8216 × 10−8 |
| 1128 | 8.2968 × 1002 | 3.5634 × 101 | 2.6395 × 100 | 2.2914 × 10−1 | 2.1474 × 10−2 | 2.1067 × 10−3 | 2.1310 × 10−4 | 2.2035 × 10−5 | 2.3165 × 10−6 | 2.4671 × 10−7 | 2.6550 × 10−8 |
| 1146 | 8.4768 × 1002 | 3.7803 × 101 | 2.9010 × 100 | 2.6067 × 10−1 | 2.5276 × 10−2 | 2.5652 × 10−3 | 2.6840 × 10−4 | 2.8704 × 10−5 | 3.1210 × 10−6 | 3.4376 × 10−7 | 3.8259 × 10−8 |
| 1164 | 8.6567 × 1002 | 4.0045 × 101 | 3.1804 × 100 | 2.9548 × 10−1 | 2.9615 × 10−2 | 3.1059 × 10−3 | 3.3578 × 10−4 | 3.7104 × 10−5 | 4.1682 × 10−6 | 4.7432 × 10−7 | 5.4538 × 10−8 |
| 1182 | 8.8367 × 1002 | 4.2360 × 101 | 3.4782 × 100 | 3.3380 × 10−1 | 3.4544 × 10−2 | 3.7402 × 10−3 | 4.1741 × 10−4 | 4.7609 × 10−5 | 5.5203 × 10−6 | 6.4836 × 10−7 | 7.6941 × 10−8 |
| 1200 | 9.0166 × 1002 | 4.4748 × 101 | 3.7950 × 100 | 3.7584 × 10−1 | 4.0124 × 10−2 | 4.4808 × 10−3 | 5.1571 × 10−4 | 6.0659 × 10−5 | 7.2526 × 10−6 | 8.7835 × 10−7 | 1.0748 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zheng, Q.; Yu, X.; Shen, Y.; Li, K. Numerical Calculation and 3-D Imaging of the Arrhenius Temperature Integral. Separations 2023, 10, 480. https://doi.org/10.3390/separations10090480
Zhang W, Zheng Q, Yu X, Shen Y, Li K. Numerical Calculation and 3-D Imaging of the Arrhenius Temperature Integral. Separations. 2023; 10(9):480. https://doi.org/10.3390/separations10090480
Chicago/Turabian StyleZhang, Wei, Qiaoyu Zheng, Xiaobing Yu, Yansong Shen, and Kui Li. 2023. "Numerical Calculation and 3-D Imaging of the Arrhenius Temperature Integral" Separations 10, no. 9: 480. https://doi.org/10.3390/separations10090480






