A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model
Abstract
:1. Introduction
2. Preliminaries
3. Governing Equation of Fractional Viscoelastic Plate
4. Numerical Algorithm for Bernstein Polynomials
4.1. Bernstein Polynomials
4.2. Function Approximation
4.3. Differential Operator Matrix of Bernstein Polynomials
4.3.1. Integer Differential Operator Matrix
4.3.2. Fractional Differential Operator Matrix
4.4. Discretizationdiscretization Governing Equation
5. Error Analysis and Mathematical Example
5.1. Error Bound
5.2. Mathematical Example
6. Numerical Analysis
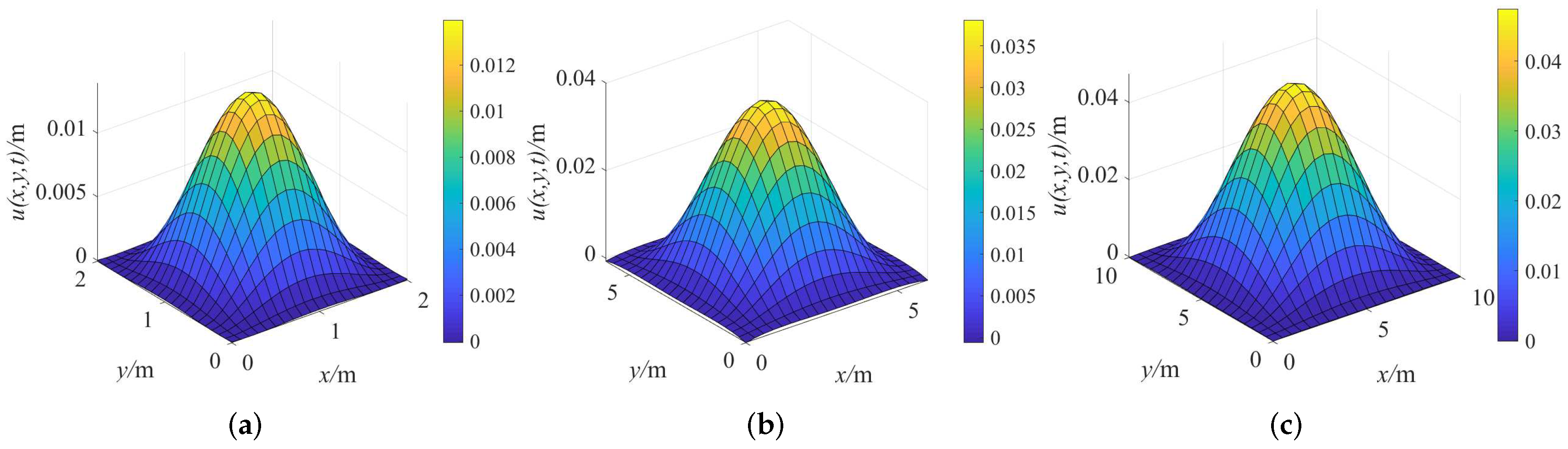
6.1. Influence of Different Simple Harmonic Loads on Plate Displacement
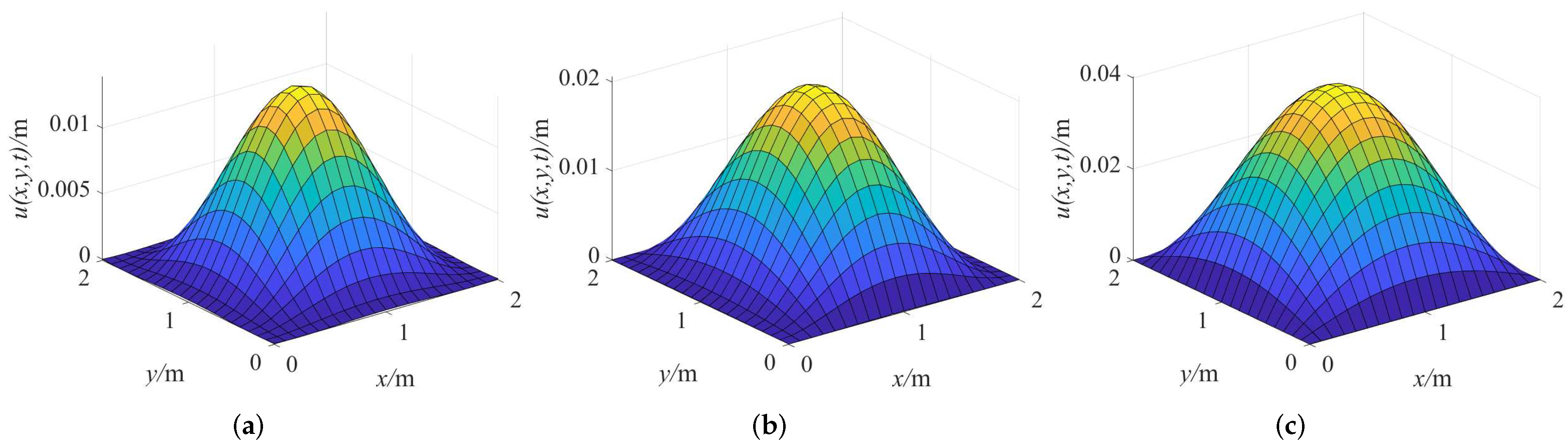
6.2. Influence of Side 0 of the Plate on Plate Displacement
6.3. Influence of Boundary Conditions on Plate Displacement
6.4. Influence of Plate Thickness on Stress
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, D.P.; Lei, Y.J.; Shen, Z.B. Semi-analytical solution for vibration of nonlocal piezoelectric Kirchhoff plates resting on viscoelastic foundation. J. Appl. Comput. Mech. 2018, 4, 202–205. [Google Scholar] [CrossRef]
- Shafei, E.; Faroughi, S.; Rabczuk, T. Nonlinear transient vibration of viscoelastic plates: A NURBS-based isogeometric HSDT approach. Comput. Math. Appl. 2018, 84, 1–15. [Google Scholar] [CrossRef]
- Ziaee, S. Linear free vibration of micro-/nano-plates with cut-out in thermal environment via modified couple stress theory and Ritz method. Ain Shams Eng. J. 2018, 9, 2373–2381. [Google Scholar] [CrossRef]
- Cadou, J.M.; Ounis, H.; Boutyour, E.H.; Potier-Ferry, M. Asymptotic numerical method and Padé approximants for eigenvalue.Application in linear vibration of plates and shells. Mech. Res. Commun. 2020, 106, 103538. [Google Scholar] [CrossRef]
- Babahammou, A.; Benamar, R. Linear and nonlinear vibrations of isotropic rectangular plates resting on full or partial line supports. Mater Today Proc. 2022, in press. [Google Scholar] [CrossRef]
- Cho, J.R. Nonlinear free vibration of functionally graded CNT-reinforced composite plates. Compos. Struct. 2022, 281, 115101. [Google Scholar] [CrossRef]
- Quan, T.Q.; Ha, D.T.T.; Duc, N.D. Analytical solutions for nonlinear vibration of porous functionally graded sandwich plate subjected to blast loading. Thin Wall Struct. 2022, 170, 108606. [Google Scholar] [CrossRef]
- Datta, N.; Praharaj, R.K. Dynamic response of fractionally damped viscoelastic plates subjected to a moving point load. J. Vib. Acoust. 2020, 142, 041002. [Google Scholar] [CrossRef]
- Katsikadelis, J.T.; Babouskos, N.G. Post-buckling analysis of viscoelastic plates with fractional derivative models. Eng. Anal. Bound. Elem. 2010, 34, 1038–1048. [Google Scholar] [CrossRef]
- Fan, W.P.; Jiang, X.Y.; Qi, H.T. Parameter estimation for the generalized fractional element network Zener model based on the Bayesian method. Physica A 2015, 427, 40–49. [Google Scholar] [CrossRef]
- Pan, W.Q.; Li, T.Z.; Wang, Y. The multi-switching sliding mode combination synchronization of fractional order non-identical chaotic system with stochastic disturbances and unknown parameters. Fractal Fract. 2022, 6, 102. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0 < α < 2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3237–3241. [Google Scholar] [CrossRef]
- Zhang, X.F.; Huang, W.K. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Rouzegar, J.; Vazirzadeh, M.; Heydari, M.H. A fractional viscoelastic model for vibrational analysis of thin plate excited by supports movement. Mech. Res. Commun. 2020, 110, 103618. [Google Scholar] [CrossRef]
- Permoon, M.R.; Farsadi, T. Free vibration of three-layer sandwich plate with viscoelastic core modelled with fractional theory. Mech. Res. Commun. 2021, 116, 103766. [Google Scholar] [CrossRef]
- Praharaj, R.K.; Datta, N. On the transient response of plates on fractionally damped viscoelastic foundation. Comput. Appl. Math. 2020, 39, 256. [Google Scholar] [CrossRef]
- Ai, Z.Y.; Jiang, Y.H.; Zhao, Y.Z.; Mu, J.J. Time-dependent performance of ribbed plates on multi-layered fractional viscoelastic cross-anisotropic saturated soils. Eng. Anal. Bound. Elem. 2022, 137, 1–15. [Google Scholar] [CrossRef]
- Sene, N.; Fall, A.N. Homotopy perturbation ρ-Laplace transform method and its application to the fractional diffusion equation and the fractional diffusion-reaction equation. Fractal Fract. 2019, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Zainal, N.H.; Kiliçman, A. Solving fractional partial differential equations with corrected Fourier series method. Abstr. Appl. Anal. 2014, 2014, 958931. [Google Scholar] [CrossRef] [Green Version]
- Qiu, W.L.; Xu, D.; Chen, H.F.; Guo, J. An alternating direction implicit Galerkin finite element method for the distributed-order time-fractional mobile–immobile equation in two dimensions. Comput. Math. Appl. 2020, 80, 3156–3172. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.A.T. Numerical study of the nonlinear anomalous reaction–subdiffusion process arising in the electroanalytical chemistry. J. Comput. Sci.-Neth. 2021, 53, 101394. [Google Scholar] [CrossRef]
- Mohamadi, A.; Shahgholi, M.; Ghasemi, F.A. Free vibration and stability of an axially moving thin circular cylindrical shell using multiple scales method. Meccanica 2019, 54, 2227–2246. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D. Variational iteration method combined with new transform to solve fractional partial differential equations. Univ. J. Math. Appl. 2018, 1, 113–120. [Google Scholar] [CrossRef]
- Wang, Y.H.; Chen, Y.M. Dynamic analysis of the viscoelastic pipeline conveying fluid with an improved variable fractional order model based on shifted Legendre polynomials. Fractal Fract. 2019, 3, 52. [Google Scholar] [CrossRef] [Green Version]
- Hashim, I.; Sharadga, M.; Syam, M.I.; Al-Refai, M. A reliable approach for solving delay fractional differential equations. Fractal Fract. 2022, 6, 124. [Google Scholar] [CrossRef]
- Cao, J.W.; Chen, Y.M.; Wang, Y.H.; Zhang, H. Numerical analysis of nonlinear variable fractional viscoelastic arch based on shifted Legendre polynomials. Math. Method Appl. Sci. 2021, 11, 8798–8813. [Google Scholar] [CrossRef]
- Wang, J.S.; Liu, L.Q.; Chen, Y.M.; Ke, X.H. Numerical solution for fractional partial differential equation with Bernstein polynomials. J. Electron. Sci. Technol. 2014, 12, 331–338. [Google Scholar] [CrossRef]
- Khan, H.; Alipour, M.; Jafari, H.; Khan, R.A. Approximate analytical solution of a coupled system of fractional partial differential equations by Bernstein polynomials. Int. J. Appl. Comput. Math. 2016, 2, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Heydari, M.H.; Avazzadeh, A.; Yang, Y. Numerical treatment of the space-time fractal-fractional model of nonlinear advection-diffusion-reaction equation through the Bernstein polynomials. Fractals 2020, 28, 2040001. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Liu, D.Y.; Boutat, D. Numerical study of a class of variable order nonlinear fractional differential equation in terms of Bernstein polynomials. Ain Shams Eng. J. 2018, 9, 1235–1241. [Google Scholar] [CrossRef] [Green Version]
- Yi, M.X.; Huang, J. Wavelet operational matrix method for solving fractional differential equations with variable coefficients. Appl. Math. Comput. 2014, 230, 383–394. [Google Scholar] [CrossRef]
- Chen, Y.M.; Sun, Y.N.; Liu, L.Q. Numerical solution of fractional partial differential equations with variable coefficients using generalized fractional-order Legendre functions. Appl. Math. Comput. 2014, 244, 847–858. [Google Scholar] [CrossRef]
- Malara, M.; Spanos, P.D. Nonlinear random vibrations of plates endowed with fractional derivative elements. Probabilist. Eng. Mech. 2018, 54, 2–8. [Google Scholar] [CrossRef]
- Timosenko, S.P. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Jiang, Q.; Zhou, Z.D.; Yang, F.P. The method of fundamental solutions for two-dimensional elasticity problems based on the Airy stress function. Eng. Anal. Bound. Elem. 2021, 130, 220–237. [Google Scholar] [CrossRef]
- Khataybeh, S.N.; Hashim, I.; Alshbool, M. Solving directly third-order ODEs using operational matrices of Bernstein polynomials method with applications to fluid flow equations. J. King Saud Univ. Sci. 2019, 31, 822–826. [Google Scholar] [CrossRef]
- Kiasat, M.S.; Zamani, H.A.; Aghdam, M.M. On the transient response of viscoelastic beams and plates on viscoelastic medium. Int. J. Mech. Sci. 2014, 83, 133–145. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.Z.; Wang, G.W. Numerical algorithm for time-fractional Sawada-Kotera equation and Ito equation with Bernstein polynomials. Appl. Math. Comput. 2018, 338, 1–11. [Google Scholar] [CrossRef]
- Kadkhoda, N. A numerical approach for solving variable order differential equations using Bernstein polynomials. Alex. Eng. J. 2020, 59, 3041–3047. [Google Scholar] [CrossRef]
- Rouzegar, J.; Davoudi, M. Forced vibration of smart laminated viscoelastic plates by RPT finite element approach. Acta Mech. Sin. 2020, 36, 933–949. [Google Scholar] [CrossRef]




| Physical Quantity | Symbol | Value | Dimension |
|---|---|---|---|
| Fractional order | 0.75 | 1 | |
| Length | a | 2 | |
| Width | b | 2 | |
| Thickness | h | 0.02 | |
| Density of the plate | 7850 | ||
| Poisson’s ratio | v | 0.3 | 1 |
| Young’s modulus | E | ||
| Damping coefficient | 1 |
| 0 | 0 | ||||
| 0 | 0 | ||||
| 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Xie, J.; Qu, J.; Chen, Y. A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model. Fractal Fract. 2022, 6, 150. https://doi.org/10.3390/fractalfract6030150
Jin S, Xie J, Qu J, Chen Y. A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model. Fractal and Fractional. 2022; 6(3):150. https://doi.org/10.3390/fractalfract6030150
Chicago/Turabian StyleJin, Suhua, Jiaquan Xie, Jingguo Qu, and Yiming Chen. 2022. "A Numerical Method for Simulating Viscoelastic Plates Based on Fractional Order Model" Fractal and Fractional 6, no. 3: 150. https://doi.org/10.3390/fractalfract6030150






