Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Microstructure of the Fabricated Ceramics
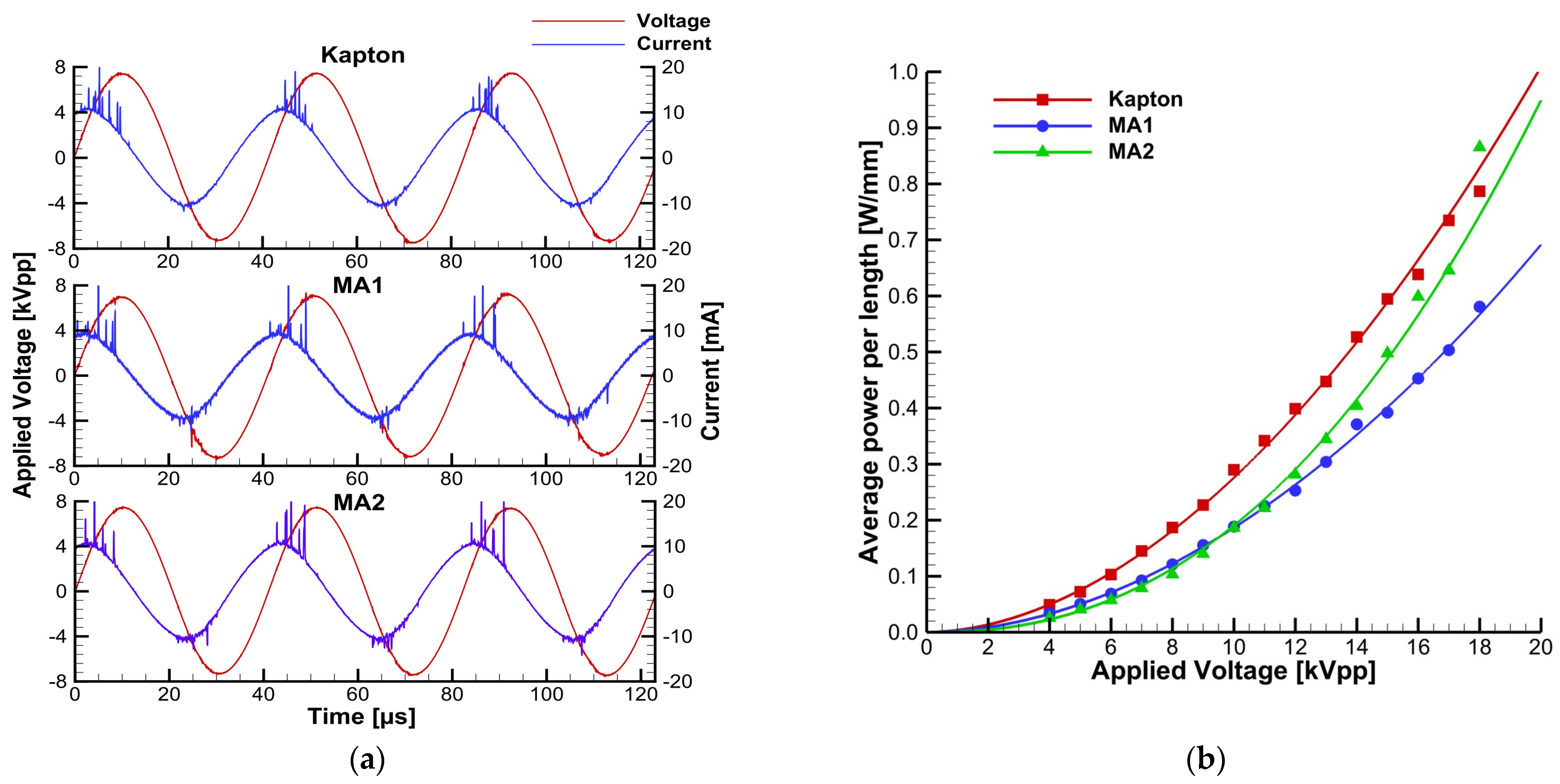
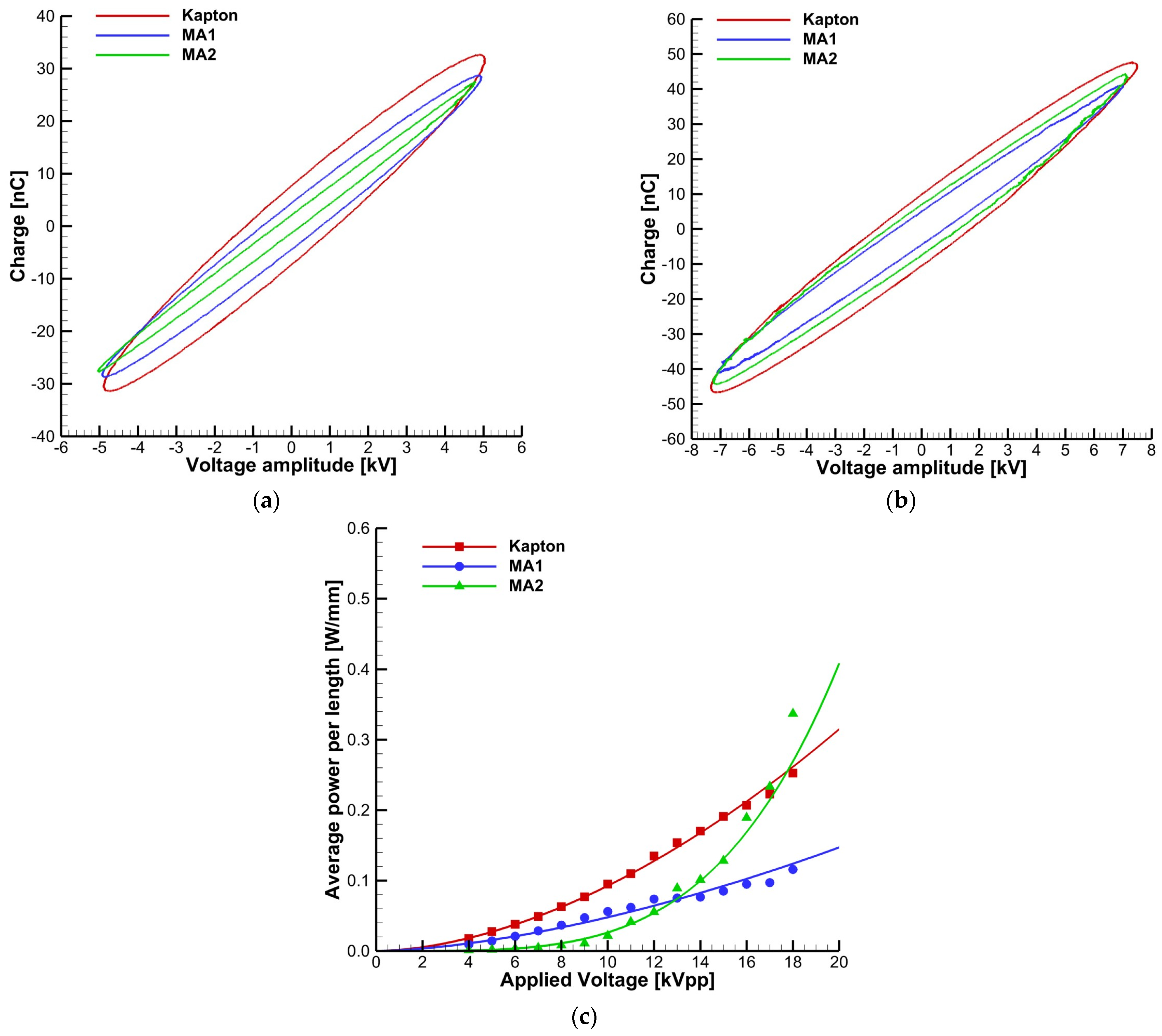
3.2. Plasma Actuators Electrical Characterization
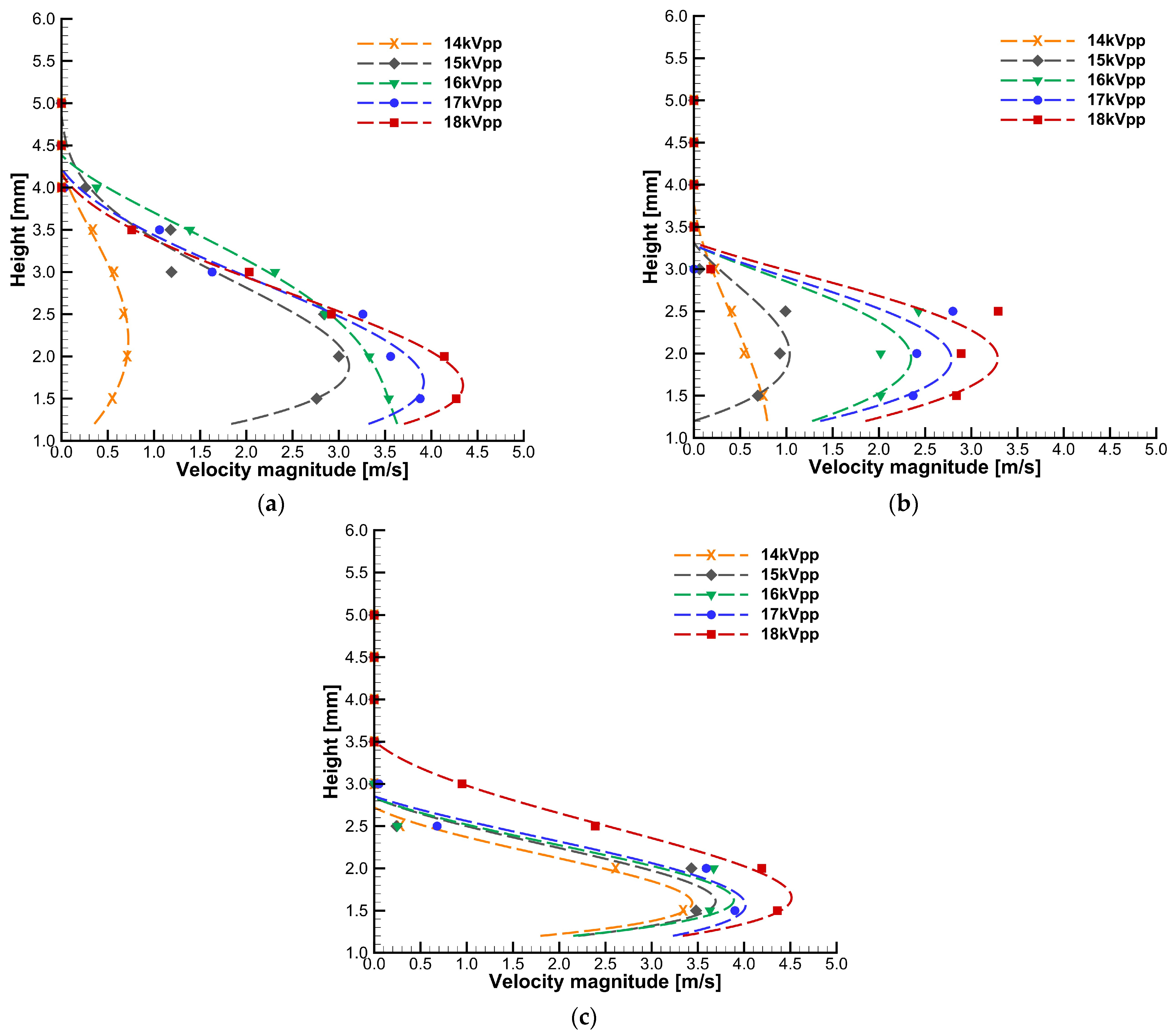
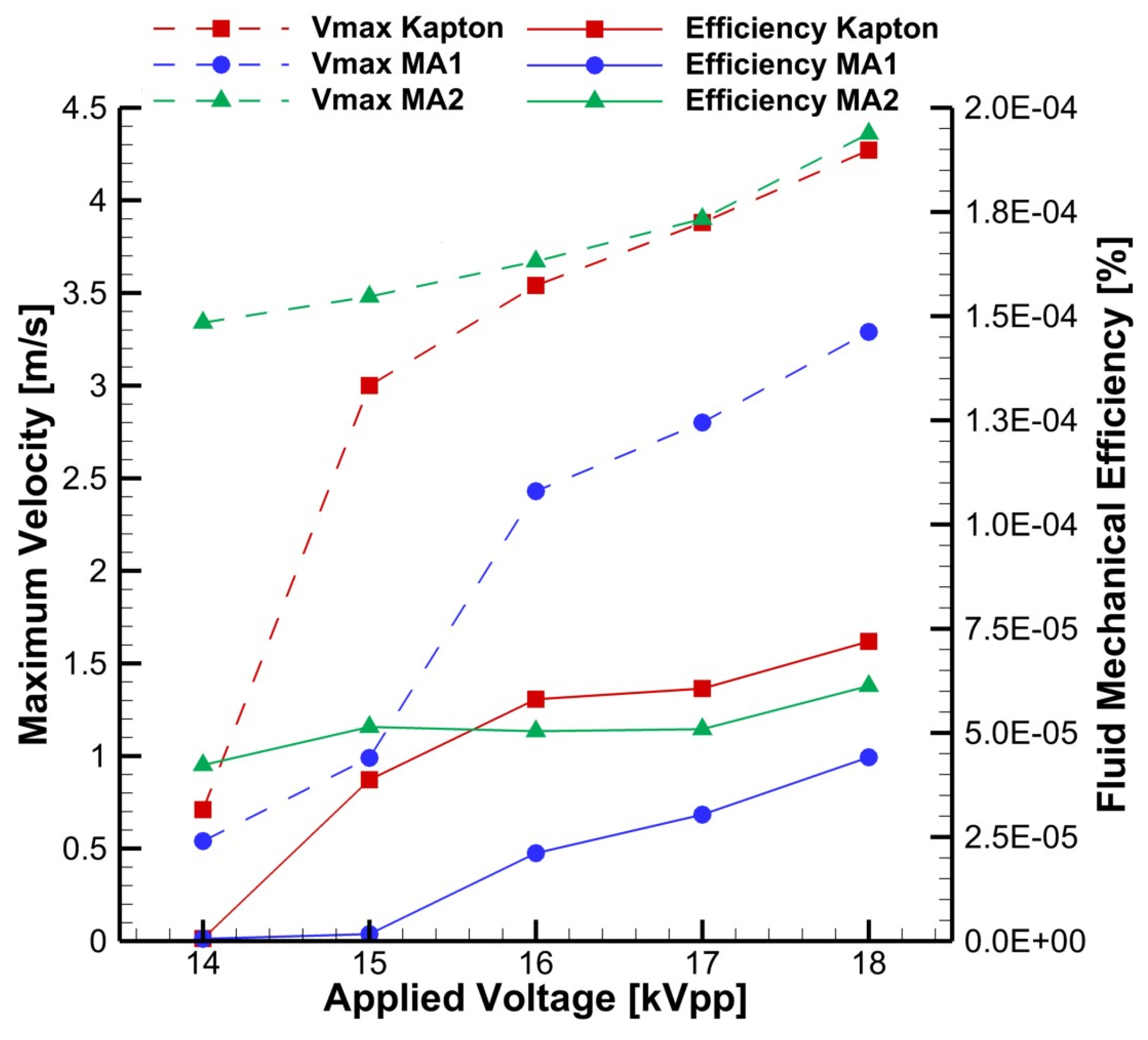
3.3. Plasma-Induced Flow Mechanical Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clyde Warsop, Active Flow Control Using MEMS. In MEMS Aerospace Applications, RTO/NATO. Available online: https://apps.dtic.mil/sti/citations/tr/ADA425494 (accessed on 1 February 2004).
- Wang, J.; Feng, L. Introduction. In Flow Control Techniques and Applications; Cambridge University Press (CUP): Cambridge, UK, 2018; pp. 1–22. ISBN 9781107161566. [Google Scholar]
- Batikh, A.; Baldas, L.; Colin, S. Application of Active Flow Control on Aircrafts—State of the Art. 2017. Available online: https://hal.science/hal-01820331 (accessed on 20 September 2023).
- Bouremel, Y.; Li, J.; Zhao, Z.; Debiasi, M. Effects of AC Dielectric Barrier Discharge Plasma Actuator Location on Flow Separation and Airfoil Performance. Procedia Eng. 2013, 67, 270–278. [Google Scholar] [CrossRef]
- Viguera, R.; Anzai, Y.; Sasaki, Y.; Nonomura, T. Experimental Observations of Transient Flows in Separation Control Using a Plasma Actuator. Actuators 2023, 12, 218. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Wang, X.; Wang, W.; Tang, K.; Li, H. Turbulent boundary layer separation control using plasma actuator at Reynolds number 2000000. Chin. J. Aeronaut. 2016, 29, 1237–1246. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V.; Roy, S. Control of transitional and turbulent flows using plasma-based actuators, Collection of Technical Papers. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, CA, USA, 5–8 June 2006; Volume 2, pp. 1087–1108. [Google Scholar] [CrossRef]
- Al-Sadawi, L.; Chong, T.P.; Kim, J.H. Aero-dynamic noise reduction by plasma actuators for a flat plate with blunt trailing edge. J. Sound Vib. 2019, 439, 173–193. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, C.-Y. Flow control of a D-shaped bluff body using different DBD plasma actuators. J. Fluids Struct. 2021, 103, 103292. [Google Scholar] [CrossRef]
- Konstantinidis, E. Active Control of Bluff-Body Flows Using Plasma Actuators. Actuators 2019, 8, 66. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Experimental transition delay using glow-discharge plasma actuators. Exp. Fluids 2007, 42, 653–657. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Active cancellation of artificially introduced Tollmien–Schlichting waves using plasma actuators. Exp. Fluids 2007, 44, 795–806. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Experimental damping of boundary-layer oscillations using DBD plasma actuators. Int. J. Heat Fluid Flow 2009, 30, 394–402. [Google Scholar] [CrossRef]
- Kim, D.; Do, H.; Choi, H. Drag reduction on a three-dimensional model vehicle using a wire-to-plate DBD plasma actuator. Exp. Fluids 2020, 61, 135. [Google Scholar] [CrossRef]
- Wang, C.-C.; Wen, C.-P. Aerodynamic drag reduction for a truck model using DBD plasma actuators. Adv. Mech. Eng. 2022, 14, 16878132221087852. [Google Scholar] [CrossRef]
- Liu, Y.; Kolbakir, C.; Hu, H.; Hu, H. A comparison study on the thermal effects in DBD plasma actuation and electrical heating for aircraft icing mitigation. Int. J. Heat Mass Transf. 2018, 124, 319–330. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Meng, X.; Cai, J.; Hu, H. Aerodynamic and Thermal Effects of Plasma Actuators on Anti-icing over an Airfoil. Lect. Notes Electr. Eng. 2019, 459, 1008–1019. [Google Scholar] [CrossRef]
- Meng, X.; Hu, H.; Li, C.; Abbasi, A.A.; Cai, J.; Hu, H. Mechanism study of coupled aerodynamic and thermal ef-fects using plasma actuation for anti-icing. Phys. Fluids 2019, 31, 37103. [Google Scholar] [CrossRef]
- Kaneko, Y.; Nishida, H.; Tagawa, Y. Visualization of the Electrohydrodynamic and Thermal Effects of AC-DBD Plasma Actuators of Plate- and Wire-Exposed Electrodes. Actuators 2022, 11, 38. [Google Scholar] [CrossRef]
- Rodrigues, F.; Abdollahzadehsangroudi, M.; Nunes-Pereira, J.; Páscoa, J. Recent Developments on Dielectric Barrier Discharge (DBD) Plasma Actuators for Icing Mitigation. Actuators 2023, 12, 5. [Google Scholar] [CrossRef]
- Xie, L.; Liang, H.; Zong, H.; Liu, X.; Li, Y. Multipurpose distributed dielectric-barrier-discharge plasma actua-tion: Icing sensing, anti-icing, and flow control in one. Phys. Fluids 2022, 34, 071701. [Google Scholar] [CrossRef]
- Thomas, F.O.; Corke, T.C.; Iqbal, M.; Kozlov, A.; Schatzman, D. Optimization of Dielectric Barrier Discharge Plasma Actuators for Active Aerodynamic Flow Control. AIAA J. 2009, 47, 2169–2178. [Google Scholar] [CrossRef]
- Hink, R.; Pipa, A.V.; Schäfer, J.; Caspari, R.; Weichwald, R.; Foest, R.; Brandenburg, R. Influence of dielectric thickness and electrode structure on the ion wind generation by micro fabricated plasma actuators. J. Phys. D Appl. Phys. 2020, 53, 405201. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Rigit, A.R.H.; La, K.C.; Bong, D.B.L. Degradation of a dielectric barrier discharge plasma actuator. In Proceedings of the IEEE International Conference on Properties and Applications of Dielectric Materials, Harbin, China, 19–23 July 2009; pp. 569–572. [Google Scholar] [CrossRef]
- Hanson, R.E.; Houser, N.M.; Lavoie, P. Dielectric material degradation monitoring of dielectric barrier dis-charge plasma actuators. J. Appl. Phys. 2014, 115, 43301. [Google Scholar] [CrossRef]
- Pons, J.; Oukacine, L.; Moreau, E.; Tatibouet, J.-M. Observation of Dielectric Degradation After Surface Dielectric Barrier Discharge Operation in Air at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2008, 36, 1342–1343. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Experimental Analysis of Alternative Dielectric Materials for DBD Plasma Actuators. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar]
- Rodrigues, F.F.; Pereira, J.N.; Abdollahzadeh, M.; Pascoa, J.; Mendez, S.L. Comparative Evaluation of Dielectric Materials for Plasma Actuators Active Flow Control and Heat Transfer Applications. In Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, Virtual, 10–12 August 2021. [Google Scholar] [CrossRef]
- Nunes-Pereira, J.; Rodrigues, F.F.; Abdollahzadehsangroudi, M.; Páscoa, J.C.; Lanceros-Mendez, S. Improved performance of polyimide Cirlex-based dielectric barrier discharge plasma actuators for flow control. Polym. Adv. Technol. 2021, 33, 1278–1290. [Google Scholar] [CrossRef]
- Shvydyuk, K.O.; Rodrigues, F.F.; Nunes-Pereira, J.; Páscoa, J.C.; Lanceros-Mendez, S.; Silva, A.P. Long-lasting ceramic composites for surface dielectric barrier discharge plasma actuators. J. Eur. Ceram. Soc. 2023, 43, 6112–6121. [Google Scholar] [CrossRef]
- Shvydyuk, K.O.; Nunes-Pereira, J.; Rodrigues, F.F.; Silva, A.P. Review of Ceramic Composites in Aeronautics and Aerospace: A Multifunctional Approach for TPS, TBC and DBD Applications. Ceramics 2023, 6, 195–230. [Google Scholar] [CrossRef]
- C20 Standard Test Methods for Apparent Porosity, Water Absorption, Apparent Specific Gravity, and Bulk Density of Burned Refractory Brick and Shapes by Boiling Water. Available online: https://www.astm.org/c0020-00r22.html (accessed on 20 September 2023).
- Ashpis, D.E.; Laun, M.C.; Griebeler, E.L.; Zheng, B.; Ke, X.; Ge, C.; Zhu, Y.; Wu, Y.; Liu, F.; Luo, S.; et al. Progress Toward Accurate Measurement of Dielectric Barrier Discharge Plasma Actuator Power. AIAA J. 2017, 55, 2254–2268. [Google Scholar] [CrossRef] [PubMed]
- Kriegseis, J.; Grundmann, S.; Tropea, C. Power consumption, discharge capacitance and light emission as measures for thrust production of dielectric barrier discharge plasma actuators. J. Appl. Phys. 2011, 110, 013305. [Google Scholar] [CrossRef]
- Pons, J.; Moreau, E.; Touchard, G. Asymmetric surface dielectric barrier discharge in air at atmospheric pressure: Electrical properties and induced airflow characteristics. J. Phys. D Appl. Phys. 2005, 38, 3635–3642. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C. Implementation of Stair-Shaped Dielectric Layers in Micro- and Macroplasma Actuators for Increased Efficiency and Lifetime. J. Fluids Eng. 2020, 142, 104502. [Google Scholar] [CrossRef]
- Somton, K.; Dateraksa, K.; Laoratanakul, P.; McCuiston, R. Shrinkage and properties of die pressed alumina produced from different granule sources. AIP Conf. Proc. 2020, 2279, 060003. [Google Scholar] [CrossRef]
- Pribyl, R.; Stastny, P.; Pazderka, M.; Kelar, J.; Tucekova, Z.K.; Zemanek, M.; Trunec, M.; Cernak, M. Properties of MgAl2O4 doped alumina barrier layers for dielectric barrier discharge. J. Phys. D Appl. Phys. 2020, 53, 505202. [Google Scholar] [CrossRef]
- Lindner, M.; Pipa, A.V.; Brandenburg, R.; Schreiner, R. Expansion of surface barrier discharge scrutinized. Plasma Sources Sci. Technol. 2022, 31, 105018. [Google Scholar] [CrossRef]
- Synek, P.; Zemánek, M.; Kudrle, V.; Hoder, T. Advanced electrical current measurements of microdischarges: Evidence of sub-critical pulses and ion currents in barrier discharge in air. Plasma Sources Sci. Technol. 2018, 27, 045008. [Google Scholar] [CrossRef]
- Synek, P.; Akishev, Y.S.; Petryakov, A.; Trushkin, N.; Vorac, J.; Hoder, T. Electrical analysis and ultra-fast sequential imaging of surface barrier discharge with streamer-leader sequence generated with 100 kHz frequency at the water interface. Plasma Sources Sci. Technol. 2019, 28, 095018. [Google Scholar] [CrossRef]
- Roth, J.R.; Dai, X.; Rahel, J.; Shermann, D.M. The physics and phenomenology of paraelectric One Atmosphere Uniform Glow Discharge Plasma (OAUGDPTM) actuators for aerodynamic flow control. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit-Meeting Papers, Reno, NV, USA, 10–13 January 2005; pp. 14057–14068. [Google Scholar] [CrossRef]
- Wilde, N.D.; Xu, H.; Gomez-Vega, N.; Barrett, S.R.H. A model of surface dielectric barrier discharge power. Appl. Phys. Lett. 2021, 118, 154102. [Google Scholar] [CrossRef]
- Birey, H. Thickness dependence of the dielectric constant and resistance of Al2O3 films. J. Appl. Phys. 1977, 48, 5209–5212. [Google Scholar] [CrossRef]
- Wang, X.; Engel, J.; Liu, C. Liquid crystal polymer (LCP) for MEMS: Processes and applications. J. Micromech. Microeng. 2003, 13, 628–633. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Li, Y.; Wang, P.; He, Y. 3D printing of ceramics: A review. J. Eur. Ceram. Soc. 2018, 39, 661–687. [Google Scholar] [CrossRef]
- Audier, P.; Fénot, M.; Bénard, N.; Moreau, E. Film cooling effectiveness enhancement using surface dielectric barrier discharge plasma actuator. Int. J. Heat Fluid Flow 2016, 62, 247–257. [Google Scholar] [CrossRef]
- Li, G.; Wang, Q.; Huang, Y.; Zhang, H. Large eddy simulation of film cooling effectiveness on a turbine vane pressure side with a saw-tooth plasma actuator. Aerosp. Sci. Technol. 2021, 112, 106615. [Google Scholar] [CrossRef]
- Liu, P.; He, L.; Zhao, B. Discharge and Optical Emission Spectrum Characteristics of a Coaxial Dielectric Barrier Discharge Plasma-Assisted Combustion Actuator. J. Spectrosc. 2020, 2020, 6034848. [Google Scholar] [CrossRef]
- Khasare, S.; Bagherighajari, F.; Dolati, F.; Mahmoudimehr, J.; Páscoa, J.; Abdollahzadehsangroudi, M. The effect of the dielectric barrier discharge plasma actuator in the control of non-reactive flow in a non-premixed bluff body burner. Phys. Fluids 2023, 35, 075135. [Google Scholar] [CrossRef]
- Ran, J.; Zhang, X.; Ge, D.; Li, X.; Li, X. Effect of Dielectric Surface Morphology on Dielectric Barrier Discharge Mode in Air at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2020, 49, 214–218. [Google Scholar] [CrossRef]
- Ran, J.; Li, C.; Ma, D.; Luo, H.; Li, X. Homogeneous dielectric barrier discharges in atmospheric air and its influencing factor. Phys. Plasmas 2018, 25, 033511. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, F.F.; Shvydyuk, K.O.; Nunes-Pereira, J.; Páscoa, J.C.; Silva, A.P. Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics 2024, 7, 192-207. https://doi.org/10.3390/ceramics7010012
Rodrigues FF, Shvydyuk KO, Nunes-Pereira J, Páscoa JC, Silva AP. Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics. 2024; 7(1):192-207. https://doi.org/10.3390/ceramics7010012
Chicago/Turabian StyleRodrigues, Frederico F., Kateryna O. Shvydyuk, João Nunes-Pereira, José C. Páscoa, and Abílio P. Silva. 2024. "Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications" Ceramics 7, no. 1: 192-207. https://doi.org/10.3390/ceramics7010012
APA StyleRodrigues, F. F., Shvydyuk, K. O., Nunes-Pereira, J., Páscoa, J. C., & Silva, A. P. (2024). Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics, 7(1), 192-207. https://doi.org/10.3390/ceramics7010012









