Thermodynamic Characteristics of Phenacetin in Solid State and Saturated Solutions in Several Neat and Binary Solvents
Abstract
:1. Introduction
2. Results and Discussion
2.1. Thermochemical Analysis of Phenacetin
2.2. Thermodynamics of Phenacetin Melting
2.3. Ideal Solubility of Phenacetin
2.4. Solubility of Phenacetin in Neat Solvents
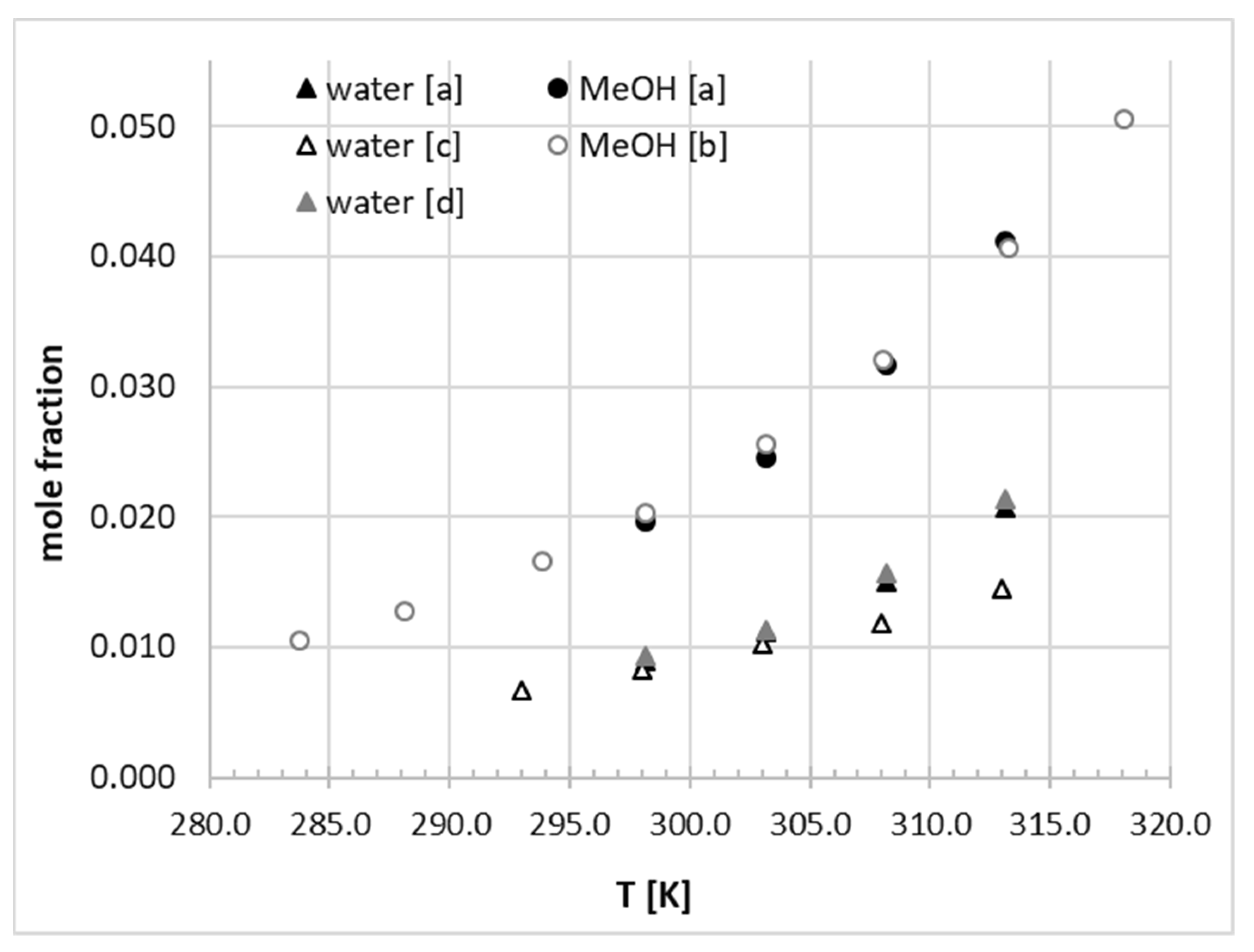
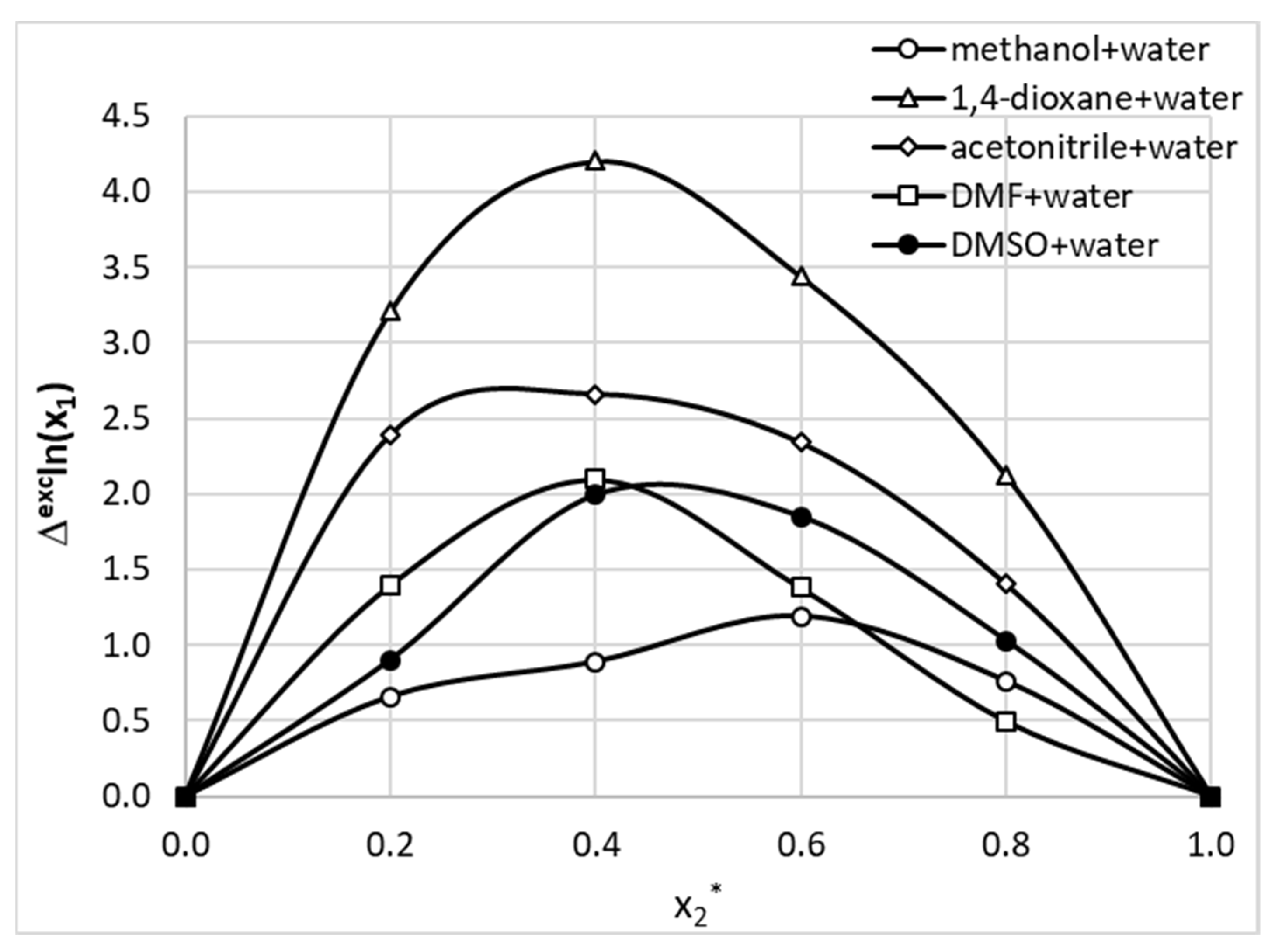
2.5. Solubility of Phenacetin in Aqueous Organic Solvent Binary Mixtures
3. Materials and Methods
3.1. Solubility Determination and Thermodynamic Measurements
3.1.1. Chemicals
3.1.2. Phenacetin Solubility Determination
3.1.3. FTIR-ATR Analysis of Sediments
3.1.4. Differential Scanning Calorimetry (DSC) Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Clissold, S.P. Paracetamol and Phenacetin. Drugs 1986, 32, 46–59. [Google Scholar] [CrossRef]
- Chandrasekharan, N.V.; Dai, H.; Roos, K.L.T.; Evanson, N.K.; Tomsik, J.; Elton, T.S.; Simmons, D.L. COX-3, a cyclooxygenase-1 variant inhibited by acetaminophen and other analgesic/antipyretic drugs: Cloning, structure, and expression. Proc. Natl. Acad. Sci. USA 2002, 99, 13926–13931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, C.B.; Jollow, D.J. The role of N-hydroxyphenetidine in phenacetin-induced hemolytic anemia. Toxicol. Appl. Pharmacol. 1991, 111, 1–12. [Google Scholar] [CrossRef]
- Peters, G.; Baechtold-Fowler, N.; Bonjour, J.P.; Chométy-Diézi, F.; Filloux, B.; Guidoux, R.; Guignard, J.P.; Peters-Haefeli, L.; Roch-Ramel, F.; Schelling, J.L.; et al. General and renal toxicity of phenacetin, paracetamol and some anti-mitotic agents in the rat. Arch. Toxicol. 1972, 28, 225–269. [Google Scholar] [CrossRef]
- Easley, J.L.; Condon, B.F. Phenacetin-induced Methemoglobinemia and Renal Failure. Anesthesiology 1974, 41, 99–100. [Google Scholar] [CrossRef]
- McLaughlin, J.K.; Mandel, J.S.; Blot, W.J.; Schuman, L.M.; Mehl, E.S.; Fraumeni, J.F. A Population-Based Case-Control Study of Renal Cell Carcinoma. J. Natl. Cancer Inst. 1984, 72, 275–284. [Google Scholar] [CrossRef] [PubMed]
- McCredie, M.; Ford, J.; Stewart, J. Risk Factors for Cancer of the Renal Parenchyma. J. Urol. 1989, 141, 1272–1273. [Google Scholar] [CrossRef]
- Khan, S.; Batchelor, H.; Hanson, P.; Perrie, Y.; Mohammed, A.R. Physicochemical characterisation, drug polymer dissolution and in vitro evaluation of phenacetin and phenylbutazone solid dispersions with polyethylene glycol 8000. J. Pharm. Sci. 2011, 100, 4281–4294. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yi, J.-M.; Liu, Y.-J.; Liu, Y.-B.; Zhang, P.-L. Solubility and micronisation of phenacetin in supercritical carbon dioxide. Chem. Pap. 2013, 67, 517–525. [Google Scholar] [CrossRef]
- Ismail, S.; Shawky, S.; Hafez, E. A New Approach for Enhancing the Dissolution Rate of Phenacetin. Drug Dev. Ind. Pharm. 1987, 13, 2147–2158. [Google Scholar] [CrossRef]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef]
- Junyaprasert, V.B.; Morakul, B. Nanocrystals for enhancement of oral bioavailability of poorly water-soluble drugs. Asian J. Pharm. Sci. 2015, 10, 13–23. [Google Scholar] [CrossRef] [Green Version]
- Fulas, O.A.; Laferrière, A.; Ayoub, G.; Gandrath, D.; Mottillo, C.; Titi, H.M.; Stein, R.S.; Friščić, T.; Coderre, T.J. Drug-nutraceutical co-crystal and salts for making new and improved bi-functional analgesics. Pharmaceutics 2020, 12, 1144. [Google Scholar] [CrossRef]
- Grant, D.; Mehdizadeh, M.; Chow, A.-L.; Fairbrother, J. Non-linear van’t Hoff solubility-temperature plots and their pharmaceutical interpretation. Int. J. Pharm. 1984, 18, 25–38. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, and p-toluic acid, and magnesium-DL-aspartate in water from T = (278 to 348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Manzurola, E.; Apelblat, A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, p-toluic acid, calcium-l-lactate, calcium gluconate, magnesium-dl-aspartate, and magnesium-l-lactate in water. J. Chem. Thermodyn. 2002, 34, 1127–1136. [Google Scholar] [CrossRef]
- Buchowski, H.; Ksiazczak, A.; Pietrzyk, S. Solvent activity along a saturation line and solubility of hydrogen-bonding solids. J. Phys. Chem. 1980, 84, 975–979. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Jouyban, A.; Acree, W. Prediction of drug solubility in ethanol-ethyl acetate mixtures at various temperatures using the Jouyban-Acree model. J. Drug Deliv. Sci. Technol. 2007, 17, 159–160. [Google Scholar] [CrossRef] [Green Version]
- Aydi, A.; Ayadi, C.; Ghachem, K.; Al-Khazaal, A.Z.; Delgado, D.R.; Alnaief, M.; Kolsi, L. Solubility, Solution Thermodynamics, and Preferential Solvation of Amygdalin in Ethanol + Water Solvent Mixtures. Pharmaceuticals 2020, 13, 395. [Google Scholar] [CrossRef]
- Przybyłek, M.; Walczak, P.; Ziółkowska, D.; Grela, I.; Cysewski, P. Studies on the solid–liquid equilibria and intermolecular interactions Urea binary mixtures with Sulfanilamide and Sulfacetamide. J. Chem. Thermodyn. 2021, 153, 106308. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alsarra, I.; Alshehri, S. Solubility Data, Solubility Parameters and Thermodynamic Behavior of An Antiviral Drug Emtricitabine in Different Pure Solvents: Molecular Understanding of Solubility and Dissolution. Molecules 2021, 26, 746. [Google Scholar] [CrossRef]
- Cysewski, P.; Walczak, P.; Ziółkowska, D.; Grela, I.; Przybyłek, M. Experimental and theoretical studies on the Sulfamethazine-Urea and Sulfamethizole-Urea solid-liquid equilibria. J. Drug Deliv. Sci. Technol. 2021, 61, 102186. [Google Scholar] [CrossRef]
- Jeliński, T.; Bugalska, N.; Koszucka, K.; Przybyłek, M.; Cysewski, P. Solubility of sulfanilamide in binary solvents containing water: Measurements and prediction using Buchowski-Ksiazczak solubility model. J. Mol. Liq. 2020, 319, 114342. [Google Scholar] [CrossRef]
- Ravi, M.; Julu, T.; Kim, N.A.; Park, K.E.; Jeong, S.H. Solubility Determination of c-Met Inhibitor in Solvent Mixtures and Mathematical Modeling to Develop Nanosuspension Formulation. Molecules 2021, 26, 390. [Google Scholar] [CrossRef] [PubMed]
- Abbott, S. Solubility Science: Principles and Practice; Destech Publications: Lancaster, PA, USA, 2017; ISBN 9781605954844. [Google Scholar]
- Pappa, G.D.; Voutsas, E.C.; Magoulas, K.; Tassios, D.P. Estimation of the Differential Molar Heat Capacities of Organic Compounds at Their Melting Point. Ind. Eng. Chem. Res. 2005, 44, 3799–3806. [Google Scholar] [CrossRef]
- Martínez, F.; Gomez, A. Thermodynamic Study of the Solubility of Some Sulfonamides in Octanol, Water, and the Mutually Saturated Solvents. J. Solut. Chem. 2001, 30, 909–923. [Google Scholar] [CrossRef]
- Perlovich, G.; Kurkov, S.V.; Kinchin, A.N.; Bauer-Brandl, A. Thermodynamics of solutions III: Comparison of the solvation of (+)-naproxen with other NSAIDs. Eur. J. Pharm. Biopharm. 2004, 57, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Sha, J.; Ma, T.; Zhao, R.; Zhang, P.; Sun, R.; Jiang, G.; Wan, Y.; He, H.; Yao, X.; Li, Y.; et al. The dissolution behaviour and apparent thermodynamic analysis of doxifluridine in twelve pure solvents at various temperatures. J. Chem. Thermodyn. 2020, 144, 106073. [Google Scholar] [CrossRef]
- Shakeel, F.; Alshehri, S.; Ibrahim, M.A.; Altamimi, M.; Haq, N.; Elzayat, E.M.; Shazly, G.A. Solubilization and thermodynamic properties of simvastatin in various micellar solutions of different non-ionic surfactants: Computational modeling and solubilization capacity. PLoS ONE 2021, 16, e0249485. [Google Scholar] [CrossRef]
- Sadeghi, M.; Rasmuson, Å.C. On the estimation of crystallization driving forces. CrystEngComm 2019, 21, 5164–5173. [Google Scholar] [CrossRef]
- Camacho, D.M.; Roberts, K.J.; More, I.; Lewtas, K.; Lewtas, K. Solubility and Nucleation of Methyl Stearate as a Function of Crystallization Environment. Energy Fuels 2018, 32, 3447–3459. [Google Scholar] [CrossRef]
- Baena, Y.; Pinzón, J.A.; Barbosa, H.J.; Martínez, F. Temperature-dependence of the solubility of some acetanilide derivatives in several organic and aqueous solvents. Phys. Chem. Liq. 2004, 42, 603–613. [Google Scholar] [CrossRef]
- Chang, Q.-L.; Li, Q.-S.; Wang, S.; Tian, Y.-M. Solubility of Phenacetinum in Methanol, Ethanol, 1-Propanol, 1-Butanol, 1-Pentanol, Tetrahydrofuran, Ethyl Acetate, and Benzene between 282.65 K and 333.70 K. J. Chem. Eng. Data 2007, 52, 1894–1896. [Google Scholar] [CrossRef]
- Cárdenas, Z.J.; Almanza, O.A.; Jouyban, A.; Martínez, F.; Acree, W.E., Jr. Solubility and preferential solvation of phenacetin in methanol + water mixtures at 298.15 K. Phys. Chem. Liq. 2018, 56, 16–32. [Google Scholar] [CrossRef]
- Peña, M.; Escalera, B.; Reíllo, A.; Sánchez, A.; Bustamante, P. Thermodynamics of Cosolvent Action: Phenacetin, Salicylic Acid and Probenecid. J. Pharm. Sci. 2009, 98, 1129–1135. [Google Scholar] [CrossRef] [PubMed]
- Mantheni, D.R.; Maheswaram, M.P.K.; Munigeti, R.; Perera, I.; Riga, A.; Alexander, K.S. Solid- and liquid-state studies of a wide range of chemicals by isothermal and scanning dielectric thermal analysis. J. Therm. Anal. Calorim. 2013, 115, 2253–2260. [Google Scholar] [CrossRef]
- Umnahanant, P.; Chickos, J. Vaporization and Sublimation Enthalpies of Acetanilide and Several Derivatives by Correlation Gas Chromatography. J. Chem. Eng. Data 2012, 57, 1331–1337. [Google Scholar] [CrossRef]
- Baird, J.A.; Van Eerdenbrugh, B.; Taylor, L. A Classification System to Assess the Crystallization Tendency of Organic Molecules from Undercooled Melts. J. Pharm. Sci. 2010, 99, 3787–3806. [Google Scholar] [CrossRef]
- Miyako, Y.; Khalef, N.; Matsuzaki, K.; Pinal, R. Solubility enhancement of hydrophobic compounds by cosolvents: Role of solute hydrophobicity on the solubilization effect. Int. J. Pharm. 2010, 393, 48–54. [Google Scholar] [CrossRef]
- Vecchio, S.; Tomassetti, M. Vapor pressures and standard molar enthalpies, entropies and Gibbs energies of sublimation of three 4-substituted acetanilide derivatives. Fluid Phase Equilibria 2009, 279, 64–72. [Google Scholar] [CrossRef]
- Wassvik, C.M.; Holmén, A.G.; Draheim, R.; Artursson, P.; Bergström, C.A.S. Molecular characteristics for solid-state limited solubility. J. Med. Chem. 2008, 51, 3035–3039. [Google Scholar] [CrossRef] [PubMed]
- Wassvik, C.M.; Holmén, A.G.; Bergström, C.A.S.; Zamora, I.; Artursson, P. Contribution of solid-state properties to the aqueous solubility of drugs. Eur. J. Pharm. Sci. 2006, 29, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, S.; Catalani, A.; Rossi, V.; Tomassetti, M. Thermal analysis study on vaporization of some analgesics. Acetanilide and derivatives. Thermochim. Acta 2004, 420, 99–104. [Google Scholar] [CrossRef]
- Manzo, R.H.; Ahumada, A.A. Effects of Solvent Medium on Solubility. V: Enthalpic and Entropic Contributions to the Free Energy Changes of Di-substituted Benzene Derivatives in Ethanol: Water and Ethanol: Cyclohexane Mixtures. J. Pharm. Sci. 1990, 79, 1109–1115. [Google Scholar] [CrossRef]
- Nordström, F.L.; Rasmuson, Å.C. Determination of the activity of a molecular solute in saturated solution. J. Chem. Thermodyn. 2008, 40, 1684–1692. [Google Scholar] [CrossRef]
- Svärd, M.; Valavi, M.; Khamar, D.; Kuhs, M.; Rasmuson, Å.C. Thermodynamic Stability Analysis of Tolbutamide Polymorphs and Solubility in Organic Solvents. J. Pharm. Sci. 2016, 105, 1901–1906. [Google Scholar] [CrossRef] [Green Version]
- Svärd, M.; Hjorth, T.; Bohlin, M.; Rasmuson, Å.C. Calorimetric Properties and Solubility in Five Pure Organic Solvents of N-Methyl-d-Glucamine (Meglumine). J. Chem. Eng. Data 2016, 61, 1199–1204. [Google Scholar] [CrossRef] [Green Version]
- Neau, S.H.; Flynn, G.L. Solid and Liquid Heat Capacities of n-Alkyl Para-aminobenzoates Near the Melting Point. Pharm. Res. 1990, 7, 1157–1162. [Google Scholar] [CrossRef]
- Hojjati, H.; Rohani, S. Measurement and Prediction of Solubility of Paracetamol in Water−Isopropanol Solution. Part 2. Prediction. Org. Process. Res. Dev. 2006, 10, 1110–1118. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Wu, M. Estimation of the ideal solubility (crystal–liquid fugacity ratio) of organic compounds. J. Pharm. Sci. 2010, 99, 1100–1106. [Google Scholar] [CrossRef]
- Alvarez, V.H.; Saldaña, M.D.A. Modeling Solubility of Polycyclic Aromatic Compounds in Subcritical Water. Ind. Eng. Chem. Res. 2011, 50, 11396–11405. [Google Scholar] [CrossRef]
- Prausintz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Bondi, A. Estimation of Heat Capacity of Liquids. Ind. Eng. Chem. Fundam. 1966, 5, 442–449. [Google Scholar] [CrossRef]
- Mackay, D.; Bobra, A.; Chan, D.W.; Shiu, W.Y. Vapor-pressure correlations for low-volatility environmental chemicals. Environ. Sci. Technol. 1982, 16, 645–649. [Google Scholar] [CrossRef]
- Mishra, D.S.; Yalkowsky, S.H. Ideal Solubility of a Solid Solute: Effect of Heat Capacity Assumptions. Pharm. Res. 1992, 9, 958–959. [Google Scholar] [CrossRef] [PubMed]
- Hildebrandt, J.H.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions; Van Nostrand Reinhold: New York, NY, USA, 1970. [Google Scholar]
- Neau, S.H.; Bhandarkar, S.V.; Hellmuth, E.W. Differential Molar Heat Capacities to Test Ideal Solubility Estimations. Pharm. Res. 1997, 14, 601–605. [Google Scholar] [CrossRef]
- Jia, R.; Sun, K.; Li, R.; Zhang, Y.; Wang, W.; Yin, H.; Fang, D.; Shi, Q.; Tan, Z. Heat capacities of some sugar alcohols as phase change materials for thermal energy storage applications. J. Chem. Thermodyn. 2017, 115, 233–248. [Google Scholar] [CrossRef]
- Mealey, D.; Svärd, M.; Rasmuson, Å.C. Thermodynamics of risperidone and solubility in pure organic solvents. Fluid Phase Equilibria 2014, 375, 73–79. [Google Scholar] [CrossRef]
- Bustamante, C.; Bustamante, P. Nonlinear Enthalpy–Entropy Compensation for the Solubility of Phenacetin in Dioxane–Water Solvent Mixtures. J. Pharm. Sci. 1996, 85, 1109–1111. [Google Scholar] [CrossRef]
- Jouyban, A. Handbook of Solubility Data for Pharmaceuticals; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Jouyban, A.; Fakhree, M.A.A. Experimental and Computational Methods Pertaining to Drug Solubility. In Toxicity and Drug Testing; Acree, W.E., Ed.; InTech: Rijeka, Croatia, 2012; pp. 187–218. ISBN 978-953-51-0004-1. [Google Scholar]
- Jouyban, A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Procek, D.; Dratwa, A. Solubility of Sulfanilamide and Sulfacetamide in neat solvents: Measurements and interpretation using theoretical predictive models, first principle approach and artificial neural networks. Fluid Phase Equilibria 2021, 529, 112883. [Google Scholar] [CrossRef]
- Svärd, M.; Ahuja, D.; Rasmuson, Å.C. Calorimetric Determination of Cocrystal Thermodynamic Stability: Sulfamethazine–Salicylic Acid Case Study. Cryst. Growth Des. 2020, 20, 4243–4251. [Google Scholar] [CrossRef]
- Svärd, M.; Zeng, L.; Valavi, M.; Krishna, G.R.; Rasmuson, Å.C. Solid and Solution State Thermodynamics of Polymorphs of Butamben (Butyl 4-Aminobenzoate) in Pure Organic Solvents. J. Pharm. Sci. 2019, 108, 2377–2382. [Google Scholar] [CrossRef] [PubMed]
- Cheuk, D.; Svärd, M.; Rasmuson, Å.C. Thermodynamics of the Enantiotropic Pharmaceutical Compound Benzocaine and Solubility in Pure Organic Solvents. J. Pharm. Sci. 2020, 109, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Thati, J.; Rasmuson, Å.C. Thermodynamics of molecular solids in organic solvents. J. Chem. Thermodyn. 2012, 48, 150–159. [Google Scholar] [CrossRef]
- Chase, M. NIST-JANAF Thermochemical Tables, 4th ed.; American Institute of Physics: College Park, MD, USA, 1998. [Google Scholar]
- Grønvold, F. Heat capacity of indium from 300 to 1000 K. J. Therm. Anal. Calorim. 1978, 13, 419–428. [Google Scholar] [CrossRef]








| Tm [K] | ΔHm [kJ/mol] |
|---|---|
| 408.05 (±0.19) (1), 407.65 (2), 407.00 (3,4), 409.00 (5), 407.60 (6), 409.60 (7), 408.30 (8), 407.40 (9), 410.20 (10), 407.20 (11), 407.70 (12) | 32.45 (±0.24) (1), 30.72 (2), 28.79 (3), 32.00 (4), 31.50 (5), 36.93 (6), 30.00 (7), 28.75 (8), 34.10 (9), 21.40 (10), 31.25 (11), 32.33 (12) |
| Model | q * [kJ·mol−1] | r * [kJ·mol−1·K−1] | |
|---|---|---|---|
| 1 | experimentally derived linear trend | 12.68 | 0.523 |
| 2 | 12.68 | zero | |
| 3 | 79.52 | zero | |
| 4 | zero | zero | |
| T [K] | 298.15 | 303.15 | 308.15 | 313.15 |
|---|---|---|---|---|
| water (10) | 0.89 ± 0.05 | 1.11 ± 0.05 | 1.50 ± 0.05 | 2.07 ± 0.09 |
| acetonitrile | 11.81 ± 0.73 | 13.69 ± 0.28 | 16.10 ± 0.80 | 19.01 ± 0.45 |
| 1,4-dioxane | 9.1 ± 0.5 | 12.4 ± 0.5 | 16.2 ± 0.6 | 20.3 ± 0.6 |
| DMF | 73.7 ± 1.6 | 86.9 ± 3.1 | 104.7 ± 3.3 | 124.6 ± 3.5 |
| DMSO | 34.1 ± 3.2 | 52.7 ± 2.7 | 77.2 ± 2.9 | 108.1 ± 5.0 |
| methanol | 19.6 ± 1.4 | 24.6 ± 1.2 | 31.6 ± 1.2 | 41.2 ± 1.1 |
| x2* | 298.15 | 303.15 | 308.15 | 313.15 |
|---|---|---|---|---|
| acetonitrile + water | ||||
| 0.2 | 25.9 ± 1.0 | 34.5 ± 0.5 | 46.0 ± 1.7 | 62.8 ± 2.3 |
| 0.4 | 90.1 ± 2.9 | 107.3 ± 4.2 | 132.8 ± 4.6 | 165.4 ± 4.7 |
| 0.6 | 173.6 ± 5.0 | 202.9 ± 6.2 | 246.3 ± 2.9 | 300.3 ± 6.2 |
| 0.8 | 180.8 ± 3.0 | 216.7 ± 5.2 | 269.2 ± 5.4 | 336.2 ± 11.7 |
| 1,4-dioxane + water | ||||
| 0.2 | 55.7 ± 2.3 | 64.2 ± 2.6 | 79.2 ± 1.9 | 99.9 ± 1.7 |
| 0.4 | 379.5 ± 12.7 | 433.2 ± 14.9 | 508.1 ± 7.0 | 616.1 ± 8.7 |
| 0.6 | 446.3 ± 13.0 | 504.2 ± 13.1 | 600.0 ± 8.3 | 739.8 ± 14.5 |
| 0.8 | 302.1 ± 7.9 | 358.0 ± 11.7 | 427.6 ± 9.7 | 510.7 ± 10.6 |
| 0.0 | 0.9 ± 0.0 | 1.1 ± 0.1 | 1.5 ± 0.0 | 2.1 ± 0.1 |
| DMF + water | ||||
| 0.2 | 13.8 ± 2.7 | 33.2 ± 2.1 | 61.1 ± 1.9 | 105.2 ± 3.0 |
| 0.4 | 106.6 ± 4.7 | 138.8 ± 4.7 | 183.4 ± 4.6 | 252.8 ± 4.5 |
| 0.6 | 199.3 ± 10.9 | 268.2 ± 8.8 | 364.7 ± 11.8 | 498.6 ± 9.7 |
| 0.8 | 315.7 ± 16.5 | 434.3 ± 24.7 | 591.2 ± 20.6 | 791.5 ± 14.8 |
| DMSO + water | ||||
| 0.2 | 7.2 ± 0.3 | 10.6 ± 0.5 | 15.0 ± 0.3 | 19.7 ± 0.7 |
| 0.4 | 70.5 ± 2.5 | 85.6 ± 1.1 | 102.7 ± 1.8 | 121.9 ± 2.7 |
| 0.6 | 200.5 ± 3.2 | 243.4 ± 8.8 | 297.6 ± 2.4 | 358.4 ± 6.6 |
| 0.8 | 290.2 ± 15.0 | 407.4 ± 19.7 | 552.7 ± 7.7 | 741.8 ± 15.9 |
| MeOH + water | ||||
| 0.2 | 5.1 ± 0.5 | 7.3 ± 0.6 | 10.4 ± 0.5 | 14.7 ± 0.5 |
| 0.4 | 18.8 ± 0.5 | 22.6 ± 0.9 | 28.3 ± 0.4 | 35.2 ± 1.0 |
| 0.6 | 74.6 ± 1.7 | 84.0 ± 3.5 | 97.4 ± 4.5 | 122.1 ± 1.1 |
| 0.8 | 142.6 ± 4.0 | 167.5 ± 5.5 | 210.0 ± 2.5 | 264.2 ± 6.5 |
| Cosolvent | J0 103 | J1 | J2 103 | RMSD | MAPE |
|---|---|---|---|---|---|
| methanol | 1.149 | −12.40 | 0.759 | 0.10 | 1.23 |
| 1,4-dioxane | 4.615 | −1899.17 | 0.570 | 0.07 | 1.47 |
| acetonitrile | 3.063 | −1511.42 | 1.836 | 0.07 | 1.15 |
| DMF | 2.309 | −2257.29 | 0.989 | 0.22 | 2.85 |
| DMSO | 2.217 | −168.14 | −1.001 | 0.09 | 1.33 |
| Property | Relative Difference | Mean Value | |||||
|---|---|---|---|---|---|---|---|
| 2 ÷ 1 | 3 ÷ 1 | 4 ÷ 1 | 1 | 2 | 3 | 4 | |
| ∆Gfus [kJ/mol] | 4.1% | −9.3% | 6.6% | 8.20 | 8.53 | 7.44 | 8.74 |
| %H [%] | −1.1% | 1.2% | −1.4% | 58.6% | 58.0% | 59.3% | 57.8% |
| xid | −12.6% | 36.1% | −19.6% | 0.036 | 0.032 | 0.050 | 0.029 |
| ln(γ)[water] | −2.2% | 5.1% | −3.6% | 6.02 | 5.88 | 6.32 | 5.80 |
| ln(γ)[methanol] | −21.3% | 49.4% | −34.8% | 0.62 | 0.49 | 0.93 | 0.41 |
| ln(γ)[DMSO] | −188.2% | 435.4% | −306.5% | 0.07 | −0.06 | 0.38 | −0.15 |
| ln(γ)[DMF] | 19.0% | −43.9% | 30.9% | −0.70 | −0.83 | −0.39 | −0.92 |
| ln(γ)[dioxane] | −9.6% | 22.2% | −15.6% | 1.39 | 1.25 | 1.69 | 1.17 |
| ln(γ)[acetonitrile] | −11.8% | 27.2% | −19.2% | 1.13 | 1.00 | 1.44 | 0.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Przybyłek, M.; Kowalska, A.; Tymorek, N.; Dziaman, T.; Cysewski, P. Thermodynamic Characteristics of Phenacetin in Solid State and Saturated Solutions in Several Neat and Binary Solvents. Molecules 2021, 26, 4078. https://doi.org/10.3390/molecules26134078
Przybyłek M, Kowalska A, Tymorek N, Dziaman T, Cysewski P. Thermodynamic Characteristics of Phenacetin in Solid State and Saturated Solutions in Several Neat and Binary Solvents. Molecules. 2021; 26(13):4078. https://doi.org/10.3390/molecules26134078
Chicago/Turabian StylePrzybyłek, Maciej, Anna Kowalska, Natalia Tymorek, Tomasz Dziaman, and Piotr Cysewski. 2021. "Thermodynamic Characteristics of Phenacetin in Solid State and Saturated Solutions in Several Neat and Binary Solvents" Molecules 26, no. 13: 4078. https://doi.org/10.3390/molecules26134078
APA StylePrzybyłek, M., Kowalska, A., Tymorek, N., Dziaman, T., & Cysewski, P. (2021). Thermodynamic Characteristics of Phenacetin in Solid State and Saturated Solutions in Several Neat and Binary Solvents. Molecules, 26(13), 4078. https://doi.org/10.3390/molecules26134078








