IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility
Abstract
:1. Introduction
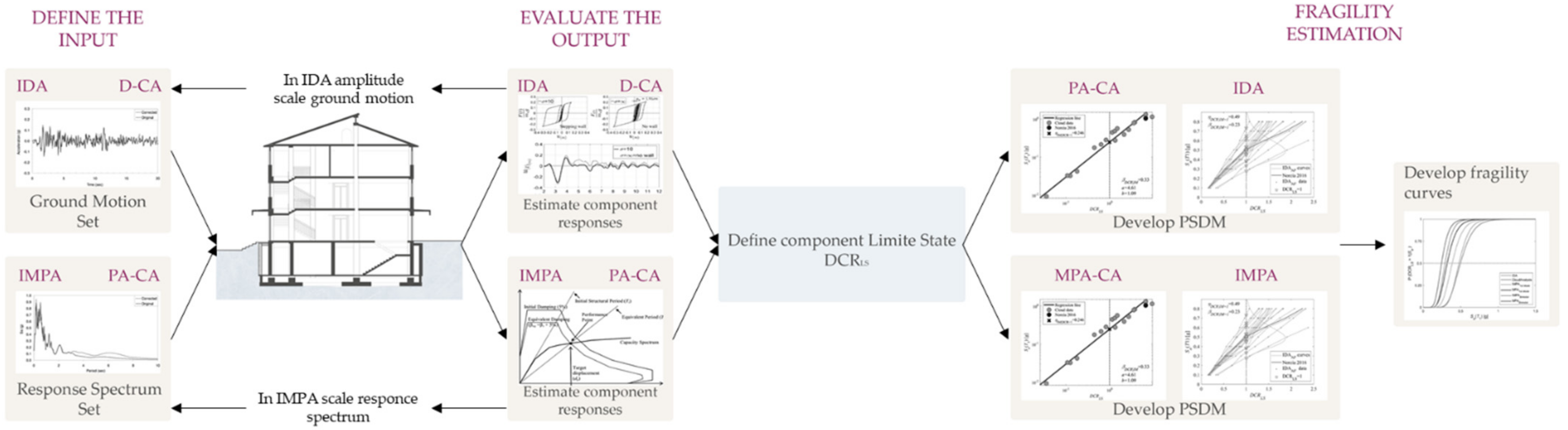
2. Methodology
2.1. Choice of Engineering Demand Parameter and Intensity Measure
2.2. Record Selection
2.3. Performed Nonlinear Analysis
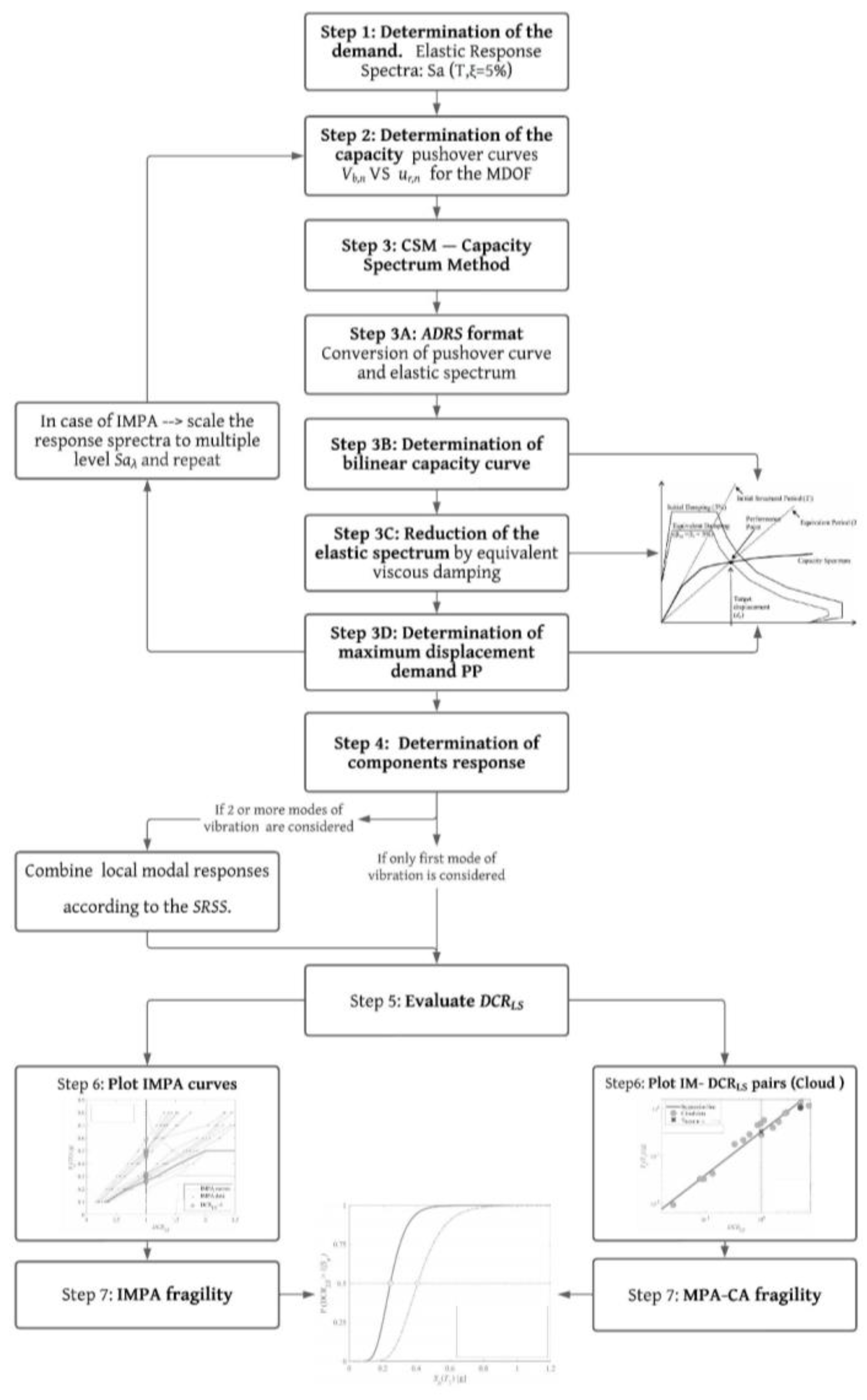
2.3.1. Cloud-Based Analysis
- Determine demand: elastic response spectrum (T, ξ = 5%);
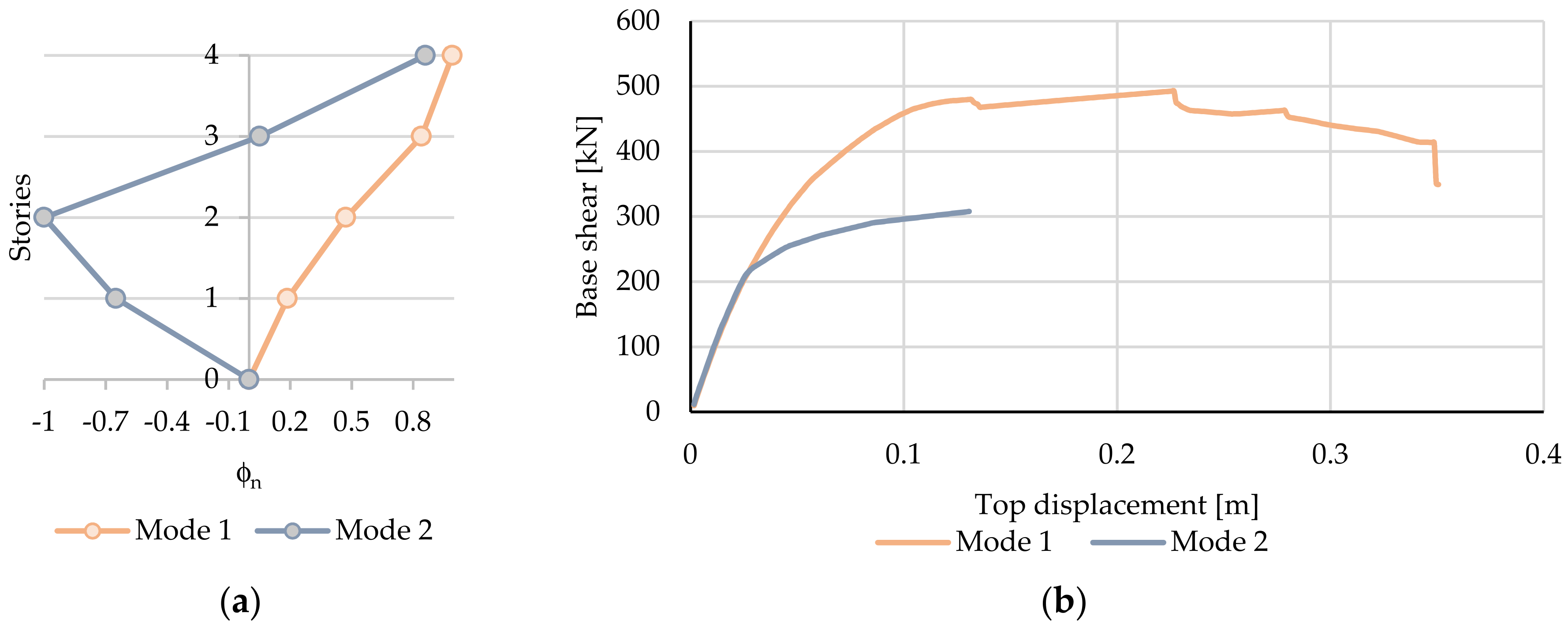
- Evaluate the capacity via pushover curves in terms of base shear Vb,n versus top displacement ur,n for the MDOF structure subjected to lateral forces profile proportional to nth mode shape;
- Determine maximum demand in terms of top displacement via the capacity spectrum method:
- Convert the pushover curve of the nth mode shape to a capacity curve in the ADRS format by (Equations (6)–(9)):where Mtot is the total mass of the structure, ϕn is the nth natural vibration mode, ϕn,r is the amplitude of the nth natural vibration mode at the roof of the structure, and Γn and αn are the modal participation factor and modal mass of the nth mode, respectively;
- Convert 5% damped response spectrum from the standard pseudo-acceleration Sa versus the period of vibration T format to the ADRS format by (Equation (10)):where SD(T) is the displacement spectrum;
- Plot demand and capacity diagrams together in the ADRS space. Determine the bilinear capacity curve. Iteratively determine the displacement demand for the nth mode shape. In this step, the dynamic analyses of a sequence of equivalent linear systems with successively updated values of equivalent viscous damping are involved;
- Reduce the elastic spectrum by the equivalent viscous damping (Equation (11));
- Determinate the performance point or the maximum expected demand in terms of top displacement;
- Convert displacement demand found in step 3 to global top displacement and individual component of local deformation (i.e., interstory drift) for the nth mode shape;
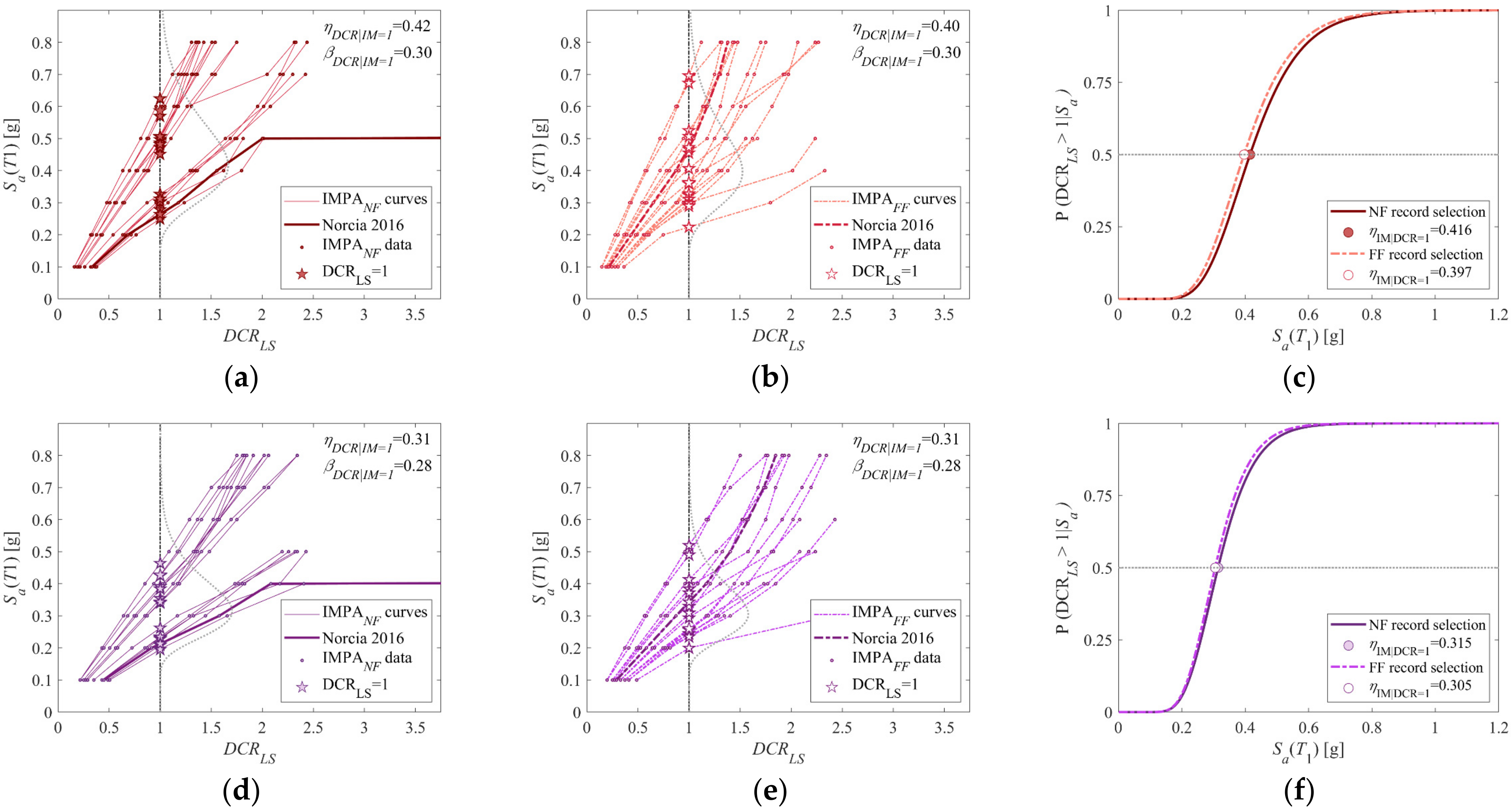
- Evaluate maximum demand to capacity ratio values according to Equation (1). If two or more modes of vibration are considered, combine the local modal responses according to the square-root-of-sum-of-squares (SRSS);
- Estimate parameters of the linear regression model in the logarithm scale to fit the pairs of demand to capacity ratio (DCRLS) and IM;
- Draw structural fragility curve according to Equation (5).
2.3.2. Incremental Dynamic Analysis (IDA)
2.3.3. Incremental Modal Pushover Analysis (IMPA)
3. Numerical Application
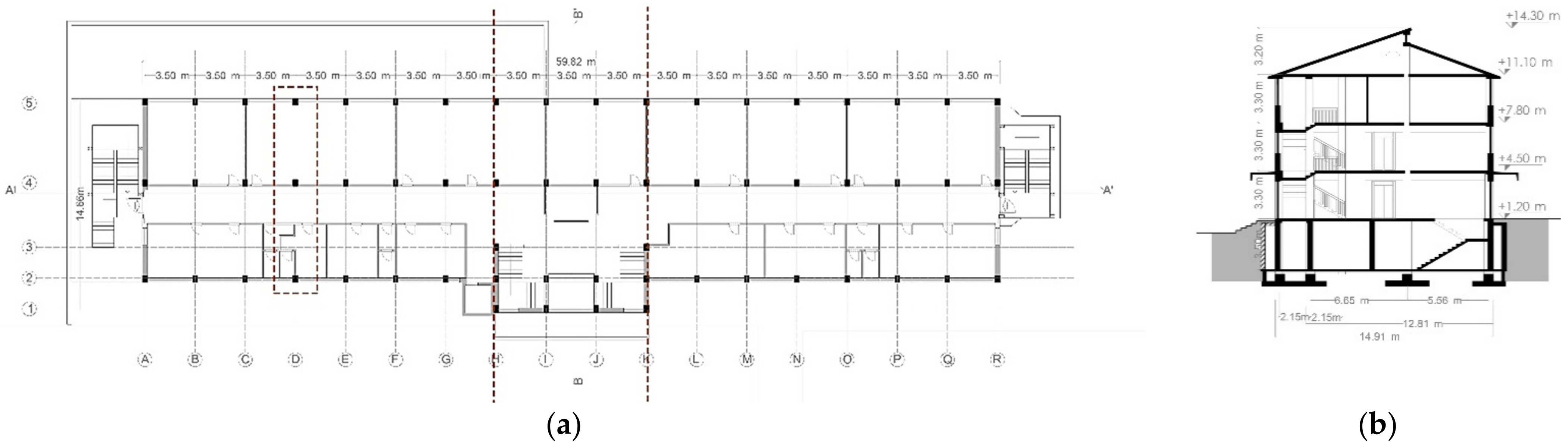
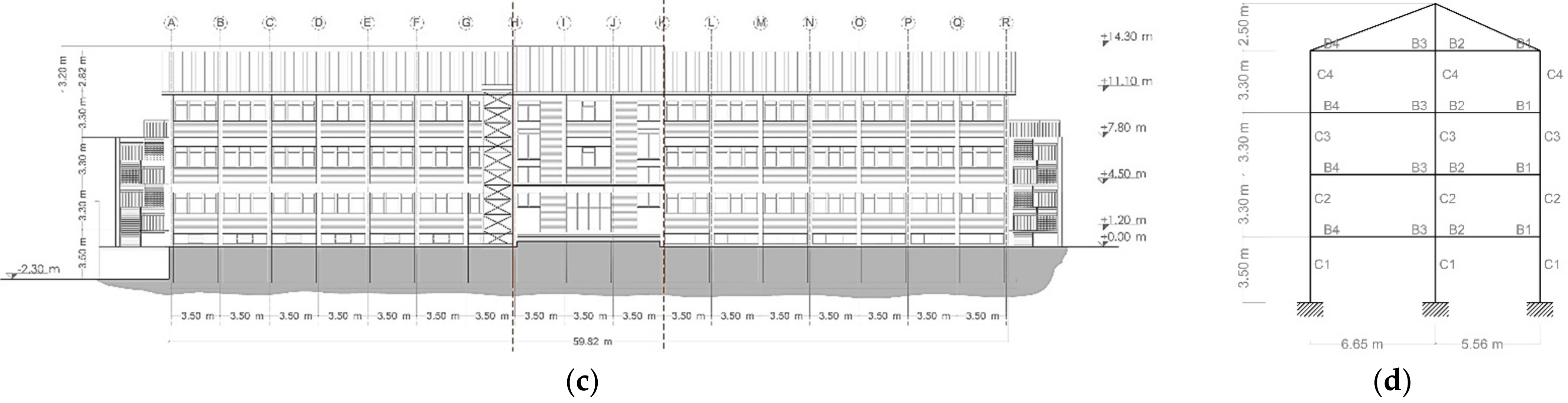
3.1. Frame Description
3.2. FE Model Description
4. Results
4.1. Nonlinear Static Analysis Results
4.2. Nonlinear Dynamic Analysis Results
5. Conclusions
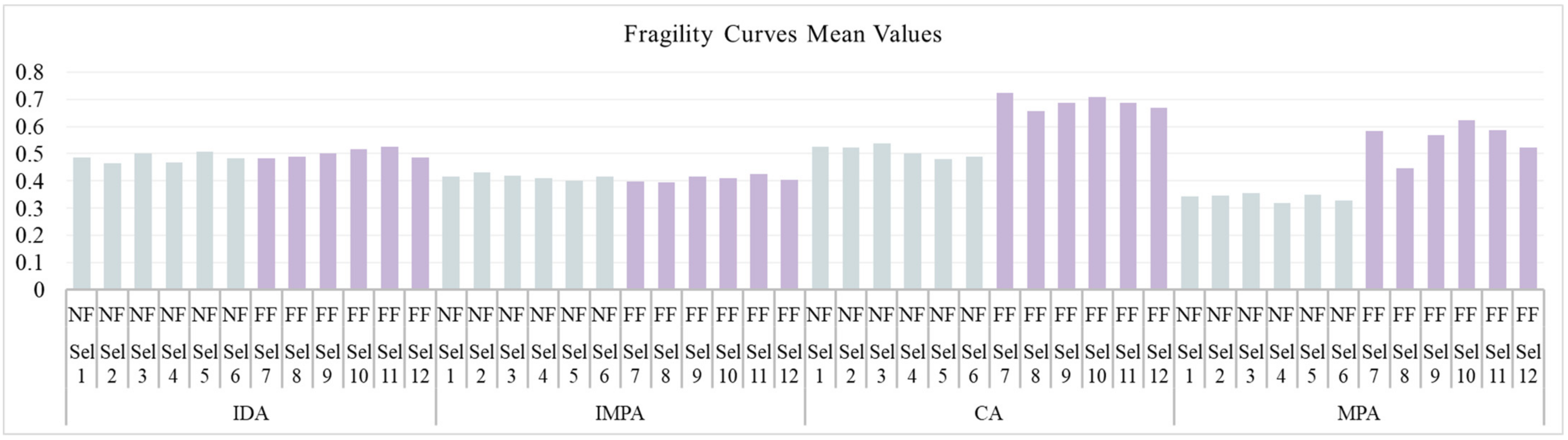
- Comparison of fragility curves shows that, in the case of methodologies distinguished by scaling (in terms of accelerograms (IDA) or response spectra (IMPA)), near-fault records and far-field record selections have led to nearly equivalent results. In contrast, the results in terms of fragility when using records without scaling, i.e., in D-CA and MPA-CA, show clear differences in the whole range of intensities;
- Fragility curves that only consider the contribution of the first mode in determining DCRLS have led to more accurate results in relation to IDA, so the inclusion of higher mode contributions does not seem to be essential for low to medium buildings (up to nine stories [20]);
- A total number of 12 subsets have been extracted from the main 210 set of records and exanimated, but results are not fully reported in this paper. The results have shown that D-CA leads to a smaller vulnerability than MPA-CA and IMPA in all selection and for the whole range of intensities. Methodologies based on the pushover analysis, on the contrary, have led to more conservative results, especially for 16% and 50% fractiles;
- IDA shows less sensitivity to record-to-record variability. It should be noted, however, that IMPA, despite its slightly greater sensitivity, has the advantage of a large reduction in the computational effort required to perform the structural analysis. In IMPA, the total time required relates mostly to the post-processing phase, which is no different for small 2D frames or more complex 3D buildings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krawinkler, H. Challenges and Progress in Performance-Based Earthquake Engineering. In Proceedings of the International Seminar on Seismic Engineering for Tomorrow—In Honor of Professor Hiroshi Akiyama, Tokyo, Japan, 26 November 1999. [Google Scholar]
- Applied Technology Council. ATC-20 Procedures for Postearthquake Safety Evaluation of Buildings; Applied Technology Council: Redwood City, CA, USA, 1989. [Google Scholar]
- FEMA. NEHRP Guidelines for the Seismic Rehabilitation of Buildings; Prepared by the Applied Technology Council; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 1997; p. 273. [Google Scholar]
- SEAOC Vision 2000 Committee. Performance Based Seismic Engineering of Buildings; Soulages, J., Ed.; Structural Engineers Association of California: Sacramento, CA, USA, 1995; Volume 2. [Google Scholar]
- Porter, K.A. An overview of PEER’s Performance-Based Earthquake Engineering Methodology. In Proceedings of the 9th International Conference on Applications of Statistics and Probability in Civil Engineering, San Francisco, CA, USA, 6–9 July 2003; pp. 1–8. [Google Scholar]
- Whitman, R.V.; Biggs, J.M.; Brennan, J.E., III; Cornell, C.A.; De Neufville, R.L.; Vanmarcke, E.H. Seismic design decision analysis. J. Struct. Div. 1975, 101, 1067–1084. [Google Scholar] [CrossRef]
- Kennedy, R.; Ravindra, M. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1984, 79, 47–68. [Google Scholar] [CrossRef]
- Kennedy, R.P.; Cornell, C.A.; Campbell, R.D.; Kaplan, S.; Perla, H.F. Probabilistic seismic safety study of an existing nucle-ar power plant. Nucl. Eng. Des. 1980, 59, 315–338. [Google Scholar] [CrossRef]
- Muntasir Billah, A.H.M.; Shahria Alam, M. Seismic fragility assessment of highway bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2015, 11, 804–832. [Google Scholar] [CrossRef]
- Nazri, F.M.; Miari, M.; Kassem, M.M.; Tan, C.-G.; Farsangi, E.N. Probabilistic Evaluation of Structural Pounding Between Adjacent Buildings Subjected to Repeated Seismic Excitations. Arab. J. Sci. Eng. 2018, 44, 4931–4945. [Google Scholar] [CrossRef]
- Farsangi, E.N.; Yang, T.; Tasnimi, A. Influence of concurrent horizontal and vertical ground excitations on the collapse margins of non-ductile RC frame buildings. Struct. Eng. Mech. 2016, 59, 653–669. [Google Scholar] [CrossRef]
- Kassem, M.; Nazri, F.M.; Farsangi, E.N. The seismic vulnerability assessment methodologies: A state-of-the-art review. Ain Shams Eng. J. 2020, 11, 849–864. [Google Scholar] [CrossRef]
- Farsangi, E.N.; Tasnimi, A.A.; Mansouri, B. Fragility assessment of RC-MRFs under concurrent vertical-horizontal seismic action effects. Comput. Concr. 2015, 16, 99–123. [Google Scholar] [CrossRef]
- Kassem, M.M.; Nazri, F.M.; Farsangi, E.N. The efficiency of an improved seismic vulnerability index under strong ground motions. Structures 2020, 23, 366–382. [Google Scholar] [CrossRef]
- Farsangi, E.N.; Takewaki, I.; Yang, T.Y.; Astaneh-Asl, A.; Gardoni, P. Resilient Structures and Infrastructure; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Dehghani, S.; Fathizadeh, S.; Yang, T.; Farsangi, E.N.; Vosoughi, A.; Hajirasouliha, I.; Málaga-Chuquitaype, C.; Takewaki, I. Performance evaluation of curved damper truss moment frames designed using equivalent energy design procedure. Eng. Struct. 2020, 226, 111363. [Google Scholar] [CrossRef]
- Rakicevic, Z.; Bogdanovic, A.; Farsangi, E.N.; Sivandi-Pour, A. A hybrid seismic isolation system toward more resilient structures: Shaking table experiment and fragility analysis. J. Build. Eng. 2021, 38, 102194. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C.A. Effects of random connection fractures on the demands and reliability for a 3-story pre-Northridge SMRF structure. In Proceedings of the 6th US National Conference on Earthquake Engineering, El Cerrito, CA, USA, 31 May–4 June 1998; pp. 1–12. [Google Scholar]
- Vamvatsikos, D.; Cornell, C. Applied Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Han, S.W.; Chopra, A.K. Approximate incremental dynamic analysis using the modal pushover analysis procedure. Earthq. Eng. Struct. Dyn. 2006, 35, 1853–1873. [Google Scholar] [CrossRef]
- Mackie, K.R.; Stojadinović, B. Comparison of Incremental Dynamic, Cloud, And Stripe Methods for Computing Probabilistic Seismic Demand Models. In Proceedings of the 2005 Structures Congress: Metropolis and Beyond & 2005 Forensic Engineering Symposium, New York, NY, USA, 20–24 April 2005. [Google Scholar]
- Kiani, J.; Khanmohammadi, M. New Approach for Selection of Real Input Ground Motion Records for Incremental Dynamic Analysis (IDA). J. Earthq. Eng. 2015, 19, 592–623. [Google Scholar] [CrossRef]
- Jalayer, F.; Ebrahimian, H.; Miano, A.; Manfredi, G.; Sezen, H. Analytical fragility assessment using unscaled ground motion records. Earthq. Eng. Struct. Dyn. 2017, 46, 2639–2663. [Google Scholar] [CrossRef]
- Shome, N.; Cornell, C.A.; Bazzurro, P.; Carballo, J.E. Earthquakes, records, and nonlinear responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- Iervolino, I.; Cornell, C.A. Record Selection for Nonlinear Seismic Analysis of Structures. Earthq. Spectra 2005, 21, 685–713. [Google Scholar] [CrossRef] [Green Version]
- Shome, N.; Cornell, C.A. Probabilistic Seismic Demand Analysis of Nonlinear Structures; RMS-35, RMS Program; Stanford University: Stanford, CA, USA, 1999; p. 320. [Google Scholar]
- Vargas-Alzate, Y.F.; Hurtado, J.E. Efficiency of intensity measures considering near-and far-fault ground motion records. Geosciences 2021, 11, 234. [Google Scholar] [CrossRef]
- Bradley, B.A. A critical examination of seismic response uncertainty analysis in earthquake engineering. Earthq. Eng. Struct. Dyn. 2013, 42, 1717–1729. [Google Scholar] [CrossRef] [Green Version]
- Luco, N.; Bazzurro, P. Does amplitude scaling of ground motion records result in biased nonlinear structural drift responses? Earthq. Eng. Struct. Dyn. 2007, 36, 1813–1835. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A.; Shome, N.; Carballo, J.E. Three Proposals for Characterizing MDOF Nonlinear Seismic Response. J. Struct. Eng. 1998, 124, 1281–1289. [Google Scholar] [CrossRef]
- Jalayer, F. Direct Probabilistic Seismic Analysis: Implementing Non-Linear Dynamic Assessments. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Miano, A.; Jalayer, F.; Ebrahimian, H.; Prota, A. Nonlinear Dynamic Analysis Procedure With A Limited Number of Analyses and Scaling. In Proceedings of the 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Crete, Greece, 24–26 June 2019. [Google Scholar]
- Mander, J.B. Fragility curve development for assessing the seismic vulnerability of highway bridges. Res. Prog. 1999, 89. Available online: https://www.semanticscholar.org/paper/Fragility-Curve-Development-for-Assessing-the-of-Mander/02d6253500a128cf1a9daf75172d965e6a43e7d1 (accessed on 15 February 2022).
- Shinozuka, M.; Feng, M.Q.; Kim, H.-K.; Kim, S.-H. Nonlinear Static Procedure for Fragility Curve Development. J. Eng. Mech. 2000, 126, 1287–1295. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Shinozuka, M. Nonlinear Static Procedure for Seismic Vulnerability Assessment of Bridges. Comput. Civ. Infrastruct. Eng. 2007, 22, 293–305. [Google Scholar] [CrossRef]
- Rossetto, T.; Gehl, P.; Minas, S.; Galasso, C.; Duffour, P.; Douglas, J.; Cook, O. FRACAS: A capacity spectrum approach for seismic fragility assessment including record-to-record variability. Eng. Struct. 2016, 125, 337–348. [Google Scholar] [CrossRef]
- Dolšek, M.; Fajfar, P. IN2-A simple alternative for IDA. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; pp. 1–6. [Google Scholar]
- Faella, C.; Lima, C.; Martinelli, E. Non-linear Static Methods For Seismic Fragility Analysis And Reliability Evaluation of Existing Structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008; pp. 12–17. [Google Scholar]
- Jalayer, F.; Ebrahimian, H.; Miano, A. N2 with Cloud: A Non-Linear Dynamic Analysis Procedure for the Equivalent SDOF System; Pisa University Press: Pisa, Italy, 2019; pp. 215–225. [Google Scholar]
- Bergami, A.V.; Liu, X.; Nuti, C. Evaluation of a modal pushover based incremental analysis. In Proceedings of the ACE, Vietri sul Mare, Italy, 12–13 June 2015. [Google Scholar]
- Jalayer, F.; De Risi, R.; Manfredi, G. Bayesian Cloud Analysis: Efficient structural fragility assessment using linear regression. Bull. Earthq. Eng. 2014, 13, 1183–1203. [Google Scholar] [CrossRef]
- MIT Ministry of Infrastructures and Transportation. Istruzioni per l’Applicazione delle Nuove Norme Tecniche per le Costruzioni di Cui al Decreto Ministeriale 14 Gennaio 2008; Consiglio Superiore dei Lavori Pubblici. GU Serie Generale No. 47 del 26-02-2009—Suppl. Ordinario No. 27; Ordinario No. 27; No. 617 of 2/2/2009; Italy. 2009. Available online: http://www.cngeologi.it/wp-content/uploads/2016/06/Circ.-esplicativa-NTC-2008-n%C2%B0-617-del-02_02_2009.pdf (accessed on 15 February 2022).
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.J.; Donahue, J.L. NGA-West2 database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- Luzi, L.; Pacor, F.; Puglia, R. Italian Accelerometric Archive v 3.0—Istituto Nazionale di Geofisica e Vulcanologia; Istituto Nazionale di Geofisica e Vulcanologia, Dipartimento della Protezione Civile Nazionale: Rome, Italy, 2019. [Google Scholar] [CrossRef]
- EN 1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Somerville, P.G. Characterizing Near-Fault Ground Motion for the Design and Evaluation of Bridges. In Proceedings of the 3rd National Seismic Conference and Workshop on Bridges and Highways, Portland, OR, USA, 28 April–1 May 2002; Volume 28, pp. 1371–1448. [Google Scholar]
- Shahi, S.K.; Baker, J.W. An efficient algorithm to identify strong velocity pulses in multi-component ground-motions. Bull. Seismol. Soc. Am. 2013, 104, 2456–2466. [Google Scholar] [CrossRef]
- Ertuncay, D.; Malisan, P.; Costa, G.; Grimaz, S. Impulsive Signals Produced by Earthquakes in Italy and their Potential Relation with Site Effects and Structural Damage. Geosciences 2021, 11, 261. [Google Scholar] [CrossRef]
- Miano, A.; Jalayer, F.; Ebrahimian, H.; Prota, A. Cloud to IDA: Efficient fragility assessment with limited scaling. Earthq. Eng. Struct. Dyn. 2017, 47, 1124–1147. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. Capacity-Demand-Diagram Methods for Estimating Seismic Deformation of Inelastic Structures: SDF Systems; Report No. PEER1999/02; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 1999. [Google Scholar]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2001, 31, 561–582. [Google Scholar] [CrossRef] [Green Version]
- Freeman, S.A. The capacity spectrum method. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- ATC-40. Seismic Evaluation and Retrofit of Concrete Buildings; Applied Technology Council: Redwood City, CA, USA, 1996. [Google Scholar]
- Porter, K.; Kennedy, R.; Bachman, R. Creating Fragility Functions for Performance-Based Earthquake Engineering. Earthq. Spectra 2007, 23, 471–489. [Google Scholar] [CrossRef]
- Bergami, A.V.; Liu, X.; Nuti, C. Proposal and Application of the Incremental Modal Pushover Analysis (IMPA). In Proceedings of the IABSE Conference Conference-Structural Engineering: Providing Solutions to Global Challenges, Geneva, Switzerland, 23–25 September 2015. [Google Scholar]
- Bergami, A.V.; Forte, A.; Lavorato, D.; Nuti, C. The Incremental Modal Pushover Analysis (IMPA): Proposal and Application. In Proceedings of the 16WCEE, Santiago de, Chile, Chile, 9–13 January 2017. [Google Scholar]
- Bergami, A.; Fiorentino, G.; Lavorato, D.; Briseghella, B.; Nuti, C. Application of the Incremental Modal Pushover Analysis to Bridges Subjected to Near-Fault Ground Motions. Appl. Sci. 2020, 10, 6738. [Google Scholar] [CrossRef]
- Bergami, A.V.; Nuti, C.; Lavorato, D.; Fiorentino, G.; Briseghella, B. IMPAβ: Incremental Modal Pushover Analysis for Bridges. Appl. Sci. 2020, 10, 4287. [Google Scholar] [CrossRef]
- Bergami, A.V.; Pelle, A.; Fiorentino, G.; Lavorato, D.; Giaccu, G.F.; Quaranta, G.; Briseghella, B.; Nuti, C. Seismic assessment of corroded concrete bridges using incremental modal pushover analysis. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2021; pp. 1–29. [Google Scholar]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research (PEER) Center. 2006, pp. 137–158. Available online: https://opensees.berkeley.edu/OpenSees/manuals/usermanual/OpenSeesCommandLanguageManualJune2006.pdf (accessed on 15 February 2022).
- Priestley, M.J.N.; Park, R. Strength and ductility of concrete bridge columns under seismic loading. Struct. J. 1987, 84, 61–76. [Google Scholar]
- Scott, M.H.; Fenves, G.L. Plastic Hinge Integration Methods for Force-Based Beam–Column Elements. J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Scott, M.H.; Ryan, K.L. Moment-Rotation Behavior of Force-Based Plastic Hinge Elements. Earthq. Spectra 2013, 29, 597–607. [Google Scholar] [CrossRef] [Green Version]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members; University of Toronto: Toronto, ON, Canada, 2000. [Google Scholar]
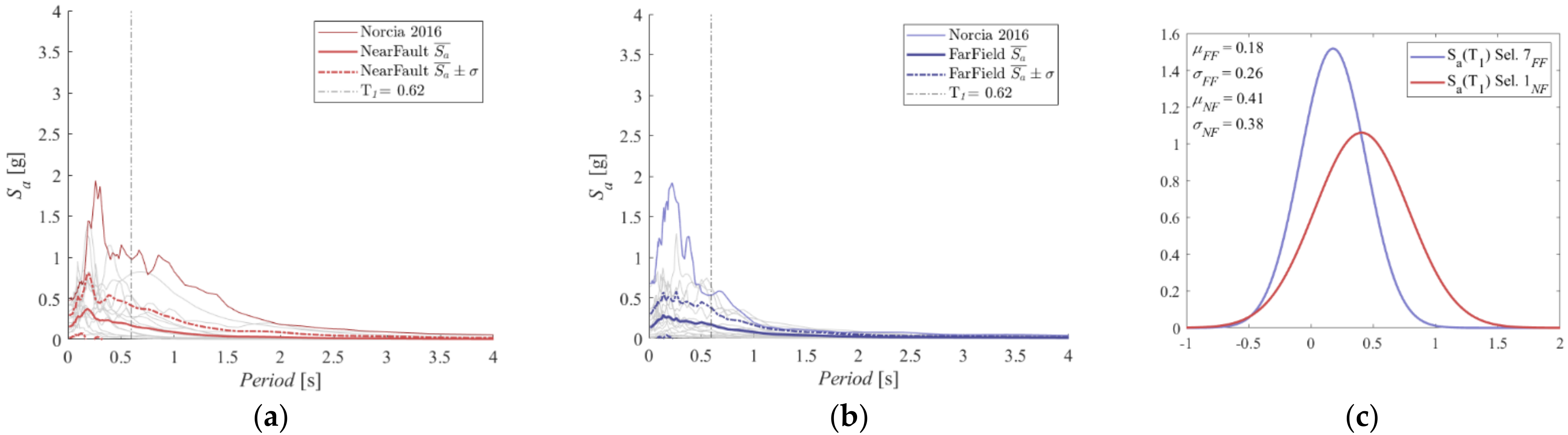




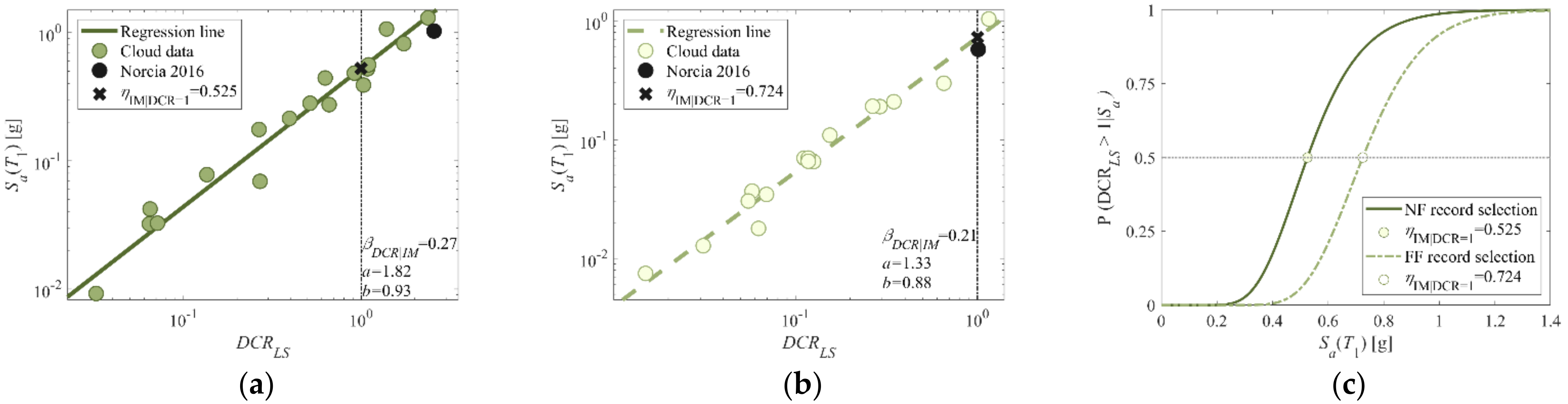
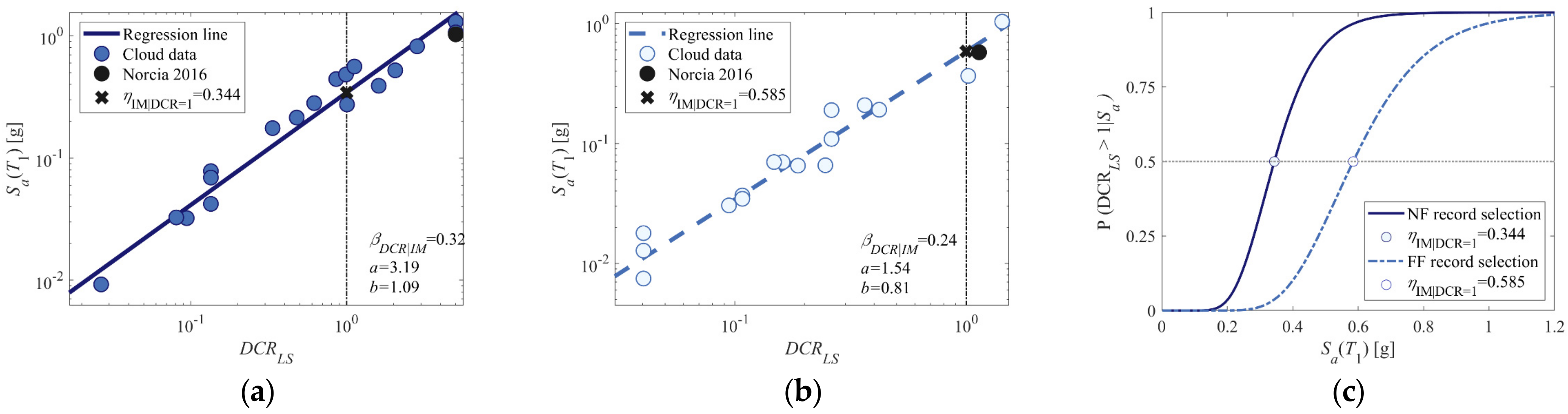
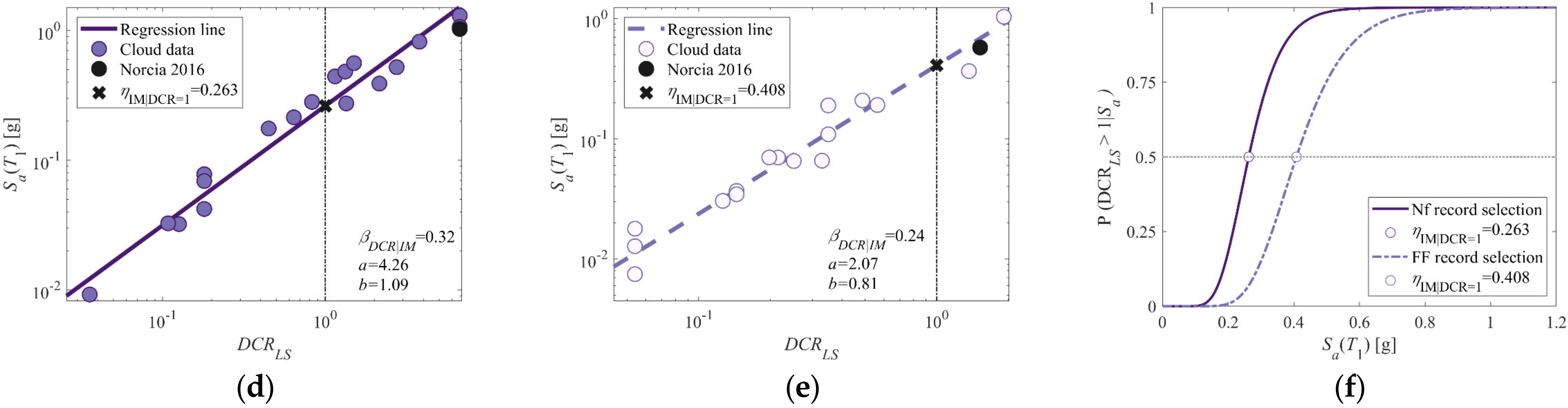

| File ID | Earthquake Name | RSN | Year | Mech. | Mw | Rjb [km] | Vs,30 [m/s] | DS-595 [s] | DS-575 [s] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | “Oroville-01” | 106 | 1975 | Normal | 5.89 | 7.79 | 680.37 | 3.4 | 1.5 |
| 2 | “Oroville-03” | 114 | 1975 | Normal | 4.7 | 7.35 | 418.97 | 4.4 | 1.3 |
| 3 | “Santa Barbara” | 136 | 1978 | Reverse Oblique | 5.92 | 0 | 514.99 | 7.5 | 4.3 |
| 4 | “Tabas_Iran” | 139 | 1978 | Reverse | 7.35 | 0 | 471.53 | 11.3 | 6.7 |
| 5 | “Helena_Montana-01” | 1 | 1935 | Strike-slip | 6 | 2.07 | 593.35 | 2.5 | 1.2 |
| 6 | “Dursunbey_Turkey” | 144 | 1979 | Normal | 5.34 | 5.57 | 585.04 | 2.5 | 1.4 |
| 7 | “Coyote Lake” | 145 | 1979 | Strike-slip | 5.74 | 5.3 | 561.43 | 8.5 | 2.7 |
| 8 | “Norcia_Italy” | 156 | 1979 | Normal | 5.9 | 1.41 | 585.04 | 5.7 | 2.7 |
| 9 | “Livermore-02” | 222 | 1980 | Strike-slip | 5.42 | 7.94 | 550.88 | 4.5 | 1.1 |
| 10 | “Anza (Horse Canyon)-01” | 226 | 1980 | Strike-slip | 5.19 | 5.85 | 617.78 | 2.4 | 1.1 |
| 11 | “Mammoth Lakes-06” | 249 | 1980 | Strike-slip | 5.94 | 6.45 | 373.18 | 5.1 | 2.5 |
| 12 | “Izmir_Turkey” | 134 | 1977 | Normal | 5.3 | 0.74 | 535.24 | 1.6 | 0.3 |
| 13 | “Mammoth Lakes-07” | 253 | 1980 | Strike-slip | 4.73 | 3.86 | 377.41 | 10.2 | 3.1 |
| 14 | Imperial Valley-02 | 6 | 1940 | Strike-Slip | 6.95 | 6.09 | 213.44 | 24.2 | 17.7 |
| 15 | Chalfant Valley-04 | 563 | 1986 | Strike-Slip | 5.44 | 8.88 | 316.19 | 17.1 | 7.7 |
| 16 | Kalamata, Greece-01 | 564 | 1986 | Normal | 6.2 | 6.45 | 382.21 | 6.1 | 1.9 |
| 17 | Kalamata, Greece-02 | 565 | 1986 | Normal | 5.4 | 4 | 382.21 | 4.2 | 1 |
| 18 | Loma Prieta | 752 | 1989 | Reverse Oblique | 6.93 | 8.65 | 288.62 | 13.2 | 5.6 |
| 19 | Central Italy | n.a. | 2016 | Normal | 6.5 | 4.6 | 498 | n.a. | n.a. |
| 20 | “Kern County” | 15 | 1952 | Reverse | 7.36 | 38.42 | 385.43 | 30.3 | 10.7 |
| 21 | “Lytle Creek” | 49 | 1970 | Reverse Oblique | 5.33 | 42.14 | 667.13 | 5.1 | 2.9 |
| 22 | “Santa Barbara” | 135 | 1978 | Reverse Oblique | 5.92 | 23.75 | 465.51 | 7 | 3.4 |
| 23 | “San Fernando” | 81 | 1971 | Reverse | 6.61 | 35.54 | 529.09 | 13.7 | 7.1 |
| 24 | “Northern Calif-07” | 101 | 1975 | Strike-slip | 5.2 | 28.73 | 567.78 | 5.7 | 4.3 |
| 25 | “Oroville-02” | 108 | 1975 | Normal | 4.79 | 12.07 | 377.25 | 7.1 | 3.3 |
| 26 | “Friuli_ Italy-01” | 125 | 1976 | Reverse | 6.5 | 14.97 | 505.23 | 4.9 | 2.5 |
| 27 | “Coyote Lake” | 152 | 1979 | Strike-slip | 5.74 | 20.44 | 362.98 | 8.2 | 3.9 |
| 28 | “Norcia_ Italy” | 157 | 1979 | Normal | 5.9 | 13.21 | 535.24 | 10.5 | 5.9 |
| 29 | “Anza (Horse Canyon)-01” | 225 | 1980 | Strike-slip | 5.19 | 12.24 | 724.89 | 2.1 | 0.7 |
| 30 | “Victoria_ Mexico” | 265 | 1980 | Strike-slip | 6.33 | 13.8 | 471.53 | 8.2 | 4.4 |
| 31 | “Mammoth Lakes-04” | 241 | 1980 | Strike-slip | 5.7 | 12.75 | 537.16 | 11.5 | 3.4 |
| 32 | “Mammoth Lakes-09” | 274 | 1980 | Strike-slip | 4.85 | 10.96 | 377.41 | 16 | 7.7 |
| 33 | “Almiros_ Greece” | 279 | 1980 | Normal | 5.2 | 13.25 | 412.68 | 10 | 4.6 |
| 34 | “Coalinga-02” | 370 | 1983 | Reverse | 5.09 | 24.23 | 467.03 | 13.7 | 8.6 |
| 35 | “Borah Peak_ ID-02” | 442 | 1983 | Normal | 5.1 | 16.31 | 468.44 | 5 | 2.3 |
| 36 | Central Italy | n.a. | 2016 | Normal | 6.5 | 26.9 | n.a. | n.a. | n.a. |
| Sel. 1 NF | Sel. 2 NF | Sel. 3 NF | Sel. 4 NF | Sel. 5 NF | Sel. 6 NF | Sel. 7 FF | Sel. 8 FF | Sel. 9 FF | Sel. 10 FF | Sel. 11 FF | Sel. 12 FF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μRjb | 4.84 | 4.31 | 4.73 | 4.63 | 4.56 | 4.28 | 20.80 | 19.55 | 19.32 | 20.89 | 19.66 | 18.84 |
| σRjb | 2.95 | 3.04 | 3.19 | 3.08 | 2.97 | 3.04 | 10.09 | 8.97 | 6.68 | 9.84 | 9.19 | 6.44 |
| μMw | 5.83 | 5.88 | 6.03 | 5.86 | 5.92 | 5.85 | 5.73 | 5.80 | 5.64 | 5.72 | 5.54 | 5.72 |
| σMw | 0.72 | 0.77 | 0.71 | 0.82 | 0.82 | 0.82 | 0.75 | 0.73 | 0.59 | 0.60 | 0.56 | 0.60 |
| μSa | 0.41 | 0.44 | 0.45 | 0.45 | 0.49 | 0.46 | 0.18 | 0.23 | 0.22 | 0.19 | 0.19 | 0.21 |
| σSa | 0.39 | 0.40 | 0.37 | 0.44 | 0.40 | 0.42 | 0.26 | 0.26 | 0.29 | 0.27 | 0.27 | 0.27 |
| Methodology | IDA | IMPA1 | D-CA | MPA1-CA | IDA | IMPA1 | D-CA | MPA1-CA | IDA | IMPA1 | D-CA | MPA1-CA | IDA | IMPA1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fractile | 0.16 | 0.16 | 0.16 | 0.16 | 0.5 | 0.5 | 0.5 | 0.5 | 0.84 | 0.84 | 0.84 | 0.84 | β | β |
| [g] | % | % | % | [g] | % | % | % | [g] | % | % | % | |||
| Sel. 1 NF | 0.388 | −20% | 1% | −34% | 0.487 | −15% | 8% | −29% | 0.602 | 15% | 44% | −5% | 0.23 | 0.29 |
| Sel. 2 NF | 0.353 | −13% | 3% | −33% | 0.464 | −7% | 12% | −25% | 0.609 | 32% | 62% | 8% | 0.27 | 0.35 |
| Sel. 3 NF | 0.396 | −21% | 7% | −38% | 0.500 | −16% | 8% | −29% | 0.632 | 12% | 38% | 1% | 0.24 | 0.29 |
| Sel. 4 NF | 0.354 | −15% | 5% | −46% | 0.466 | −12% | 8% | −32% | 0.615 | 20% | 45% | 15% | 0.28 | 0.31 |
| Sel. 5 NF | 0.399 | −30% | −11% | −42% | 0.506 | −21% | −5% | −31% | 0.641 | 14% | 28% | 3% | 0.24 | 0.37 |
| Sel. 6 NF | 0.382 | −19% | −4% | −40% | 0.482 | −14% | 1% | −32% | 0.608 | 15% | 34% | −4% | 0.23 | 0.29 |
| Sel. 7 FF | 0.401 | −27% | 43% | 8% | 0.481 | −18% | 50% | 21% | 0.577 | 12% | 90% | 63% | 0.18 | 0.30 |
| Sel. 8 FF | 0.376 | −26% | 32% | −28% | 0.488 | −19% | 35% | −9% | 0.634 | 14% | 78% | 50% | 0.26 | 0.35 |
| Sel. 9 FF | 0.398 | −23% | 44% | 3% | 0.501 | −17% | 37% | 14% | 0.631 | 13% | 64% | 58% | 0.23 | 0.31 |
| Sel. 10 FF | 0.402 | −30% | 46% | −2% | 0.515 | −21% | 37% | 21% | 0.659 | 16% | 65% | 91% | 0.25 | 0.38 |
| Sel. 11 FF | 0.429 | −26% | 34% | −3% | 0.525 | −19% | 31% | 12% | 0.643 | 7% | 57% | 58% | 0.20 | 0.29 |
| Sel. 12 FF | 0.387 | −22% | 47% | −1% | 0.485 | −17% | 38% | 8% | 0.607 | 11% | 62% | 49% | 0.23 | 0.29 |
| μ [g] | 0.39 | 0.30 | 0.47 | 0.31 | 0.49 | 0.41 | 0.60 | 0.45 | 0.62 | 0.56 | 0.76 | 0.65 | ||
| σ | 0.02 | 0.01 | 0.10 | 0.09 | 0.02 | 0.01 | 0.10 | 0.12 | 0.02 | 0.02 | 0.09 | 0.17 | ||
| CoV | 0.05 | 0.05 | 0.21 | 0.29 | 0.04 | 0.03 | 0.16 | 0.27 | 0.03 | 0.04 | 0.12 | 0.27 |
| Methodology | Near-Fault Record (Sel. 1) | Far-Field Record (Sel. 7) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| η16% [g] | η50% [g] | η84% [g] | β | RMSD | η16% [g] | η50% [g] | η84% [g] | β | RMSD | |
| IDA | 0.388 | 0.487 | 0.612 | 0.22 | - | 0.481 | 0.401 | 0.577 | 0.18 | - |
| D-CA | 1% | 8% | 15% | 0.26 | 8% | 43% | 50% | 58% | 0.21 | 41% |
| MPA1-CA | −34% | −29% | −24% | 0.33 | 11% | 8% | 21% | 36% | 0.24 | 20% |
| MPA2-CA | −50% | −46% | −42% | 0.33 | 15% | −24% | −15% | −5% | 0.24 | 5% |
| IMPA1 | −20% | −15% | −9% | 0.28 | 6% | −27% | −18% | −7% | 0.30 | 6% |
| IMPA2 | −39% | −35% | −32% | 0.27 | 13% | −42% | −37% | −30% | 0.28 | 12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contiguglia, C.P.; Pelle, A.; Briseghella, B.; Nuti, C. IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility. Appl. Sci. 2022, 12, 3687. https://doi.org/10.3390/app12073687
Contiguglia CP, Pelle A, Briseghella B, Nuti C. IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility. Applied Sciences. 2022; 12(7):3687. https://doi.org/10.3390/app12073687
Chicago/Turabian StyleContiguglia, Carlotta Pia, Angelo Pelle, Bruno Briseghella, and Camillo Nuti. 2022. "IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility" Applied Sciences 12, no. 7: 3687. https://doi.org/10.3390/app12073687
APA StyleContiguglia, C. P., Pelle, A., Briseghella, B., & Nuti, C. (2022). IMPA versus Cloud Analysis and IDA: Different Methods to Evaluate Structural Seismic Fragility. Applied Sciences, 12(7), 3687. https://doi.org/10.3390/app12073687








