Outlook for Offshore Wind Energy Development in Mexico from WRF Simulations and CMIP6 Projections
Abstract
1. Introduction
- Identification of marine regions in Mexico with significant wind energy potential using 40 years of high spatial resolution numerical simulations with the WRF model.
- Evaluation of the feasibility of developing offshore wind farms in these regions based on the analysis of bathymetric data and the availability of nearby transmission lines.
- Assessment of the ability of the CMIP6 models to reproduce the climatic characteristics of the wind field in the identified regions. This evaluation is conducted by comparing CMIP6 data with the monthly climatologies of wind magnitude obtained from the WRF simulations.
- Obtaining future projections for the regions in Mexico with high offshore wind potential from the results provided by the CMIP6 models that exhibited the best performance. In this study, data from the SSP5-8.5 scenario, representing the most severe future climate projection, are analyzed.
2. Data and Methods
2.1. WRF Simulations
2.2. CMIP6 Models
2.3. Methods
2.3.1. Regridding CMIP6 Data to the WRF Grid
2.3.2. Application of the Power Law Method
2.3.3. Bias Correction and Variability Adjustment of CMIP6 Models
Bias Calculation
Bias and Variability Adjustment
2.3.4. Statistical Metrics
3. Results
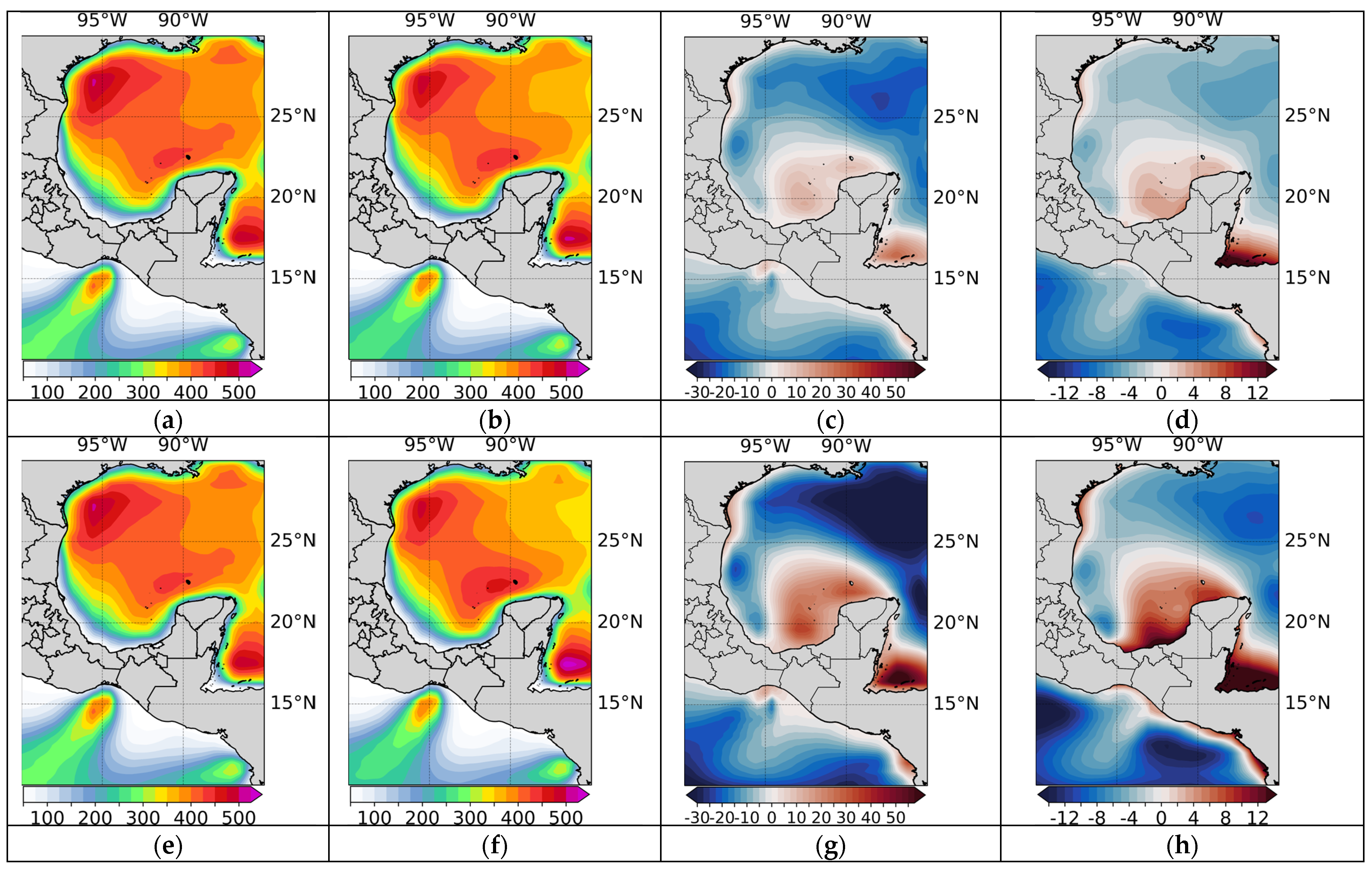
3.1. Identification of Areas with High Offshore Wind Potential in Mexico
3.2. Bathymetry and Transmission Lines
| Water Depth Range (m) | Foundation Technology |
|---|---|
| 0–30 | Monopile/Gravity |
| 30–50 | Jacket/Tripod |
| 50–120 | Floating Structures (Tension Leg Platform and/or Semi-Submersible Type) |
| >120 | Floating Structures (Spar Type) |

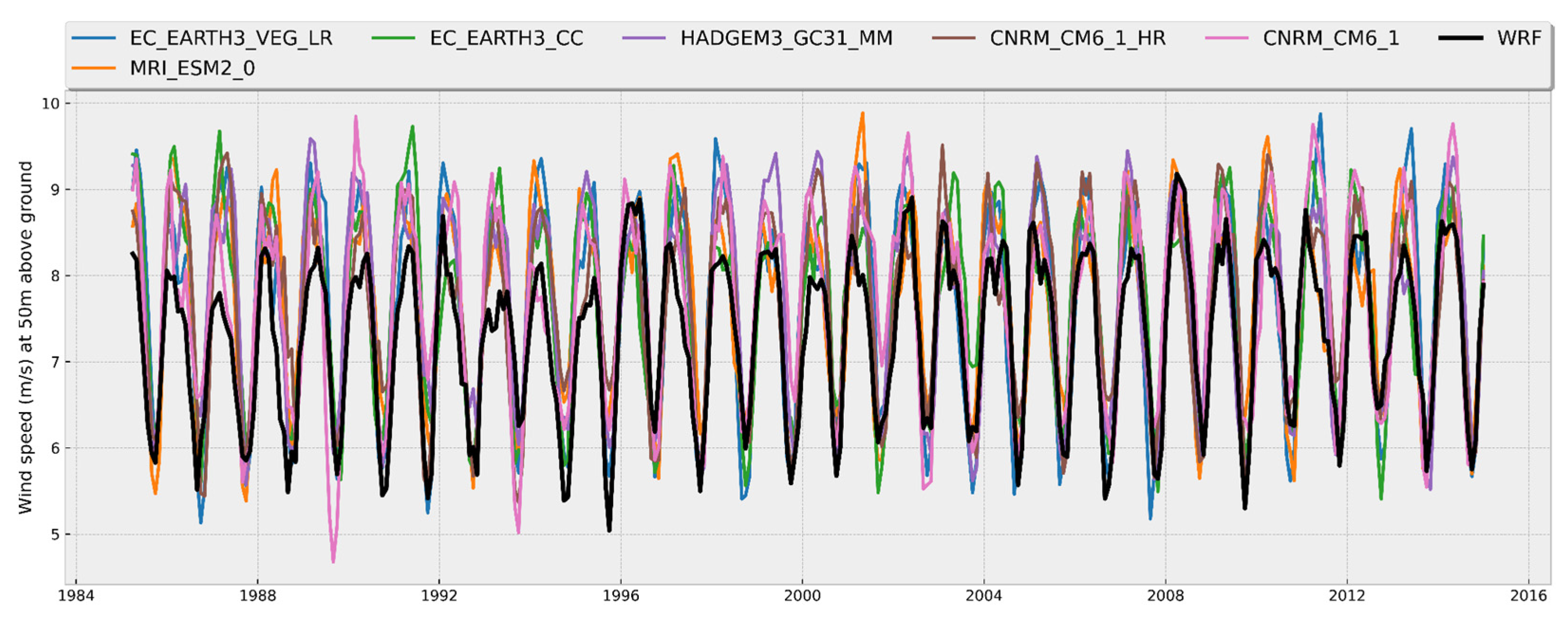
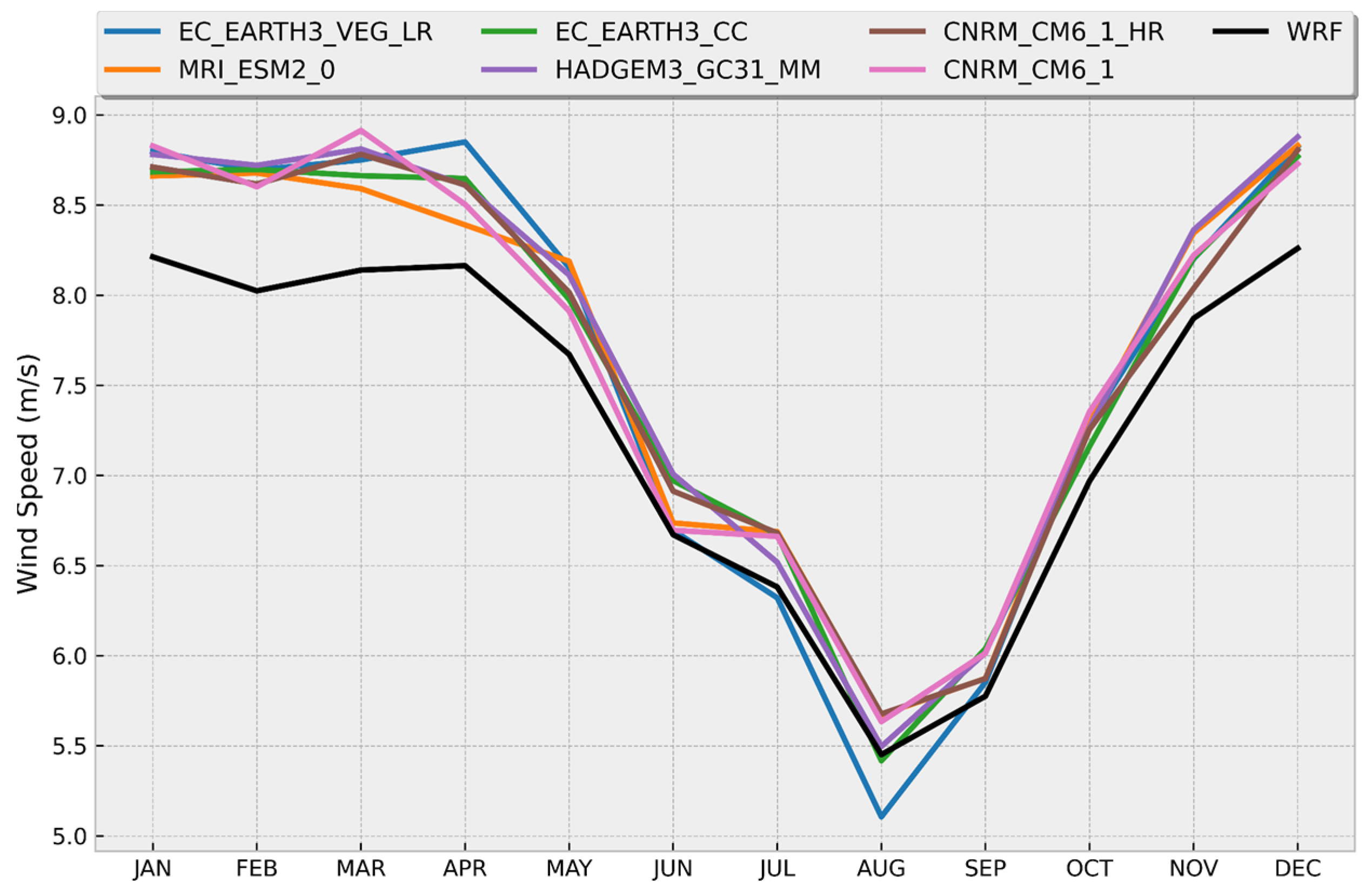
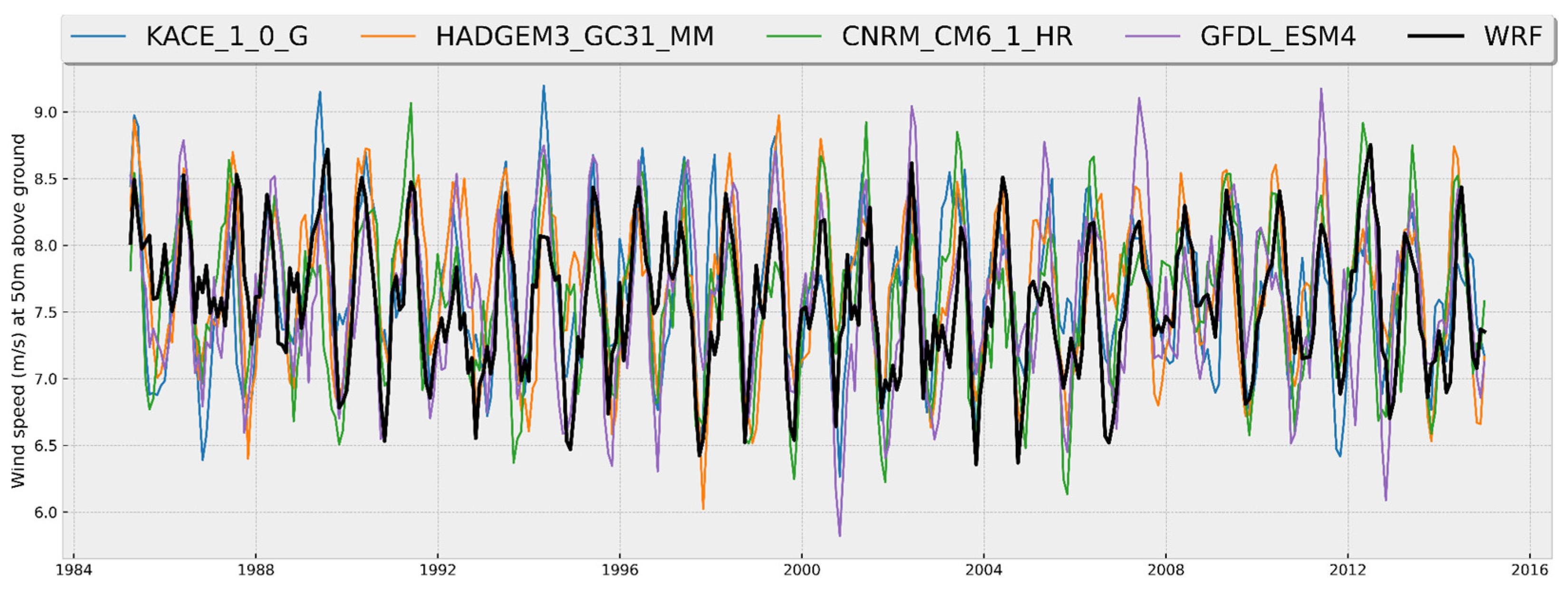
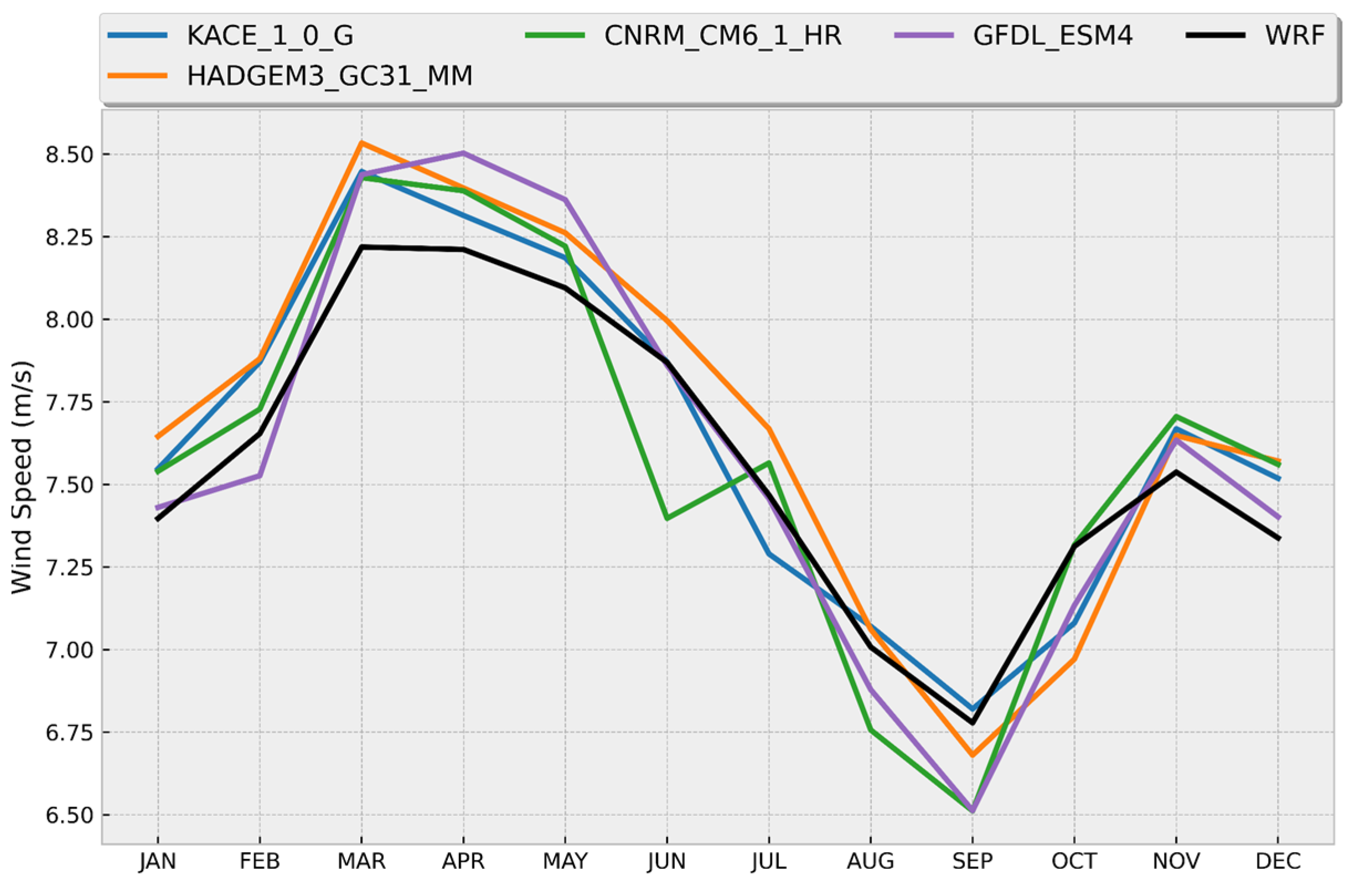
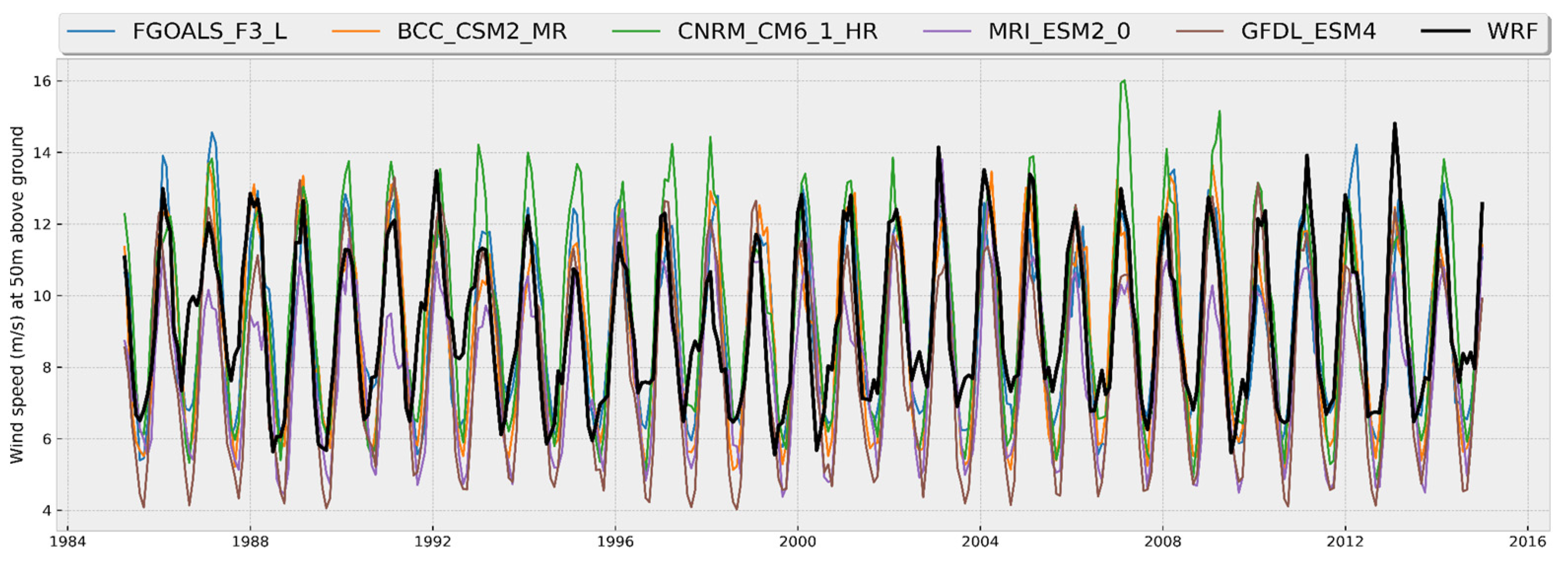
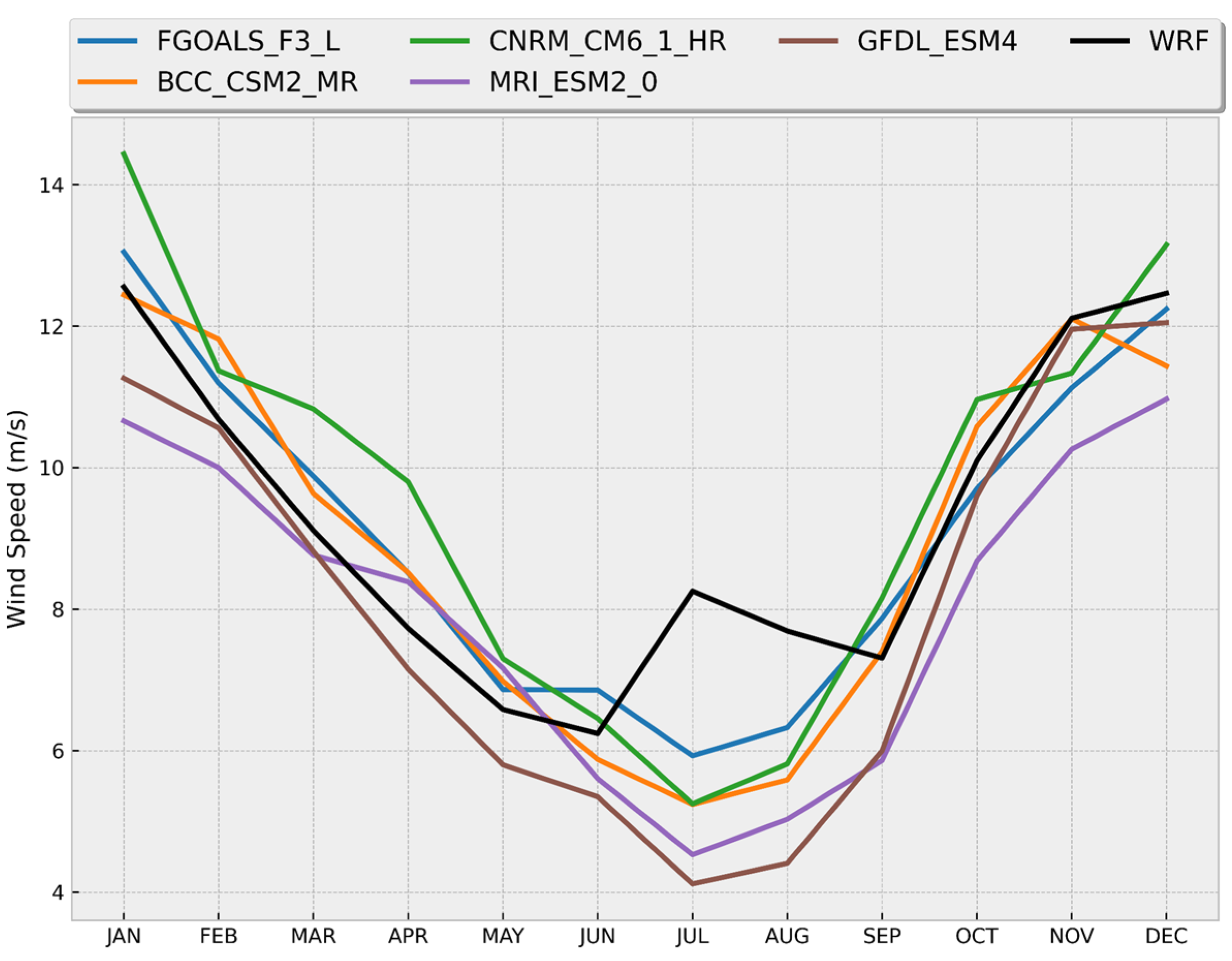
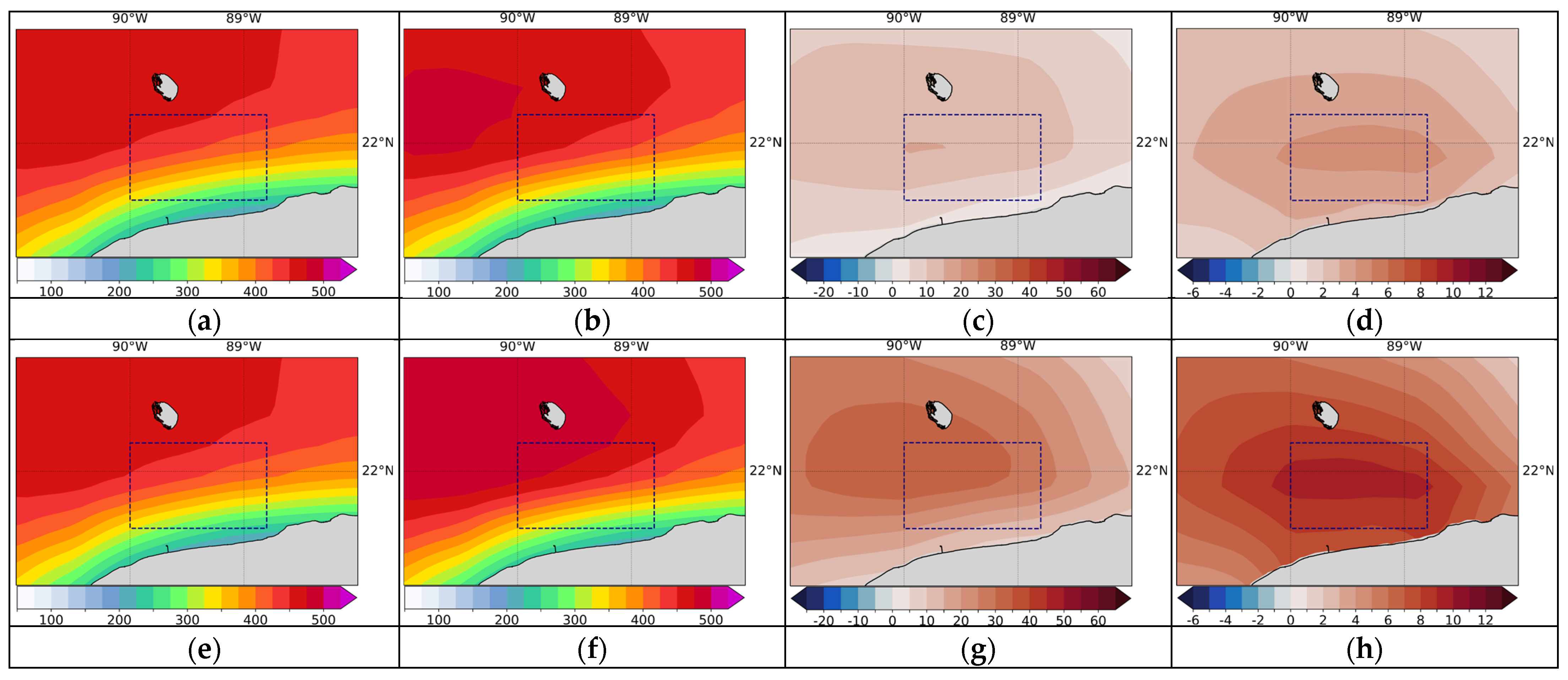
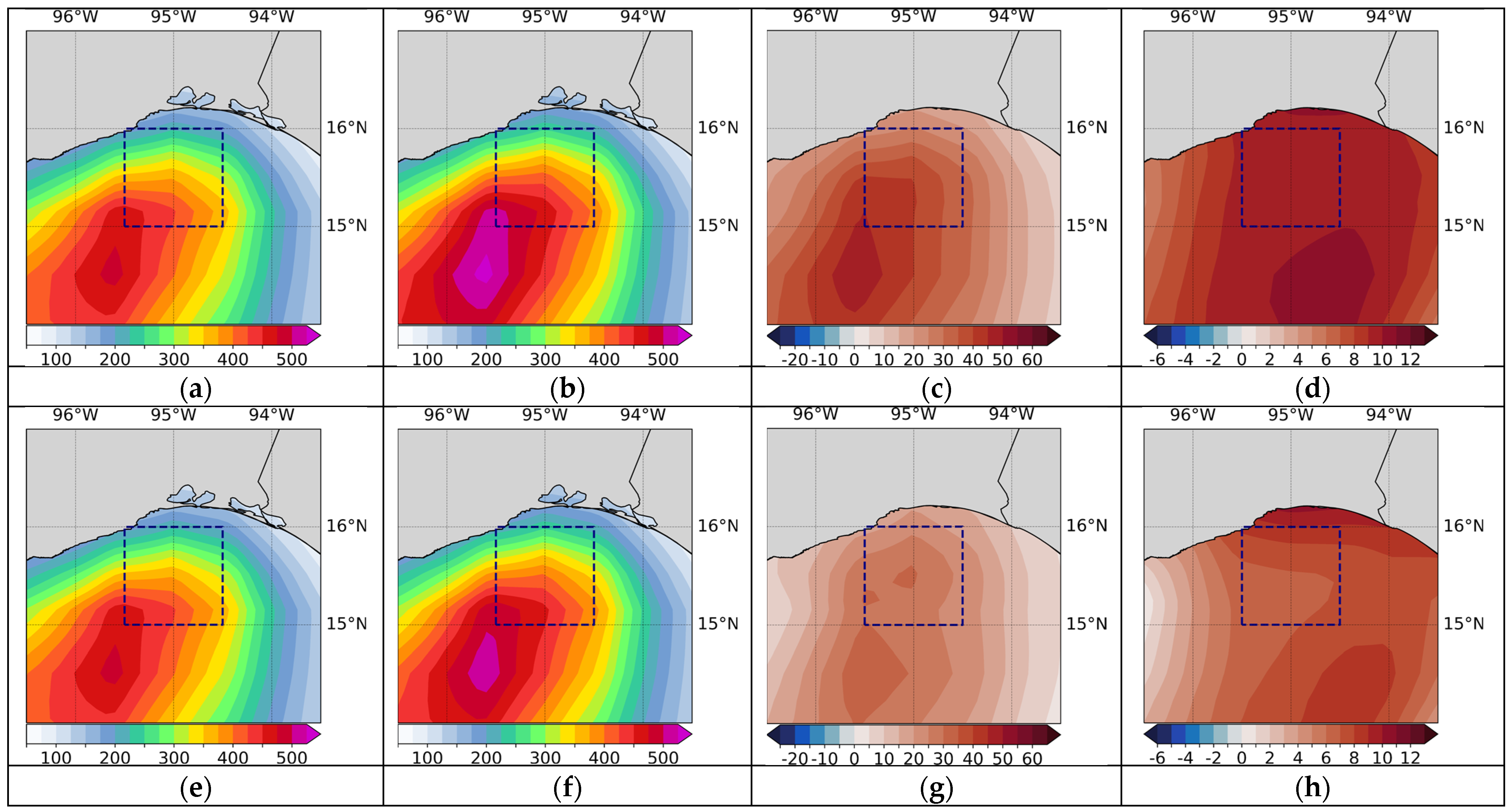
3.3. Comparison between CMIP6 Models and WRF
3.4. CMIP6 Ensembles: Projecting Future Wind Power
3.4.1. Ensemble Average
3.4.2. Weighted Average Ensemble
4. Discussion
- (1)
- Identification of high wind potential areas and recommendations for foundation technologies: Three areas with significant offshore wind potential in Mexico were identified through relatively high spatial resolution (~10 km) numerical simulations with the WRF model for the 40-year period of 1979–2018: the north coast of Tamaulipas (Zone I), the northwest coast of Yucatan (Zone II), and the Gulf of Tehuantepec (Zone III). These areas have been studied in other works under different approaches. Among them, Canul-Reyes et al. [9] assessed offshore wind potential in the Gulf of Mexico based on data from the ERA5 and MERRA2 reanalyses (~30 and 50 km resolution, respectively), identifying promising areas for development based on geographical restrictions, wind speed analysis, and capacity factor seasonal variability. They identified the north coast of the Tamaulipas state and the northwest of the Yucatan peninsula as the areas with the greatest potential for offshore wind energy development in the Gulf of Mexico.
- (2)
- Model performance: A comparative analysis was carried out of the time series of monthly averages and annual cycles of wind magnitude at 50 m above the surface, obtained from the WRF data and the best performing CMIP6 models in the three zones of interest for the historical period 1985–2014. The results indicated that, in general, the CMIP6 models adequately reproduce seasonal variations and annual cycles, although not necessarily the interannual variability, with a certain over or underestimation of the values depending on the time of year and the particular zone. Each zone shows particular behaviors throughout the year in terms of the variable analyzed. For example, the annual cycle in Zone I (see Figure 6) shows a range of values approximately between 5.50 and 8.30 m/s, with stronger winds between December and April and weaker ones in August and September. In Zone II, winds with a greater interannual variation are observed compared to the other two zones (see Figure 7), which influenced the lower values of the correlation coefficient we obtained. Its annual cycle shows a smaller range of variation, with values between approximately 6.75 and 8.25 m/s; however, the most intense winds occur between March and May and not during the winter months (see Figure 8). This is a zone that is predominantly affected by the easterly trade winds which flow parallel to the coast throughout the year, while in Zone I the predominant winds change direction throughout the year and most of the time flow from sea to land coming from the southeast [68]. The above indicates that the dynamic processes that determine the high wind potential in both areas are different. The results obtained in the present study are in accordance with the analyses of the monthly averages of the capacity factor in these two areas of the Gulf of Mexico carried out by Canul-Reyes et al. [9]. In general, they obtained the maximum values between March and April and the minimum values from July to September in those regions, which coincides with our analysis of the annual cycle of wind magnitude.
- (3)
- Future projections of offshore wind energy potential: In this work, two types of CMIP6 model ensembles were tested in order to analyze the future projections of offshore wind potential considering a short-term (2040–2069) and a long-term (2070–2099) period under the SSP5-8.5 scenario: the ensemble average and the weighted average ensemble. The latter was obtained by calculating the contribution of each CMIP6 model according to its similarity with the climatological conditions of the wind magnitude computed from the WRF reference model for each of the three analyzed zones. To do this, the smallest MAPE values for each zone were considered (see Table 6, Table 7 and Table 8). The result is a weighted-average ensemble which assigns specific weights to each model, prioritizing those that showed better performance in each area, unlike the ensemble average that considers them all equally. In this sense, we consider that the weighted average ensemble yields more consistent, reliable, and robust results compared to the average ensemble.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Department of Energy. How Wind Can Help Us Breathe Easier. Energy.gov. Available online: https://www.energy.gov/eere/wind/articles/how-wind-can-help-us-breathe-easier (accessed on 7 September 2023).
- Marvel, K.; Kravitz, B.; Caldeira, K. Geophysical limits to global wind power. Nat. Clim. Chang. 2013, 3, 118–121. [Google Scholar] [CrossRef]
- Bailey, H.; Brookes, K.L.; Thompson, P.M. Assessing environmental impacts of offshore wind farms: Lessons learned and recommendations for the future. Aquat. Biosyst. 2014, 10, 8. [Google Scholar] [CrossRef] [PubMed]
- Leung, D.Y.; Yang, Y. Wind energy development and its environmental impact: A review. Renew. Sustain. Energy Rev. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Ellis, G.; Ferraro, G. The Social Acceptance of Wind Energy; Technical Report. JRC Science for Policy Report; European Commission: Brussels, Belgium, 2016. [CrossRef]
- Wind Europe. Wind Energy in Europe: 2022 Statistics and the Outlook for 2023–2027. Available online: https://windeurope.org/intelligence-platform/product/wind-energy-in-europe-2022-statistics-and-the-outlook-for-2023-2027/#downloads (accessed on 7 September 2023).
- Huacuz, J.M. The road to green power in Mexico—Reflections on the prospects for the large-scale and sustainable implementation of renewable energy. Energy Policy 2005, 33, 2087–2099. [Google Scholar] [CrossRef]
- Bracho, R.; Alvarez, J.; Aznar, A.; Brancucci, C.; Brinkman, G.; Cooperman, A.; Flores-Espino, F.; Frazier, W.; Gearhart, C.; Guerra Fernandez, O.J.; et al. Mexico Clean Energy Report; (No. NREL/TP-7A40-82580), National Renewable Energy Lab. (NREL): Golden, CO, USA, 2022. [Google Scholar]
- Canul-Reyes, D.A.; Rodríguez-Hernández, O.; Jarquin-Laguna, A. Potential zones for offshore wind power development in the Gulf of Mexico using reanalyses data and capacity factor seasonal analysis. Energy Sustain. Dev. 2022, 68, 211–219. [Google Scholar] [CrossRef]
- Arenas-López, J.P.; Badaoui, M. Analysis of the offshore wind resource and its economic assessment in two zones of Mexico. Sustain. Energy Technol. Assess. 2022, 52, 101997. [Google Scholar] [CrossRef]
- Bernal-Camacho, D.F.; Fontes, J.V.; Mendoza, E. A Technical Assessment of Offshore Wind Energy in Mexico: A Case Study in Tehuantepec Gulf. Energies 2022, 15, 4367. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Wind resource evolution in Europe under different scenarios of climate change characterised by the novel Shared Socioeconomic Pathways. Energy Convers. Manag. 2021, 234, 113961. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Climate change impacts on wind energy resources in North America based on the CMIP6 projections. Sci. Total Environ. 2022, 806, 150580. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Zha, J.; Li, Z.; Azorin-Molina, C.; Deng, K.; Minola, L.; Chen, D. Evaluation of global terrestrial near-surface wind speed simulated by CMIP6 models and their future projections. Ann. N. Y. Acad. Sci. 2022, 1518, 249–263. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X. Future projections of offshore wind energy resources in China using CMIP6 simulations and a deep learning-based downscaling method. Energy 2021, 217, 119321. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; (No. NCAR/TN-475+STR), University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Fernández-González, S.; Martín, M.L.; García-Ortega, E.; Merino, A.; Lorenzana, J.; Sánchez, J.L.; Valero, F.; Rodrigo, J.S. Sensitivity analysis of the WRF model: Wind-resource assessment for complex terrain. J. Appl. Meteorol. Climatol. 2018, 57, 733–753. [Google Scholar] [CrossRef]
- Li, J.; Zheng, X.; Zhang, C.; Chen, Y. Impact of land-use and land-cover change on meteorology in the Beijing–Tianjin–Hebei Region from 1990 to 2010. Sustainability 2018, 10, 176. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Tovar-Pescador, J. Influence of land-use misrepresentation on the accuracy of WRF wind estimates: Evaluation of GLCC and CORINE land-use maps in southern Spain. Atmos. Res. 2015, 157, 17–28. [Google Scholar] [CrossRef]
- Durán, P.; Meißner, C.; Rutledge, K.; Fonseca, R.; Martin-Torres, J.; Adaramola, M.S. Meso-microscale coupling for wind resource assessment using averaged atmospheric stability conditions. Meteorol. Z. 2019, 28, 273–291. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Sīle, T.; Witha, B.; Davis, N.N.; Dörenkämper, M.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; Olsen, B.T.; et al. The making of the New European Wind Atlas—Part 1: Model sensitivity. Geosci. Model Dev. 2020, 13, 5053–5078. [Google Scholar] [CrossRef]
- Rodrigo, J.S.; Arroyo RA, C.; Witha, B.; Dörenkämper, M.; Gottschall, J.; Avila, M.; Arnqvist, J.; Hahmann, A.; Sile, T. The new European wind atlas model chain. J. Phys. Conf. Ser. 2020, 1452, 012087. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The making of the new European wind atlas—Part 2: Production and evaluation. Geosci. Model Dev. 2020, 13, 5079–5102. [Google Scholar] [CrossRef]
- Chang, T.J.; Chen, C.L.; Tu, Y.L.; Yeh, H.T.; Wu, Y.T. Evaluation of the climate change impact on wind resources in Taiwan Strait. Energy Convers. Manag. 2015, 95, 435–445. [Google Scholar] [CrossRef]
- IOA Group of UNAM. Available online: http://grupo-ioa.atmosfera.unam.mx/ (accessed on 31 July 2023).
- Instituto de Ciencias de la Atmósfera y Cambio Climático (ICAyCC) de la UNAM. Available online: https://www.atmosfera.unam.mx/ (accessed on 31 July 2023).
- López-Espinoza, E.D.; Zavala-Hidalgo, J.; Mahmood, R.; Gómez-Ramos, O. Assessing the impact of land use and land cover data representation on weather forecast quality: A case study in central Mexico. Atmosphere 2020, 11, 1242. [Google Scholar] [CrossRef]
- Rivera-Martínez, S. Análisis del uso de Suelo y Vegetación en México Entre 1968 y 2011 para su uso en un Modelo de Pronóstico Meteorológico. Bachelor’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, Mexico, 2018. [Google Scholar]
- Jurado de Larios, O.E. Sensibilidad del Modelo WRF ante Condiciones Iniciales y de Frontera: Un Estudio de Caso en el Valle de México. Master’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, Mexico, 2017. [Google Scholar]
- Allende-Arandía, M.E.; Zavala-Hidalgo, J.; Torres-Freyermuth, A.; Appendini, C.M.; Cerezo-Mota, R.; Taylor-Espinosa, N. Sea-land breeze diurnal component and its interaction with a cold front on the coast of Sisal, Yucatan: A case study. Atmos. Res. 2020, 244, 105051. [Google Scholar] [CrossRef]
- Meza-Carreto, J. Evaluación del Desempeño del Modelo WRF para Reproducir las Variaciones de la Temperatura en México durante la Década de los 80. Master’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, Mexico, 2018. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Miztli—LANCAD. Available online: http://www.lancad.mx/ (accessed on 18 February 2023).
- Mahmood, R.; Leeper, R.; Quintanar, A.I. Sensitivity of planetary boundary layer atmosphere to historical and future changes of land use/land cover, vegetation fraction, and soil moisture in Western Kentucky, USA. Glob. Planet. Chang. 2011, 78, 36–53. [Google Scholar] [CrossRef]
- Anderson, J.R. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976; Volume 964.
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Tokarska, K.B.; Stolpe, M.B.; Sippel, S.; Fischer, E.M.; Smith, C.J.; Lehner, F.; Knutti, R. Past warming trend constrains future warming in CMIP6 models. Sci. Adv. 2020, 6, eaaz9549. [Google Scholar] [CrossRef] [PubMed]
- WCRP CMIP6 Data Request. 2019. Available online: https://cmip.llnl.gov/cmip6/data-request/ (accessed on 17 January 2023).
- O’Neill, B.C.; Tebaldi, C.; Van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The scenario model intercomparison project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Ridder, N.N.; Pitman, A.J.; Ukkola, A.M. Do CMIP6 climate models simulate global or regional compound events skillfully? Geophys. Res. Lett. 2021, 48, e2020GL091152. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Change 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Tebaldi, C.; Debeire, K.; Eyring, V.; Fischer, E.; Fyfe, J.; Friedlingstein, P.; Knutti, R.; Lowe, J.; O’Neill, B.; Sanderson, B.; et al. Climate model projections from the scenario model intercomparison project (ScenarioMIP) of CMIP6. Earth Syst. Dyn. Discuss. 2020, 12, 253–293. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S), Climate Data Store (CDS). CMIP6 Climate Projections. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.c866074c?tab=overview (accessed on 31 August 2023).
- The NCAR Command Language (Version 6.6.2) [Software]; UCAR/NCAR/CISL/TDD: Boulder, CO, USA, 2019. Available online: https://www.ncl.ucar.edu/ (accessed on 17 January 2023).
- Hahmann, A.N.; García-Santiago, O.; Peña, A. Current and future wind energy resources in the North Sea according to CMIP6. Wind Energy Sci. 2022, 7, 2373–2391. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Costoya, X.; DeCastro, M.; Gómez-Gesteira, M. Wind energy resource over Europe under CMIP6 future climate projections: What changes from CMIP5 to CMIP6. Renew. Sustain. Energy Rev. 2021, 151, 111594. [Google Scholar] [CrossRef]
- Islam, M.R.; Saidur, R.; Rahim, N.A. Assessment of wind energy potentiality at Kudat and Labuan, Malaysia using Weibull distribution function. Energy 2011, 36, 985–992. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Ma, K. Wind speed probability distribution estimation and wind energy assessment. Renew. Sustain. Energy Rev. 2016, 60, 881–899. [Google Scholar] [CrossRef]
- Miao, H.; Xu, H.; Huang, G.; Yang, K. Evaluation and future projections of wind energy resources over the Northern Hemisphere in CMIP5 and CMIP6 models. Renew. Energy. 2023, 211, 809–821. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ogunjobi, K.O.; Abolude, A.T.; Salack, S. Projected changes in wind speed and wind energy potential over West Africa in CMIP6 models. Environ. Res. Lett. 2021, 16, 044033. [Google Scholar] [CrossRef]
- Navarro-Racines, C.E.; Tarapues-Montenegro, J.E.; Ramírez-Villegas, J.A. Bias-Correction in the CCAFS-Climate Portal: A Description of Methodologies; Decision and Policy Analysis (DAPA) Research Area; International Center for Tropical Agriculture (CIAT): Cali, DC, USA, 2015. [Google Scholar]
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Skaugen, T.E. Downscaling RCM precipitation to the station scale using quantile mapping—A comparison of methods. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 6185–6201. [Google Scholar]
- Li, D.; Feng, J.; Xu, Z.; Yin, B.; Shi, H.; Qi, J. Statistical bias correction for simulated wind speeds over CORDEX-East Asia. Earth Space Sci. 2019, 6, 200–211. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Cassisi, C.; Montalto, P.; Aliotta, M.; Cannata, A.; Pulvirenti, A. Similarity measures and dimensionality reduction techniques for time series data mining. In Advances in Data Mining Knowledge Discovery and Applications; IntechOpen: Rijeka, Croatia, 2012; pp. 71–96. [Google Scholar] [CrossRef]
- Morley, S.K.; Brito, T.V.; Welling, D.T. Measures of model performance based on the log accuracy ratio. Space Weather 2018, 16, 69–88. [Google Scholar] [CrossRef]
- Mori, U.; Mendiburu, A.; Lozano, J.A. Distance Measures for Time Series in R: The TSdist Package. R J. 2016, 8, 451. [Google Scholar] [CrossRef]
- Mohammadi, K.; Mostafaeipour, A. Using different methods for comprehensive study of wind turbine utilization in Zarrineh, Iran. Energy Convers. Manag. 2013, 65, 463–470. [Google Scholar] [CrossRef]
- Davis, N.N.; Badger, J.; Hahmann, A.N.; Hansen, B.O.; Mortensen, N.G.; Kelly, M.; Larsén, X.G.; Olsen, B.T.; Floors, R.; Lizcano, G.; et al. The Global Wind Atlas: A high-resolution dataset of climatologies and associated web-based application. Bull. Am. Meteorol. Soc. 2023, 104, E1507–E1525. [Google Scholar] [CrossRef]
- Lantz, E.J.; Roberts, J.O.; Nunemaker, J.; DeMeo, E.; Dykes, K.L.; Scott, G.N. Increasing Wind Turbine Tower Heights: Opportunities and Challenges. 2019. Available online: https://www.osti.gov/biblio/1515397 (accessed on 10 October 2023).
- Krontiris, A.; Sandeberg, P. La tecnología HVDC para el sector de energía eólica marina está madurando. Revista ABB 2018, 3, 36–43. [Google Scholar]
- Nagababu, G.; Naidu, N.K.; Kachhwaha, S.S.; Savsani, V. Feasibility study for offshore wind power development in India based on bathymetry and reanalysis data. Energy Sources A Recovery Util. Environ. Eff. 2017, 39, 497–504. [Google Scholar] [CrossRef]
- Romero-Centeno, R.; Zavala-Hidalgo, J.; Gallegos, A.; O’Brien, J.J. Isthmus of Tehuantepec wind climatology and ENSO signal. J. Clim. 2003, 16, 2628–2639. [Google Scholar] [CrossRef]
- Ibrahim, A.; Abutarboush, H.; Mohamed, A.; Fouad, M.; El-Kenawy, E. An optimized ensemble model for prediction of the bandwidth of metamaterial antenna. CMC—Comput. Mater. Contin. 2022, 71, 199–213. [Google Scholar]
- Romero Centeno, R.; Zavala Hidalgo, J. (Eds.) Meteorología; En S. Z. Herzka, R.A. Zaragoza Álvarez, E.M. Peters y G. Hernández Cárdenas. (Coord. Gral.); Atlas de línea base ambiental del golfo de México (tomo I); Consorcio de Investigación del Golfo de México: Mexico City, Mexico, 2021. [Google Scholar]
- Thomas, B.; Costoya, X.; Decastro, M.; Insua-Costa, D.; Senande-Rivera, M.; Gómez-Gesteira, M. Downscaling CMIP6 climate projections to classify the future offshore wind energy resource in the Spanish territorial waters. J. Clean. Prod. 2023, 433, 139860. [Google Scholar] [CrossRef]
- Claro, A.; Santos, J.A.; Carvalho, D. Assessing the Future Wind Energy Potential in Portugal Using a CMIP6 Model Ensemble and WRF High-Resolution Simulations. Energies 2023, 16, 661. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Climate-change impacts on offshore wind resources in the Mediterranean Sea. Energy Convers. Manag. 2023, 291, 117231. [Google Scholar] [CrossRef]
- Shen, C.; Duan, Q.; Miao, C.; Xing, C.; Fan, X.; Wu, Y.; Han, J. Bias correction and ensemble projections of temperature changes over ten subregions in CORDEX East Asia. Adv. Atmos. Sci. 2020, 37, 1191–1210. [Google Scholar] [CrossRef]
- Long, Y.; Xu, C.; Liu, F.; Liu, Y.; Yin, G. Evaluation and projection of wind speed in the arid region of northwest China based on CMIP6. Remote Sens. 2021, 13, 4076. [Google Scholar] [CrossRef]





| Parameterization Scheme | Scheme Used |
|---|---|
| Land Surface Model | Noah-MP |
| Surface Layer Model | MM5 Monin-Obukhov |
| Microphysics | WRF Single-moment 3-class |
| Shortwave Radiation | Dudhia Shortwave Scheme |
| Longwave Radiation | RRTM Longwave Scheme |
| Planetary Boundary Layer | Yonsei University Scheme (YSU) |
| Convection | Kain-Fritsch Scheme |
| Modeling Center/Nation | Model Name | Horizontal Resolution |
|---|---|---|
| Commonwealth Scientific and Industrial Research Organization/Australia | access_cm2, access_esm1_5 | 1.25° × 1.875°, 1.25° × 1.875° |
| Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research/Germany | awi_cm_1_1_mr, awi_esm_1_1_lr | 0.94° × 0.94°, 1.8° × 1.8° |
| Beijing Climate Center China Meteorological Administration/China | bcc_csm2_mr, bcc_esm1 | 1.125° × 1.125°, 2.81° × 2.81° |
| Canadian Centre for Climate Modelling and Analysis/Canada | canesm5_canoe | 2.8° × 2.8° |
| National Center for Atmospheric Research, Climate and Global Dynamics Laboratory/USA | cesm2, cesm2_fv2, cesm2_waccm, cesm2_waccm_fv2 | 0.94° × 1.25°, 2.5° × 1.8°, 0.94° × 1.25°, 2.5° × 1.8° |
| Fondazione Centro Euro-Mediterraneo sui Cambiamenti Climatici/Italy | cmcc_cm2_hr4, cmcc_cm2_sr5, cmcc_esm2 | 0.94° × 0.94°, 0.94° × 0.94°, 0.94° × 0.94° |
| Centre National de Recherches Météorologiques–Centre Européen de Recherche et de Formation Avancée en Calcul Scientifique/France | cnrm_cm6_1, cnrm_cm6_1_hr, cnrm_esm2_1 | 1.4° × 1.4°, 0.50° × 0.50°, 1.4° × 1.4° |
| LLNL (Lawrence Livermore National Laboratory, Livermore, CA 94550, USA); ANL (Argonne National Laboratory, Argonne, IL 60439, USA); BNL (Brookhaven National Laboratory, Upton, NY 11973, USA); LANL (Los Alamos National Laboratory, Los Alamos, NM 87545, USA); LBNL (Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA); ORNL (Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA); PNNL (Pacific Northwest National Laboratory, Richland, WA 99352, USA); SNL (Sandia National Laboratories, Albuquerque, NM 87185, USA) | e3sm_1_0, e3sm_1_1, e3sm_1_1_eca | 0.94° × 0.94°, 0.94° × 0.94°, 1.25° × 1.875° |
| Fondazione Centro Euro-Mediterraneo sui Cambiamenti Climatici/Italy | fgoals_f3_l | 1.125° × 1.125° |
| Geophysical Fluid Dynamics Laboratory/USA | fgoals_g3 | 2.5° × 1.875° |
| Geophysical Fluid Dynamics Laboratory/USA | gfdl_esm4 | 0.94° × 0.94° |
| German Climate Computing Center/Germany | hadgem3_gc31_ll, hadgem3_gc31_mm | 2.5° × 2.5°, 2.5° × 2.5° |
| Institute for Global Environmental Strategies/Japan | inm_cm4_8, inm_cm5_0 | 2.0° × 2.5°, 2.0° × 2.5° |
| Institute of Numerical Mathematics, Russian Academy of Sciences/Russia | iitm_esm | 0.94° × 0.94° |
| Institut Pierre-Simon Laplace/France | ipsl_cm5a2_inca, ipsl_cm6a_lr | 1.4° × 1.4°, 1.4° × 1.4° |
| Japan Agency for Marine-Earth Science and Technology/Japan | kace_1_0_g | 1.125° × 1.125° |
| Korea Institute of Ocean Science and Technology/South Korea | kiost_esm | 1.5° × 1.5° |
| Max Planck Institute for Meteorology/Germany | mpi_esm1_2_hr, mpi_esm1_2_lr | 0.94° × 0.94°, 0.94° × 0.94° |
| Meteorological Research Institute/Japan | mri_esm2_0 | 0.94° × 0.94° |
| Norwegian Computing Center/Norway | noresm2_lm, noresm2_mm | 1.25° × 1.875°, 1.25° × 1.875° |
| Research Institute for Global Change/Japan | sam0_unicon | 1.25° × 1.875° |
| The Australian National University/Australia | taiesm1 | 1.875° × 3.75° |
| National Institute for Environmental Studies/Japan | ukesm1_0_ll | 2.5° × 2.5° |
| European consortium of national meteorological services and research institutes | EC-Earth3, EC-Earth3-Veg, EC-Earth3-AerChem, EC-Earth3-CC | 0.94° × 0.94°, 0.94° × 0.94°, 0.94° × 0.94°, 0.94° × 0.94° |
| First Institute of Oceanography, State Oceanic Administration, Qingdao National Laboratory for Marine Science and Technology/China | fio_esm_2_0 | 0.94° × 0.94° |
| Metric | Description | Formula |
|---|---|---|
| Pearson Correlation Coefficient () | Pearson’s correlation helps assess how related two time series are in a linear sense. R is a dimensionless quantity. | |
| Mean Absolute Error (MAE) | MAE provides a robust measure of accuracy, as it does not disproportionately penalize large errors. | |
| Mean Absolute Percentage Error (MAPE) | MAPE provides a measure of how closely predictions align with actual values in terms of percentage error. It is scale-independent, facilitating comparisons across different types of datasets. | |
| Root Mean Square Deviation (RMSD) | RMSD indicates the typical magnitude of errors and penalizes large errors significantly. | |
| Minkowski Distance | The Minkowski Distance, with its adjustable parameter, serves as a versatile metric and offers a generalized approach to distances. It effectively measures dissimilarity between time series, considering both the magnitude and trend of the data, and it is an effective tool for identifying systematic error patterns in comparing similarities between datasets. Like other distances, Minkowski is limited to comparing equal-length time series. In this study, a Minkowski Distance with was employed. This choice increased the metric’s sensitivity to discrepancies in extreme values within the time series. | corresponds to the Manhattan distance; corresponds to the Euclidean distance; and provides a more general distance metric that can adapt to various data characteristics. |
| Zone Name | Coordinates of the Vertices |
|---|---|
| Tamaulipas | (24.94, −97.12), (25.89, −97.12), (24.94, −95.97), (25.89, −95.97) |
| Yucatán | (21.5, −90), (22.25, −90), (21.5, −88.8), (22.25, −88.8) |
| Tehuantepec | (15, −94.5), (16, −94.5), (15, −95.5), (16, −95.5) |
| Model | MAPE | Pearson Correlation | RMSD (m/s) | MAE (m/s) | Minkowski Distance (m/s) |
|---|---|---|---|---|---|
| EC_EARTH3_VEG_LR | 7.619 | 0.855 | 0.700 | 0.553 | 2.452 |
| MRI_ESM2_0 | 7.665 | 0.829 | 0.691 | 0.544 | 2.529 |
| EC_EARTH3_CC | 7.821 | 0.826 | 0.700 | 0.563 | 2.291 |
| HADGEM3_GC31_MM | 7.933 | 0.852 | 0.702 | 0.572 | 2.423 |
| CNRM_CM6_1_HR | 7.967 | 0.824 | 0.701 | 0.568 | 2.479 |
| CNRM_CM6_1 | 8.025 | 0.833 | 0.717 | 0.573 | 2.459 |
| Model | MAPE | Pearson Correlation | RMSD (m/s) | MAE (m/s) | Minkowski Distance (m/s) |
|---|---|---|---|---|---|
| KACE_1_0_G | 5.018 | 0.594 | 0.481 | 0.378 | 1.825 |
| HADGEM3_GC31_MM | 5.024 | 0.639 | 0.473 | 0.375 | 1.717 |
| CNRM_CM6_1_HR | 5.133 | 0.587 | 0.489 | 0.388 | 1.885 |
| GFDL_ESM4 | 5.352 | 0.622 | 0.492 | 0.403 | 1.698 |
| Model | MAPE | Pearson Correlation | RMSD (m/s) | MAE (m/s) | Minkowski Distance (m/s) |
|---|---|---|---|---|---|
| FGOALS_F3_L | 11.996 | 0.802 | 1.379 | 1.070 | 5.126 |
| BCC_CSM2_MR | 13.404 | 0.817 | 1.430 | 1.162 | 5.043 |
| CNRM_CM6_1_HR | 15.248 | 0.789 | 1.656 | 1.334 | 5.814 |
| MRI_ESM2_0 | 17.555 | 0.759 | 1.914 | 1.594 | 6.089 |
| GFDL_ESM4 | 17.761 | 0.827 | 1.878 | 1.549 | 6.592 |
| Model | Zona I | Zona II | Zona III |
|---|---|---|---|
| BCC_CSM2_MR | ✓ | ||
| EC_EARTH3_VEG_LR | ✓ | ||
| MRI_ESM2_0 | ✓ | ✓ | |
| EC_EARTH3_CC | ✓ | ||
| HADGEM3_GC31_MM | ✓ | ✓ | |
| CNRM_CM6_1_HR | ✓ | ✓ | ✓ |
| CNRM_CM6_1 | ✓ | ||
| FGOALS_F3_L | ✓ | ||
| GFDL_ESM4 | ✓ | ✓ | |
| KACE_1_0_G | ✓ |
| Description | Equation |
|---|---|
| Equation for calculating the weights based on the inverse of the squared MAPE. | |
| Equation for normalizing the weights. | |
| Equation for calculating the weighted ensemble using the normalized weights. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meza-Carreto, J.; Romero-Centeno, R.; Figueroa-Espinoza, B.; Moreles, E.; López-Villalobos, C. Outlook for Offshore Wind Energy Development in Mexico from WRF Simulations and CMIP6 Projections. Energies 2024, 17, 1866. https://doi.org/10.3390/en17081866
Meza-Carreto J, Romero-Centeno R, Figueroa-Espinoza B, Moreles E, López-Villalobos C. Outlook for Offshore Wind Energy Development in Mexico from WRF Simulations and CMIP6 Projections. Energies. 2024; 17(8):1866. https://doi.org/10.3390/en17081866
Chicago/Turabian StyleMeza-Carreto, Jaime, Rosario Romero-Centeno, Bernardo Figueroa-Espinoza, Efraín Moreles, and Carlos López-Villalobos. 2024. "Outlook for Offshore Wind Energy Development in Mexico from WRF Simulations and CMIP6 Projections" Energies 17, no. 8: 1866. https://doi.org/10.3390/en17081866
APA StyleMeza-Carreto, J., Romero-Centeno, R., Figueroa-Espinoza, B., Moreles, E., & López-Villalobos, C. (2024). Outlook for Offshore Wind Energy Development in Mexico from WRF Simulations and CMIP6 Projections. Energies, 17(8), 1866. https://doi.org/10.3390/en17081866





