Stability Analysis of Plate—Screw Fixation for Femoral Midshaft Fractures
Abstract
:1. Introduction
2. Materials and Methods
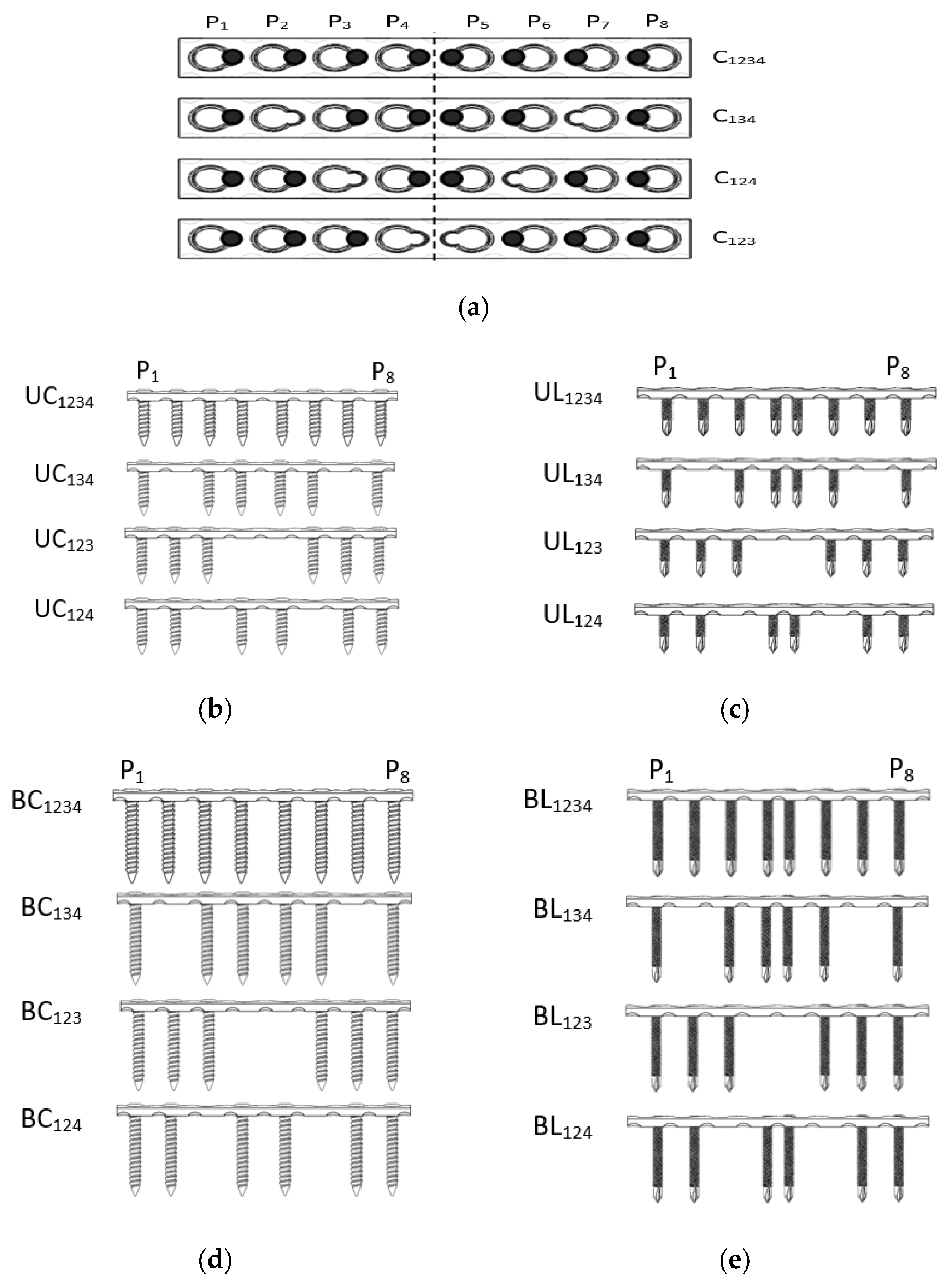
2.1. Implant–Bone Fixation System
2.2. 3D Model of Implant–Bone Configuration
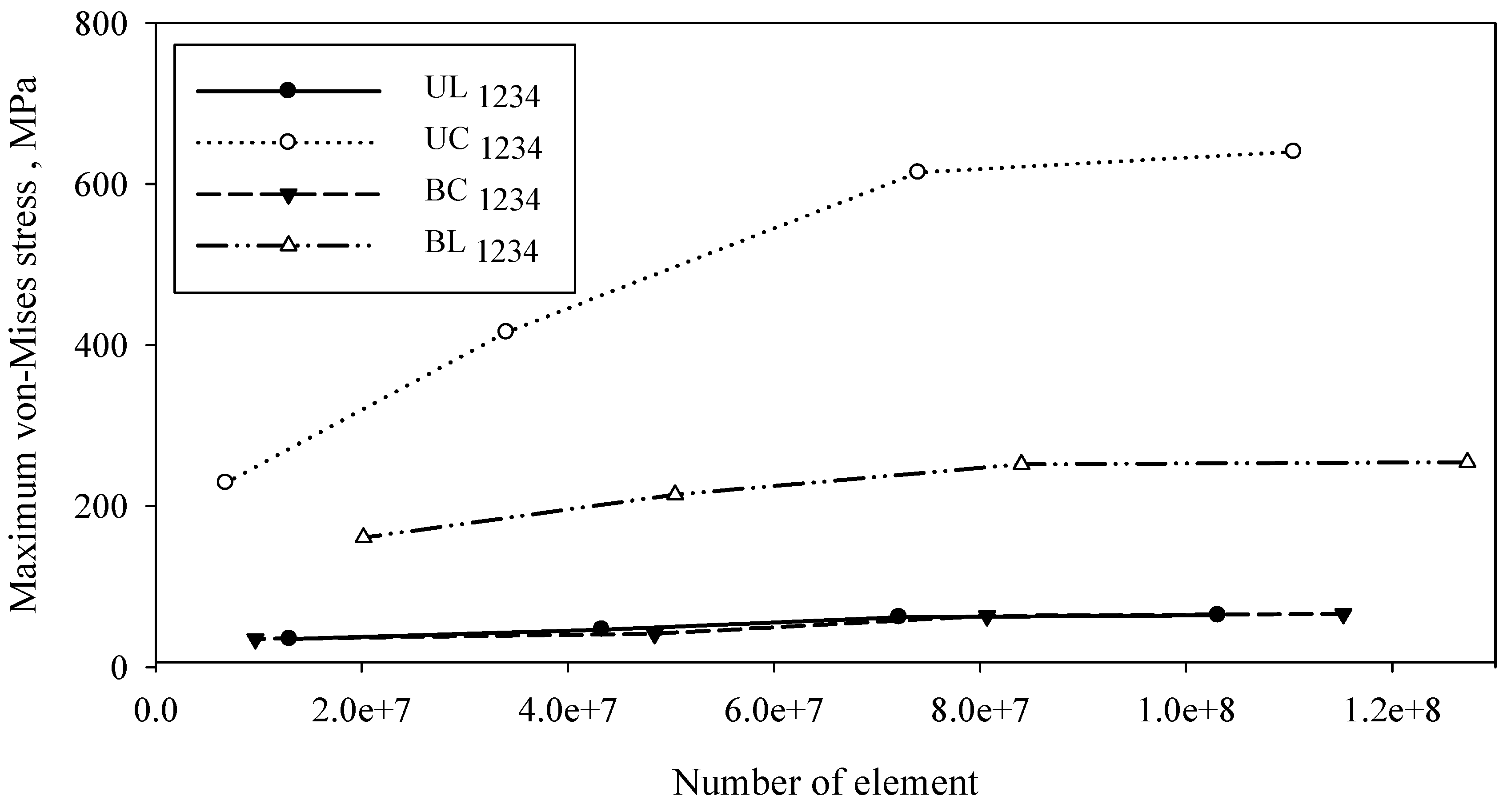
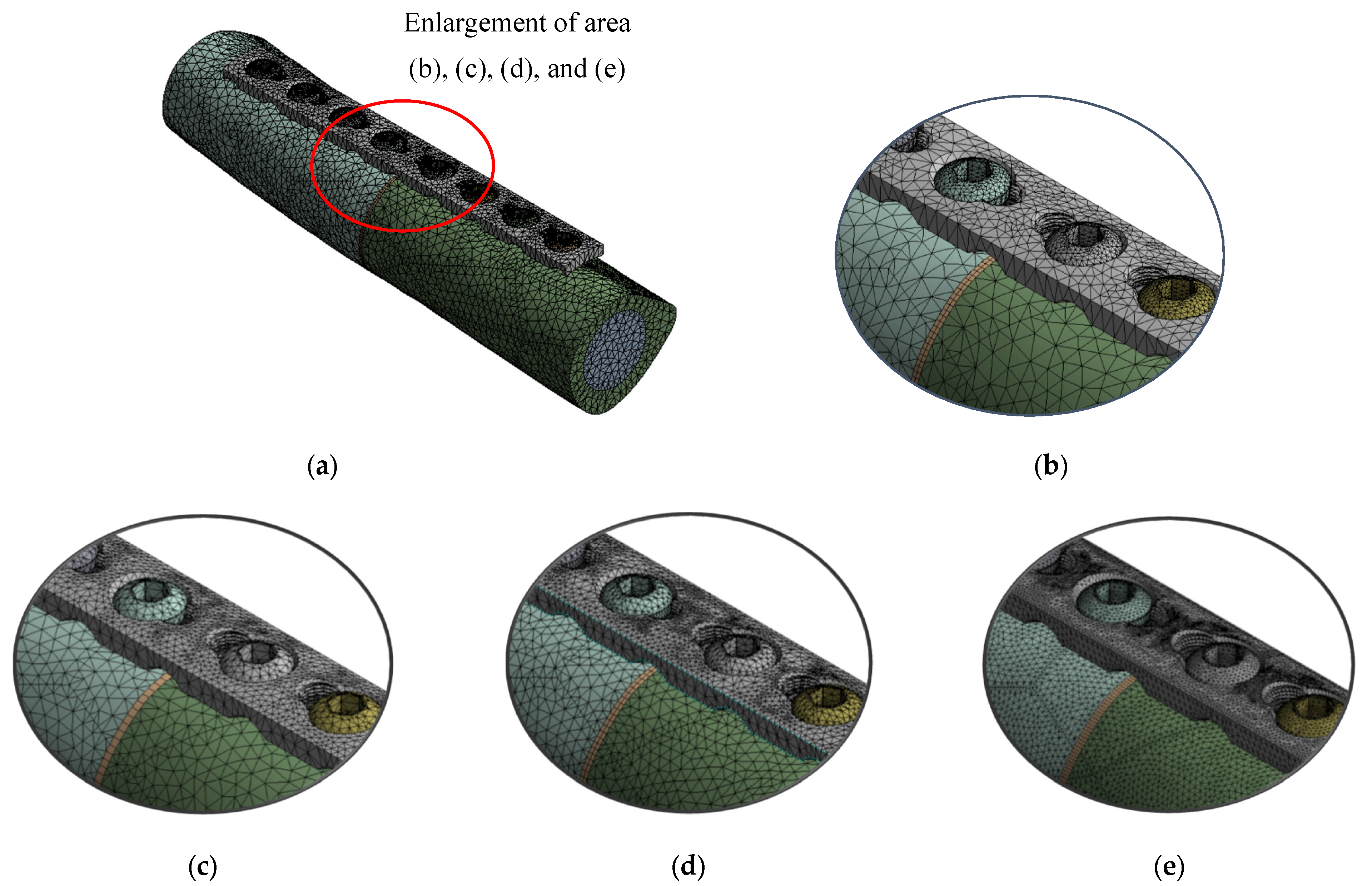
2.3. Mesh and Validation
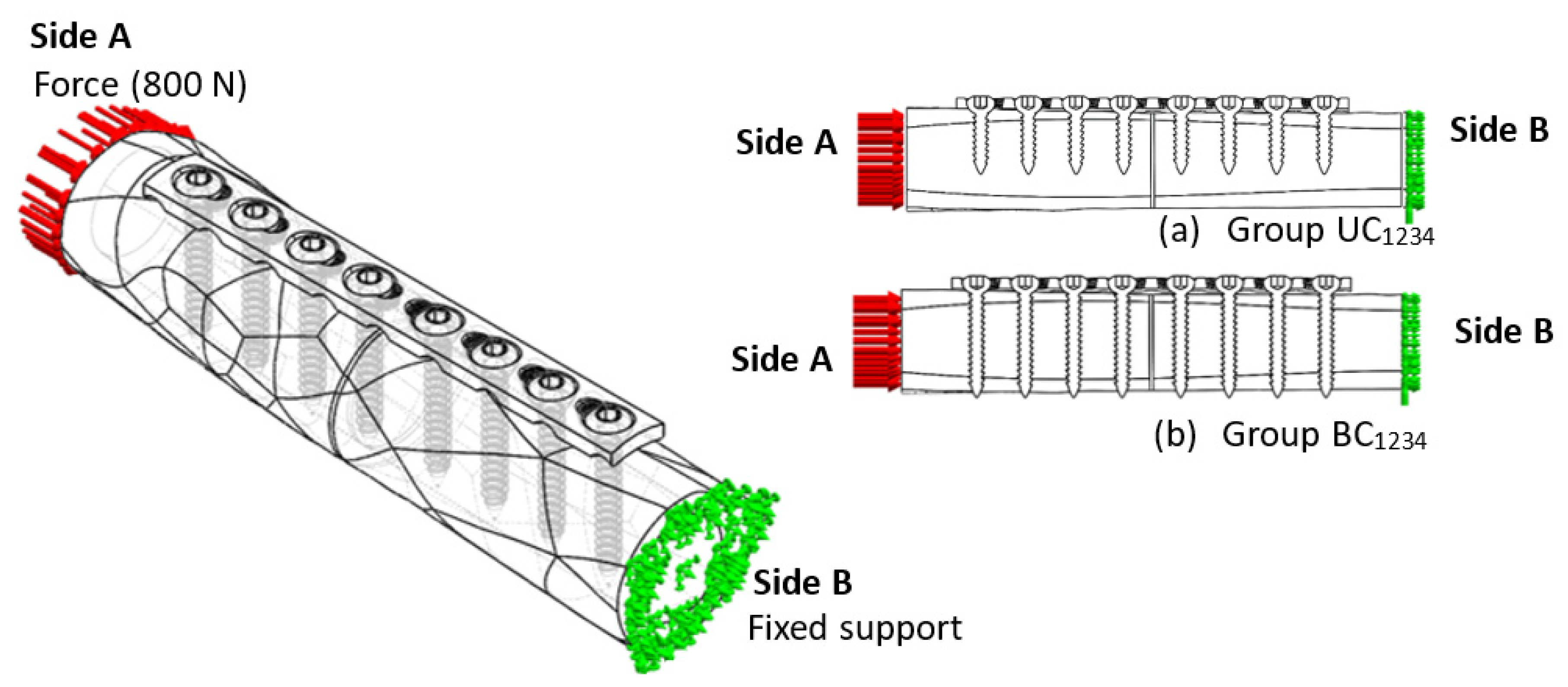
2.4. Fixation Interface Condition
2.5. FE Simulation of Compression Load
2.6. Identification of Material Properties
2.7. Stability Characterisation
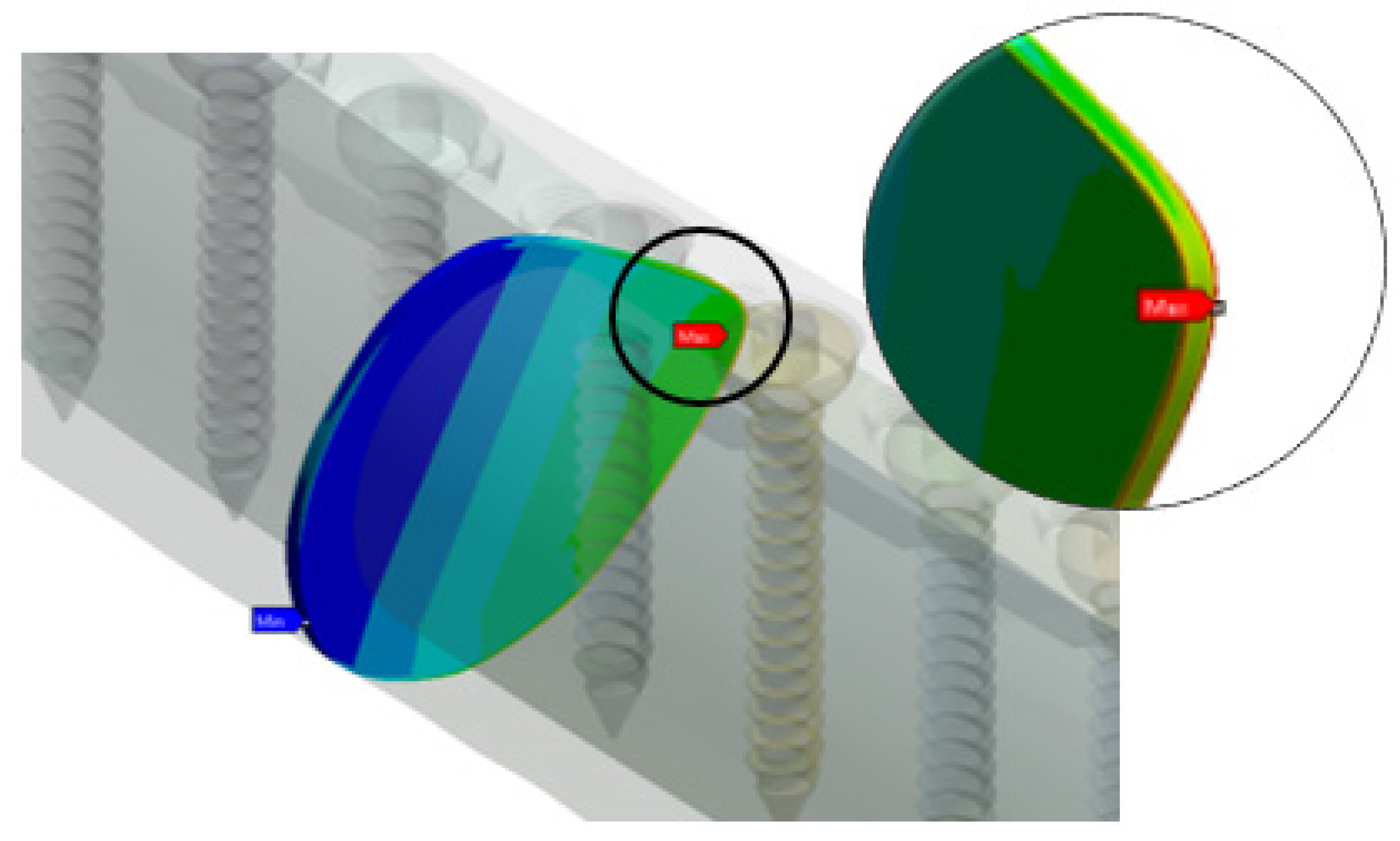
2.7.1. Implant Stress Analysis
2.7.2. Working Length Measurement
2.7.3. Interfragmentary Strain Measurement
2.7.4. Stability Classification
3. Results and Discussion
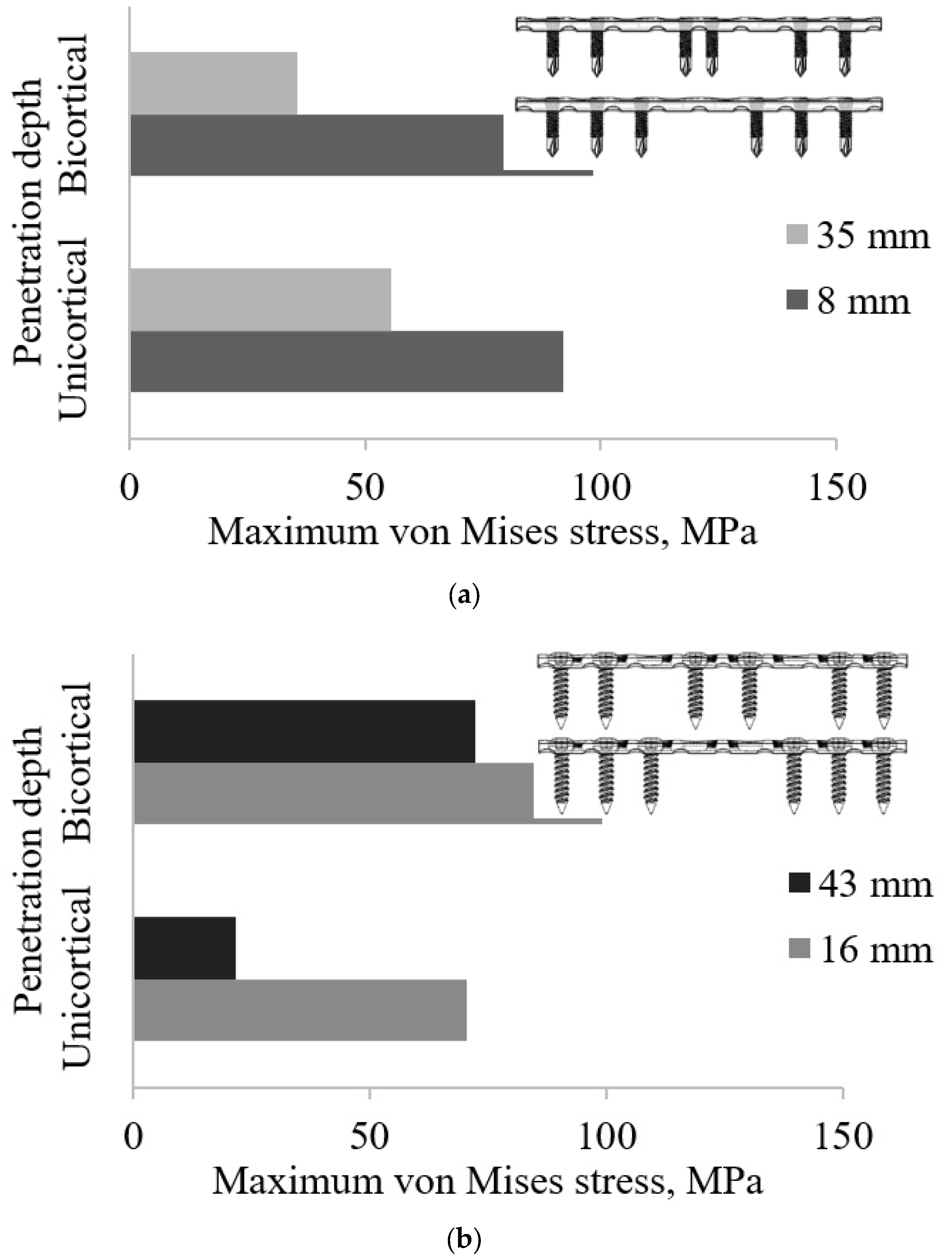
3.1. Effect of Screw Types and Penetration Depth Configuration
3.2. Effect of Implant Type (Unicortical) on the Stress Distribution of Screw and LCP Plate
3.3. Effect of Implant Type (Bicortical) on the Stress Distribution of Screw and LCP Plate
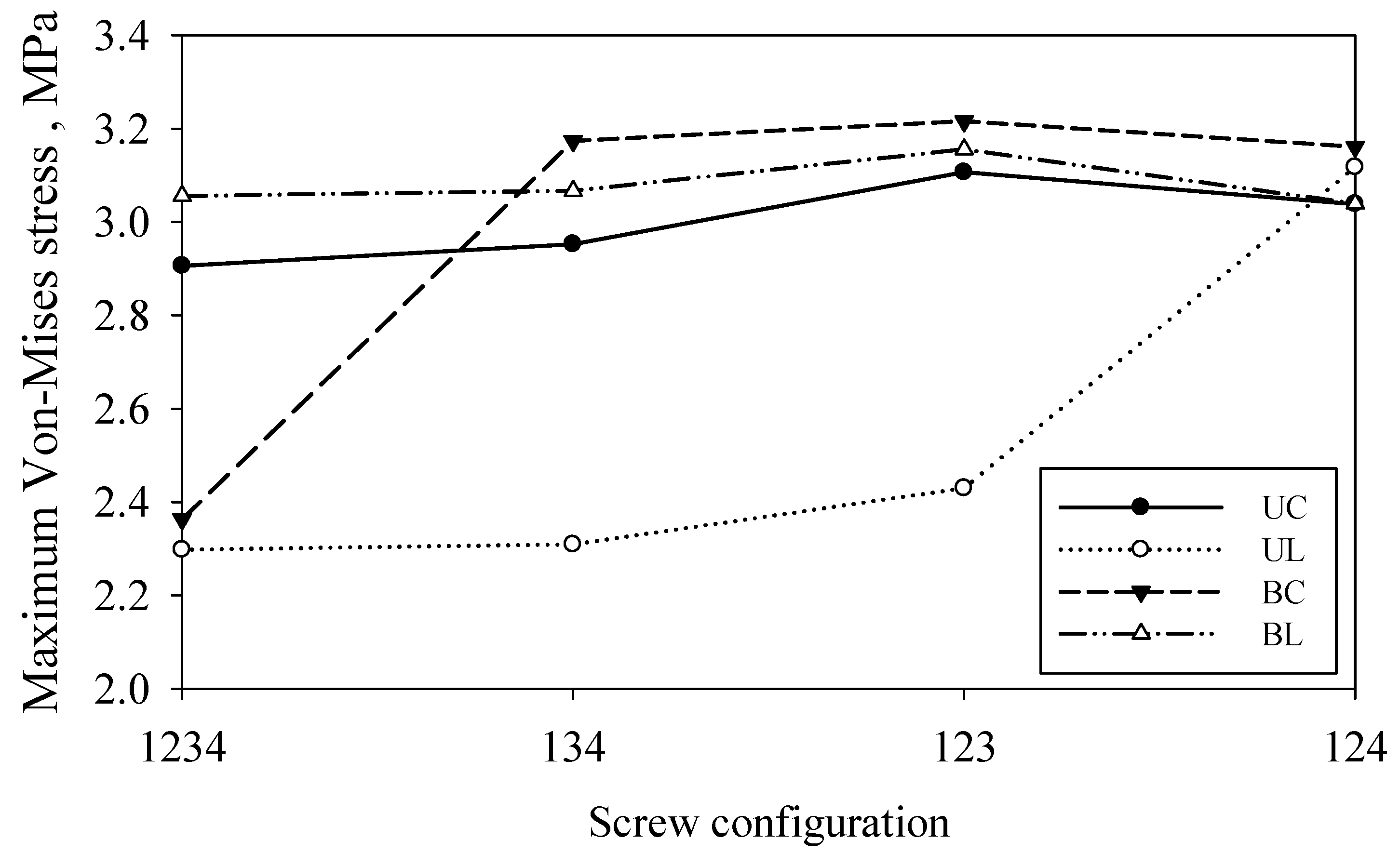
3.4. Effect of Working Length as a Function of Screw Configurations on Plate Stress
3.5. Effect of Screw Configuration on the Callus Stress
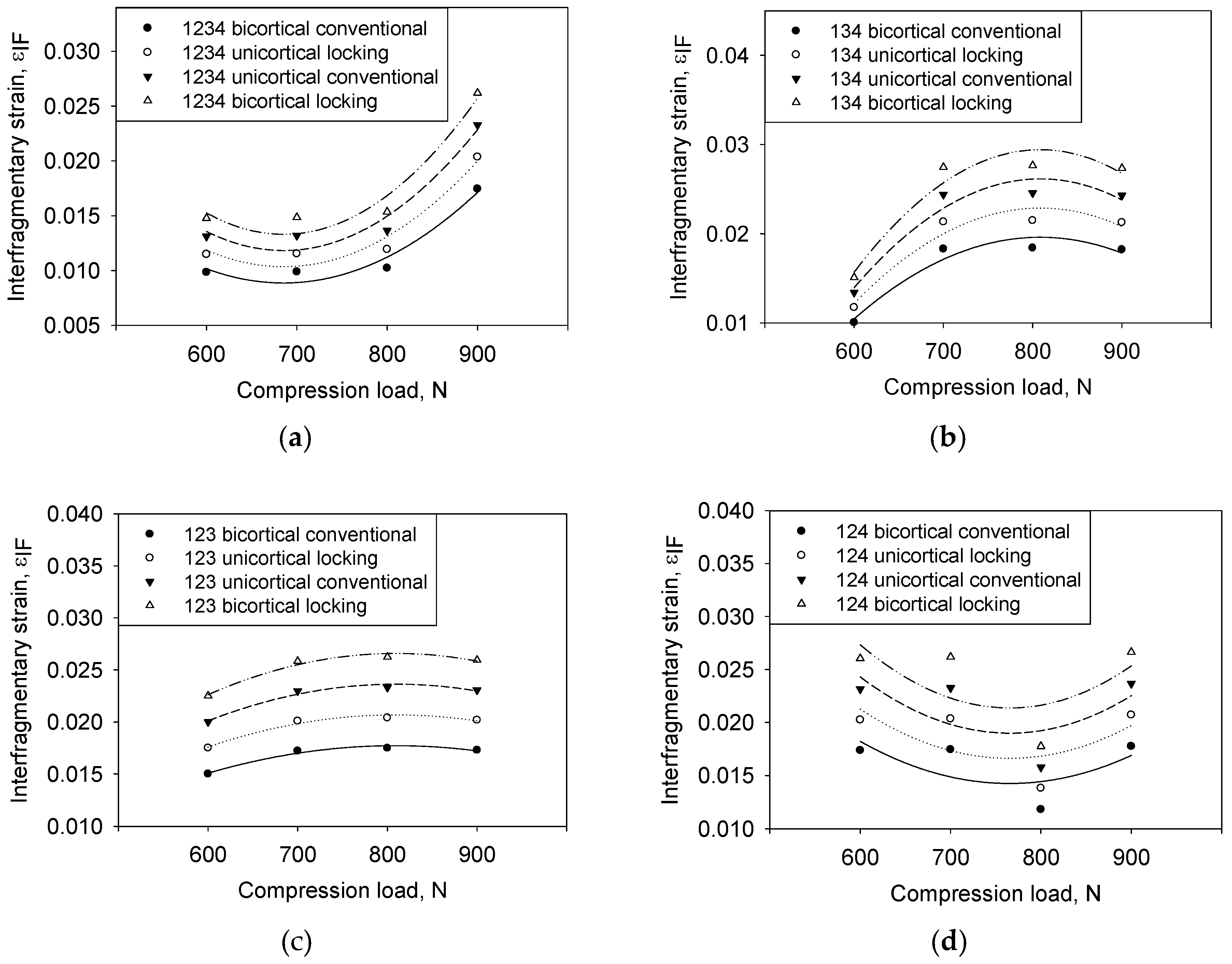
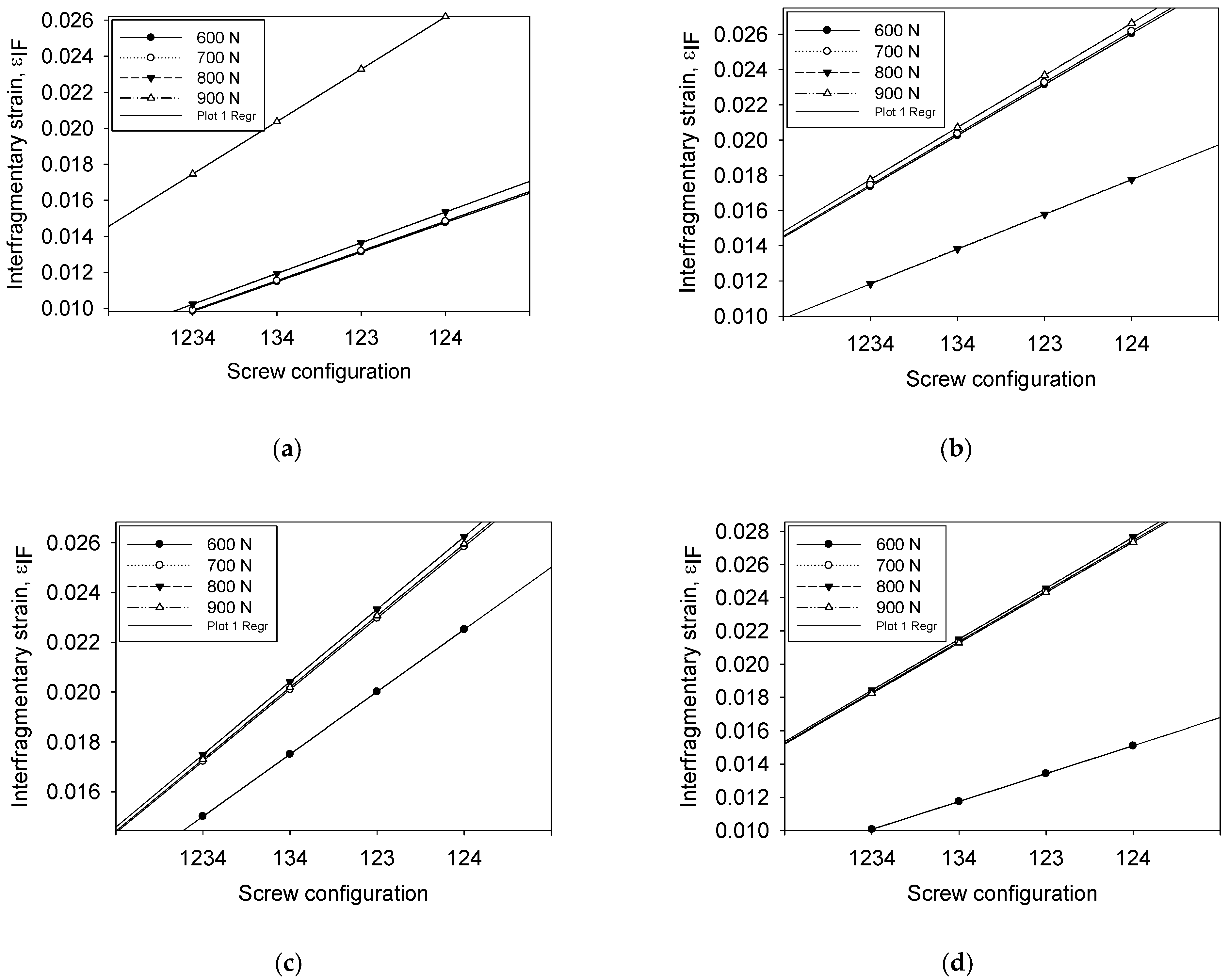
3.6. Interfragmentary Strain as a Function of Screw Configuration
3.7. Interfragmentary Strain as a Function of Compression Loading
3.8. Interfragmentary Strain as a Function of Compression Loading
3.9. Correlation between the Controllable Parameters on Interfragmentary Strain as Stability Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alemdar, C.; Azboy, I.; Atiç, R.; Özkul, E.; Gem, M.; Kapukaya, A. Management of infectious fractures with ‘Non-Contact Plate’ (NCP) method. Acta Orthop. Belg. 2015, 81, 523–529. [Google Scholar]
- Ito, K.; Perren, S.M. Biology of fracture healing. J. Trauma Orthop. 2017, 5, 48–52. [Google Scholar]
- Hammarstedt, J.E.; Redshaw, J.T., Jr.; Schimoler, P.J.; Westrik, E.R.; Andreini, D.; Kharlamov, A.; Miller, M.C. Biomechanical analysis of stability of joint depression calcaneal fractures:Fixation with locking compression plate alone compared with addition of supplemental oblique screw. J. Clin. Orthop. Trauma 2022, 33, 101998. [Google Scholar] [CrossRef]
- Kuan, F.; Hsu, K.; Hong, C.; Chen, Y.; Chiang, C.; Chang, H.; Su, W. Biomechanical comparisons of hook plate and screw fixations in split-type greater tuberosity fractures of the humerus. J. Shoulder Elb. Surg. 2021, 31, 1308–1315. [Google Scholar] [CrossRef]
- Jang, Y.; Kim, D. Biomechanical study of Proximal humeral fracture fixation: Locking plate with medial support screw vs. locking plate with intramedullary fibular graft. Clin. Biomech. 2021, 90, 105510. [Google Scholar] [CrossRef]
- Rosa, N.; Marta, M.; Vaz, M.; Tavares, S.M.O.; Simoes, R.; Magalhaes, F.D.; Marques, A.T. Intramedullary nailing biomechanics: Evolution and challenges. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 295–308. [Google Scholar] [CrossRef]
- Fernandes, M.G.; Alves, J.L.; Fonseca, E.M.M. Diaphyseal femoral fracture: 3D biomodel and intramedullary nail created by additive manufacturing. Int. J. Mater. Eng. Innov. 2016, 7, 130–142. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Gill, S.P.S.; Singh, P.; Raj, M.; Gupta, A. Evaluation of Implant Failure in Long Bones Fractures—A Retrospective Study. Indian J. Orthop. Surg. 2016, 2, 64–68. [Google Scholar] [CrossRef]
- Eberle, S.; Gerber, C.; von Oldenburg, G.; Hogel, F.; Augat, P. A biomechanical evaluation of orthopaedic implants for hip fractures by finite element analysis and in-vitro tests. J. Eng. Med. 2010, 224, 1141–1152. [Google Scholar] [CrossRef]
- Gefen, A. Computational simulations of stress shielding and bone resorption around existing and computer-designed orthopaedic screws. Med. Biol. Eng. Comput. 2002, 40, 311–322. [Google Scholar] [CrossRef]
- Stephan, M. Internal Fixation of Long Bone Fractures: The Scientific Basis of Biological Internal Fixation. J. Bone Jt. Surg. 2007, 84, 1–24. [Google Scholar]
- Fitzpatrick, D.C.; Doornink, J.; Madey, S.M.; Bottlang, M. Relative stability of conventional and locked plating fixation in a model of the osteoporotic femoral diaphysis. Clin. Biomech. 2009, 24, 203–209. [Google Scholar] [CrossRef]
- Niemeyer, P.; Südkamp, N.P. Principles and clinical application of the locking compression plate (LCP). Acta Chir. Orthop. Traumatol. Cech. 2006, 73, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Lofaj, F.; Kucera, J.; Nemeth, D.; Kvetkova, L. Finite element analysis of stress distributions in mono- and bi-cortical dental implants. Mater. Sci. Eng. C 2015, 50, 85–96. [Google Scholar] [CrossRef]
- Marsico, V.d.S.; Lehmann, R.B.; Claro, C.A.d.A.; Amaral, M.; Vitti, R.P.; Neves, A.C.C.; Concilio, L.R.d.S. Three-dimensional finite element analysis of occlusal splint and implant connection on stress distribution in implant–supported fixed dental prosthesis and peri-implantal bone. Mater. Sci. Eng. C 2017, 80, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Tschegg, E.K.; Herndler, S.; Weninger, P.; Jamek, M.; Stanzl-Tschegg, S.; Redl, H. Stiffness analysis of tibia-implant system under cyclic loading. Mater. Sci. Eng. C 2008, 28, 1203–1208. [Google Scholar] [CrossRef]
- Gepreel, M.A.-H.; Niinomi, M. Biocompatibility of Ti-alloys for long-term implantation. J. Mech. Behav. Biomed. Mater. 2013, 20, 407–415. [Google Scholar] [CrossRef]
- Berger, L.; Fischerauer, S.; Weiß, B.; Celarek, A.; Castellani, C.; Weinberg, A.-M.; Tschegg, E. Unlocked and locked elastic stable intramedullary nailing in an ovine tibia fracture model: A biomechanical study. Mater. Sci. Eng. C 2014, 40, 267–274. [Google Scholar] [CrossRef]
- Shah, F.A.; Trobos, M.; Thomsen, P.; Palmquist, A. Commercially pure titanium (cp-Ti) versus titanium alloy (Ti6Al4V) materials as bone anchored implants—Is one truly better than the other? Mater. Sci. Eng. C 2016, 62, 960–966. [Google Scholar] [CrossRef]
- Nareliya, R.; Kumar, V. Biomechanical Analysis of Human Femur: A Review. J. Biomed. Bioeng. 2012, 3, 67–70. [Google Scholar]
- Hoskins, W.; Bingham, R.; Griffin, X.L. Distal femur fractures in adults. Orthop. Trauma 2017, 31, 93–101. [Google Scholar] [CrossRef]
- Lin, D.; Li, Q.; Li, W.; Ichim, I.; Swain, M. Evaluation of dental implant induced bone remodelling by using 2D Finite element. Proceeding of the 5th Australasian Congress on Applied Mechanics, ACAM 2007, Brisbane, Australia, 10–12 December 2007. [Google Scholar]
- Cheng, H.; Peng, B.; Chen, M.; Huang, C.; Lin, Y.; Shen, Y. Influence of Deformation and Stress between Bone and Implant from Various Bite Forces by Numerical Simulation Analysis. BioMed Res. Int. 2017, 2017, 2827953. [Google Scholar] [CrossRef]
- Norris, B.L.; Lang, G.; Russell, T.A.T.; Rothberg, D.L.; Ricci, W.M.; Borrelli, J. Absolute Versus Relative Fracture Fixation: Impact on Fracture Healing. J. Orthop. Trauma 2018, 32, S12–S16. [Google Scholar] [CrossRef] [PubMed]
- Khader, B.A.; Towler, M.R. Common treatments and procedures used for fractures of the distal radius and scaphoid: A review. Mater. Sci. Eng. C 2017, 74, 422–433. [Google Scholar] [CrossRef] [PubMed]
- Piotrowski, B.; Baptista, A.A.; Patoor, E.; Bravetti, P.; Eberhardt, A.; Laheurte, P. Interaction of bone-dental implant with new ultra low modulus alloy using a numerical approach. Mater. Sci. Eng. C 2014, 38, 151–160. [Google Scholar] [CrossRef]
- Dantas, T.A.; Abreu, C.; Costa, M.; Miranda, G.; Silva, F.; Dourado, N.; Gomes, J. Bioactive materials driven primary stability on titanium biocomposites. Mater. Sci. Eng. C 2017, 77, 1104–1110. [Google Scholar] [CrossRef]
- Didier, P.; Piotrowski, B.; Fischer, M.; Laheurte, P. Mechanical stability of custom-made implants: Numerical study of anatomical device and low elastic Young’s modulus alloy. Mater. Sci. Eng. C 2017, 74, 399–409. [Google Scholar] [CrossRef]
- Revathi, A.; Borrás, A.D.; Muñoz, A.I.; Richard, C.; Manivasagam, G. Degradation mechanisms and future challenges of titanium and its alloys for dental implant applications in oral environment. Mater. Sci. Eng. C 2017, 76, 1354–1368. [Google Scholar] [CrossRef]
- Pater, T.J.; Grindel, S.I.; Schmeling, G.J.; Wang, M. Stability of unicortical locked fixation versus bicortical non-locked fixation for forearm fractures. Bone Res. 2014, 2, 14014. [Google Scholar] [CrossRef]
- Erani, P.; Baleani, M. Achievable accuracy of hip screw holding power estimation by insertion torque measurement. Clin. Biomech. 2018, 52, 57–65. [Google Scholar] [CrossRef]
- Gautschi, O.P.; Schatlo, B.; Schaller, K.; Tessitore, E. Clinically relevant complications related to pedicle screw placement in thoracolumbar surgery and their management: A literature review of 35,630 pedicle screws. Neurosurg. Focus 2011, 31, E8. [Google Scholar] [CrossRef]
- Femur 3D CAD Model Library, GrabCAD. Available online: https://grabcad.com/library/femur--1 (accessed on 8 August 2018).
- Stainless Steel Small Fragment Locking Compression Plate (LCP) System. 2013, p. 1. Available online: http://synthes.vo.llnwd.net/o16/LLNWMB8/US%20Mobile/Synthes%20North%20America/Product%20Support%20Materials/Technique%20Guides/DSUSTRM10161165%20Rev%20C.pdf (accessed on 20 April 2018).
- Meinberg, E.; Agel, J.; Roberts, C. Fracture and Dislocation Classification Compendium 2018. J. Orthop. Trauma 2018, 32, S1–S10. [Google Scholar] [CrossRef]
- Ahmad, M.; Nanda, R.; Bajwa, A.S.; Candal-Couto, J.; Green, S.; Hui, A.C. Biomechanical testing of the locking compression plate: When does the distance between bone and implant significantly reduce construct stability? Injury 2007, 38, 358–364. [Google Scholar] [CrossRef]
- Oh, J.-K.; Sahu, D.; Ahn, Y.-H.; Lee, S.-J.; Tsutsumi, S.; Hwang, J.-H.; Jung, D.-Y.; Perren, S.M.; Oh, C.-W. Effect of Fracture Gap on Stability of Compression Plate Fixation: A Finite Element Study. J. Orthop. Res. 2010, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Chung, C. A simplified application (APP) for the parametric design of screw-plate fi xation of bone fractures. J. Mech. Behav. Biomed. Mater. 2017, 77, 642–648. [Google Scholar] [CrossRef] [PubMed]
- Bitter, T.; Khan, I.; Marriott, T.; Lovelady, E.; Verdonschot, N.; Janssen, D. Finite element wear prediction using adaptive meshing at the modular taper interface of hip implants. J. Mech. Behav. Biomed. Mater. 2018, 77, 616–623. [Google Scholar] [CrossRef]
- Geraldes, D.M.; Phillips, A.T.M. A comparative study of orthotrophic and isotropic bone adaptation in the femur. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 873–889. [Google Scholar] [CrossRef] [PubMed]
- Robinson, A.F.; Quinn, S. Stress analysis of implant-bone fixation at different fracture angle. J. Phys. Conf. Ser. 2017, 908, 012019. [Google Scholar]
- Weiss, D.B.; Kaar, S.G.; Frankenburg, E.P.; Karunakar, M.A. Locked versus unlocked plating with respect to plate length in an ulna fracture model. Bull. NYU Hosp. Jt. Dis. 2008, 66, 5–8. [Google Scholar]
- Moazen, M.; Mak, J.H.; Jones, A.C.; Jin, Z.; Wilcox, R.K.; Tsiridis, E. Evaluation of a new approach for modelling the screw-bone interface in a locking plate fixation: A corroboration study. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2013, 227, 746–756. [Google Scholar] [CrossRef]
- Bagheri, Z.S.; Bougherara, H.; Zdero, R. Thermographic Stress Analysis of Whole Bones and Implants. In Experimental Methods in Orthopaedic Biomechanics; Elsevier: Amsterdam, The Netherlands, 2017; pp. 49–64. [Google Scholar]
- Egol, K.A.; Kubiak, E.N.; Fulkerson, E.; Kummer, F.J.; Koval, K.J. Biomechanics of locked plates and screws. J. Orthop. Trauma 2004, 18, 488–493. [Google Scholar] [CrossRef]
- Stoffel, K.; Dieter, U.; Stachowiak, G.; Gächter, A.; Kuster, M.S. Biomechanical testing of the LCP—How can stability in locked internal fixators be controlled? Injury 2003, 34, B11–B19. [Google Scholar] [CrossRef]
- MacLeod, A.R.; Simpson, A.H.R.W.; Pankaj, P. Age-related optimization of screw placement for reduced loosening risk in locked plating. J. Orthop. Res. 2016, 34, 1856–1864. [Google Scholar] [CrossRef] [PubMed]
- Chao, P.; Conrad, B.P.; Lewis, D.D.; Horodyski, M.; Pozzi, A. Effect of plate working length on plate stiffness and cyclic fatigue life in a cadaveric femoral fracture gap model stabilized with a 12-hole 2.4 mm locking compression plate. BMC Vet. Res. 2013, 9, 125. [Google Scholar] [CrossRef] [PubMed]
- Shea, T.M.; Laun, J.; Gonzalez-Blohm, S.A.; Doulgeris, J.J.; Lee, W.E.; Aghayev, K.; Vrionis, F.D. Designs and techniques that improve the pullout strength of pedicle screws in osteoporotic vertebrae: Current status. Biomed Res. Int. 2014, 2014, 748393. [Google Scholar] [CrossRef] [PubMed]
- Fouad, H. Effects of the bone-plate material and the presence of a gap between the fractured bone and plate on the predicted stresses at the fractured bone. Med. Eng. Phys. 2010, 32, 783–789. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Shih, K.S.; Hsu, C.C.; Cho, T. Simulation-based particle swarm optimization and mechanical validation of screw position and number for the fixation stability of a femoral locking compression plate. Med. Eng. Phys. 2014, 36, 57–64. [Google Scholar] [CrossRef]
- Perren, S.M. Fracture healing—The evolution of our understanding. Acta Chir. Orthop. Traumatol. Cech. 2008, 75, 241–246. [Google Scholar] [CrossRef]
- Lacroix, D.; Prendergast, P.J. A mechano-regulation model for tissue differentiation during fracture healing: Analysis of gap size and loading. J. Biomech. 2002, 35, 1163–1171. [Google Scholar] [CrossRef]
- Henschel, J.; Tsai, S.; Fitzpatrick, D.C.; Marsh, J.L.; Madey, S.M.; Bottlang, M. Comparison of 4 Methods for Dynamization of Locking Plates: Differences in the Amount and Type of Fracture Motion. J. Orthop. Trauma 2017, 31, 531–537. [Google Scholar] [CrossRef]
- Schulte, F.A.; Ruffoni, D.; Lambers, F.M.; Christen, D.; Webster, D.J.; Kuhn, G.; Müller, R. Local Mechanical Stimuli Regulate Bone Formation and Resorption in Mice at the Tissue Level. PLoS ONE 2013, 8, e62172. [Google Scholar]


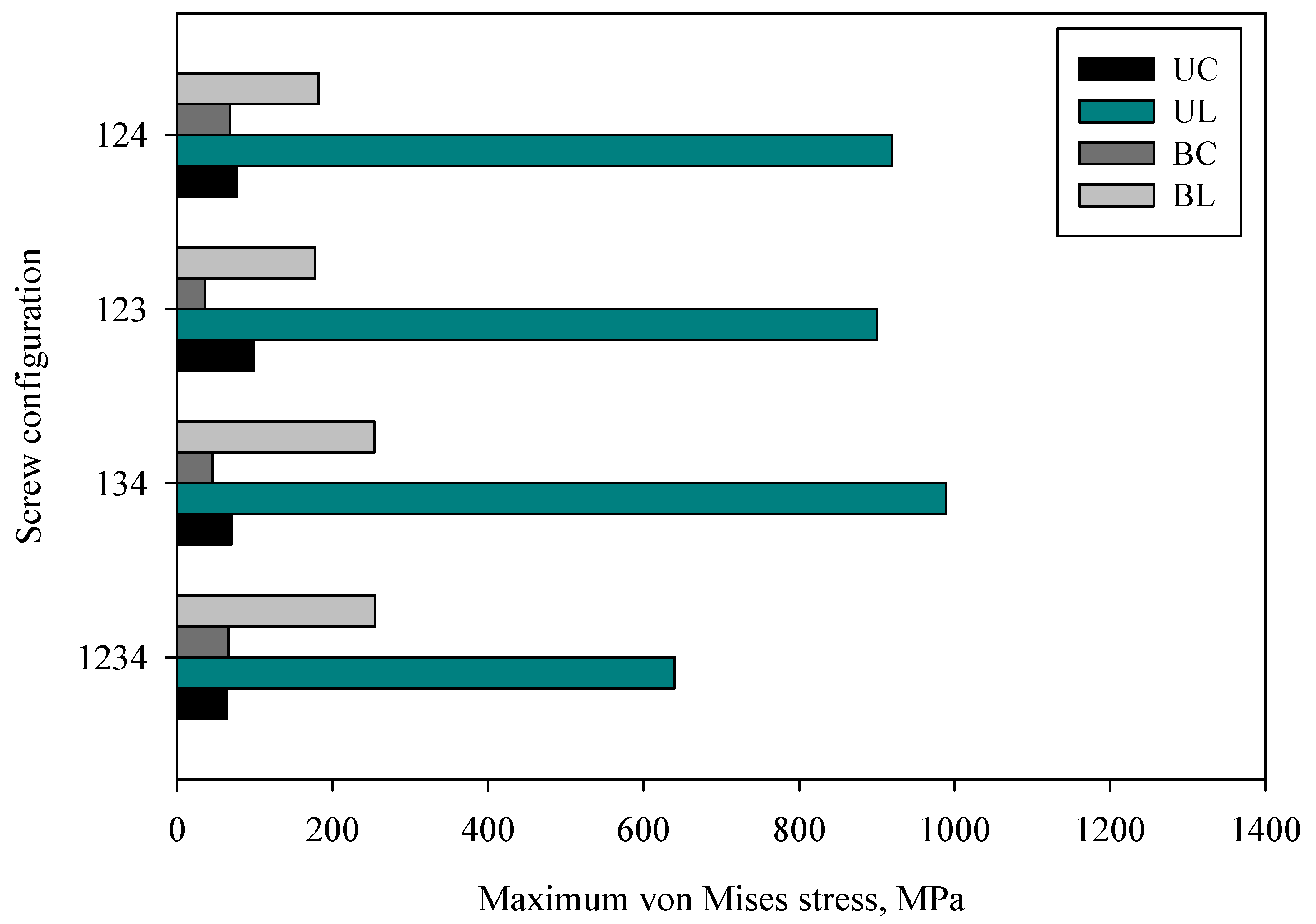


| Type of Configuration | Size Element | Mesh Node | Mesh Element |
|---|---|---|---|
| UC1234 | 0.4 | 1,749,365 | 1,030,853 |
| UL1234 | 1,897,652 | 1,104,719 | |
| BC1234 | 1,954,078 | 1,152,557 | |
| BL1234 | 2,171,312 | 1,272,999 | |
| UC1234 | 0.6 | 975,134 | 572,176 |
| UL1234 | 1,010,747 | 582,995 | |
| BC1234 | 1,215,571 | 717,126 | |
| BL1234 | 1,448,019 | 847,188 | |
| UC1234 | 0.8 | 647,338 | 379,441 |
| UL1234 | 674,924 | 388,894 | |
| BC1234 | 811,360 | 477,850 | |
| BL1234 | 1,054,827 | 616,522 | |
| UC1234 | 1 | 490,809 | 290,207 |
| UL1234 | 524,384 | 129,887 | |
| BC1234 | 648,844 | 385,956 | |
| BL1234 | 900,669 | 527,306 |
| Component | Relationship | Remark |
|---|---|---|
| Screw–bone (i.e., screw threads) | Rigid (bonded contact) | Fixed all degrees of freedom |
| Plate–bone | Contact pair | Initially bonded |
| Fracture surface | Contact pair | Initially bonded |
| Plate–screw (conventional) | Contact pair | Provide a universal connection between the screw control node and nodes on the bearing surface of the plate. |
| Plate–screw (locked) | Rigid | Provide a rigid connection between the screw control node and nodes on the bearing surface of the plate. |
| Material | Young’s Modulus, E (GPa) | Poisson’s Ratio (ʋ) | Shear Modulus (GPa) |
|---|---|---|---|
| Trabecular | ETb = 1.1 | ʋTb = 0.3 | - |
| Callus | Ecallus = 0.2 | ʋcallus = 0.3 | - |
| Cortical bone (Longitudinal transverse) | E3 = 20.0 | ʋ12 = 0.376 | G12 = 4.53 |
| E1 = 12.0 | ʋ23 = 0.235 | G23 = 4.53 | |
| E2 = 12.0 | ʋ23 = 0.376 | G13 = 4.53 | |
| Stainless steel | Es.s = 200 | ʋS.S = 0.3 | - |
| Implant Type | Screw Configuration | |||
|---|---|---|---|---|
| 1234 | 134 | 123 | 124 | |
| Group UC | * 0.0175 | 0.0204 | 0.0233 | 0.0262 |
| Group UL | * 0.0184 | 0.0215 | 0.0246 | 0.0276 |
| Group BC | * 0.0102 | * 0.0119 | * 0.0136 | * 0.0154 |
| Group BL | * 0.0118 | * 0.0138 | * 0.0158 | * 0.0178 |
| Screw Type | Screw Configuration | |||
|---|---|---|---|---|
| 1234 | 134 | 123 | 124 | |
| Group UC | 3.87 × 10−6 | 5.39 × 10−6 | 2.00 × 10−7 | 2.64 × 10−5 |
| Group UL | 2.96 × 10−6 | 4.12 × 10−6 | 1.53 × 10−7 | 2.02 × 10−5 |
| Group BC | 2.18 × 10−6 | 3.03 × 10−6 | 1.12 × 10−7 | 1.49 × 10−5 |
| Group BL | 4.90 × 10−6 | 6.82× 10−6 | 2.53 × 10−7 | 3.35 × 10−5 |
| Screw Configuration | 1234 | 134 | 123 | 124 |
|---|---|---|---|---|
| Regression | 0.0256 | 0.0264 | 0.0003 | 0.6632 |
| Normality test (Shapiro–Wilk) | * 0.4186 | * 0.4186 | * 0.4183 | * 0.4186 |
| Constant variance test | 0.7048 | 0.0059 | 0.0072 | 0.9432 |
| Standard error estimation | 0.0019 | 0.0022 | 0.0004 | 0.0049 |
| Implant Type | Compression Load (N) | |||
|---|---|---|---|---|
| 600 | 700 | 800 | 900 | |
| Group UC | 2.50 × 10−3 | 3.05 × 10−3 | 3.07 × 10−3 | 3.04 × 10−3 |
| Group UL | 1.68 × 10−3 | 2.91 × 10−3 | 1.97 × 10−3 | 2.96 × 10−3 |
| Group BC | 1.64 × 10−3 | 1.65 × 10−3 | 1.71 × 10−3 | 2.91 × 10−3 |
| Group BL | 2.89 × 10−3 | 2.91 × 10−3 | 1.97 × 10−3 | 2.96 × 10−3 |
| Screw Type | UC | UL | BC | BL |
|---|---|---|---|---|
| Correlation | 1.000 ** | −0.997 ** | −0.371 | 0.338 |
| Significant value | 0.000 | 0.003 | 0.629 | 0.662 |
| Compression Load | 600 N | 700 N | 800 N | 900 N |
|---|---|---|---|---|
| Correlation | −0.371 | −0.997 ** | −1.000 ** | 0.338 |
| Significant value | 0.629 | 0.003 | 0.000 | 0.662 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basirom, I.; Daud, R.; Ijaz, M.F.; Rojan, M.A.; Basaruddin, K.S. Stability Analysis of Plate—Screw Fixation for Femoral Midshaft Fractures. Materials 2023, 16, 5958. https://doi.org/10.3390/ma16175958
Basirom I, Daud R, Ijaz MF, Rojan MA, Basaruddin KS. Stability Analysis of Plate—Screw Fixation for Femoral Midshaft Fractures. Materials. 2023; 16(17):5958. https://doi.org/10.3390/ma16175958
Chicago/Turabian StyleBasirom, Izzawati, Ruslizam Daud, Muhammad Farzik Ijaz, Mohd Afendi Rojan, and Khairul Salleh Basaruddin. 2023. "Stability Analysis of Plate—Screw Fixation for Femoral Midshaft Fractures" Materials 16, no. 17: 5958. https://doi.org/10.3390/ma16175958
APA StyleBasirom, I., Daud, R., Ijaz, M. F., Rojan, M. A., & Basaruddin, K. S. (2023). Stability Analysis of Plate—Screw Fixation for Femoral Midshaft Fractures. Materials, 16(17), 5958. https://doi.org/10.3390/ma16175958





