Theoretical Investigation on Indirect Tensile Strength of Concrete with Rectangular Cross-Section under Locally Distributed Load
Abstract
:1. Introduction
2. Trigonometric Series Solution of the Indirect Tensile Strength of Rectangular Test Blocks
2.1. Brief Description of the Theoretical Solution Method for Indirect Tensile Strength of Rectangular Specimen
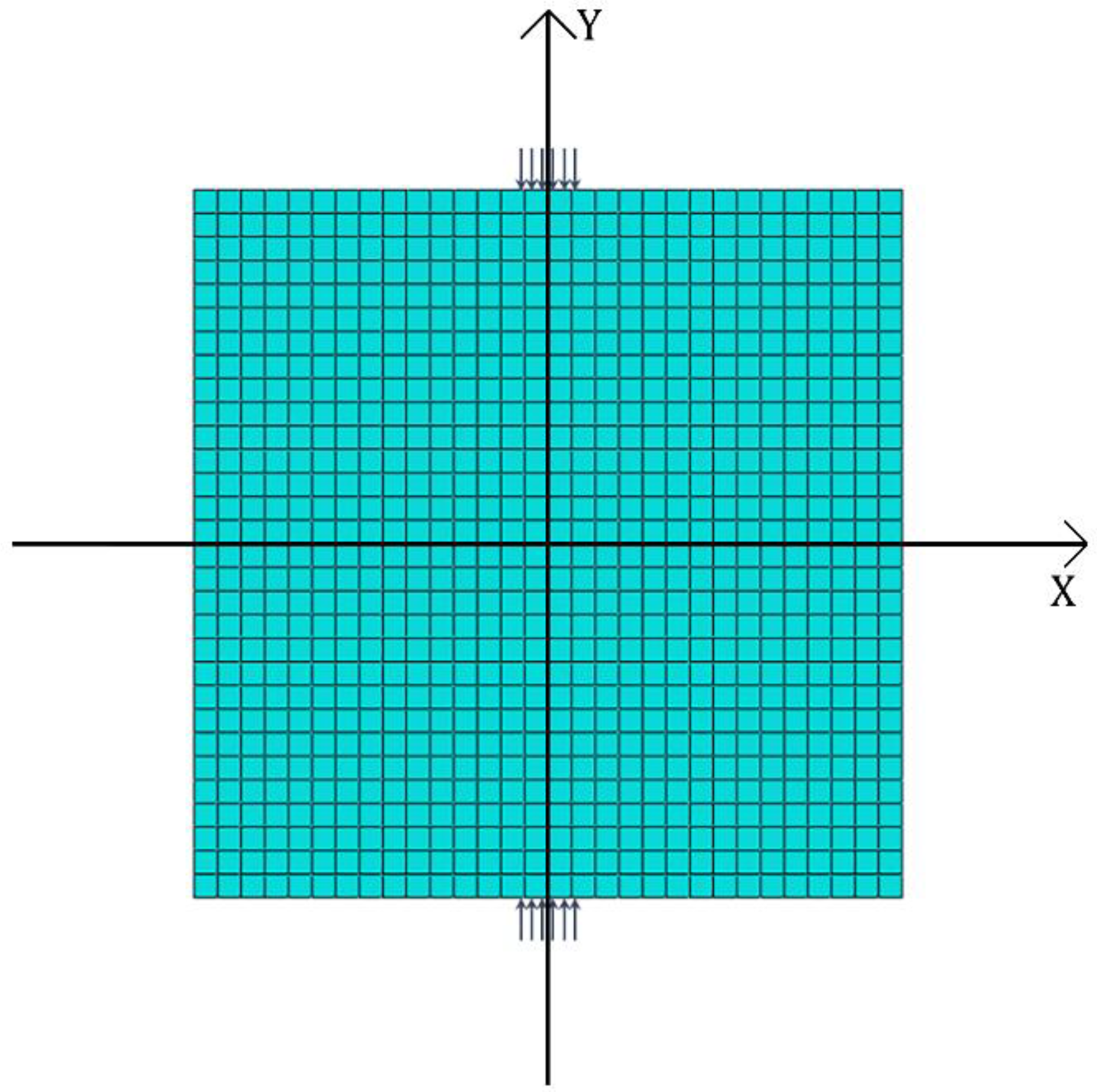
2.2. Theoretical Solutions for Rectangular Test Blocks under Locally Distributed Loads
3. Verification of Theoretical Results
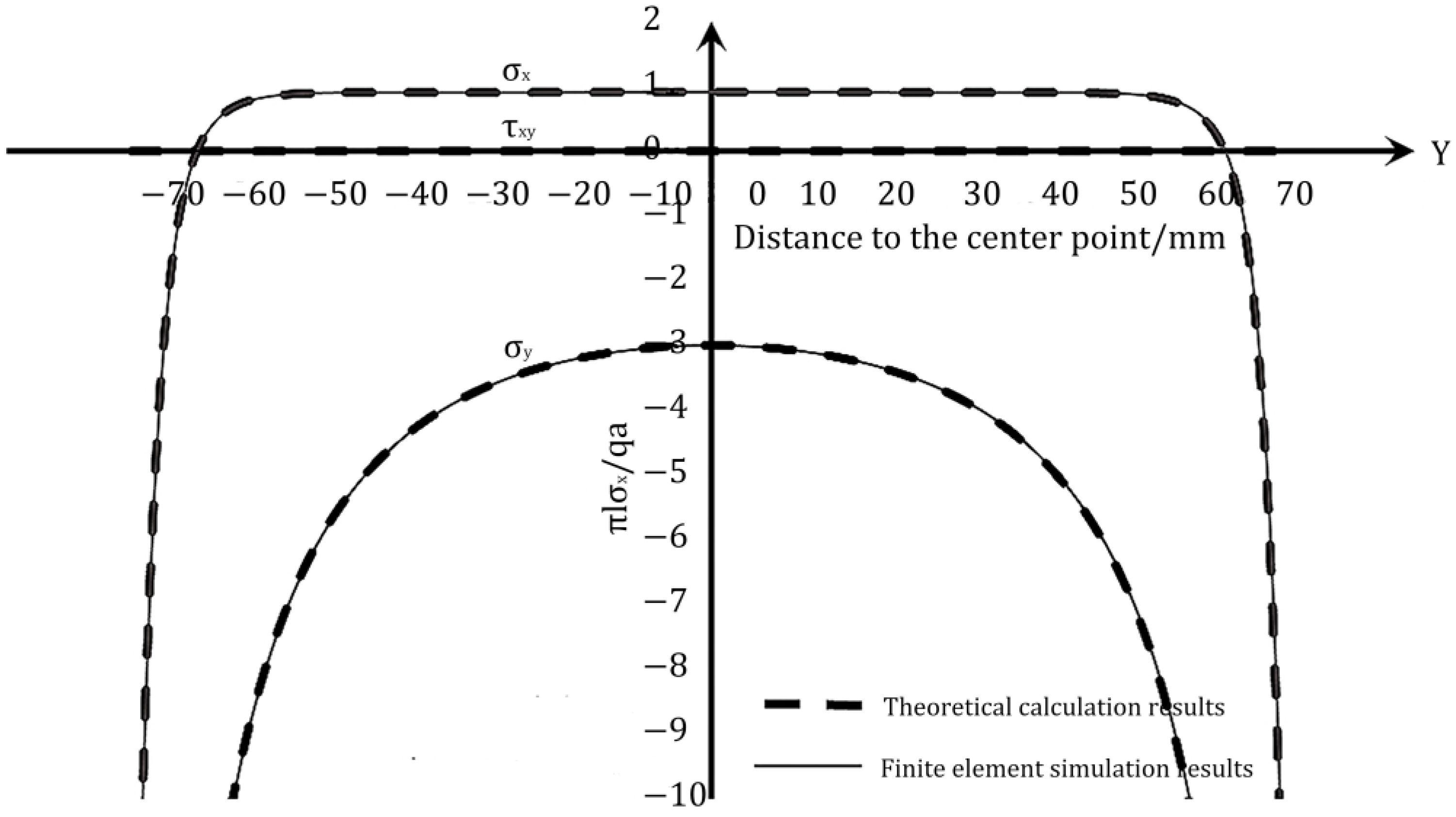
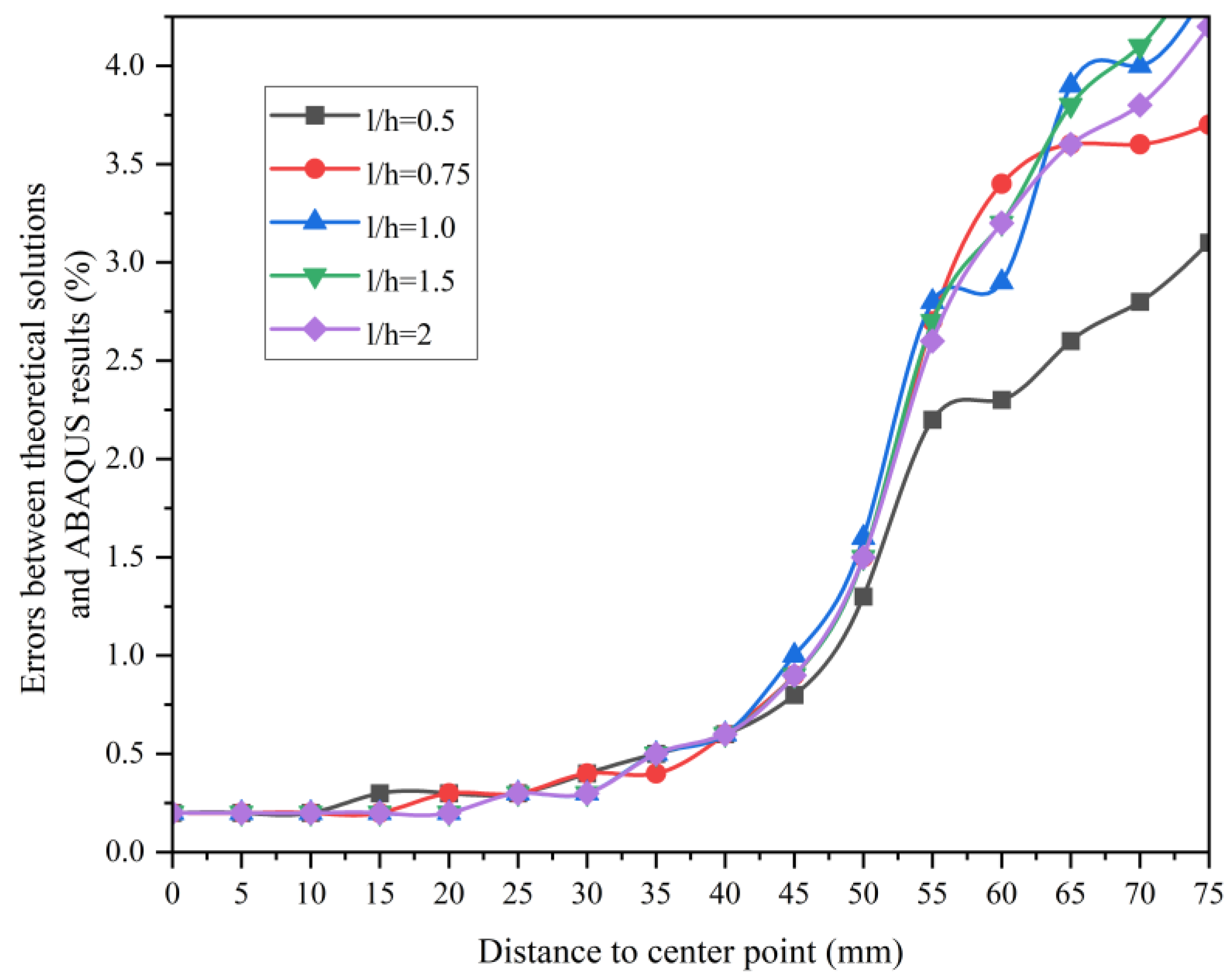
3.1. Comparison of Theoretical Solutions and Finite Element Simulation Tests
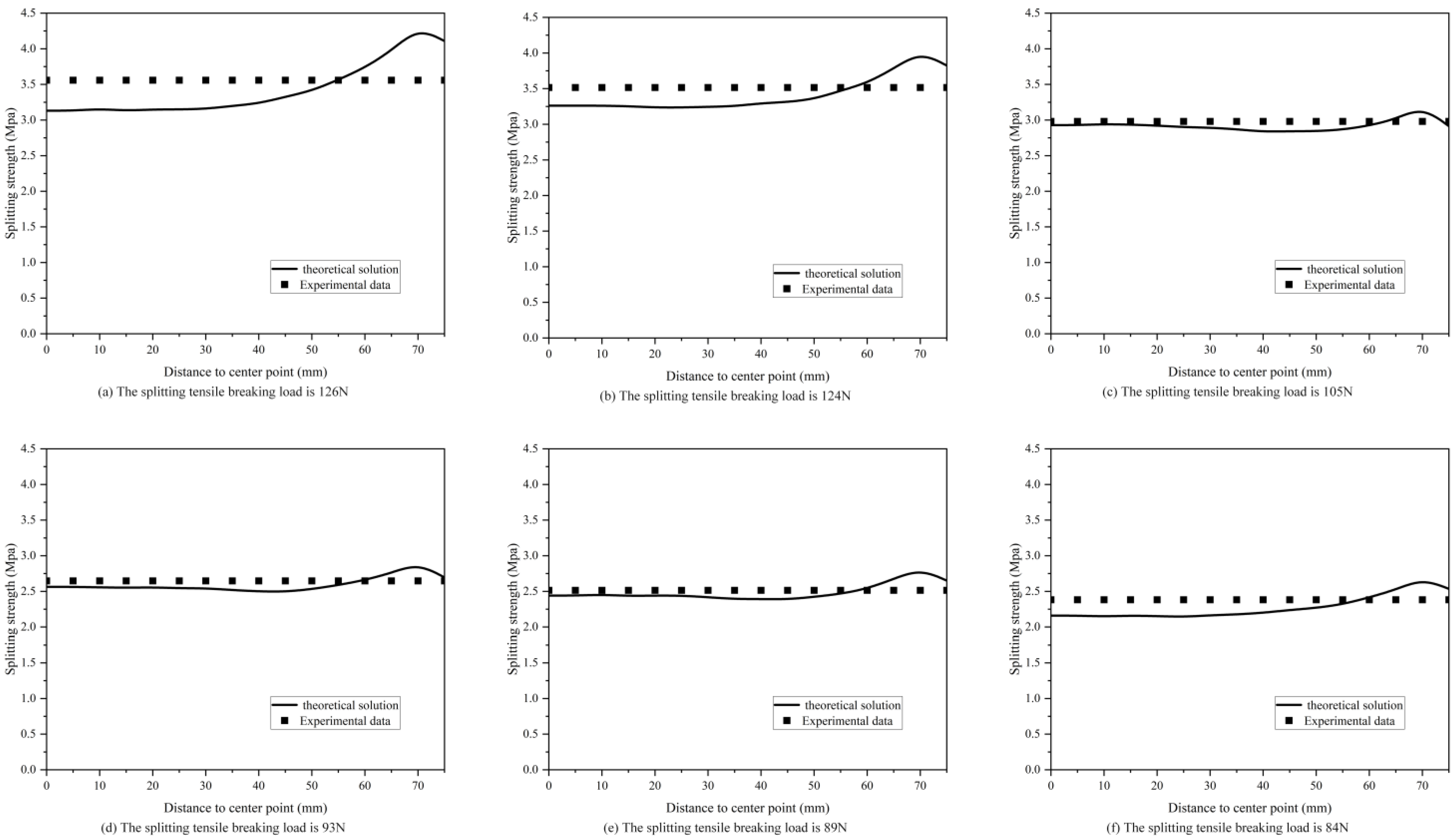
3.2. Comparison between Theoretical Solutions and Experimental Results
4. Theoretical Analysis of Tensile Strength of Rectangular Test Blocks under Locally Distributed Load
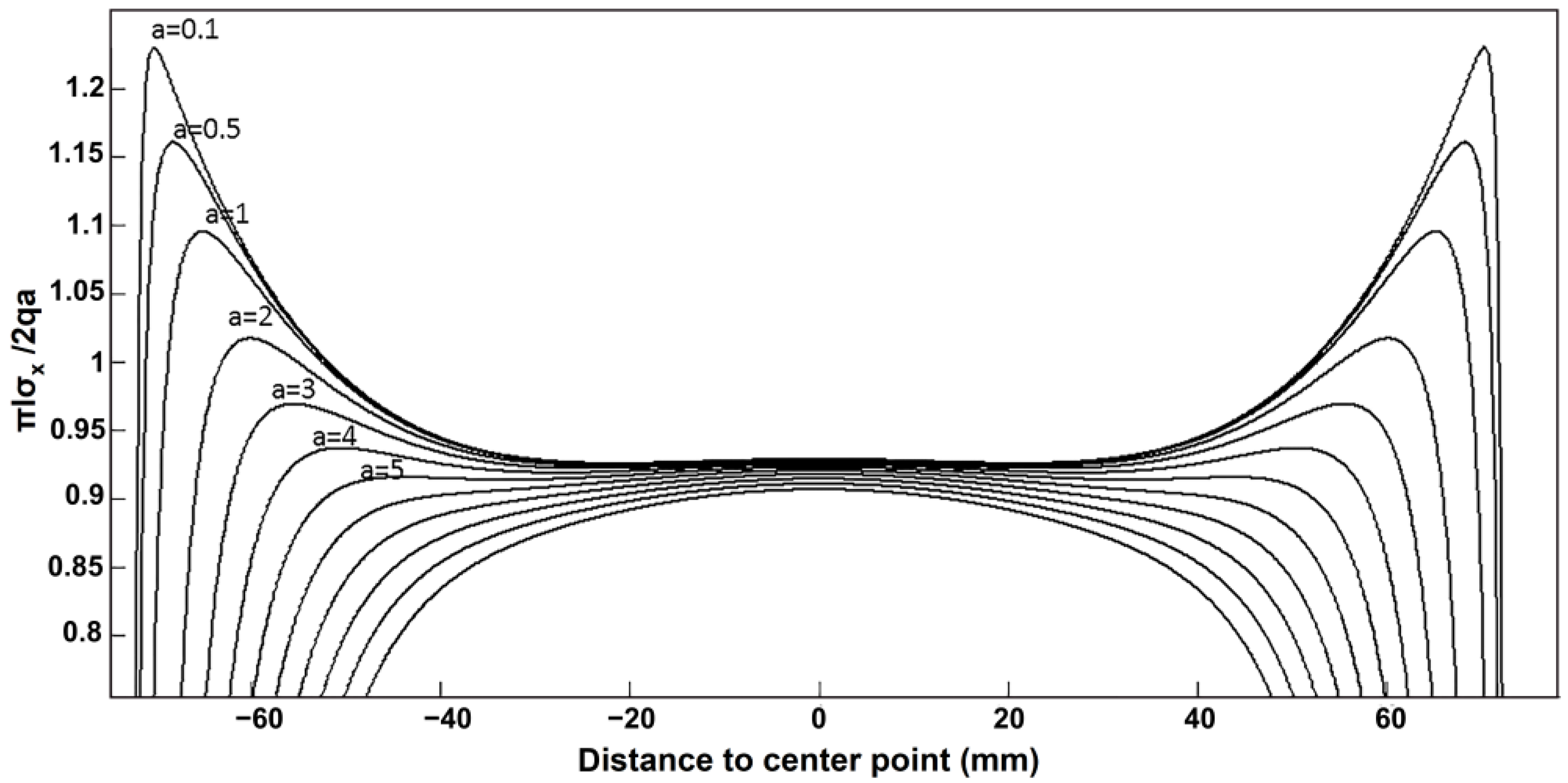
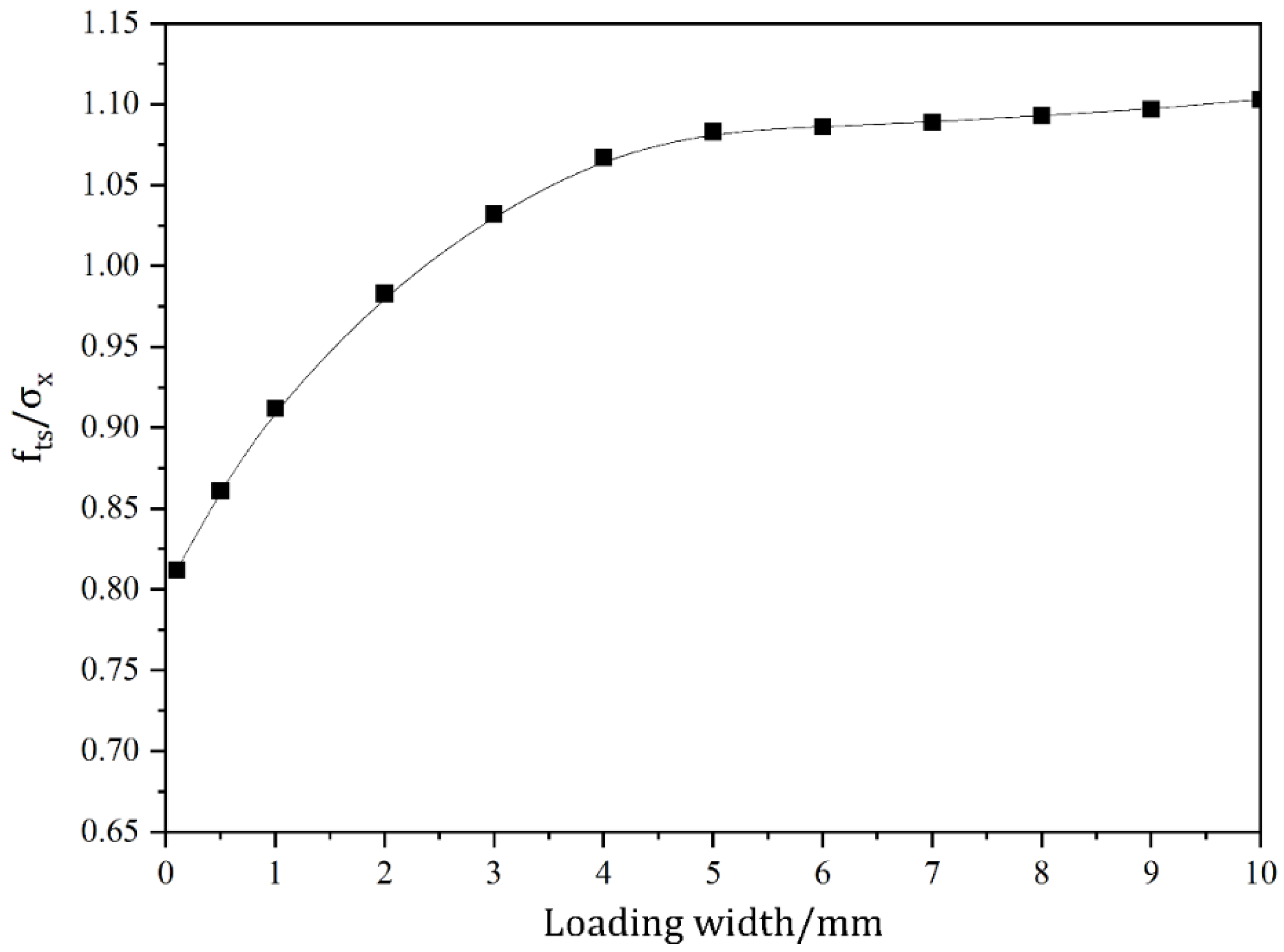
4.1. Effect of Local Loading Width on Tensile Strength
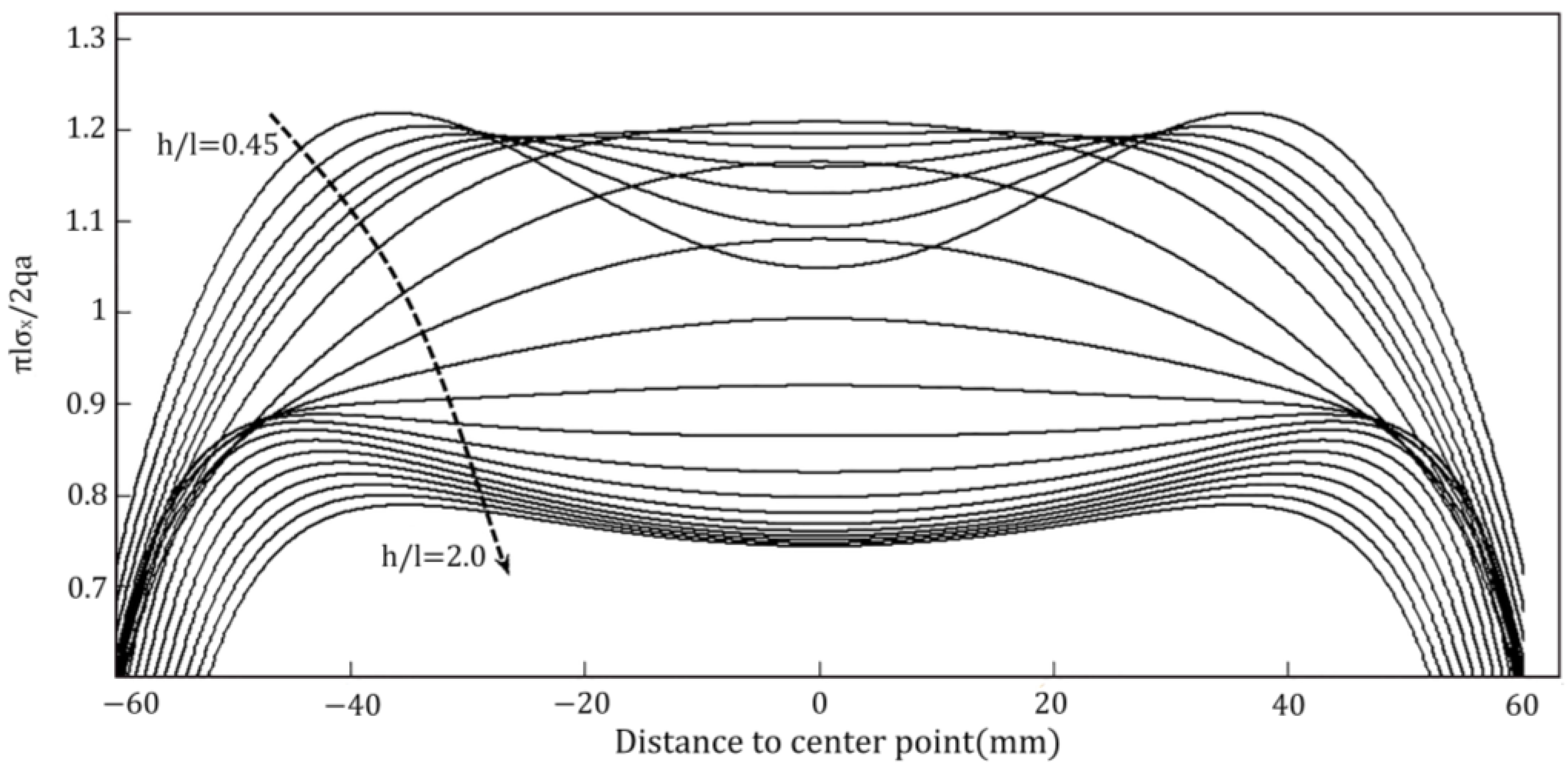
4.2. Effect of Length-to-Height Ratio of Rectangular Test Blocks on Tensile Strength
5. Conclusions
- The measured tensile strength of the specimens increases with the increase in the load action width. When the width of load action is less than 6% of the side length of the added specimen, the stress concentration near the loading point is obvious and the measured tensile strength value is small. If the width of load action is too small, it will cause stress concentration damage near the loading point and make the splitting tensile strength test invalid.
- The width of the load action has a greater influence on the location of the cracking point. With the increase in the width of the load action, the cracking point gradually moves from both sides to the center. The measured tensile strength presents an increasing trend with the increase in the loading width, and the rate of increase will gradually stabilize.
- The measured tensile strength increases with the increase in the aspect ratio. When h/l < 0.6, the measured tensile strength increases first and then decreases; when h/l > 0.6, the measured tensile strength manifests an increasing trend, and the increase rate is greater when 0.6 < h/l < 1.1 than when h/l > 1.1.
- The length-to-height ratio has a greater influence on the location of the crack initiation point of the specimen. With the increase in the length-to-height ratio, the location of the crack initiation point first moves from both sides to the center point, and then moves from the center point to both sides.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, R.H.; Duan, K.; Zhang, Q.Y. Effect of Heterogeneity in Micro-Structure and Micro-Strength on the Discrepancies Between Direct and Indirect Tensile Tests on Brittle Rock. Rock Mech. Rock Eng. 2022, 55, 981–1000. [Google Scholar] [CrossRef]
- Yang, R.; Li, W.; Li, Y.; Fang, S.; Zhu, Y. Comparative analysis on dynamic tensile mechanical properties of three kinds of rocks. J. China Coal Soc. 2020, 45, 3107–3118. [Google Scholar]
- Shukur, M.H.; Ibrahim, K.A.; Al-Darzi, S.Y.; Salih, O.A. Mechanical properties of concrete using different types of recycled plastic as an aggregate replacement. Cogent Eng. 2023, 10, 2243735. [Google Scholar] [CrossRef]
- Wessling, A.; Larsson, S.; Kajberg, J. A statistical bonded particle model study on the effects of rock heterogeneity and cement strength on dynamic rock fracture. Comput. Part. Mech. 2023. [Google Scholar] [CrossRef]
- Caverzan, A.; Peroni, M.; Solomos, G. Compressive behaviour of dam concrete at higher strain rates. Eur. Phys. J.-Spec. Top. 2016, 225, 283–293. [Google Scholar] [CrossRef]
- Truong, V.D.; Kim, D.J. A review paper on direct tensile behavior and test methods of textile reinforced cementitious composites. Compos. Struct. 2021, 19, 501–515. [Google Scholar] [CrossRef]
- Yoo, P.J.; Kim, T.W. Strengthening of hot-mix asphalt mixtures reinforced by polypropylene-impregnated multifilament glass fibres and scraps. Constr. Build. Mater. 2015, 75, 415–420. [Google Scholar] [CrossRef]
- Majedi, M.R.; Afrazi, M.; Fakhimi, A. A Micromechanical Model for Simulation of Rock Failure Under High Strain Rate Loading. Int. J. Civ. Eng. 2021, 47, 2271–2278. [Google Scholar] [CrossRef]
- Al Houri, A.; Habib, A.; Elzokra, A.; Habib, M. Tensile Testing of Soils: History, Equipment and Methodologies. Civ. Eng. J.-Tehran 2020, 6, 591–601. [Google Scholar] [CrossRef]
- Demirdag, S.; Tufekci, K.; Sengun, N.; Efe, T.; Altindag, R. IOP in Determination of the Direct Tensile Strength of Granite Rock by Using a New Dumbbell Shape and its Relationship with Brazilian Tensile Strength, World Multidisciplinary Earth Sciences Symposium (WMESS), Prague, Czech Republic, 3–7 September 2018; IOP Publishing Ltd.: Prague, Czech Republic, 2018. [Google Scholar]
- Rafiee, R.; Abbasi, F. Numerical and Experimental Analyses of the Hoop Tensile Strength of Filament-Wound Composite Tubes. Mech. Compos. Mater. 2020, 56, 423–436. [Google Scholar] [CrossRef]
- Kumar, A.; Liu, Y.Y.C.; Dolbow, J.E.; Lopez-Pamies, O. The strength of the Brazilian fracture test. J. Mech. Phys. Solids 2023, 182, 105473. [Google Scholar] [CrossRef]
- Slowik, M.; Akram, A. Length Effect at Testing Splitting Tensile Strength of Concrete. Materials 2022, 15, 250. [Google Scholar] [CrossRef] [PubMed]
- Cakiroglu, C.; Aydin, Y.; Bekdas, G.; Geem, Z.W. Interpretable Predictive Modelling of Basalt Fiber Reinforced Concrete Splitting Tensile Strength Using Ensemble Machine Learning Methods and SHAP Approach. Materials 2023, 16, 4578. [Google Scholar] [CrossRef] [PubMed]
- de-Prado-Gil, J.; Palencia, C.; Jagadesh, P.; Martínez-García, R. A Comparison of Machine Learning Tools That Model the Splitting Tensile Strength of Self-Compacting Recycled Aggregate Concrete. Materials 2022, 15, 4164. [Google Scholar] [CrossRef] [PubMed]
- Guzmán-Torres, J.A.; Domínguez-Mota, F.J.; Alonso-Guzmán, E.M.; Martínez-Molina, W. Modeling Tensile Strength of Concrete Using Support Vector Regression. ACI Mater. J. 2022, 119, 25–37. [Google Scholar]
- Behnood, A.; Verian, K.P.; Gharehveran, M.M. Evaluation of the splitting tensile strength in plain and steel fiber-reinforced concrete based on the compressive strength. Constr. Build. Mater. 2015, 98, 519–529. [Google Scholar] [CrossRef]
- Van Cauwelaert, F. The split tensile test applied to rectangular concrete blocks—Numerical and analytical approach. Mater. Struct. 1996, 29, 494–499. [Google Scholar] [CrossRef]
- Chai, Q.; Huang, S.; Wan, F.; Wu, F.; Feng, L. A new experimental method to measure and calculate the tensile strength of concrete. Front. Mater. 2023, 10, 1216747. [Google Scholar] [CrossRef]
- Ince, R.; Gör, M.; Eren, M.E.; Alyamaç, K.E. The Effect of Size on the Splitting Strength of Cubic Concrete Members. Strain 2015, 51, 135–146. [Google Scholar] [CrossRef]
- Luan, C.; Wang, Q.; Yang, F.; Zhang, K.; Utashev, N.; Dai, J.; Shi, X. Practical Prediction Models of Tensile Strength and Reinforcement-Concrete Bond Strength of Low-Calcium Fly Ash Geopolymer Concrete. Polymers 2021, 13, 875. [Google Scholar] [CrossRef]
- Huang, X.; Jiang, J.; Sun, T.; Jiang, W. Orthogonal experiment on mechanical properties of basalt fiber-carbon fiber/slag concrete. Acta Mater. Compos. Sin. 2020, 37, 1743–1753. [Google Scholar]
- Karczmarzyk, S. An exact elastodynamic solution to vibration problems of a composite structure in the plane stress state. J. Sound Vibr. 1996, 196, 85–96. [Google Scholar] [CrossRef]
- Zhong, W.; Yao, W. New solution system for plate bending and its application. Acta Mech. Sin. 1999, 31, 173–184. [Google Scholar]
- Yu, T.; Zhong, Z. A general solution of a clamped functionally graded cantilever-beam under uniform loading. Acta Mech. Solida Sin. 2006, 27, 15–20. [Google Scholar]
- Rocco, C.; Guinea, G.V.; Planas, J.; Elices, M. Review of the splitting-test standards from a fracture mechanics point of view. Cem. Concr. Res. 2001, 31, 73–82. [Google Scholar] [CrossRef]
- Feng, L.; Yuan, Q.; Ma, Y.; Shi, C. Experimental Study on Mechanical Property of Rubber Concrete. J. Yangtze River Sci. Res. Inst. 2015, 32, 115–118. [Google Scholar]
- Tang, T. Effects of load-distributed width on split tension of unnotched and notched cylindrical specimens. J. Test. Eval. 1994, 22, 401–409. [Google Scholar]
- Rocco, C.; Guinea, G.V.; Planas, J.; Elices, M. Mechanisms of rupture in splitting tests. ACI Mater. J. 1999, 49, 340–353. [Google Scholar]
- Wu, Z.Y.; Zhang, J.H.; Yu, H.F.; Fang, Q.; Ma, H.Y.; Chen, L. Three-Dimensional Mesoscopic Investigation on the Impact of Specimen Geometry and Bearing Strip Size on the Splitting-Tensile Properties of Coral Aggregate Concrete. Engineering 2022, 17, 110–122. [Google Scholar] [CrossRef]
- Mostafa, I.T.; Mousa, S.; Mohamed, H.M.; Benmokrane, B. Behavior of high-strength concrete (HSC) box girders reinforced with GFRP bars, ties, and spirals under torsion. Struct. Concr. 2023, 294, 116726. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Y.J.; Zhang, W.; Zhu, L. Property Assessment of High-Performance Concrete Containing Three Types of Fibers. Steel Compos. Struct. 2023, 48, 17. [Google Scholar] [CrossRef]
- Jafaria, A.; Beheshtib, M.; Shahmansouric, A.A.; Bengar, H.A. Plastic hinge length for coupled and hybrid-coupled shear walls. Steel Compos. Struct. 2023, 48, 367–383. [Google Scholar]
- Khalili, A.; Nateghi-Alahi, F. Finite element analysis of RC moment-resisting frames to assess effective slab width; a parametric study. Structures 2023, 57, 105113. [Google Scholar] [CrossRef]




| a/mm | 0.1 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fts/σx | 0.812 | 0.861 | 0.912 | 0.983 | 1.032 | 1.067 | 1.083 | 1.086 | 1.089 | 1.093 | 1.097 | 1.103 |
| h/l | h (mm) | l (mm) | Loading Width (mm) | Distributed Load Values (MPa) |
|---|---|---|---|---|
| 0.50 | 150.00 | 75.00 | 15.00 | 66.67 |
| 0.75 | 150.00 | 112.50 | 22.50 | 44.44 |
| 1.00 | 150.00 | 150.00 | 30.00 | 33.33 |
| 1.25 | 150.00 | 187.50 | 37.50 | 26.67 |
| 1.50 | 150.00 | 225.00 | 45.00 | 22.22 |
| 1.75 | 150.00 | 262.50 | 52.50 | 19.05 |
| 2.00 | 150.00 | 300.00 | 60.00 | 16.67 |
| d (mm) | h/l = 0.5 | h/l = 0.75 | h/l = 1 | h/l = 1.25 | h/l = 1.5 | h/l = 1.75 | h/l = 2 |
|---|---|---|---|---|---|---|---|
| 0 | 0.068% | 0.066% | 0.072% | 0.050% | 0.006% | 0.001% | 0.021% |
| 5 | 0.069% | 0.065% | 0.072% | 0.050% | 0.006% | 0.002% | 0.021% |
| 10 | 0.071% | 0.064% | 0.072% | 0.049% | 0.005% | 0.002% | 0.021% |
| 15 | 0.074% | 0.062% | 0.071% | 0.049% | 0.003% | 0.003% | 0.022% |
| 20 | 0.077% | 0.058% | 0.070% | 0.049% | 0.000% | 0.005% | 0.023% |
| 25 | 0.078% | 0.051% | 0.069% | 0.049% | 0.003% | 0.006% | 0.025% |
| 30 | 0.077% | 0.041% | 0.069% | 0.050% | 0.008% | 0.009% | 0.026% |
| 35 | 0.072% | 0.026% | 0.070% | 0.053% | 0.013% | 0.012% | 0.028% |
| 40 | 0.060% | 0.003% | 0.075% | 0.058% | 0.021% | 0.016% | 0.028% |
| 45 | 0.036% | 0.033% | 0.087% | 0.067% | 0.033% | 0.023% | 0.026% |
| 50 | 0.010% | 0.093% | 0.115% | 0.085% | 0.068% | 0.053% | 0.010% |
| 55 | 0.100% | 0.240% | 0.246% | 0.973% | 0.141% | 0.026% | 0.044% |
| 60 | 0.330% | 3.924% | 0.036% | 0.067% | 0.011% | 0.005% | 0.019% |
| 65 | 2.984% | 0.128% | 0.097% | 0.061% | 0.024% | 0.058% | 0.087% |
| 70 | 0.066% | 0.000% | 0.005% | 0.152% | 0.345% | 0.511% | 0.564% |
| 75 | 3.996% | 4.048% | 4.233% | 4.532% | 4.864% | 5.207% | 5.567% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Xu, J.; Sun, L.; Yue, J.; Zang, Q. Theoretical Investigation on Indirect Tensile Strength of Concrete with Rectangular Cross-Section under Locally Distributed Load. Materials 2023, 16, 7671. https://doi.org/10.3390/ma16247671
Wang Z, Xu J, Sun L, Yue J, Zang Q. Theoretical Investigation on Indirect Tensile Strength of Concrete with Rectangular Cross-Section under Locally Distributed Load. Materials. 2023; 16(24):7671. https://doi.org/10.3390/ma16247671
Chicago/Turabian StyleWang, Ziran, Jialin Xu, Linhao Sun, Jinchao Yue, and Quansheng Zang. 2023. "Theoretical Investigation on Indirect Tensile Strength of Concrete with Rectangular Cross-Section under Locally Distributed Load" Materials 16, no. 24: 7671. https://doi.org/10.3390/ma16247671
APA StyleWang, Z., Xu, J., Sun, L., Yue, J., & Zang, Q. (2023). Theoretical Investigation on Indirect Tensile Strength of Concrete with Rectangular Cross-Section under Locally Distributed Load. Materials, 16(24), 7671. https://doi.org/10.3390/ma16247671





