Next Article in Journal
Effects of Different Altitudes on Castanopsis hystrix, the Top Community-Building Species in Southern Subtropical China: Rhizospheric Soil Chemical Properties and Soil Microbiota
Next Article in Special Issue
A Copula Approach for Predicting Tree Sap Flow Based on Vapor Pressure Deficit
Previous Article in Journal
Response of Forest Bird Communities to Managed Landscapes in the Acadian Forest
Previous Article in Special Issue
The Water Dynamics of Norway Spruce Stands Growing in Two Alpine Catchments in Austria
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 15
Issue 1
10.3390/f15010186
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characteristics and Estimation of the Time of Concentration for Small Forested Catchments in Steep Mountainous Terrain

by
Sooyoun Nam
,
Honggeun Lim
,
Byoungki Choi
,
Qiwen Li
,
Haewon Moon
and
Hyung Tae Choi
*
Forest Environment and Conservation Department, National Institute of Forest Science, Seoul 02455, Republic of Korea
*
Author to whom correspondence should be addressed.
Forests 2024, 15(1), 186; https://doi.org/10.3390/f15010186
Submission received: 30 November 2023 / Revised: 12 January 2024 / Accepted: 15 January 2024 / Published: 17 January 2024
(This article belongs to the Special Issue Hydrological Modelling of Forested Ecosystems)
Browse Figures
Versions Notes

Abstract

:
Accurate modeling of flood flow hydrographs for small forested catchments in steep mountainous terrain is challenging because of large errors in the estimation of response time using existing empirical equations. The time of concentration (TC) for a catchment is a widely used time parameter for estimating peak discharges in hydrological designs. In this study, we developed an estimated TC using readily available mountain catchment variables, a small catchment, steep slope, and narrow valley, using empirical equations. For our approach, we used directly measured data from 39 forested catchments (area: 0.02–9.69 km2) during 3648 observed rainfall events over a 10-year observation period. Based on the uncertainties inherent in the empirical equation, the estimated TC values were compared and analyzed through multiple regression and two different modified empirical modelling equations using our observed catchment parameters. The mean TC was significantly correlated with catchment size and stream length but negatively correlated with stream slope (p < 0.01). As a result, the mean TC estimated using the three modelling equations with catchment variables was qualitatively similar and had relative differences ranging from −12.5 to 15.5 min (−49 to 56%). Therefore, the models (particularly modeling equations with multiple regression, a modified empirical formula, and modified SCS Lag) can efficiently determine the TC and can be used in any small forested catchment in steep mountainous terrain.

1. Introduction

Hydrological analyses require one or more time-scale parameters as inputs [1]. Time responses are fundamental parameters for hydrologists to design floods because the amount of precipitation may not cause a flood risk; however, the runoff distribution may cause a flood risk [2]. Consequently, the design of a flood requires the time response of the catchment [3,4]. Among these parameters, the time of concentration (TC) is most frequently utilized [5,6]. The TC of a catchment is the time required for the runoff to travel from the most hydraulically distant point to the outlet of the catchment [5,7,8,9,10]. The TC is a specific value for a specific catchment and rainfall condition, and represents the steady-state hydraulic condition formed in the catchment [11]. Furthermore, the TC reflects the speed at which a catchment responds to rainfall events [12]; hence, it is important in hydrological analyses [13]. Zolghadr et al. [2] explained that the estimated TC leads to the accurate design of flood control structures and preparation of flood hazard maps and facilitates decision making by local authorities before floods. Hence, the estimated TC is essential for understanding the formulation of flood-forecasting models for the implementation of flood-warning systems [14,15].
Recognizing its importance, earlier attempts have been made to develop empirical methods for estimating TC within a catchment [13,16]. In addition, the input parameters can be used to derive or estimate TC using different empirical equations under various catchment topographical conditions [13,16]. For instance, McCuen [4] reported that empirical equations for estimating TC are based on four input parameters: slope, catchment size, flow resistance, and water input. Other empirical equations have been developed for catchments in which channel flow dominates [7,17,18,19]. Previous studies have indicated that empirical equations are typically developed using regression analysis with input parameters, such as catchment and channel parameters, including the catchment area, channel length, channel slope, and catchment shape parameters [4,7,19,20]. Although these formulas are well-accepted by the applied hydrology community, information on their technical foundations is limited [16]. Wait and Simonton [21] explained that each formula depends on a catchment’s unique physical characteristics, such as its area, flow path lengths, characterizations of storage capacity and catchment slope.
On the Korean Peninsula, 63.1% of land is covered by forests located in mountainous terrain [22]. The topography is characterized by steep hills with a narrow valley; the topography can be attributed to rapid flood TC and high peak flow [23,24]. Most residents in this area live near the main channel with steep slopes (>30°) that are susceptible to slope failure of the mountainous areas [25,26]. Kim et al. [27] reported that perceptions of the degree of unsafety were higher (48–57%) among residents of eastern and mountainous areas, which are affected annually by sediment and flooding disasters caused by typhoons and heavy rainfall, than among western residents (38–46%). Min et al. [28] also explained that the living zone for residents was located in the watershed, and a provincial area was formed by the boundary of the mountainous region. In addition, most of the heavy rainfall occurs primarily in the summer season (June–September) as a result of the East Asian monsoon, during which time the Korean Peninsula is also impacted by the passage of severe tropical typhoons [29]. Similarly, Kim et al. [27] reported that typhoon-induced heavy rainfall associated with the East Asian monsoon climate is one of the most important factors affecting sediment disasters such as landslides, slope failure, and debris flows in the Korean Peninsula. Further, Kim et al. [30] explained that the Korean Peninsula experiences annual flood damage from the East Asian monsoon, and the flood damage costs caused by rainstorms and typhoons account for most damage losses caused by natural disasters. For these reasons, South Korea is classified as a nation with very high-water erosion vulnerability [31,32,33].
Owing to the numerous definitions and related estimation procedures available in the literature [34,35], which result in substantially different design values of TC, estimating TC remains as one of the most ambiguous and uncertain concepts in modern hydrology [16]. Many researchers have developed empirical equations using experimental and analytical methods [7,36,37,38,39,40]; however, these approaches are not effective for estimating TC in steep forested catchments. This is because in steep mountainous catchments it is difficult to directly measure discharge using conventional techniques [41]. Therefore, the objectives of this study were to (1) indicate event-driven TC characteristics with rainfall-runoff events and (2) develop an estimated TC based on empirical equations and a regression equation using catchment parameters. In our approach, we used directly measured data from 39 forested catchments over a 10-year observation period.

2. Materials and Methods

2.1. Study Sites

This study was conducted in 39 forested catchments, ranging from 0.02 to 9.69 km2, located in a mountainous region in South Korea (Figure 1). This area was managed by the National Institute of Forest Science (NiFoS). Six climate classes from the Köppen–Geiger classification system [42,43] occur within the observed forested catchments. The major climate types are warm temperate and snow. The climate classes are further sub-classified by their precipitation and temperature condition [44]. The six climate zones are Cfa (warm temperate, fully humid, and hot summer), Cwa (warm temperate, winter dry, and hot summer) Dfa (snow, fully humid, and hot summer), Dfb (snow, fully humid, and warm summer) Dwa (snow, winter dry, and hot summer), and Dwb (snow, winter dry, and warm summer) (Table 1). According to the weather stations of the Korea Meteorological Administration, the mean annual precipitation ± standard deviation (SD) in this region from 2003 to 2022 was 1348.6 ± 357.9 mm (minimum–maximum values: 589.2–2314.5 mm), of which 46–68% occurred from July to September. The mean annual temperature ± SD was 12.0 ± 1.3 °C (9.1–15.6 °C). The catchment elevations range from 59 to 1560 m above sea level, with a slope gradient ranging from 20.0 to 34.9°. The underlying geology comprises igneous, sedimentary, and metamorphic rocks. The catchment was mainly covered by 31–50-year-old stands (IV–VII) (71%) based on forest type map (1:5000). Most catchments are dominated by broadleaved and mixed forests (e.g., Quercus spp., Pinus densiflora, and Larix kaempferi), except for C3, C6, C9, and C21, which are covered by coniferous forests (e.g., Pinus koraiensis, Abies holophylla, and Pinus densiflora). Stream channels were 0.3–5.3 km in length and 0.1–0.5 m/m in slope (Table 1). The streamside vegetation consisted of forest cover and an understory that changed to open or closed types with seasonal distribution (e.g., [45]).

2.2. Field Observation

For all monitored catchments, we used stream gauging stations managed by the NiFoS (Figure 2a,b). Water level in the sharp-crested weirs (i.e., 90° V-notch, 120° V-notch, and rectangular sharp-crested weirs) were measured using capacitance water level recorder (OTT-Orpheus Mini Water Level Logger, OTT Messtechnik, Kempten, Germany). Because maximum water levels differed in various catchments, the sizes of weirs varied [46], particularly these weirs have simplicity, easy maintenance, and good flow measurement precision [47]. Weirs are located on exposed solid bedrock in the stream channel. The water level was measured at 10 min intervals for each catchment outlet. Precipitation was measured at 10 min intervals using a HOBO tipping-bucket rain gauge (RG3, Onset Computer Corporation, Bourne, MA, USA) located in an open area of each catchment outlet.
The event-driven TC was analyzed using rainfall events observed from 2010 to 2021. To examine the appropriate estimated TC equation response to rainfall events, we analyzed the variables of rainfall events and catchment. The rainfall event variables included total precipitation, maximum 10 min precipitation intensity, one day antecedent precipitation index (API1), duration of precipitation, and total stream water level. In this study, we considered API1 to be the sum of precipitation during the preceding day. We assumed that API1 was better than API5 in the forested mountainous catchments [23]. The catchment variables included catchment size, slope gradient, stream slope, and stream length [7,11,48].

2.3. Data Analysis

When selecting a design flood using a modelling empirical equation, the duration of the designed precipitation should be determined; therefore, it is necessary to recommend an appropriate TC for the catchment [49]. Numerous formulas for estimating TC have been developed for different land uses and geometries [11]. This is because the surface flow is dominant, and empirical formulas using the stream slope and length are effective for mountain streams [2,49]. The estimated values were compared to the observed values [1,2,50]. The catchment variables used for this were the slope gradient, stream slope, and stream length associated with a deep relationship to TC for determining an appropriate modeling equation [4,7,17,18,19]. The selected formula, their necessary explanations, and references are listed in Table 2 [7,13,36,39,40,51,52,53,54,55]. The reference empirical equations for estimating TC were based on four types of input parameters: slope, catchment size, flow resistance, and water input (Table 2). Several empirical equations are applicable to natural basins that are commonly used for natural catchments in South Korea (e.g., [32,56,57,58]).
The residual between observed and estimated TC values was determined as follows:
R e s i d u a l = y i − y i ^
where y i is the observed TC value at time i (min), and y i ^ is the estimated TC value at time i (min).
To evaluate the advantages and disadvantages of the proposed estimation TC modeling equation in the present study, we used the mean of absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and Nash–Sutcliffe efficiency (NSE) [48,59], which were determined as follows:
M A E = 1 N ∑ i = 1 N y i − y i ^
R M S E = 1 N ∑ i = 1 N y i − y i ^ 2
M A P E = 1 N ∑ i = 1 N y i − y i ^ y i
N S E = 1 − ∑ i = 1 N y i − y i ^ 2 ∑ i = 1 N y i − y i ¯ 2
where y i ¯ is the mean of the observed TC value (min) and N is the total number of rainfall events. MAE, RMSE, NSE, and MAPE are commonly used metrics to compare the values predicted by a model with the values actually observed (e.g., [48,59,60,61]). If the results of MAE, RMSE, and MAPE are closer to 0 and NSE is closer to 1, then the prediction accuracy of the model is higher (e.g., [59,62]).
All statistical analyses were performed using R version 4.1.2 (R Foundation for Statistical Computing, Vienna, Austria) and IBM SPSS Statistics 19 (IBM Corp., Armonk, NY, USA).

3. Results

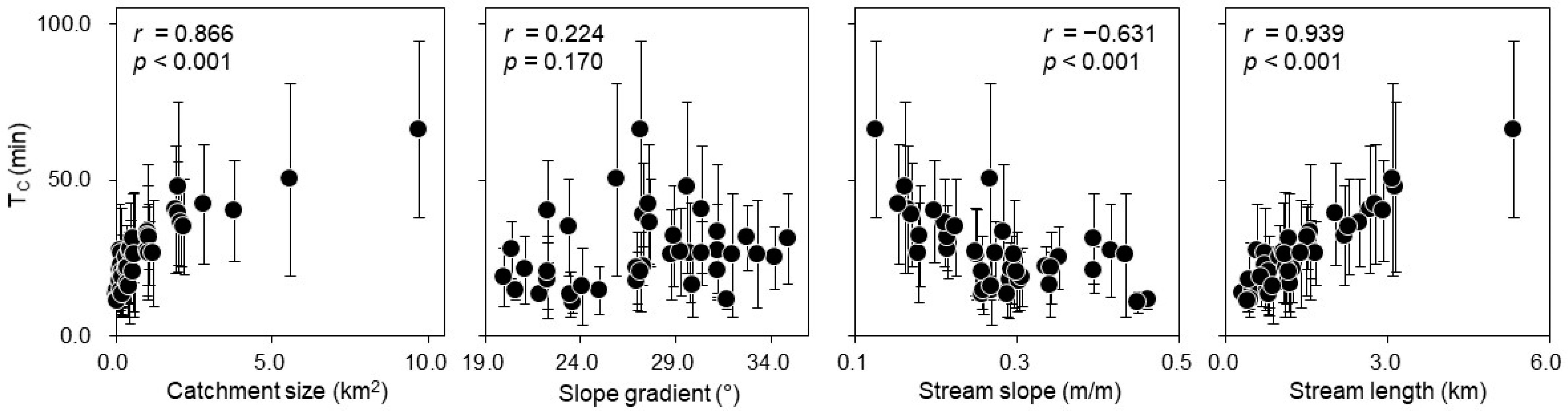
3.1. Characteristics of Time of Concentration by Catchment Variables

During the monitoring period from 2010 to 2021, we observed 3648 rainfall events. Table 3 lists the rainfall event variables; TC ranged from 5.0 to 115.4 min. Rainfall event characteristics included the total precipitation and maximum (max.) 10 min precipitation intensity, duration of precipitation, and one day antecedent precipitation. The total precipitation during the observed rainfall events was 2.2–698.4 mm with 1.7–29.5 mm of max. 10 min precipitation intensity. The duration of precipitation and one-day preceding precipitation was 0.1–12.1 hr and 0.0–258.3 mm, respectively (Table 3).
The mean TC ranged from 11.0 to 66.2 min with a 0.02–9.69 km2 catchment size, 20.0–34.9° slope gradient, 0.1–0.5 m/m stream slope, and 0.3–5.3 km stream length for 39 forested catchments (Figure 3). From the detected TC changes due to the catchment variables (e.g., [1]), a correlation analysis was performed between the TC and spatial variables (i.e., catchment size, slope gradient, stream slope, and stream length). The TC significantly correlated with the catchment size and stream length but negatively correlated with the stream slope (p < 0.01) (Figure 3).

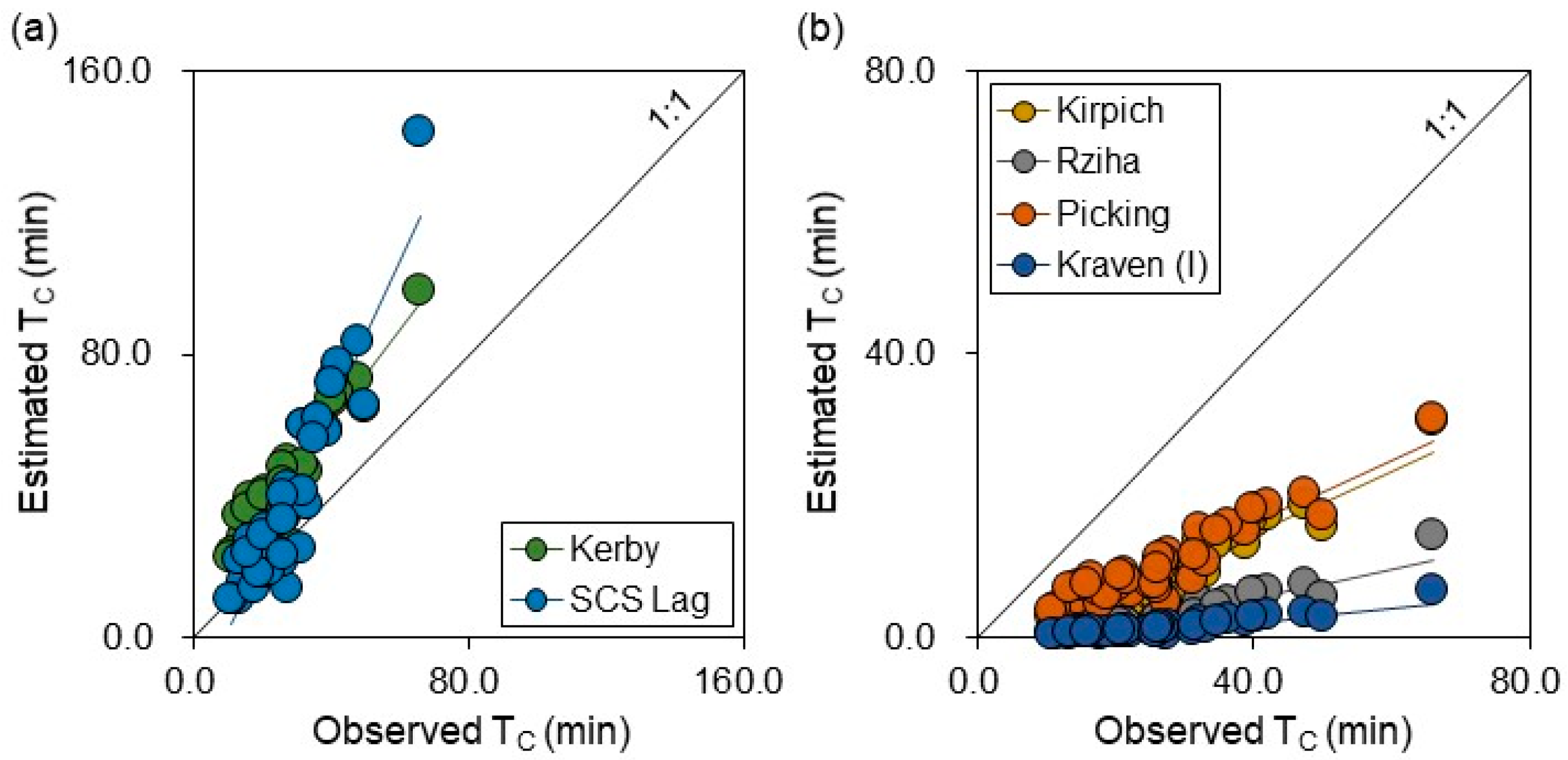
3.2. Interaction of Empirical Formulas and the Time of Concentration

Based on the results of the correlation analysis, the different methods for estimating TC (six empirical formulas; Table 2) were applied to 39 forested mountain catchments using their appropriate catchment parameters. The reference empirical equation is based on the physical characteristics of catchments, including their size, stream slope, stream length, land cover, and use (e.g., [11,13,63,64]). The estimated values were then compared with the observed values. The formulae were carefully selected to be as consistent as possible with the information and data available from the catchments. The selected formulae, their necessary explanations, and references are listed in Table 2.
In this study, we integrated the following concepts for the variables along with a practical procedure for their estimation using readily available catchment characteristic variables, with the aim of standardizing this key parameter for practitioners [65]. To derive or estimate different catchment topographic data using different methods (Table 2), empirical equations can be used to determine how variables estimated using different methods impact the estimation of TC for small forested catchments in steep mountainous terrain.
Table 4 shows that the statistical measures selected to assess the reference empirical equations in this study were the residual (min), MAE, RMSE, MAPE, and NSE. The residual between the observation and estimation of mean TC for six reference empirical equations ranged from −76.3 to 59.8 min with −154 to 99% relative differences (Table 4). The MAE ranged from 9.63 to 25.75, the RMSE ranged from 18.12 to 27.85, the MAPE ranged from 0.39 to 0.96, and the NSE ranged from −4.58 to −1.36. These findings indicate that the estimated accuracy was low due to over- and underestimated TC (Figure 4a,b). The TC estimated by Kraven (I)’s equations showed the highest differences (MAE: 25.75, RMSE: 27.85, MAPE: 0.96, and NSE: −4.58) among six empirical formulas indicates that, among the equations analyzed, this was the slowest compared to the observed TC (Table 4). In the present study, the observed TC was based on mean TC values.

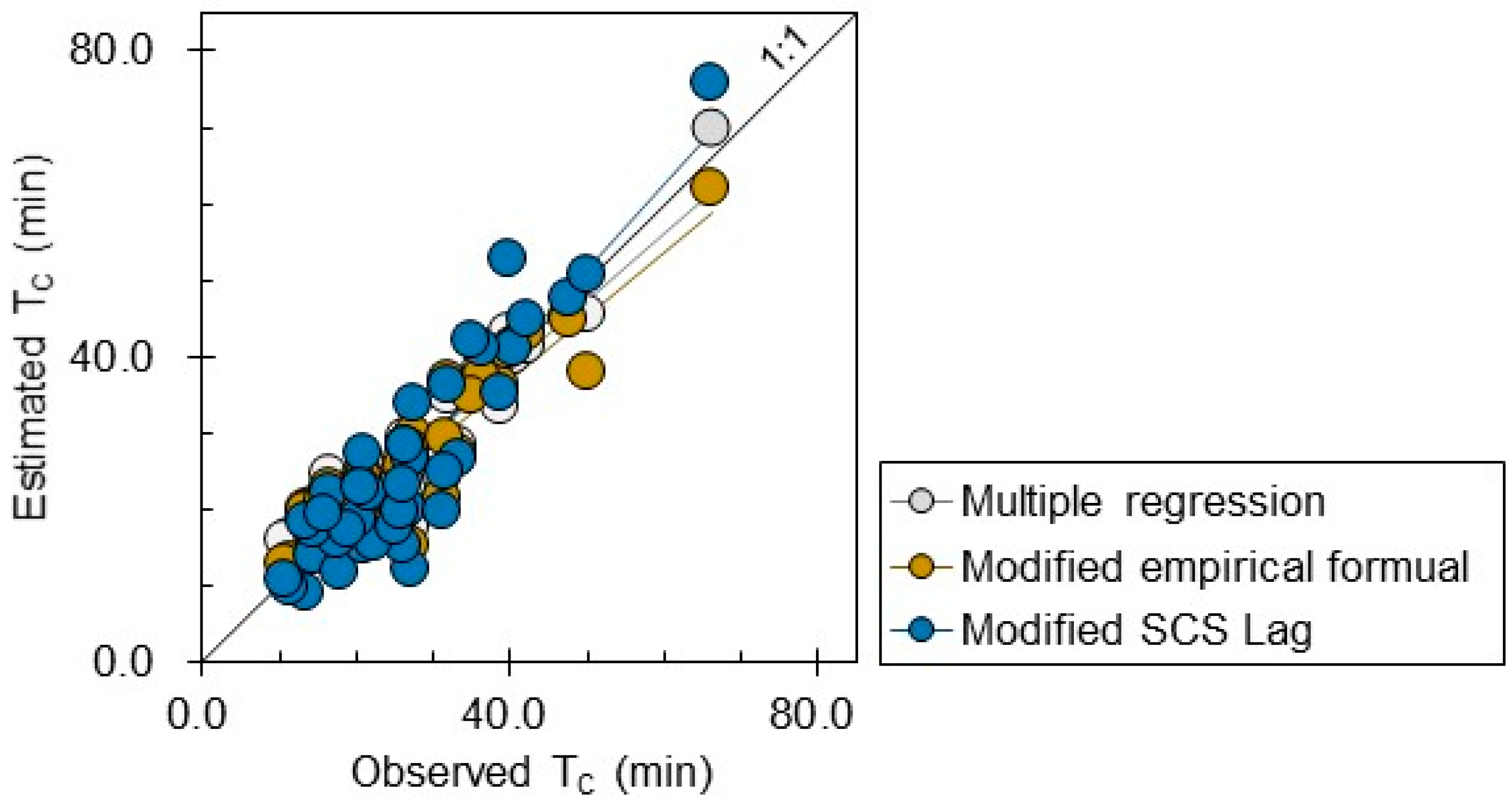
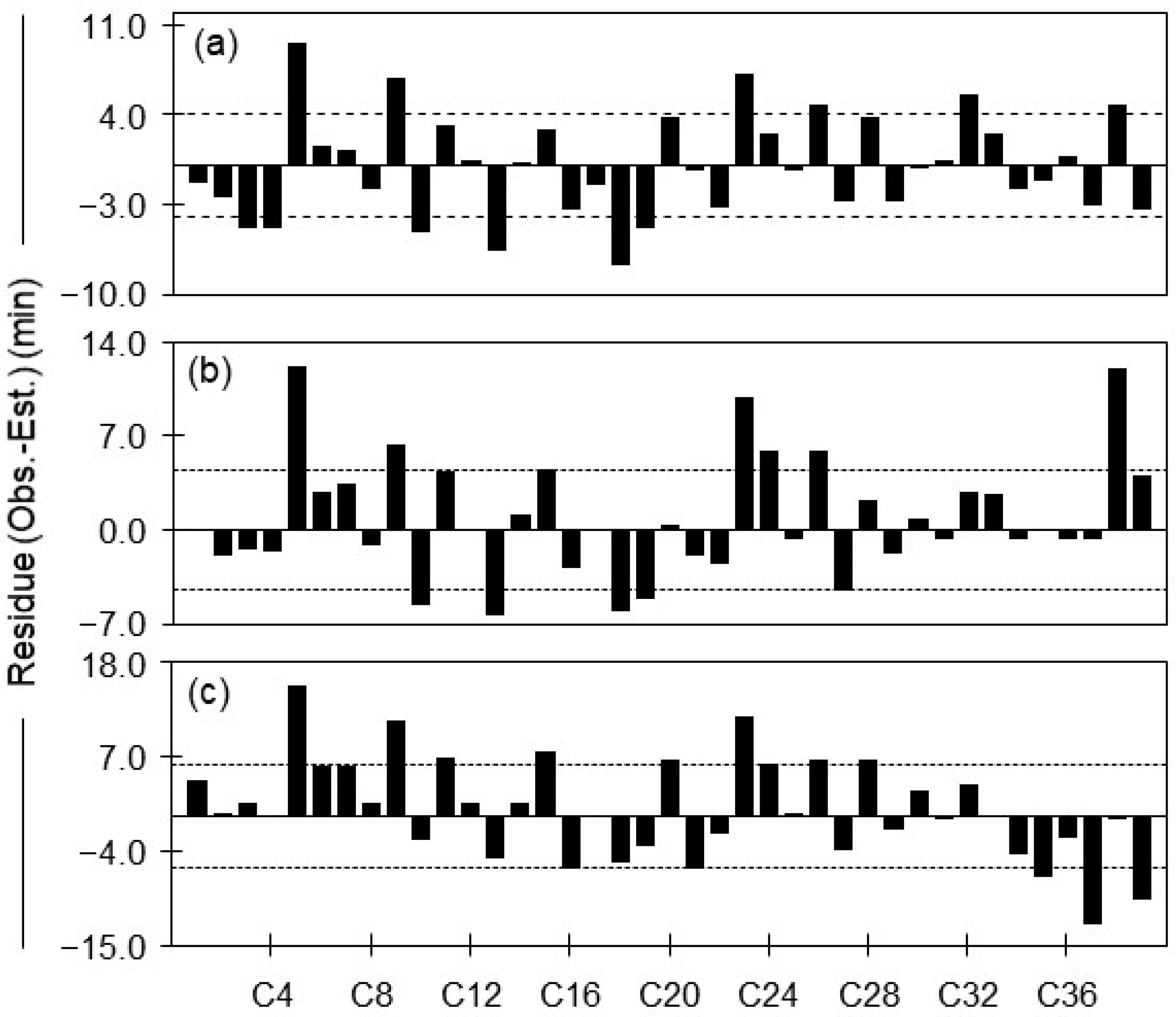
3.3. Relationship between Observed and Estimated Time of Concentration

Each empirical equation was developed in a particular region with specific physical and climatic characteristics (Table 4 and Figure 4). Thus, based on the multiple regression equation from the correlation analysis (Figure 3) and the reference empirical equations (Figure 4), we identified practical approaches for estimating TC (Figure 5 and Table 5). Here, the multiple regression equation with the three catchment variables (catchment size, stream slope, and length) rendered significant results with a 0.883 coefficient of determination (R2) at a 99% significance level with 1.945–8.386 of variance inflation factor (VIF). Moreover, in the case of the VIFs ≤ 10, it can be concluded that there is no serious case of multicollinearity [66,67]. The VIFs show how much the variance of the multiple regression equation is inflated or enhanced due to the presence of multicollinearity [67,68].
Figure 5 shows the relationship between the observed and estimated TC based on multiple regression, the modified empirical formula, and the modified SCS Lag [49]. Using the multiple regression model, the estimated TC (mean ± SD) was 27.1 ± 11.0 min (range: 14.9–69.7 min). With the two modified models, the values were 26.2 ± 10.6 min (12.6–62.0 min) and 26.1 ± 14.2 min (9.0–75.8 min) for the empirical formula and SCS Lag, respectively.
The residual between the observed and estimated TC for the multiple regression equation ranged from −7.8 to 9.7 min (Table 5 and Figure 6a). The modified empirical formula model ranged from −6.4 to 12.3 min (Figure 6b) and the SCS Lag model ranged from −12.5 to 15.5 min (Figure 6c). The Tc estimated using catchment variables developed by the three modeling equations was qualitatively similar and had relative differences ranging from −49 to 56%. Using the multiple regression model, the MAE, RMSE, MAPE, and NSE values were 3.30, 4.02, 0.15, and 0.88, respectively (Table 4). The values of MAE, RMSE, MAPE, and NSE in two modified modeling equations were 3.35, 4.56, 0.14, and 0.85 in the empirical formula and 4.77, 6.04, 0.19, and 0.74 in SCS Lag. In other words, regarding the assessment with respect to the residual, MAE, RMSE, MAPE, and NSE, the three equations showed relatively high accuracy in estimating TC (Table 4).

4. Discussion

4.1. Influence of Spatial Variations in Time of Concentration

An increased TC is catchment topography, which is one of the most important factors to consider when dealing with flood responses [69]. For instance, Gregory and Arnold [70] argued that TC with increasing precipitation and intensity involves higher discharge and flow velocity because of the faster saturation of the soil in rural catchments. Gericke and Smithers [71] indicated that design flood events have a specific magnitude–frequency relationship in each location and a certain sensitivity to time parameters. Thus, catchment response time parameters should be considered as major inputs required for catchment characteristics, such as catchment length and slope (e.g., [7,72]). Several studies have also reported on the importance of TC, which is the time it takes for the precipitation that falls at the most distant point of the catchment to reach the control section [35,71,73].
The results of our correlation analysis (Figure 3) can be attributed to hydrologic processes in hillslopes and zero-order catchments (unchannelized hollows), which can control streamflow generation [74,75]. In particular, we found that our small forested catchments (0.02–9.69 km2) were located in steep mountainous terrain with 0.07 m/m stream slope (Table 1), which could propagate much faster in channel flow [50]. By moving downstream, the flow velocity increases because the decrease in depth overcompensates for the decrease in channel slope [76]. This can also affect the velocity of the surface flow, leading to low infiltration rates [77]. For instance, Caruso and Down [78] reported that the high intensity and frequency of storm events in the maritime South Pacific and steep terrain in many parts of New Zealand lead to large and frequent floods in many areas. Uwizeyimana et al. [79] classified the land use and slope of a catchment in Rwanda, where they found an increase in runoff in dry soil environments, which was more expressive on high slopes. Azizian [80] also suggested that models should be analyzed based on their physical characteristics and compatibility with the studied region. Finally, the instantaneous nature of their occurrence and their high capacity for transport usually lead to flash floods that cause environmental, economic, and human losses [81].

4.2. Identification of Practical Approaches for Estimating the Time of Concentration

We evaluated the estimations for TC modeling equations in the present study (Table 4). The estimated accuracy of the empirical equations of Kerby and Kerby overestimated the TC (Figure 4a), while the other four empirical equations underestimated these values (Figure 4b). These results indicate that these equations are indicative of other empirical equations that were not evaluated in this study. This is because the origin of the empirical equations was uncertain; the method might not be developed from actual data analysis but from observations. Moreover, the method lacks an apparent physical basis and is dependent upon the unit system indicated [13]. Similarly, Zolghadr et al. [2] explained that the empirical equations are site-specific and may not be suitable from a climatic and hydrological perspective for many other areas, and it is difficult to determine the accuracy for an area of interest. In other words, the application of the reference empirical equations was limited to different climatic characteristics including runoff, area, and length [2,7,34]. For each empirical equation, there were some restrictions that limit its applicability, such as the regional location of the catchment, valid ranges of the catchment area, mainstream slope, and dominant flow regime (i.e., sheet, shallow concentrated, or channel flow) [1]. Therefore, the differences between the TC values obtained through observation and the reference empirical equation-based catchment characteristics were considered minor sources of error in relation to other uncertainties inherent in TC estimation. We also concluded that if a proper correction variable is introduced into the formulation, then the bias will be minimized, which will result in improved functionality and higher accuracy (e.g., [1,13,48]).
Based on these characteristics, a multiple regression equation was used as the appropriate catchment parameters including catchment size, stream slope, and length (Figure 3). This was because relationships of catchment scales and processes in geomorphology, and hydrology can contribute to our understanding of major advances in developing a functional and dynamic perspective from up- to down-stream connections [82,83]. Schumm and Lichty [84] indicated the dependent and independent processes of landform evolution at various spatial scales. Church and Mark [85] explained the proportional characteristics of landforms and their behaviors at different scales. Gomi et al. [86] reviewed that hydrologic and geomorphic processes differed by headwaters (≤1 km2 in catchment area) and network systems (>1 km2 in catchment area). Over 60% of our study catchments were distributed in a 1 km2 area with various stream lengths (Table 1). In other words, our catchment had complex terrain characteristics with relatively confined and steep valleys, influenced by the nature and rapidity of the hydrological responses. Thus, the multiple regression model allowed us to compare the relative contribution of each independent variable in the prediction of the dependent variable (Table 5). Additionally, we modified the empirical formula using the relationship between the stream slope and length and referred to it as the modified SCS Lag [49]. In general, the SCS Lag method is widely utilized in view of its reported applicability across a varied range of topography and catchment sizes [21]. Several studies have explained that the empirical formula using stream length and slope was applied to the main channel length and main channel slope in small catchments in Tennessee from 0.004 to 0.45 km2, with slopes from 3 to 12% [7,13,65]. McCuen et al. [5] also commented on how the empirical formula had the smallest bias for catchments with considerable channel flow. From Kim et al. [49], the modified SCS Lag was identified for six small forested catchments (area: 0.14–0.39 km2) with slopes of over 30%. Because the equation was developed from heavily forested catchments to meadows, smooth land surfaces and large paved areas, modified SCS lag would be feasible to TC in small forested catchment [49]. In addition, several researchers indicated that the best performing empirical equations were modified by adjusting their formulas to minimize bias and improve accuracy, which were considered minor sources of error in relation to other uncertainties inherent in time parameter estimation. [1,11,13,23,87]. Zahraei et al. [87] also suggested that when empirical equations were applied for other areas, their accuracy needs to be evaluated, and, if necessary, their equations should be modified. As illustrated in Figure 5 and Figure 6, the relationship between the observed and estimated TC using three different modeling equations was suitable for determining reliable model performance, reflecting each other’s different catchment variables [4,7,19,20]. Moreover, the morphometric characteristics of catchments strongly influence their runoff behavior [77,88,89].
The differences in the formation of empirical models may have been caused by the TC of the three modeling equations through applying variables such as catchment size, stream slope, and stream length (e.g., [11,90,91]). For instance, Kaufmann de Almeida et al. [48] explained that their equations used only morphological characteristics, whereas others combined morphological characteristics with hydrological data from the study area. Sharifi and Hosseini [1] also showed variability in their results obtained using empirical and semi-empirical methods. Yogi et al. [92] indicated that the models can provide a process that allows for more accurate analyses of drainage in forested mountain catchments, attributing the advantages to a more accurate choice of hydrological parameters.
In this study, we examined how parameters estimated using different methods impact the estimation of TC for small forested catchments in steep mountainous terrains (e.g., [1,13,48]). As mentioned above, there are modified empirical equations for estimating TC, and the equations primarily developed for specific spatial characteristics include steep slopes and short stream channel lengths within a relatively small catchment (e.g., [41]). These results suggest that the compiled TC estimation equations can be used for consultation with researchers and designers who need to estimate the TC for a region with specific characteristics, allowing for the verification of potential areas for further research (e.g., [48,93,94]). Therefore, the above results indicate that the estimated TC was appropriate for each catchment variable. Finally, because of steep stream gradient profiles [95], the high intensity of precipitation in such catchments [96] can lead to high flow velocities and extreme peak discharges, which are usually associated with destructive torrents and floods [97,98].

5. Summary and Conclusions

We demonstrated the applicability of estimating the time of concentration (TC) in 39 forested mountain catchments during 3648 rainfall events over a 10-year observation period. Our main findings were as follows: (1) the mean TC was significantly correlated with catchment size and stream length, and negatively correlated with stream slope (p < 0.01); (2) selected reference empirical equations did not fit our study sites because they over- or under-overestimated TC values; and (3) regarding model prediction accuracy, the MAE, RMSE, and MAPE were closer to 0 and NSE was closer to 1, indicating that the multiple regression, modified empirical formula, and modified SCS Lag were appropriate modeling equations for estimating the TC in this region. This could be associated with the application of catchment variables, particularly catchment size, stream slope, and stream length, to steep mountain catchments. In particular, catchment characteristics can alter flow paths due to small size, steep slope, and narrow and short stream channels for small forested catchments in steep mountainous terrain. Our results indicate that the unique aspects of our study design allowed us to identify the best-performing model using multiple regression and two modified empirical equations based on longitudinal observation data. Further examination of the performance of the estimated TC and its standard incorporation into the output modules for reasonable flood events will broaden the basis for interpreting the expected value ranges for well-functioning steep mountain catchments under specific climate, topography, and vegetation conditions. In addition, ongoing research suggests that the adaptation of varying TC within well-known modeling approaches should ensure physical consistency and reliable estimations in the context of hydrological design and flood risk evaluations.

Author Contributions

Conceptualization, S.N. and H.T.C.; methodology, S.N. and H.L.; software, S.N., H.L. and H.T.C.; validation, S.N.; formal analysis, S.N. and H.L.; investigation, S.N., H.L. and H.T.C.; resources, S.N., H.L. and H.T.C.; data curation, S.N., H.L. and H.T.C.; writing—original draft preparation, S.N. and H.T.C.; writing—review and editing, S.N., B.C., Q.L. and H.M.; visualization-n, S.N., H.L. and B.C.; supervision, S.N. and H.T.C.; project administration, S.N., H.L., B.C. and H.T.C.; funding acquisition, H.T.C. All authors have read and agreed to the published version of the manuscript.

Funding

This study was carried out with the support of the “R&D Program for Forest Science Technology (Project No. 2021343B10-2323-CD01)” provided by the Korea Forest Service (Korea Forestry Promotion Institute).

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not available publicly as they are from a project for obtaining specific research results and because of the intellectual property rights at the National Institute of Forest Science. When the project is completed, it is planned to be publicly provided through the institution’s original and independent system.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sharifi, S.; Hosseini, S.M. Methodology for identifying the best equations for estimating the time of concentration of watersheds in a particular region. J. Irrig. Drain. Eng. 2011, 137, 712–719. [Google Scholar] [CrossRef]
  2. Zolghadr, M.; Rafiee, M.R.; Esmaeilmanesh, F.; Fathi, A.; Tripathi, R.P.; Rathnayake, U.; Gunakala, S.R.; Azamathulla, H.M. Computation of time of concentration based on two-dimensional hydraulic simulation. Water 2022, 14, 3155. [Google Scholar] [CrossRef]
  3. Singh, V.P. Hydrologic Systems: Rainfall Runoff Modeling; Prentice Hall Publication: Bergen, NJ, USA, 1988; Volume 1, p. 960. [Google Scholar]
  4. McCuen, R.H. Hydrologic Design and Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
  5. McCuen, R.H.; Wong, S.L.; Rawls, W.J. Estimating urban time of concentration. J. Hydraul. Eng. 1984, 110, 887–904. [Google Scholar] [CrossRef]
  6. Wong, T.S.W. Evolution of kinematic wave time of concentration formulas for overland flow. J. Hydrol. Eng. 2009, 14, 739–744. [Google Scholar] [CrossRef]
  7. Kirpich, Z.P. Time of concentration of small agricultural watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
  8. Bell, F.C.; Kar, S.O. Characteristic response times in design flood estimation. J. Hydrol. 1969, 8, 173–196. [Google Scholar] [CrossRef]
  9. Garg, S.K. Irrigation Engineering and Hydraulic Structures; Khanna Publishers: New Delhi, India, 2001. [Google Scholar]
  10. Saghafian, B.; Julien, P.Y.; Rajaie, H. Runoff hydrograph simulation based on time variable isochrone technique. J. Hydrol. 2002, 261, 193–203. [Google Scholar] [CrossRef]
  11. Kang, J.H.; Kayhanian, M.; Stenstrom, M.K. Predicting the existence of stormwater first flush from the time of concentration. Water Res. 2008, 42, 220–228. [Google Scholar] [CrossRef]
  12. Pavlovic, S.B.; Moglen, G.E. Discretization issues in travel time calculation. J. Hydrol. Eng. 2008, 13, 71–79. [Google Scholar] [CrossRef]
  13. Fang, X.; Thompson, D.B.; Cleveland, T.G.; Pradhan, P.; Malla, R. Time of concentration estimated using watershed parameters determined by automated and manual methods. J. Irrig. Drain Eng. 2008, 134, 202–211. [Google Scholar] [CrossRef]
  14. Montesarchio, V.; Ridolfi, E.; Russo, F.; Napolitano, F. Rainfall threshold definition using an entropy decision approach and radar data, Nat. Hazards Earth Syst. Sci. 2011, 11, 2061–2074. [Google Scholar] [CrossRef]
  15. Alfieri, L.; Salamon, P.; Pappenberger, F.; Wetterhall, F.; Thielen, J. Operational early warning systems for water-related hazards in Europe. Environ. Sci. Policy 2012, 21, 35–49. [Google Scholar] [CrossRef]
  16. Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Time of concentration: A paradox in modern hydrology. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef]
  17. Williams, G.B. Flood discharges and the dimensions of spillways in India. Engineering 1922, 134, 321. [Google Scholar]
  18. Johnstone, D.; Cross, W.P. Elements of Applied Hydrology; Ronald Press: New York, NY, USA, 1949. [Google Scholar]
  19. Haktanir, T.; Sezen, N. Suitability of two-parameter gamma and three-parameter beta distributions as synthetic unit hydrographs in Anatolia. Hydrol. Sci. J. 1990, 352, 167–184. [Google Scholar] [CrossRef]
  20. Wu, I.P. Design hydrographs for small watersheds in Indiana. J. Hydr. Div. 1963, 89, 36–65. [Google Scholar] [CrossRef]
  21. Wait, I.W.; Simonton, D.S. Evaluation of the SCS Lag Time Method for Steep, Rural Watersheds. In Proceedings of the World Environmental and Water Resources Congress, Austin, TX, USA, 17–21 May 2015; pp. 2558–2567. [Google Scholar]
  22. Korea Forest Service (KFS). Statistical Yearbook of Forestry 2023; Korea Forest Service: Daejeon, Republic of Korea, 2023; No. 23; pp. 24–25. (In Korean)
  23. Oh, K.D.; Jun, B.H.; Han, H.G.; Jung, S.W.; Cho, Y.H.; Park, S.Y. Curve number for a small forested mountainous catchment. J. Korea Water Resour. Assoc. 2005, 38, 605–616. (In Korean) [Google Scholar] [CrossRef]
  24. Passalacqua, P.; Tarolli, P.; Foufoula-Georgiou, E. Testing space-scale methodologies for automatic geomorphic feature extraction from lidar in a complex mountainous landscape. Water Resour. Res. 2010, 46, W11535. [Google Scholar]
  25. Ministry of Land, Transport and Maritime Affairs (MLTM). Investigation on the Typhoon and Heavy Rainfall; MLTM: Sejong, Republic of Korea, 2006; p. 497. (In Korean)
  26. Pradhan, A.M.S.; Kim, Y.T. Relative effect method of landslide susceptibility zonation in weathered granite soil: A case study in Deokjeok-ri Creek, South Korea. Nat. Hazards 2014, 72, 1189–1217. [Google Scholar] [CrossRef]
  27. Kim, S.W.; Lee, J.H.; Chun, K.W. Recent increases in sediment disasters in response to climate change and land use, and the role of watershed management strategies in Korea. Int. J. Eros. Control Eng. 2008, 1, 44–53. [Google Scholar] [CrossRef]
  28. Min, K.H.; Son, Y.H.; Furuya, K. (2019). Categorizing Types of Transition Areas in Biosphere Reserves: A Case Study of the Baekdudaegan Mountain Ranges in South Korea. Int. Rev. Spat. Plan. Sustain. Dev. 2019, 7, 83–100. [Google Scholar]
  29. Kim, M.S.; Onda, Y.; Uchida, T.; Kim, J.K. Effects of soil depth and subsurface flow along the subsurface topography on shallow landslide predictions at the site of a small granitic hillslope. Geomorphology 2016, 271, 40–54. [Google Scholar] [CrossRef]
  30. Kim, N.W.; Won, Y.S.; Chung, I.M. The scale of typhoon RUSA. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3147–3182. [Google Scholar]
  31. United States Department of Agriculture (USDA); Natural Resources Conservation Service (NRCS). National Engineering Handbook: Part 630—Hydrology National Engineering Handbook; US Government Printing Office: Washington, DC, USA, 2004; pp. 1–424.
  32. Lee, G.; Yu, W.; APIP, K.J. Catchment-scale soil erosion and sediment yield simulation using a spatially distributed erosion model. Environ. Earth Sci. 2013, 70, 33–47. [Google Scholar] [CrossRef]
  33. Research Institute for Gangwon (RIG). Watershed Service and Reward in Drinking Water Source (Policy Memo 298); Gangwon Institute: Chuncheon, Republic of Korea, 2013; pp. 1–11. (In Korean) [Google Scholar]
  34. McCuen, R.H. Uncertainty analyses of watershed time parameters. J. Hydrol. Eng. 2009, 14, 490–498. [Google Scholar] [CrossRef]
  35. Gericke, O.J.; Smithers, J.C. Review of methods used to estimate catchment response time for the purpose of peak discharge estimation. Hydrol. Sci. J. 2014, 59, 1935–1971. [Google Scholar] [CrossRef]
  36. Kerby, W.S. Time of concentration for overland flow. Civ. Eng. 1959, 29, 60. [Google Scholar]
  37. Dooge, J.C.I. Synthetic Unit Hydrographs Based on Triangular Inflow. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1956; p. 103. [Google Scholar]
  38. Chow, V.T. Hydrologic Determination of Waterway Areas for the Design of Drainage Structures in Small Drainage Basins; Engineering Experiment Station. Bulletin; University of Illinois: Chicago, IL, USA, 1962; No. 462. [Google Scholar]
  39. Rziha, F. Eisenbahn-Unter-Und Oberbau; Verlag der KK Hof-und Staatsdr: Vienna, Austria, 1876; Volume 1. [Google Scholar]
  40. Japan Society of Civil Engineers (JSCE). The Collection of Hydraulic Formulae; Japan Society of Civil Engineers: Tokyo, Japan, 1999. [Google Scholar]
  41. Asfaha, T.G.; Frankl, A.; Haile, M.; Zenebe, A.; Nyssen, J. Determinants of peak discharge in steep mountain catchments–Case of the Rift Valley escarpment of Northern Ethiopia. J. Hydrol. 2015, 529, 1725–1739. [Google Scholar] [CrossRef]
  42. Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
  43. Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
  44. Ryberg, K.R.; Akyuez, F.A.; Wiche, G.J.; Lin, W. Changes in seasonality and timing of peak streamflow in snow and semi-arid climates of the north-central United States, 1910–2012. Hydrol. Process. 2016, 30, 1208–1218. [Google Scholar] [CrossRef]
  45. Nam, S.; Jang, S.J.; Chun, K.W.; Lee, J.U.; Kim, S.W. Seasonal water temperature variations in response to air temperature and precipitation in a forested headwater stream and an urban river: A case study from the Bukhan River basin, South Korea. Forest Sci. Technol. 2021, 17, 46–55. [Google Scholar] [CrossRef]
  46. Gomi, T.; Asano, Y.; Uchida, T.; Onda, Y.; Sidle, R.C.; Miyata, S.; Kosugi, K.; Mizugaki, S.; Fukuyama, T.; Fukushima, T. Evaluation of storm runoff pathways in steep nested catchments draining a Japanese cypress forest in central Japan: A geochemical approach. Hydrol. Process. 2010, 24, 550–566. [Google Scholar] [CrossRef]
  47. Martinez, J.; Reca, J.; Morillas, M.T.; Lopez, J.G. Design and calibration of a compound sharp-crested weir. J. Hydraul. Eng. 2005, 131, 112–116. [Google Scholar] [CrossRef]
  48. Kaufmann de Almeida, I.; Kaufmann Almeida, A.; Garcia Gabas, S.; Alves Sobrinho, T. Performance of methods for estimating the time of concentration in a watershed of a tropical region. Hydrol. Sci. J. 2017, 62, 2406–2414. [Google Scholar] [CrossRef]
  49. Kim, J.; Choi, H.T.; Lim, H. Evaluation on the application of the estimation of time of concentration using real rainfall-runoff events in small forest watershed. J. Korean Soc. Hazard Mitig. 2015, 15, 199–206. [Google Scholar] [CrossRef]
  50. Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the time of concentration: Shedding light on a paradox. Hydrol. Sci. J. 2018, 63, 721–2740. [Google Scholar] [CrossRef]
  51. Kent, K.M. Travel time, time of concentration and lag. In National Engineering Handbook; NRCS: Washington, DC, USA, 1972; Volume 4. [Google Scholar]
  52. Cronshey, R.; McCuen, R.H.; Miller, N.; Rawls, W.; Robbins, S.; Woodward, D. Urban Hydrology for Small Watersheds (TR-55); Natural Resources Conservation Service: Washington, DC, USA, 1986.
  53. Woodward, D.E. Part 630 Hydrology National Engineering Handbook-Chapter 15 Time of Concentration; United States Department of Agriculture: Washington, DC, USA, 2010; p. 29.
  54. Pinto, N.L.S.; Holtz, A.C.T.; Martins, J.A.; Gomide, F.L.S. Hidrologia Básica; Editora Blucher: São Paulo, SP, Brasil, 1976; p. 304. [Google Scholar]
  55. Silveira, A.L.L. Desempenho de Fórmulas de Tempo de Concentração em Bacias Urbanas e Rurais. RBRH Rev. Bras. De Recur. Hidr. 2005, 10, 5–29. [Google Scholar] [CrossRef]
  56. Jeong, J.H.; Keum, J.H.; Yoon, Y.N. Development of an estimation method for travel time. J. Korea Water Resour. Assoc. 2002, 35, 715–727. (In Korean) [Google Scholar] [CrossRef]
  57. Jung, C.Y.; Choi, G.W.; Han, M.S.; and Jung, S.M. Estimation of time of concentration for stream at island near coastal region. J. Korean Soc. Hazard Mitig. 2007, 7, 151–158. (In Korean) [Google Scholar]
  58. Kwon, K.D.; Lee, J.H.; Kang, M.J.; Jee, H.K. Effect of estimation for time of concentration on the design flood. Korean Wetl. Soc. 2014, 16, 125–137. (In Korean) [Google Scholar]
  59. Yan, J.; Liu, J.; Yu, Y.; Xu, H. Water Quality Prediction in the Luan River Based on 1-DRCNN and BiGRU Hybrid Neural Network Model. Water 2021, 13, 1273. [Google Scholar] [CrossRef]
  60. Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic modeling of the Iroquois River Watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 361–375. [Google Scholar]
  61. Yndman, R.J. Another look at forecast accuracy metrics for intermittent demand. Foresight 2006, 4, 43–46. [Google Scholar]
  62. Yang, H.; Lim, H.; Moon, H.; Li, Q.; Nam, S.; Choi, B.; Choi, H.T. Identifying the minimum number of flood events for reasonable flood peak prediction of ungauged forested catchments in South Korea. Forests 2023, 14, 1131. [Google Scholar] [CrossRef]
  63. Salimi, E.T.; Nohegar, A.; Malekian, A.; Hoseini, M.; Holisaz, A. Estimating time of concentration in large watersheds. Paddy Water Environ. 2017, 15, 123–132. [Google Scholar] [CrossRef]
  64. Fan, J.; Galoie, M.; Motamedi, A.; Huang, J. Assessment of land cover resolution impact on flood modeling uncertainty. Hydrol. Res. 2021, 52, 78–80. [Google Scholar] [CrossRef]
  65. Perdikaris, J.; Gharabaghi, B.; Rudra, R. Reference Time of Concentration Estimation for Ungauged Catchments. Earth Sci. Res. 2018, 7, 58. [Google Scholar] [CrossRef]
  66. Montgomery, D.C.; Askin, R.G. Problems of nonnormality and multicollinearity for forecasting methods based on least squares. AIIE Trans. 1981, 13, 102–115. [Google Scholar] [CrossRef]
  67. Baig, M.A.; Zaman, Q.; Baig, S.A.; Qasim, M.; Khalil, U.; Khan, S.A.; Ali, S. Regression analysis of hydro-meteorological variables for climate change prediction: A case study of Chitral Basin, Hindukush region. Sci. Total Environ. 2021, 793, 148595. [Google Scholar] [CrossRef]
  68. Cho, J.H.; Lee, J.H. Multiple linear regression models for predicting nonpoint-source pollutant discharge from a highland agricultural region. Water 2018, 10, 1156. [Google Scholar] [CrossRef]
  69. Abdulkareem, J.H.; Pradhan, B.; Sulaiman, W.N.A.; Jamil, N.R. Development of lag time and time of concentration for a tropical complex catchment under the influence of long-term land use/land cover (LULC) changes. Arab. J. Geosci. 2019, 12, 101. [Google Scholar] [CrossRef]
  70. Gregory, R.L.; Arnold, C.B. Run-off–rational runoff formulas. Trans. ASCE 1932, 96, 1038–1099. [Google Scholar]
  71. Gericke, O.J.; Smithers, J.C. Are estimates of catchment response time inconsistent as used in current flood hydrology practice in South Africa? J. S. Afr. Inst. Civ. Eng. 2016, 58, 2–15. [Google Scholar] [CrossRef]
  72. Soil Conservation Service (SCS). SCS National Engineering Handbook; Section 4. Hydrology, Soil Conservation Service, United States Department of Agriculture (USDA): Washington, DC, USA, 1972.
  73. United States Department of Agriculture (USDA). Time of concentration (Chapter 15, Section 4, Part 630). In National Engineering Handbook; Woodward, D.E., Ed.; USDA NRCS: Washington, DC, USA, 2010; pp. 1–15. [Google Scholar]
  74. Tsukamoto, Y.; Ohta, T.; Noguchi, H. Hydrological and Geomorphological Study of Debris Slides on Forested Hillslope in Japan. In Recent Developments in the Explanation and Prediction of Erosion and Sediment Yield; Walling, D.E., Ed.; IAHS Publication 137; IAHS Press: Wallingford, UK, 1982; pp. 89–98. [Google Scholar]
  75. Sidle, R.C.; Tsuboyama, Y.; Noguchi, S.; Hosoda, I.; Fujieda, M.; Shimizu, T. Streamflow generation in steep headwaters: A linked hydro-geomorphic paradigm. Hydrol. Process. 2000, 14, 369–385. [Google Scholar] [CrossRef]
  76. Leopold, L.B.; Maddock, T., Jr. The Hydraulic Geometry of Stream Channels and Some Geomorphologic Implications; U.S. Geological Survey Professional Paper; United States Geological Survey (USGS): Reston, VA, USA, 1953; No. 252; p. 56.
  77. Bao, Q.; Laituri, M. The effects of watershed characteristics on storm runoff relationships in Vietnam. J. Environ. Sci. Water Res. 2013, 2, 40–52. [Google Scholar]
  78. Caruso, B.S.; Down, P.W. Rehabilitation and flood management planning in a steep, boulder-bedded stream. Environ. Manag. 2007, 40, 256–271. [Google Scholar] [CrossRef]
  79. Uwizeyimana, D.; Mureithi, S.M.; Mvuyekure, S.M.; Karuku, G.; Kironchi, G. Modelling surface runoff using the soil conservation service-curve number method in a drought prone agro-ecological zone in Rwanda. Int. Soil Water Conserv. Res. 2019, 7, 9–17. [Google Scholar] [CrossRef]
  80. Azizian, A. Uncertainty analysis of time of concentration equations based on frst-order-analysis (FOA) method. Am. J. Eng. Appl. Sci. 2018, 11, 327–341. [Google Scholar] [CrossRef]
  81. Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaskovicova, L.; Bloschl, G.; Borga, M.; Dumitrescu, A.; et al. Compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
  82. Hynes, H.B.N. The stream and its valley. Proc. Int. Assoc. Theor. Appl. Limnol. 1975, 19, 1–15. [Google Scholar] [CrossRef]
  83. Vannote, R.L.; Minshall, W.G.; Cummins, K.W.; Sedell, J.R.; Cushing, C.E. The river continuum concept. Can. J. Fish. Aquat. Sci. 1980, 37, 130–137. [Google Scholar] [CrossRef]
  84. Schumm, S.A.; Lichty, R.W. Time, space and causality in geomorphology. Am. J. Sci. 1965, 263, 110–119. [Google Scholar] [CrossRef]
  85. Church, M.; Mark, D.M. On size and scale in geomorphology. Prog. Phys. Geogr. 1980, 4, 342–390. [Google Scholar] [CrossRef]
  86. Gomi, T.; Sidle, R.C.; Richardson, J.S. Understanding processes and downstream linkages of headwater systems. Bioscience 2002, 52, 905–916. [Google Scholar] [CrossRef]
  87. Zahraei, A.; Baghbani, R.; Linhoss, A. Applying a graphical method in evaluation of empirical methods for estimating time of concentration in an Arid Region. Water 2021, 13, 2624. [Google Scholar] [CrossRef]
  88. Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees. Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
  89. Andreassian, V. Waters and forests: From historical and controversy to scientific debate. J. Hydrol. 2004, 291, 1–27. [Google Scholar] [CrossRef]
  90. Upegui, J.J.V.; Gutiérrez, A.B. Estimación del Tiempo de Concentración y Tiempo de Rezago em la Cuenca Experimental Urbana de la Quebrada San Luis, Manizales. Dyna 2011, 78, 58–71. [Google Scholar]
  91. Liang, J.; Melching, C.S. Comparison of computed and experimentally assessed times of concentration for a V-shaped laboratory watershed. J. Hydrol. Eng. 2012, 17, 1389–1396. [Google Scholar] [CrossRef]
  92. Yogi, F.; Correa, C.J.P.; Arruda, E.M.; Tonello, K.C. Sensitivity analysis of rainfall–runoff parameters models to estimate flows. Appl. Water Sci. 2021, 11, 25. [Google Scholar] [CrossRef]
  93. Beven, K.J. A history of the concept of time of concentration. Hydrol. Earth Syst. Sci. 2020, 24, 2655–2670. [Google Scholar] [CrossRef]
  94. Almeida, A.K.; de Almeida, I.K.; Guarienti, J.A.; Gabas, S.G. The time of concentration application in studies around the world: A review. Environ. Sci. Pollut. Res. 2022, 29, 8126–8172. [Google Scholar] [CrossRef]
  95. Markewich, H.W.; Pavich, M.J.; Buell, G. Contrasting soils and landscapes of the Piedmont and Coastal Plain, eastern United States. Geomorphology 1990, 3, 417–447. [Google Scholar] [CrossRef]
  96. Buytaert, W.; Celleri, R.; de Bievre, B.; Cisneros, F.; Wyseure, G.; Deckers, J.; Hofstede, R. Human impact on hydrology of the Andean páramos. Earth Sci. Rev. 2006, 79, 53–72. [Google Scholar] [CrossRef]
  97. Weingartner, R.; Barben, M.; Spreafico, M. Floods in mountain areas-an overview based on examples from Switzerland. J. Hydrol. 2003, 282, 10–24. [Google Scholar] [CrossRef]
  98. Ruiz-Villanueva, V.; Diez-Herrero, A.; Stoffel, M.; Bollschweiler, M.; Bodoque, J.M.; Ballesteros, J.A. Dendrogeomorphic analysis of flash floods in a small ungauged mountain catchment (Central Spain). Geomorphology 2010, 118, 383–392. [Google Scholar] [CrossRef]
Forests 15 00186 g001
Figure 1. Location of observed forested catchments (C1–C39) in steep mountainous terrain.
Figure 1. Location of observed forested catchments (C1–C39) in steep mountainous terrain.
Forests 15 00186 g001
Forests 15 00186 g002
Figure 2. Views of stream gauging stations in (a) C19 and (b) C27 among observed forested catchments (C1–C39). 120° V-notch and rectangular sharp-crested weirs were installed in C19 and C27.
Figure 2. Views of stream gauging stations in (a) C19 and (b) C27 among observed forested catchments (C1–C39). 120° V-notch and rectangular sharp-crested weirs were installed in C19 and C27.
Forests 15 00186 g002
Forests 15 00186 g003
Figure 3. Relationship of time of concentration (TC) to catchment variables, catchment size, slope gradient, stream slope, and stream length. The r and p values indicate correlation coefficient and significance. The TC was based on mean value of TC.
Figure 3. Relationship of time of concentration (TC) to catchment variables, catchment size, slope gradient, stream slope, and stream length. The r and p values indicate correlation coefficient and significance. The TC was based on mean value of TC.
Forests 15 00186 g003
Forests 15 00186 g004
Figure 4. Relationship between the observed and estimated time of concentration (TC) using six reference empirical equations: (a) over- and (b) underestimated TC. The different empirical equations referred to [7,13,36,39,40,51,52,53,54,55].
Figure 4. Relationship between the observed and estimated time of concentration (TC) using six reference empirical equations: (a) over- and (b) underestimated TC. The different empirical equations referred to [7,13,36,39,40,51,52,53,54,55].
Forests 15 00186 g004
Forests 15 00186 g005
Figure 5. Relationship between observed and estimated time of concentration (TC) based on multiple regression, modified empirical formula, and modified SCS Lag [49].
Figure 5. Relationship between observed and estimated time of concentration (TC) based on multiple regression, modified empirical formula, and modified SCS Lag [49].
Forests 15 00186 g005
Forests 15 00186 g006
Figure 6. Differences between observed (Obs.) and estimated (Est.) TC values by (a) multiple regression, (b) modified empirical formula, and (c) modified SCS Lag. The C1–C39 indicates the study catchments based on ordering catchment size, from 0.02 to 9.69 km2 (see, Table 1). The horizontal dashed lines indicate the standard deviation of the residuals.
Figure 6. Differences between observed (Obs.) and estimated (Est.) TC values by (a) multiple regression, (b) modified empirical formula, and (c) modified SCS Lag. The C1–C39 indicates the study catchments based on ordering catchment size, from 0.02 to 9.69 km2 (see, Table 1). The horizontal dashed lines indicate the standard deviation of the residuals.
Forests 15 00186 g006
Table 1. Summary table for observed forested catchments in steep mountainous terrain.
Table 1. Summary table for observed forested catchments in steep mountainous terrain.
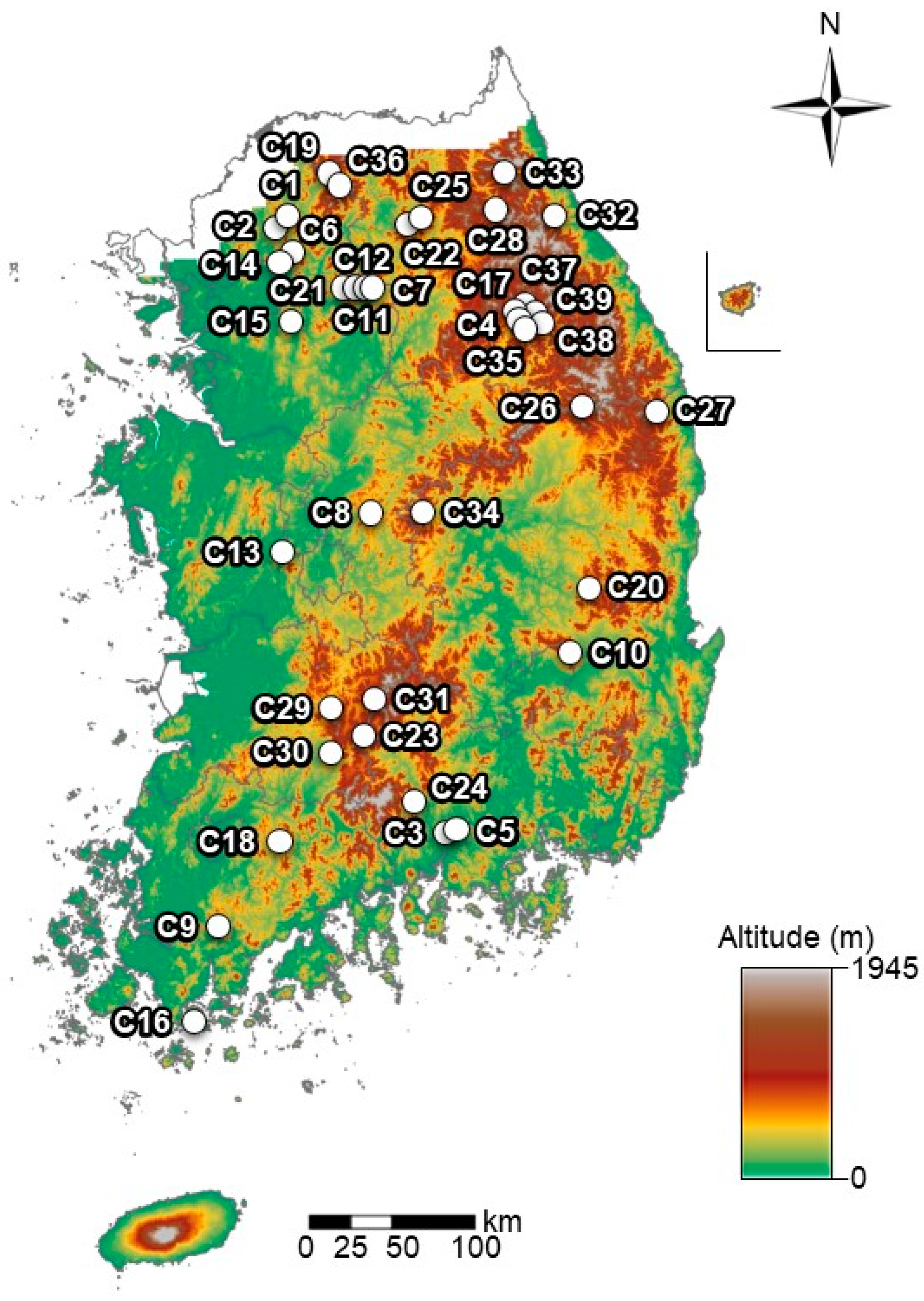
SiteLocationClimate ClassArea
(km2)		Altitude
(m)		Slope
Gradient (°) *		Soil Depth
(cm) *		Underlying
Geology		Forest TypeAge ClassStream Length
(km)		Stream Slope
(m/m) *
C1GGDwa0.02120–20821.938.7IgBFV0.30.3
C2GGDwa0.04120–27220.632.7IgMFV0.50.3
C3GNCwa0.05146–36631.731.7SedCFIV0.50.5
C4GWDwb0.061120–132023.667.3SedBFVI0.40.5
C5GNCwa0.12160–41531.227.4SedMFIV0.60.4
C6GGDwa0.13165–30622.363.6MetaCFV0.50.3
C7GGDwa0.13681–100931.276.6MetaBFIV0.80.4
C8CBDwa0.15303–54527.055.9SedMFV0.80.3
C9JBCfa0.17146–34528.852.3IgCFI0.70.3
C10GBCwa0.18494–71625.062.1IgBFIV0.80.3
C11GGDwa0.19694–95527.383.7MetaBFV0.70.4
C12GGDwa0.20695–91922.362.6MetaMFIV0.80.3
C13SSCwa0.2259–31023.540.4IgBFV0.80.3
C14GGDwa0.24241–46020.066.2MetaBFVII0.70.3
C15GGDwa0.34260–63734.256.7MetaBFV1.00.4
C16JNCfa0.35124–51521.144.9IgBFIV1.30.3
C17GWDwb0.41960–136827.074.9IgBFVII1.10.4
C18JNCwa0.41326–76529.928.2MetaBFIII1.20.4
C19GWDwb0.45680–93624.155.7IgBFV0.90.3
C20GBCwa0.46386–60029.856.1SedMFIV1.10.2
C21GGDwa0.47546–91920.465.2MetaCFIV1.60.2
C22GWDwa0.55270–64827.271.3MetaMFV1.20.3
C23JBDwb0.56745–123534.963.5MetaBFIV1.20.4
C24GNCwa0.59495–100032.031.4IgBFV1.10.5
C25GWDwa1.01282–68729.370.0MetaMFV1.50.3
C26GBDwb1.02861–134031.264.9MetaBFV1.60.3
C27GBDfb1.03472–91528.964.5MetaMFVI2.20.2
C28GWDwb1.06490–84532.855.1IgMFVI1.50.2
C29JBDwb1.07511–100330.452.2MetaBFV1.70.3
C30JBDwb1.21405–85033.338.2MetaMFV1.40.3
C31JBDwb1.92570–106530.471.8IgMFIV2.70.2
C32GWDfa1.98210–60027.337.6MetaMFV2.10.2
C33GWDfb1.99580–115529.655.0IgMFIV3.20.2
C34CBDwa2.09325–90127.749.7IgMFV2.50.2
C35GWDwb2.19627–119023.456.4SedMFV2.30.2
C36GWDwb2.81430–91527.657.0IgMFV2.80.2
C37GWDwb3.80726–136522.373.9SedMFIV2.90.2
C38GWDwb5.57672–156025.962.9SedMFV3.10.3
C39GWDwb9.69600–137527.271.9SedMFV5.30.1
Note: GG: Gyeonggi-do; GW: Gangwon-do; CB: Chungcheongbuk-do; CN: Chungcheongnam-do; SS: Sejong special self-governing city GB: Gyeongsangbuk-do; GN: Gyeongsangnam-do; JB: Jeollabuk-do; JN: Jeollanam-do; Cfa: warm temperate, fully humid, and hot summer; Cwa: warm temperate, winter dry and hot summer; Dfa: snow, fully humid, and hot summer; Dfb: snow, fully humid, and warm summer; Dwa: snow, winter dry, and hot summer; Dwb: snow, winter dry, and warm summer. Ig: igneous rock; Sed: sedimentary rock; Meta: metamorphic rock; BF: broadleaved forest; MF: mixed forest; CF: coniferous forest; I: 1–10 year; III: 21–30 year; IV: 31–40 year; V: 41–50 year; VII: 61–70 year. Climate class is according to the Köppen–Geiger classification system [42,43]. Age class was classified as 10-year intervals through forest type map (1:5000). Range from minimum to maximum values. Asterisk (*) indicates the mean values.
Table 2. Summary of the reference empirical equations to estimate time of concentration in this study.
Table 2. Summary of the reference empirical equations to estimate time of concentration in this study.
Equation Name
[References]		Formulas for TCVariables and UnitsRemarks
Kirpich
[7,13]		 T C = 3.978 L 0.77 S 0.385 TC: time of concentration (min)
L: channel length (km)
S: channel slope (m/m)		Tennessee small catchments (0.004–0.45 km2) and slope (3–12%)
Kerby
[36]		 T C = 1.4394 60 n L S 0.467 TC: time of concentration (hr)
L: flow path length (m)
S: flow path average slope (m/m)
n: roughness coefficient		Developed in catchments from the United States with area (<0.04 km2) and slope (<1%)
SCS Lag
[51,52,53]		 T C = 0.057 L 0.8 ( 1000 / C N − 9 ) 0.7 S 0.5 TC: time of concentration (hr)
CN: runoff curve number
L: flow length (km)
S: average watershed slope (m/m)		Developed in 24 rural basins in the United States with area (<8.09 km2)
Rziha
[39]		 T C = 0.0139 L S 0.6 TC: time of concentration (hr)
L: stream length (km)
S: stream slope (m/m)		Natural upstream
(S ≥ 1/200)
Picking
[54,55]		 T C = 5.3 60 L 2 S 1 3 TC: time of concentration (hr)
L: length of the main stream (km)
S: average slope of the main (m/m)		Data of rural basins
Kraven (I)
[40]		 T C = 0.0074 L S 0.515 TC: time of concentration (hr)
L: stream length (km)
S: stream slope (m/m)		Natural downstream
(S < 1/200)
Table 3. Summary table for time of concentration (TC) with rainfall event response.
Table 3. Summary table for time of concentration (TC) with rainfall event response.
YearnPT (mm)P10 (mm)PD (hr)API1 (mm)TC (min)
2010–2021364838.3 ± 41.9 (2.2–698.4)5.0 ± 3.7
(1.7–29.5)		1.0 ± 0.9
(0.1–12.1)		10.6 ± 21.1
(0.0–253.8)		25.5 ± 19.1
(5.0–115.4)
Note: PT: total precipitation; P10: maximum 10 min precipitation intensity; PD: duration of precipitation; API1: one day antecedent precipitation. n: number of observed storm events. Mean ± standard deviation. Bracket: minimum–maximum values.
Table 4. Differences between time of concentration values obtained by observation and reference empirical equations.
Table 4. Differences between time of concentration values obtained by observation and reference empirical equations.
Equation Name [References]Residual (min)MAERMSEMAPENSE
Kirpich [7,13]18.3 ± 6.8 (8.1–35.8)9.6319.550.39−1.75
Kerby [36]−17.1 ± 7.0 (−31.7–0.4)17.1518.510.70−1.47
SCS Lag [51,52,53]−10.4 ± 16.2 (−76.3–13.3)12.6819.230.39−1.66
Rziha [39]24.2 ± 9.4 (10.4–52.0)24.2325.970.91−3.85
Picking [54,55]16.8 ± 6.8 (6.6–35.4)16.8118.120.63−1.36
Kraven (I) [40]25.8 ± 10.6 (10.7–59.8)25.7527.850.96−4.58
Note: Mean ± standard deviation. Bracket: minimum–maximum values. The detailed information on reference empirical equations is in Table 1. MAE: mean of absolute error; RMSE: root mean square error; MAPE: mean absolute percentage error; NSE: Nash–Sutcliffe efficiency.
Table 5. Summary of estimated model analyses between multiple regression, modified empirical formula, and modified SCS Lag.
Table 5. Summary of estimated model analyses between multiple regression, modified empirical formula, and modified SCS Lag.
EquationResidual
(min)		MAERMSEMAPENSEComments
T C = 0.246 A − 0.023 S + 10.462 L + 11.516 −0.04 ± 4.0
(−7.8–9.7)		3.304.020.150.88Multiple regression
T C = 14.486 L 0.468 S 0.348 0.9± 4.5
(−6.4–12.3)		3.354.560.140.85Modified empirical formula
T C = l 0.8 ( 1000 / C N − 9 ) 0.7 1140 Y 0.5 × 60 −1.0 ± 6.0
(−12.5–15.5)		4.776.040.190.74Modified SCS Lag
Note: MAE: mean of absolute error; RMSE: root mean square error; MAPE: mean absolute percentage error; NSE: Nash–Sutcliffe efficiency; TC: time of concentration (min); A: catchment size (km2); S: stream slope (m/m); L: stream length (km); l: flow length (ft); CN: curve number; Y: average catchment land slope (%). Modified SCS Lag was referred by [49]. Mean ± standard deviation. Bracket: minimum–maximum values.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Nam, S.; Lim, H.; Choi, B.; Li, Q.; Moon, H.; Choi, H.T. Characteristics and Estimation of the Time of Concentration for Small Forested Catchments in Steep Mountainous Terrain. Forests 2024, 15, 186. https://doi.org/10.3390/f15010186

AMA Style

Nam S, Lim H, Choi B, Li Q, Moon H, Choi HT. Characteristics and Estimation of the Time of Concentration for Small Forested Catchments in Steep Mountainous Terrain. Forests. 2024; 15(1):186. https://doi.org/10.3390/f15010186

Chicago/Turabian Style

Nam, Sooyoun, Honggeun Lim, Byoungki Choi, Qiwen Li, Haewon Moon, and Hyung Tae Choi. 2024. "Characteristics and Estimation of the Time of Concentration for Small Forested Catchments in Steep Mountainous Terrain" Forests 15, no. 1: 186. https://doi.org/10.3390/f15010186

APA Style

Nam, S., Lim, H., Choi, B., Li, Q., Moon, H., & Choi, H. T. (2024). Characteristics and Estimation of the Time of Concentration for Small Forested Catchments in Steep Mountainous Terrain. Forests, 15(1), 186. https://doi.org/10.3390/f15010186

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop