The Performance Enhancement of a Vehicle Suspension System Employing an Electromagnetic Inerter
Abstract
1. Introduction
2. Basic Structure and Working Principle of Electromagnetic Inerter
3. Parametric Sensitivity Analysis of Fluid Inerter
4. The Influence of External Circuits on the Output Characteristics of the Device
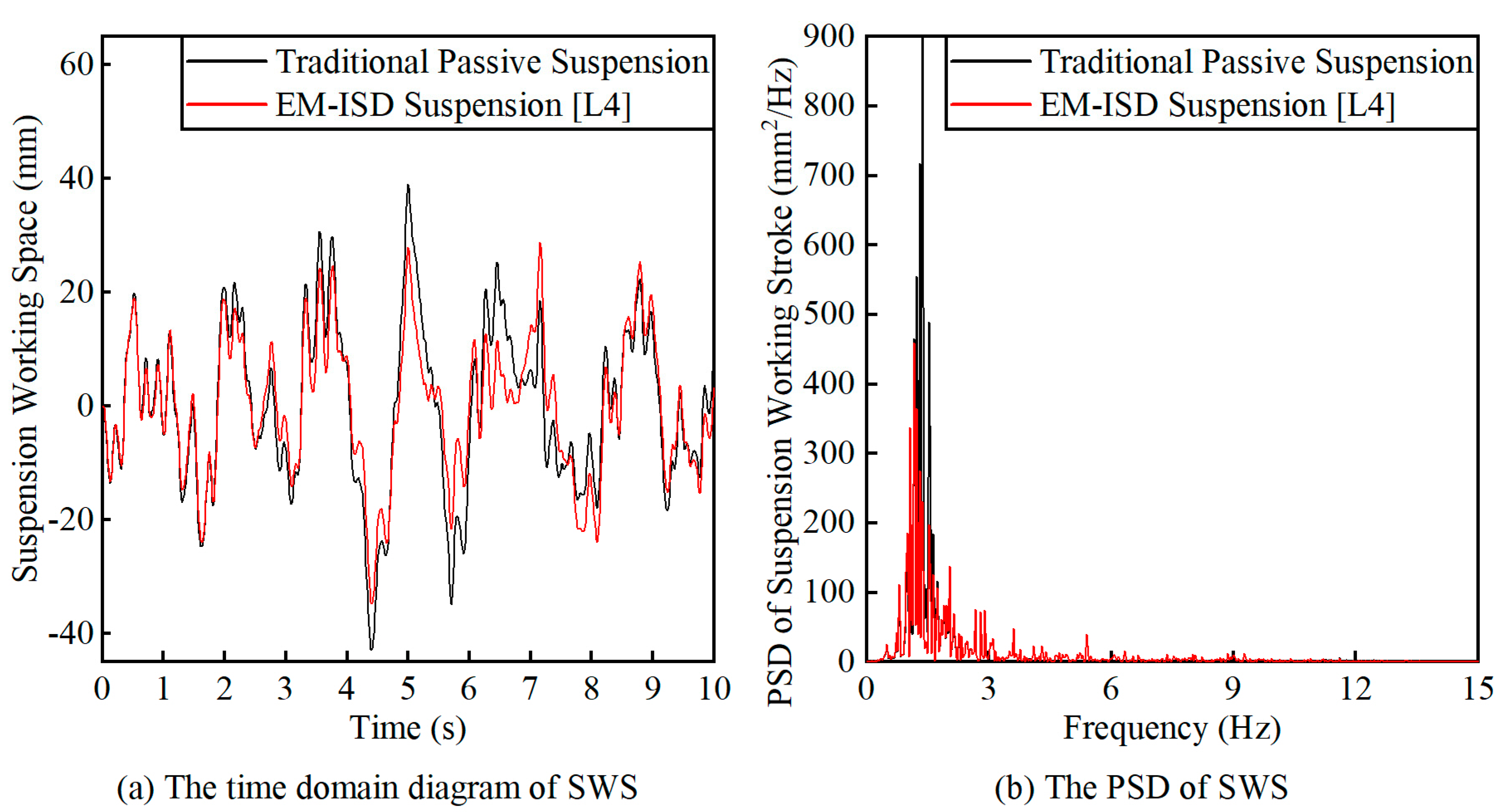
5. Quarter Vehicle Model with Electromagnetic Inerter–Spring–Damper (EM-ISD) Suspension System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, M.C. Synthesis of Mechanical Networks: The Inerter. IEEE Trans. Autom. Control. 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Chang, Y.; Zhou, J.; Wang, K.; Xu, D. A Quasi-Zero-Stiffness Dynamic Vibration Absorber. J. Sound Vib. 2021, 494, 115859. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, Z.; Wang, Z.; Li, G. Study of Longitudinal–Vertical Dynamics for In-Wheel Motor-Driven Electric Vehicles. Automot. Innov. 2021, 4, 227–237. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Lee, H.P.; Yang, Y.; Zhang, X. A Review of the Inerter and Inerter-Based Vibration Isolation: Theory, Devices, and Applications. J. Frankl. Inst. 2022, 359, 7677–7707. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Zhang, R. Optimal Design and Seismic Performance of Tuned Fluid Inerter Applied to Structures with Friction Pendulum Isolators. Soil Dyn. Earthq. Eng. 2020, 132, 106099. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-Induced Vibration Mitigation in Tall Buildings Using the Tuned Mass-Damper-Inerter. J. Struct. Eng. 2017, 143, 04017127. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S. Cable vibration mitigation by using an H-bridge-based electromagnetic inerter damper with energy harvesting function. Struct. Control Health Monit. 2022, 29, e3120. [Google Scholar] [CrossRef]
- Sun, L.; Hong, D.; Chen, L. Cables Interconnected with Tuned Inerter Damper for Vibration Mitigation. Eng. Struct. 2017, 151, 57–67. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, Z.; Qiao, H.; De Domenico, D. Seismic Protection of Reinforced Concrete Continuous Girder Bridges with In-erter-Based Vibration Absorbers. Soil Dyn. Earthq. Eng. 2023, 164, 107526. [Google Scholar] [CrossRef]
- Luo, J.; Macdonald, J.H.G.; Jiang, J.Z. Identification of Optimum Cable Vibration Absorbers Using Fixed-Sized-Inerter Layouts. Mech. Mach. Theory 2019, 140, 292–304. [Google Scholar] [CrossRef]
- Chen, H.; Su, W.; Wang, F. Modeling and Analyses of a Connected Multi-Car Train System Employing the Inerter. Adv. Mech. Eng. 2017, 9, 168781401770170. [Google Scholar] [CrossRef]
- Wang, F.; Liao, M.; Liao, B.; Su, W.; Chan, H.A. The Performance Improvements of Train Suspension Systems with Mechanical Networks Employing Inerters. Veh. Syst. Dyn. 2009, 47, 805–830. [Google Scholar] [CrossRef]
- He, H.; Li, Y.; Jiang, J.Z.; Burrow, S.; Neild, S.; Conn, A. Using an Inerter to Enhance an Active-Passive-Combined Vehicle Suspension System. Int. J. Mech. Sci. 2021, 204, 106535. [Google Scholar] [CrossRef]
- Shen, Y.; Jia, M.; Yang, X.; Liu, Y.; Chen, L. Vibration Suppression Using a Mechatronic PDD-ISD-Combined Vehicle Suspension System. Int. J. Mech. Sci. 2023, 250, 108277. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, A.; Du, F.; Yang, X.; Liu, Y.; Chen, L. Optimal design and dynamic performance analysis of semi-active vehicle air ISD suspension. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Chen, M.Z.Q.; Li, Z.; Sun, Y. Load Mitigation for a Barge-Type Floating Offshore Wind Turbine via Inerter-Based Passive Structural Control. Eng. Struct. 2018, 177, 198–209. [Google Scholar] [CrossRef]
- Sarkar, S.; Fitzgerald, B. Fluid Inerter for Optimal Vibration Control of Floating Offshore Wind Turbine Towers. Eng. Struct. 2022, 266, 114558. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, J.Z.; Neild, S. Inerter-Based Configurations for Main-Landing-Gear Shimmy Suppression. J. Aircr. 2017, 54, 684–693. [Google Scholar] [CrossRef]
- Asai, T.; Sugiura, K. Numerical Evaluation of a Two-Body Point Absorber Wave Energy Converter with a Tuned Inerter. Renew. Energy 2021, 171, 217–226. [Google Scholar] [CrossRef]
- Nemoto, Y.; Takino, M.; Tsukamoto, S.; Asai, T. Numerical Study of a Point Absorber Wave Energy Converter with Tuned Variable Inerter. Ocean. Eng. 2022, 257, 111696. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Houghton, N.E.; Smith, M.C. Experimental Testing and Analysis of Inerter Devices. J. Dyn. Syst. Meas. Control 2009, 131, 011001. [Google Scholar] [CrossRef]
- Siami, A.; Karimi, H.R. Modelling and Identification of the Hysteretic Dynamics of Inerters. Designs 2020, 4, 27. [Google Scholar] [CrossRef]
- Wang, F.; Hong, M.; Lin, T. Designing and Testing a Hydraulic Inerter. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 66–72. [Google Scholar] [CrossRef]
- Swift, S.J.; Smith, M.C.; Glover, A.R.; Papageorgiou, C.; Gartner, B.; Houghton, N.E. Design and Modelling of a Fluid Inerter. Int. J. Control 2013, 86, 2035–2051. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, W. Modeling, Testing, and Characteristic Analysis of a Planetary Flywheel Inerter. Shock Vib. 2018, 2018, 2631539. [Google Scholar] [CrossRef]
- John, E.D.A.; Wagg, D.J. Design and Testing of a Frictionless Mechanical Inerter Device Using Living-Hinges. J. Frankl. Inst. 2019, 356, 7650–7668. [Google Scholar] [CrossRef]
- Málaga Chuquitaype, C.; Menendez Vicente, C.; Thiers Moggia, R. Experimental and Numerical Assessment of the Seismic Response of Steel Structures with Clutched Inerters. Soil Dyn. Earthq. Eng. 2019, 121, 200–211. [Google Scholar] [CrossRef]
- Lazarek, M.; Brzeski, P.; Perlikowski, P. Design and Identification of Parameters of Tuned Mass Damper with Inerter Which Enables Changes of Inertance. Mech. Mach. Theory 2018, 119, 161–173. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Z.; Hu, N.; Yang, Y.; Yin, Z. Study of Dynamic Breakdown of Inerter and the Improved Design. Mech. Syst. Signal Process. 2022, 167, 108520. [Google Scholar] [CrossRef]
- Chillemi, M.; Furtmüller, T.; Adam, C.; Pirrotta, A. Nonlinear Mechanical Model of a Fluid Inerter. Mech. Syst. Signal Process. 2023, 188, 109986. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, J.Z.; Titurus, B.; Harrison, A. Model Identification Methodology for Fluid-Based Inerters. Mech. Syst. Signal Process. 2018, 106, 479–494. [Google Scholar] [CrossRef]
- Liu, X.; Titurus, B.; Jiang, J.Z. Generalisable Model Development for Fluid-Inerter Integrated Damping Devices. Mech. Mach. Theory 2019, 137, 1–22. [Google Scholar] [CrossRef]
- Wang, F.; Chan, H. Vehicle Suspensions with a Mechatronic Network Strut. Veh. Syst. Dyn. 2011, 49, 811–830. [Google Scholar] [CrossRef]
- Firestone, F.A. A New Analogy Between Mechanical and Electrical Systems. J. Acoust. Soc. Am. 1933, 4, 249–267. [Google Scholar] [CrossRef]
- Shen, Y.; Shi, D.; Chen, L.; Liu, Y.; Yang, X. Modeling and Experimental Tests of Hydraulic Electric Inerter. Sci. China Technol. Sci. 2019, 62, 2161–2169. [Google Scholar] [CrossRef]
- Zuo, L.; Scully, B.; Shestani, J.; Zhou, Y. Design and Characterization of an Electromagnetic Energy Harvester for Vehicle Suspensions. Smart Mater. Struct. 2010, 19, 045003. [Google Scholar] [CrossRef]
- Rhinefrank, K.; Schacher, A.; Prudell, J.; Brekken, T.K.A.; Stillinger, C.; Yen, J.Z.; Ernst, S.G.; von Jouanne, A.; Amon, E.; Paasch, R.; et al. Comparison of Direct-Drive Power Takeoff Systems for Ocean Wave Energy Applications. IEEE J. Ocean. Eng. 2012, 37, 35–44. [Google Scholar] [CrossRef]
- Orkisz, P.; Sapiński, B. Vibration Reduction System with a Linear Motor: Operation Modes, Dynamic Performance, Energy Consumption. Energies 2022, 15, 1910. [Google Scholar] [CrossRef]
- Wen, X.; Li, Y.; Yang, C. Design, Modeling, and Characterization of a Tubular Linear Vibration Energy Harvester for Integrated Active Wheel System. Automot. Innov. 2021, 4, 413–429. [Google Scholar] [CrossRef]
- Luo, C.; Yang, X.; Jia, Z.; Liu, C. Layout Optimization and Performance Analysis of Vehicle Suspension System Using an Electromagnetic Inerter. World Electr. Veh. J. 2023, 14, 318. [Google Scholar] [CrossRef]
- Glover, A.R.; Smith, M.C.; Houghton, N.E.; Long, P.J.G. Force-Controlling Hydraulic Device. UK. Patent GB0913759D0, 6 August 2009. [Google Scholar]
- Shen, Y.; Hua, J.; Fan, W.; Liu, Y.; Yang, X.; Chen, L. Optimal Design and Dynamic Performance Analysis of a Fractional-Order Electrical Network-Based Vehicle Mechatronic ISD Suspension. Mech. Syst. Signal Process. 2023, 184, 109718. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, R.; Yang, Y.; Wang, S. Simulation Study of Heavy Vehicle Road-Friendliness under Bilateral Tracks’ Excitation. Adv. Mater. Res. 2013, 680, 422–428. [Google Scholar] [CrossRef]
- Chillemi, M. Experimental and Numerical Investigation of a Fluid Inerter for Structural Control. J. Sound Vib. 2024, 573, 118222. [Google Scholar] [CrossRef]
- Wiseman, Y. Efficient Embedded Computing Component for Anti-Lock Braking System. Int. J. Control. Autom. 2018, 11, 1–10. [Google Scholar]
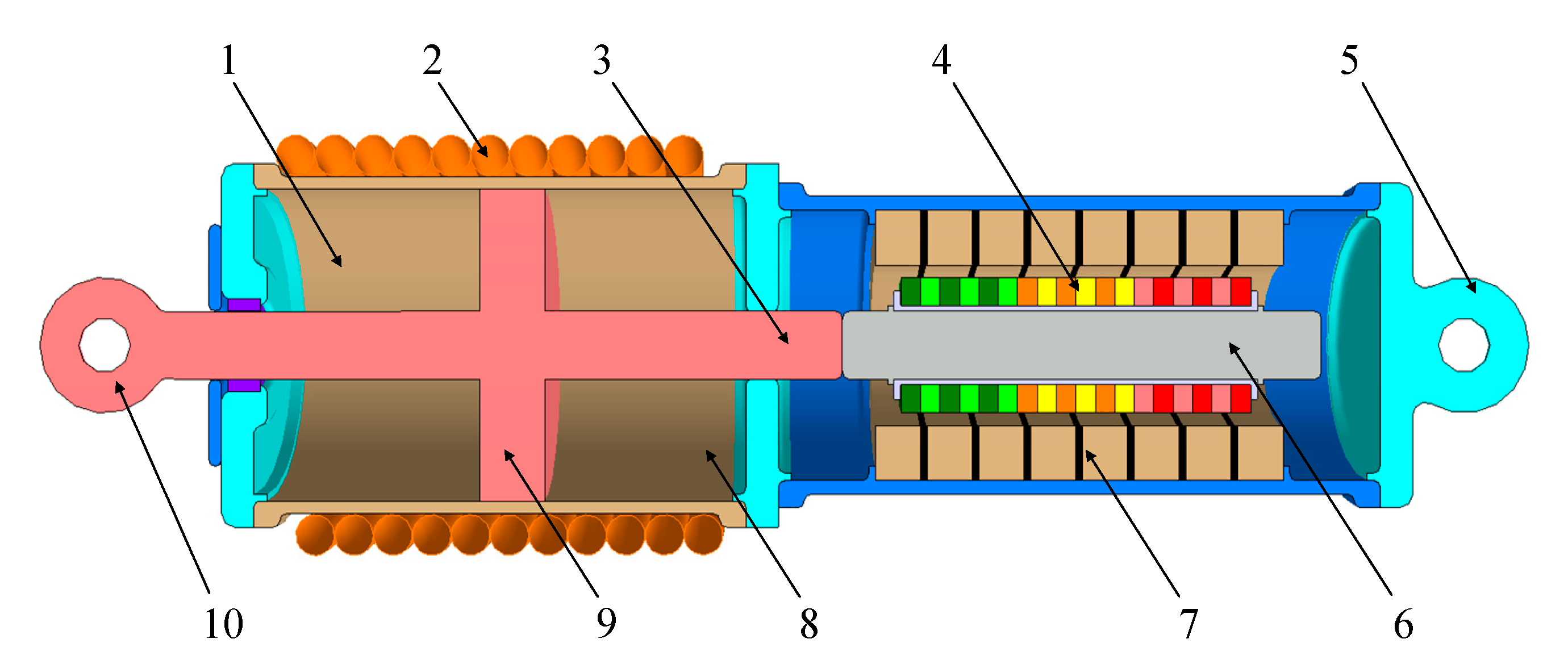

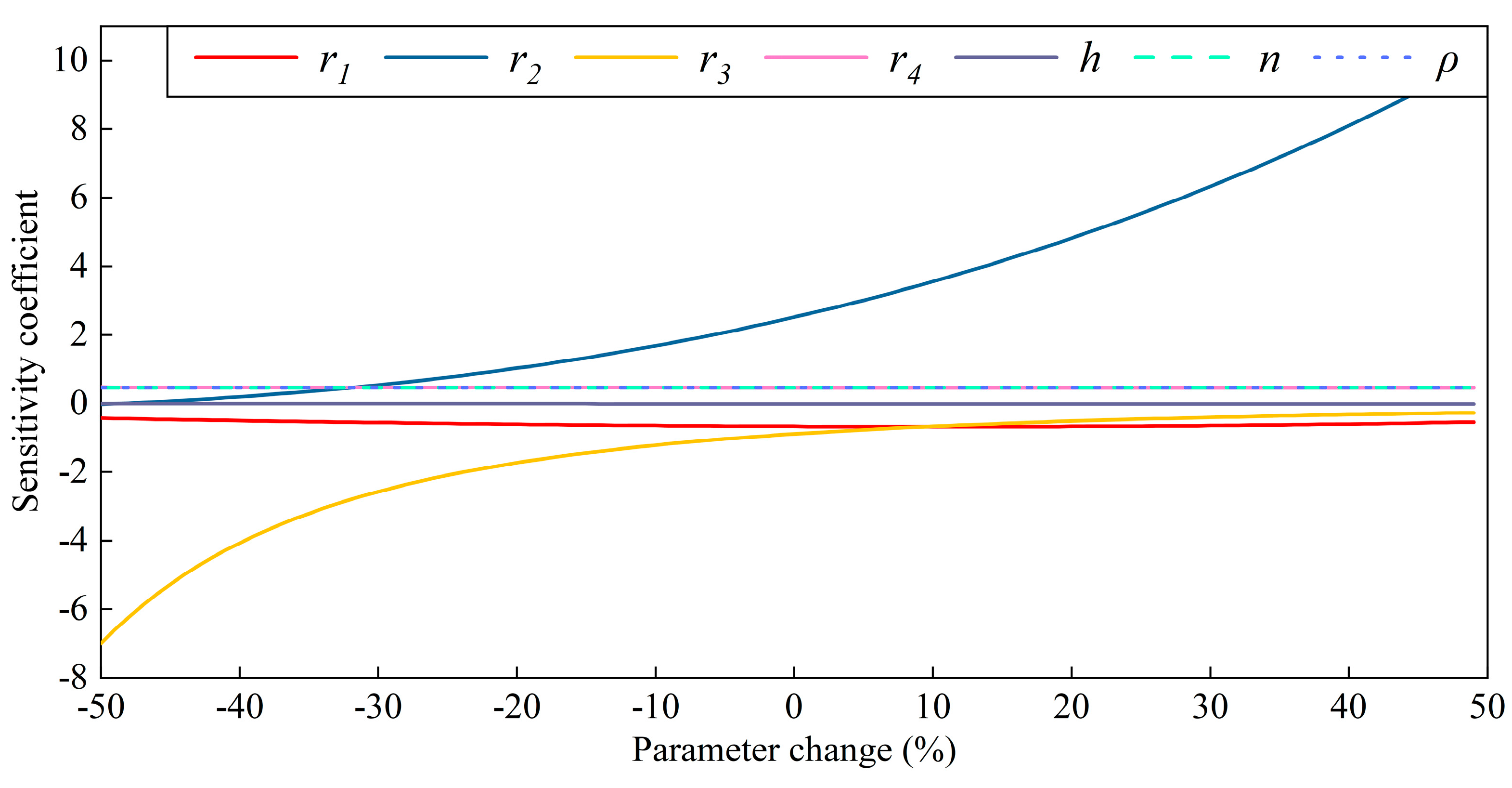




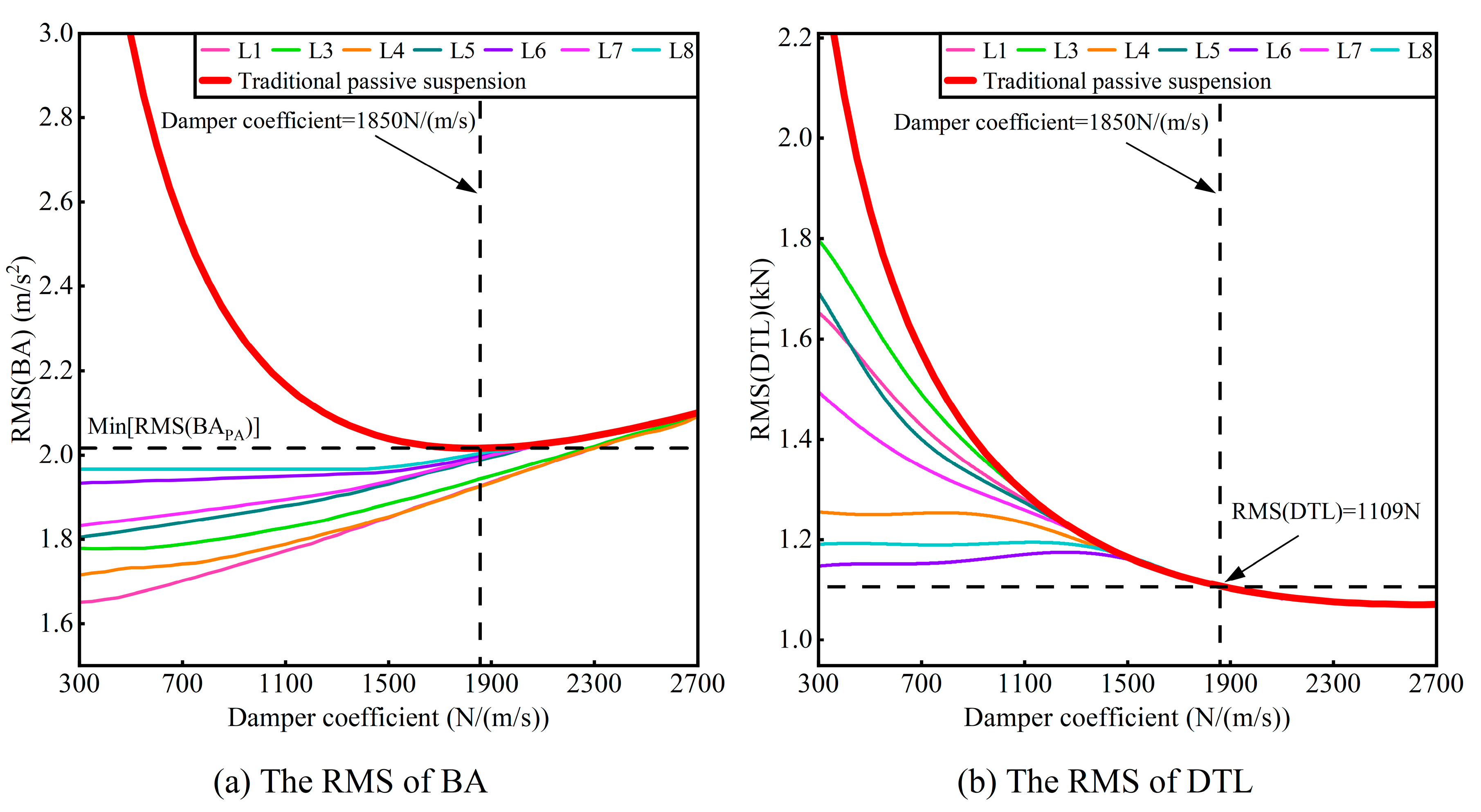

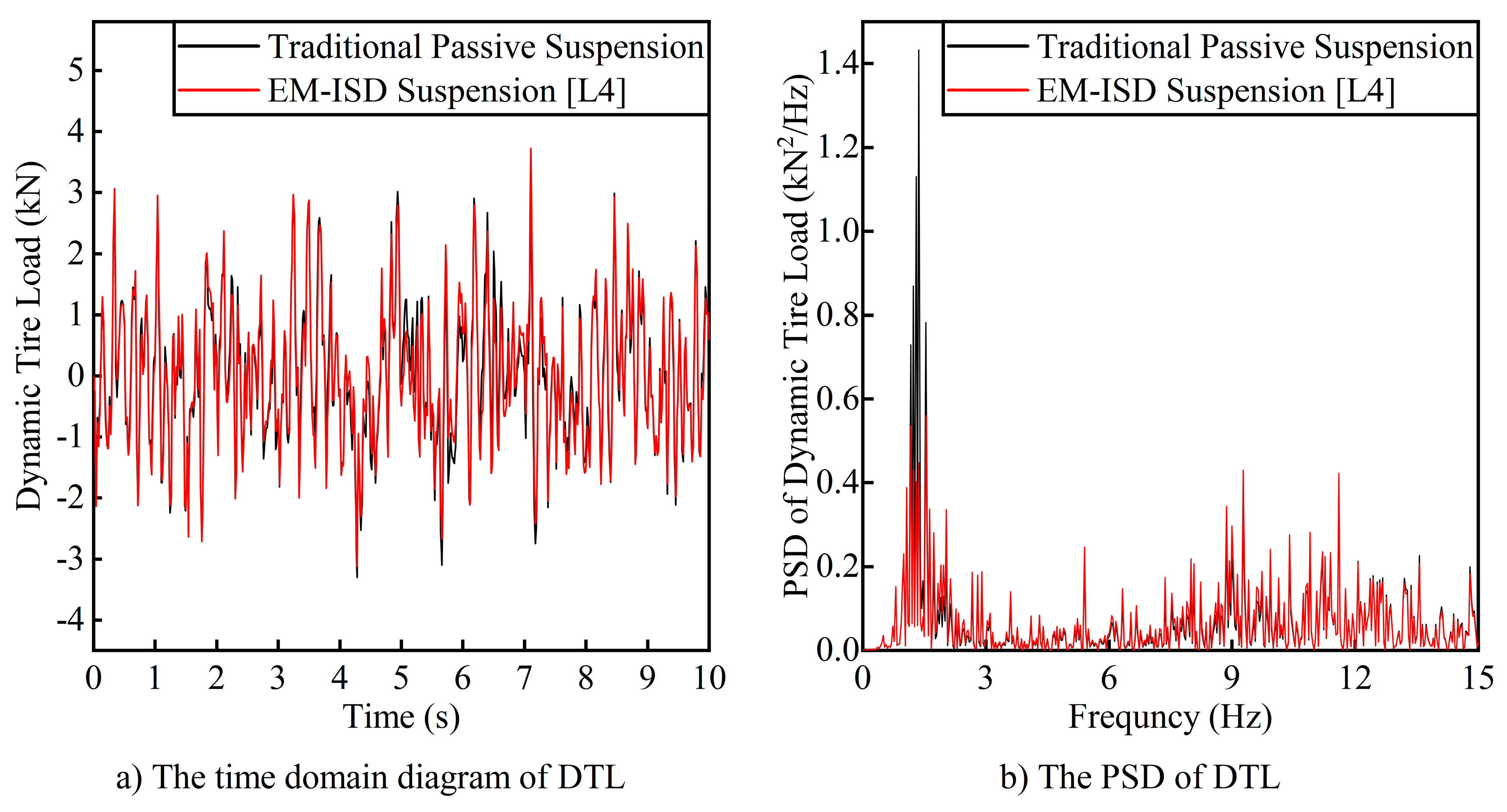
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Inner radius of the hydraulic cylinder | r1 | m | 0.04 |
| Radius of the piston rod | r2 | m | 0.0125 |
| Inner radius of helix tube | r3 | m | 0.0085 |
| The radius of rotation of helix tube | r4 | m | 0.078 |
| Lead of the helix tube | h | m | 0.0095 |
| The number of turns of the helical tube | n | - | 7 |
| Fluid density | ρ | kg/m3 | 690 |
| Voltage coefficient | Ke | V/(m/s) | 100 |
| Force coefficient | Kt | N/A | 81 |
| Resistance of the external circuit (resistance only) | R | Ω | 5 |
| Capacitance size of external circuit (capacitance only) | C | F | 0.015 |
| Inductance size of external circuit (inductance only) | L | H | 2 |
| Parameter [Unit] | Value |
|---|---|
| Suspension spring stiffness k [N/m] | 35,000 |
| Tire equivalent stiffness kt [N/m] | 190,000 |
| Sprung mass ms [kg] | 400 |
| Unsprung mass mu [kg] | 45 |
| Damping coefficient of EM-ISD suspension c [N/(m/s)] | 300–2700 (step size: 50) |
| Parameter [Unit] | Value |
|---|---|
| Inertance coefficient [kg] | 6.8 |
| Inductance [H] | 1.8 |
| Capacitance [mF] | 7.2 |
| Resistance [Ω] | 54 |
| Damping coefficient [N/(m/s)] | 1850 |
| Structure | RMS(BA) [m/s2] | RMS(DTL) [N] | RMS(SWS) [mm] | MAX(SWS) [mm] |
|---|---|---|---|---|
| Traditional passive suspension | 2.016359 | 1097.28 | 15.828 | 0.048 |
| EM-ISD suspension (L4) | 1.921581 | 1097.16 | 13.644 | 0.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Yang, X.; Jia, Z.; Liu, C.; Yang, Y. The Performance Enhancement of a Vehicle Suspension System Employing an Electromagnetic Inerter. World Electr. Veh. J. 2024, 15, 162. https://doi.org/10.3390/wevj15040162
Luo C, Yang X, Jia Z, Liu C, Yang Y. The Performance Enhancement of a Vehicle Suspension System Employing an Electromagnetic Inerter. World Electric Vehicle Journal. 2024; 15(4):162. https://doi.org/10.3390/wevj15040162
Chicago/Turabian StyleLuo, Chen, Xiaofeng Yang, Zhihong Jia, Changning Liu, and Yi Yang. 2024. "The Performance Enhancement of a Vehicle Suspension System Employing an Electromagnetic Inerter" World Electric Vehicle Journal 15, no. 4: 162. https://doi.org/10.3390/wevj15040162
APA StyleLuo, C., Yang, X., Jia, Z., Liu, C., & Yang, Y. (2024). The Performance Enhancement of a Vehicle Suspension System Employing an Electromagnetic Inerter. World Electric Vehicle Journal, 15(4), 162. https://doi.org/10.3390/wevj15040162






