Numerical Simulations for Damage and Failure of a Polymer Material Subjected to Thermal Fatigue Loading
Abstract
1. Introduction
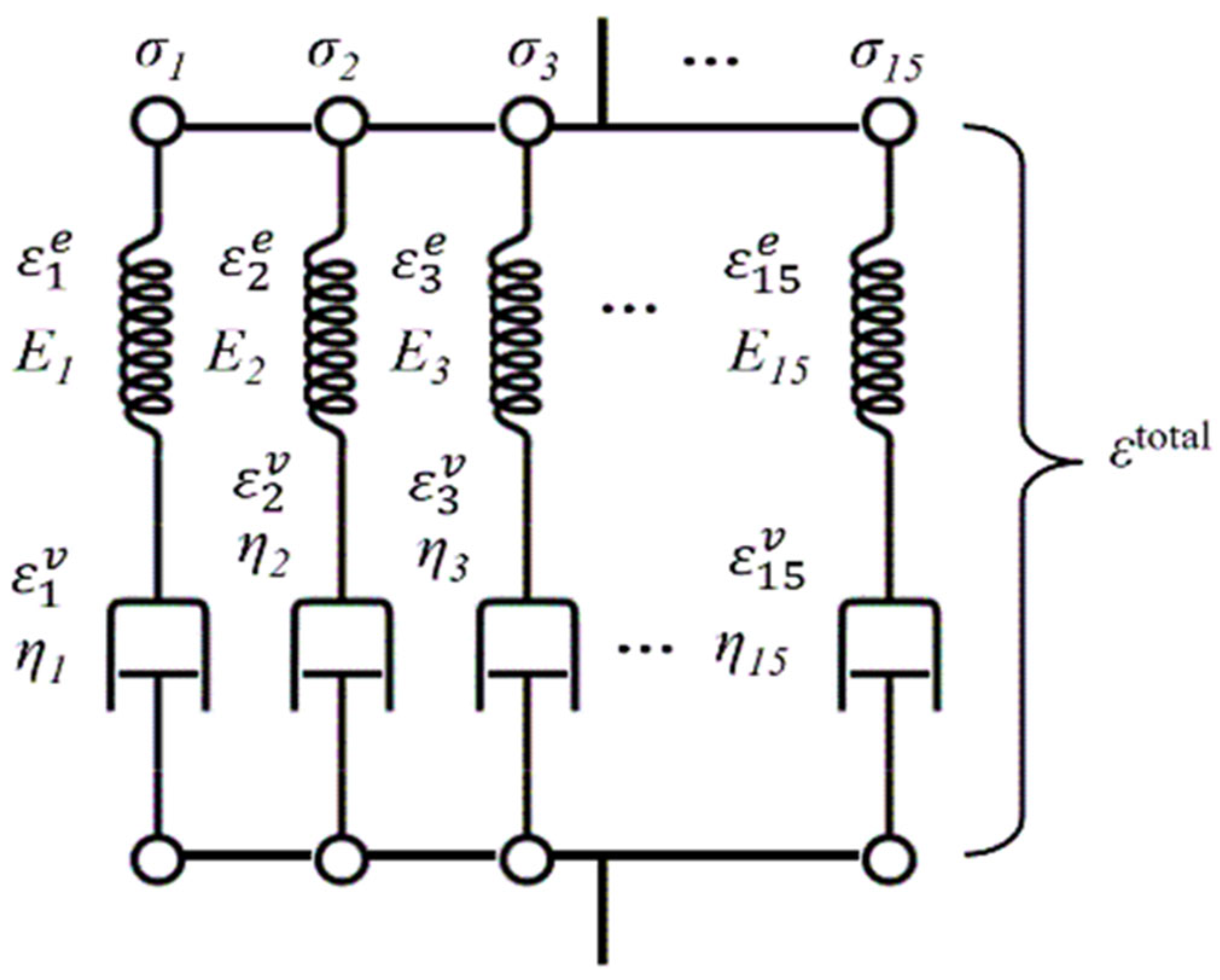
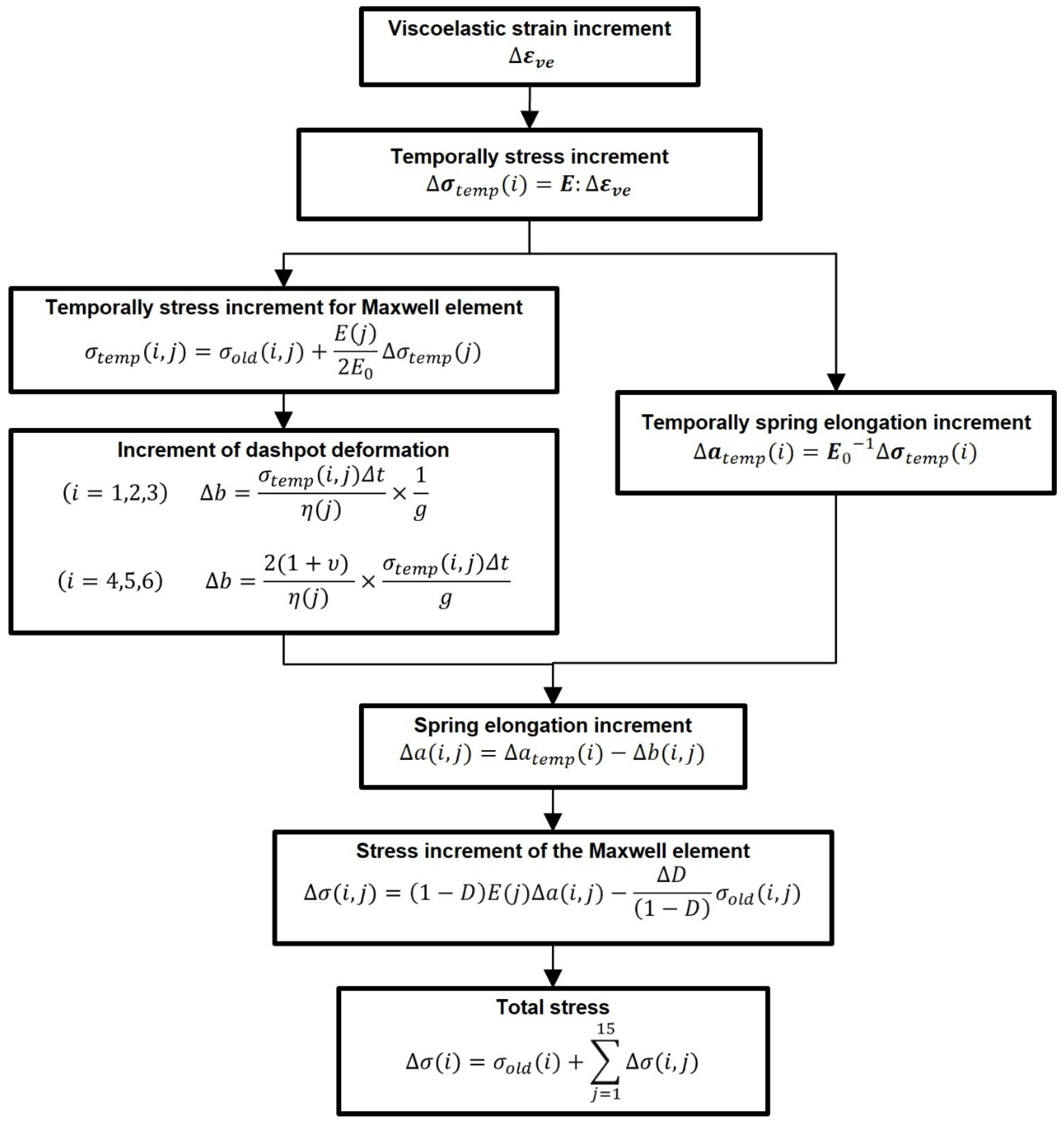
2. Governing Equations and Material Parameters Used in This Study
3. Heat Cycle Failure Simulation with Fixed Displacement for Surface Nodes
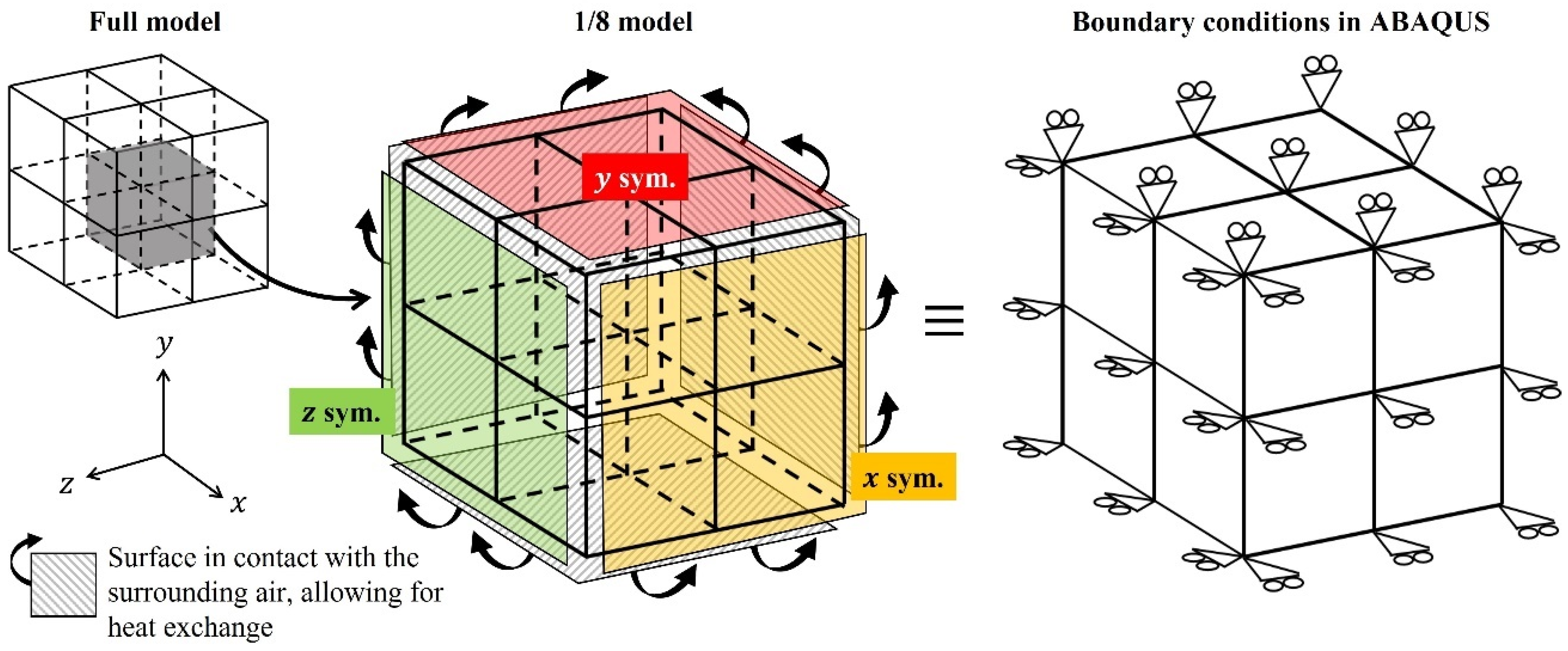
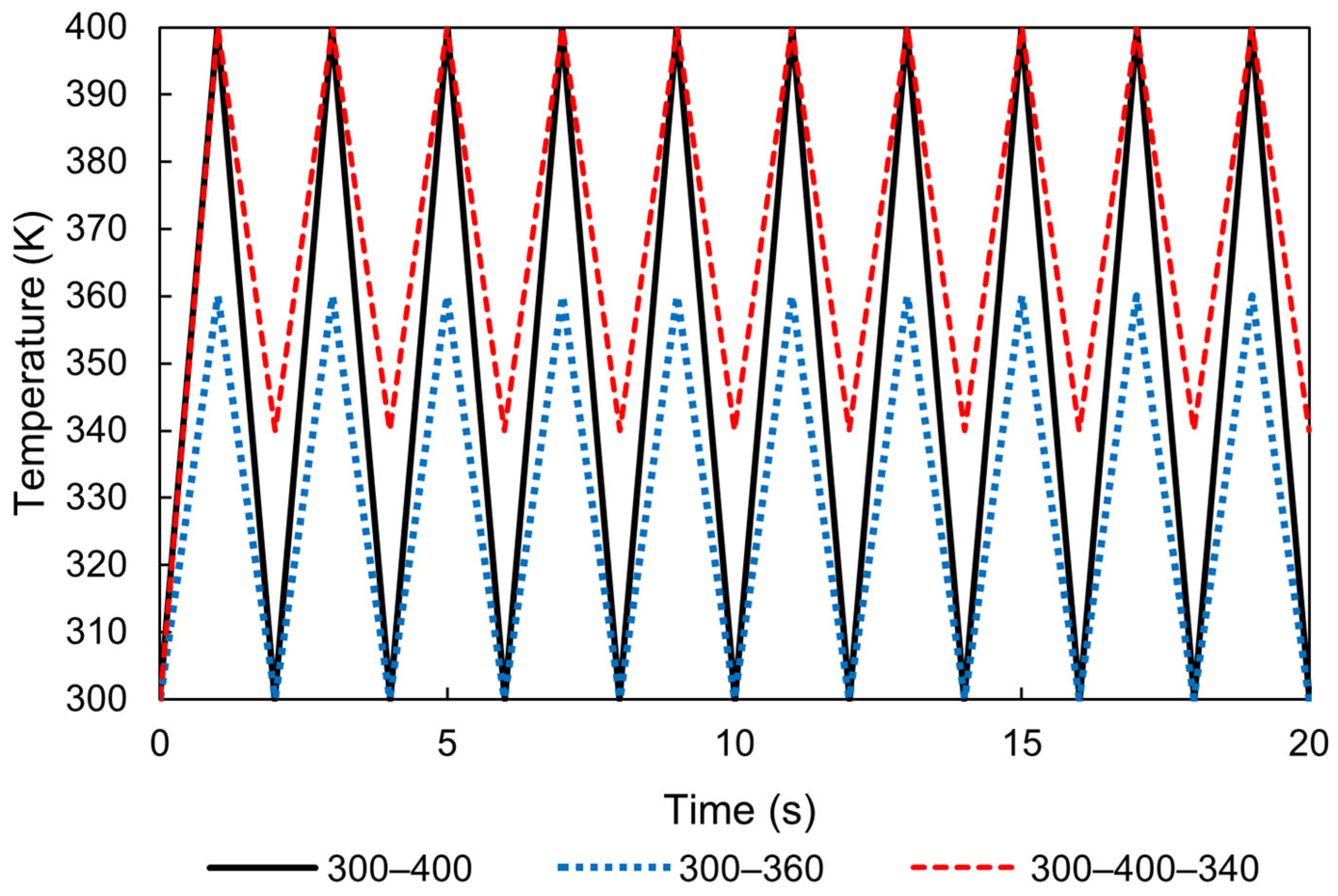
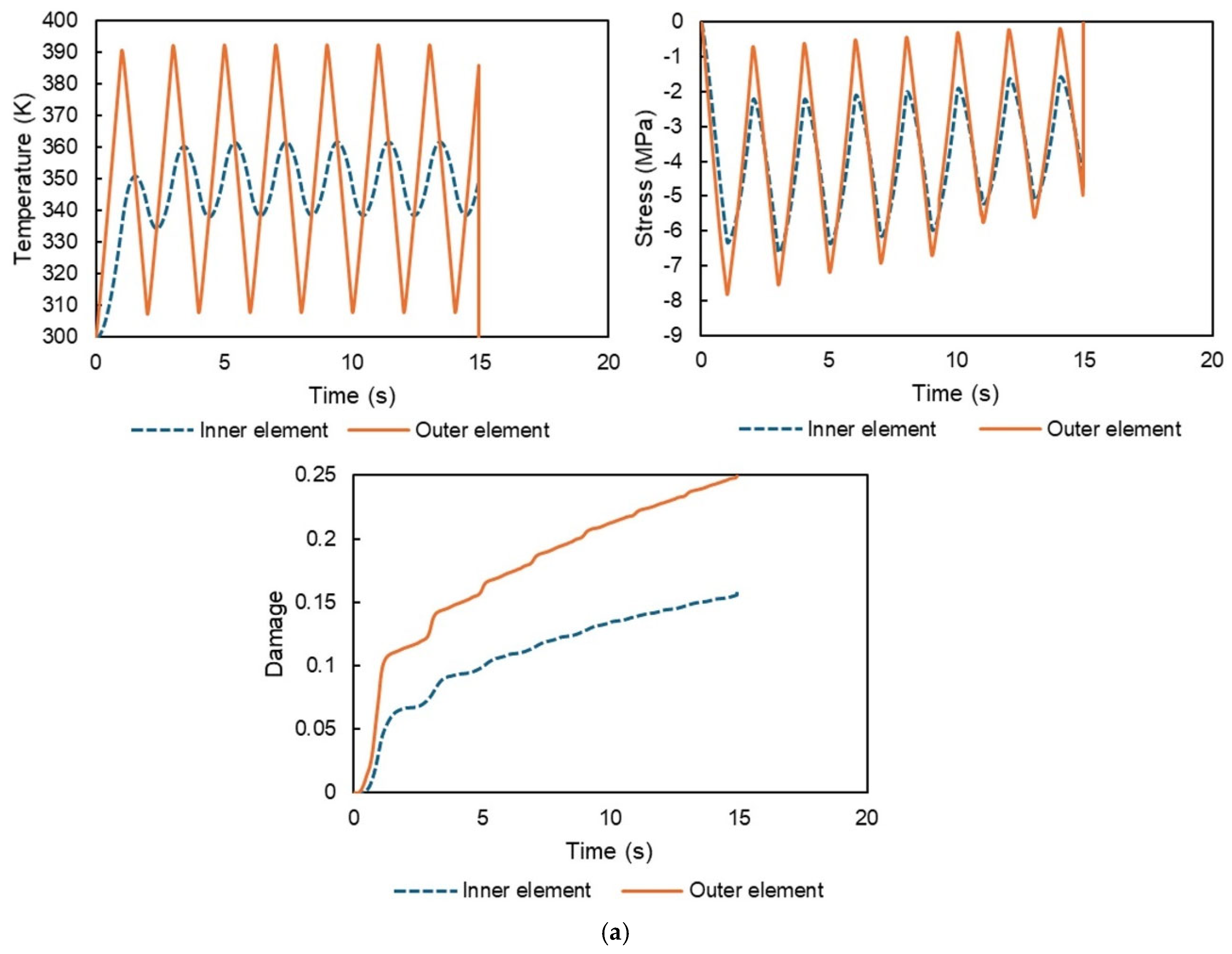
3.1. Numerical Conditions
3.2. Numerical Results
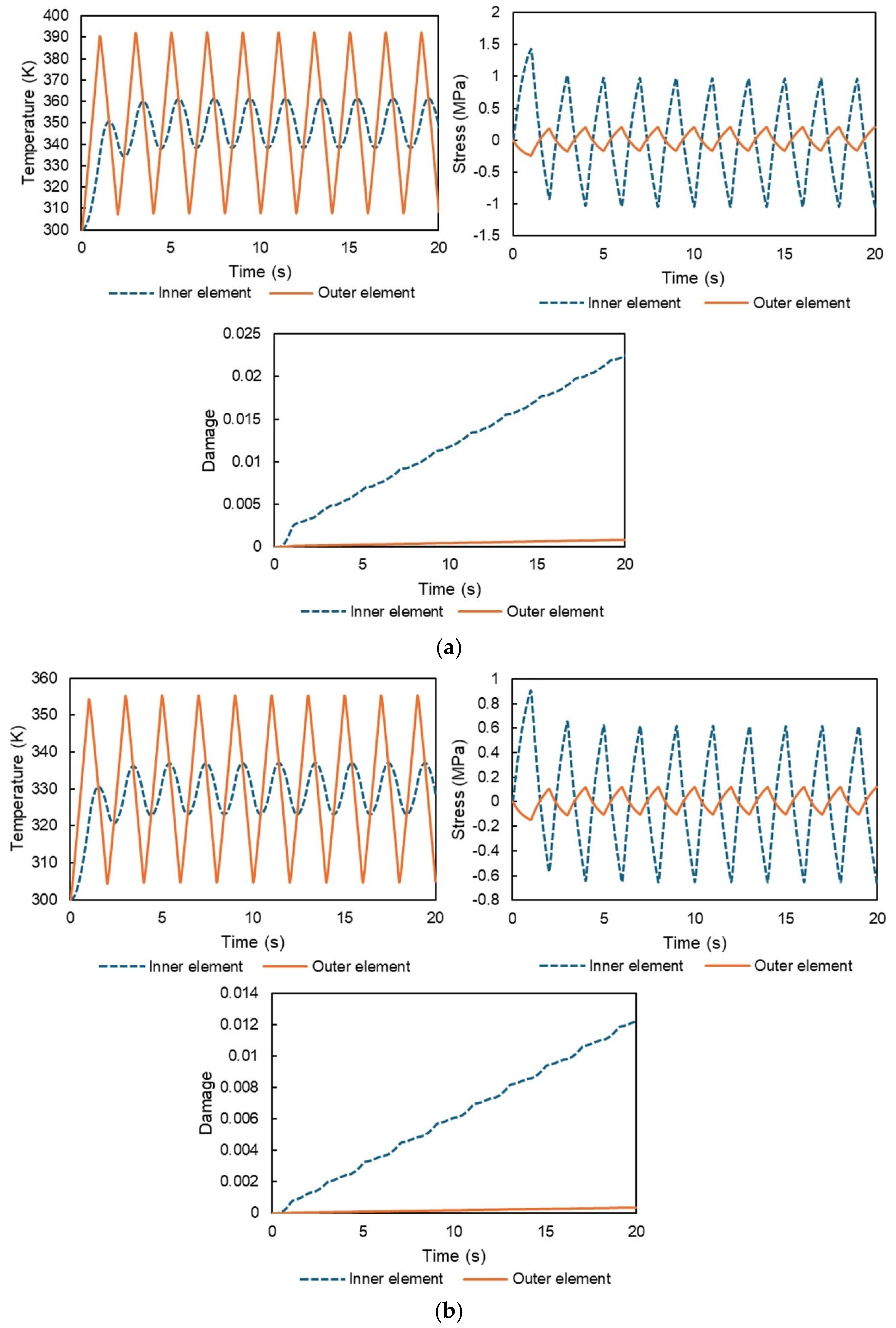
4. Heat Cycle Simulation with No Displacement Constraints
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Biernacki, K.; Szyszkowski, W.; Yannacopoulos, S. Experimental study of large-scale model composite materials under thermal fatigue. Compos. Part A Appl. Sci. Manuf. 1999, 30, 1027–1034. [Google Scholar] [CrossRef]
- Shin, K.B.; Kim, C.G.; Hong, C.S.; Lee, H.H. Prediction of failure thermal cycles in graphite/epoxy composite materials under simulated low earth orbit environments. Compos. Part B Eng. 2000, 31, 223–235. [Google Scholar] [CrossRef]
- Kobayashi, S.; Terada, K.; Ogihara, S.; Takeda, N. Damage-mechanics analysis of matrix cracking in cross-ply CFRP laminates under thermal fatigue. Compos. Sci. Technol. 2001, 61, 1735–1742. [Google Scholar] [CrossRef]
- Kobayashi, S.; Terada, K.; Takeda, N. Evaluation of long-term durability in high-temperature resistant CFRP laminates under thermal fatigue loading. Compos. Part B Eng. 2003, 34, 753–759. [Google Scholar] [CrossRef]
- Smmazçelik, T.; Çoban, O.; Bora, M.Ö.; Günay, V.; Cürgül, I. The effects of thermal cycles on the impact fatigue properties of thermoplastic matrix composites. Appl. Compos. Mater. 2008, 15, 99–113. [Google Scholar] [CrossRef]
- Deng, J.; Song, Y.; Xu, Z.; Nie, Y.; Lan, Z. Thermal aging effects on the mechanical behavior of glass-fiber-reinforced polyphenylene sulfide composites. Polymers 2022, 14, 1275. [Google Scholar] [CrossRef]
- Lizarralde, I.; Sapountzi, E.; Bénéthuilière, T.; Sket, F.; González, C. An X-ray computed tomography analysis of damage induced by thermal cycling in non-crimp fabric composites. Compos. Part A Appl. Sci. Manuf. 2022, 152, 106699. [Google Scholar] [CrossRef]
- Zrida, H.; Fernberg, P.; Ayadi, Z.; Varna, J. Microcracking in thermally cycled and aged carbon fibre/polyimide laminates. Int. J. Fatigue 2017, 94, 121–130. [Google Scholar] [CrossRef]
- Ajaja, J.; Barthelat, F. Damage accumulation in a carbon fiber fabric reinforced cyanate ester composite subjected to mechanical loading and thermal cycling. Compos. Part B Eng. 2016, 90, 523–529. [Google Scholar] [CrossRef]
- Zhang, C.; Binienda, W.K.; Morscher, G.N.; Martin, R.E.; Kohlman, L.W. Experimental and FEM study of thermal cycling induced microcracking in carbon/epoxy triaxial braided composites. Compos. Part A Appl. Sci. Manuf. 2013, 46, 34–44. [Google Scholar] [CrossRef]
- Qiu, Z.; Wu, D.; Zhang, Y.; Liu, C.; Qian, Y.; Cai, D. On the mechanical behavior of carbon fiber/epoxy laminates exposed in thermal cycling environments. Thin-Walled Struct. 2024, 196, 111481. [Google Scholar] [CrossRef]
- Boccaccini, A.R.; Strutt, A.J.; Vecchio, K.S.; Mendoza, D.; Chawla, K.K.; Ponton, C.B.; Pearce, D.H. Behavior of Nicalon™-fiber-reinforced glass-matrix composites under thermal cycling conditions. Compos. Part A Appl. Sci. Manuf. 1998, 29, 1343–1352. [Google Scholar] [CrossRef]
- Kobayashi, S.; Shimpo, T.; Goto, K. Microscopic damage behavior in carbon fiber reinforced plastic laminates for a high-accuracy antenna in a satellite under cyclic thermal loading. Adv. Compos. Mater. 2019, 28, 259–269. [Google Scholar] [CrossRef]
- Mosallam, A.S.; Xin, H.; Salama, M.A.; Altunişik, A.C.; Adanur, S.; Elmikawi, M. Residual mechanical properties of triaxial CFRP laminates after thermal cycling and ultraviolet radiation exposure of composite bridge members. Structures 2021, 30, 166–173. [Google Scholar] [CrossRef]
- Park, S.Y.; Choi, H.S.; Choi, W.J.; Kwon, H. Effect of vacuum thermal cyclic exposures on unidirectional carbon fiber/epoxy composites for low earth orbit space applications. Compos. Part B Eng. 2012, 43, 726–738. [Google Scholar] [CrossRef]
- Shivakumar, K.N.; Holloway, G. Effect of thermal fatigue on tensile and flexural properties of carbon/cyanate ester pultruded composite. J. Reinf. Plast. Compos. 2009, 28, 675–689. [Google Scholar] [CrossRef]
- Hancox, N.L. Thermal effects on polymer matrix composites: Part 1. Thermal cycling. Mater. Des. 1998, 19, 85–91. [Google Scholar] [CrossRef]
- Qin, G.; Na, J.; Mu, W.; Tan, W. Effect of thermal cycling on the degradation of adhesively bonded CFRP/aluminum alloy joints for automobiles. Int. J. Adhes. Adhes. 2019, 95, 102439. [Google Scholar] [CrossRef]
- Azimpour-Shishevan, F.; Akbulut, H.; Mohtadi-Bonab, M.A. The effect of thermal shock cycling on low-velocity impact behavior of carbon fiber reinforced epoxy composites. J. Dyn. Behav. Mater. 2019, 5, 161–169. [Google Scholar] [CrossRef]
- Glaoui, B.; Merbouh, M.; van de Ven, M.; Chailleux, E.; Youcefi, A. How thermal fatigue cycles change the rheological behavior of polymer modified bitumen? Energy Procedia 2013, 36, 844–851. [Google Scholar] [CrossRef]
- Sauer, J.A.; Richardson, G.C. Fatigue of polymers. Int. J. Fract. 1980, 16, 499–532. [Google Scholar] [CrossRef]
- Naga, S.A.R.; El-Sayed, T.A. Fatigue Failure in Polymeric Materials: Insights from Experimental Testing. J. Fail. Anal. Prev. 2024, 24, 922–935. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106178. [Google Scholar] [CrossRef]
- Takase, N.; Koyanagi, J.; Mori, K.; Sakai, T. Molecular dynamics simulation for evaluating fracture entropy of a polymer material under various combined stress states. Materials 2021, 14, 1884. [Google Scholar] [CrossRef]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107204. [Google Scholar] [CrossRef]
- Sakai, T.; Takase, N.; Oya, Y.; Koyanagi, J. A possibility for quantitative detection of mechanically-induced invisible damage by thermal property measurement via entropy generation for a polymer material. Materials 2022, 15, 737. [Google Scholar] [CrossRef]
- Deng, H.; Mochizuki, A.; Fikry, M.; Abe, S.; Ogihara, S.; Koyanagi, J. Numerical and experimental studies for fatigue damage accumulation of CFRP cross-ply laminates based on entropy failure criterion. Materials 2023, 16, 388. [Google Scholar] [CrossRef]
- Deng, H.; Toda, K.; Sato, M.; Koyanagi, J. Micro-scale numerical simulation of fatigue failure for CFRP subjected to multiple-amplitude cyclic loadings based on entropy damage criterion. Materials 2023, 16, 6120. [Google Scholar] [CrossRef]
- Kagawa, H.; Umezu, Y.; Sakaue, K.; Koyanagi, J. Numerical simulation for the tensile failure of randomly oriented short fiber reinforced plastics based on a viscoelastic entropy damage criterion. Compos. Part C Open Access 2023, 10, 100342. [Google Scholar] [CrossRef]
- Li, Y.; Deng, H.; Takamura, M.; Koyanagi, J. Durability analysis of CFRP adhesive joints: A study based on entropy damage modeling using FEM. Materials 2023, 16, 6821. [Google Scholar] [CrossRef]
- Kudo, N.; Fujita, R.; Oya, Y.; Sakai, T.; Nagano, H.; Koyanagi, J. Identification of invisible fatigue damage of thermosetting epoxy resin by non-destructive thermal measurement using entropy generation. Adv. Compos. Mater. 2024, 33, 233–249. [Google Scholar] [CrossRef]
- Sakai, T.; Oya, Y.; Koyanagi, J. Evaluation of volumetric strain on polyamide 6 by thermodynamic entropy generation. Exp. Mech. 2024, 64, 105–111. [Google Scholar] [CrossRef]
- Yamada, N.; Morita, M.; Takamura, M.; Murashima, T.; Oya, Y.; Koyanagi, J. Molecular dynamics simulation of cumulative microscopic damage in a thermosetting polymer under cyclic loading. Polymers 2024, 16, 1813. [Google Scholar] [CrossRef] [PubMed]
- Iwamoto, S.; Oya, Y.; Koyanagi, J. Evaluation of microscopic damage of PEEK polymers under cyclic loadings using molecular dynamics simulations. Polymers 2022, 14, 4955. [Google Scholar] [CrossRef]
- Mohammadi, M.; Naderi, M.H.; Soltanolkotabi, M. Effects of a classical homogeneous gravitational field on the cavity-field entropy and generation of the Schrödinger-cat states in the Jaynes-Cummings model. Eur. Phys. J. D 2008, 47, 295–302. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. Real-time fatigue life monitoring based on thermodynamic entropy. Struct. Health Monit. 2011, 10, 189–197. [Google Scholar] [CrossRef]
- Amooie, M.A.; Khonsari, M.M. On the effect of environmental temperature on fracture fatigue entropy. Int. J. Fatigue 2023, 168, 107411. [Google Scholar] [CrossRef]
- Amooie, M.A.; Wilson, P.J.; Mahmoudi, A.; Azizian-Farsani, E.; Khonsari, M.M. On the measurement of total entropy generation for determining fatigue fracture. Int. J. Fatigue 2024, 189, 108578. [Google Scholar] [CrossRef]
- Hajshirmohammadi, B.; Khonsari, M.M. On the entropy of fatigue crack propagation. Int. J. Fatigue 2020, 133, 105413. [Google Scholar] [CrossRef]
- Hebert, J.; Khonsari, M.M. Effect of surface roughness and polishing orientation on fatigue life and fracture fatigue entropy. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1514–1530. [Google Scholar] [CrossRef]
- Hebert, J.; Khonsari, M.M. Dislocation-based entropy as a criterion for fracture. Theor. Appl. Fract. Mech. 2024, 133, 104548. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Jirandehi, A.P.; Amooie, M.A.; Khonsari, M.M. Entropy-based damage model for assessing the remaining useful fatigue life. Int. J. Damage Mech. 2024, 33, 223–244. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Khosravani, M.R.; Khonsari, M.M.; Reinicke, T. On the evaluation of entropy threshold for debonding during crack propagation using DIC technique. Eng. Fract. Mech. 2023, 288, 109361. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the application of fracture fatigue entropy to variable frequency and loading amplitude. Theor. Appl. Fract. Mech. 2018, 98, 30–37. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the application of fracture fatigue entropy to multiaxial loading. Int. J. Fatigue 2021, 150, 106321. [Google Scholar] [CrossRef]
- Nourian-Avval, A.; Khonsari, M.M. Rapid prediction of fatigue life based on thermodynamic entropy generation. Int. J. Fatigue 2021, 145, 106105. [Google Scholar] [CrossRef]
- Wei, W.; He, L.; Chen, M.; Chen, X.; Liang, R.; Zou, L.; Yang, X. A two-scale thermodynamic entropy model for rapid high-cycle fatigue property evaluation of welded joints. Eng. Fract. Mech. 2023, 292, 109614. [Google Scholar] [CrossRef]
- Fauthan, M.A.; Abdullah, S.; Abdullah, M.F. Entropy generation approach for evaluating energy dissipation and temperature rise to predict the fatigue life behavior in magnesium alloy. J. Mater. Res. Technol. 2023, 26, 4387–4404. [Google Scholar] [CrossRef]
- Sato, M.; Imai, E.; Koyanagi, J.; Ishida, Y.; Ogasawara, T. Evaluation of the interfacial strength of carbon-fiber-reinforced temperature-resistant polymer composites by the micro-droplet test. Adv. Compos. Mater. 2017, 26, 465–476. [Google Scholar] [CrossRef]
- Koyanagi, J.; Hatta, H.; Ogawa, F.; Kawada, H. Time-dependent reduction of tensile strength caused by interfacial degradation under constant strain duration in UD-CFRP. J. Compos. Mater. 2007, 41, 3007–3026. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A thermo-viscoelastic analysis of process-induced residual stress in fibre-reinforced polymer-matrix composites. Mater. Sci. Eng. A 2007, 452–453, 483–498. [Google Scholar] [CrossRef]
- Barcenas, L.; Khoun, L.; Hubert, P. Thermoviscoelastic modelling of highly reactive thermoset resins for liquid moulding applications. Compos. Part A Appl. Sci. Manuf. 2024, 185, 108350. [Google Scholar] [CrossRef]
- Zhi, J.; Yang, B.; Li, Y.; Tay, T.E.; Tan, V.B.C. Multiscale thermo-mechanical analysis of cure-induced deformation in composite laminates using Direct FE2. Compos. Part A Appl. Sci. Manuf. 2023, 173, 107704. [Google Scholar] [CrossRef]



| Maxwell Elements | Elasticity | Damage Variables | ||||
|---|---|---|---|---|---|---|
| [MPa] | [MPa∙s] | [MPa] | 4260 | [kJ] | 100 | |
| 1 | 284 | 4.5 × 102 | 0.33 | [K] | 300 | |
| 2 | 284 | 3.3 × 103 | 4 | |||
| 3 | 284 | 1.2 × 105 | Nonlinearity | 0.25 | ||
| 4 | 284 | 1.9 × 106 | [MPa] | 70 | [kJ] | 0.4 |
| 5 | 284 | 1.8 × 107 | 2 | |||
| 6 | 284 | 1.4 × 108 | 7 | |||
| 7 | 284 | 8.5 × 108 | ||||
| 8 | 284 | 5.0 × 109 | Thermal Parameters | |||
| 9 | 284 | 3.0 × 1010 | [J/kg∙K] | 1130 | ||
| 10 | 284 | 1.9 × 1011 | [kg/m3] | 0.0014 | ||
| 11 | 284 | 1.4 × 1016 | [W/m2·K] | 1 | ||
| 12 | 284 | 1.3 × 1019 | [W/m·K] | 0.3 | ||
| 13 | 284 | 2.1 × 1022 | Thermal expansion coefficient [/K] | 4 × 10−5 | ||
| 14 | 284 | 1.3 × 1026 | ||||
| 15 | 284 | 2.5 × 1029 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koyanagi, J.; Sugiyama, T.; Fikry, M.J.M.; Li, Y.; Tsukada, T. Numerical Simulations for Damage and Failure of a Polymer Material Subjected to Thermal Fatigue Loading. Polymers 2025, 17, 1153. https://doi.org/10.3390/polym17091153
Koyanagi J, Sugiyama T, Fikry MJM, Li Y, Tsukada T. Numerical Simulations for Damage and Failure of a Polymer Material Subjected to Thermal Fatigue Loading. Polymers. 2025; 17(9):1153. https://doi.org/10.3390/polym17091153
Chicago/Turabian StyleKoyanagi, Jun, Takumu Sugiyama, M. J. Mohammad Fikry, Yutong Li, and Takuhei Tsukada. 2025. "Numerical Simulations for Damage and Failure of a Polymer Material Subjected to Thermal Fatigue Loading" Polymers 17, no. 9: 1153. https://doi.org/10.3390/polym17091153
APA StyleKoyanagi, J., Sugiyama, T., Fikry, M. J. M., Li, Y., & Tsukada, T. (2025). Numerical Simulations for Damage and Failure of a Polymer Material Subjected to Thermal Fatigue Loading. Polymers, 17(9), 1153. https://doi.org/10.3390/polym17091153







