A Solution of the Junction Riemann Problem for 1D Hyperbolic Balance Laws in Networks including Supersonic Flow Conditions on Elastic Collapsible Tubes
Abstract
:1. Introduction
2. Materials and Methods
2.1. 1D Mathematical Models in Arteries and Veins
2.1.1. Elastic Mechanical Properties of Vessels and Tube Laws
2.1.2. Conservation-Law Form
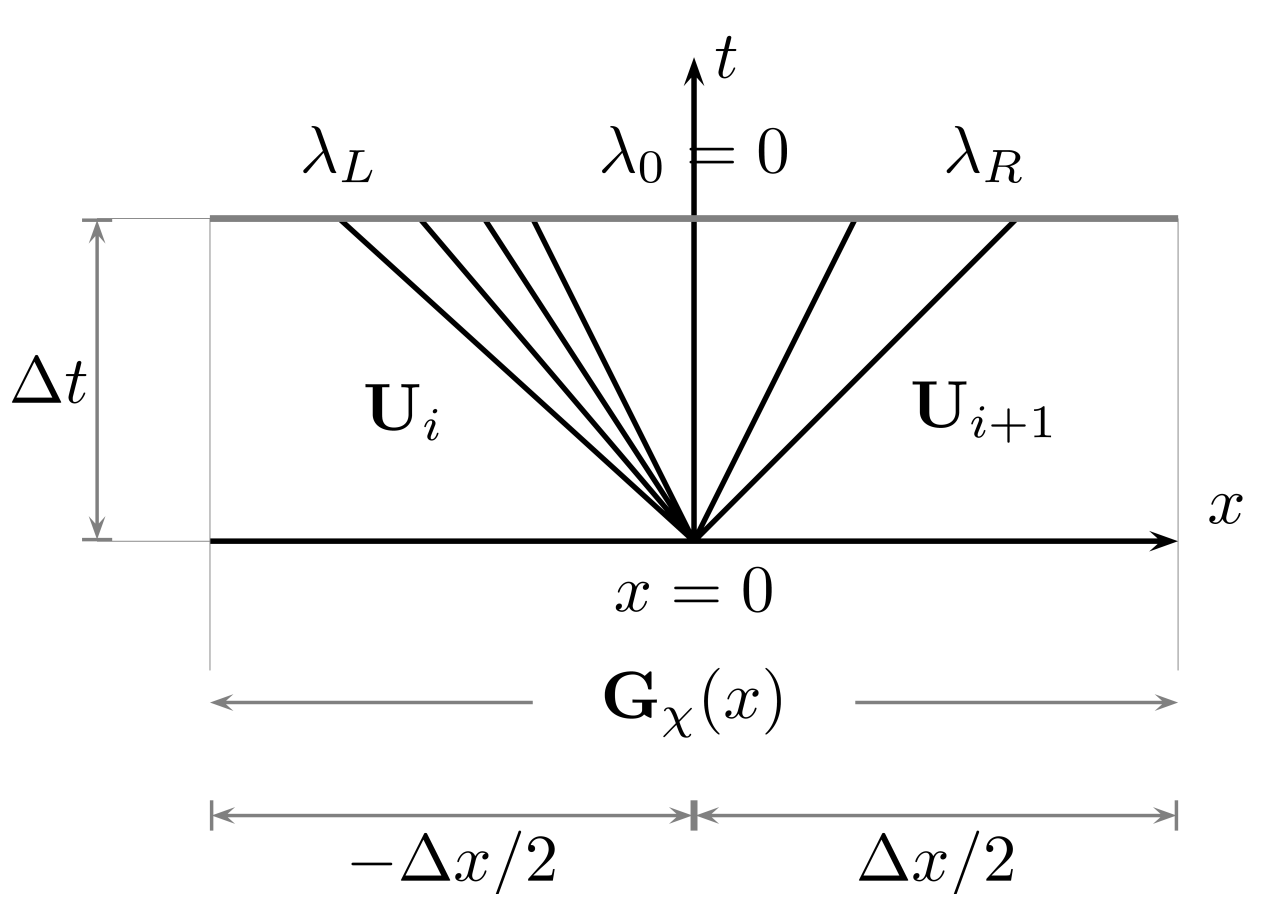
2.2. Numerical Method
2.2.1. Numerical Computation of Fluxes at the Inner Interfaces
2.2.2. The HLLS Solver
2.3. External Boundary Conditions at the Inflow-Outflow Sections of the Network
2.3.1. Non-Linear Waves: Shocks and Rarefactions
- In the case of a rarefaction in a k vessel, the solution is given by the characteristic field [24,25],and the jump condition across the rarefaction in invariant form becomes:with the following entropy condition:Considering that along the rarefaction waves the vessel area decreases, the equation in (42) can be written asor written asif expressed using variations in u. Both results suggest that velocity and flow variations must ensure:and, therefore, during the suction produced by a decompression wave, the vessel area decreases while flow and velocity increased/decreased for backward/forward waves, respectively.
- If the solution in a k vessel is a shock of celerity S, that will travel in the direction, the Rankine–Hugoniot (RH) condition provides the solution. Solutions for right and left traveling shock waves can be defined using the following function [24,25]:withwhere the shock speed is given by:under the following entropy conditions:The RH condition applied to the mass conservation equation in combination with the direction of the advance of the shock or compression wave, leads to the following expression:and considering that in (48), we find that in boundary cells,Therefore, velocity and flow variations must ensure:and for compression waves, the vessel area increases while flow and velocity are decreased/increased for backward/forward waves, respectively.
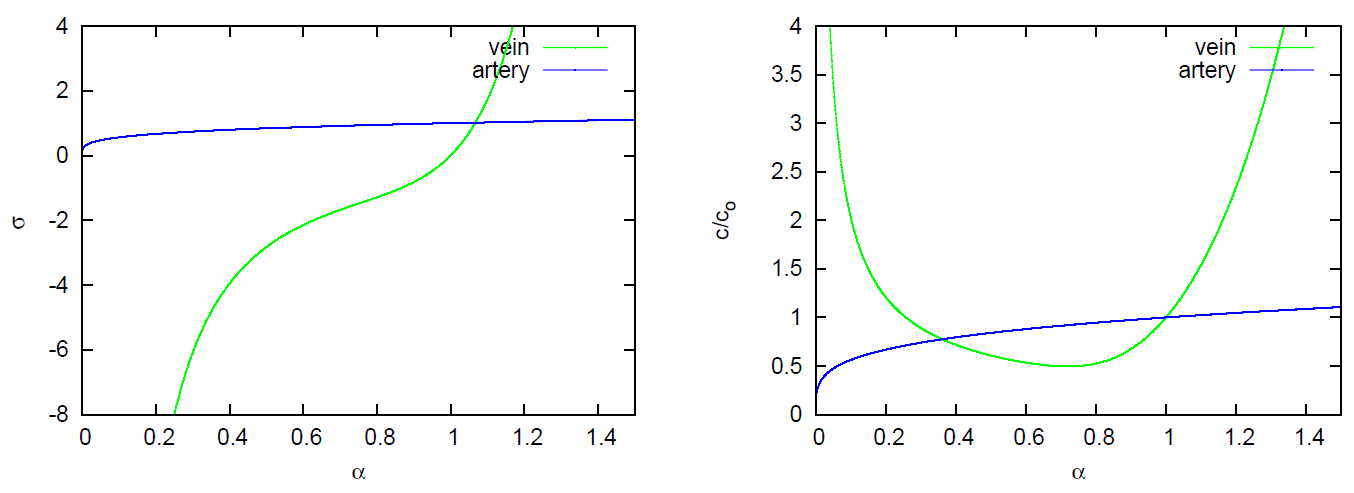
2.3.2. Pulse Wave Velocity in Arteries and Veins
2.3.3. Outflow and Inflow Boundary Conditions in the Subsonic Flow Regime
2.3.4. Limitation of Boundary Conditions at Outflow Sections
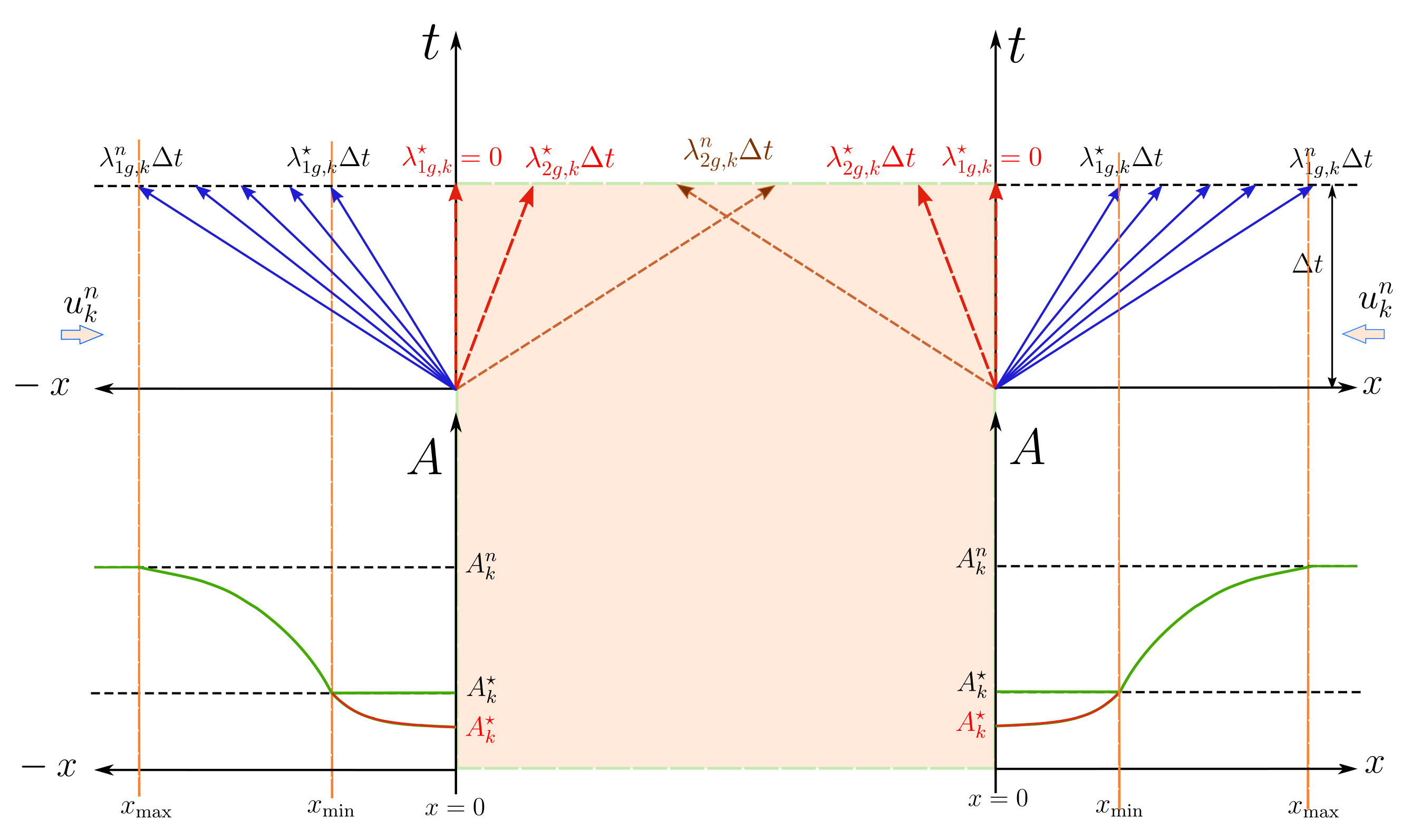
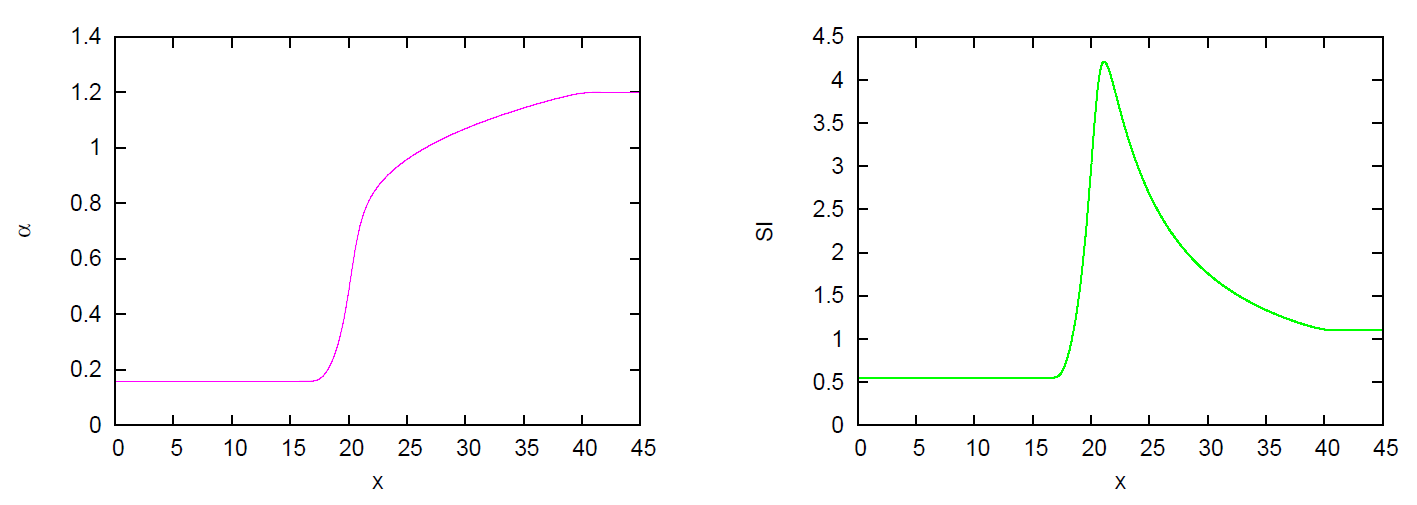
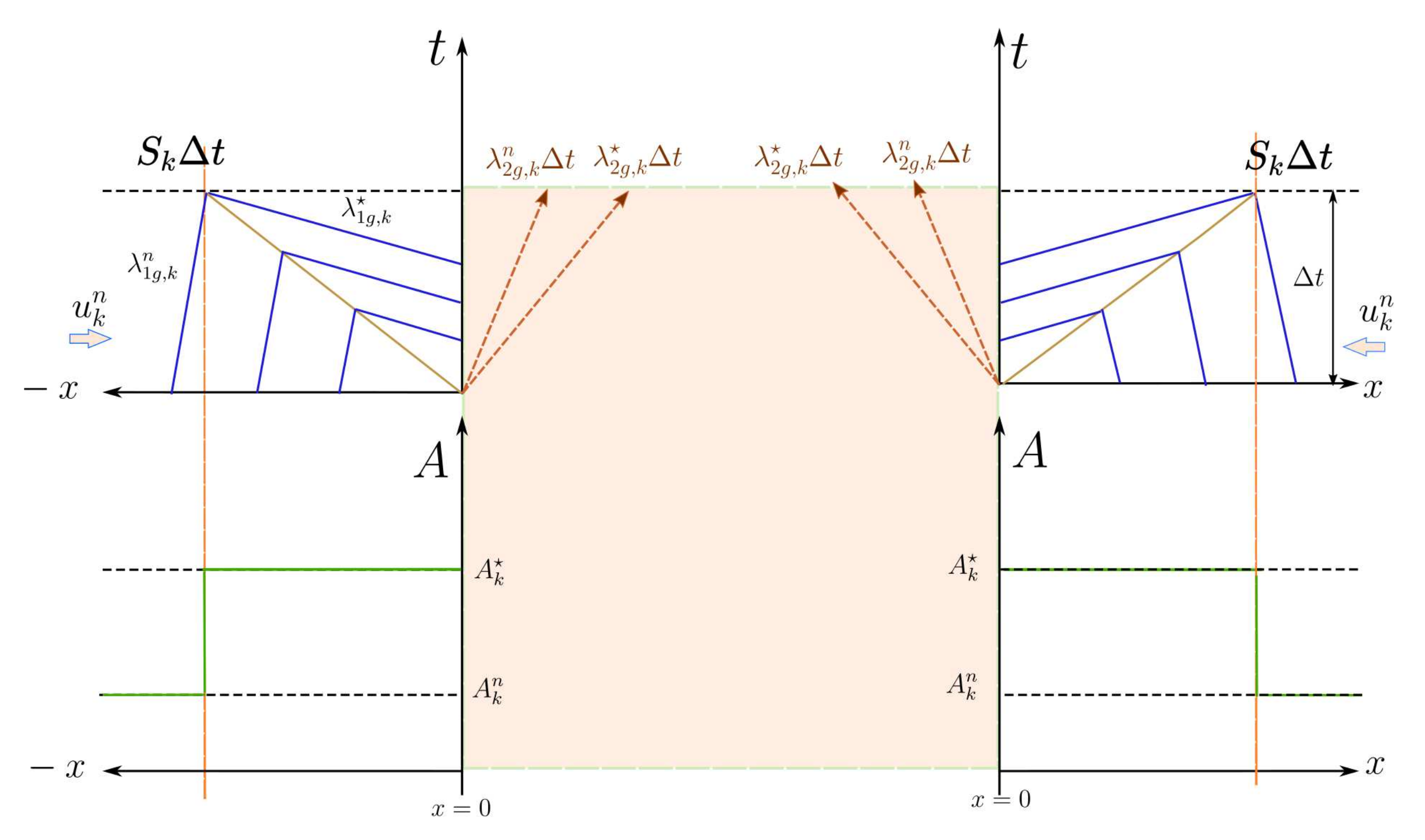
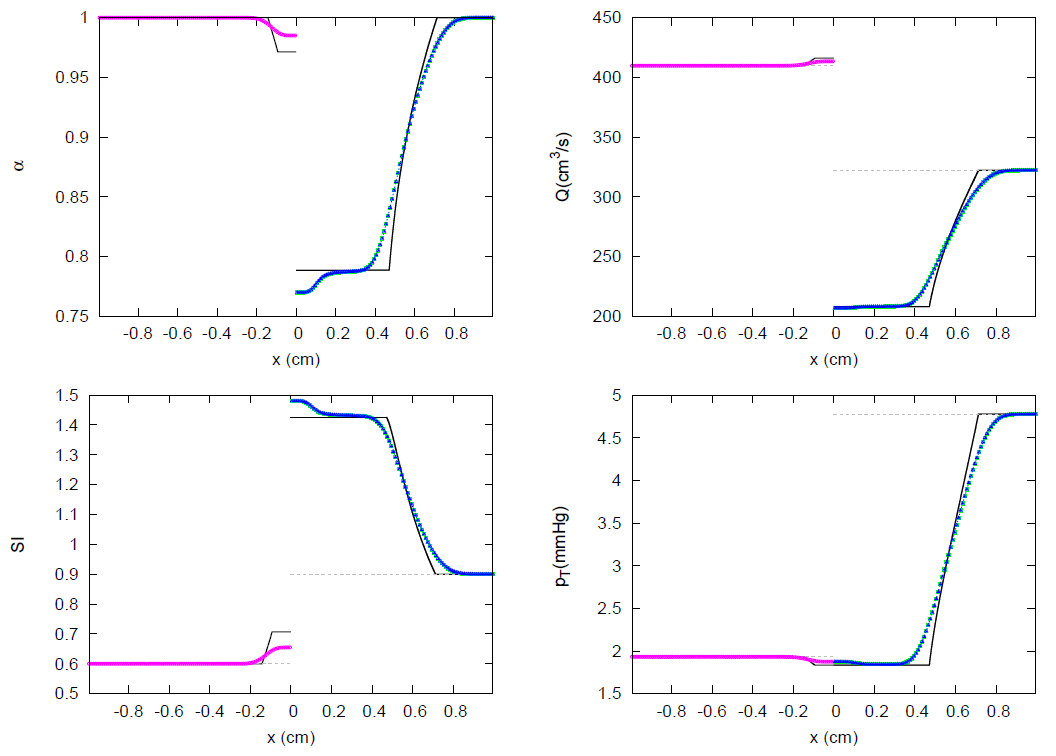
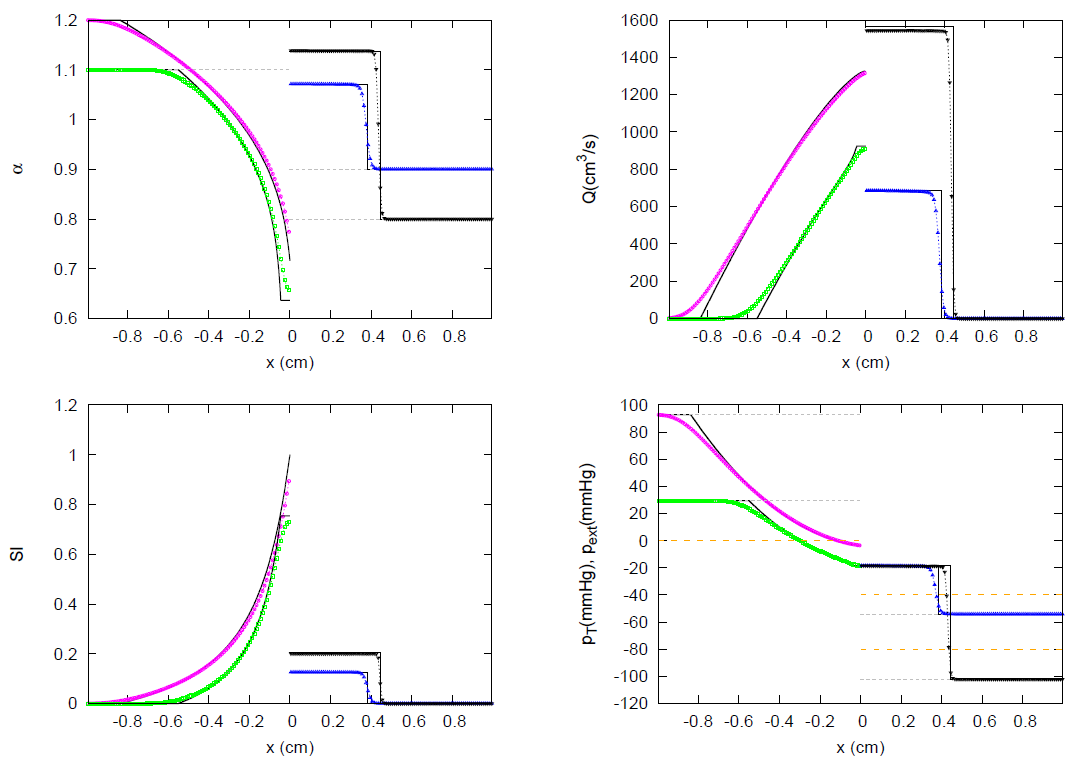
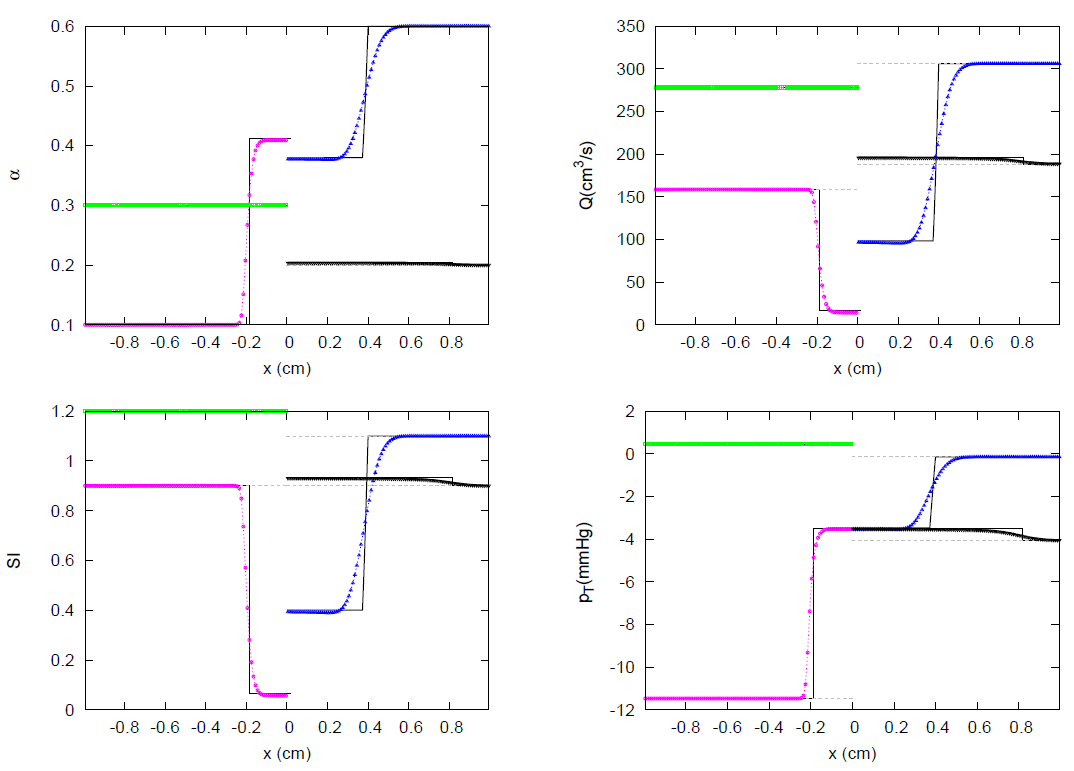
- Case A1. Decompression waves under initial subsonic conditions, (Figure 6).Suction is generated in the outflow section and a rarefaction or decompression wave appears according to (47). The value of the increases in the direction with . As the solution can be only developed in the inner region of the vessel, , the value of the speed index at the boundary, , must be limited to conditions of sonic flow:Therefore, a critical limit in the velocity and flow, and , appears when imposing the boundary condition:Then, if the limit in (61) is exceeded, the solution is given by the functionand the solution for flow is given by .
- Case A2. Decompression waves under initial supersonic conditions, (Figure 7).For a supersonic initial state, both celerities and fall outside the domain of computation and the limit in (61) has already been exceeded. Further acceleration/deceleration would mean to force the development of the solution outside the vessel. Under these conditions no information can travel inside the domain and the initial state cannot change. We cannot specify any boundary conditions [35].
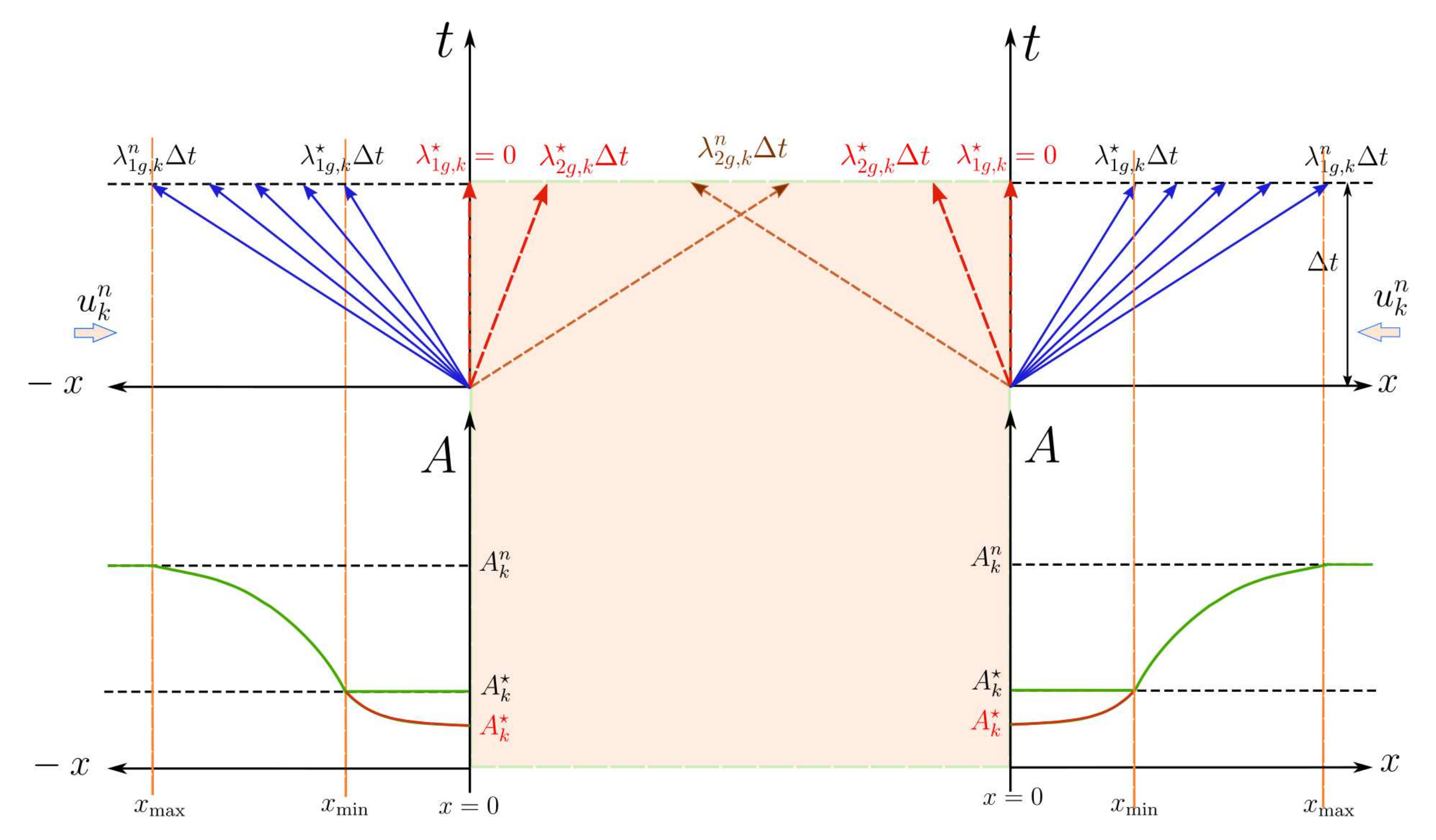
- Case B1. Compression waves under initial subsonic conditions, (Figure 8).When the flow is decelerated/accelerated at the boundary in presence of backward/forward wave, the vessel area increases. The value of the decreases in the direction and sonic conditions cannot be achieved.
- Case B2. Compression waves under initial supersonic conditions, (Figure 9). For a supersonic initial state, the wave falls outside the computational domain. When the flow is decelerated at the boundary, the shock must satisfy the entropy condition in (51), ensuring . Therefore, sonic conditions cannot be achieved.
2.3.5. Limitation of Boundary Conditions at Inflow Sections
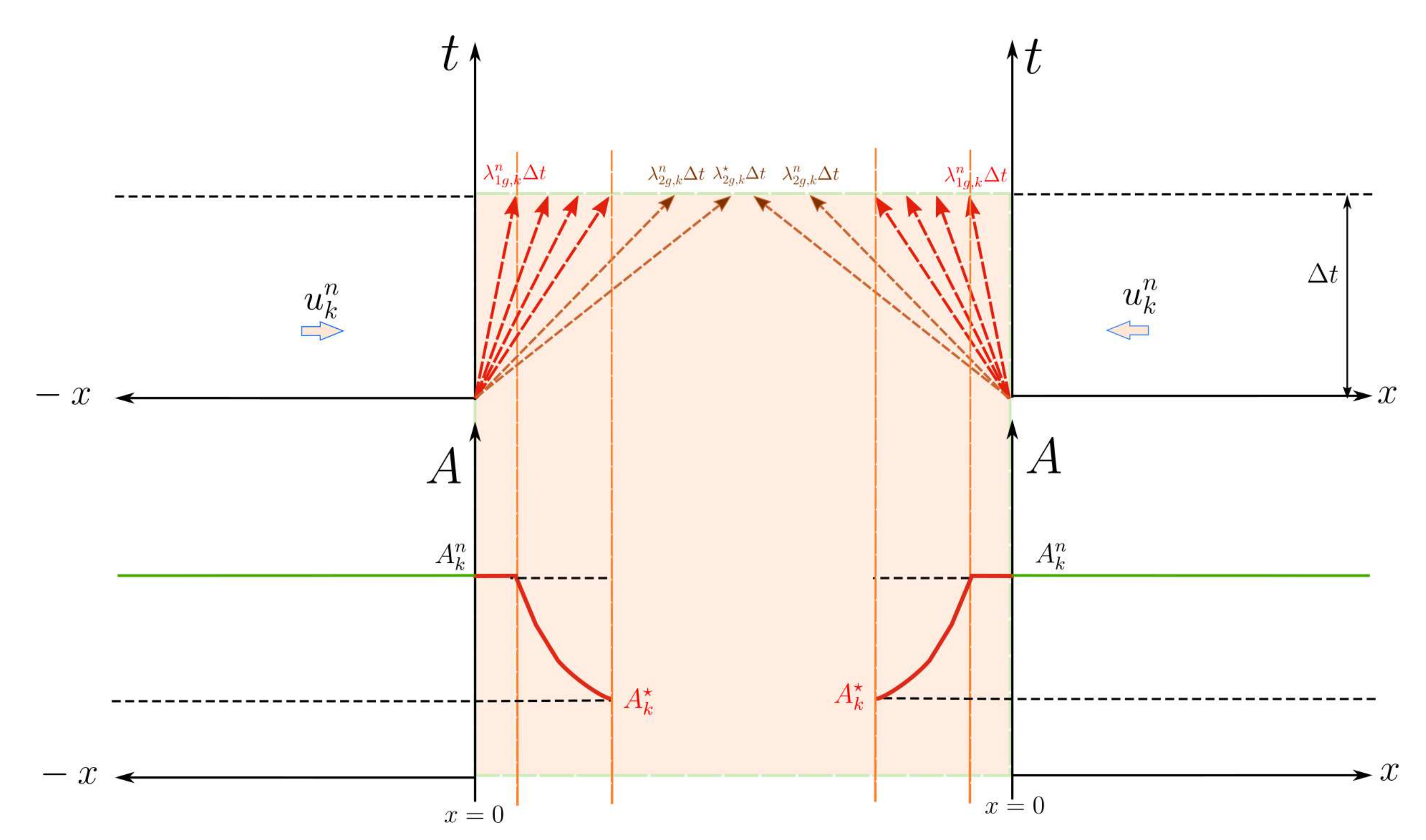
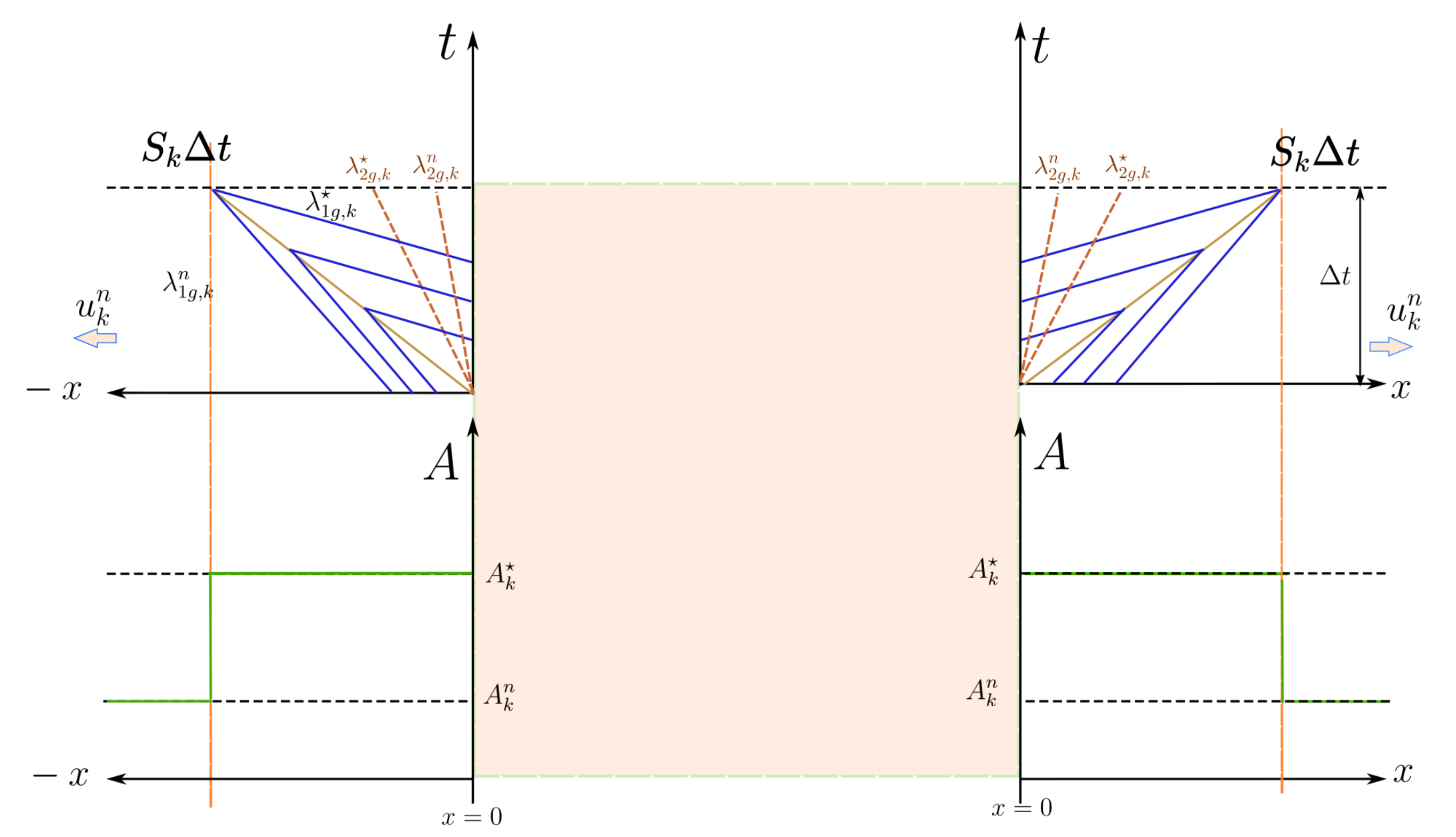
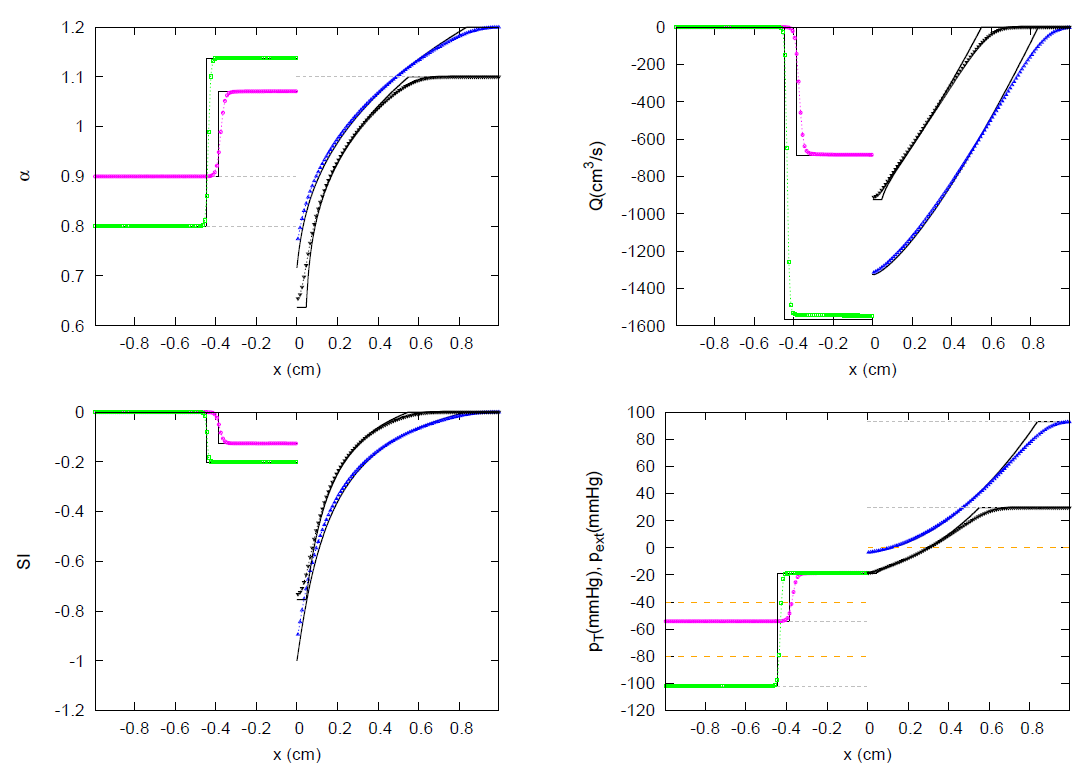
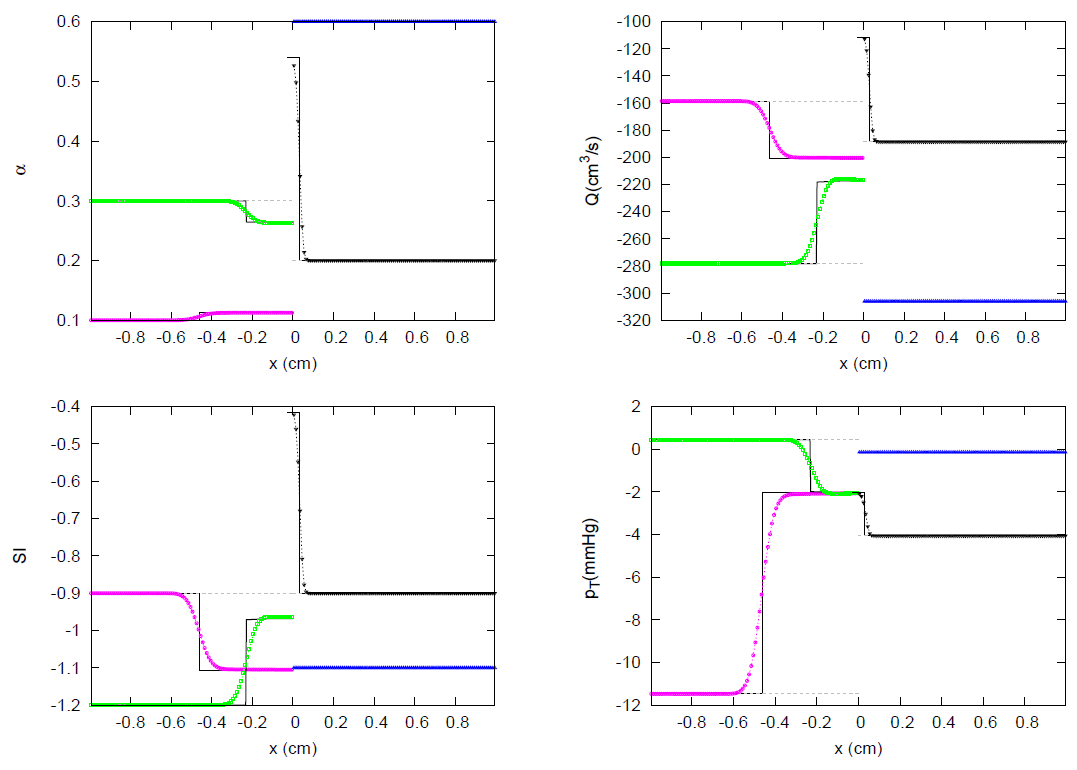
- Case C1. Compression waves under initial subsonic conditions, (Figure 10).Under these conditions, the vessel area increases and the solution is a shock or compression wave moving in the direction, where .
- Case C2. Compression waves under initial supersonic conditions, (Figure 11).
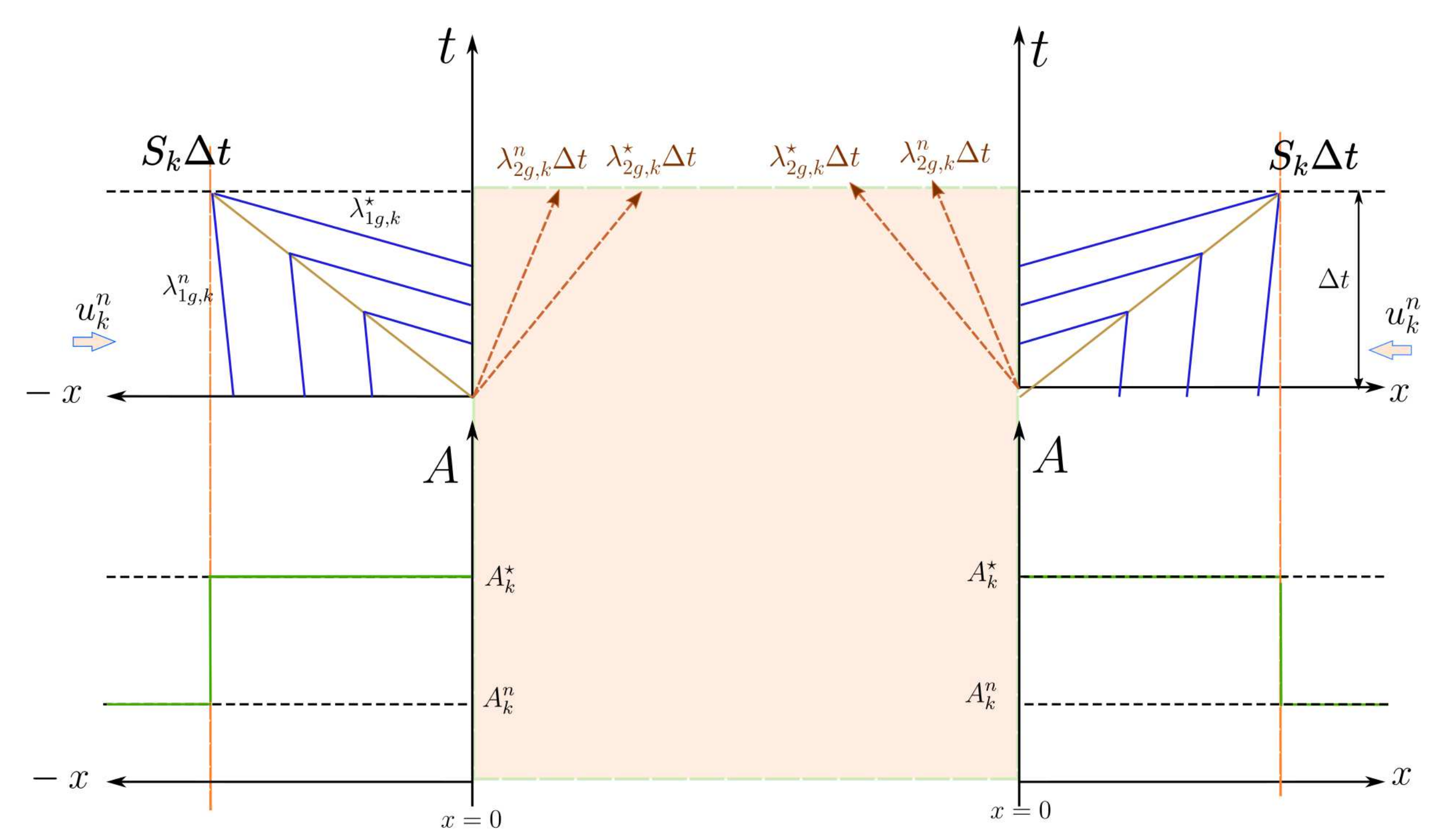
- Case D1. Decompression waves under initial subsonic conditions, (Figure 12).In the subsonic range, we find that . The limiting value of is given by , or , and represents a condition of reversal flow. When this limit is exceeded, sonic conditions must be imposed, and the solution is given by function in (63).
- Case D2. Decompression waves under initial supersonic conditions, (Figure 13).Again, the limiting state, a condition of reversal flow, is provided by and, if exceeded, the solution is given by function in (63).
2.3.6. Outflow and Inflow Boundary Conditions including Subsonic, Sonic and Supersonic Flow
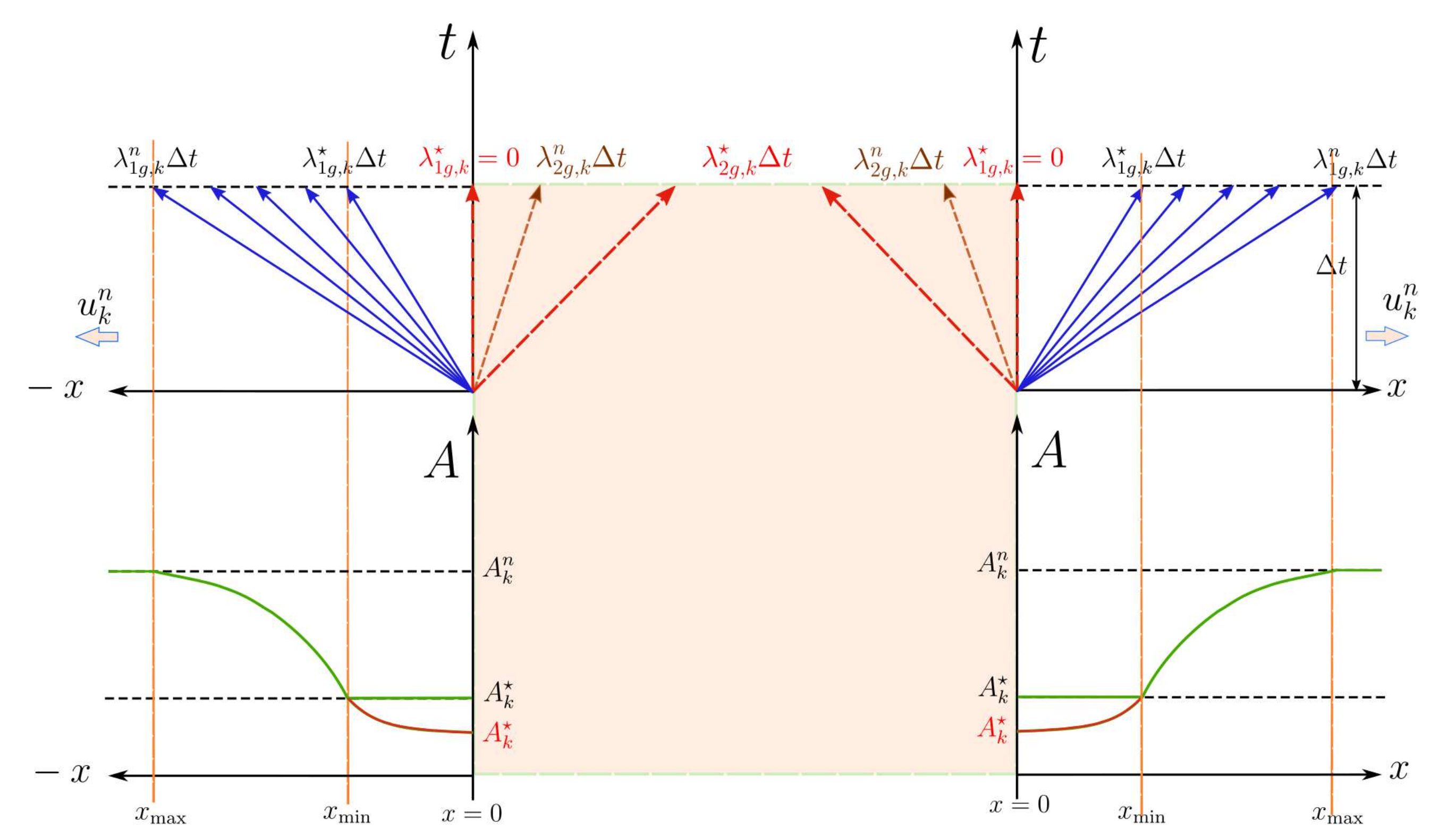
- If , at outflow boundary conditions:
- The acceleration/deceleration of the flow generated by a backward/forward wave can be imposed provided that the limiting value of flow in (62) is not exceeded, leading to a decompression wave (case A1).
- The deceleration/acceleration of the flow generated by a backward/forward wave can be imposed leading to a compression wave (case B1), and no sonic limitation appears.
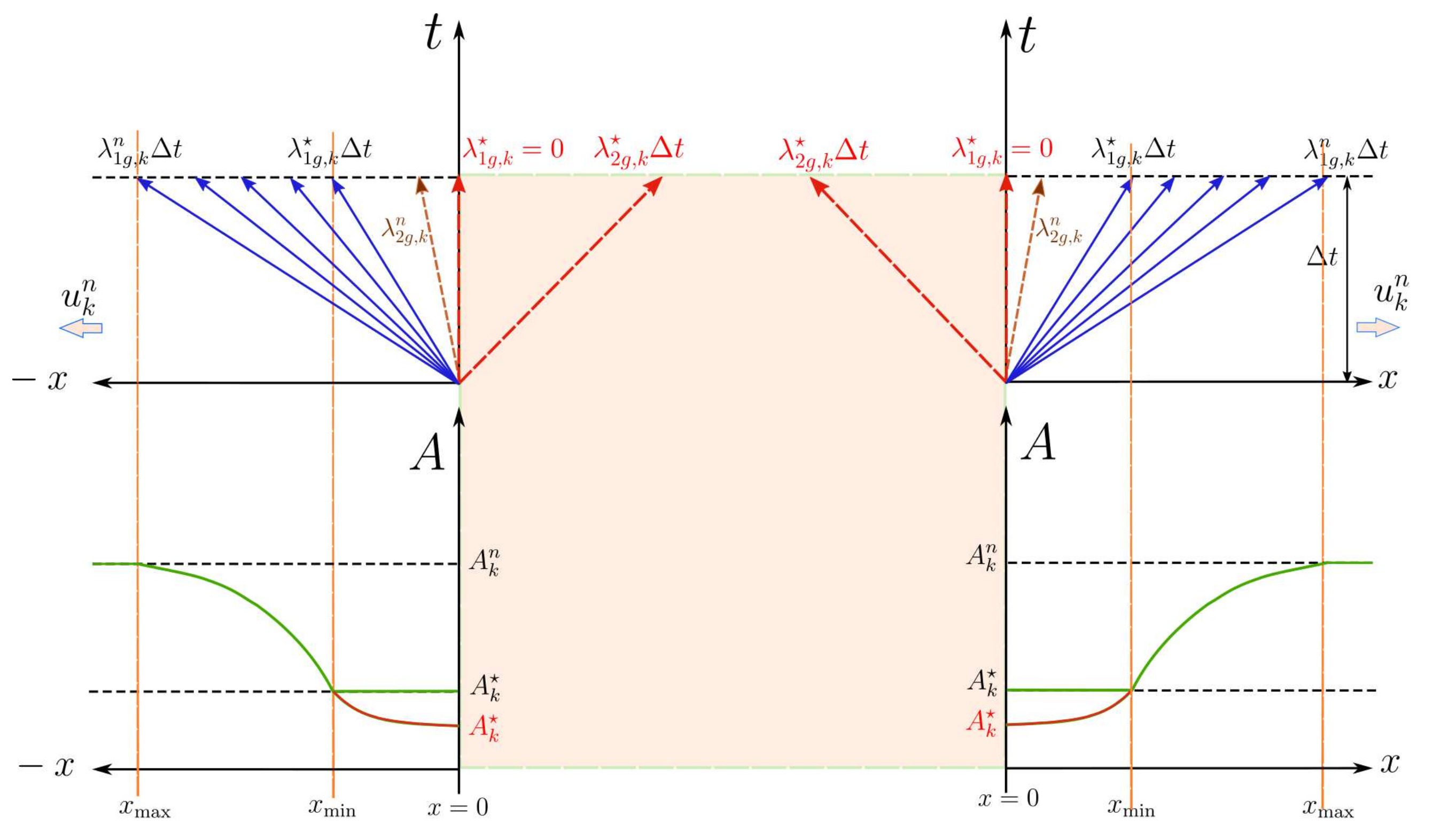
- If , at inflow boundary conditions:
- Flow deceleration/acceleration, generated by a backward/forward wave can be imposed leading to a compression wave (case C1).
- Flow acceleration/deceleration, generated by a backward/forward wave leads to a decompression wave. Flow at the boundary must by limited by the function in (63) (case D1).
- If , at outflow boundary conditions:
- The acceleration/deceleration of the flow cannot be imposed, as no information can arrive to the inner domain of the vessel (case A2), .
- The deceleration/acceleration of the flow, generated by a backward/forward wave can be imposed if leading to a compression wave with a suitable value of celerity (case B2), .
- If , in inflow boundary conditions:
- The deceleration/acceleration of the flow generated by a backward/forward wave can be imposed, leading to a compression wave, provided that both flow and area are imposed (case C2), .
- The deceleration of the flow can be imposed, leading to a decompression wave (case D2) limited by the function in (63).
- The target functions in system (55) must be redefined to ensure limitation of sonic flow in cases A1, D1 y D2.
- Unfeasible acceleration/deceleration, in supersonic outflow sections in case A2 must be avoided, the target functions in system (55) must be redefined to include this case.
- In case C2, involving a supersonic inflow section, both area and flow rate must be imposed. In this case, the system of equations in (55) is useless.
Initial Values and Relaxation Parameters
- if , the solution will be a rarefaction,
- if , the solution will be a shock.
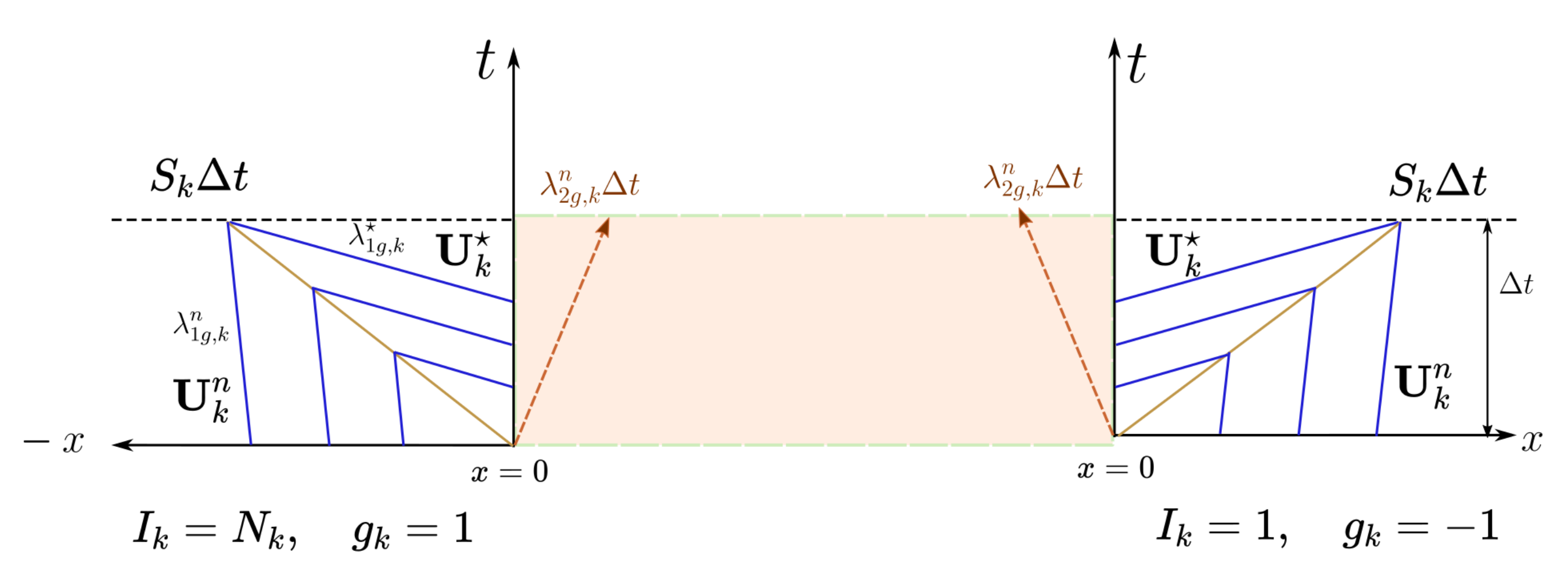
2.4. Solution of the JRP
2.4.1. Solution of the JRP under Subsonic Flow Conditions
2.4.2. Solution of the JRP under Subsonic and Supersonic Flow Conditions
Courant–Friedrichs–Lewy (CFL) Condition
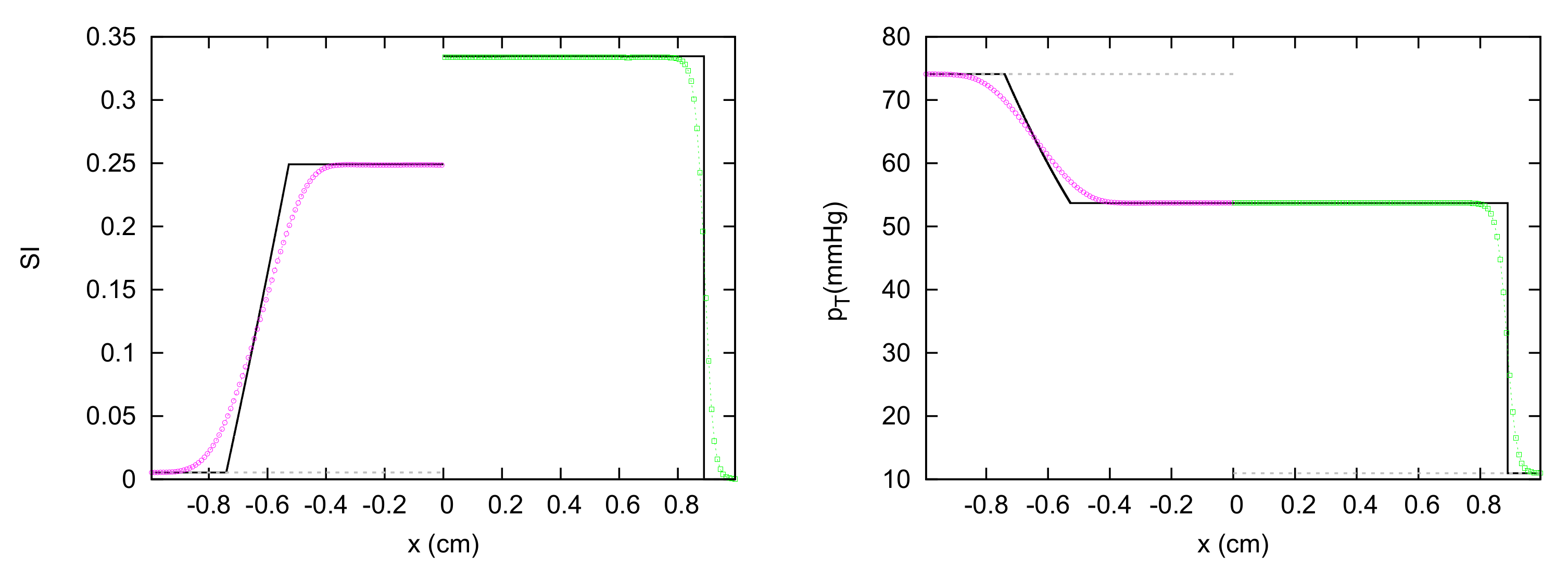
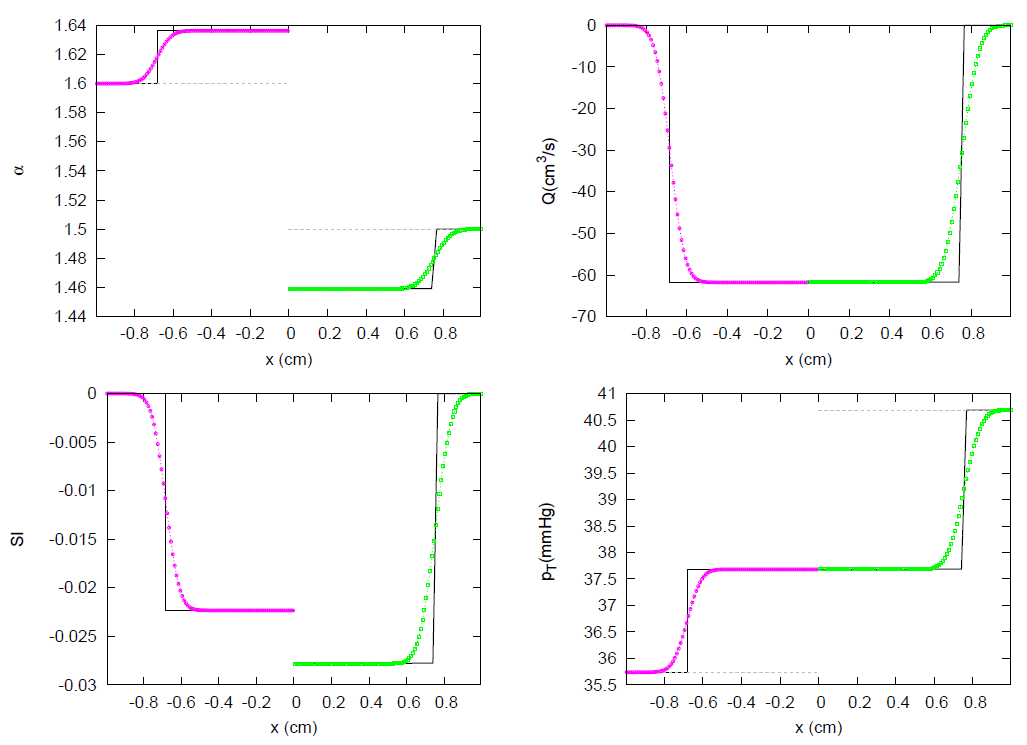
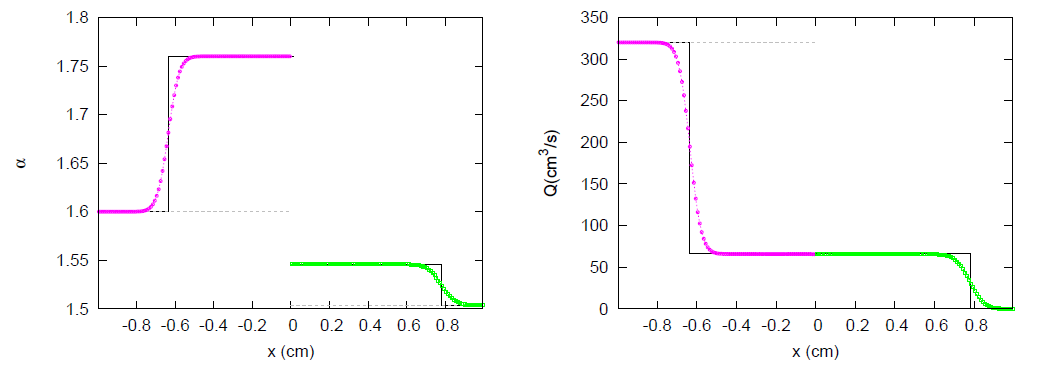
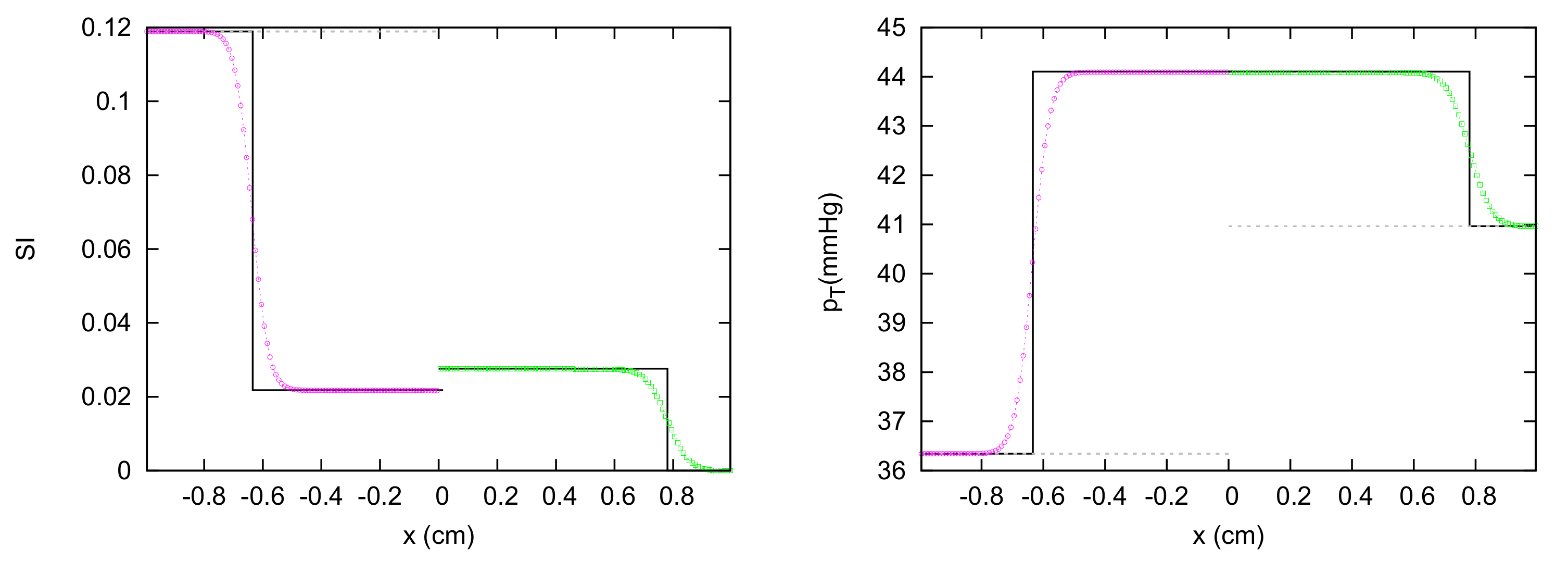
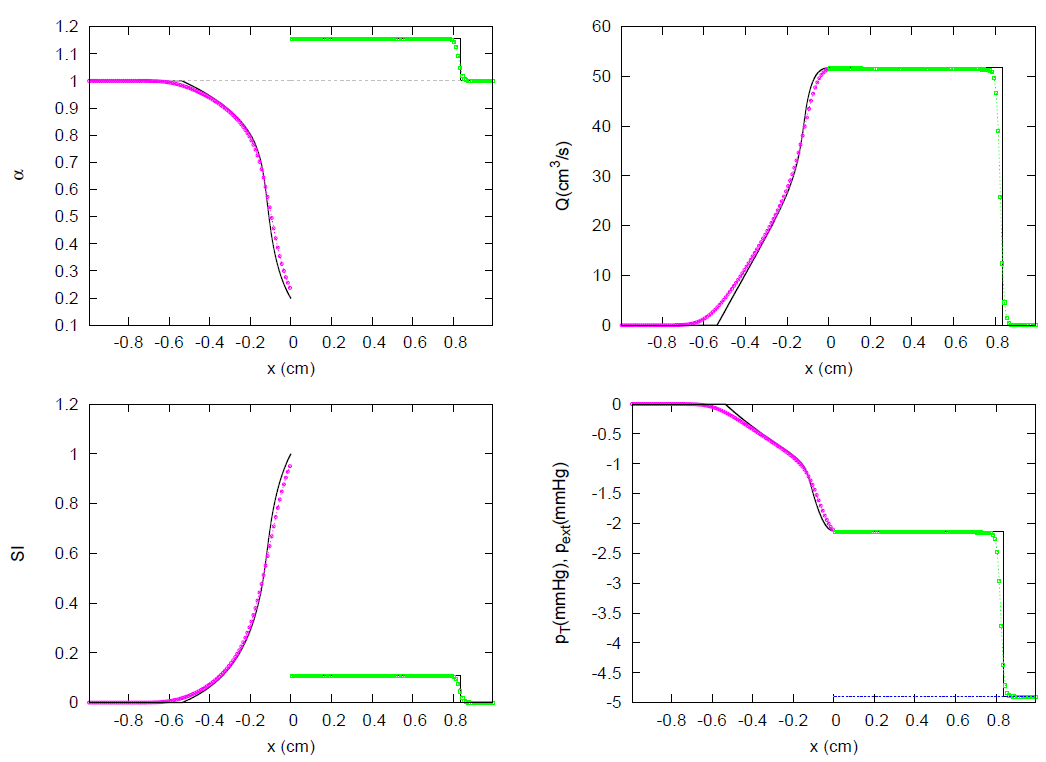
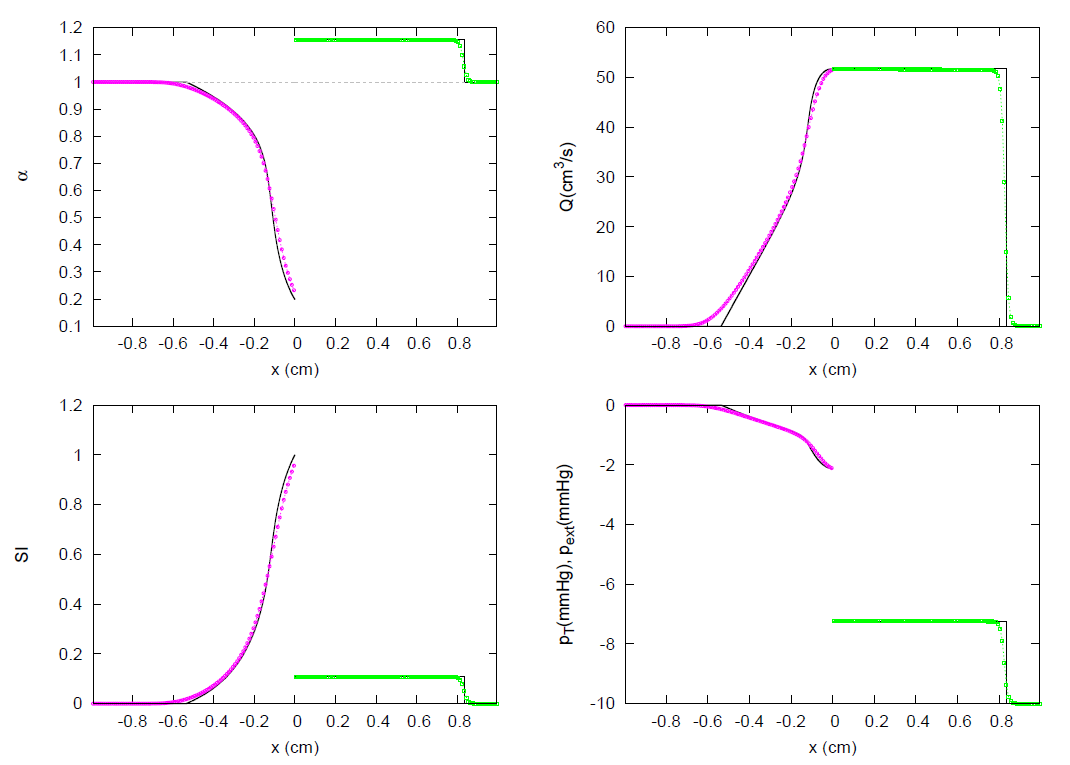
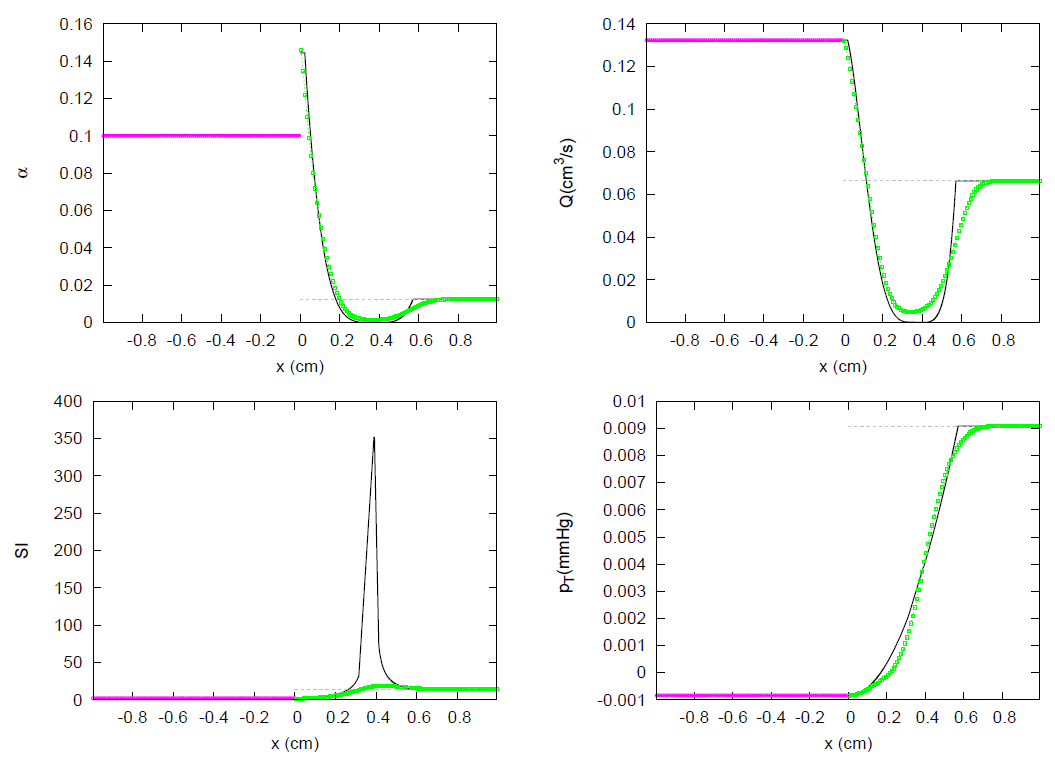
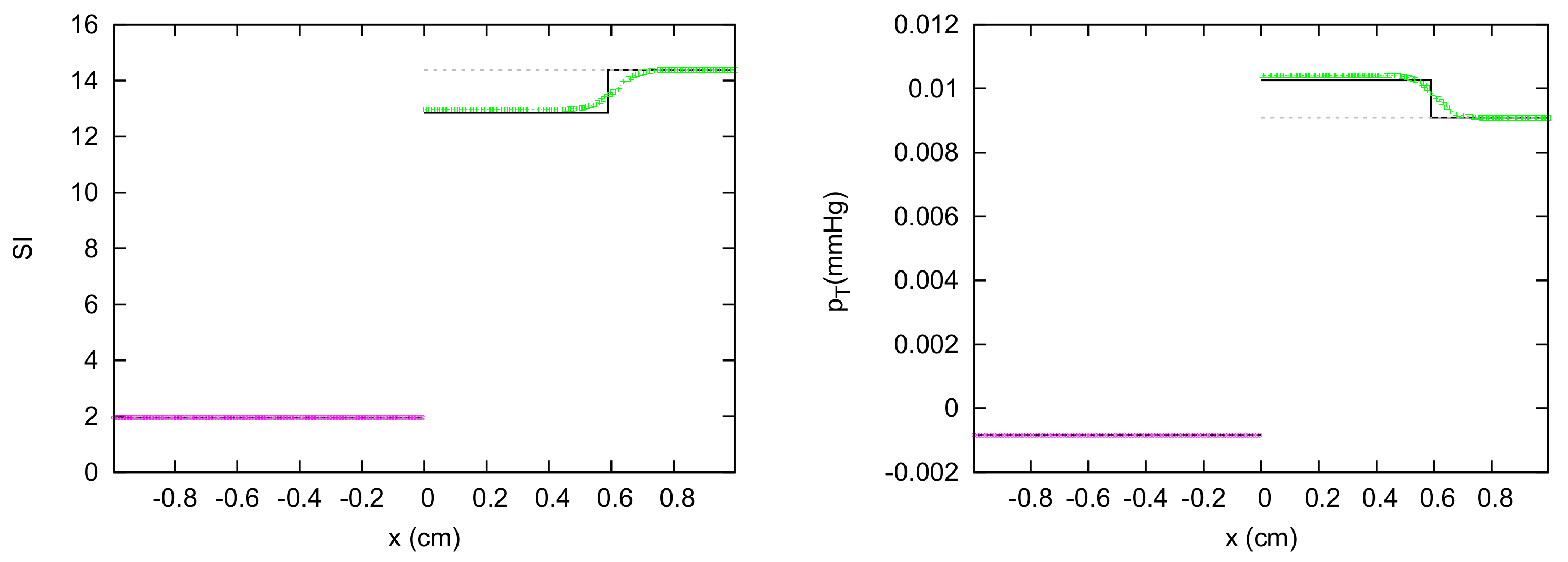
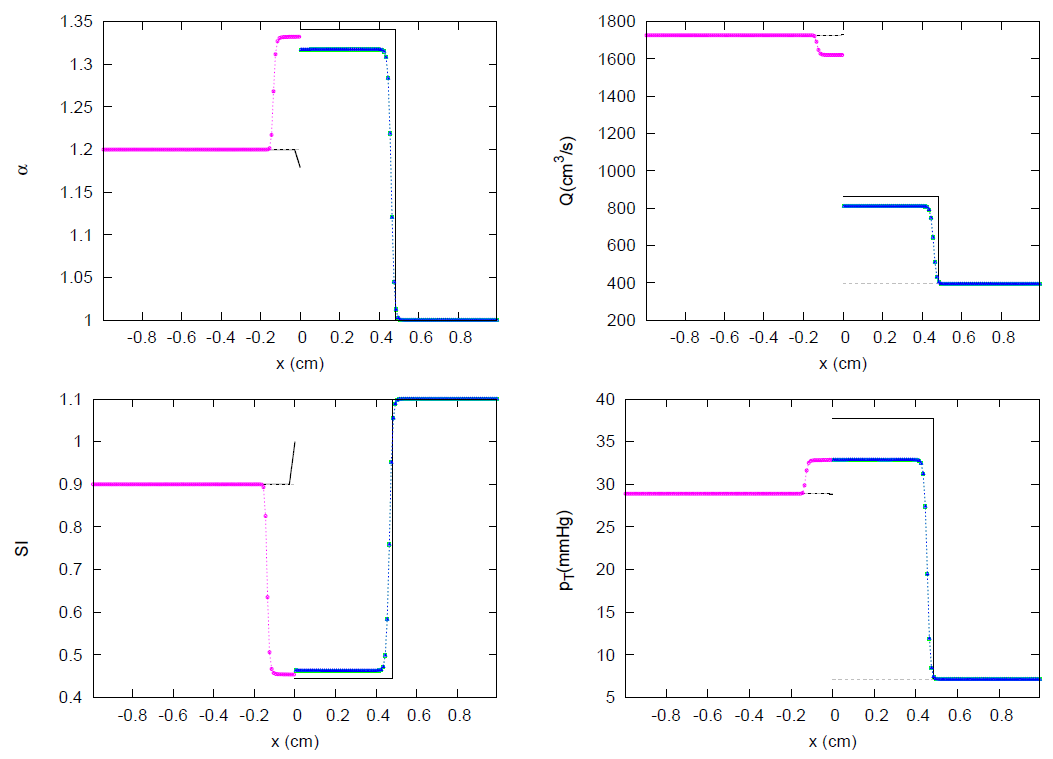
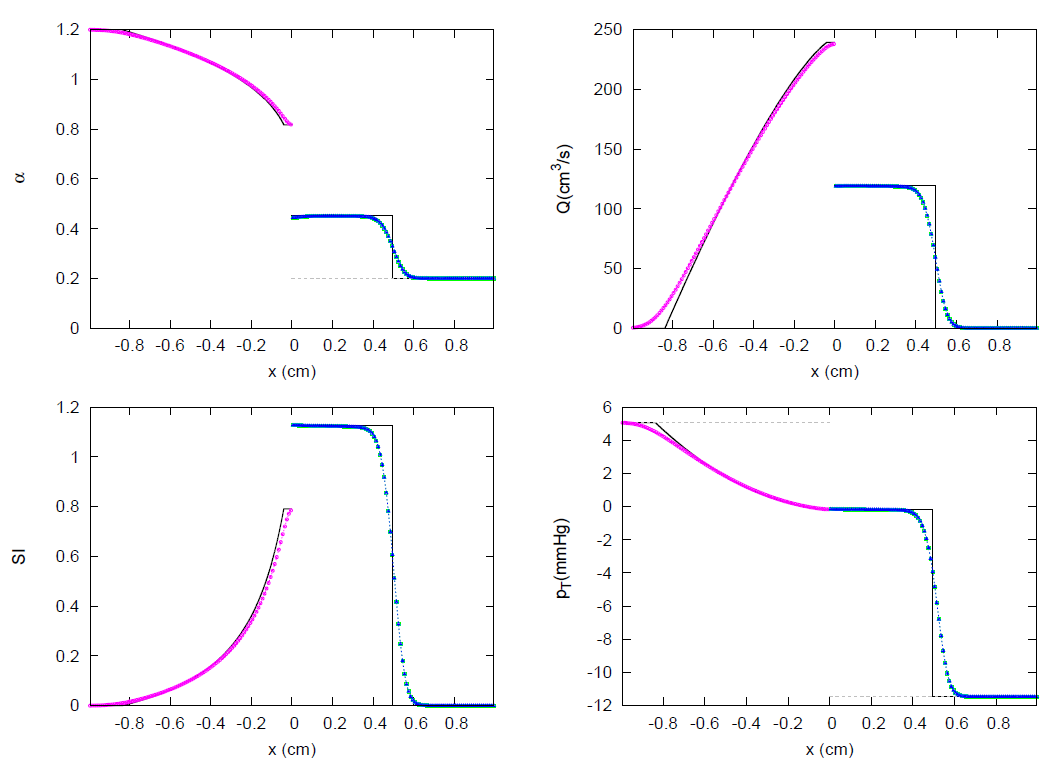
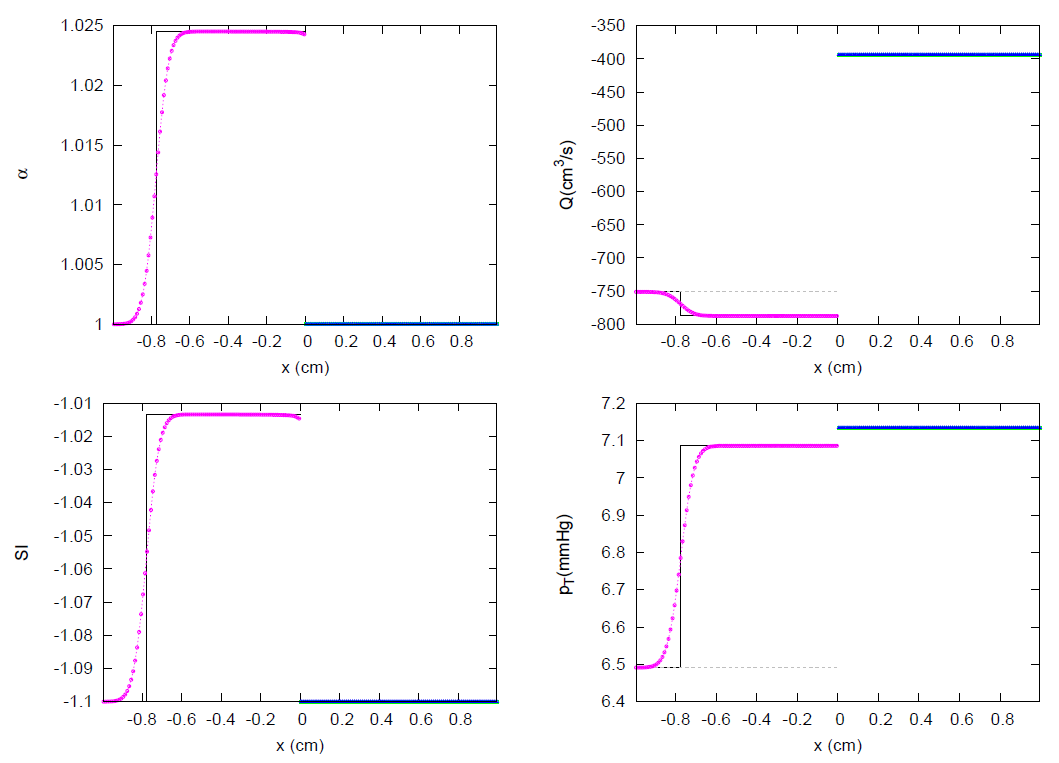
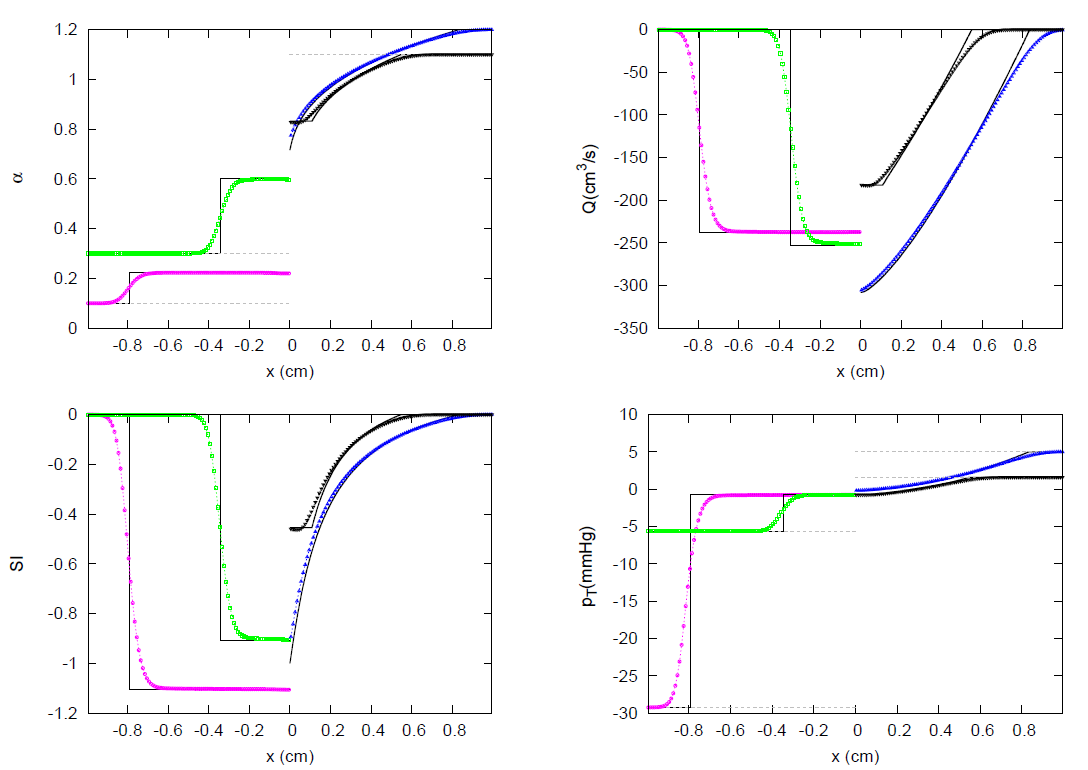
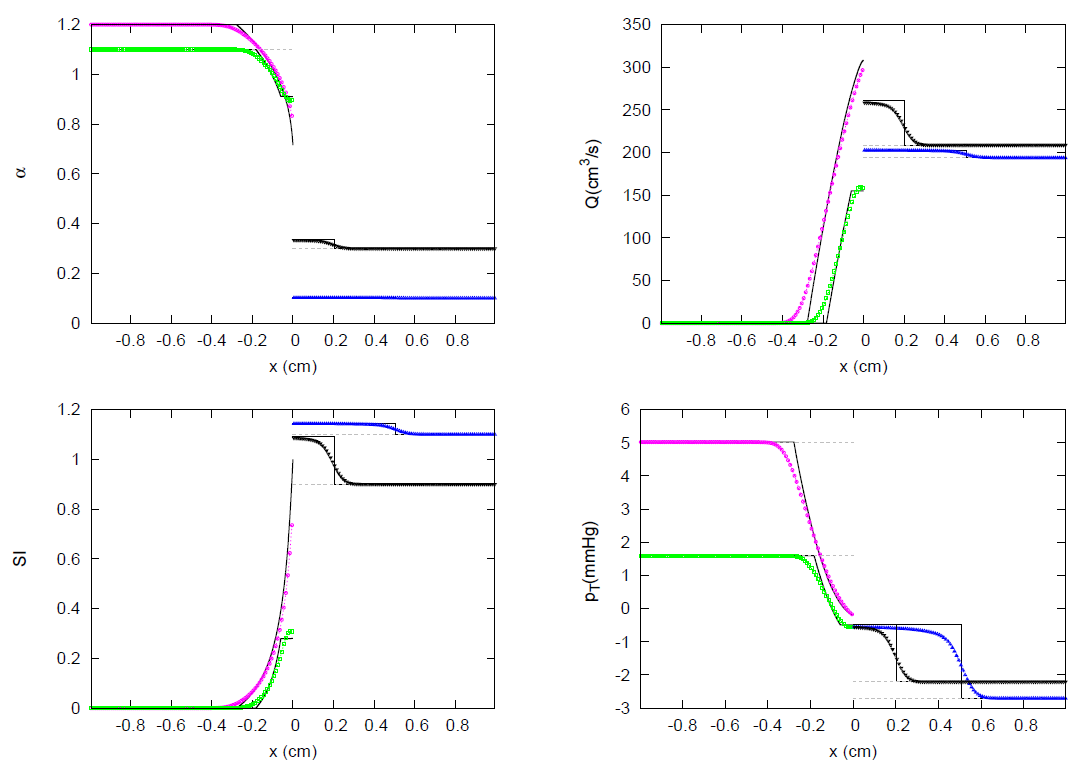
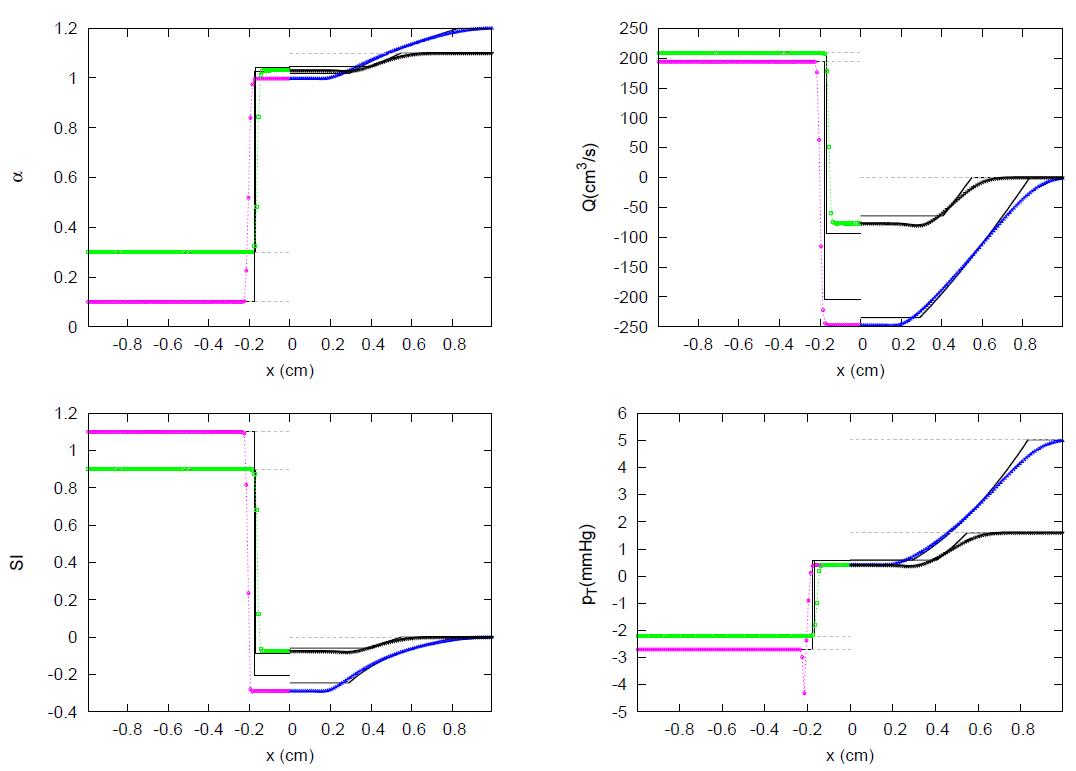
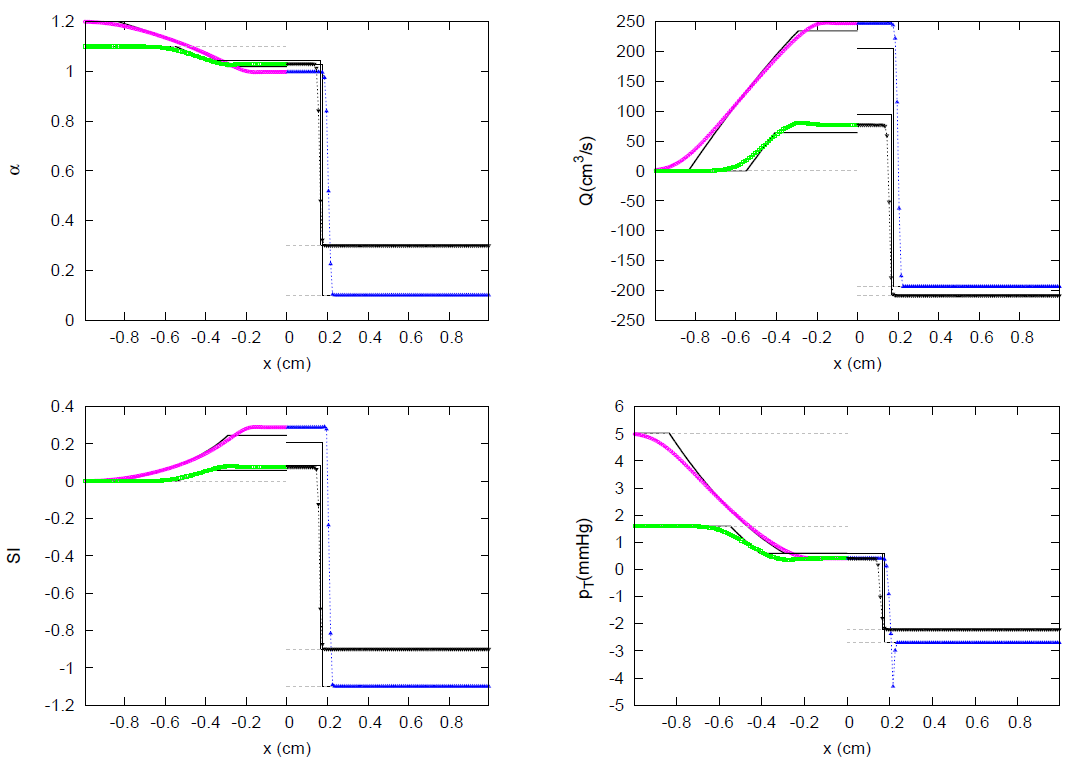
3. Results
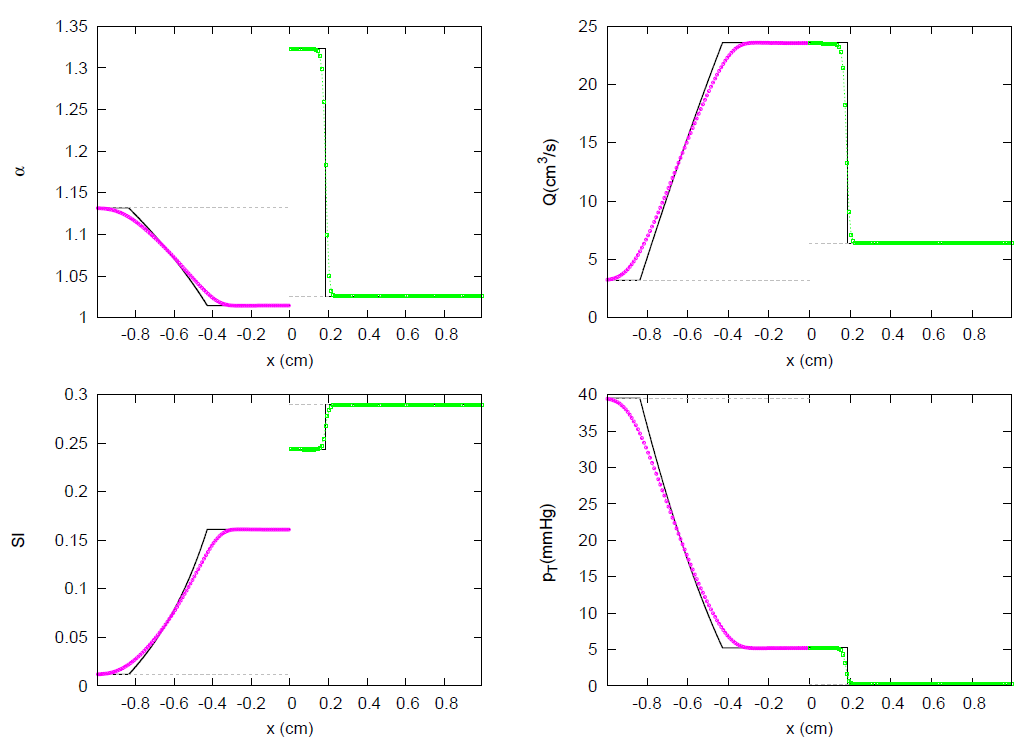
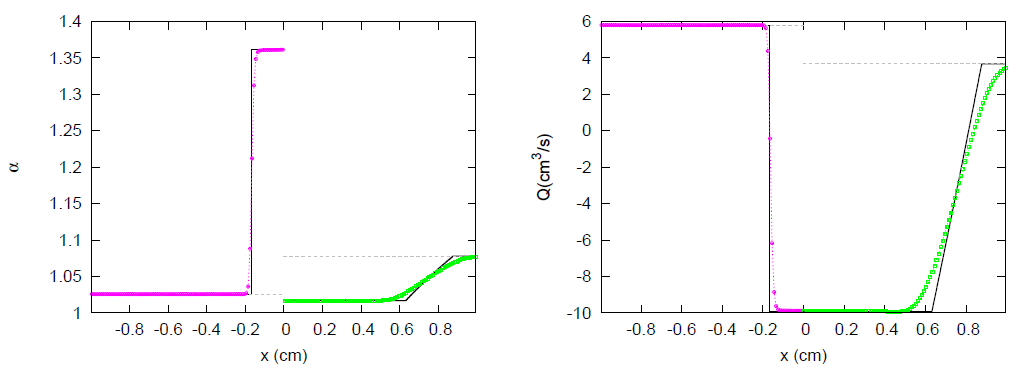
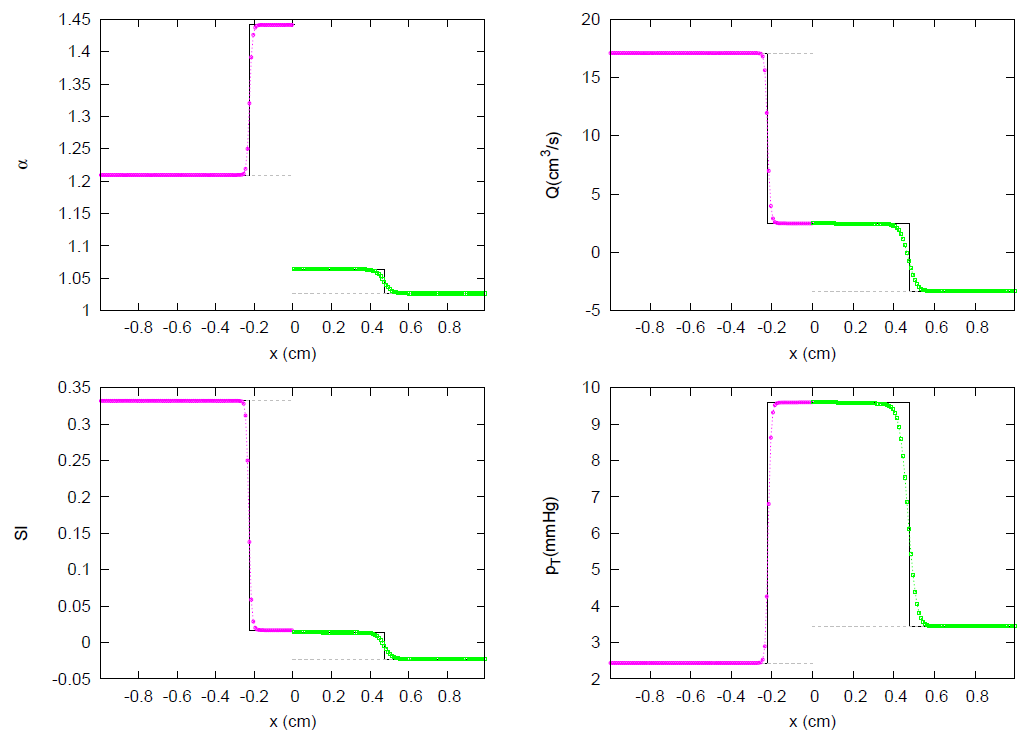
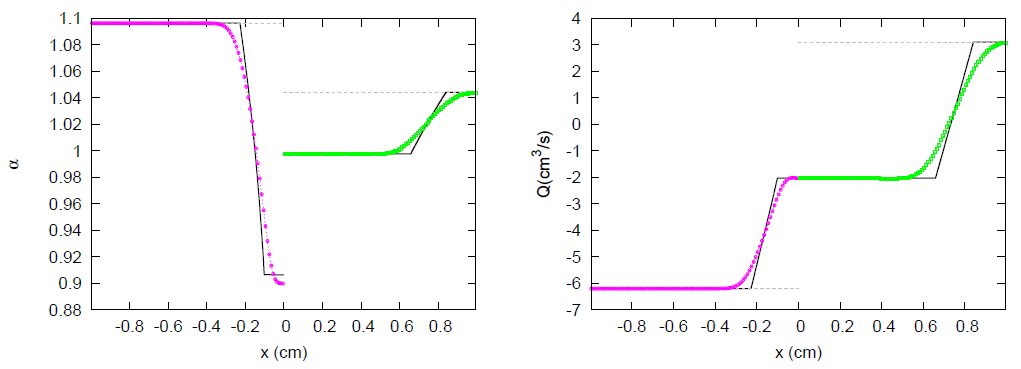
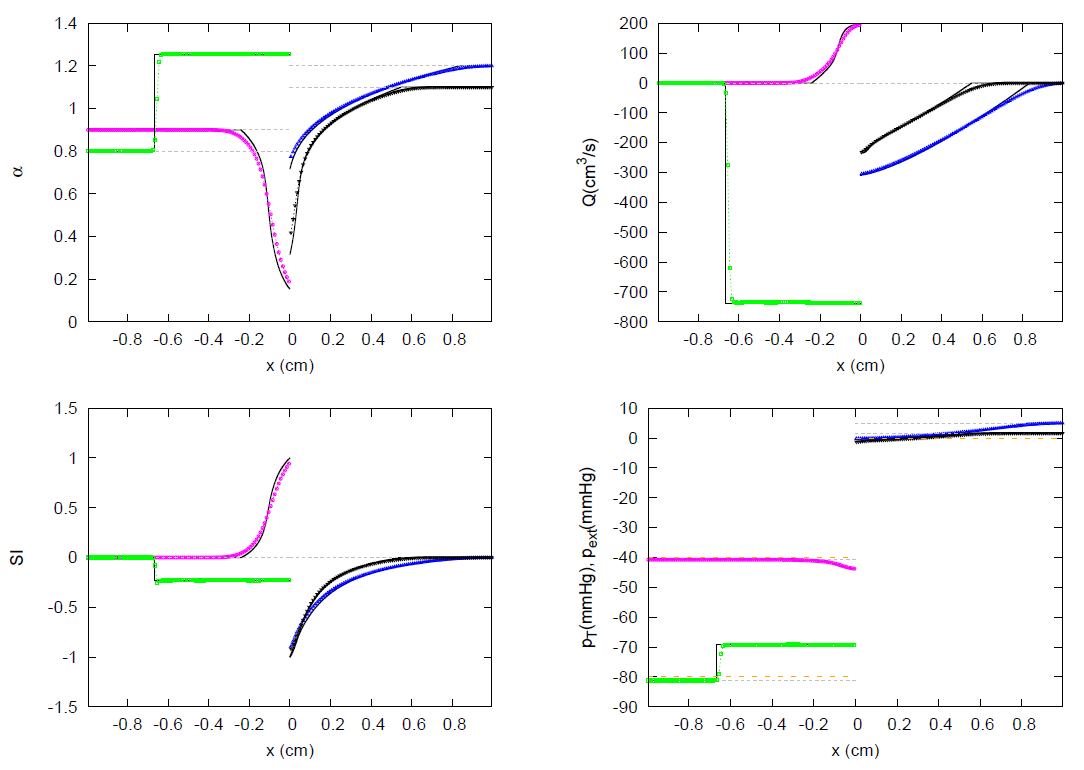
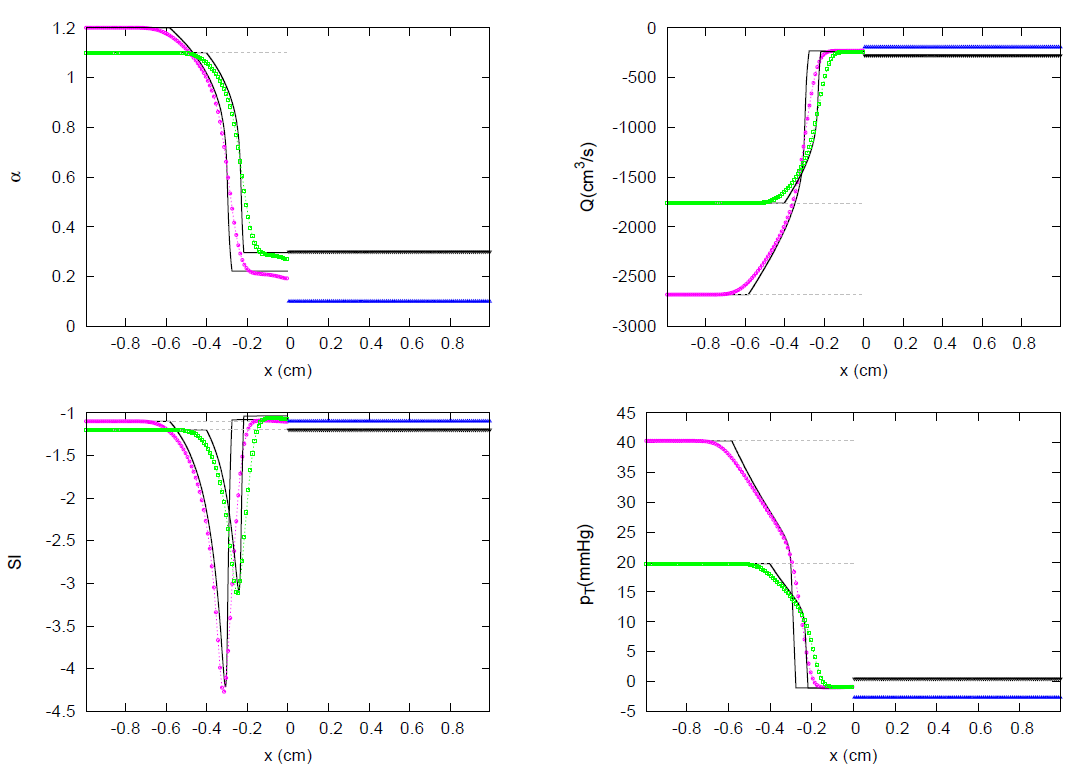
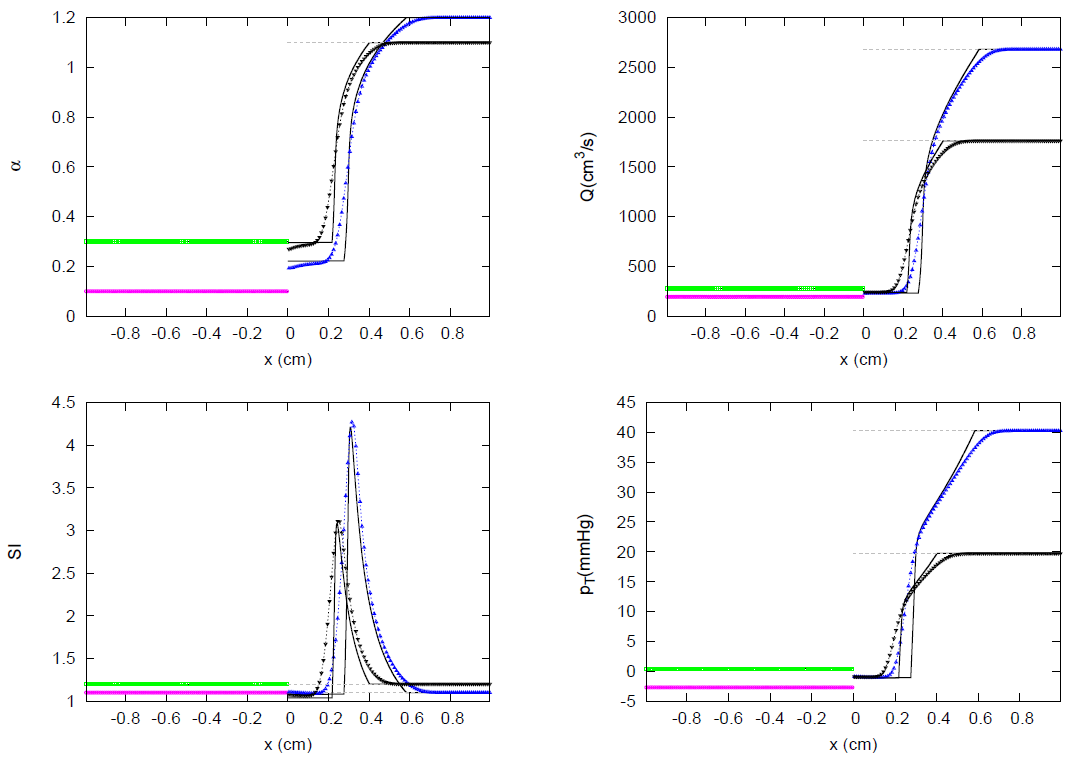
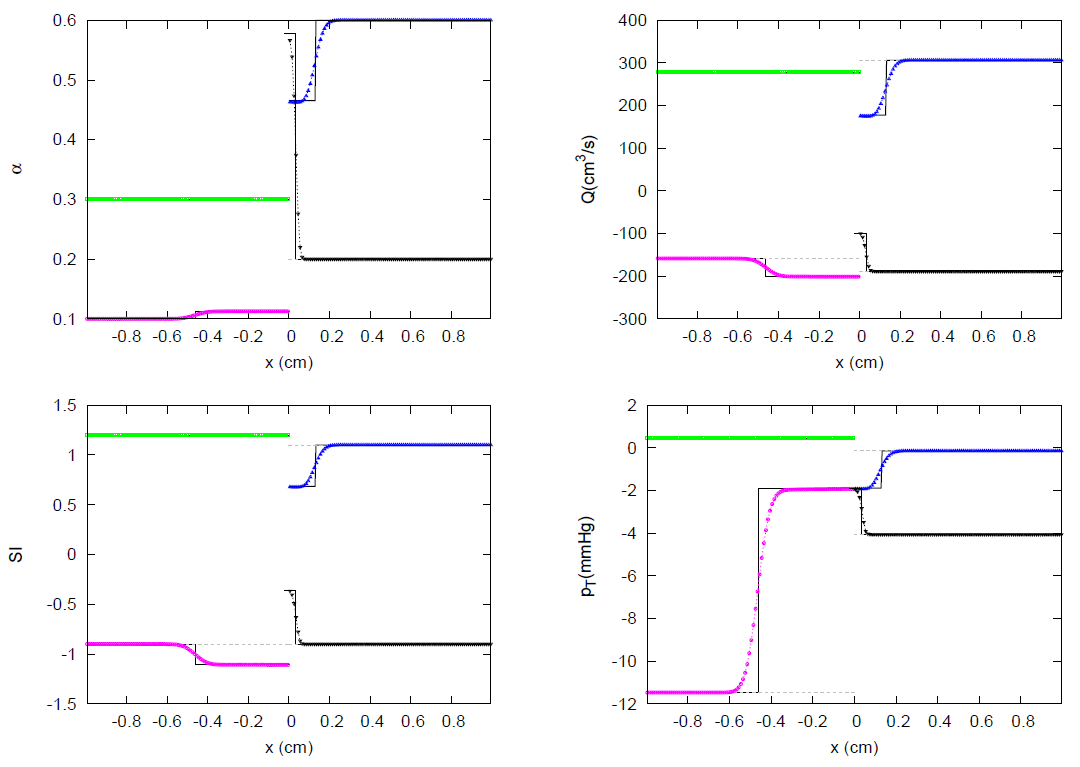
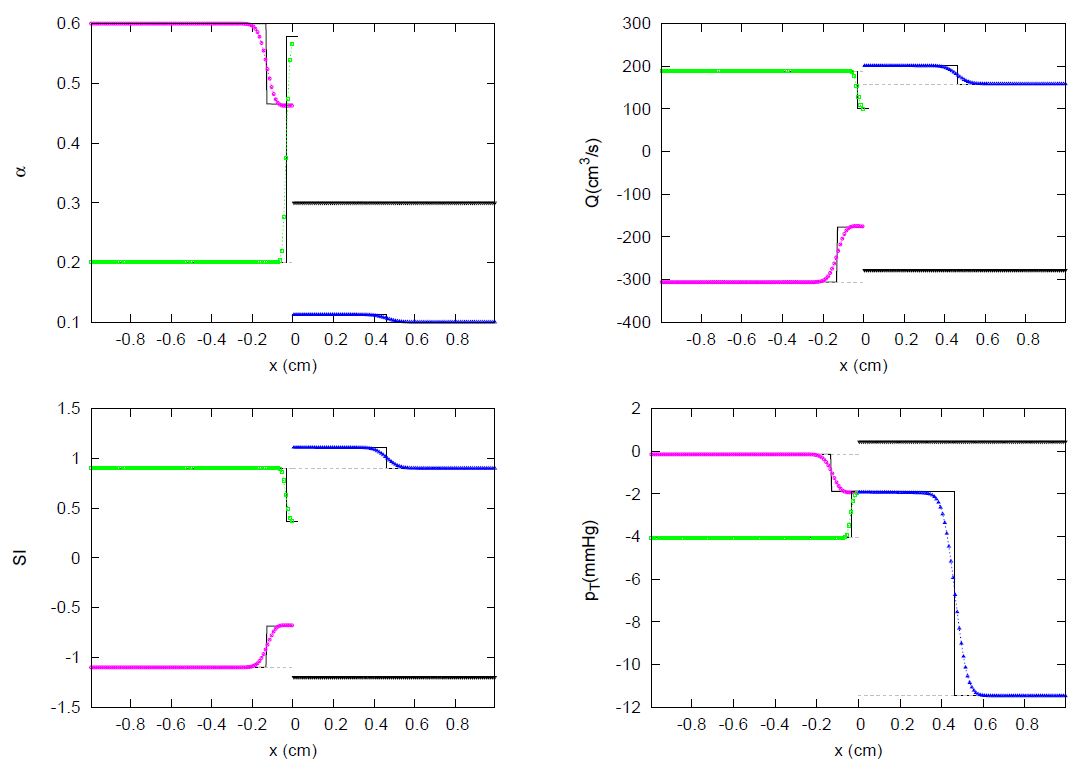
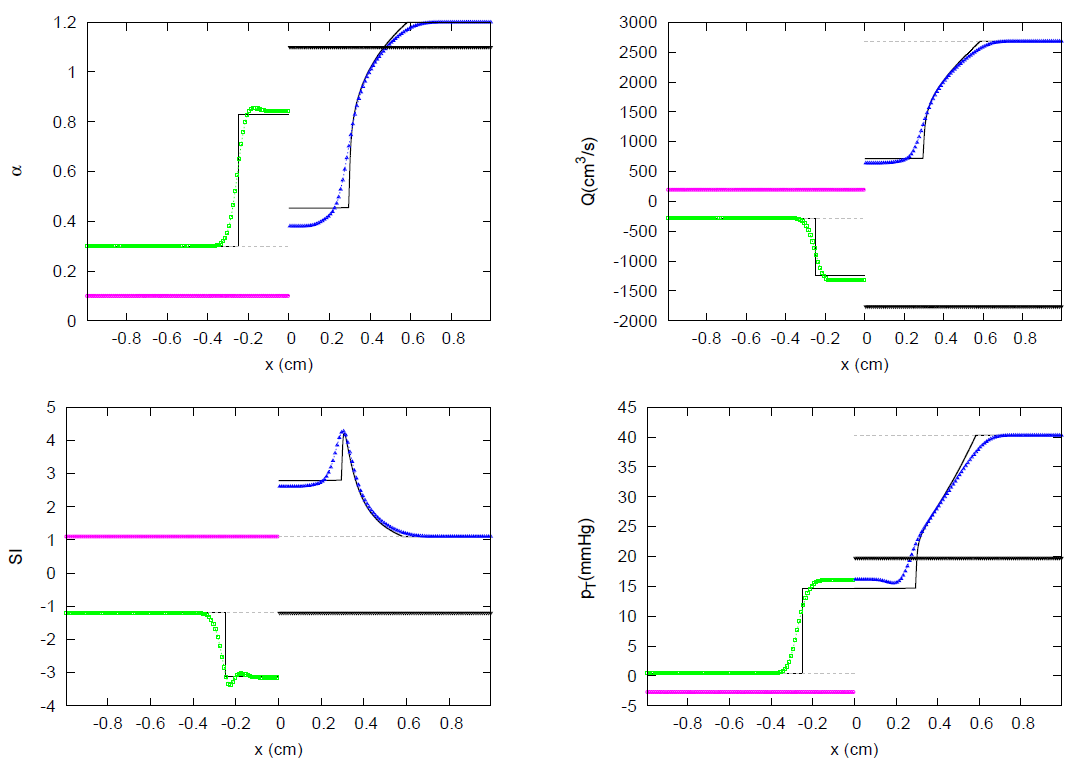
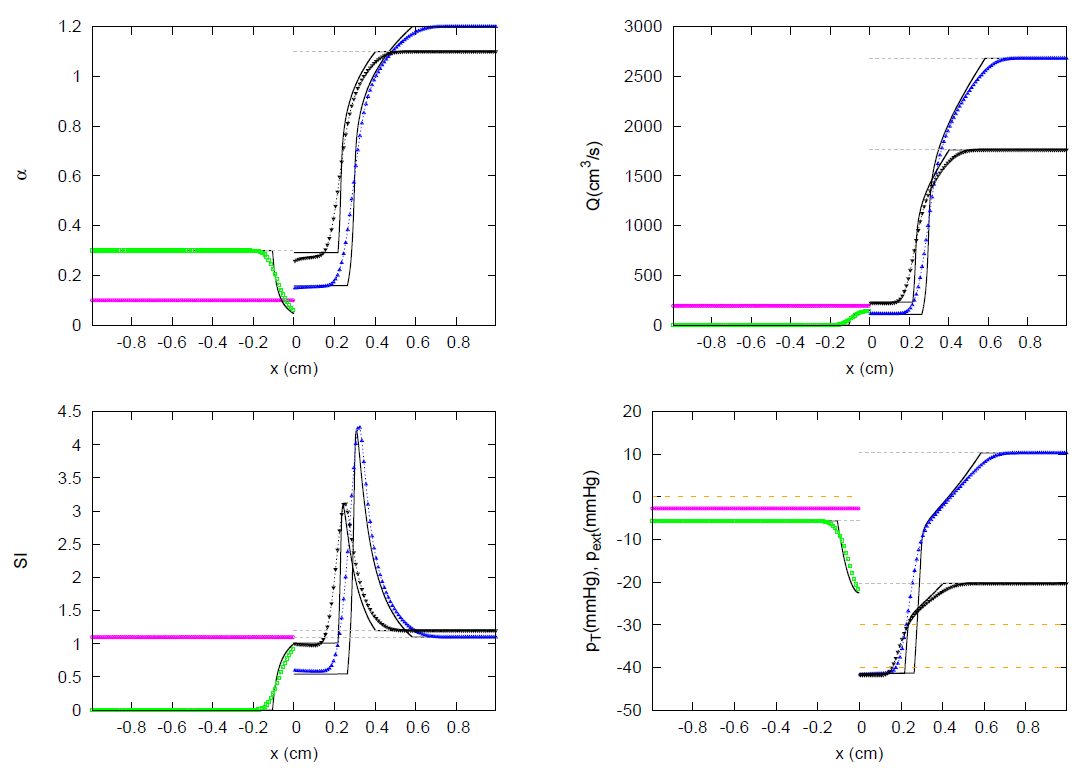
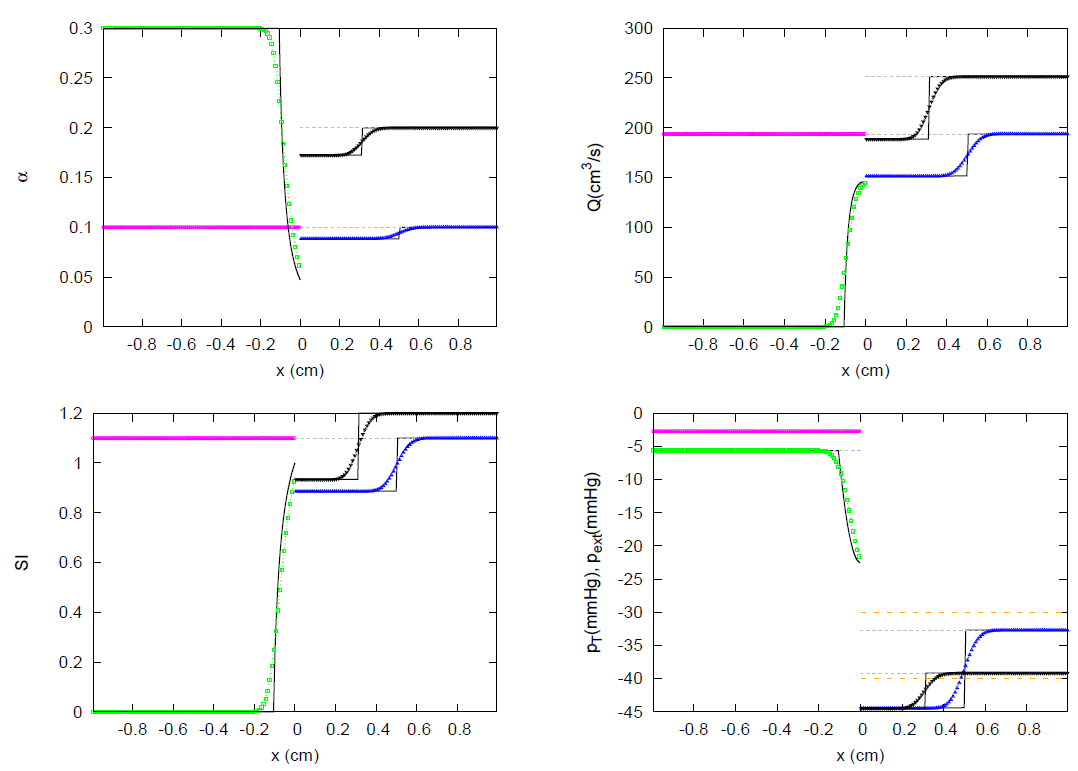
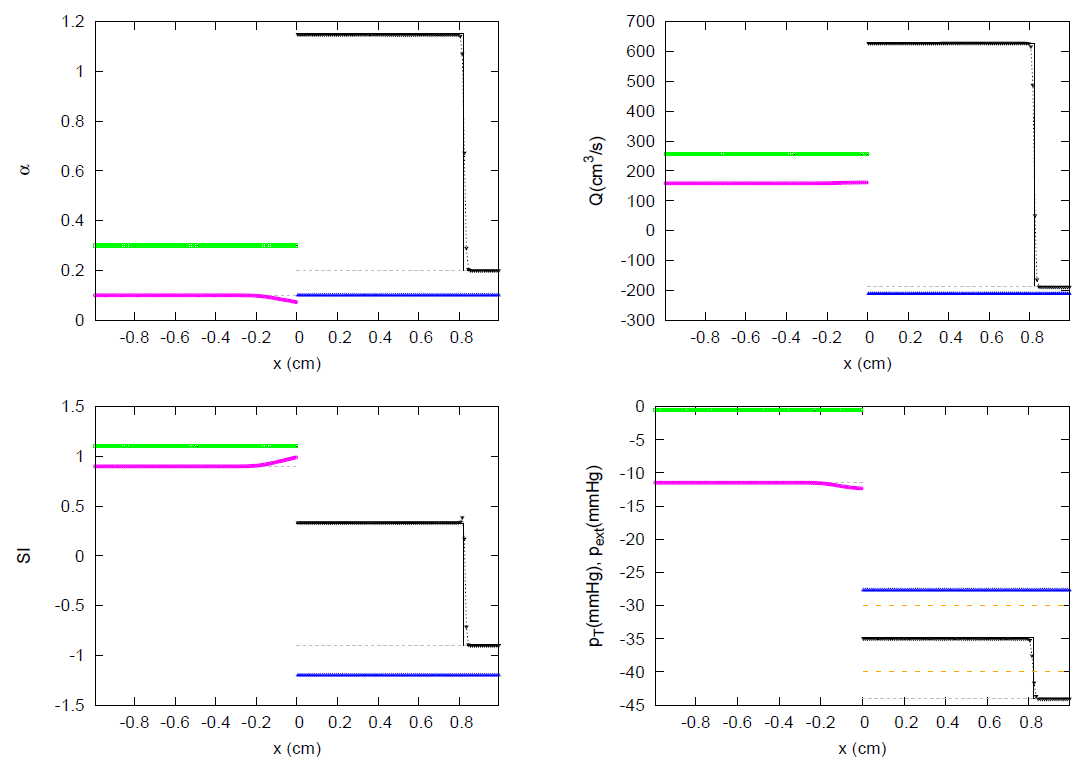
3.1. JRP with Two Vessels
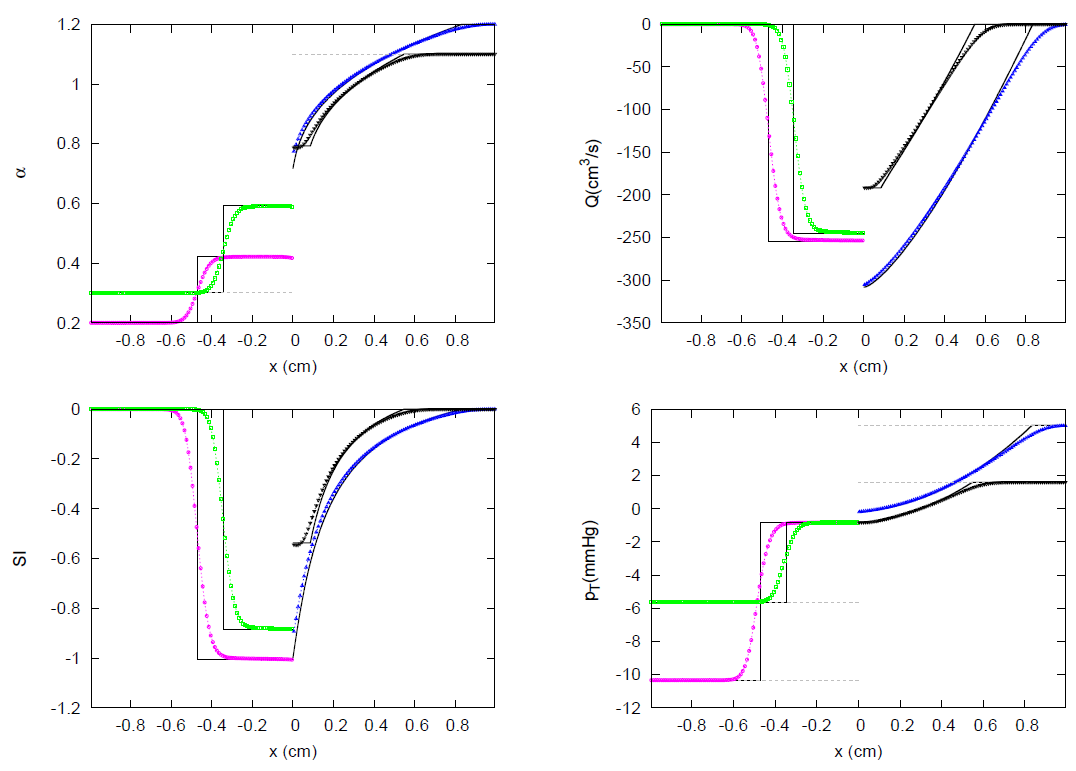
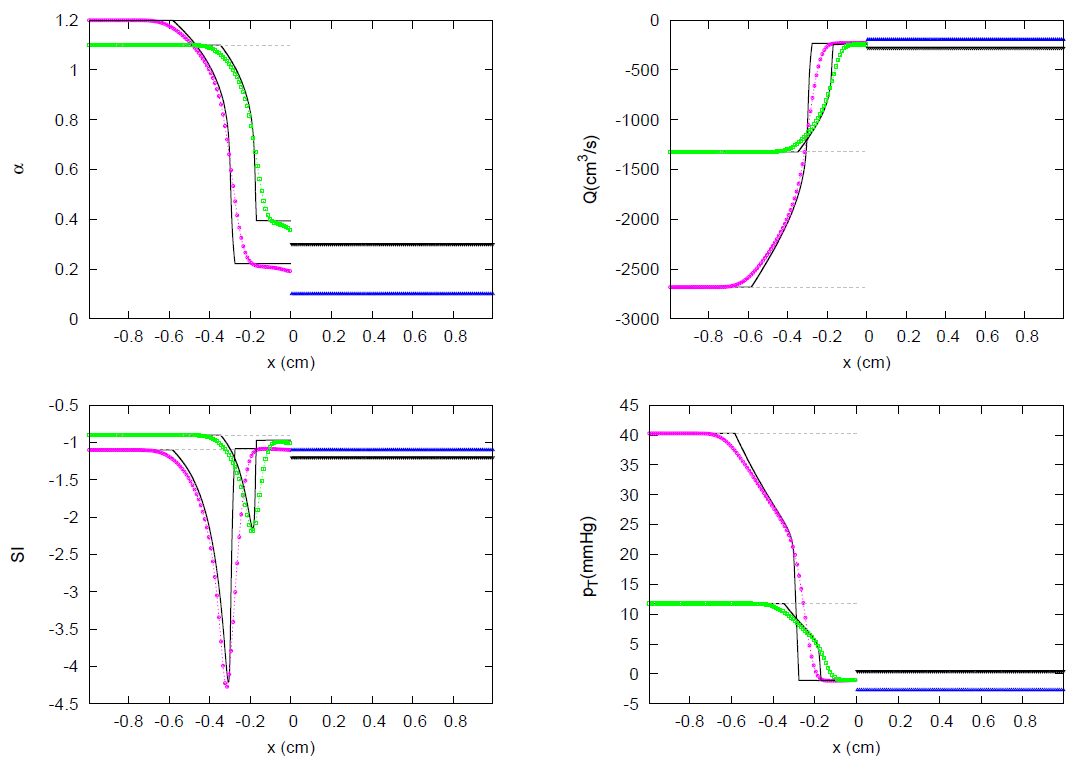
3.2. JRP with Three Vessels
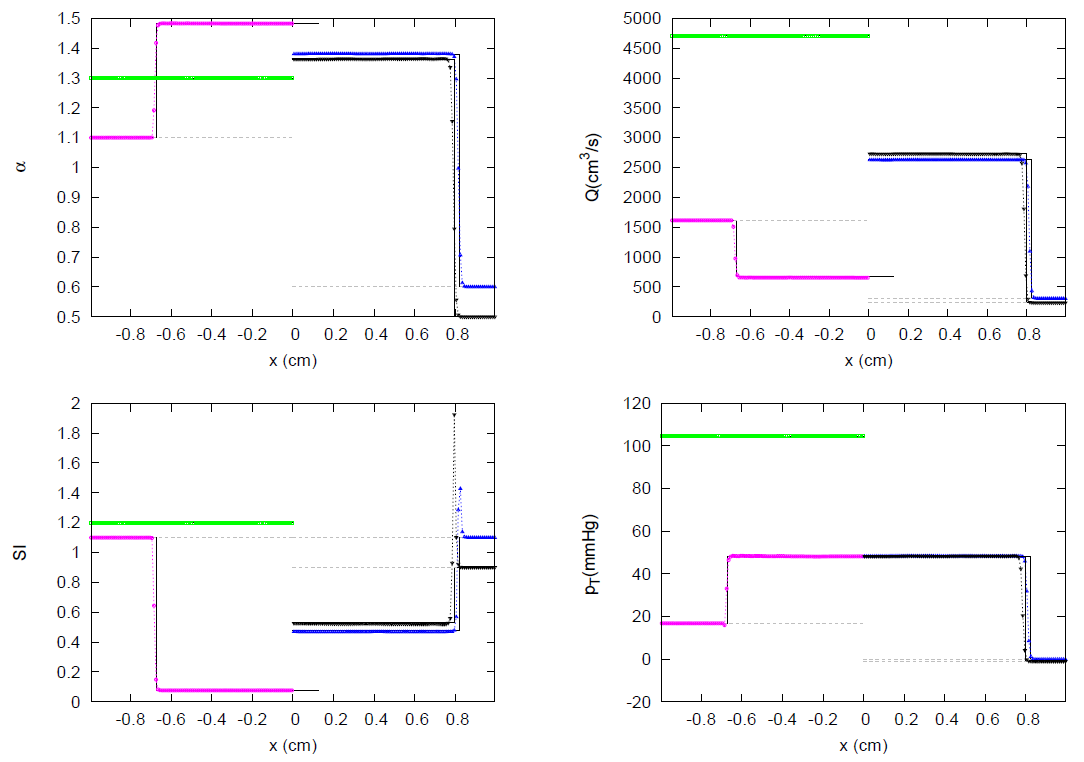
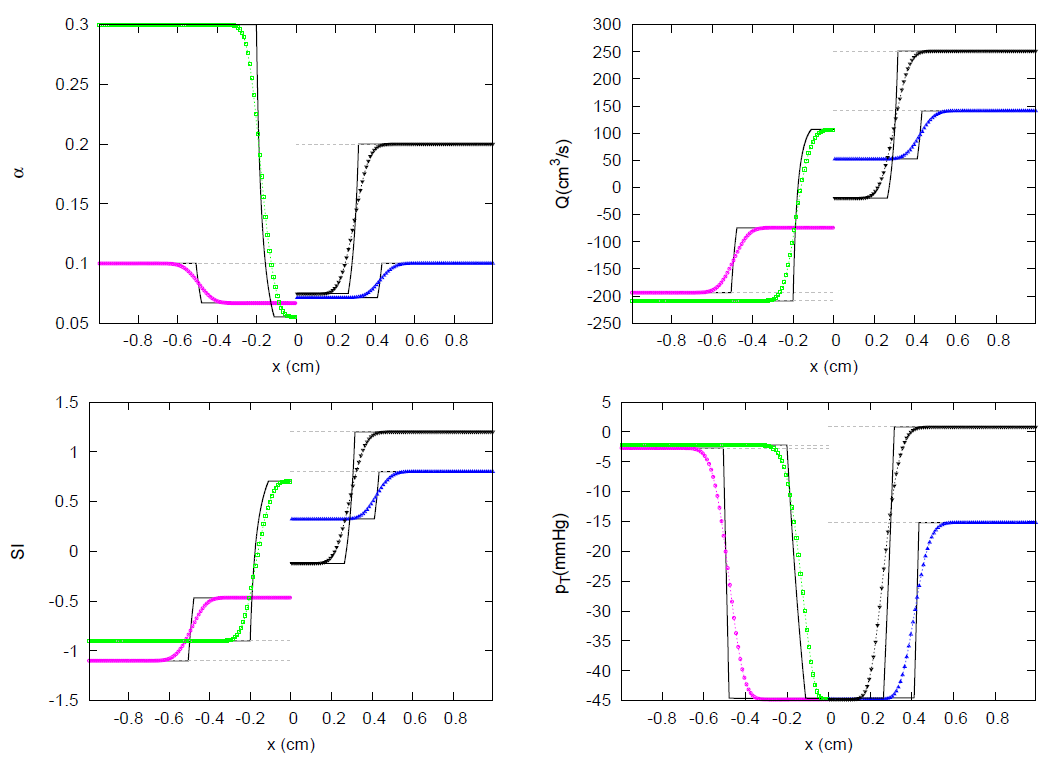
3.3. JRP with Four Vessels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Invariant Integration
- The domain of integration in is divided in divisions, of lenghtOver each division, a Gauss-Legendre quadrature is used to approximate the solution. In the Gauss quadrature rule, the most common domain of integration is taken as , so the rule is stated aswhich is exact for polynomials of degree or less. If a fifth order is selected (), three integration points are requiredwith their respective weightsThe integral over must be changed into an integral over a general interval for when applying the Gaussian quadrature rule, leading to
- Once an initial evaluation of is performed, , the number of divisions is doubled and the procedure is repeated to obtain new evaluation of . If the difference between these two approximations is sufficiently small,we assume that the last value is accurate enough and we proceed with the resolution of the system of equations. Otherwise, the number of divisions is doubled until the tolerance is reached.
References
- Bellamoli, F.; Müller, L.O.; Toro, E.F. A numerical method for junctions in networks of shallow-water channels. Appl. Math. Comput. 2018, 337, 190–213. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Parker, K. Wave propagation in a model of the arterial circulation. J. Biomech. 2004, 37, 457–470. [Google Scholar] [CrossRef]
- Xiao, N.; Alastruey, J.; Alberto Figueroa, C. A systematic comparison between 1-D and 3-D hemodynamics in compliant arterial models. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 204–231. [Google Scholar] [CrossRef] [Green Version]
- Morgan, P.; Parker, K. A mathematical model of flow through a collapsible tube—I. Model and steady flow results. J. Biomech. 1989, 22, 1263–1270. [Google Scholar] [CrossRef]
- Pedley, T.; Luo, X. Modelling flow and oscillations in collapsible tubes. Theor. Comput. Fluid Dyn. 1998, 10, 277–294. [Google Scholar] [CrossRef]
- Bassez, S.; Flaud, P.; Chauveau, M. Modeling of the deformation of flexible tubes using a single law: Application to veins of the lower limb in man. J. Biomech. Eng. 2001, 123, 58–65. [Google Scholar] [CrossRef]
- Marchandise, E.; Flaud, P. Accurate modelling of unsteady flows in collapsible tubes. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 279–290. [Google Scholar] [CrossRef]
- Ho, H.; Mithraratne, K.; Hunter, P. Numerical Simulation of Blood Flow in an Anatomically-Accurate Cerebral Venous Tree. IEEE Trans. Med. Imaging 2013, 32, 85–91. [Google Scholar] [CrossRef]
- Müller, L.O.; Toro, E.F. A global multiscale mathematical model for the human circulation with emphasis on the venous system. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 681–725. [Google Scholar] [CrossRef] [PubMed]
- Müller, L.O.; Toro, E.F. Enhanced global mathematical model for studying cerebral venous blood flow. J. Biomech. 2014, 47, 3361–3372. [Google Scholar] [CrossRef] [PubMed]
- Mynard, J.P.; Smolich, J.J. One-Dimensional Haemodynamic Modeling and Wave Dynamics in the Entire Adult Circulation. Ann. Biomed. Eng. 2015, 43, 1443–1460. [Google Scholar] [CrossRef]
- Elshobaki, M.; Valiani, A.; Caleffi, V. Numerical modelling of open channel junctions using the Riemann problem approach. J. Hydraul. Res. 2019, 57, 662–674. [Google Scholar] [CrossRef]
- Zhang, X.; Noda, S.; Himeno, R.; Liu, H. Gravitational effects on global hemodynamics in different postures: A closed-loop multiscale mathematical analysis. Acta Mech. Sin. 2017, 33, 595–618. [Google Scholar] [CrossRef]
- Sherwin, S.; Franke, V.; Peiró, J.; Parker, K. One-dimensional modelling of a vascular network in space-time variables. J. Eng. Math. 2003, 47, 217–250. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Formaggia, L.; Peiró, J.; Franke, V. Computational modelling of 1D blood flow with variable mechanical properties and its application to the simulation of wave propagation in the human arterial system. Int. J. Numer. Methods Fluids 2003, 43, 673–700. [Google Scholar] [CrossRef]
- Joseph, E. Flaherty, J.B.K.; Rubinow, S.I. Post Buckling Behavior of Elastic Tubes and Rings with Opposite Sides in Contact. SIAM J. Appl. Math. 1972, 23, 446–455. [Google Scholar] [CrossRef]
- Elad, D.; Katz, D.; Kimmel, E.; Einav, S. Numerical schemes for unsteady fluid flow through collapsible tubes. J. Biomed. Eng. 1991, 13, 10–18. [Google Scholar] [CrossRef]
- Brook, B.; Pedley, T. A model for time-dependent flow in (giraffe jugular) veins: Uniform tube properties. J. Biomech. 2002, 35, 95–107. [Google Scholar] [CrossRef]
- Quarteroni, A.; Formaggia, L. Mathematical Modelling and Numerical Simulation of the Cardiovascular System. In Computational Models for the Human Body; Elsevier: Amsterdam, The Netherlands, 2004; Volume 12, pp. 3–127. [Google Scholar] [CrossRef]
- Miglio, E.; Perotto, S.; Saleri, F. Model coupling techniques for free-surface flow problems: Part I. Nonlinear Anal. Theory Methods Appl. 2005, 63, e1885–e1896. [Google Scholar] [CrossRef]
- Bermúdez, A.; López, X.; Vázquez-Cendón, M.E. Treating network junctions in finite volume solution of transient gas flow models. J. Comput. Phys. 2017, 344, 187–209. [Google Scholar] [CrossRef]
- Fullana, J.M.; Zaleski, S. A branched one-dimensional model of vessel networks. J. Fluid Mech. 2009, 621, 183–204. [Google Scholar] [CrossRef]
- Huang, P.G.; Muller, L.O. Simulation of one-dimensional blood flow in networks of human vessels using a novel TVD scheme. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02701. [Google Scholar] [CrossRef]
- Müller, L.O.; Blanco, P.J. A high order approximation of hyperbolic conservation laws in networks: Application to one-dimensional blood flow. J. Comput. Phys. 2015, 300, 423–437. [Google Scholar] [CrossRef]
- Toro, E.F.; Siviglia, A. Flow in Collapsible Tubes with Discontinuous Mechanical Properties: Mathematical Model and Exact Solutions. Commun. Comput. Phys. 2013, 13, 361–385. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Murillo, J.; García-Navarro, P. Augmented versions of the HLL and HLLC Riemann solvers including source terms in one and two dimensions for shallow flow applications. J. Comput. Phys. 2012, 231, 6861–6906. [Google Scholar] [CrossRef]
- Murillo, J.; Navas-Montilla, A.; García-Navarro, P. Formulation of exactly balanced solvers for blood flow in elastic vessels and their application to collapsed states. Comput. Fluids 2019, 186, 74–98. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; Leer, B.V. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. A Roe type energy balanced solver for 1D arterial blood flow and transport. Comput. Fluids 2015, 117, 149–167. [Google Scholar] [CrossRef]
- LeVeque, R.J. Balancing Source Terms and Flux Gradients in High-Resolution Godunov Methods: The Quasi-Steady Wave-Propagation Algorithm. J. Comput. Phys. 1998, 146, 346–365. [Google Scholar] [CrossRef] [Green Version]
- LeVeque, R.J. Finite-Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Energy balance numerical schemes for shallow water equations with discontinuous topography. J. Comput. Phys. 2013, 236, 119–142. [Google Scholar] [CrossRef]
- Thompson, K.W. Time-dependent boundary conditions for hyperbolic systems, II. J. Comput. Phys. 1990, 89, 439–461. [Google Scholar] [CrossRef]




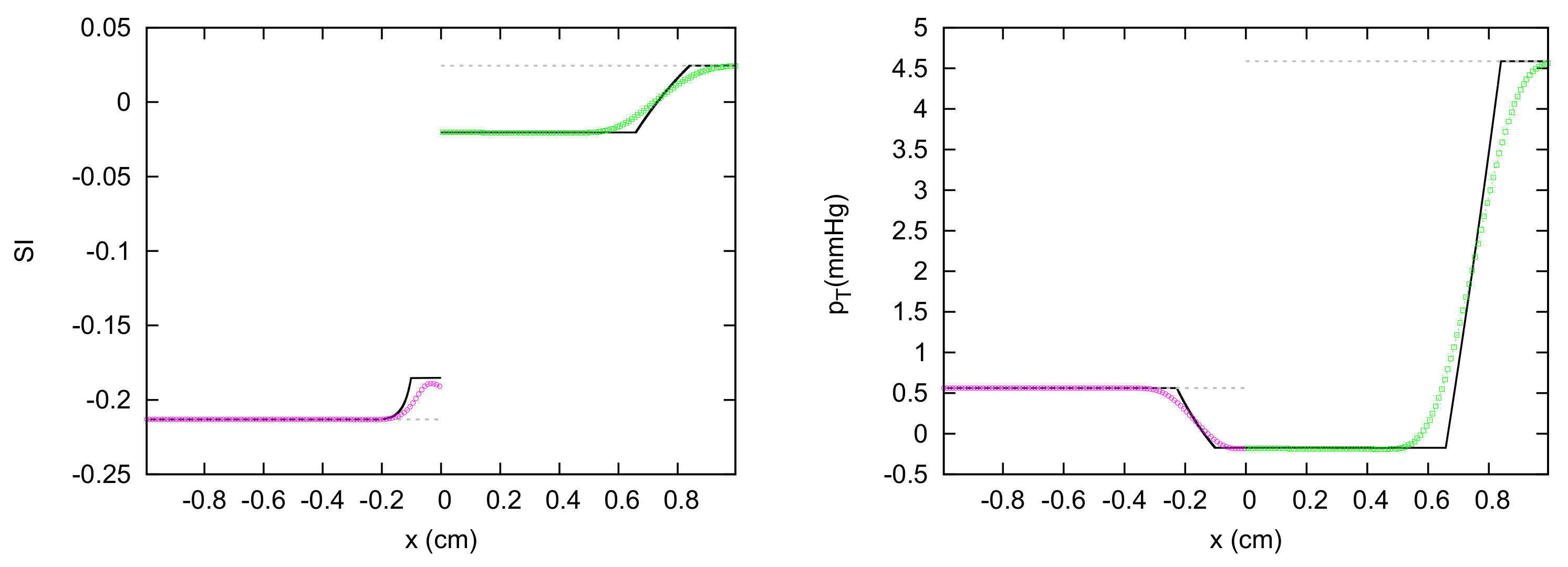
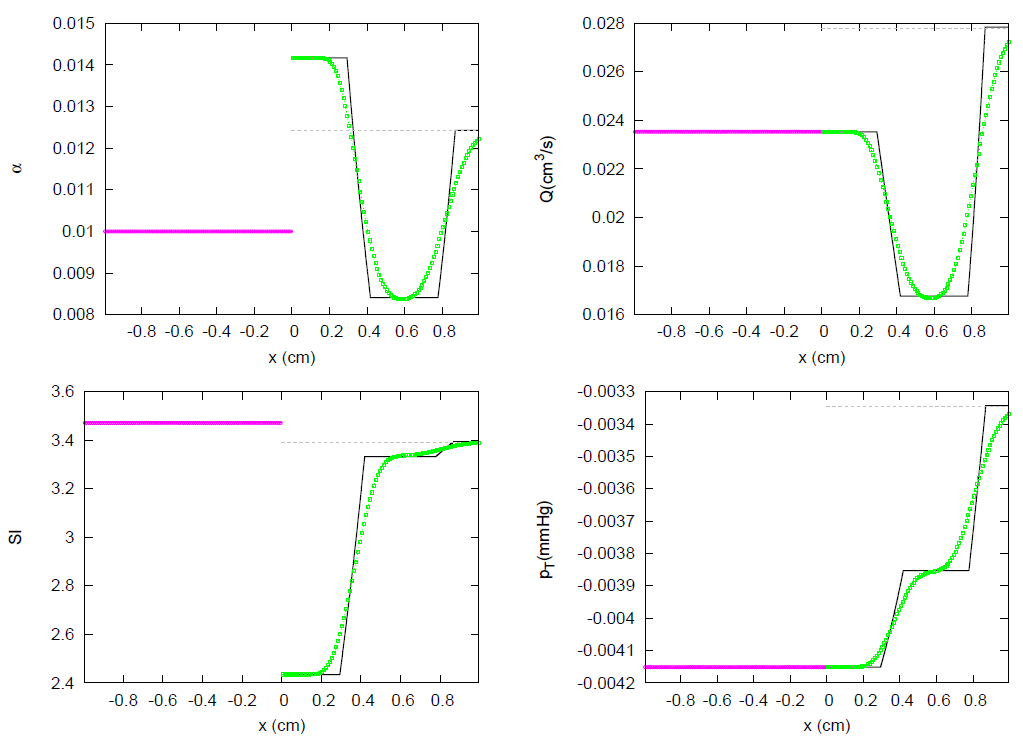

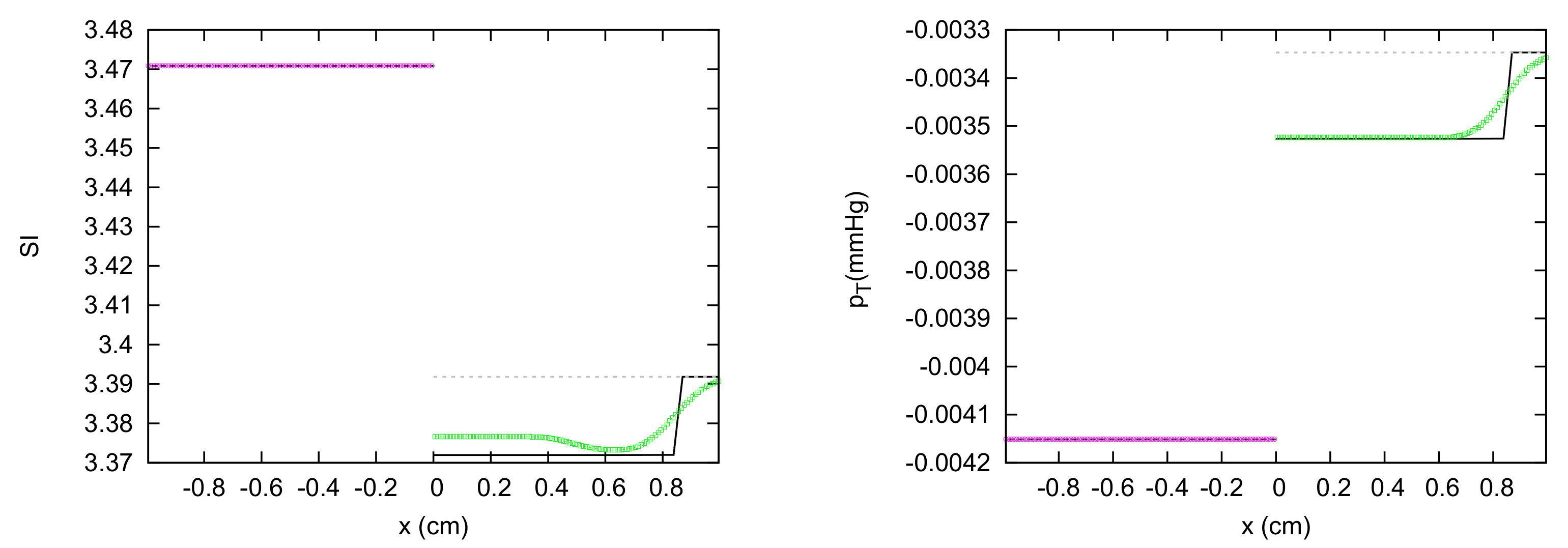

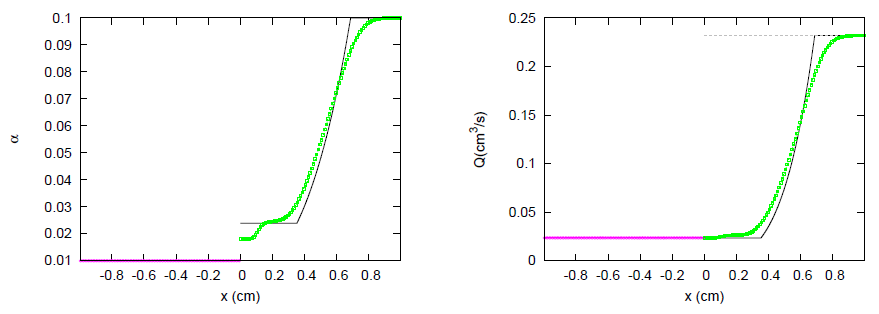



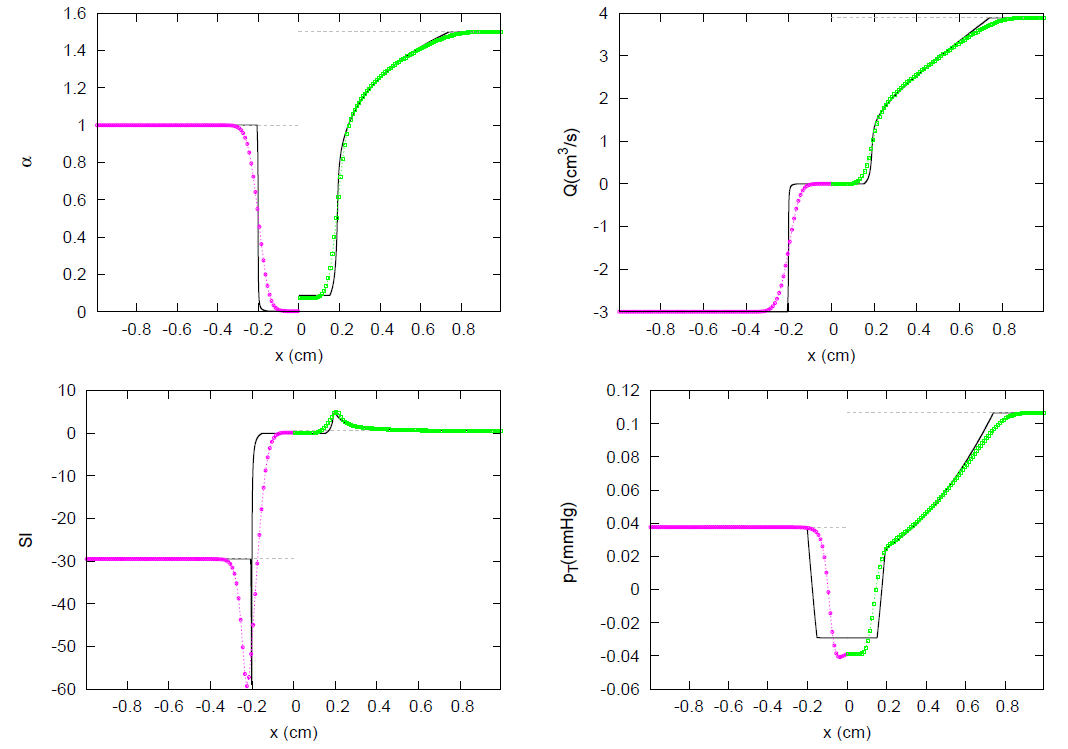
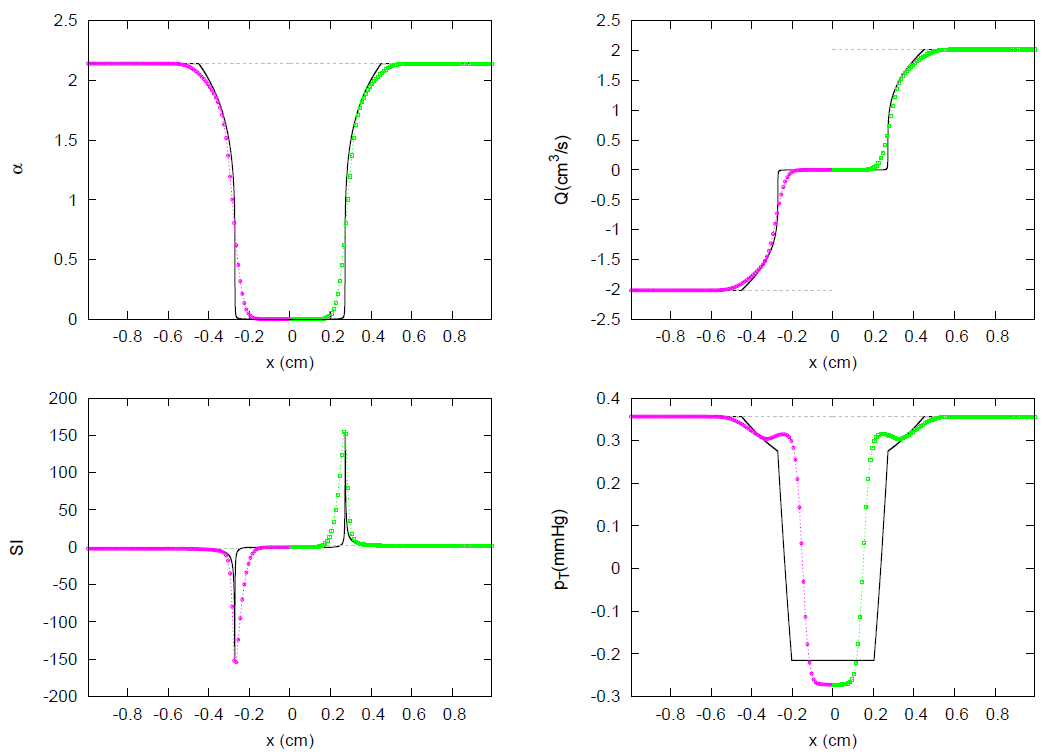
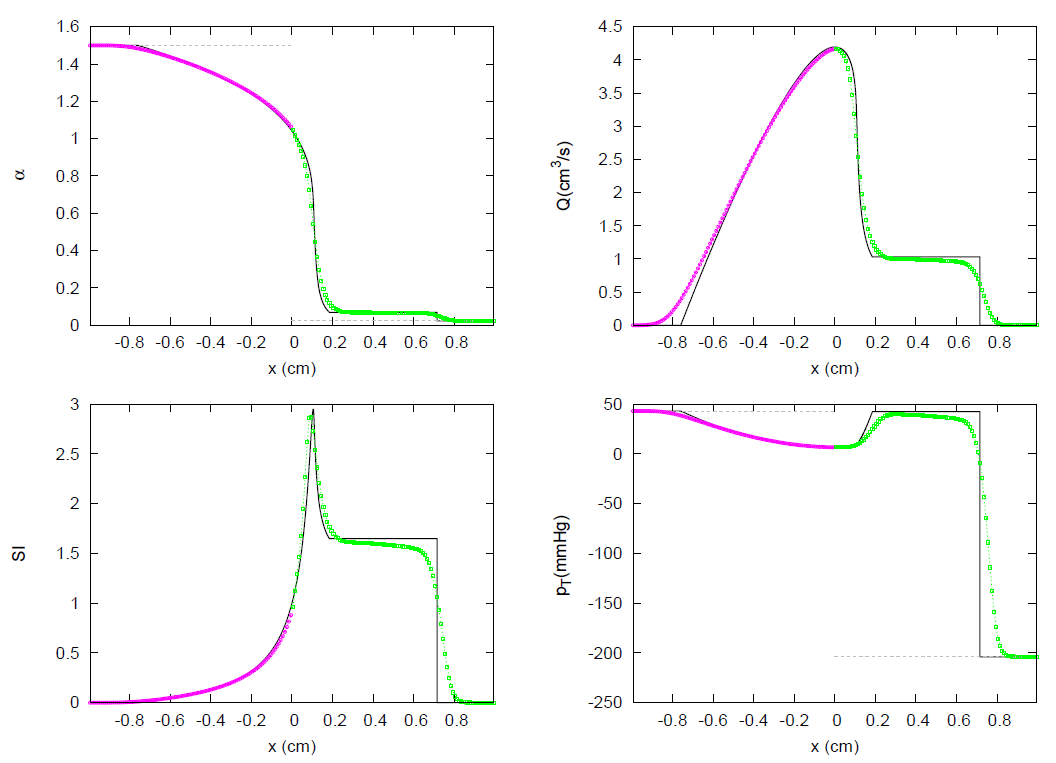
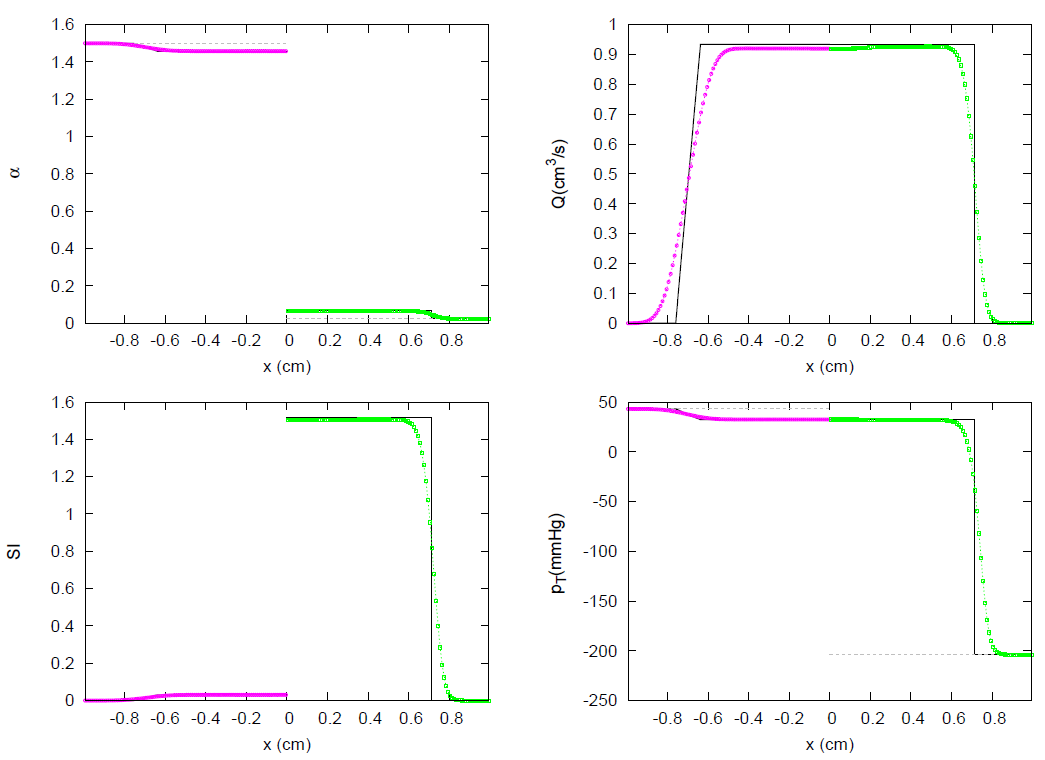
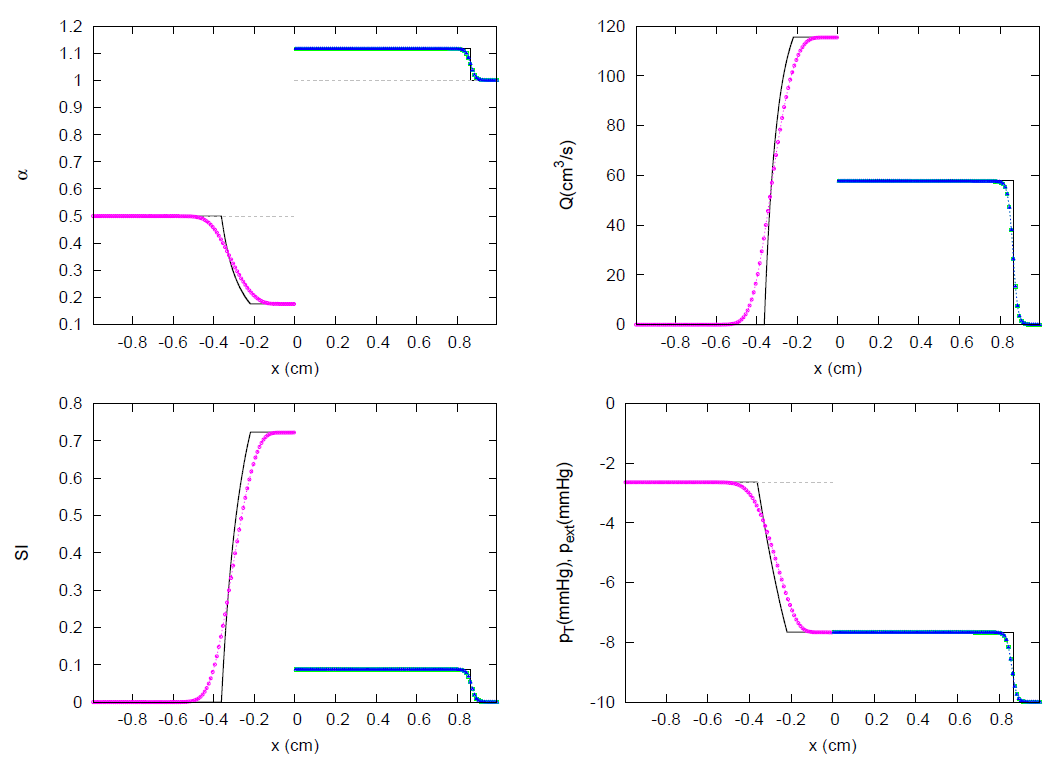

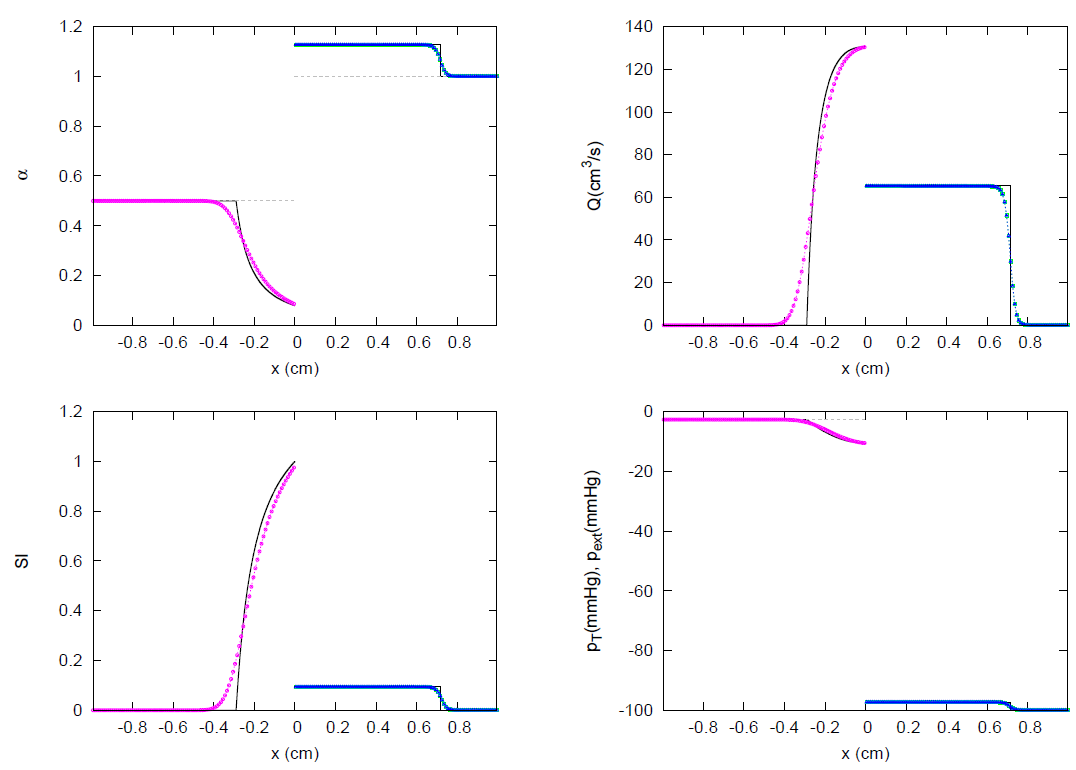

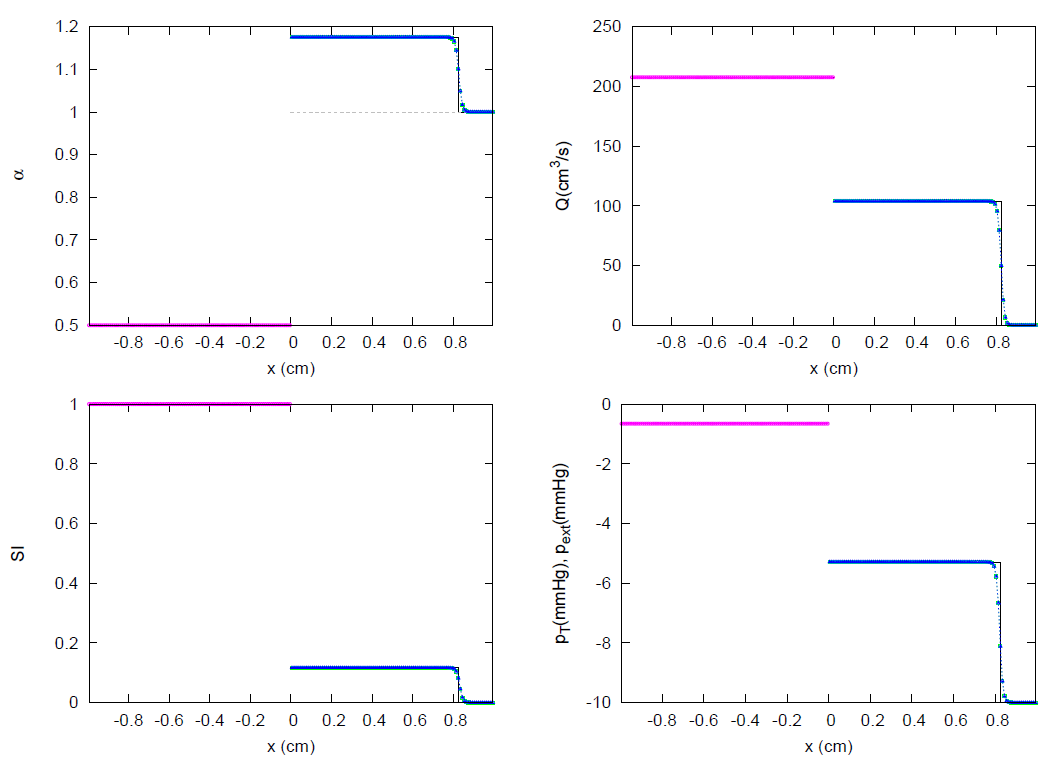
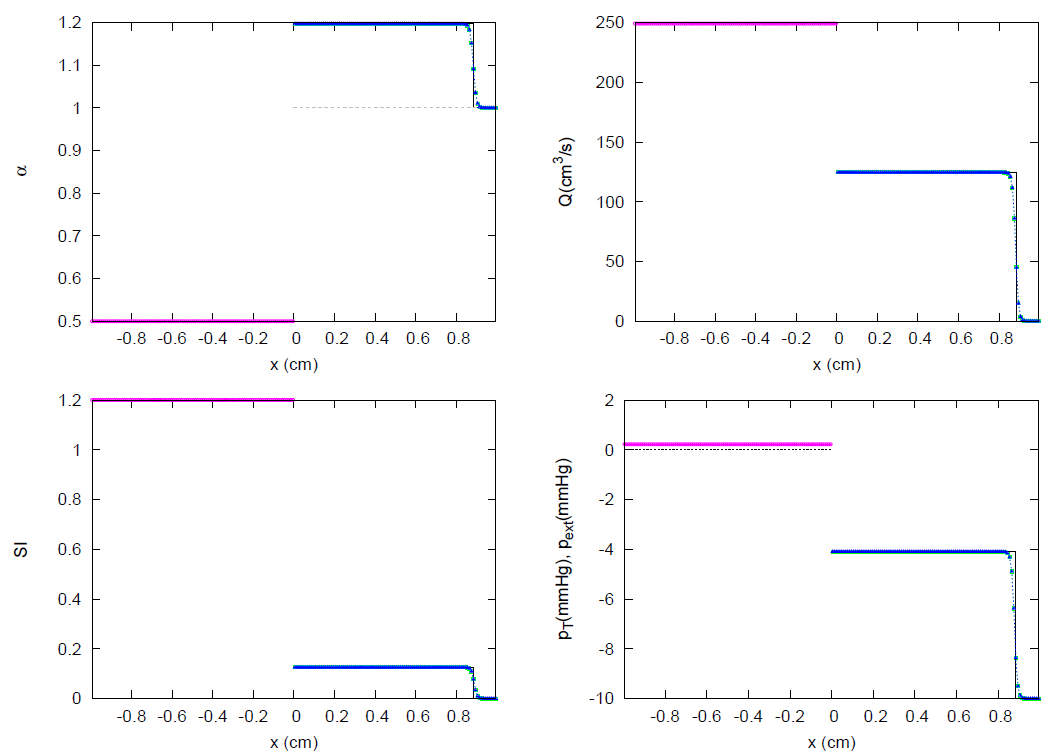







| Test Case | k | m | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2V0 | 1 | 1 | 25.231 | 299.07 | 0.0 | 0.0 | 0.01 | 2.400 | 0.5 | 0.0 |
| 2 | −1 | 22.568 | 346.41 | 0.0 | 5.0 | 0.01 | 1.909 | 0.5 | 0.0 | |
| 2V1 | 1 | 1 | 25.231 | 299.07 | 0.0 | 0.0 | 0.01 | 2.400 | 0.5 | 0.0 |
| 2 | −1 | 22.568 | 346.41 | 0.0 | 0.0 | 0.00 | 1.125 | 0.5 | 0.0 | |
| 2V2 | 1 | 1 | 25.231 | 299.07 | 0.0 | 0.0 | 0.00 | 1.600 | 0.5 | 0.0 |
| 2 | −1 | 22.568 | 346.41 | 0.0 | 0.0 | 0.00 | 1.500 | 0.5 | 0.0 | |
| 2V3 | 1 | 1 | 25.231 | 299.07 | 0.0 | 0.0 | 0.12 | 1.600 | 0.5 | 0.0 |
| 2 | −1 | 22.568 | 346.41 | 0.0 | 0.0 | 0.00 | 1.504 | 0.5 | 0.0 | |
| 2V4 | 1 | 1 | 6.000 | 479.58 | 0.0 | 0.0 | 0.01 | 1.132 | 10.0 | −1.5 |
| 2 | −1 | 6.293 | 61.91 | 0.0 | 0.0 | 0.29 | 1.026 | 10.0 | −1.5 | |
| 2V5 | 1 | 1 | 6.000 | 61.91 | 0.0 | 0.0 | 0.29 | 1.026 | 10.0 | −1.5 |
| 2 | −1 | 6.148 | 619.14 | 0.0 | 0.0 | 0.01 | 1.078 | 10.0 | −1.5 | |
| 2V6 | 1 | 1 | 6.000 | 61.91 | 0.0 | 0.0 | 0.33 | 1.210 | 10.0 | −1.5 |
| 2 | −1 | 6.434 | 391.58 | 0.0 | 0.0 | −0.02 | 1.027 | 10.0 | −1.5 | |
| 2V7 | 1 | 1 | 6.000 | 61.91 | 0.0 | 0.0 | −0.21 | 1.096 | 10.0 | −1.5 |
| 2 | −1 | 6.148 | 339.12 | 0.0 | 0.0 | 0.02 | 1.044 | 10.0 | −1.5 | |
| 2V8 | 1 | 1 | 11.284 | 2.14 | 0.0 | 0.0 | 3.47 | 0.010 | 0.5 | 0.0 |
| 2 | −1 | 11.284 | 1.98 | 0.0 | 0.0 | 3.39 | 0.012 | 0.5 | 0.0 | |
| 2V9 | 1 | 1 | 11.284 | 2.14 | 0.0 | 0.0 | 3.47 | 0.010 | 0.5 | 0.0 |
| 2 | −1 | 11.284 | 1.98 | 0.0 | 0.0 | 2.09 | 0.100 | 0.5 | 0.0 | |
| SubAtm1 | 1 | 1 | 15.958 | 107.24 | 0.0 | 0.0 | 0.00 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 15.958 | 107.24 | 0.0 | −4.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| SubAtm2 | 1 | 1 | 15.958 | 107.24 | 0.0 | 0.0 | 0.00 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 15.958 | 107.24 | 0.0 | −4.9 | 0.00 | 1.000 | 10.0 | −1.5 | |
| SubAtm3 | 1 | 1 | 15.958 | 107.24 | 0.0 | 0.0 | 0.00 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 15.958 | 107.24 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| Collapse1 | 1 | 1 | 11.284 | 1.21 | 0.0 | 0.0 | 1.95 | 0.100 | 0.5 | 0.0 |
| 2 | −1 | 11.284 | 1.11 | 0.0 | 0.0 | 14.38 | 0.012 | 0.5 | 0.0 | |
| Collapse2 | 1 | 1 | 6.180 | 0.34 | 0.0 | 0.0 | −29.49 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 5.046 | 3.39 | 0.0 | 0.0 | 0.54 | 1.500 | 10.0 | −1.5 | |
| Collapse3 | 1 | 1 | 2.000 | 0.36 | 0.0 | 0.0 | −2.01 | 2.140 | 10.0 | −1.5 |
| 2 | −1 | 2.000 | 0.36 | 0.0 | 0.0 | 2.01 | 2.140 | 10.0 | −1.5 | |
| Collapse4 | 1 | 1 | 2.000 | 107.24 | 0.0 | 0.0 | 0.00 | 1.500 | 10.0 | −1.5 |
| 2 | −1 | 2.000 | 107.24 | 0.0 | 0.0 | 0.00 | 0.024 | 10.0 | −1.5 |
| Test Case | k | m | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3V1 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.00 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3V2 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.00 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −40.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −40.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3V3 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.00 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −100.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −100.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3V4 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.95 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −100.0 | 0.90 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −100.0 | 0.90 | 1.000 | 10.0 | −1.5 | |
| 3V5 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 1.00 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3V6 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 1.20 | 0.500 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | −10.0 | 0.00 | 1.000 | 10.0 | −1.5 | |
| 3V7 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.60 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 0.90 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 0.90 | 1.000 | 10.0 | −1.5 | |
| 3V8 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.90 | 1.200 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 1.10 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 1.10 | 1.000 | 10.0 | −1.5 | |
| 3V9 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 0.00 | 0.200 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 0.00 | 0.200 | 10.0 | −1.5 | |
| 3V10 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | 1.10 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 1.10 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | 1.10 | 1.000 | 10.0 | −1.5 | |
| 3V11 | 1 | 1 | 27.000 | 119.27 | 0.0 | 0.0 | −1.10 | 1.000 | 10.0 | −1.5 |
| 2 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | −1.10 | 1.000 | 10.0 | −1.5 | |
| 3 | −1 | 19.092 | 125.04 | 0.0 | 0.0 | −1.10 | 1.000 | 10.0 | −1.5 |
| Test Case | k | m | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4V1 | 1 | 1 | 30.500 | 511.00 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 511.00 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 511.00 | 0.0 | −40.0 | 0.00 | 0.900 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 511.00 | 0.0 | −80.0 | 0.00 | 0.800 | 10.0 | −1.5 | |
| 4V2 | 1 | 1 | 30.500 | 511.00 | 0.0 | −40.0 | 0.00 | 0.900 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 511.00 | 0.0 | −80.0 | 0.00 | 0.800 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 511.00 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 511.00 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V3 | 1 | 1 | 30.500 | 118.72 | 0.0 | −40.0 | 0.00 | 0.900 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | −40.0 | 0.00 | 0.800 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V4 | 1 | 1 | 30.500 | 118.72 | 0.0 | −40.0 | 0.00 | 0.900 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | −80.0 | 0.00 | 0.800 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V5 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.300 | 10.0 | −1.5 | |
| 4V6 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V7 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V8 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 4V9 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.300 | 10.0 | −1.5 | |
| 4V10 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 |
| Test Case | k | m | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4V11 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.300 | 10.0 | −1.5 | |
| 4V12 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 4V13 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 1.100 | 10.0 | −1.5 | |
| 4V14 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 4V15 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 1.200 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 1.100 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 4V16 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 1.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 1.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.600 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.500 | 10.0 | −1.5 | |
| 4V17 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.600 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.200 | 10.0 | −1.5 | |
| 4V18 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.600 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.200 | 10.0 | −1.5 | |
| 4V19 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.600 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.200 | 10.0 | −1.5 | |
| 4V20 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.600 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.200 | 10.0 | −1.5 |
| Test Case | k | m | n | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4V21 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.600 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.200 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 4V22 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.20 | 1.100 | 10.0 | −1.5 | |
| 4V23 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | −30.0 | 1.10 | 1.200 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | −40.0 | 1.20 | 1.100 | 10.0 | −1.5 | |
| 4V24 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.00 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | −30.0 | 1.10 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | −40.0 | 1.20 | 0.200 | 10.0 | −1.5 | |
| 4V25 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.90 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | −30.0 | −1.20 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | −40.0 | −0.90 | 0.200 | 10.0 | −1.5 | |
| 4V26 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 30.0 | 0.90 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.80 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | −40.0 | −1.20 | 0.200 | 10.0 | −1.5 | |
| 4V27 | 1 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −1.10 | 0.100 | 10.0 | −1.5 |
| 2 | 1 | 30.500 | 118.72 | 0.0 | 0.0 | −0.90 | 0.300 | 10.0 | −1.5 | |
| 3 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 0.80 | 0.100 | 10.0 | −1.5 | |
| 4 | −1 | 30.500 | 118.72 | 0.0 | 0.0 | 1.20 | 0.200 | 10.0 | −1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murillo, J.; García-Navarro, P. A Solution of the Junction Riemann Problem for 1D Hyperbolic Balance Laws in Networks including Supersonic Flow Conditions on Elastic Collapsible Tubes. Symmetry 2021, 13, 1658. https://doi.org/10.3390/sym13091658
Murillo J, García-Navarro P. A Solution of the Junction Riemann Problem for 1D Hyperbolic Balance Laws in Networks including Supersonic Flow Conditions on Elastic Collapsible Tubes. Symmetry. 2021; 13(9):1658. https://doi.org/10.3390/sym13091658
Chicago/Turabian StyleMurillo, Javier, and Pilar García-Navarro. 2021. "A Solution of the Junction Riemann Problem for 1D Hyperbolic Balance Laws in Networks including Supersonic Flow Conditions on Elastic Collapsible Tubes" Symmetry 13, no. 9: 1658. https://doi.org/10.3390/sym13091658
APA StyleMurillo, J., & García-Navarro, P. (2021). A Solution of the Junction Riemann Problem for 1D Hyperbolic Balance Laws in Networks including Supersonic Flow Conditions on Elastic Collapsible Tubes. Symmetry, 13(9), 1658. https://doi.org/10.3390/sym13091658






