Next Article in Journal
Performance Requirements and Optimum Mix Proportion of High-Volume Fly Ash 3D Printable Concrete
Previous Article in Journal
Numerical Modeling of Four-Pile Caps Using the Concrete Damaged Plasticity Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 14
Issue 7
10.3390/buildings14072067
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A New Type of Wharf and a Study of Its Mechanical Properties by FE (Finite Element) and Experimental Methods

by
Xiang He
1,
Xia Qin
1,
Mian Huang
1,
Xiaoli Xie
2,*,
Chenhao Du
2 and
Wenyang Fan
3
1
School of Architectural Engineering, Nanning College for Vocational Technology, Nanning 530000, China
2
College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China
3
Guangxi Vocational and Technical College of Communications, Nanning 530004, China
*
Author to whom correspondence should be addressed.
Buildings 2024, 14(7), 2067; https://doi.org/10.3390/buildings14072067 (registering DOI)
Submission received: 4 May 2024 / Revised: 27 June 2024 / Accepted: 2 July 2024 / Published: 6 July 2024
(This article belongs to the Section Building Structures)
Browse Figures
Versions Notes

Abstract

:
Due to the limitations of planar mode wharfs, this paper proposes a new type of wharf—the three-dimensional cantilevered wharf. The proposed wharf is defined as an improvement of the traditional wharf, extending the traditional wharf upward and cantilevering out to the sea. The three-dimensional cantilevered wharf is a composite truss structure that meets structural and functional requirements. The composite truss structure is formed by connecting the beams of frame structures as a whole. The material consumption of the three-dimensional cantilevered wharf is decreased by controlling stresses and optimizing components. A finite element model of the proposed wharf, with a length of 200 m, width of 105 m, and cantilever length of 80 m, was established to analyze the basic mechanical performance. In this paper, the force distribution of the pile foundation, the vertical force transfer efficiency of web members, the structural stiffness, and the natural frequencies of the proposed wharf are analyzed. Tests regarding the stress and stiffness of different plane cantilever trusses are carried out, and finite element analysis is used for comparison. The test results show that the high-rise cantilever truss has a great in-plane stiffness and a reasonable component stress distribution. Additionally, the three-dimensional cantilevered wharf significantly improves the utilization efficiency of the wharf.

1. Introduction

With the development of economic globalization and international trade, ocean transportation has become the most essential route to address logistics [1,2,3]. The port, as an important hub of ocean transportation, is the distribution center of import and export cargoes; it is a place for freighters to berth, load, and unload cargoes, move passengers, and renew provisions. Since the 1980s, many ports have been built all over the world to improve logistics capability, such as the Port of Rotterdam in the Netherlands, the Port of Shanghai in China, the Port of Singapore, and the Hong Kong Port. Over the last two centuries, trade has grown remarkably. Nowadays, approximately a quarter of total global production is exported. According to WTO statistics (Figure 1), the world merchandise trade volume decreased by 1.2% in 2023 but will increase by 2.6% and 3.3% respectively in 2024 and 2025. A larger-scale modern port can more orient such an increase in demand, as it is trade-driven.
The wharf plays a key role in ports. The wharf can be classified into two broad categories: vertical-face wharves and sloping wharves, according to the vertical section type. The vertical-face wharf is widely applied in seaports or deep-water river ports. With sufficiently large and deep water areas, it is convenient for large ships to moor and operate. The sloping wharf is applied in geographical locations with large water level drops due to its strong adaptability to water level fluctuation [4,5]. Therefore, it has become the main form of wharf in mountainous areas.
Most of the active wharves and wharves under construction are in the planar mode. Although many scholars are committed to innovating wharf structure and improving loading and unloading efficiency, breakthrough progress has not been achieved. At present, fully automated container wharves are being further researched, but most are limited to the plane mode [6,7]. Chang et al. [8] predicted the integrated scheduling problem at automatic container wharves. Combining the characteristics of automatic container wharves to study the integrated scheduling problem was suggested in their research. The integrated scheduling problem of the wharf can be solved by algorithm computation and simulation checking [9] However, loading and unloading efficiency cannot be significantly improved by optimizing the operation process. The planar dispatch scheduling of the traditional plane wharves cannot take full advantage of the space resources above the wharf. The layout of container yards, train lines, sorting centers, etc., is rigid and is prone to conflicts on the plane. It is difficult to upgrade the berth of the traditional wharf once it is completed. Also, the limited operational radius and single-line operation mode of the cranes reduce the loading and unloading efficiency. Therefore, a three-dimensional wharf is needed so that it can more reasonably satisfy the functions of the port.
In terms of structure, most wharves are composed of substructures and superstructures, such as high-pile wharves. The superstructure consists of beams and prestressed concrete hollow slabs [10]. Wharf reconstruction measures have been researched [11], such as in gravity wharves and high-pile wharves. At present, rock-socketed pile forks and raking piles have been proposed to be used in the substructure of the vertical wharf. A vertical-faced frame container wharf has been proposed as well [12]. It improves the efficiency and transportation capacity of the port and can better meet the requirements of economic development. A semi-covered type of sheet pile wharf was suggested along with its corresponding calculation method for design by Liu et al. [13]. Boroschek et al. [14] present the damping characteristic results of a 375 m long pile-supported wharf structure under forced excitation. The substructure reconstruction contributes significantly to the durability, economy, and expansibility of the wharf [15] but has no effect on the loading and unloading efficiency. From the aforementioned studies, it should be noted that most of the past research focused on the study of the supporting system of the wharf, while only a few studies on the superstructure of the wharf are available.
The frame structure is a parallelogram structure mainly composed of beams and columns, which constitutes a load-bearing system. It is widely applied in high-rise and multi-increment buildings. The structural feature is that the main beams of each layer do not form as a whole but act independently. A truss is a plane structure composed of straight bars, and it has triangular elements in general. Truss members mainly bear axial tension or pressure, to make full use of the strength of materials to give full play to the role of materials, save materials, and reduce the weight of the structure [16,17]. Truss structures originated in ancient Rome, and after continuous development, they have been widely used in various fields, such as large-space roofs, industrial workshops, bridges, aircraft, cranes, and so on. In addition, the researcher of this article applies the truss concept to the optimization of suspension bridge structures [18]. Though the research on single trusses has been quite thorough, there are still many areas to be researched and developed for truss systems. Moreover, heretofore, the truss structure has not been applied in the wharf.
Based on the advantages of the truss [18], a new type of wharf—a three-dimensional cantilevered wharf—is proposed to solve the problems in wharves, as shown in Figure 1. In the new wharf, the superstructure is a composite truss structure system with common chords. It is formed by connecting the main beams on each floor of the frame structure with diagonal web members into a whole (making the parallelogram frame structure into a stable triangular structure). The structural system has exceptionally high load-bearing capacity and excellent spanning ability, which is attributed to its larger beam height. Hence, the structure can obtain more space and a longer cantilever. This new design allows the wharf to have more berths, higher loading and unloading efficiency, and a larger storage yard area. In addition, a three-dimensional intermodal transport can be formed. This article details the structural form and mechanical principles of this new wharf design. It shows how the mechanical properties are investigated by using the finite element method. The methods of transportation, storage, and berthing are also mentioned in the article, and the rationality of the structural system is also investigated via experimentation.

2. Structural Form and Methodology

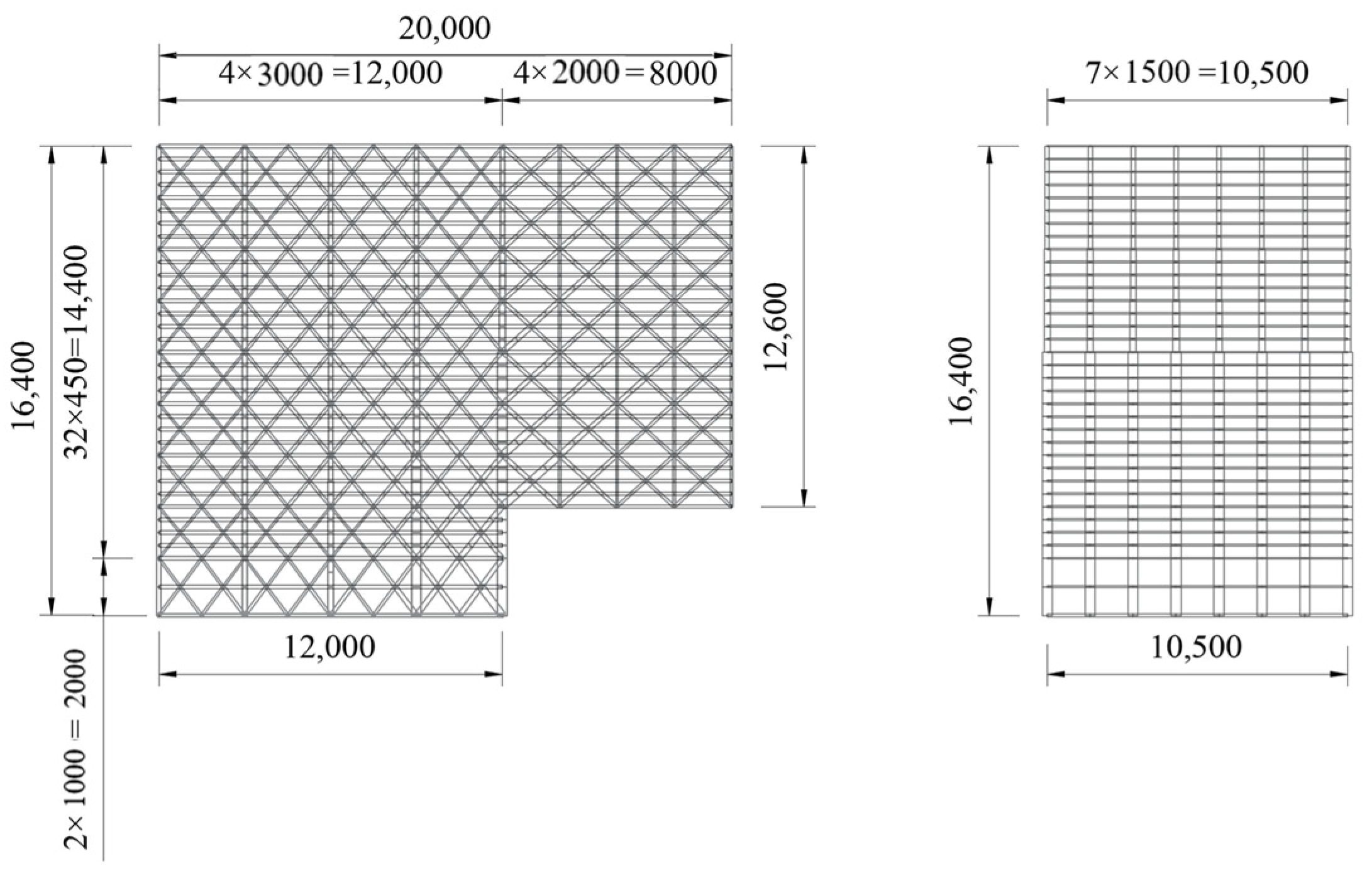
2.1. Structural Assumptions

Generally, a truss has greater stiffness than a same-size frame. Appropriate truss application can greatly improve structural stiffness. With this background knowledge, this paper presents a new type of wharf structure called a three-dimensional cantilevered wharf. The proposed wharf’s substructure is similar to that of a high-pile wharf. In contrast, it uses a kind of frame-truss composite structure to innovate the wharf superstructure. A three-dimensional cantilevered wharf is primarily composed of a foundation, columns, beams, plates, and web members. It applies web members on several perpendicular planes in the frame to form local trusses. From the side view, the web members brace the frame into an overall truss. Additionally, to meet the requirements of the wharf, it has an ultra-long cantilever section, relying on its advantage of high in-plane stiffness.
The upper frame-truss composite structure is made of steel to control the weight. The bearing capacity of the pile foundation is designed according to the requirements of the superstructure. Except for the cantilever segment, columns are supported directly by the pile foundation. Therefore, the concrete surface of a traditional high-pile wharf is transformed into a frame-truss composite structure. Through bracing the steel beams between two floors by web members into trusses, the single beam height of the frame becomes the overall beam height of the truss, which can enhance the bending resistance capacity.
Based on this new structure type, a three-dimensional cantilevered wharf (as shown in Figure 2) has the following advantages compared with the traditional high-pile wharf. Firstly, it transforms a planar wharf into a stereo wharf, which greatly increases its available space and scheduling flexibility. Secondly, the frame-truss composite structure has good performance in bearing and integrity, and so can well transfer the load to the foundation vertically and horizontally along the truss. Thirdly, a three-dimensional cantilevered wharf has more berths and can set up berths for ships with different tonnage according to different cantilever heights. What is more, it can realize interchange transport, even train and truck layered cooperative operation, as shown in Figure 3.

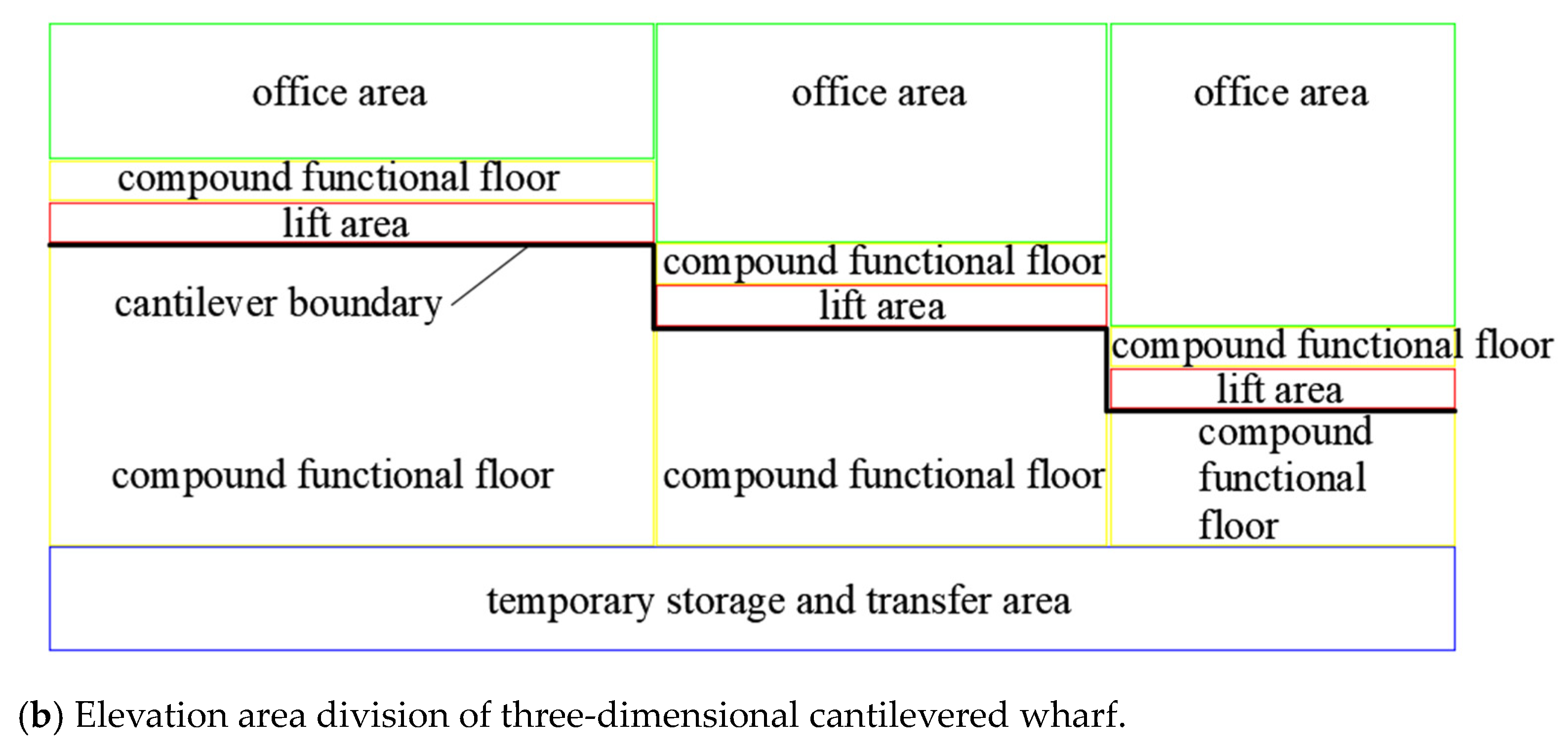
2.2. Division of Port Functional Area

The plane and elevation area division of the port is shown in Figure 4. The plane layout is roughly planned for the following parts: heavy container yard, empty container yard, berths, office area, loading and unloading area, and traffic routes. The elevation area division is about the floor function division of a three-dimensional cantilevered wharf. It can be seen that the port has a small footprint and can realize three-dimensional space utilization.

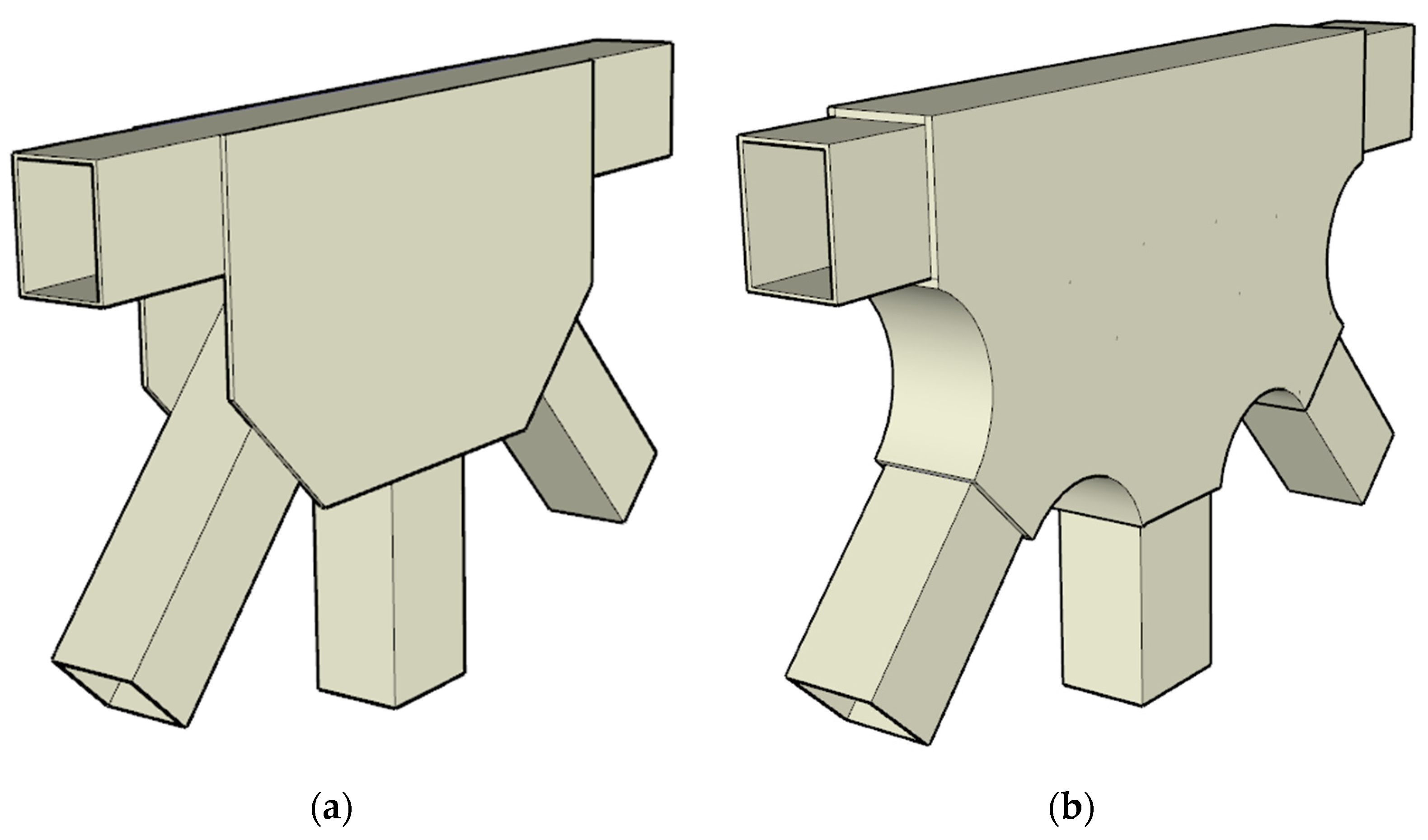
2.3. Connection of Web Member and Beam

In the three-dimensional cantilevered wharf, the web member is connected to the main beam by the truss joint plate or the integral joint, as shown in Figure 5. The former is more conducive to on-site assembly, and the latter can be prefabricated in a factory. The web members can be bolted or welded to the gusset plates; the welding length and the number of bolts are determined by the force of web member.
The new design of the wharf has to address challenges including wind resistance, earthquake resistance, steel corrosion, enormous vertical forces on the foundation, etc. The wind-resistant behavior of the structure can be improved by controlling the span-height ratio and cantilever length of the structure. The impact of earthquakes on the structure can be weakened through the use of elastic foundation settings. The coastal geology makes it difficult to bear enormous vertical forces. Therefore, a foundation reinforcement is required, which will also increase the cost. The steel anti-corrosion technology developed by Hou [19,20] can be applied to the offshore steel structure wharf.
Most of the active wharves and wharves under construction have a planar mode. The new design of the wharf is a three-dimensional wharf, which allows the wharf to have more berths, higher loading and unloading efficiency, and a larger storage yard area. Besides, a three-dimensional intermodal transport can be formed. Its construction cost exceeds that of a traditional wharf. This research does not provide a detailed analysis of its cost. The details will be further researched in the future.

3. Finite Element Analysis

A three-dimensional cantilevered wharf example is established for stiffness, strength, and dynamic characteristics analysis. It is divided into three parts according to different cantilever heights. The lowest cantilever height part is selected to perform finite element analysis (FEA) by MIDAS (Midas Civil 2021) to demonstrate the feasibility of the structure.

3.1. Calculation Models for Three-Dimensional Cantilevered Wharf

As shown in Figure 6, the cantilever height of the wharf model is 38 m. Its length is 200 m, and its width is 105 m. Its shore segment and cantilever segment include compartments of 15 m × 30 m and 15 m × 20 m. The total height of the wharf model was 164 m, the height of the bottom two floors was 10 m, and the height of the top three floors was 4.5 m, which is applicable to different functions. The bottom floor was covered with 15 cm of concrete floor above concrete beams. The superstructure components’ cross-section adopted a steel ribbed box, except for the floor slab. The substructure of the wharf adopts a 36 m deep high-pile foundation. Inclined piles are used to fix the vertical piles, and the vertical piles are designed according to the requirement of bearing capacity. Detailed parameters of the three partial models are summarized in Table 1. The material properties are listed in Table 2. Some components are inevitably subjected to high axial forces, such as seaward columns and cantilever web members, etc., thus using high-strength steel to ensure the strength demand.
Midas finite element software (Midas Civil 2021) is used to analyze the strength of each component of the wharf model, and the stiffness, dynamic characteristics, and seismic response of the structure are tested. In the finite element models, beams, columns, and diagonal web members are simulated by beam elements (approximate size of the global seed is 0.5 m), while the floor is simulated by plate elements (approximate size of the global seed is 0.5 m), as shown in Figure 7.
For boundary conditions, all the pile foot nodes are fixed, and we use nodal elastic support to simulate the soil boundary condition of the pile side according to the codes [21,22]. The structural load grade refers to the code and the loads specified, and their combinations are described below.
  • Floor live load: The bottom two floors are loaded with a fully uniform distributed load of 5 kN/m2, and the rest are 3.5 kN/m2.
  • Hanging load: A 40-ton hanging load is applied at the maximum cantilever length.
  • Wind load: The offward wind load is 0.66 kN/m2, and the shoreline wind load is 0.16 kN/m2.
  • Snow load: The uniform snow load is 0.4 kN/m2.
  • Temperature effect: The initial temperature was 15 °C, which was increased by 25 °C and then decreased by 20 °C.
  • Seismic load: The seismic load magnitude is 8.
  • The following load combinations are used:
    -
    Combination I: 1.2 dead load + 1.4 floor live load + 0.7 hanging load + 0.6 wind load + 0.7 snow load + 0.6 temperature effect;
    -
    Combination II: dead load + 0.6 floor live load + 0.6 hanging load + 0.2 snow load + 0.4 temperature effect + seismic load;
    -
    Combination III: 1.2 dead load + 1.3 seismic load.

3.2. FEA Results

3.2.1. Analysis of Support Reaction Force, Structural Internal Force, and Stresses

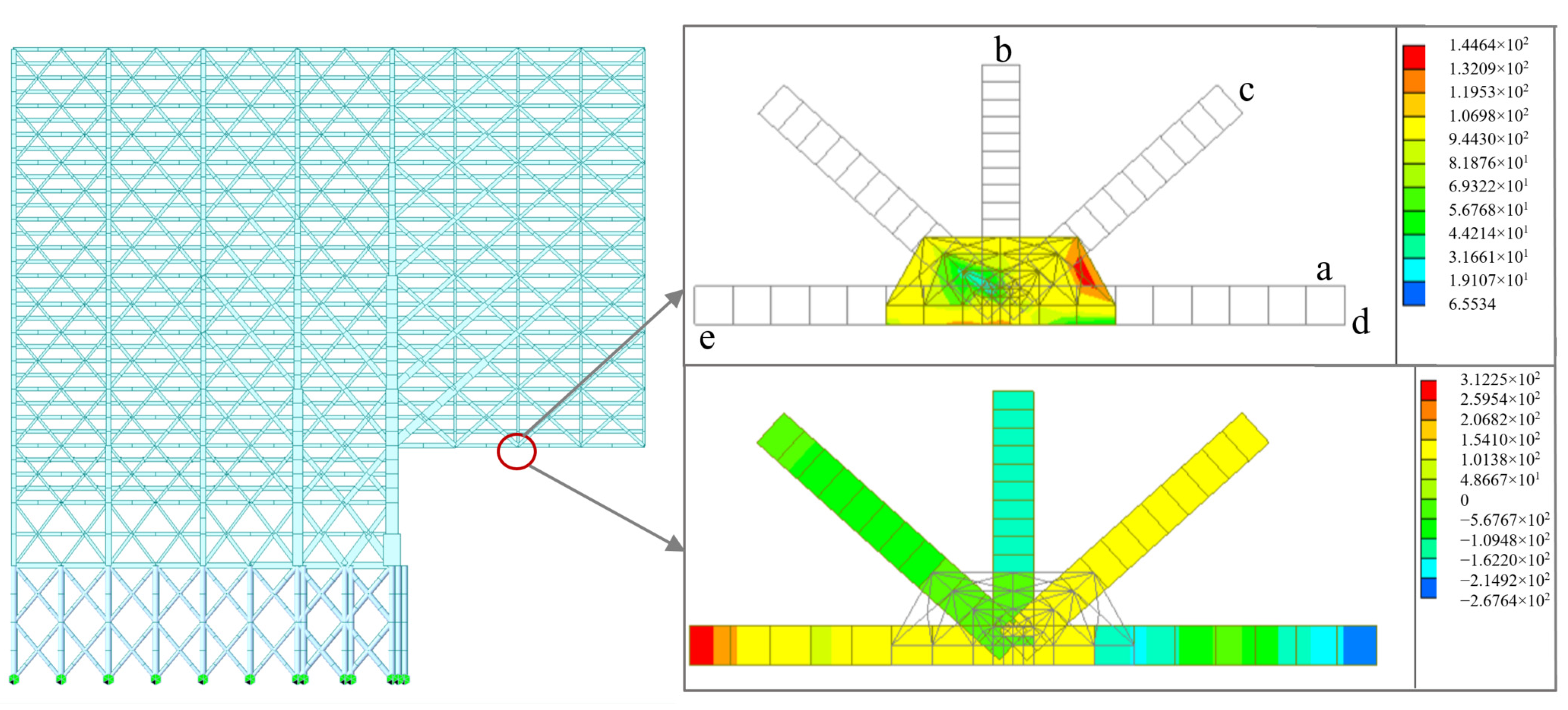
(1)
Pile block force
After the finite element analysis of Midas (Midas Civil 2021), the vertical force values of the pile block (the rows 1, 3, 5, 7, and 9 of piles are directly below columns, and the rest are below web members) of the models under load combination I and Combination II are obtained.
As is shown in Figure 8 and Table 3, the maximum vertical force is generated in off-ward columns, which is more than twice the others. The offward column foot’s force accounts for 51.78% of the total under load Combination I and 51.68% under Combination II. The vertical force on the top of the second-row pile accounts for 6.10% and 5.03%. The second row of columns’ foot bearing force accounts for 19.17% and 17.03%. Other pile block forces are small, accounting for 22.95% and 26.25% in total.
Therefore, conclusions can be drawn from the values that the pile below the column needs to bear more vertical force than the pile below the web member. Web members such as branches transmit the internal forces into columns, connecting the cantilever segment to the shore segment and allocating the load to the adjacent columns.
(2)
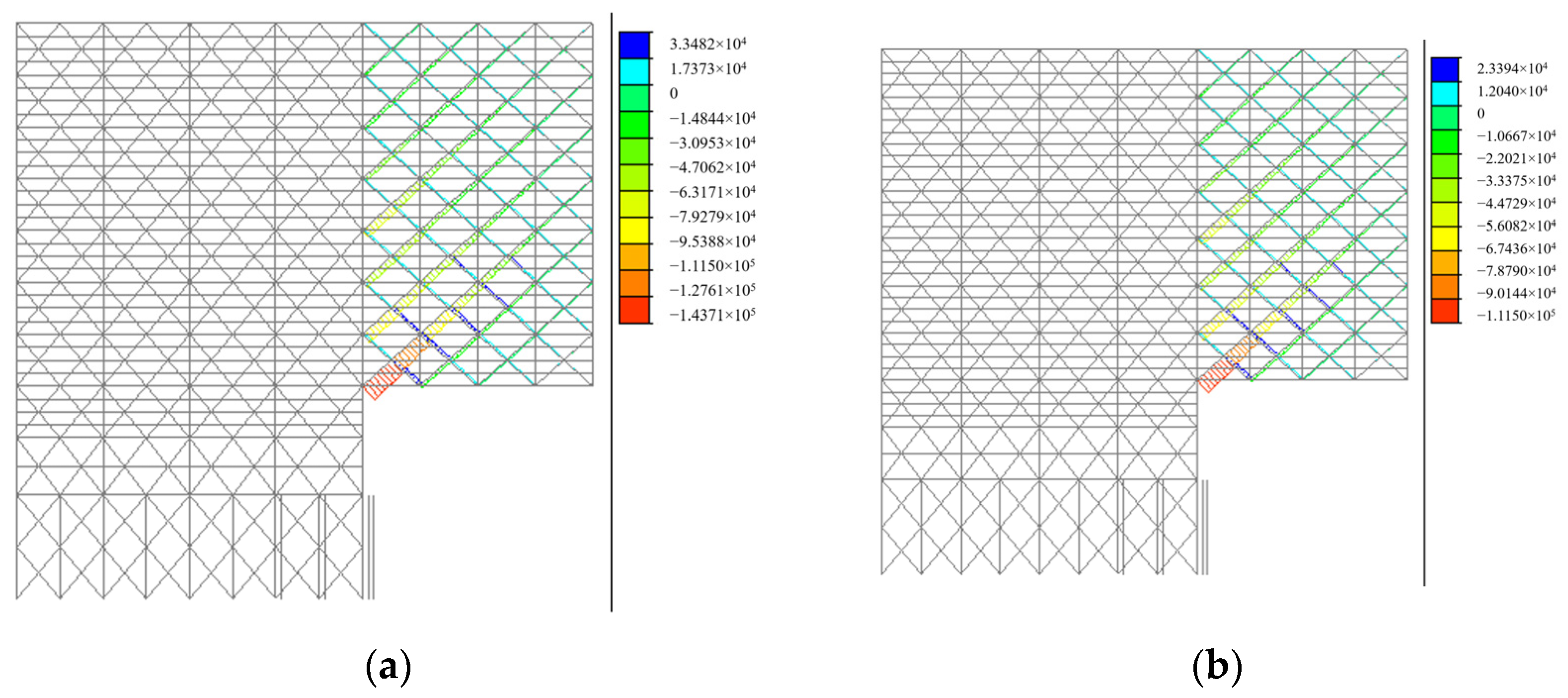
Structural internal force
The structural internal forces for a set value of the axial force of the web member and shearing force of the cantilever segment of the main beam under load combination I and combination II are listed in Figure 9 and Table 4 to illustrate the force transfer characteristics.
The obtained results suggest that under load combination I, the maximum shearing force of the cantilever segment main beam is 1286 kN, and the maximum axial force of the web member is 143,715 kN, with a vertical component of 96,164 kN. Under load combination II, for the main beam, the maximum shearing force is 883 kN, and the maximum axial force of the web member is 101,497 kN, with a 67,915 kN vertical component. According to Table 3, The vertical force transmitted by the web member accounted for, respectively, 95.76% and 95.84% under load combination I and combination II.
It can be concluded from the internal force result that most of the vertical force of the cantilever segment is transmitted by the web member, and the formed truss makes the cantilever segment and the shore segment concatenated as a whole. Therefore, the super-long cantilever segment can be established.
(3)
Structural stresses
Structural stresses can be a reference for the form of structural arrangement. To prevent structural strength failure, the tensile and compressive stresses of steel structures are controlled below 305 MPa, the compressive stress of concrete is controlled below 26.8 MPa, and the tensile stress below 2.39 MPa. Table 5 lists the stresses of the columns, beams, and diagonal web members of the wharf models under load Combinations I, II, and III. It can be seen that the maximum structural stress of 302.7 MPa occurs in columns under load combination I. Under load combination III, the maximum tensile and compressive stresses of the web members are 106.4 MPa and 151.0 MPa, respectively. The structural stresses are small and can meet the demand of fatigue strength requirements.
(4)
Stress analysis of joint connections
As shown in Figure 10, a joint is selected from the overall analysis model (using the (a) connection form in Figure 5). Based on the Saint-Venant principle, a truncated member is placed 2 m away from the joint, which can avoid the influence of stress concentration on the joint caused by the cross-section a to e. The joint is analyzed by applying displacement boundary conditions at sections a to e. The applied displacements are the displacements from the sections a to e in the overall analysis model. The joint analysis model is modeled by the Midas plate element, with 1207 elements.
This indicates that under the load combination I, the maximum stress of the joint plate is 144.6 MPa, and the maximum stress of the members is 312 MPa. This is mainly due to stress concentration caused by displacement boundary conditions in sections a to e. Except for the high stress near the cross-section, the stresses in other areas are within 220 MPa.
The new type of wharf—three-dimensional—involves a lot of joint connection forms, and only a simple static analysis of the joint is included here. The connection forms, static performance, seismic performance, and other aspects of the joints will be further researched in the future.

3.2.2. Analysis of Structural Stiffness

Table 6 presents the floor deflection under live load. The maximum deflection occurs at the top floor of the cantilever segment, which is 22.70 mm.

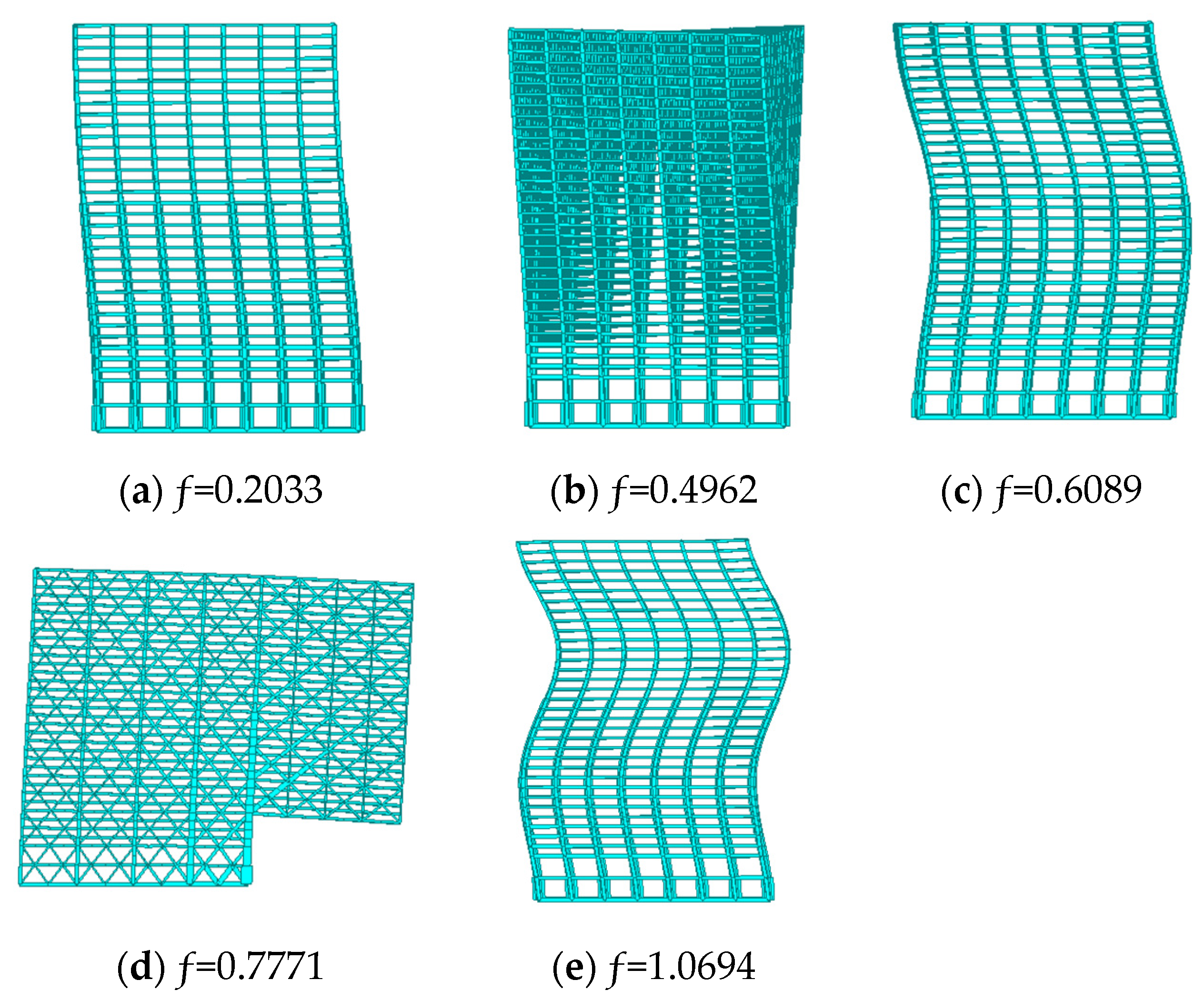
3.2.3. Analysis of Structural Frequency

The dynamic responses (Figure 11) of the structures are analyzed using the linear elasticity principle. The pile foundation is not considered in the eigenvalue calculation, and all the degrees of freedom of the tower foot nodes are fixed. Figure 6 displays the first five natural vibration modes. It is shown that the first shoreline plane vibration frequency is 0.2033 Hz, and the first cantilever plane vibration frequency is 0.7771 Hz. These results indicate that the cantilever frequency of the structure is much larger than the shoreline plane frequency. Therefore, the web members have a significant effect in increasing cantilever plane frequency.

4. Stress and Stiffness Test of Plane Truss

4.1. Test Model Parameters and Load Conditions

The load-bearing characteristic and in-plane stiffness performance of the structure are verified by a single perpendicular plane cantilever loading test. The center-line size of a unit truss is 3.2 m × 0.35 m. The chord section is 60 mm × 30 mm × 3.5 mm, and the web member section is 30 mm × 30 mm × 3.5 mm. The angle between the web member and chord rod is 60°. Test models with height–cantilever ratios of 0.29, 0.58, 0.87, and 1.16 were constructed:
  • Test model I: A unit truss with 1.2 m cantilever segment. The size of test model I is 3.2 m × 0.35 m, and the height–cantilever ratio is 0.29. Load 2 tons on the cantilever segment end.
  • Test model II: Two vertical overlap unit trusses with 1.2 m cantilever segment. The size of test model II is 3.2 m × 0.7 m, and the height–cantilever ratio is 0.58. Load 4 tons on the cantilever segment end.
  • Test model III: Three vertical overlap unit trusses with 1.2 m cantilever segment. The size of the test model III is 3.2 m × 1.05 m, and the height–cantilever ratio is 0.87. Load 6 tons on the cantilever segment end.
  • Test model IV: Four vertical overlap unit trusses with 1.2 m cantilever segment. The size of test model IV is 3.2 m × 1.4 m, and the height–cantilever ratio is 1.16. Load 8 tons on the cantilever segment end.
The main parameters of the two models are listed in Table 6.
The DH3821-Net static strain and stress testing acquisition system is used to collect strain data, as shown in Figure 12. Electronic dial indicators are used to collect displacement. The data are collected after 2 min of loading at each stage (the component enters a stable deformation state).

4.2. Arrangement of Measuring Points

Figure 13 indicates the arrangement of test points. It is shown that the arrangement principle of stress and deflection test points are as follows: (1) Chord stress test points: ① Right section of the middle of a simply supported segment. ② Right section of the cantilever support line. ③ Right section of the middle of the cantilever segment. (2) Chord deflection test points: ① The middle of a simply supported segment. ② The middle of the cantilever segment. ③ The end of the cantilever segment. (3) Web member stress test point: Each unit truss has two test points.
The actual test model and the jack loading equipment are shown in Figure 14. By loading at the end of the cantilever segment, we could analyze the stress and deflection characteristics of the truss. The main parameters of the four models are listed in Table 7.

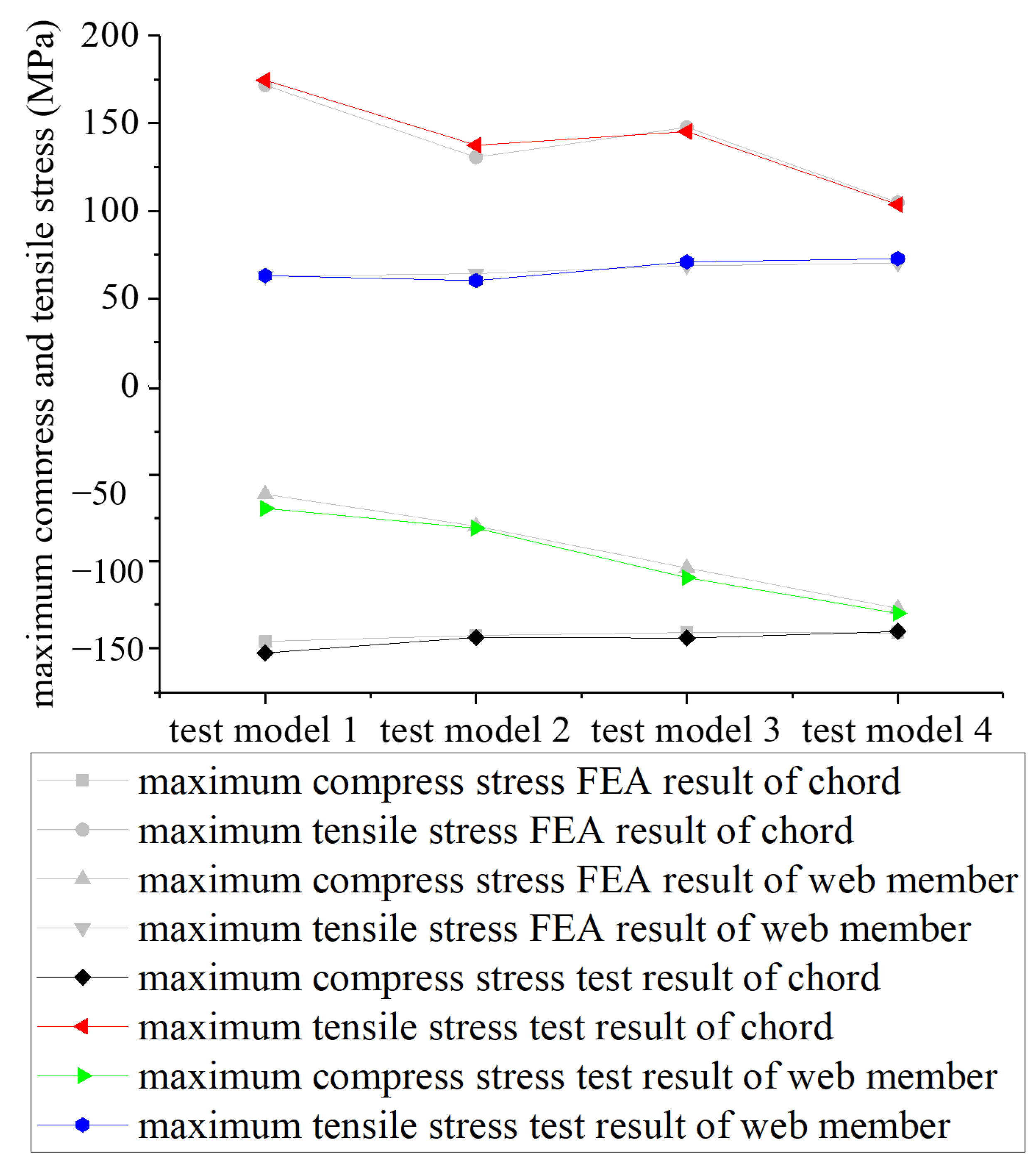
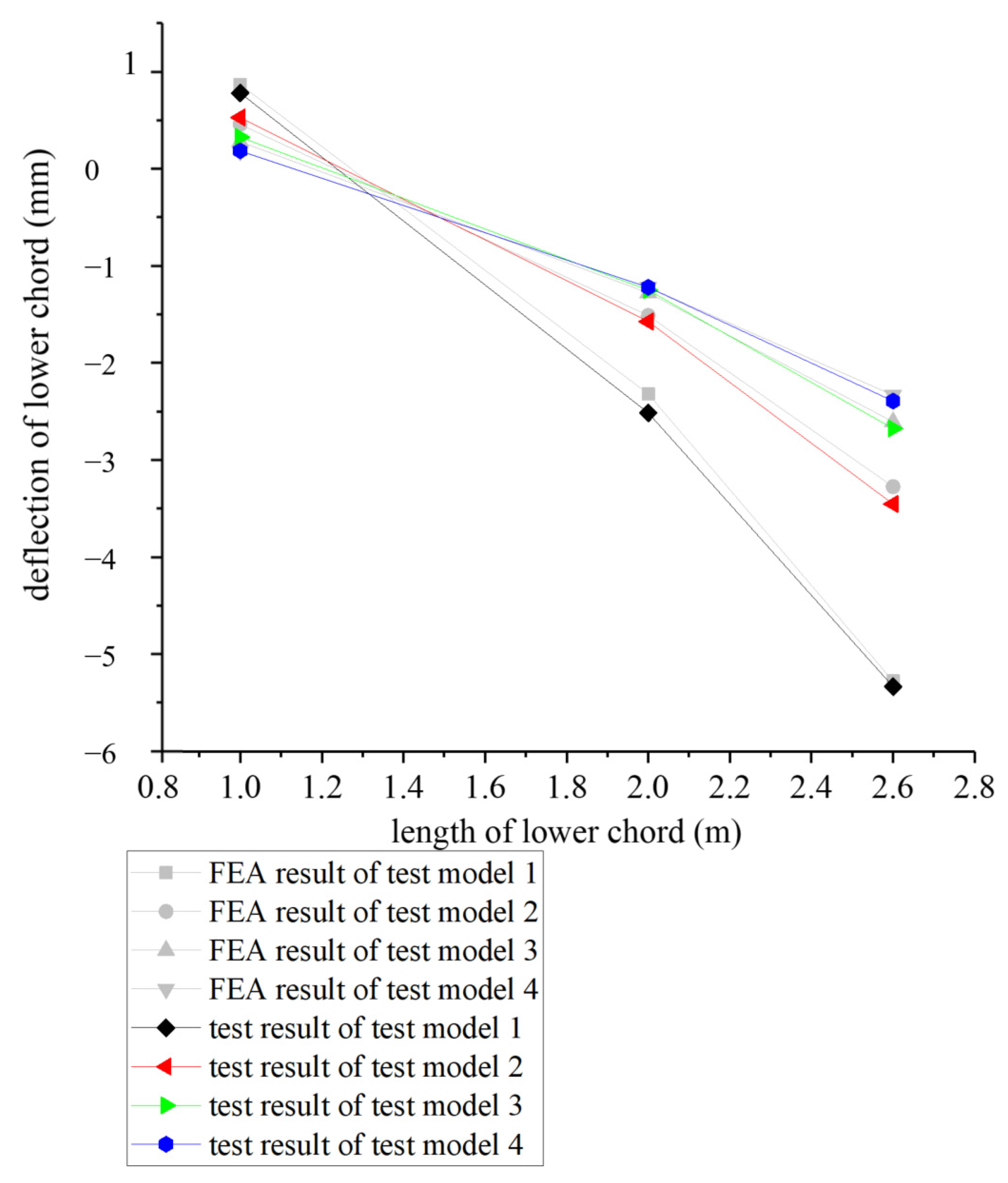
4.3. Test Results

Table 8 and Table 9 list the stress results. The maximum stress results given by MIDAS and the experiments of test models I, II, III, and IV under loads of 2, 4, 6, and 8 tons are compared in Figure 15. Notice that the maximum stress of the chord occurs at the cantilever support line. With the increase of the height–cantilever ratio of the test models, the maximum stress shows a decreasing trend. Meanwhile, the maximum stress of web members increases so that the stress level of components of the truss is average.
Table 10 lists the deflection results; the corresponding comparison is shown in Figure 16. The maximum deflection of test models I, II, III, and IV is, respectively, −5.31 mm, −3.35 mm, −2.71 mm, and −2.49 mm. All occur at the end of the upper chord cantilever segment. Notice that with the increase of the height–cantilever ratio of the test model, its in-plane stiffness is greatly improved.
During the actual experimental tests, the failure modes that were observed are as shown in Figure 17. The failure mode is out-of-plane instability. Therefore, in the new design of the wharf, the main beam is connected by horizontal members to form a whole, thereby improving the overall stability of the structure.

4.4. Test Conclusion

In terms of the analysis of the test data above, with the increase of the height–cantilever ratio of the truss, the strength and in-plane stiffness are greatly improved. The stress magnitude of the chord and the belly become closer.

5. Conclusions

A new type of wharf model with an 80 m cantilever length and 164 m height is set up to study the mechanical properties. An experimental study was carried out to validate the new type of wharf. The main observations from this study are listed below:
  • The piles and columns at the intersection of the shore segment and cantilever segment need to bear about half of the load. Therefore, it needs to be strengthened. Web members transmit the vertical forces into the column, so the pile below the column essentially needs to bear more vertical force than the pile below the web member.
  • In the cantilever segment, the web members can transfer vertical force more efficiently than the beams. The vertical force transmitted by the former accounts for more than 90%. So, the super-long cantilever is based on the proposed wharf structure.
  • The three-dimensional cantilevered wharf has good mechanical properties and economic performance. It transforms the planar wharf mode into a three-dimensional wharf mode, which improves the space utilization efficiency.
Overall, it can be summarized that the proposed wharf type has the feasibility to replace the conventional wharf scheme. Therefore, the operation mode of the wharf can be changed into a three-dimensional mode, which greatly improves the efficiency of the wharf within a limited area.

Author Contributions

Conceptualization, X.X.; methodology, X.Q.; validation, M.H. and W.F.; resources, X.Q.; data curation, C.D.; writing—original draft, X.H. and C.D.; writing—review and editing, M.H.; visualization, W.F.; supervision, X.X.; project administration, X.H.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.

Funding

National Natural Science Foundation of China [Nos. 12162004, 11562001] and the Research Project of Humanities and Social Sciences of the Ministry of Education [23YJCZH073].

Data Availability Statement

Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, K.; Chen, D.; Sun, X.; Yang, Z. Container Ocean-transportation System Design with the factors of demand fluctuation and choice inertia of shippers. Transp. Res. Part E Logist. Transp. Rev. 2016, 95, 267–281. [Google Scholar] [CrossRef]
  2. Kim, T.; Lee, W.D. Review on applications of machine learning in coastal and ocean engineering. J. Ocean Eng. Technol. 2022, 36, 194–210. [Google Scholar] [CrossRef]
  3. Yu, D.; Ye, J. Numerical modelling of the creep subsidence of an ocean lighthouse constructed on a reclaimed Coral Reef Island. KSCE J. Civ. Eng. 2021, 25, 1191–1203. [Google Scholar] [CrossRef]
  4. Chen, C.; Melville, B.W.; Nandasena, N.A.K.; Shamseldin, A.Y.; Wotherspoon, L. Experimental study of uplift loads due to tsunami bore impact on a wharf model. Coast. Eng. 2016, 117, 126–137. [Google Scholar] [CrossRef]
  5. Jia, C.; Yi, X.Y.; Guo, C.; Tan, H. Influence of wave direction on uplift force of sloping high piled wharf. J. Coast. Res. 2016, 2016, 1442–1446. [Google Scholar] [CrossRef]
  6. Lu, Y. The Optimization of automated container terminal scheduling based on proportional fair priority. Math. Probl. Eng. 2022, 2022, 7889048. [Google Scholar] [CrossRef]
  7. Nikolaieva, L.L.; Omelchenko, T.Y.; Haichenia, O.V. Hierarchical Management System for Container Vessels Automated Cargo Handling. J. ETA Marit. Sci. 2024, 12, 25–35. [Google Scholar] [CrossRef]
  8. Chang, Y.M.; Zhu, X.N.; Wang, L. Review on integrated scheduling of container terminals. J. Traffic Transp. Eng. 2019, 19, 136–146. (In Chinese) [Google Scholar]
  9. Niu, B.; Liu, Q.; Wang, Z.; Tan, L.; Li, L. Multi-objective bacterial colony optimization algorithm for integrated container terminal scheduling problem. Nat. Comput. 2021, 20, 89–104. [Google Scholar] [CrossRef]
  10. Zhou, Y.; Zheng, Y.; Liu, Y.; Pan, T.; Zhou, Y. A hybrid methodology for structural damage detection uniting FEM and 1D-CNNs: Demonstration on typical high-pile wharf. Mech. Syst. Signal Process. 2022, 168, 108738. [Google Scholar] [CrossRef]
  11. Madabhushi, G.S.; Boksmati, J.I.; Torres, S.G. Numerical and centrifuge modeling of gravity wharf structures subjected to seismic loading. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
  12. Dai, J.; Wang, D.Y.; Zuo, X.F.; He, T. A new overhead vertical wharf in inland rivers of Three Gorges Reservoir. Yangtze River 2014, 45, 44–47. (In Chinses) [Google Scholar]
  13. Liu, Y.X.; Wu, L.D.; Li, Y.Y. A new type of wharf structure the structure of semi—Covered type of deep water sheet pile wharf. Port Eng. Technol. 2005, 2002, 16–19. (In Chinses) [Google Scholar]
  14. Boroschek, R.L.; Baesler, H.; Vega, C. Experimental evaluation of the dynamic properties of a wharf structure. Eng. Struct. 2011, 33, 344–356. [Google Scholar] [CrossRef]
  15. Xie, Y.F.; Liu, C.L.; Gao, S.Y.; Tang, J.P.; Chen, Y. Lateral load bearing capacity of offshore high-piled wharf with batter piles. Ocean Eng. 2017, 142, 377–387. [Google Scholar] [CrossRef]
  16. Mai, H.T.; Lieu, Q.X.; Kang, J.; Lee, J. A novel deep unsupervised learning-based framework for optimization of truss structures. Eng. Comput. 2023, 39, 2585–2608. [Google Scholar] [CrossRef]
  17. Yao, H.; Huang, Y.; Ma, W.; Liang, L.; Zhao, Y. Dynamic Analysis of a Large Deployable Space Truss Structure Considering Semi-Rigid Joints. Aerospace 2023, 10, 821. [Google Scholar] [CrossRef]
  18. Qin, X.; Liang, M.Z.; Xie, X.L.; Song, H.L. Mechanical performance analysis and stiffness test of a new type of suspension bridge. Front. Struct. Civ. Eng. 2021, 15, 1160–1180. [Google Scholar] [CrossRef]
  19. Hou, B.R.; Li, X.; Ma, X.; Du, C.; Zhang, D.; Zheng, M.; Ma, F. The cost of corrosion in China. Npj Mater. Degrad. 2017, 1, 4. [Google Scholar] [CrossRef]
  20. Qian, B.; Hou, B.R.; Zheng, M. The inhibition effect of tannic acid on mild steel corrosion in seawater wet/dry cyclic conditions. Corros. Sci. 2013, 72, 1–9. [Google Scholar] [CrossRef]
  21. GB50017–2017; Standard for Design of Steel Structures. China Architecture & Publishing & Media Co., Ltd.: Beijing, China, 2017.
  22. GB50009-2012; Load Code for the Design of Buildings Structures. China Architecture & Publishing & Media Co., Ltd.: Beijing, China, 2012.
Buildings 14 02067 g001
Figure 1. WTO statistics.
Figure 1. WTO statistics.
Buildings 14 02067 g001
Buildings 14 02067 g002
Figure 2. Three-dimensional cantilevered wharf.
Figure 2. Three-dimensional cantilevered wharf.
Buildings 14 02067 g002
Buildings 14 02067 g003
Figure 3. Three-dimensional intermodal transport.
Figure 3. Three-dimensional intermodal transport.
Buildings 14 02067 g003
Buildings 14 02067 g004aBuildings 14 02067 g004b
Figure 4. Division of port functional areas.
Figure 4. Division of port functional areas.
Buildings 14 02067 g004aBuildings 14 02067 g004b
Buildings 14 02067 g005
Figure 5. Example of joint connection: (a) joint plate connection; (b) integral joint.
Figure 5. Example of joint connection: (a) joint plate connection; (b) integral joint.
Buildings 14 02067 g005
Buildings 14 02067 g006
Figure 6. Wharf model elevation and side layout (unit: cm).
Figure 6. Wharf model elevation and side layout (unit: cm).
Buildings 14 02067 g006
Buildings 14 02067 g007
Figure 7. The finite element mesh model of the new wharf.
Figure 7. The finite element mesh model of the new wharf.
Buildings 14 02067 g007
Buildings 14 02067 g008
Figure 8. Vertical force of pile block: (a) load combination I and (b) load combination II.
Figure 8. Vertical force of pile block: (a) load combination I and (b) load combination II.
Buildings 14 02067 g008
Buildings 14 02067 g009aBuildings 14 02067 g009b
Figure 9. Structural internal force of cantilever segment (unit: kN): (a) axial force of web member under load combination I; (b) axial force of web member under load combination II; (c) vertical shearing force of main beam under load combination I; (b) vertical shearing force of main beam under load combination II.
Figure 9. Structural internal force of cantilever segment (unit: kN): (a) axial force of web member under load combination I; (b) axial force of web member under load combination II; (c) vertical shearing force of main beam under load combination I; (b) vertical shearing force of main beam under load combination II.
Buildings 14 02067 g009aBuildings 14 02067 g009b
Buildings 14 02067 g010
Figure 10. The stress distribution of the joint (MPa): a–e are the cross-section numbers.
Figure 10. The stress distribution of the joint (MPa): a–e are the cross-section numbers.
Buildings 14 02067 g010
Buildings 14 02067 g011
Figure 11. Natural vibration modes: (a–e) the first five natural vibration modes and frequencies for the structure.
Figure 11. Natural vibration modes: (a–e) the first five natural vibration modes and frequencies for the structure.
Buildings 14 02067 g011
Buildings 14 02067 g012
Figure 12. The DH3821-Net static strain and stress testing acquisition system.
Figure 12. The DH3821-Net static strain and stress testing acquisition system.
Buildings 14 02067 g012
Buildings 14 02067 g013aBuildings 14 02067 g013b
Figure 13. Test point layout.
Figure 13. Test point layout.
Buildings 14 02067 g013aBuildings 14 02067 g013b
Buildings 14 02067 g014
Figure 14. Loading equipment: (a) test model and equipment; (b) jack; (c) oil hydraulic pump.
Figure 14. Loading equipment: (a) test model and equipment; (b) jack; (c) oil hydraulic pump.
Buildings 14 02067 g014
Buildings 14 02067 g015
Figure 15. Maximum stress of test model.
Figure 15. Maximum stress of test model.
Buildings 14 02067 g015
Buildings 14 02067 g016
Figure 16. Deflection of test model lower chord.
Figure 16. Deflection of test model lower chord.
Buildings 14 02067 g016
Buildings 14 02067 g017
Figure 17. The failure modes of the test model.
Figure 17. The failure modes of the test model.
Buildings 14 02067 g017
Table 1. Sectional properties and material consumption of each component.
Table 1. Sectional properties and material consumption of each component.
ComponentSection FormMaterialArea (m2)Ixx (m4)Iyy (m4)Izz (m4)Amount of Steel Used (t)Amount of Concrete Used (m3)
columnbox sectionQ4200.02900.0001520.0001020.00010224,683-
concrete filled steel box columnconcrete filled steel boxQ420 and C402.997.9594.5914.59121258308
main beambox sectionQ4200.05070.0005270.0007160.00022261,288-
secondary beambox sectionQ4200.01400.0002850.0006700.0001011649-
foundation main beamrectangularC401.620.3000.4370.109-3278
web memberbox sectionQ4200.01160.02740.01830.018344,987-
pile foundationcircularC603.141.5710.7850.785-22,579
floor slab-C40-----102,707
Note: The total consumption of Q420 steel was 134,732 t, and that of concrete was 136,872 m3.
Table 2. Material properties.
Table 2. Material properties.
TypeElastic Modulus E (GPa)Compressive Strength fc (MPa)Tensile Strength ft (MPa)Unit Weight γ (kN/m3)
C4032.519.11.7125.49
C603627.52.0425.49
Q235206.0321521576.98
Q420210.0637537576.98
Table 3. The vertical force distribution of each pile.
Table 3. The vertical force distribution of each pile.
Vertical ForceLoad Combination ILoad Combination II
Vertical Force (kN)Percentage (%)Vertical Force (kN)Percentage (%)
the first row of offward piles4,356,69751.783,676,22051.68
the second row of piles513,0586.10357,8085.03
the third row of piles1,612,47819.171,211,58617.03
the rest of piles1,931,21122.951,867,17826.25
Table 4. The vertical force distribution of each member for the cantilever segment.
Table 4. The vertical force distribution of each member for the cantilever segment.
Cantilever Segment Internal ForceLoad Combination ILoad Combination II
Shearing Force of Main Beam (kN)Axial Force of Web Member (kN)Vertical Component of Web Member (kN)Shearing Force of Main Beam (kN)Axial Force of Web Member (kN)Vertical Component of Web Member (kN)
maximum value1286143,71596,164883101,49767,915
summarized value112,0383,783,2932,531,51776,2612,623,1551,755,233
Vertical force percentage4.24%/95.76%4.16%/95.84%
Table 5. The distributed stresses of main components under load combinations I, II, and III.
Table 5. The distributed stresses of main components under load combinations I, II, and III.
Main ComponentsLoad Combination ILoad Combination IILoad Combination III
Compressive Stress (MPa)Tensile Stress (MPa)Compressive Stress (MPa)Tensile Stress (MPa)Compressive Stress (MPa)Tensile Stress (MPa)
column−302.7180.9−231.3127.8−216.8108.1
main beam−239.1270.9−167.2180.6−144.1149.0
web member−268.8196.3−176.3127.4−151.0106.4
Table 6. Structural displacement.
Table 6. Structural displacement.
Part of StructureMaximum Deflection of Floor Slab (mm)Maximum Vertical Deformation of Column (mm)Relative Deflection (mm)
second floor of shore segment21.235.3115.92
top floor of shore segment53.6240.0113.61
top floor of cantilever segment112.3489.6422.70
Table 7. Main sectional property and material consumption of four models.
Table 7. Main sectional property and material consumption of four models.
ComponentSection TypeSection Dimensions (mm)MaterialModel 1 (t)Model 2 (t)Model 3 (t)Model 4 (t)
chordbox-shaped section60 × 30 × 3.5Q235 steel0.02920.04380.05840.0730
web memberreal-circular section30 × 30 × 3.5Q235 steel0.01880.03760.05640.0751
vertical memberreal-circular section50 × 50 × 4Q235 steel0.00570.01140.01720.0229
Table 8. Stress distribution of test points of chords.
Table 8. Stress distribution of test points of chords.
ComponentStress (MPa)
Middle of Simply Supported SegmentCantilever Segment
Cantilever Support LineRight Section of the Middle
test model I
chord 172.1174.655.4
chord 2−70.2−152.2−70.8
test model II
chord 360.3137.565.0
chord 4−1.056.7−22.2
chord 5−68.8−143.4−64.5
test model III
chord 664.1145.250.2
chord 720.758.422.5
chord 8−21.5−62.4−32.6
chord 9−55.3−143.7−55.0
test model IV
chord 1056.8103.663.2
chord 1127.373.120.5
chord 122.640.2−4.5
chord 13−28.0−53.3−32.4
chord 14−44.8−140.0−52.9
Table 9. Stress distribution of test points of web members.
Table 9. Stress distribution of test points of web members.
Test PointStressTest PointStress
test model I
163.12−69.7
test model II
3−75.0458.1
560.26−81.0
test model III
765.18−72.4
9−71.01070.9
1162.812−109.3
test model IV
13−82.21448.7
15−89.11672.8
1767.318−90.1
1958.720−129.6
Table 10. Deflections of different chords.
Table 10. Deflections of different chords.
ComponentDeflection (mm)
Simply Supported SegmentCantilever Segment
MiddleEnd
test model I
chord 10.73−2.56−5.33
chord 20.71−2.55−5.34
test model II
chord 30.47−1.58−3.57
chord 40.43−1.58−3.52
chord 50.46−1.62−3.48
test model III
chord 60.27−1.35−2.83
chord 70.25−1.36−2.82
chord 80.24−1.32−2.74
chord 90.26−1.30−2.71
test model IV
chord 100.06−1.24−2.60
chord 110.07−1.30−2.62
chord 120.11−1.31−2.47
chord 130.08−1.27−2.41
chord 140.12−1.27−2.43
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

He, X.; Qin, X.; Huang, M.; Xie, X.; Du, C.; Fan, W. A New Type of Wharf and a Study of Its Mechanical Properties by FE (Finite Element) and Experimental Methods. Buildings 2024, 14, 2067. https://doi.org/10.3390/buildings14072067

AMA Style

He X, Qin X, Huang M, Xie X, Du C, Fan W. A New Type of Wharf and a Study of Its Mechanical Properties by FE (Finite Element) and Experimental Methods. Buildings. 2024; 14(7):2067. https://doi.org/10.3390/buildings14072067

Chicago/Turabian Style

He, Xiang, Xia Qin, Mian Huang, Xiaoli Xie, Chenhao Du, and Wenyang Fan. 2024. "A New Type of Wharf and a Study of Its Mechanical Properties by FE (Finite Element) and Experimental Methods" Buildings 14, no. 7: 2067. https://doi.org/10.3390/buildings14072067

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop