Sustainable Structural System Selection Using Hybrid Fuzzy Multi-Criteria Decision Model Based on Seismic Performance
Abstract
:1. Introduction
2. Literature Review
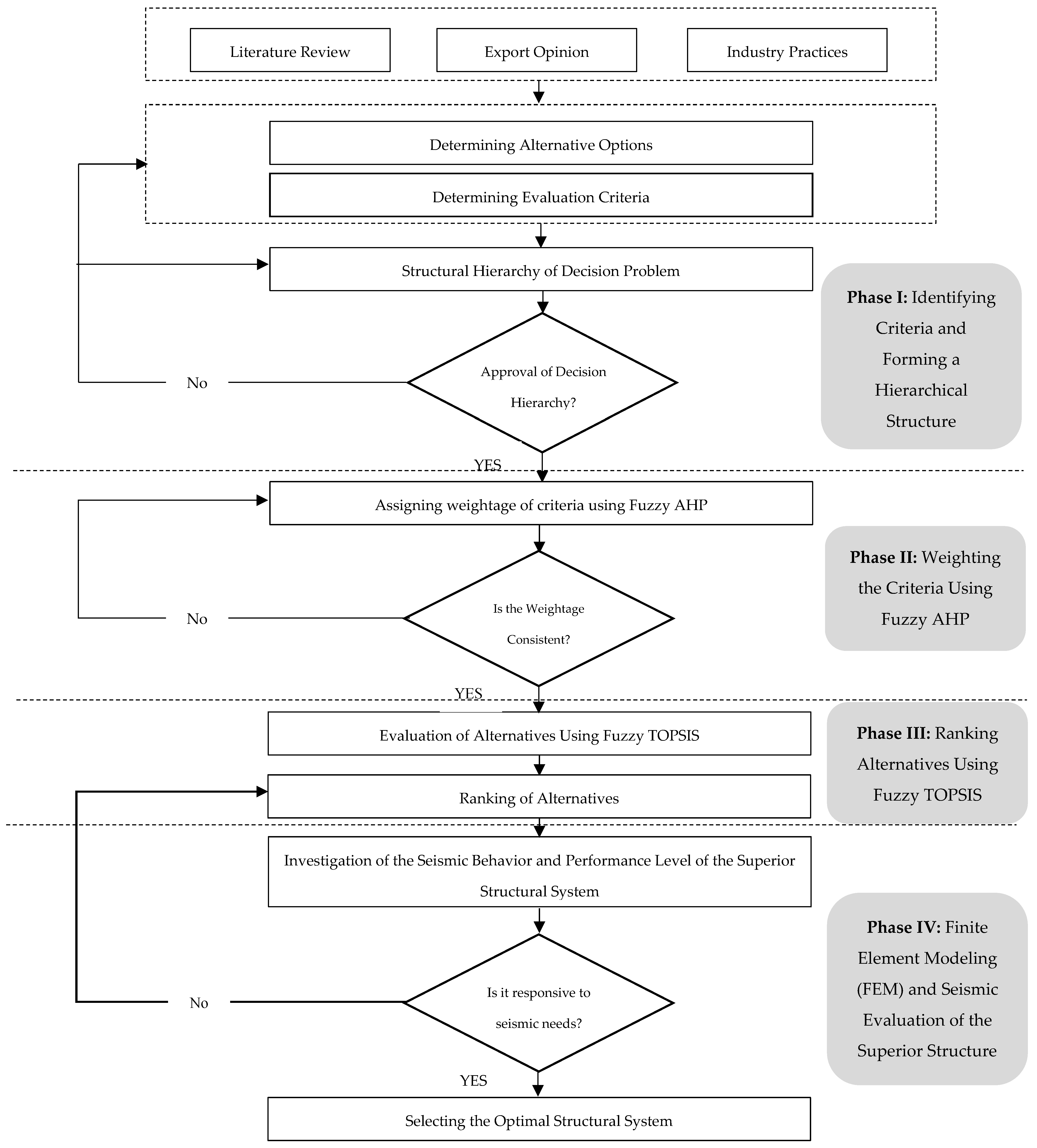
3. Methods
3.1. Identification and Preparation of Required Information
3.2. Hybrid MCDM Method
3.2.1. Fuzzy AHP Method
3.2.2. Fuzzy TOPSIS Method
4. Research Findings and Discussion
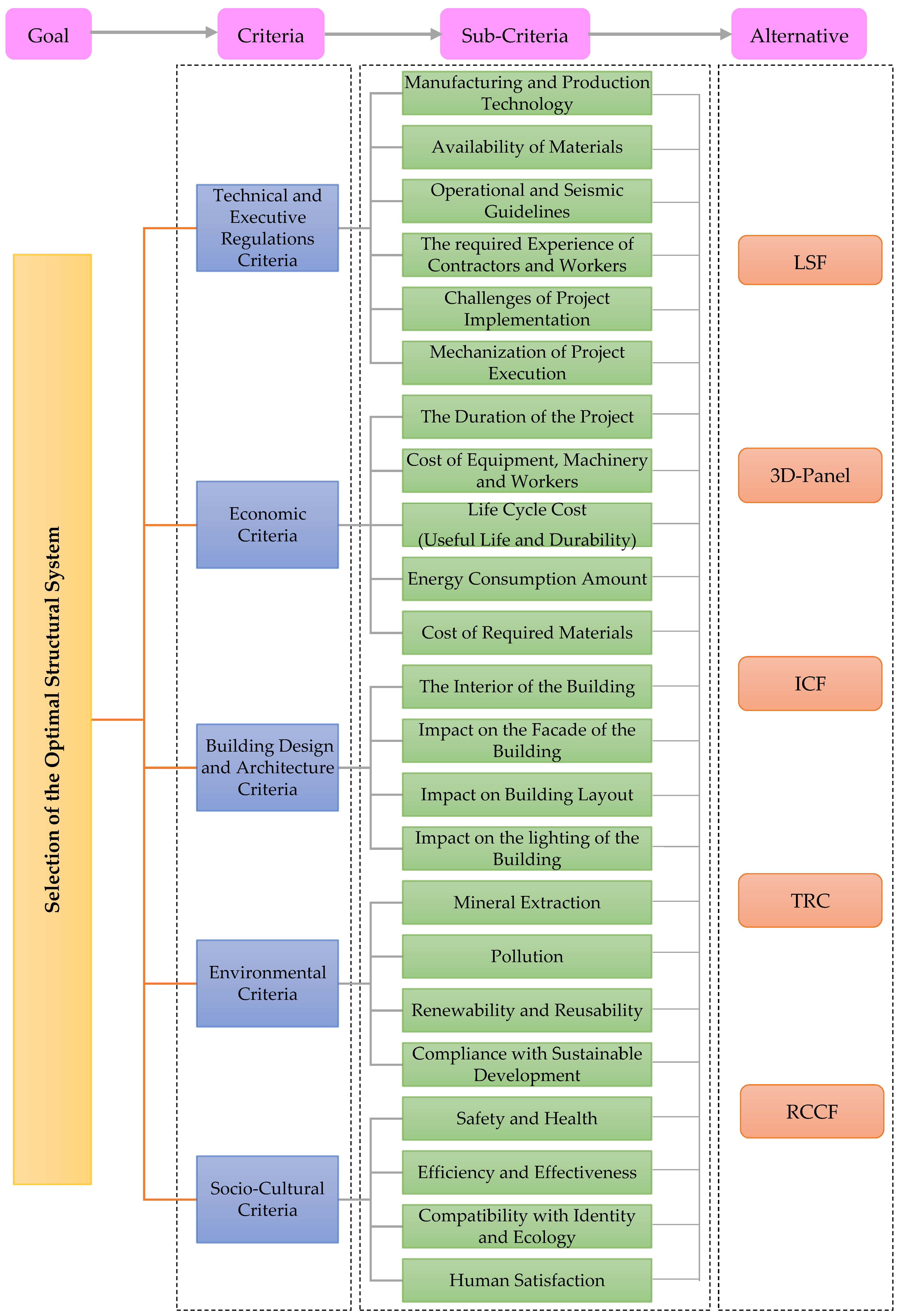
4.1. Identification of Criteria, Sub-Criteria, and Alternatives (Phase I)
4.2. Prioritizing Criteria and Sub-Criteria (Phase II)
4.3. Prioritizing Structural Systems (Phase III)
4.4. Case Study: Numerical Modeling and Seismic Performance Evaluation (Phase IV)

4.4.1. Fundamental Principles
Stiffness
Ductility
Response Modification Factor
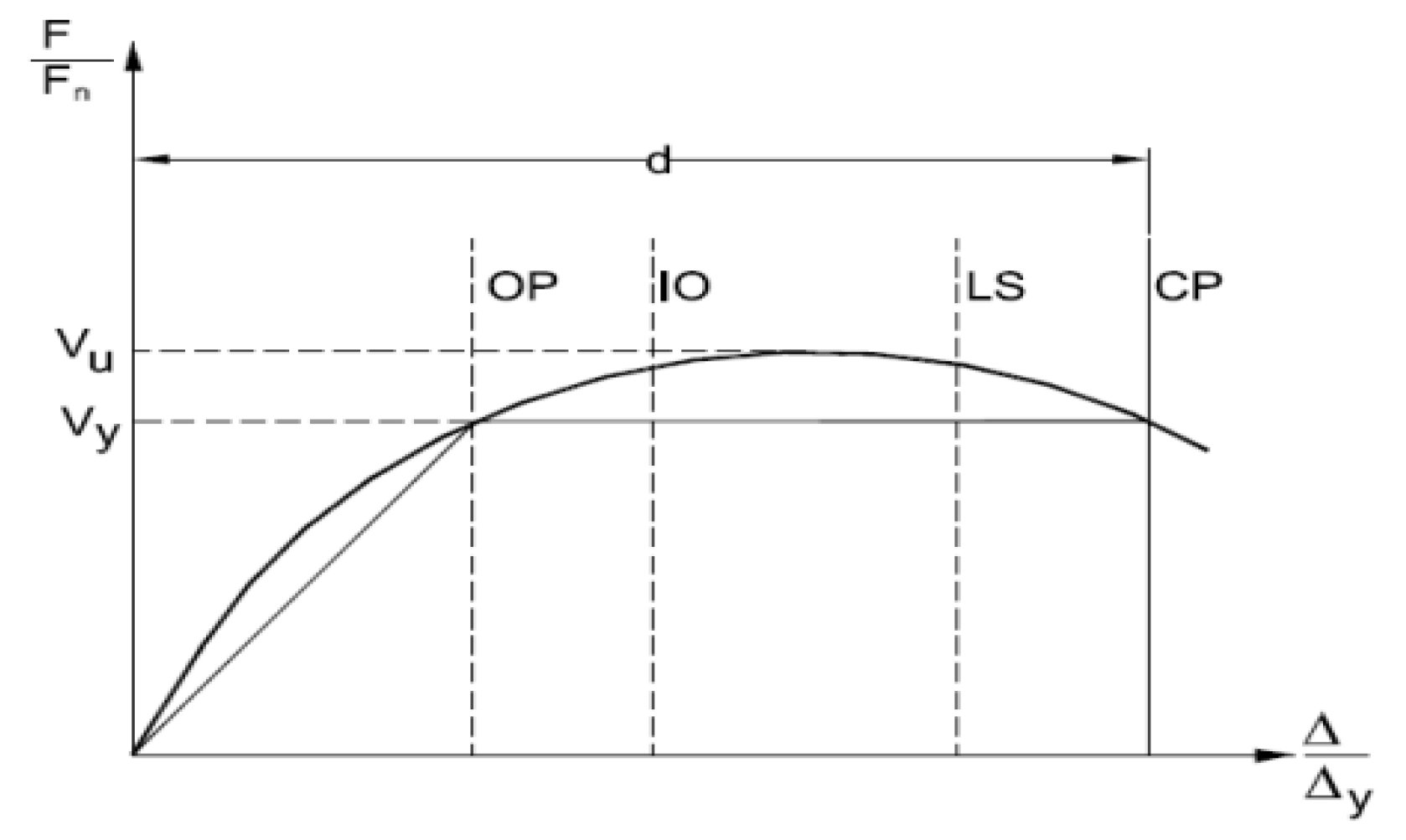
Performance Level
| Equations | Description | Step | |
|---|---|---|---|
| (25) | These equations link structural displacements to base shear, utilizing the effective mass index, participation factor, base shear, total construction weight, and roof form shape. The capacity curve is created using the pushover method, plotting base shear against roof displacement. | 1 | |
| (26) | |||
| where α1, PF1, V, W, and φ1,roof represent the effective mass index in the first mode, the participation factor in the first mode, base shear, total construction weight (including a percentage of live load), and the first mode form shape in the roof floor, respectively. | |||
| The seismic demand curve is derived from the elastic design spectrum with 5% damping, adjusted using structural behavior reduction coefficients. | 2 | ||
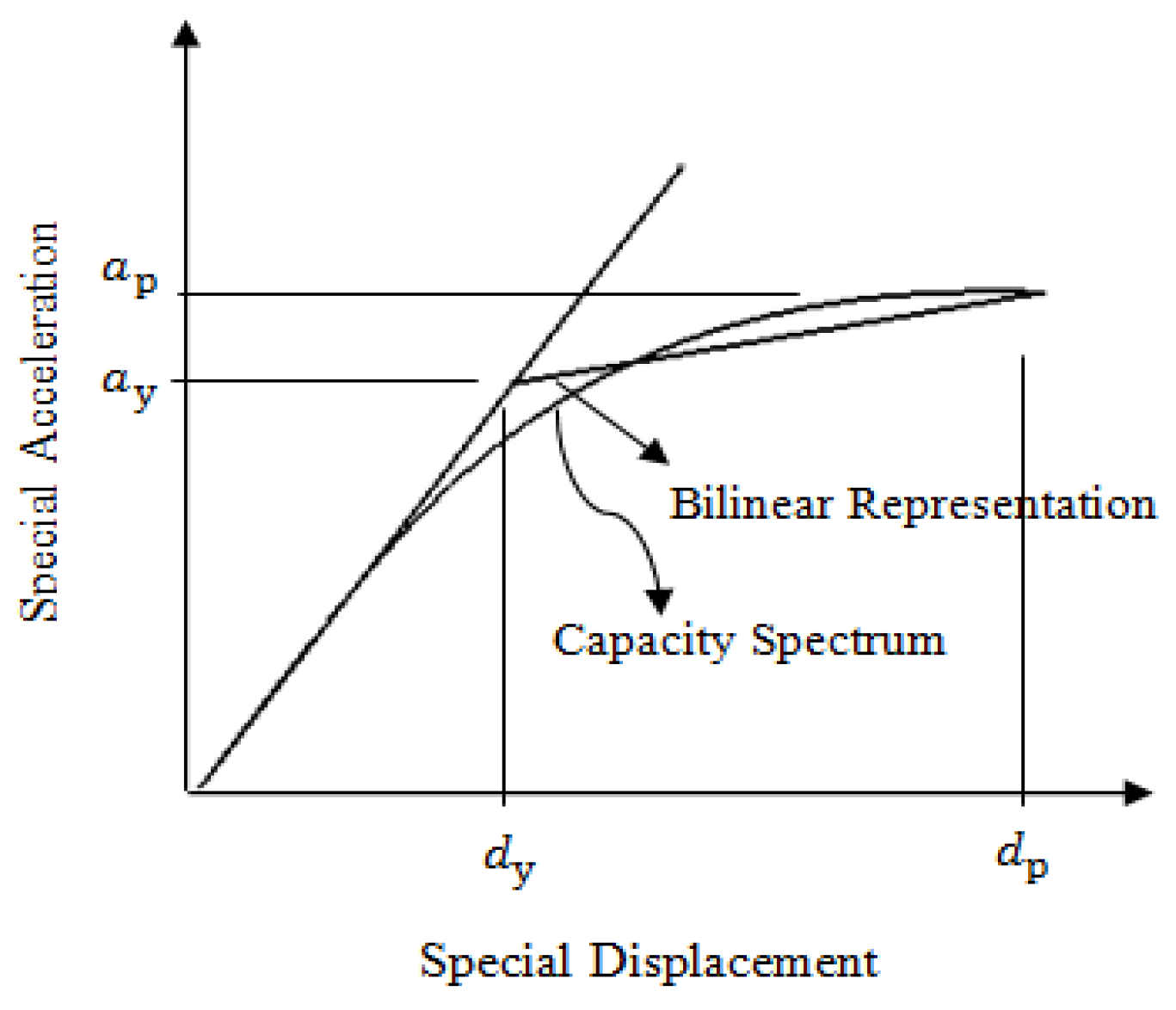
| (27) | Using this equation, the equivalent damping, period, and yield points are calculated from the capacity curve, allowing for the estimation of energy absorption by the structure. Parameters for converting ideal hysteresis diagrams to a parallelogram and other specifics are shown in Figure 10 (data from [97]). | 3 | |
| The coefficient of kh was utilized to transform the ideal Hysteresis diagram into a parallelogram, with other parameters detailed in Figure 10. | |||
| (28) | These equations are used to plot the reduced acceleration displacement response spectrum (ADRS), calculating effective damping and spectrum reduction coefficients. | 4 | |
| (29) | |||
| Target displacement (dpi) is determined, where the capacity curve intersects the reduced Sa − Sd spectrum. The corresponding forces are assessed through non-linear static analysis (refer to [97]). | 5 | ||
| An iterative process ensures accuracy by comparing dpi with initial assumptions and repeating the previous steps until convergence is achieved. | 6 | ||
4.4.2. Finite Element Modeling
Verification of Analytical Model by Laboratory Model
Modeling Accuracy and Experimental Comparison
Parameter Analysis

4.4.3. Findings and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdollahzadeh, G.; Taheri Amiri, M.J.; Akbari Kaffash, E.; Hemmatian, M.; Keihanfard, S. Choosing an Appropriate Factorial System through the Modern and Outmoded System by Two Approaches Anp Ahp-fuzzy. J. Math. Comput. Sci. 2013, 6, 107–117. [Google Scholar] [CrossRef]
- Afolabi, A.O.; Nnaji, C.; Okoro, C. Immersive Technology Implementation in the Construction Industry: Modeling Paths of Risk. Buildings 2022, 12, 363. [Google Scholar] [CrossRef]
- Alavi, S.M.; Naser Sadrabadi, A.; Zare Ahmadabadi, H.; Hosseini Bamakn, S.M. Recognizing and Prioritizing of Construction 4.0” Drivers in Iran for the Horizon of Twenty Years. J. Iran Futures Stud. 2022, 7, 159–178. [Google Scholar]
- Almeida, P.; Solas, M.; Andres, R.; Buhler, M.M.; Gerbert, P.; Castagnino, S.; Rothballer, C. Shaping the Future of Construction a Breakthrough in Mindset and Technology; World Economic Forum: Cologny, Switzerland, 2016. [Google Scholar] [CrossRef]
- Craveiro, F.; Duarte, J.P.; Bartolo, H.; Bartolo, P.J. Additive Manufacturing as an Enabling Technology for Digital Construction: Perspective on Construction 4.0. Autom. Constr. 2019, 103, 251–267. [Google Scholar] [CrossRef]
- Abbaszadeh, G. Pathology of mass housing projects in Iran (Mehr Housing Plan). J. Fundam. Appl. Sci. 2016, 8, 885–915. [Google Scholar] [CrossRef]
- Rezafar, A. The effect of politics on the formation of urban aesthetics, the case of Iran. Cities 2023, 132, 104095. [Google Scholar] [CrossRef]
- Rastogi, S. Construction 4.0: The 4th Generation Revolution. In Proceedings of the Indian Lean Construction Conference–ILCC, IIT Madras, Chennai, India, 27–29 July 2017; pp. C288–C298. [Google Scholar]
- Klinc, R.; Turk, Z. Construction 4.0—Digital Transformation of One of the Oldest Industries. Econ. Bus. Rev. 2019, 21, 393–410. [Google Scholar] [CrossRef]
- Mardani, A. Evaluation of Criteria Influencing industrialized building system in Iran based on Vitruvius’s Three Principles of Architecture. International. J. Archit. Eng. Urban Plan. 2023, 33, 4. [Google Scholar]
- Hashemi, A.; Noguchi, M.; Altan, H. Feasibility of Application of Modern Methods of Construction in Iran. In Proceedings of the International Conference of ZEMCH, Bari-Lecce, Italy, 22–24 September 2015. [Google Scholar]
- Su, P.; Wu, X. Construction and Quantitative Analysis of Housing Industrialization Index System. Adv. Econ. Bus. Manag. Res. 2022, 650, 18–23. [Google Scholar]
- Shen, L.F.; Deng, X.L.; Ma, C.B. Thinking of Speeding up Transformation Construction for Housing Industry–Based on the Perspective of Housing Industrialization. Adv. Mater. Res. 2013, 709, 748–751. [Google Scholar] [CrossRef]
- Huang, Z.; Fu, S. Construction Industrialization and Sustainability. In Proceedings of the International Conference on Construction and Real Estate Management, Edmonton, AB, Canada, 21–24 May 2019. [Google Scholar]
- Yunus, R.; Yang, J. Improving ecological performance of industrialized building systems in Malaysia. Constr. Manag. Econ. 2014, 32, 183–195. [Google Scholar] [CrossRef]
- Gudiene, N.; Banaitis, A.; Podvezko, V.; Banaitiene, N. Identification and evaluation of the critical success factors for construction projects in Lithuania: AHP approach. J. Civ. Eng. Manag. 2014, 20, 350–359. [Google Scholar] [CrossRef]
- Eram, T.; Mirsaeedy, L. Selection of optimal building system by using analytic hierarchy process A case study: Residential project in Gonbad-e-Kavos. In Proceedings of the 3rd International Conference on Research in Science and Technology, Berlin, Germany, 9 July 2016. [Google Scholar]
- Si, J.; Marjanovic-Halburd, M.; Nasiri, F.; Bell, S. Assessment of Building-Integrated Green Technologies: A Review and Case Study on Applications of Multi-Criteria Decision Making (MCDM) Method. Sustain. Cities Soc. 2016, 27, 106–115. [Google Scholar] [CrossRef]
- Erdogan, S.A.; Saparauskas, J.; Turskis, Z. A Multi-Criteria Decision-Making Model to Choose the Best Option for Sustainable Construction Management. Sustainability 2019, 11, 2239. [Google Scholar] [CrossRef]
- Siadati, R.; Shahhosseini, V. Comparison of Modern Structural Systems based on a Fuzzy Analytical Hierarchy Process. Indian J. Sci. Technol. 2015, 8, 1–5. [Google Scholar] [CrossRef]
- Balali, V.; Zahraie, B.; Roozbahani, A. Integration of ELECTRE III and PROMETHEE II Decision-Making Methods with an Interval Approach: Application in Selection of Appropriate Structural Systems. J. Comput. Civ. Eng. 2014, 28, 297–314. [Google Scholar] [CrossRef]
- Islam, H.; Jollands, M.; Setunge, S.; Bhuiyan, M.A. Optimization approach of balancing life cycle cost and environmental impacts on residential building design. Energy Build. 2015, 87, 282–292. [Google Scholar] [CrossRef]
- Mathiyazhagan, K.; Gnanavelbabu, A.; Lokesh Prabhuraj, B. A sustainable assessment model for material selection in construction industries perspective using hybrid MCDM approaches. J. Adv. Manag. Res. 2019, 16, 234–259. [Google Scholar] [CrossRef]
- Zumrut, I.B.; Baran, H.B.; Ozbealta, T.G. Multi–criteria decision-making approach for selecting a structural system of an industrial facility. Organ. Technol. Manag. Constr. 2022, 14, 2656–2665. [Google Scholar] [CrossRef]
- Aghazadeh, E.; Yildirim, H.; Kuruoglu, M. A Hybrid Fuzzy MCDM Methodology for Optimal Structural System Selection Compatible with Sustainable Materials in Mass-Housing Projects. Sustainability 2022, 14, 13559. [Google Scholar] [CrossRef]
- Alam Bhuiyan, M.M.; Hammad, A. A Hybrid Multi-Criteria Decision Support System for Selecting the Most Sustainable Structural Material for a Multistory Building Construction. Sustainability 2023, 15, 3128. [Google Scholar] [CrossRef]
- Jalali, G.; Araghizadeh, M.; Hashemi Fesharaki, S.J. Determination and prioritization of the most effective criteria in architectural design of office buildings from passive defense point of view by using AHP method. Emerg. Manag. 2019, 8, 67–76. [Google Scholar]
- Ahmadnejad Karimi, M.; Abadi, M.; Azimi, M. Explaining the Challenges of Using Structures in Architectural Design Case study: Architecture Students and Graduates. J. Archit. Urban Plan. 2023, 15, 43–61. [Google Scholar]
- Golabchi, M.; Mazaherian, H. New Construction Technologies; University of Tehran Press: Tehran, Iran, 2018. [Google Scholar]
- Saaty, T.L. What Is the Analytic Hierarchy Process? Springer: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Torfi, F.; Farahani, R.Z.; Rezapour, S. Fuzzy AHP to determine the relative weights of evaluation criteria and Fuzzy TOPSIS to rank the alternatives. Appl. Soft Comput. 2010, 10, 520–528. [Google Scholar] [CrossRef]
- Wang, T.C.; Lee, H.D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Kelemenis, A.; Askounis, D. A new TOPSIS-based multi-criteria approach to personnel selection. Expert Syst. Appl. 2010, 37, 4999–5008. [Google Scholar] [CrossRef]
- Hsieh, T.Y.; Lu, S.T.; Tzeng, G.H. Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Proj. Manag. 2004, 22, 573–584. [Google Scholar] [CrossRef]
- Akadiri, P.O.; Olomolaiye, P.O. Development of Sustainable Assessment Criteria for Building Materials Selection. Eng. Constr. Archit. Manag. 2012, 19, 666–687. [Google Scholar] [CrossRef]
- Edwards, K.L. Selecting materials for optimum use in engineering components. Mater. Des. 2005, 26, 469–473. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, Y.; Wang, X.J.; Chin, K.S.; Tsui, K.L. Fostering linguistic decision-making under uncertainty: A proportional interval type-2 hesitant fuzzy TOPSIS approach based on Hamacher aggregation operators and andness optimization models. Inf. Sci. 2019, 500, 229–258. [Google Scholar] [CrossRef]
- Jaskowski, P.; Biruk, S.; Bucon, R. Assessing contractor selection criteria weights with fuzzy AHP method application in group decision environment. Autom. Constr. 2010, 19, 120–126. [Google Scholar] [CrossRef]
- Jahan, A.; Ismail, M.Y.; Sapuan, S.M.; Mustapha, F. Material screening and choosing methods—A review. Mater. Des. 2010, 31, 696–705. [Google Scholar] [CrossRef]
- Vahedi Nikbakht, M.; Gheibi, M.; Montazeri, H.; Yeganeh Khaksar, R.; Moezzi, R.; Vadiee, A. Identification and Ranking of Factors Affecting the Delay Risk of High-Rise Construction Projects Using AHP and VIKOR Methods. Infrastructures 2024, 9, 24. [Google Scholar] [CrossRef]
- Road, Housing & Urban Development Research Center. New Technologies Used in the Construction Industry, 1st ed.; BHRC: Teheran, Iran, 2002. [Google Scholar]
- Nieto-Morote, A.; Ruz-Vila, F. A fuzzy multi-criteria decision-making model for construction contractor prequalification. Autom. Const. 2012, 25, 8–19. [Google Scholar] [CrossRef]
- Zhao, R.; Su, H.; Chen, X.; Yu, Y. Commercially Available Materials Selection in Sustainable Design: An Integrated Multi-Attribute Decision Making Approach. Sustainability 2016, 8, 79. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, L.L.; Chin, K.S.; Yang, Y.; Pedrycz, W.; Chang, J.P.; Martínez, L.; Skibniewski, M.J. Sustainable building material selection: An integrated multi-criteria large group decision making framework. Appl. Soft Comput. 2021, 113, 107903. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Chouinard, L.E.; Mirza, M.S. Design strategies using multi-criteria decision-making tools to enhance the performance of building façades. J. Build. Eng. 2020, 30, 101274. [Google Scholar] [CrossRef]
- Marzouk, M.M.; El Kherbawy, A.A.; Khalifa, M. Factors influencing sub–contractors selection in construction projects. HBRC J 2013, 9, 150–158. [Google Scholar] [CrossRef]
- Morzangoushi, A.; Kabiri, M.M.; Ebrahimi Dehshiri, S. Identifying and Ranking the Contractors Selecting Criteria. Indian J. Fundam. Appl. Life Sci. 2015, 5, 2410–2416. [Google Scholar]
- Nejatyan, E.; Sarvari, H.; Hosseini, S.A.; Javanshir, H. Determining the Factors Influencing Construction Project Management Performance Improvement through Earned Value-Based Value Engineering Strategy: A Delphi-Based Survey. Buildings 2023, 13, 1964. [Google Scholar] [CrossRef]
- Govindan, K.; Madan Shankar, K.; Kannan, D. Sustainable material selection for construction industry—A hybrid multi criteria decision making approach. Renew. Sustain. Energy Rev. 2016, 55, 1274–1288. [Google Scholar] [CrossRef]
- Zhong, S.; Elhegazy, H.; Elzarka, H. Key factors affecting the decision-making process for buildings projects in Egypt. Ain Shams Eng. J. 2022, 13, 101597. [Google Scholar] [CrossRef]
- Gunduz, M.; Aly, A.A.; El-Mekkawy, T. Value Engineering Factors with an Impact on Design Management Performance of Construction Projects. J. Manag. Eng. 2022, 38, 3. [Google Scholar] [CrossRef]
- Tuzkaya, G.; Gulsun, B.; Kahraman, C.; Ozgen, D. An integrated fuzzy multi–criteria decision making methodology for material handling equipment selection problem and an application. Expert Syst. Appl. 2010, 37, 2853–2863. [Google Scholar] [CrossRef]
- Mostavi, E.; Asadi, S.; Boussa, D. Development of a new methodology to optimize building life cycle cost, environmental impacts, and occupant satisfaction. Energy 2017, 121, 606–615. [Google Scholar] [CrossRef]
- Balezentis, T.; Streimikiene, D. Multi-criteria ranking of energy generation scenarios with Monte Carlo simulation. Appl. Energy 2017, 185, 862–871. [Google Scholar] [CrossRef]
- Cui, B.; Wang, S.; Sun, Y. Life-cycle cost benefit analysis and optimal design of small scale active storage system for building demand limiting. Energy 2014, 73, 787–800. [Google Scholar] [CrossRef]
- Rajeshkumar, V.; Anandaraj, S.; Kavinkumar, V.; Elango, K.S. Analysis of factors influencing formwork material selection in construction buildings. Mater. Today Proc. 2021, 37, 880–885. [Google Scholar] [CrossRef]
- Wang, P.K.; Perng, Y.H. Critical Criteria for Customer Satisfaction of Interior Design. Mater. Sci. Eng. 2019, 652, 012012. [Google Scholar] [CrossRef]
- El-Zeiny, R.M. Interior Design of Workplace and Performance Relationship: Private sector corporations in Egypt. Asian J. Environ. Behav. Stud. 2018, 3, 109–118. [Google Scholar] [CrossRef]
- Balali, A.; Valipour, A. Identification and selection of building façade’s smart materials according to sustainable development goals. Sustain. Mater. Technol. 2020, 26, e00213. [Google Scholar] [CrossRef]
- Akbari, P.; Yazdanfar, S.A.; Hosseini, S.B.; Norouzian-Maleki, S. Identification of Building Façade Functions by Using Fuzzy TOPSIS Technique. Space Ontol. Int. J. 2020, 9, 37–45. [Google Scholar]
- Singh, A.K.; Avikal, S.; Kumar, N.; Kumar, M.; Thakura, P. A fuzzy-AHP and M − TOPSIS based approach for selection of composite materials used in structural applications. Mater. Today Proc. 2020, 26, 3119–3123. [Google Scholar] [CrossRef]
- Nasser, K.; Thabet, W.; Beliveau, Y. A procedure for multi-criteria selection of building assemblies. Autom. Constr. 2003, 12, 543–560. [Google Scholar] [CrossRef]
- Wagdi, D.; Abou-Zeid, M.N.; Tarabieh, K. Materials Selection for Improved Indoor Air Quality in Residential Buildings: A Pre-occupancy Assessment. In Proceedings of the PLEA 2015 Architecture in (R.) Evolution, Bologna, Italy, 9–11 September 2015. [Google Scholar]
- Vilutiene, T.; Kumetaitis, G.; Kiaulakis, A.; Kalibatas, D. Assessing the Sustainability of Alternative Structural Solutions of a Building: A Case Study. Buildings 2020, 10, 36. [Google Scholar] [CrossRef]
- Chatterjee, P.; Chakreborty, S. Material selection using preferential ranking methods. Mater. Des. 2012, 35, 384–393. [Google Scholar] [CrossRef]
- Onut, S.; Kara, S.S.; Mert, S. Selecting the Suitable Material Handling Equipment in the Presence of Vagueness. Int. J. Adv. Manuf. Technol. 2009, 44, 818–828. [Google Scholar] [CrossRef]
- Wong, J.K.W.; Li, H. Application of the analytic hierarchy process (AHP) in multi-criteria analysis of the selection of intelligent building systems. Build. Environ. 2008, 43, 108–125. [Google Scholar] [CrossRef]
- Li, H.C.; You, J.X.; Zhen, L.; Fan, X.J. A Novel Hybrid Multiple Criteria Decision Making Model for Material Selection with Target-Based Criteria. Mater. Des. 2014, 60, 380–390. [Google Scholar] [CrossRef]
- Emovon, I.; Oghenenyerovwho, O.S. Application of MCDM Method in Material Selection for Optimal Design: A review. Results Mater. 2020, 7, 100115. [Google Scholar] [CrossRef]
- Zakeri, S.; Chatterjee, P.; Konstantas, D.; Ecer, F. A Decision Analysis Model for Material Selection Using Simple Ranking Process. Sci. Rep. 2023, 13, 8631. [Google Scholar] [CrossRef] [PubMed]
- Afrasiabi, A.; Tavana, M.; Di Caprio, D. An Extended Hybrid Fuzzy Multi-Criteria Decision Model for Sustainable and Resilient Supplier Selection. Environ. Sci. Pollut. Res. 2022, 29, 37291–37314. [Google Scholar] [CrossRef] [PubMed]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A new multi-criteria decision making approach for sustainable material selection problem: A critical study on rank reversal problem. J. Clean. Prod. 2018, 182, 466–484. [Google Scholar] [CrossRef]
- Agrawal, R. Sustainable material selection for additive manufacturing technologies: A critical analysis of rank reversal approach. J. Clean. Prod. 2021, 296, 126500. [Google Scholar] [CrossRef]
- Thakkar, J.J. Multi-Criteria Decision Making; Springer Nature: Berlin/Heidelberg, Germany; Singapore, 2021. [Google Scholar]
- Martinez, M.J. Simplified Nonlinear Finite Element Analysis of Buildings with CFS Shear Wall Panels. J. Constr. Steel Res. 2011, 67, 565–575. [Google Scholar] [CrossRef]
- Javaheri-Tafti, M.R.; Ronagh, H.R.; Behnamfar, F.; Memarzadeh, P. An experimental investigation on the seismic behavior of cold-formed steel walls sheathed by thin steel plates. Thin-Walled Struct. 2014, 80, 66–79. [Google Scholar] [CrossRef]
- Zeynalian, M.; Ronagh, H.R. Seismic performance of cold formed steel walls heathed by fibre-cement board panels. J. Constr. Steel Res. 2015, 107, 1–11. [Google Scholar] [CrossRef]
- Lotfi, M. Evaluation Performance Seismic Structures of Cold-Formed Steel (CFS). Master’s Thesis, University of Semnan, Semnan, Iran, 2014. [Google Scholar]
- Gerami, M.; Lotfi, M.; Nejat, R. Inelastic behavior of cold-formed braced walls under monotonic and cyclic loading. Int. J. Adv. Struct. Eng. 2015, 7, 181–209. [Google Scholar] [CrossRef]
- Gerami, M.; Lotfi, M. Analytical Analysis of Seismic Behavior of Cold-Formed Steel Frames with Strap Brace and Sheathings Plates. Adv. Civ. Eng. 2014, 2014, 535120. [Google Scholar] [CrossRef]
- Ayatollahi, S.R.; Usefi, N.; Ronagh, H.; Izadnia, M.; Javaheri, M.R. Performance of gypsum sheathed CFS panels under combined lateral and gravity loading. J. Constr. Steel Res. 2020, 170, 106125. [Google Scholar] [CrossRef]
- Yilmaz, F.; Mojtabaei, S.M.; Hajirasouliha, I.; Becque, J. Behaviour and performance of OSB-sheathed cold-formed steel stud wall panels under combined vertical and seismic loading. Thin-Walled Struct. 2023, 183, 110419. [Google Scholar] [CrossRef]
- COLA-UCI Light Frame Committee. Report of a Testing Program of Light-Framed Walls with Wood-Sheathed Shear Panels; Final report to the City of Los Angeles; Department of Building and Safety, Structural Engineering Association of Southern California: Irvin, CA, USA, 2001. [Google Scholar]
- Fulop, L.; Dubina, D. Performance of wall-stud cold-formed shear panels under monotonic and cyclic loading Part I: Experimental research. Thin-Walled Struct. 2004, 42, 321–338. [Google Scholar] [CrossRef]
- Fulop, L.; Dubina, D. Performance of wall-stud cold-formed shear panels under monotonic and cyclic loading Part II: Numerical modeling and performance analysis. J. Thin-Walled Struct. 2004, 42, 339–349. [Google Scholar] [CrossRef]
- NAHB. Monotonic Tests of Cold-Formed Steel Shear Walls with Openings; NAHB Research Center, Inc.: Upper Marlboro, MD, USA; The American Iron and Steel Institute, AISI Publication: Washington, DC, USA, 1997. [Google Scholar]
- Branston, A.E.; Chen, C.Y.; Boudreault, F.A.; Rogers, C. Testing of Light Gauge Steel Frame/Wood Structural Panel Shear Walls. Can. J. Civ. Eng. 2006, 33, 561–572. [Google Scholar] [CrossRef]
- Ye, J.; Wang, X.; Jian, H.; Jia, H.; Zhao, M. Cyclic performance of cold-formed steel shear walls sheathed with double-layer wallboards on both sides. Thin-Walled Struct. 2015, 92, 146–159. [Google Scholar] [CrossRef]
- Macillo, V.; Fiorino, L.; Landolfo, R. Seismic response of CFS shear walls sheathed with nailed gypsum panels: Experimental tests. Thin-Walled Struct. 2017, 120, 161–171. [Google Scholar] [CrossRef]
- Landolfo, R.; Campiche, A.; Iuorio, O.; Fiorino, L. Seismic performance evaluation of CFS strap-braced buildings through experimental tests. Structures 2021, 33, 3040–3054. [Google Scholar] [CrossRef]
- Shi, Y.; Gu, Y.; Xu, Y.; Li, H.; Yang, X. Seismic behavior of steel-sheathed cold-formed steel shear walls with reinforced end columns. J. Constr. Steel Res. 2022, 197, 107509. [Google Scholar] [CrossRef]
- Gunalan, S.; Mahendran, M. Review of current fire design rules for cold-formed steel wall systems. J. Fire Sci. 2014, 32, 3–34. [Google Scholar] [CrossRef]
- FEMA (Federal Emergency Management Agency). Guidelines for the Seismic Rehabilitation of Buildings (FEMA 273); FEMA Publication: Washington, DC, USA, 1997. [Google Scholar]
- ASTM. Standard Test Methods for Cyclic (Reversed) Load Test for Shear Resistance of Framed Walls for Buildings; ASTM Publication: West Conshohocken, PA, USA, 2007. [Google Scholar]
- Newmark, N.M.; Hall, W.J. Earthquake Spectra and Design; Earthquake Engineering Research Institute: Berkeley, CA, USA, 1982. [Google Scholar]
- Branston, A.E.; Boudreault, F.A.; Chen, C.Y.; Rogers, C.A. Light Gauge Steel Frame/Wood Structural Panel Shear Walls Design Method. Can. J. Civ. Eng. 2006, 33, 872–889. [Google Scholar] [CrossRef]
- ATC-40 (Applied Technology Council). Seismic Evaluation and Retrofit of Concrete Buildings; California Seismic Safety Commission: Grapevine, CA, USA, 1997; Available online: https://www.atcouncil.org (accessed on 13 June 2024).
- MSC Nastran. Users Guide MSC Software, Version 2012; MSC Software Corporation Publication: Santa Ana, CA, USA, 2012. [Google Scholar]
- ASTM 370; Standard Test Methods and Definitions Testing of Steel Products. ASTM Publication: West Conshohocken, PA, USA, 2006.
- Al-Kharat, M.; Rogers, C.A. Inelastic performance of cold-formed steel strap braced walls. J. Constr. Steel Res. 2007, 63, 460–474. [Google Scholar] [CrossRef]
- Hatami, S.; Rahmani, A. Determining the Lateral Resistance and Displacement of Shear Wall Panels in Cold-Formed Steel Structures. J. Comput. Methods Eng. 2012, 30, 57–73. [Google Scholar]




| Information | Structural System |
|---|---|
| This construction system enhances quality with 90% factory production, lowers dead weight by 60%, and uses bolt–nut connections on-site. It offers 10% more space due to its thinner walls, energy efficiency, and all-weather construction, reducing time and labor without heavy machinery. It promises over 50 years of durability, easy utility installation, plan flexibility, diverse material options, and eco-friendliness with minimal waste [29]. | Light Steel Frame (LSF) |
| This construction method offers easy transportation and setup, suitability for various building types, more space from thinner walls, versatility in facades, and impenetrability. It ensures a clean, debris-free workshop and uses a non-flammable, ozone-friendly modified polystyrene core [29]. | 3D Sandwich Panel (3DP) |
| The Insulating Concrete Form (ICF) system uses permanent EPS forms to construct reinforced concrete walls that are integral to the structure post-concrete pour. | Insulating Concrete Framework (ICF) |
| These forms, typically two 5-cm EPS panels linked by ties, are protected with finishes. The structural walls primarily handle and transfer loads, with uniform distribution to the foundation. This system’s high indeterminacy suggests good seismic performance [29]. | |
| The Tronco system blends traditional and modern approaches for low-rise buildings, utilizing on-site fabricated galvanized steel tubes as its core. It integrates frames for doors, windows, and utilities during construction. It has EPS panels in walls, ceilings, and hollow tube spaces, excels in energy conservation, and reduces structural weight [29]. | Tronco System (TRC) |
| The Tunnel Formwork method, a modern construction approach, utilizes concrete for load-bearing walls and ceilings, in which reinforcement, formwork, and pouring happen simultaneously. Named for its tunnel-shaped metal forms, this method eliminates beams and columns, with walls directly handling loads. It enhances seismic behavior through a box-like structure, spreads stress more evenly, increases structural indeterminacy, and delays plastic hinge formation. This method also stands out for its fast construction pace, lower concrete use than traditional frameworks, and reduced material waste [29]. | Reinforced Concrete Continuous Frame (RCCF) |
| Equations | Description | Step | |
|---|---|---|---|
| (1) | Developing a hierarchical structure and executing fuzzy scale-based comparisons among criteria or alternatives to form a pairwise comparison matrix, as displayed in Equation (1); | 1 | |
| (2) | Averaging the preferences of all decision makers as per Equation (2) to create a new pairwise comparison matrix shown in Equation (3); | 2 | |
| (3) | |||
| (4) | Calculating the geometric mean for each criterion using Equation (4); | 3 | |
| (5) | Deriving the fuzzy weights () and conducting a vector summation of each , inversely scaling the sum vector, ordering it, and finally multiplying by the reciprocal vector as shown in Equation (5); | 4 | |
| (6) | Transforming fuzzy triangular numbers into precise values using the center of area de-fuzzification technique, as detailed in Equation (6); | 5 | |
| (7) | Normalizing the crisp weights derived from the previous step using the process outlined in Equation (7). | 6 | |
| Equations | Description | Step | |
| (8) | where n denotes the number of decision alternatives and m denotes the number of decision criteria. | Build a decision matrix where nn represents the number of alternatives and mm the number of criteria; | 1 |
| (9) | Normalize the decision matrix, converting fuzzy expert opinions into a scaled matrix using Equation (9) for positive components and Equation (10) for negative components; | 2 | |
| (10) | |||
| (11) | Generate a scaled matrix v devoid of fuzzy weights, based on the vector wij as specified in Equation (11); | 3 | |
| (12) | Identify the fuzzy ideal (A+) and fuzzy anti-ideal (A−) points, defined as the maximum and minimum values in each criterion column, respectively; | 4 | |
| (13) | |||
| (14) | Compute the total distances of each alternative from the fuzzy positive ideal and the fuzzy negative ideal; | 5 | |
| (15) | |||
| (16) | Calculate the similarity index for each option relative to the ideal solution; | 6 | |
| The ranking of alternatives. | 7 | ||
| Reference(s) | Influence | Sub-Criteria (Evaluation Criteria) (Code) | Main Criteria (Code) |
|---|---|---|---|
| [35,36,37] | Beneficial criteria | Manufacturing and Production Technology | Technical and Executive Regulations Criteria |
| [38,39] | Beneficial criteria | Availability of Materials | |
| [29,40] | Beneficial criteria | Operational and Seismic Guidelines | |
| [41,42] | Beneficial criteria | The Required Experience of Contractors and Workers | |
| [43,44] | Cost criteria | Challenges of Project Implementation | |
| [45,46,47] | Beneficial criteria | Mechanization of Project Execution | |
| [47,48,49] | Cost criteria | The Duration of the Project | Economic Criteria |
| [47,48,50] | Cost criteria | Cost of Equipment, Machinery and Workers | |
| [51,52,53] | Cost criteria | Life Cycle Cost (Useful Life and Durability) | |
| [39,43,54,55] | Cost criteria | Energy Consumption Amount | |
| [35,39,44,49] | Cost criteria | Cost of Required Materials | |
| [56,57] | Beneficial criteria | The Interior of the Building | Building Design and Architecture Criteria |
| [58,59,60,61] | Beneficial criteria | Impact on the Facade of the Building | |
| [56,58] | Beneficial criteria | Impact on Building Layout | |
| [56,60] | Beneficial criteria | Impact on the lighting of the Building | |
| [35,50,51] | Cost criteria | Mineral Extraction | Environmental Criteria |
| [50,54,62,63] | Cost criteria | Pollution | |
| [50,64] | Beneficial criteria | Renewability and Reusability | |
| [37,64,65] | Beneficial criteria | Compliance with Sustainable Development | |
| [66,67,68] | Beneficial criteria | Safety and Health | Socio-cultural Criteria |
| [52,63,69] | Beneficial criteria | Efficiency and Effectiveness | |
| [39,70,71] | Beneficial criteria | Compatibility with Identity and Ecology | |
| [38,43,56,72,73] | Beneficial criteria | Human Satisfaction |
| Rank | Normalized Weight | Definitive Weight | Fuzzy Weight | Weight | ||
|---|---|---|---|---|---|---|
| General | Group | Criteria | ||||
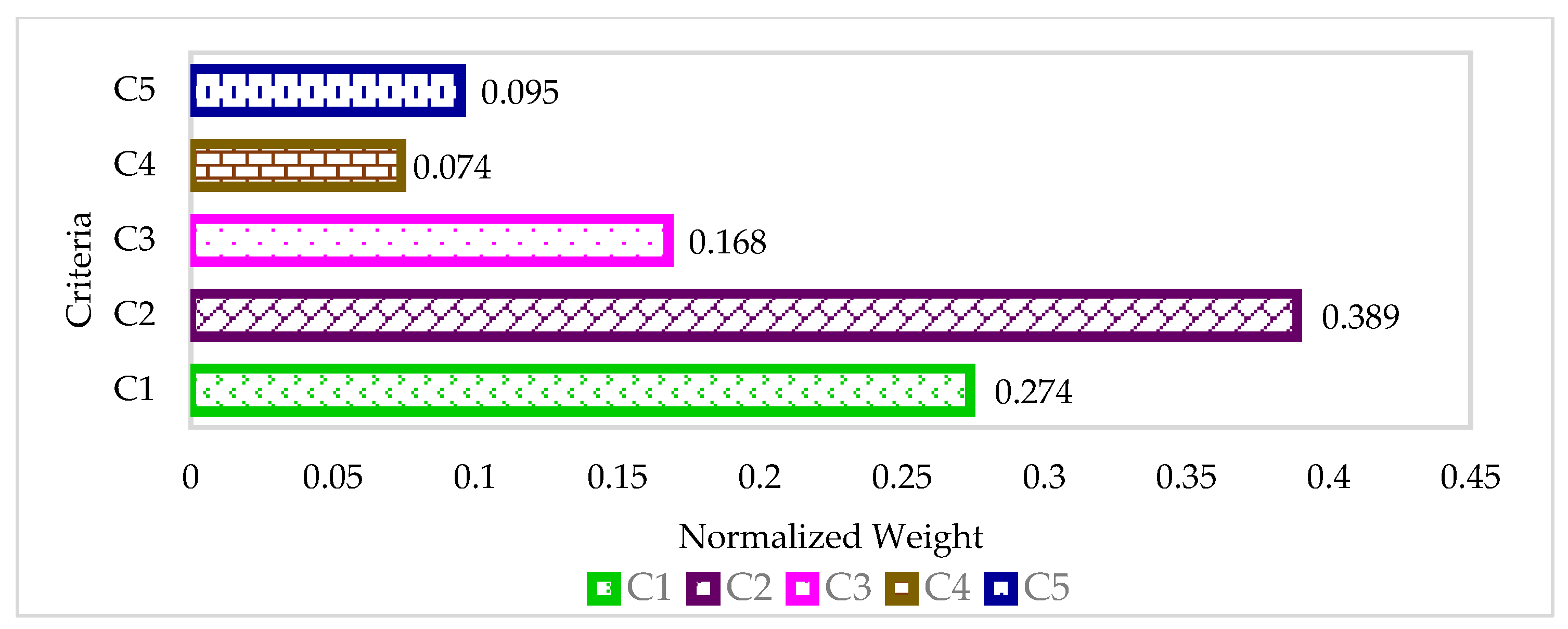
| 2 | 0.274 | 0.301 | (0.147, 0.273, 0.509) | Technical and Executive Regulations | ||
| 3 | 1 | 0.295 | 0.318 | (0.156, 0.297, 0.523) | Manufacturing and Production Technology | |
| 17 | 6 | 0.094 | 0.101 | (0.053, 0.092, 0.164) | Availability of Materials | |
| 9 | 4 | 0.146 | 0.157 | (0.083, 0.146, 0.255) | Operational and Seismic Guidelines | |
| 14 | 5 | 0.117 | 0.126 | (0.065, 0.116, 0.204) | The Required Experience of Contractors and Workers | |
| 6 | 2 | 0.178 | 0.191 | (0.094, 0.174, 0.323) | Challenges of Project Implementation | |
| 7 | 3 | 0.170 | 0.183 | (0.127, 0.174, 0.257) | Mechanization of Project Execution | |
| 1 | 0.389 | 0.426 | (0.210, 0.165, 0.315) | Economic | ||
| 1 | 1 | 0.401 | 0.442 | (0.219, 0.412, 0.726) | The Duration of the Project | |
| 2 | 2 | 0.218 | 0.240 | (0.111, 0.214, 0.421) | Cost of Equipment, Machinery, and Workers | |
| 15 | 5 | 0.080 | 0.088 | (0.048, 0.078, 0.147) | Life Cycle Cost (Useful Life and Durability) | |
| 11 | 4 | 0.100 | 0.110 | (0.056, 0.097, 0.188) | Energy Consumption Amount | |
| 4 | 3 | 0.201 | 0.222 | (0.099, 0.198, 0.391) | Cost of Required Materials | |
| 3 | 0.168 | 0.184 | (0.091, 0.165, 0.315) | Building Design and Architecture | ||
| 19 | 4 | 0.103 | 0.112 | (0.059, 0.098, 0.193) | The Interior of the Building | |
| 5 | 1 | 0.392 | 0.428 | (0.226, 0.404, 0.681) | Impact on the Facade of the Building | |
| 10 | 3 | 0.232 | 0.254 | (0.129, 0.232, 0.423) | Impact on Building Layout | |
| 8 | 2 | 0.273 | 0.299 | (0.134, 0.266, 0.529) | Impact on the Lighting of the Building | |
| 5 | 0.074 | 0.081 | (0.043, 0.071, 0.138) | Environmental | ||
| 23 | 4 | 0.116 | 0.127 | (0.065, 0.112, 0.220) | Mineral Extraction | |
| 18 | 2 | 0.258 | 0.283 | (0.133, 0.252, 0.495) | Pollution | |
| 20 | 3 | 0.221 | 0.243 | (0.117, 0.219, 0.416) | Renewability and Reusability | |
| 16 | 1 | 0.405 | 0.445 | (0.225, 0.416, 0.722) | Compliance with Sustainable Development | |
| 4 | 0.095 | 0.104 | (0.053, 0.093, 0.177) | Cultural and Social | ||
| 13 | 2 | 0.340 | 0.375 | (0.178, 0.339, 0.645) | Safety and Health | |
| 12 | 1 | 0.392 | 0.431 | (0.206, 0.400, 0.718) | Efficiency and Effectiveness | |
| 22 | 4 | 0.132 | 0.145 | (0.074, 0.127, 0.252) | Compatibility with Identity and Ecology | |
| 21 | 3 | 0.136 | 0.150 | (0.077, 0.134, 0.254) | Human Satisfaction | |
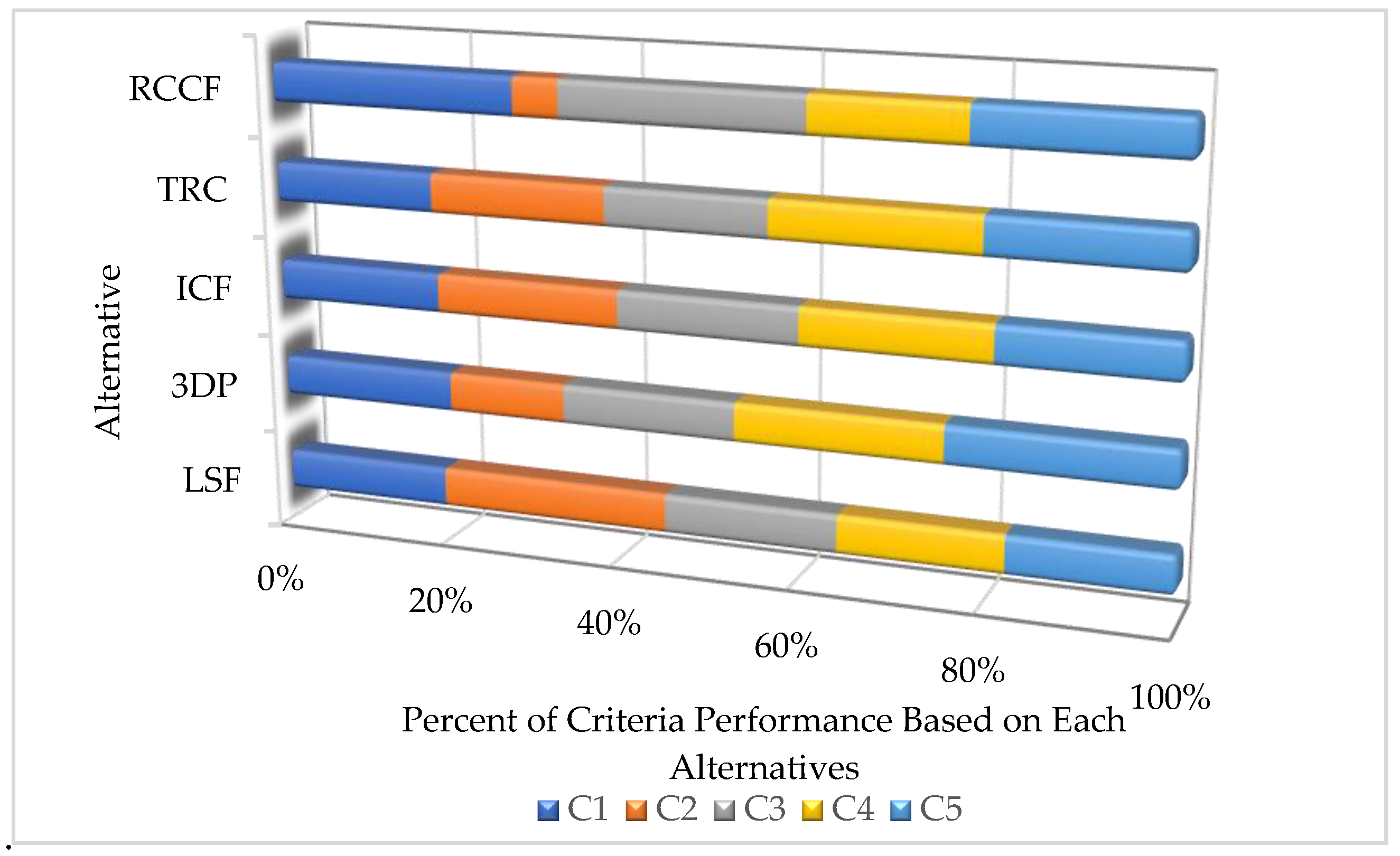
| Criteria | Alternative | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.012 | 0.006 | 0.047 | 0.023 | 0.019 | 0.051 | 0.094 | 0.009 | 0.029 | 0.012 | 0.015 | 0.005 | 0.005 | LSF | |
| 0.047 | 0.010 | 0.061 | 0.030 | 0.026 | 0.072 | 0.133 | 0.025 | 0.042 | 0.020 | 0.025 | 0.018 | 0.043 | 3DP | |
| 0.023 | 0.010 | 0.047 | 0.023 | 0.024 | 0.066 | 0.121 | 0.016 | 0.038 | 0.020 | 0.025 | 0.009 | 0.015 | ICF | |
| 0.035 | 0.010 | 0.047 | 0.023 | 0.024 | 0.072 | 0.133 | 0.016 | 0.042 | 0.020 | 0.025 | 0.014 | 0.028 | TRC | |
| 0.047 | 0.010 | 0.069 | 0.034 | 0.027 | 0.075 | 0.138 | 0.025 | 0.043 | 0.020 | 0.025 | 0.018 | 0.043 | RCCF | |
| SUM (di+) | Criteria | Alternative | ||||||||||||
| 0.397 | 0.002 | 0.002 | 0.007 | 0.009 | 0.005 | 0.003 | 0.011 | 0.005 | 0.013 | 0.011 | LSF | |||
| 0.711 | 0.009 | 0.009 | 0.019 | 0.015 | 0.016 | 0.008 | 0.015 | 0.008 | 0.032 | 0.027 | 3DP | |||
| 0.550 | 0.004 | 0.004 | 0.013 | 0.015 | 0.010 | 0.005 | 0.011 | 0.007 | 0.022 | 0.019 | ICF | |||
| 0.619 | 0.007 | 0.007 | 0.019 | 0.009 | 0.016 | 0.005 | 0.011 | 0.005 | 0.032 | 0.019 | TRC | |||
| 0.758 | 0.009 | 0.009 | 0.027 | 0.022 | 0.022 | 0.012 | 0.017 | 0.008 | 0.032 | 0.027 | RCCF | |||
| Criteria | Alternative | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.051 | 0.011 | 0.042 | 0.021 | 0.017 | 0.046 | 0.084 | 0.027 | 0.026 | 0.019 | 0.024 | 0.020 | 0.054 | LSF | |
| 0.017 | 0.007 | 0.011 | 0.006 | 0.002 | 0.005 | 0.010 | 0.012 | 0.003 | 0.011 | 0.015 | 0.006 | 0.021 | 3DP | |
| 0.041 | 0.007 | 0.042 | 0.021 | 0.005 | 0.012 | 0.023 | 0.020 | 0.007 | 0.011 | 0.015 | 0.016 | 0.047 | ICF | |
| 0.028 | 0.007 | 0.042 | 0.021 | 0.005 | 0.005 | 0.010 | 0.020 | 0.003 | 0.011 | 0.015 | 0.011 | 0.035 | TRC | |
| 0.017 | 0.007 | 0.002 | 0.001 | 0.001 | 0.002 | 0.004 | 0.012 | 0.001 | 0.011 | 0.015 | 0.009 | 0.021 | RCCF | |
| SUM (di+) | Criteria | Alternative | ||||||||||||
| 0.623 | 0.010 | 0.010 | 0.028 | 0.022 | 0.023 | 0.012 | 0.010 | 0.005 | 0.032 | 0.027 | LSF | |||
| 0.211 | 0.004 | 0.004 | 0.016 | 0.015 | 0.013 | 0.007 | 0.003 | 0.000 | 0.013 | 0.011 | 3DP | |||
| 0.402 | 0.008 | 0.008 | 0.023 | 0.015 | 0.019 | 0.010 | 0.010 | 0.001 | 0.022 | 0.019 | ICF | |||
| 0.331 | 0.006 | 0.006 | 0.016 | 0.022 | 0.013 | 0.010 | 0.010 | 0.005 | 0.013 | 0.019 | TRC | |||
| 0.164 | 0.004 | 0.004 | 0.009 | 0.009 | 0.008 | 0.004 | 0.000 | 0.000 | 0.013 | 0.011 | RCCF | |||
| Rank | CC | di- | di+ | Alternative |
|---|---|---|---|---|
| 1 | 0.611 | 0.623 | 0.397 | LSF |
| 4 | 0.229 | 0.211 | 0.711 | 3DP |
| 2 | 0.422 | 0.402 | 0.550 | ICF |
| 3 | 0.349 | 0.331 | 0.619 | TRC |
| 5 | 0.178 | 0.164 | 0.758 | RCCF |
| Nominal Grade Fy (MPa) | Dimensions (mm) | Thickness (mm) | Member |
|---|---|---|---|
| 345 | 152 × 41 × 12.7 | 1.91 | Chord studs |
| 230 | 152 × 41 × 12.7 | 1.22 | Interior studs |
| 345 | 152 × 31.8 | 1. 91 | Tracks |
| 230 | 300 × 300 | 1.91 | Connection plate |
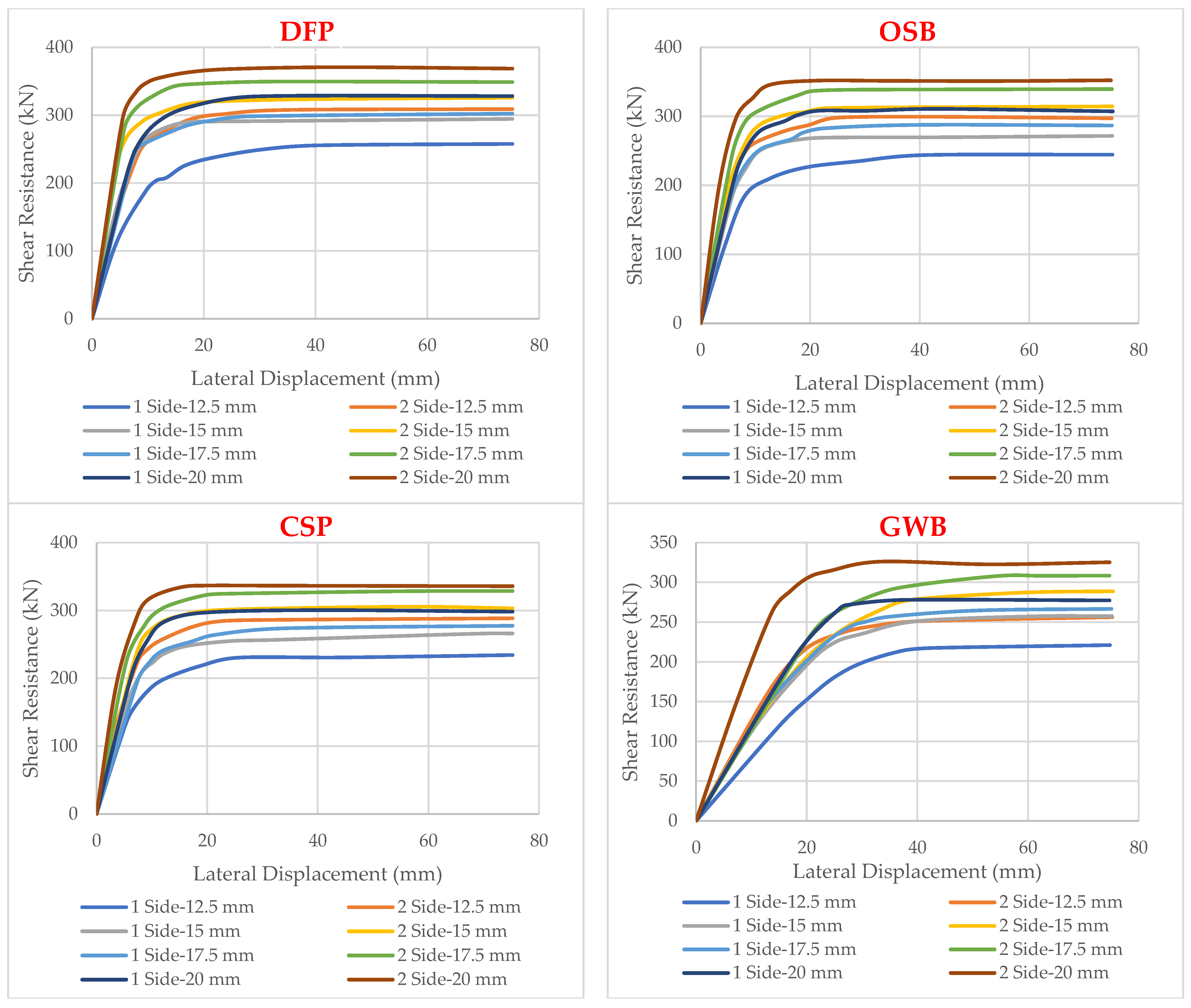
| Specimen | Thickness mm | Sy kN | Syp kN | Ke kN/mm | μ | Energy kN.mm | Kp kN/mm | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DFP | 12.5 | 214.06 | 255.76 | 9.78 | 2.41 | 16,785 | 38.26 | 83.70 | 203.87 | 25.56 | 55.89 |
| 15 | 235.13 | 280.63 | 11.08 | 2.06 | 18,761 | 50.47 | 83.79 | 223.93 | 21.95 | 63.31 | |
| 17.5 | 235.70 | 302.85 | 13.92 | 1.83 | 19,938 | 50.08 | 83.77 | 241.62 | 27.80 | 79.54 | |
| 20 | 273.35 | 322.52 | 16.93 | 1.49 | 21,228 | 60.03 | 84.75 | 260.33 | 28.20 | 96.73 | |
| OSB | 10 | 189.26 | 225.75 | 8.29 | 3.06 | 14,803 | 29.55 | 83.84 | 180.25 | 28.05 | 47.36 |
| 12.5 | 203.94 | 244.66 | 9.11 | 2.67 | 15,912 | 36.54 | 83.36 | 194.23 | 24.93 | 52.06 | |
| 15 | 229.47 | 271.48 | 10.74 | 2.38 | 18,228 | 45.02 | 84.53 | 218.54 | 23.86 | 61.37 | |
| 17.5 | 246.15 | 293.37 | 13.08 | 2.08 | 19,033 | 47.48 | 83.90 | 234.43 | 27.55 | 74.74 | |
| 20 | 265.59 | 315.96 | 16.01 | 1.70 | 20,633 | 56.91 | 84.06 | 252.94 | 28.14 | 91.50 | |
| CSP | 10 | 176.11 | 217.58 | 7.71 | 3.52 | 14,632 | 27.06 | 80.94 | 167.72 | 28.48 | 44.04 |
| 12.5 | 198.26 | 234.21 | 8.76 | 3.088 | 15,084 | 34.36 | 84.65 | 188.82 | 25.49 | 50.06 | |
| 15 | 219.82 | 265.61 | 9.93 | 2.64 | 17,971 | 41.63 | 82.76 | 209.35 | 23.85 | 56.74 | |
| 17.5 | 235.01 | 287.51 | 12.36 | 2.31 | 18,113 | 45.08 | 81.74 | 223.82 | 27.42 | 70.63 | |
| 20 | 257.03 | 307.58 | 15.50 | 1.88 | 19,146 | 54.04 | 83.57 | 244.79 | 28.68 | 88.57 | |
| GWB | 10 | 161.72 | 213.06 | 7.21 | 4.06 | 11,143 | 24.69 | 75.90 | 154.02 | 29.19 | 41.19 |
| 12.5 | 181.69 | 224.62 | 8.19 | 3.55 | 12,436 | 31.30 | 80.89 | 173.04 | 26.17 | 46.80 | |
| 15 | 212.44 | 258.68 | 9.31 | 2.86 | 14,555 | 32.99 | 82.12 | 202.32 | 28.22 | 53.20 | |
| 17.5 | 226.94 | 279.92 | 11.67 | 2.48 | 15,199 | 44.15 | 81.07 | 216.13 | 26.43 | 66.69 | |
| 20 | 241.16 | 296.45 | 14.63 | 2.02 | 15,811 | 52.92 | 81.35 | 229.68 | 27.65 | 83.62 |
| Specimen | Thickness mm | Sy kN | Syp kN | Ke kN/mm | μ | Energy kN.mm | Kp kN/mm | (%) | (%) | (%) | (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DFP | 12.5 | 247.54 | 307.69 | 15.32 | 1.62 | 2.445 | 45.26 | 80.45 | 235.75 | 33.85 | 87.54 |
| 15 | 278.18 | 326.49 | 16.41 | 1.54 | 22,025 | 63.27 | 85.20 | 264.93 | 25.94 | 93.77 | |
| 17.5 | 296.08 | 346.68 | 18.96 | 1.42 | 23,516 | 60.89 | 85.40 | 281.98 | 31.14 | 108.36 | |
| 20 | 319.12 | 371.34 | 22.85 | 1.31 | 26,045 | 72.59 | 85.94 | 303.92 | 31.05 | 130.57 | |
| OSB | 10 | 207.22 | 269.84 | 12.56 | 1.97 | 18,063 | 36.86 | 76.79 | 197.35 | 34.08 | 71.79 |
| 12.5 | 245.51 | 298.94 | 13.41 | 1.83 | 19,367 | 41.31 | 82.13 | 233.82 | 32.46 | 76.63 | |
| 15 | 269.02 | 318.36 | 15.23 | 1.72 | 21,448 | 56.15 | 84.50 | 256.21 | 27.12 | 87.03 | |
| 17.5 | 287.62 | 337.69 | 18.01 | 1.61 | 22,469 | 58.47 | 85.17 | 273.92 | 30.81 | 102.93 | |
| 20 | 306.96 | 358.98 | 21.61 | 1.49 | 25,239 | 69.78 | 85.51 | 292.34 | 30.97 | 123.50 | |
| CSP | 10 | 201.50 | 259.85 | 11.62 | 2.18 | 17,349 | 32.60 | 77.54 | 191.90 | 35.64 | 66.41 |
| 12.5 | 245.51 | 298.43 | 12.35 | 2.04 | 16,982 | 38.11 | 81.93 | 232.85 | 32.41 | 70.57 | |
| 15 | 256.34 | 309.76 | 13.89 | 1.86 | 20,784 | 51.46 | 82.75 | 244.13 | 26.99 | 79.37 | |
| 17.5 | 279.47 | 329.79 | 17.11 | 1.79 | 21,902 | 56.12 | 84.74 | 166.16 | 30.48 | 97.75 | |
| 20 | 291.83 | 341.67 | 20.09 | 1.65 | 23,863 | 66.24 | 85.41 | 277.93 | 30.32 | 114.77 | |
| GWB | 10 | 176.79 | 239.54 | 9.84 | 2.57 | 13,884 | 28.05 | 73.80 | 168.37 | 35.09 | 56.24 |
| 12.5 | 211.26 | 254.26 | 10.51 | 2.28 | 15,370 | 35.43 | 83.09 | 201.20 | 29.66 | 60.06 | |
| 15 | 239.77 | 287.81 | 12.67 | 2.09 | 17,396 | 44.76 | 83.31 | 288.35 | 28.31 | 72.40 | |
| 17.5 | 263.43 | 311.24 | 16.15 | 1.92 | 18,040 | 53.86 | 84.64 | 250.89 | 29.99 | 92.29 | |
| 20 | 278.54 | 328.27 | 19.22 | 1.77 | 18,969 | 64.88 | 84.85 | 265.28 | 29.62 | 109.82 |
| Specimen | Thickness (mm) | One-Side | Two-Side | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | R | ||||||||
| DFP | 12.5 | 2.41 | 1.95 | 2.04 | 3.99 | 1.62 | 1.50 | 2.36 | 3.53 |
| 15 | 2.06 | 1.77 | 2.24 | 3.96 | 1.54 | 1.44 | 2.65 | 3.82 | |
| 17.5 | 1.83 | 1.63 | 2.42 | 3.95 | 1.42 | 1.36 | 2.82 | 3.83 | |
| 20 | 1.49 | 1.41 | 2.60 | 3.66 | 1.31 | 1.27 | 3.04 | 3.87 | |
| OSB | 10 | 3.06 | 2.26 | 1.80 | 4.07 | 1.97 | 1.71 | 1.97 | 3.38 |
| 12.5 | 2.67 | 2.08 | 1.94 | 4.04 | 1.83 | 1.63 | 2.24 | 3.65 | |
| 15 | 2.38 | 1.94 | 2.18 | 4.23 | 1.72 | 1.56 | 2.56 | 4.00 | |
| 17.5 | 2.08 | 1.78 | 2.34 | 4.16 | 1.61 | 1.49 | 2.74 | 4.08 | |
| 20 | 1.70 | 1.55 | 2.53 | 3.92 | 1.49 | 1.41 | 2.92 | 4.11 | |
| CSP | 10 | 3.52 | 2.46 | 1.68 | 4.13 | 2.18 | 1.83 | 1.92 | 3.52 |
| 12.5 | 3.08 | 2.27 | 1.89 | 4.29 | 2.04 | 1.75 | 2.33 | 4.09 | |
| 15 | 2.64 | 2.07 | 2.09 | 4.32 | 1.86 | 1.65 | 2.44 | 4.02 | |
| 17.5 | 2.31 | 1.90 | 2.24 | 4.26 | 1.79 | 1.61 | 2.66 | 4.27 | |
| 20 | 1.88 | 1.66 | 2.45 | 4.07 | 1.65 | 1.52 | 2.78 | 4.22 | |
| GWB | 10 | 4.06 | 2.67 | 1.54 | 4.11 | 2.57 | 2.03 | 1.68 | 3.42 |
| 12.5 | 3.55 | 2.47 | 1.73 | 4.27 | 2.28 | 1.89 | 2.01 | 3.79 | |
| 15 | 2.86 | 2.17 | 2.02 | 4.39 | 2.09 | 1.78 | 2.88 | 5.14 | |
| 17.5 | 2.48 | 1.99 | 2.16 | 4.30 | 1.92 | 1.69 | 2.51 | 4.23 | |
| 20 | 2.02 | 1.74 | 2.30 | 4.01 | 1.77 | 1.59 | 2.65 | 4.22 | |
| Sheathing | Thickness (mm) | Δtarget (mm) | Δy (mm) | d | Normalized Displacement (mm) | Drift Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CP | LS | IO | OP | CP | LS | IO | OP | |||||
| GWB | 10 | 5.18 | 29.27 | 4.70 | 120.15 | 101.98 | 47.24 | 11.17 | 4.92 | 4.29 | 1.94 | 0.48 |
| 12.5 | 4.07 | 26.76 | 4.62 | 120.01 | 101.86 | 46.10 | 10.70 | 4.92 | 4.27 | 1.89 | 0.44 | |
| 15 | 2.91 | 13.74 | 4.50 | 71.73 | 60.13 | 25.34 | 5.50 | 2.94 | 2.46 | 1.04 | 0.23 | |
| 17.5 | 2.70 | 12.72 | 4.10 | 57.29 | 48.37 | 21.63 | 5.09 | 2.35 | 1.98 | 0.89 | 0.21 | |
| 20 | 2.52 | 12.04 | 3.54 | 42.64 | 36.52 | 18.16 | 4.82 | 1.75 | 1.50 | 0.74 | 0.20 | |
| CSP | 10 | 1.19 | 14.91 | 6.82 | 99.78 | 82.98 | 31.80 | 5.96 | 4.07 | 3.39 | 1.30 | 0.24 |
| 12.5 | 1.05 | 13.63 | 6.79 | 99.30 | 82.48 | 31.35 | 5.45 | 4.07 | 3.38 | 1.28 | 0.22 | |
| 15 | 0.99 | 9.39 | 6.66 | 63.70 | 52.88 | 20.26 | 3.76 | 2.61 | 2.17 | 0.83 | 0.15 | |
| 17.5 | 0.94 | 8.93 | 5.75 | 51.38 | 42.89 | 17.42 | 3.57 | 2.11 | 1.76 | 0.71 | 0.15 | |
| 20 | 0.87 | 8.51 | 4.49 | 38.24 | 32.30 | 14.46 | 3.40 | 1.57 | 1.32 | 0.59 | 0.14 | |
| OSB | 10 | 1.13 | 12.86 | 6.52 | 83.37 | 69.26 | 26.96 | 5.14 | 3.42 | 2.84 | 1.10 | 0.21 |
| 12.5 | 0.98 | 11.76 | 6.48 | 83.35 | 69.26 | 26.56 | 4.70 | 3.42 | 2.84 | 1.09 | 0.19 | |
| 15 | 0.86 | 8.19 | 6.24 | 56.81 | 47.09 | 17.91 | 3.28 | 2.33 | 1.93 | 0.73 | 0.13 | |
| 17.5 | 0.84 | 7.64 | 5.99 | 45.73 | 38.11 | 15.26 | 3.06 | 1.87 | 1.56 | 0.63 | 0.13 | |
| 20 | 0.80 | 7.44 | 4.57 | 34.04 | 28.72 | 12.76 | 2.98 | 1.39 | 1.18 | 0.52 | 0.12 | |
| DFP | 12.5 | 0.97 | 10.81 | 7.10 | 76.80 | 63.60 | 24.01 | 4.32 | 3.15 | 2.61 | 0.98 | 0.18 |
| 15 | 0.85 | 7.64 | 6.24 | 47.71 | 39.70 | 15.65 | 3.06 | 1.96 | 1.63 | 0.64 | 0.13 | |
| 17.5 | 0.83 | 7.31 | 5.34 | 39.04 | 32.69 | 13.66 | 2.92 | 1.60 | 1.34 | 0.56 | 0.12 | |
| 20 | 0.82 | 7.15 | 4.06 | 29.05 | 24.67 | 11.53 | 2.86 | 1.19 | 1.01 | 0.47 | 0.12 | |
| Sheathing | Thickness (mm) | Δtarget (mm) | Δy (mm) | d | Normalized Displacement (mm) | Drift Ratio (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CP | LS | IO | OP | CP | LS | IO | OP | |||||
| GWB | 10 | 5.18 | 29.27 | 4.70 | 120.15 | 101.98 | 47.24 | 11.17 | 4.92 | 4.29 | 1.94 | 0.48 |
| 12.5 | 4.07 | 26.76 | 4.62 | 120.01 | 101.86 | 46.10 | 10.70 | 4.92 | 4.27 | 1.89 | 0.44 | |
| 15 | 2.91 | 13.74 | 4.50 | 71.73 | 60.13 | 25.34 | 5.50 | 2.94 | 2.46 | 1.04 | 0.23 | |
| 17.5 | 2.70 | 12.72 | 4.10 | 57.29 | 48.37 | 21.63 | 5.09 | 2.35 | 1.98 | 0.89 | 0.21 | |
| 20 | 2.52 | 12.04 | 3.54 | 42.64 | 36.52 | 18.16 | 4.82 | 1.75 | 1.50 | 0.74 | 0.20 | |
| CSP | 10 | 1.19 | 14.91 | 6.82 | 99.78 | 82.98 | 31.80 | 5.96 | 4.07 | 3.39 | 1.30 | 0.24 |
| 12.5 | 1.05 | 13.63 | 6.79 | 99.30 | 82.48 | 31.35 | 5.45 | 4.07 | 3.38 | 1.28 | 0.22 | |
| 15 | 0.99 | 9.39 | 6.66 | 63.70 | 52.88 | 20.26 | 3.76 | 2.61 | 2.17 | 0.83 | 0.15 | |
| 17.5 | 0.94 | 8.93 | 5.75 | 51.38 | 42.89 | 17.42 | 3.57 | 2.11 | 1.76 | 0.71 | 0.15 | |
| 20 | 0.87 | 8.51 | 4.49 | 38.24 | 32.30 | 14.46 | 3.40 | 1.57 | 1.32 | 0.59 | 0.14 | |
| OSB | 10 | 1.13 | 12.86 | 6.52 | 83.37 | 69.26 | 26.96 | 5.14 | 3.42 | 2.84 | 1.10 | 0.21 |
| 12.5 | 0.98 | 11.76 | 6.48 | 83.35 | 69.26 | 26.56 | 4.70 | 3.42 | 2.84 | 1.09 | 0.19 | |
| 15 | 0.86 | 8.19 | 6.24 | 56.81 | 47.09 | 17.91 | 3.28 | 2.33 | 1.93 | 0.73 | 0.13 | |
| 17.5 | 0.84 | 7.64 | 5.99 | 45.73 | 38.11 | 15.26 | 3.06 | 1.87 | 1.56 | 0.63 | 0.13 | |
| 20 | 0.80 | 7.44 | 4.57 | 34.04 | 28.72 | 12.76 | 2.98 | 1.39 | 1.18 | 0.52 | 0.12 | |
| DFP | 12.5 | 0.97 | 10.81 | 7.10 | 76.80 | 63.60 | 24.01 | 4.32 | 3.15 | 2.61 | 0.98 | 0.18 |
| 15 | 0.85 | 7.64 | 6.24 | 47.71 | 39.70 | 15.65 | 3.06 | 1.96 | 1.63 | 0.64 | 0.13 | |
| 17.5 | 0.83 | 7.31 | 5.34 | 39.04 | 32.69 | 13.66 | 2.92 | 1.60 | 1.34 | 0.56 | 0.12 | |
| 20 | 0.82 | 7.15 | 4.06 | 29.05 | 24.67 | 11.53 | 2.86 | 1.19 | 1.01 | 0.47 | 0.12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lotfi, M.; Gerami, M.; Karakouzian, M. Sustainable Structural System Selection Using Hybrid Fuzzy Multi-Criteria Decision Model Based on Seismic Performance. Buildings 2024, 14, 2107. https://doi.org/10.3390/buildings14072107
Lotfi M, Gerami M, Karakouzian M. Sustainable Structural System Selection Using Hybrid Fuzzy Multi-Criteria Decision Model Based on Seismic Performance. Buildings. 2024; 14(7):2107. https://doi.org/10.3390/buildings14072107
Chicago/Turabian StyleLotfi, Mohsen, Mohsen Gerami, and Moses Karakouzian. 2024. "Sustainable Structural System Selection Using Hybrid Fuzzy Multi-Criteria Decision Model Based on Seismic Performance" Buildings 14, no. 7: 2107. https://doi.org/10.3390/buildings14072107
APA StyleLotfi, M., Gerami, M., & Karakouzian, M. (2024). Sustainable Structural System Selection Using Hybrid Fuzzy Multi-Criteria Decision Model Based on Seismic Performance. Buildings, 14(7), 2107. https://doi.org/10.3390/buildings14072107










