Local Buckling and Resistance of Continuous Steel Beams with Thin-Walled I-Shaped Cross-Sections
Abstract
:Featured Application
Abstract
1. Introduction
2. Computational Model for Local Cross-Section Buckling
3. “Local” Critical Resistance and Design Ultimate Resistance of the Cross-Section
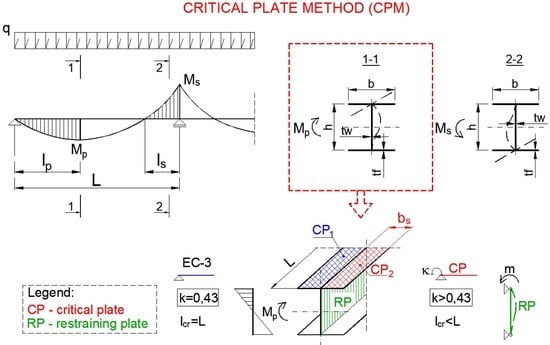
4. The Idea of the Critical Plate Method (CPM)
5. Algorithm of the CPM Method for Thin-Walled I-Cross-Sections under Bending
- (1)
- Division of the cross-section into component plates according to Figure 2;
- (2)
- Identifying CP for a “simple” cross-section based on the conditionwhere —Euler stress for the i-th plate according to the formula: .Note: for acc. to Equation (6), the critical plate (CP) is the cantilever wall of the compression flange and the rigid plate (RP) is the web;
- (3)
- Adoption of the initial CP edge restraint coefficient value (for the so-called zero step), e.g., ;
- (4)
- Estimation of the critical length () for a single half-wave of CP buckling [26] according to the formula
- (5)
- (6)
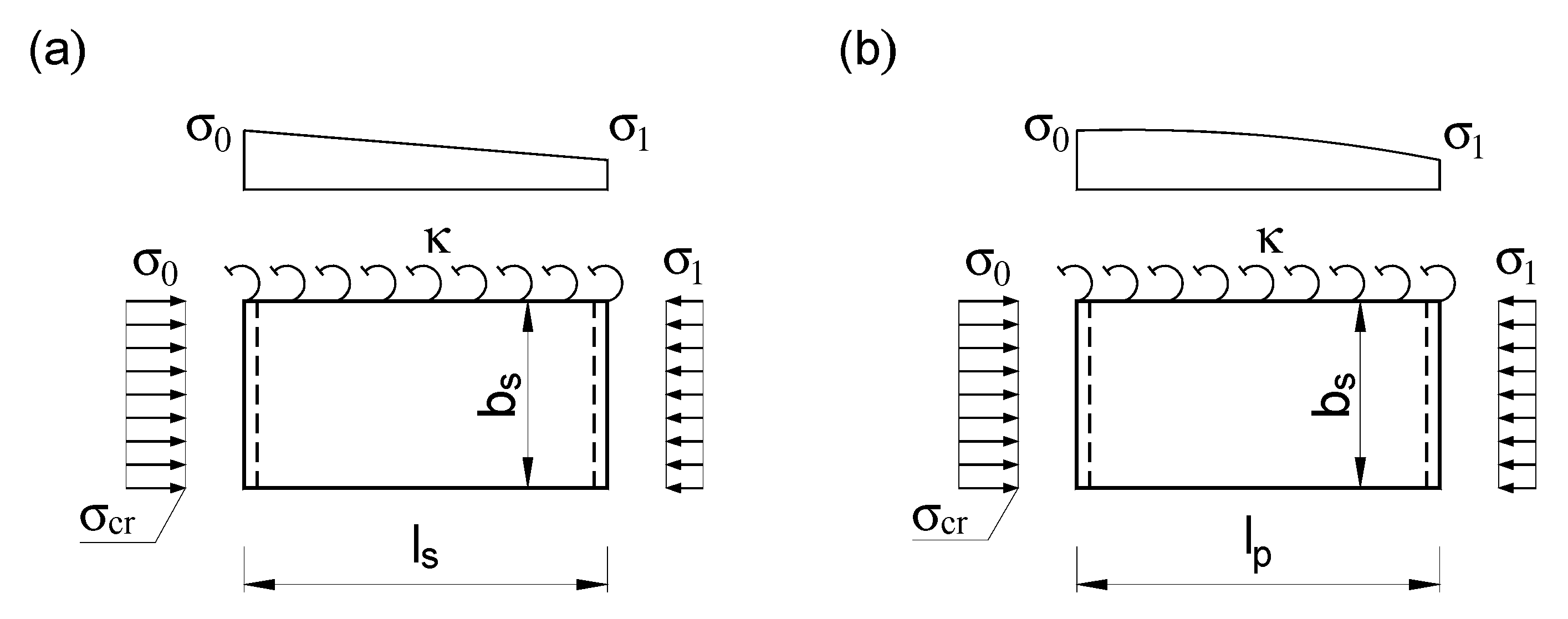
- Determination of according to the formulawhere k*—buckling coefficient according to a more accurate calculation model.The k* coefficient can be determined on the basis of Reference [26] from the following formulas:
- for linear stress distribution (Figure 3a),
- for non-linear stress distribution (according to 2° parabola, Figure 3b),where —longitudinal stress distribution coefficient (Figure 3), .The plate buckling coefficient of an elastically restrained and infinitely long cantilever plate can be determined according to Reference [26], using the formulaOn the other hand, Reference [28] presents a simplified formula for within the range in the form of
- (7)
- Estimation of the critical stress for a RP bent in its plane (width ) [32] for one half-wave of CP buckling length according to Point 4.
- (8)
- Determination of rotational spring stiffness according to Equation (17) and the restraint coefficient according to Equation (3) for the first (i = 1) and subsequent iteration steps.where —parameter of geometrical configuration of plates in contact with the j-th edge (for a welded I-section [10]; note: for an I-section made up of two channel sections , i.e., one web with thickness stabilizes one CP of the flange on one edge), RP flexural rigidity,—RP thickness;
- (9)
- Repetition of Steps (4) to (8) up to the moment when ;
- (10)
- according to Equation (11) is the sought buckling stress for CP;
- (11)
- Determination of the “local” critical resistance of the cross-section according to Equation (1);
- (12)
- Determination of the design ultimate resistance of the cross-section according to Equation (2) for the coefficient calculated with the following assumptions [10]:
- (a)
- the slenderness of the critical plate (CP) shall be determined from the buckling stress determined by Step 10 (i.e., taking into account the elastic restraint effect of the cantilever plate and the effect of longitudinal stress variation);
- (b)
- for the web (rigid plate RP), a simple support shall be provided at the same edge;
- (c)
- the boundary conditions at the other edge of the RP have a slight impact on the result of the calculations (conservatively, simple support can also be assumed here),
- (d)
- the effect of possible longitudinal stress variation in RP is insignificant and can be ignored,
- (e)
- the effective widths so determined “shall be folded” into an effective cross-section, for which is determined.
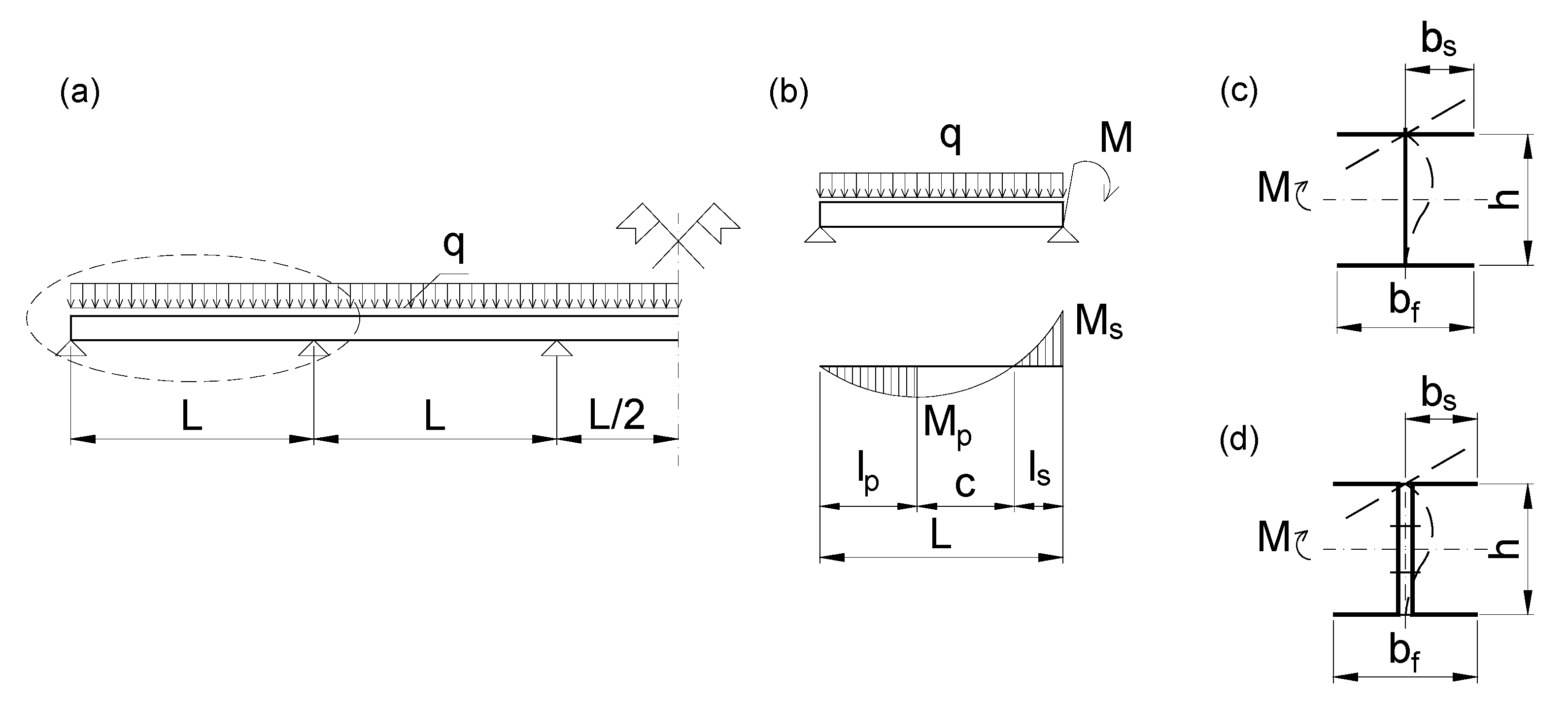
6. Calculation Method for a Continuous I-Beam
7. Example of Using CPM to Determine the Resistance of a Continuous I-Beam
7.1. Statics and Cross-Sectional Forces
7.2. Welded Section
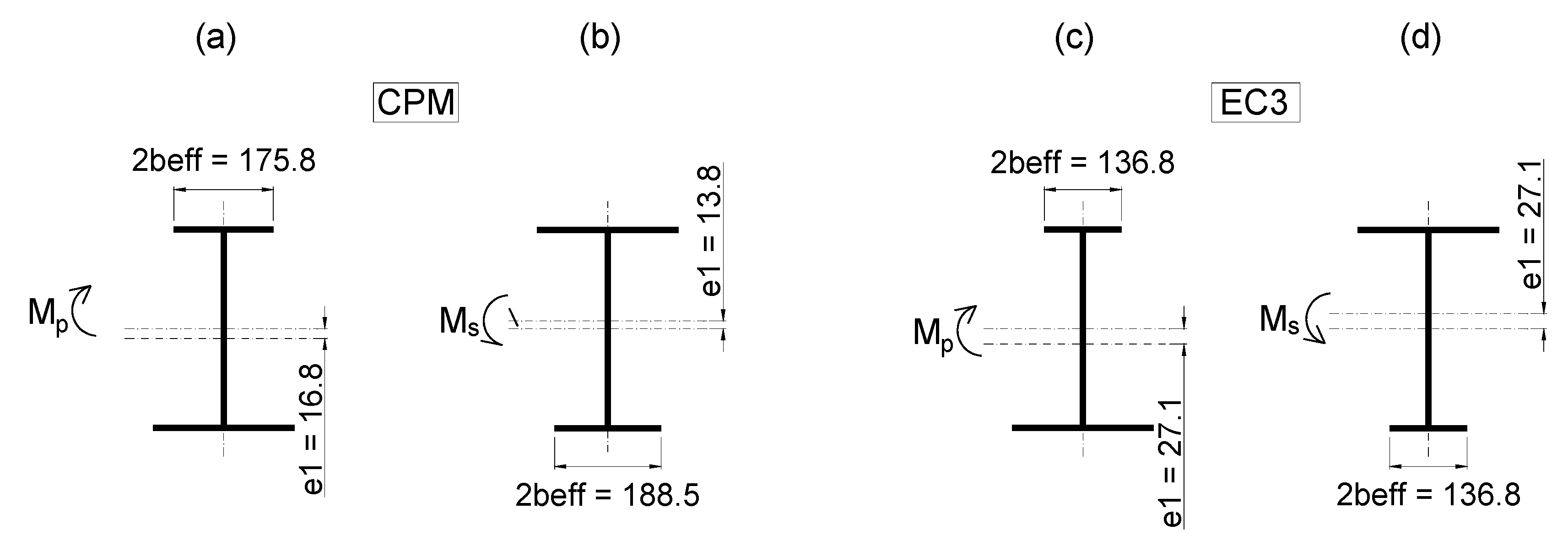
7.2.1. Calculation of Critical Resistance According to CPM
7.2.2. Finite Element and Finite Strip Analysis
7.2.3. Comparison of Critical Stress Results
7.2.4. Design Ultimate Resistance
7.3. I-Section Consisting of Two Cold-Formed Channel Sections (2C)
8. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- EN 1993-1-1, Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- EN 1993-1-3, Eurocode 3: Design of Steel Structures—Part 1-3: General rules—Supplementary Rules for Cold-Formed Members and Sheeting; European Committee for Standardization: Brussels, Belgium, 2006.
- EN 1993-1-5, Eurocode 3: Design of Steel Structures—Part 1-5: Plated Structural Elements; European Committee for Standardization: Brussels, Belgium, 2006.
- Szychowski, A. A theoretical analysis of the local buckling in thin-walled bars with open cross-section subjected to warping torsion. Thin-Walled Struct. 2014, 76, 42–55. [Google Scholar] [CrossRef]
- Kowal, Z.; Szychowski, A. Experimental determination of critical loads in thin-walled bars with Z-section subjected to warping torsion. Thin-Walled Struct. 2014, 75, 87–102. [Google Scholar] [CrossRef]
- Brzezińska, K.; Szychowski, A. Stability and resistance of steel continuous beams with thin-walled box sections. Arch. Civ. Eng. 2018, 64, 123–143. [Google Scholar] [CrossRef] [Green Version]
- Bulson, P.S. The Stability of Flat Plates; Chatto and Windus: London, UK, 1970. [Google Scholar]
- Yu, C.; Schafer, B.W. Effect of longitudinal stress gradient on the ultimate strength of thin plates. Thin-Walled Struct. 2006, 44, 787–799. [Google Scholar] [CrossRef]
- Hancock, G.J. Cold-formed steel structures. J. Constr. Steel Res. 2003, 58, 473–487. [Google Scholar] [CrossRef]
- Szychowski, A. Computation of thin-walled cross-section resistance to local buckling with the use of the Critical Plate Method. Arch. Civ. Eng. 2016, 62, 229–264. [Google Scholar] [CrossRef] [Green Version]
- Jakubowski, S. The matrix analysis of stability and free vibrations of walls of thin-walled girders. Arch. Budowy Masz. 1986, XXXIII, 357–376. (In Polish) [Google Scholar]
- Rusch, A.; Lindner, J. Load carrying capacity of thin-walled I-sections subjected to bending about the z-axis (in German). Stahlbau 1999, 68, 457–467. [Google Scholar] [CrossRef]
- Beale, R.G.; Godley, M.H.R.; Enjily, V. A theoretical and experimental investigation into cold-formed channel sections in bending with the unstiffened flanges in compression. Comput. Struct. 2001, 79, 2403–2411. [Google Scholar] [CrossRef]
- Kotełko, M.; Lim, T.H.; Rhodes, J. Post—Failure behaviour of box section beams under pure bending (an experimental study). Thin-Walled Struct. 2000, 38, 179–194. [Google Scholar]
- Jakubowski, S. Buckling of thin-walled girders under compound load. Thin-Walled Struct. 1988, 6, 129–150. [Google Scholar] [CrossRef]
- Nassar, G. Das Ausbeulen dünnwandiger Querschnitte unter einachsig aussermittiger Druckbeanspruchung. Der Stahlbau H 1965, 10, 311–316. [Google Scholar]
- Papangelis, J.P.; Hancock, G.J. Computer analysis of thin-walled structural members. Comput. Struct. 1995, 56, 157–176. [Google Scholar] [CrossRef]
- Schafer, B.W.; Ádány, S. Buckling analysis of cold-formed steel members using CUFSM: Conventional and constrained finite strip methods. In Proceedings of the Eighteenth International Specialty Conference on Cold-Formed Steel Structures, Orlando, FL, USA, 26–27 October 2006. [Google Scholar]
- Gardner, L.; Fieber, A.; Macorini, L. Formulae for calculating elastic local buckling stresses of full structural cross-sections. Structures 2019, 17, 2–20. [Google Scholar] [CrossRef]
- Ciesielczyk, K.; Rzeszut, K. Locla and distortional buckling of axially loaded cold rolled sigma profiles. Acta Mech. et Autom. 2016, 10, 218–222. [Google Scholar] [CrossRef] [Green Version]
- Fieber, A.; Gardner, L.; Macorini, L. Formulae for determining elastic local buckling half-wavelengths of structural steel cross-sections. J. Constr. Steel Res. 2019, 159, 493–506. [Google Scholar] [CrossRef]
- Seif, M.; Schafer, B.W. Local buckling of structural steel shapes. J. Constr. Steel Res. 2010, 66, 1232–1247. [Google Scholar] [CrossRef]
- Couto, C.; Vila Real, P. Numerical investigation on the influence of imperfections in the local buckling of thin-walled I-shaped sections. Thin-Walled Struct. 2019, 135, 89–108. [Google Scholar] [CrossRef]
- Yu, C.; Schafer, B.W. Effect of longitudinal stress gradients on elastic buckling of thin plates. J. Eng. Mech. ASCE 2007, 133, 452–463. [Google Scholar] [CrossRef]
- Szychowski, A. The stability of eccentrically compressed thin plates with a longitudinal free edge and with stress variation in the longitudinal direction. Thin-Walled Struct. 2008, 46, 494–505. [Google Scholar] [CrossRef]
- Szychowski, A. Stability of cantilever walls of steel thin-walled bars with open cross-section. Thin-Walled Struct. 2015, 94, 348–358. [Google Scholar] [CrossRef]
- Szychowski, A. Local buckling of cantilever wall of thin-walled member with longitudinal and transverse stress variation. Bud. i Archit. 2015, 14, 113–121. (In Polish) [Google Scholar] [CrossRef]
- Szychowski, A. Stability of eccentrically compressed cantilever wall of a thin-walled member. JCEEA 2015, XXXII, 439–457. (In Polish) [Google Scholar] [CrossRef]
- Kotełko, M. Thin-Walled Structures Resistance and Failure Mechanisms; Wydawnictwa Naukowo –Techniczne: Warsaw, Poland, 2011. (In Polish) [Google Scholar]
- Kotełko, M. Thin-walled profiles with edge stiffeners as energy absorbers. Thin-Walled Struct. Elsevier 2007, 45, 872–876. [Google Scholar]
- Kalyanaraman, V. Local buckling of cold-formed steel members. J. Struct. Div. 1979, 105, 813–828. [Google Scholar]
- Li, L.-Y.; Chen, J.-K. An analytical model for analyzing distortional buckling of cold-formed steel sections. Thin-Walled Struct. 2008, 46, 1430–1436. [Google Scholar] [CrossRef]
- Kowal, Z. The Stability of Compressed Flange of Plate Girder with a Box Cross-Section; Zeszyty Naukowe Politechniki Wrocławskiej: Budownictwo, Poland, 1965; pp. 73–85. (In Polish) [Google Scholar]
- Rykaluk, K. Residual Welding Stresses in Chosen Ultimate Bearing Capacity; Scientific Papers of the Institute of Building Engineering of Wroclaw Technical University, No 29, Series: Monographs No 11; Wroclaw Technical University: Wroclaw, Poland, 1981. (In Polish) [Google Scholar]
- Hibbitt, Karlsson & Sorensen Inc. 2000 ABAQUS/CAE User’s Manual; Hibbitt, Karlsson & Sorensen: Pawtucket, RI, USA, 2000. [Google Scholar]
- Ignatowicz, R.L. The Theoretical and Experimental Analysis of Resistance of the Cold-Formed Steel Columns with Box cross-Section. Ph.D. Thesis, Instytut Budownictwa Politechniki Wrocławskiej, Series PRE 52/99. Wrocław University of Science and Technology, Wroclaw, Poland, 1999. (In Polish). [Google Scholar]






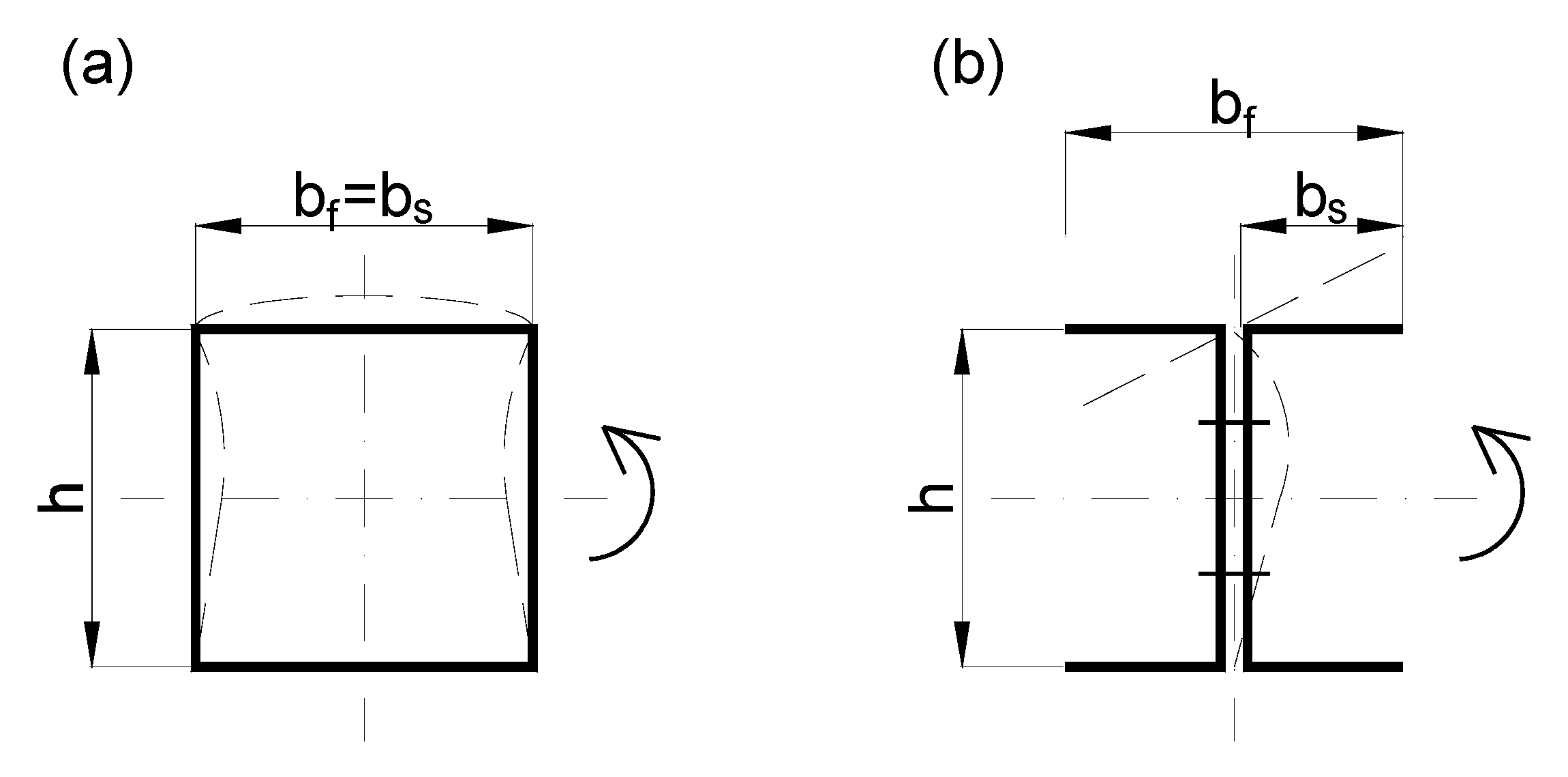


| Wall Thickness (mm) | t= | 8 | 7 | 6 | 5 |
|---|---|---|---|---|---|
| Slenderness | λ=b/t= | 15.63 | 17.86 | 20.83 | 25.00 |
| Euler stress (N/mm2) | Flange σE,i= | 778.24 | 595.84 | 437.76 | 304.00 |
| Web σE,i= | 135.11 | 103.44 | 76.00 | 52.78 | |
| Buckling coefficient | for lp: k*= | 0.800 | 0.800 | 0.800 | 0.800 |
| for ls: k*= | 0.950 | 0.950 | 0.950 | 0.950 | |
| Critical stress acc. CPM (N/mm2) | for lp: σcr,p= | 622.60 | 476.67 | 350.21 | 243.20 |
| for ls: σcr,s= | 739.08 | 565.86 | 415.73 | 288.70 | |
| Critical stress acc. EC3 (N/mm2) | σcr,0= | 334.64 | 256.21 | 188.24 | 130.72 |
| Local critical resistance (kNm) | for lp: = | 448.36 | 300.35 | 189.13 | 109.45 |
| for ls: = | 532.24 | 356.54 | 224.52 | 129.93 | |
| 240.99 | 161.44 | 101.66 | 58.83 | ||
| Critical load acc. CPM (kN/m) | for lp: = | 359.72 | 240.97 | 151.74 | 87.81 |
| for ls: = | 316.02 | 211.70 | 133.31 | 77.14 | |
| Critical load acc. EC3 (kN/m) | 143.09 | 95.85 | 60.36 | 34.93 | |
| Percentage increase of resistance (%) | 120.86 | 120.86 | 120.86 | 120.86 |
| t | s/p | ABAQUS | CPM | CUFSM | [19] | [22] | EC3 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 5 | s | 291.98 | 288.70 | 235.53 | 223.98 | 191.64 | 130.72 |
| p | 247.16 | 243.20 | |||||
| 6 | s | 418.32 | 415.73 | 339.16 | 322.53 | 275.96 | 188.24 |
| p | 355.00 | 350.21 | |||||
| 7 | s | 566.31 | 565.86 | 461.62 | 439.00 | 375.59 | 256.21 |
| p | 481.86 | 476.67 | |||||
| 8 | s | 735.48 | 739.08 | 602.92 | 573.38 | 490.58 | 334.64 |
| p | 627.53 | 622.60 | |||||
| Wall Thickness (mm) | t= | 8 | 7 | 6 | 5 |
|---|---|---|---|---|---|
| Slenderness | λ=b/t= | 15.63 | 17.86 | 20.83 | 25.00 |
| Design ultimate resistance (kNm) | for lp: = | 244.81 | 201.32 | 159.99 | 121.57 |
| for ls: = | 245.78 | 210.24 | 167.37 | 127.27 | |
| = | 208.72 | 170.89 | 135.56 | 103.16 | |
| Ultimate load acc. CPM (kN/m) | for lp: = | 196.41 | 161.52 | 128.36 | 97.54 |
| for ls: = | 145.93 | 124.83 | 99.38 | 75.57 | |
| Ultimate load acc. EC3 (kN/m) | for ls: | 123.93 | 101.47 | 80.49 | 61.25 |
| Percentage increase of resistance (%) | 17.76 | 23.02 | 23.46 | 23.37 |
| Span Length (m) | L = | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| Slenderness | λ=b/t= | 30.25 | |||
| Euler stress (N/mm2) | flange σE,i = | 207.64 | |||
| web σE,i = | 50.23 | ||||
| Length of ranges (m) | lp= | 1600 | 2000 | 2400 | 2800 |
| ls= | 843 | 1050 | 1263 | 1474 | |
| Buckling coefficient | for lp: k*= | 0.94 | 0.93 | 0.92 | 0.92 |
| for ls: k*= | 1.11 | 1.08 | 1.05 | 1.04 | |
| Critical stress acc. to CPM (N/mm2) | for lp: σcr,s= | 195.42 | 193.34 | 191.98 | 191.03 |
| for ls: σcr,s= | 230.47 | 223.70 | 218.80 | 215.20 | |
| Critical stress acc. to EC3 (N/mm2) | σcr,0= | 89.28 | |||
| “Local” critical resistance (kNm) | for lp: = | 64.13 | 63.45 | 63.00 | 62.69 |
| for ls: = | 75.63 | 73.41 | 71.80 | 70.62 | |
| 29.30 | |||||
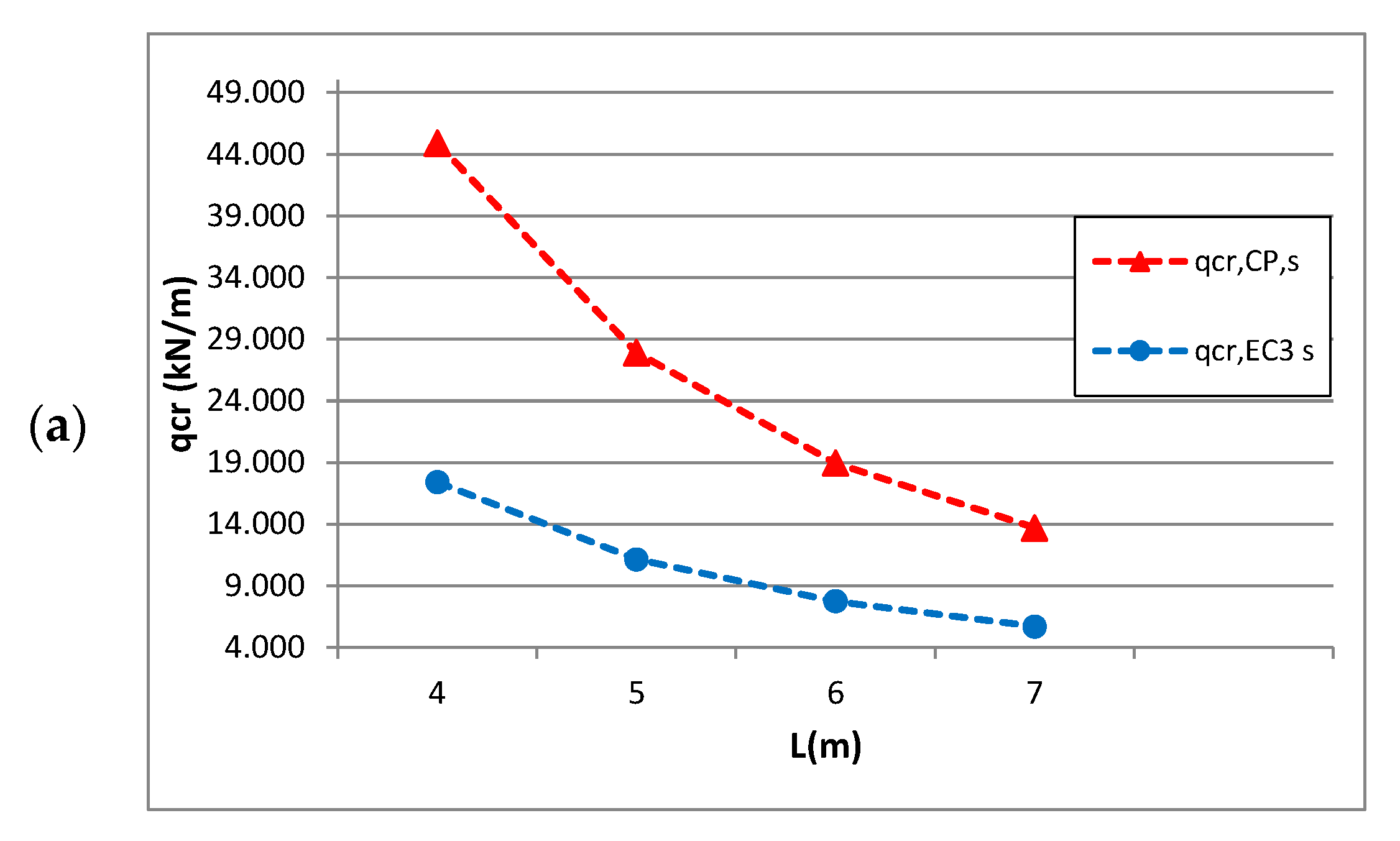
| Critical load acc. to CPM (kN/m) | for lp: = | 51.45 | 32.58 | 22.47 | 16.42 |
| for ls: = | 44.91 | 27.90 | 18.95 | 13.69 | |
| Critical load acc. to EC3 (kN/m) | 17.40 | 11.13 | 7.73 | 5.68 | |
| Percentage increment of resistance (%) | 158.13 | 150.54 | 145.06 | 141.03 | |
| Design ultimate resistance (kNm) | for lp: = | 89.15 | 88.94 | 88.80 | 88.71 |
| for ls: = | 92.43 | 91.82 | 91.38 | 91.04 | |
| 75.77 | |||||
| Ultimate load acc. to CPM (kN/m) | for lp: = | 71.52 | 45.67 | 31.67 | 23.24 |
| for ls: = | 54.88 | 34.89 | 24.11 | 17.65 | |
| Ultimate load acc. to EC3 (kN/m) | for ls: | 44.99 | 28.79 | 19.99 | 14.69 |
| Percentage increase of resistance (%) | 21.99 | 21.19 | 20.60 | 20.16 | |
| L (m) | |||||||
|---|---|---|---|---|---|---|---|
| 4 | SK | 87.09 | 101.27 | 63.85 | 60.13 | 37.91 | 1.59 |
| 2C | 64.13 | 75.63 | 29.30 | 44.91 | 17.40 | 2.58 | |
| % | −26.36 | −25.32 | −54.11 | −25.32 | −54.11 | 62.74 | |
| 5 | SK | 86.32 | 98.61 | 63.85 | 37.47 | 24.26 | 1.54 |
| 2C | 63.45 | 73.41 | 29.30 | 27.90 | 11.13 | 2.51 | |
| % | −26.49 | −25.55 | −54.11 | −25.55 | −54.11 | 62.23 | |
| 6 | SK | 85.81 | 96.74 | 63.85 | 25.53 | 16.85 | 1.52 |
| 2C | 63.00 | 71.80 | 29.30 | 18.95 | 7.73 | 2.45 | |
| % | −26.58 | −25.78 | −54.11 | −25.78 | −54.11 | 61.75 | |
| 7 | SK | 85.45 | 95.33 | 63.85 | 18.48 | 12.38 | 1.49 |
| 2C | 62.69 | 70.62 | 29.30 | 13.69 | 5.68 | 2.41 | |
| % | −26.63 | −25.92 | −54.11 | −25.92 | −54.11 | 61.43 | |
| L (m) | |||||||
|---|---|---|---|---|---|---|---|
| 4 | SK | 93.62 | 96.59 | 87.79 | 57.35 | 52.13 | 1.10 |
| 2C | 89.15 | 92.43 | 75.77 | 54.88 | 44.99 | 1.22 | |
| % | −4.78 | −4.31 | −13.69 | −4.31 | −13.70 | 10.88 | |
| 5 | SK | 93.45 | 96.06 | 87.79 | 36.50 | 33.35 | 1.09 |
| 2C | 88.94 | 91.82 | 75.77 | 34.89 | 28.79 | 1.21 | |
| % | −4.83 | −4.41 | −13.69 | −4.41 | −13.68 | 10.73 | |
| 6 | SK | 93.33 | 95.68 | 87.79 | 25.25 | 23.17 | 1.09 |
| 2C | 88.80 | 91.38 | 75.77 | 24.11 | 19.99 | 1.21 | |
| % | −4.86 | −4.50 | −13.69 | −4.50 | −13.70 | 10.66 | |
| 7 | SK | 93.25 | 95.39 | 87.79 | 18.49 | 17.02 | 1.09 |
| 2C | 88.71 | 91.04 | 75.77 | 17.65 | 14.69 | 1.20 | |
| % | −4.87 | −4.56 | −13.69 | −4.56 | −13.69 | 10.58 | |
| Wall Thickness (mm) | t = | 5 | 4 | 3 | 2 |
|---|---|---|---|---|---|
| Slenderness | λ=b/t= | 24.00 | 30.25 | 40.67 | 61.50 |
| Euler stress (N/mm2) | plate σE,i= | 329.86 | 207.64 | 114.89 | 50.23 |
| web σE,i= | 79.13 | 50.23 | 28.03 | 12.36 | |
| Buckling coefficient | for lp: k*= | 0.94 | 0.94 | 0.94 | 0.94 |
| for ls: k*= | 1.11 | 1.11 | 1.11 | 1.11 | |
| Critical stress acc. to CPM (N/mm2) | for lp: σcr,s= | 310.46 | 195.42 | 108.13 | 47.28 |
| for ls: σcr,s= | 366.13 | 230.47 | 127.52 | 55.76 | |
| Critical stress acc. to EC3 (N/mm2) | σcr,0= | 141.84 | 89.28 | 49.40 | 21.60 |
| “Local” critical resistance (kNm) | for lp: = | 126.49 | 64.13 | 26.80 | 7.86 |
| for ls: = | 149.17 | 75.63 | 31.60 | 9.28 | |
| 57.79 | 29.30 | 12.24 | 3.59 | ||
| Critical load acc. to CPM (kN/m) | for lp: = | 101.49 | 51.45 | 21.50 | 6.31 |
| for ls: = | 88.57 | 44.91 | 18.76 | 5.51 | |
| Critical load acc. to EC3 (kN/m) | 34.31 | 17.40 | 7.27 | 2.13 | |
| Percentage increment of resistance (%) | 158.13 | ||||
| Design ultimate resistance (kNm) | for lp: = | 122.56 | 89.15 | 59.47 | 34.28 |
| for ls: = | 127.15 | 92.43 | 61.51 | 35.26 | |
| 103.28 | 75.77 | 51.38 | 30.43 | ||
| Ultimate load acc. to CPM (kN/m) | for lp: = | 98.33 | 71.52 | 47.72 | 27.50 |
| for ls: = | 75.50 | 54.88 | 36.52 | 20.94 | |
| Ultimate load acc. to EC3 (kN/m) | for ls: | 61.32 | 44.99 | 30.51 | 18.07 |
| Percentage increment of resistance (%) | 23.12 | 21.99 | 19.71 | 15.87 | |
| t (mm) | |||||||
|---|---|---|---|---|---|---|---|
| 5 | SK | 169.45 | 197.05 | 124.23 | 117.00 | 73.76 | 1.59 |
| 2C | 126.49 | 149.17 | 57.79 | 88.57 | 34.31 | 2.58 | |
| % | −25.35 | −24.29 | −53.48 | −24.29 | −53.48 | 62.74 | |
| 4 | SK | 87.09 | 101.27 | 63.85 | 60.13 | 37.91 | 1.59 |
| 2C | 64.13 | 75.63 | 29.30 | 44.91 | 17.40 | 2.58 | |
| % | −26.36 | −25.32 | −54.11 | −25.32 | −54.11 | 62.74 | |
| 3 | SK | 36.88 | 42.89 | 27.04 | 25.46 | 16.05 | 1.59 |
| 2C | 26.80 | 31.60 | 12.24 | 18.76 | 7.27 | 2.58 | |
| % | −27.34 | −26.32 | −54.72 | −26.32 | −54.72 | 62.74 | |
| 2 | SK | 10.97 | 12.76 | 8.04 | 7.57 | 4.78 | 1.59 |
| 2C | 7.86 | 9.28 | 3.59 | 5.51 | 2.13 | 2.58 | |
| % | −28.31 | −27.29 | −55.32 | −27.29 | −55.32 | 62.74 | |
| t (mm) | |||||||
|---|---|---|---|---|---|---|---|
| 5 | SK | 127.41 | 131.27 | 119.58 | 77.94 | 71.00 | 1.10 |
| 2C | 122.56 | 127.15 | 103.28 | 75.50 | 61.32 | 1.23 | |
| % | −3.80 | −3.14 | −13.64 | −3.14 | −13.64 | 12.16 | |
| 4 | SK | 93.62 | 96.59 | 87.79 | 57.35 | 52.12 | 1.10 |
| 2C | 89.15 | 92.43 | 75.77 | 54.88 | 44.99 | 1.22 | |
| % | −4.78 | −4.31 | −13.69 | −4.31 | −13.69 | 10.87 | |
| 3 | SK | 62.80 | 64.75 | 59.05 | 38.45 | 35.06 | 1.10 |
| 2C | 59.47 | 61.51 | 51.38 | 36.52 | 30.51 | 1.20 | |
| % | −5.29 | −5.01 | −12.98 | −5.01 | −12.98 | 9.16 | |
| 2 | SK | 36.12 | 37.11 | 34.24 | 22.04 | 20.33 | 1.08 |
| 2C | 34.28 | 35.26 | 30.43 | 20.94 | 18.07 | 1.16 | |
| % | −5.10 | −4.99 | −11.12 | −4.99 | −11.13 | 6.91 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szychowski, A.; Brzezińska, K. Local Buckling and Resistance of Continuous Steel Beams with Thin-Walled I-Shaped Cross-Sections. Appl. Sci. 2020, 10, 4461. https://doi.org/10.3390/app10134461
Szychowski A, Brzezińska K. Local Buckling and Resistance of Continuous Steel Beams with Thin-Walled I-Shaped Cross-Sections. Applied Sciences. 2020; 10(13):4461. https://doi.org/10.3390/app10134461
Chicago/Turabian StyleSzychowski, Andrzej, and Karolina Brzezińska. 2020. "Local Buckling and Resistance of Continuous Steel Beams with Thin-Walled I-Shaped Cross-Sections" Applied Sciences 10, no. 13: 4461. https://doi.org/10.3390/app10134461