Modified Recurrence Plot for Robust Condition Monitoring of Electrode Tips in a Resistance Spot Welding System
Abstract
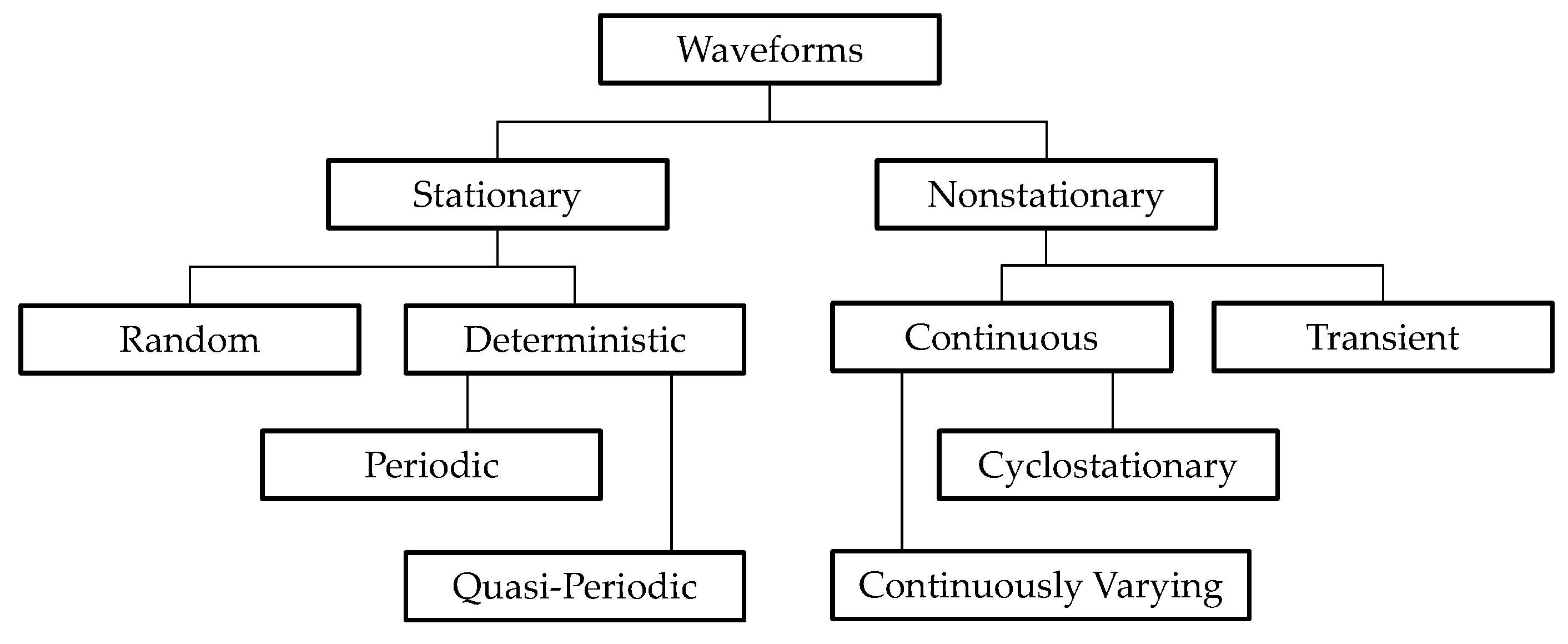
:1. Introduction
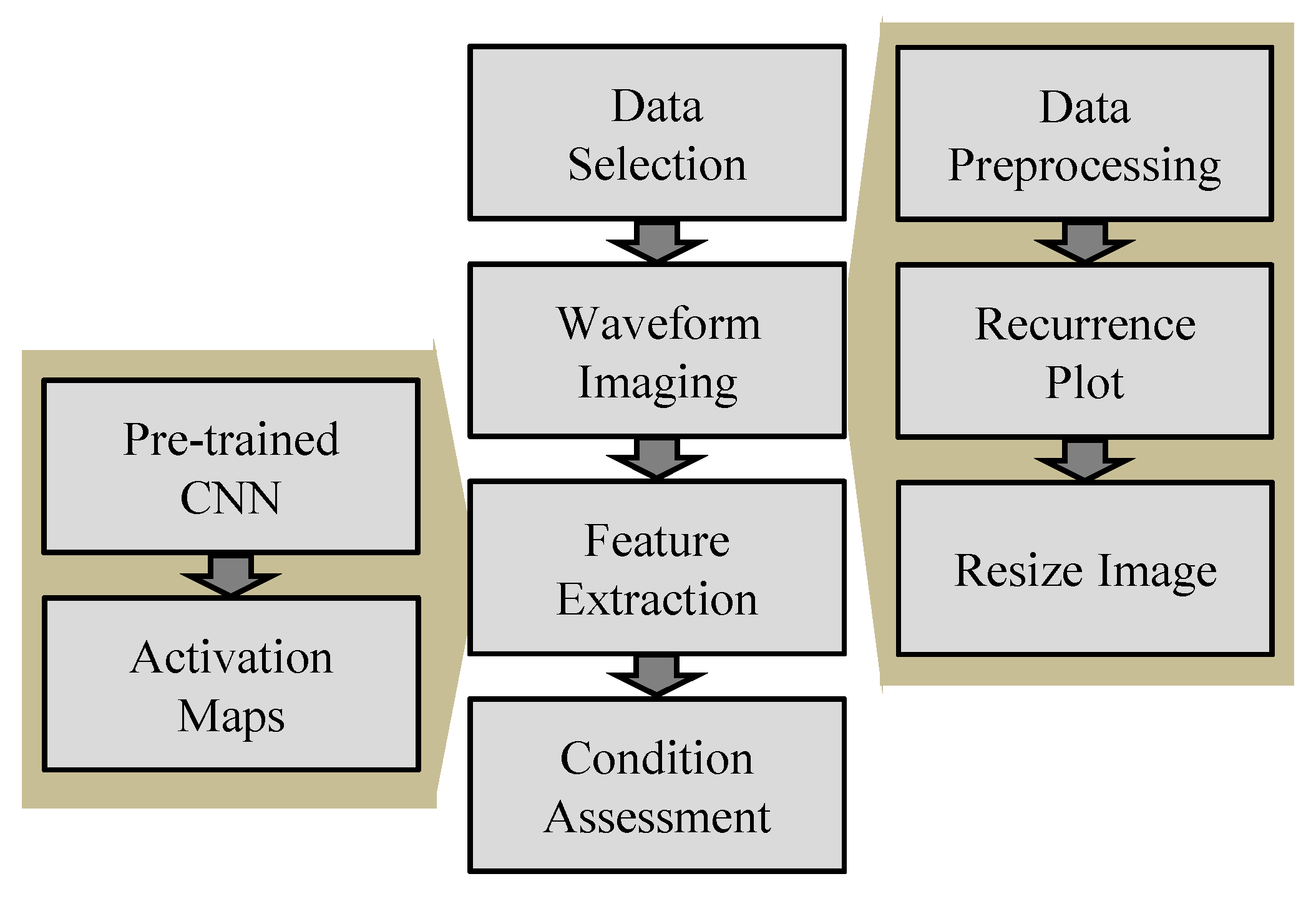
2. Proposed Methodology
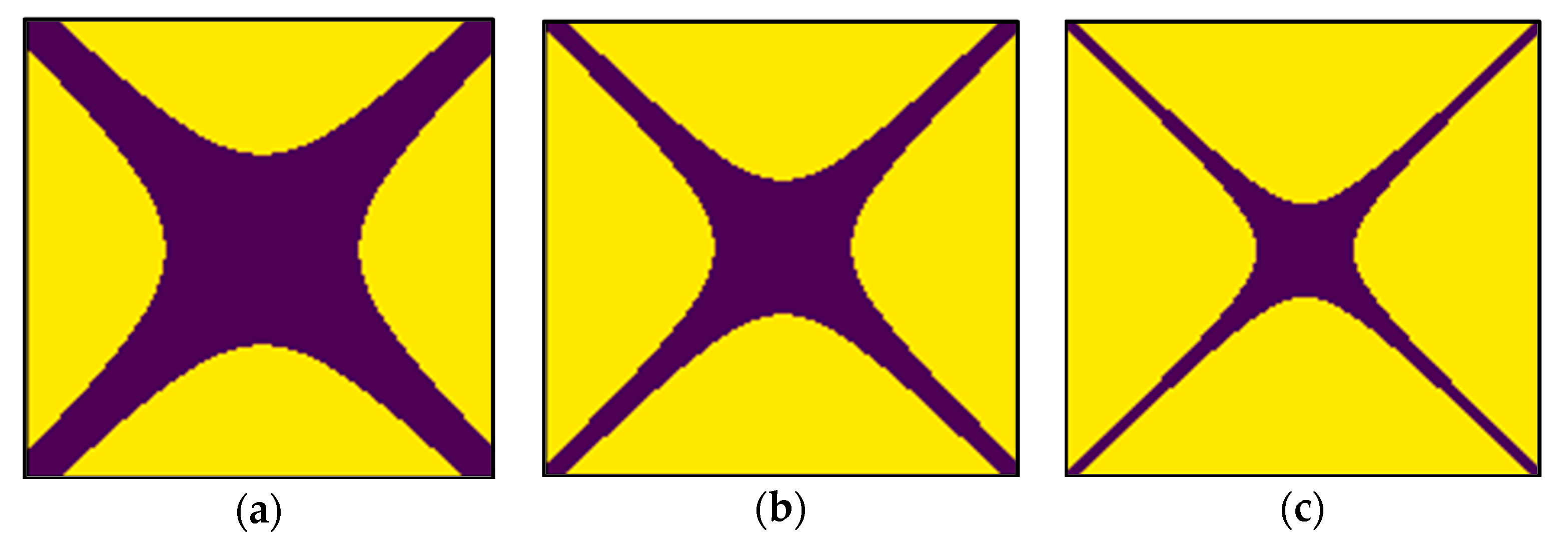
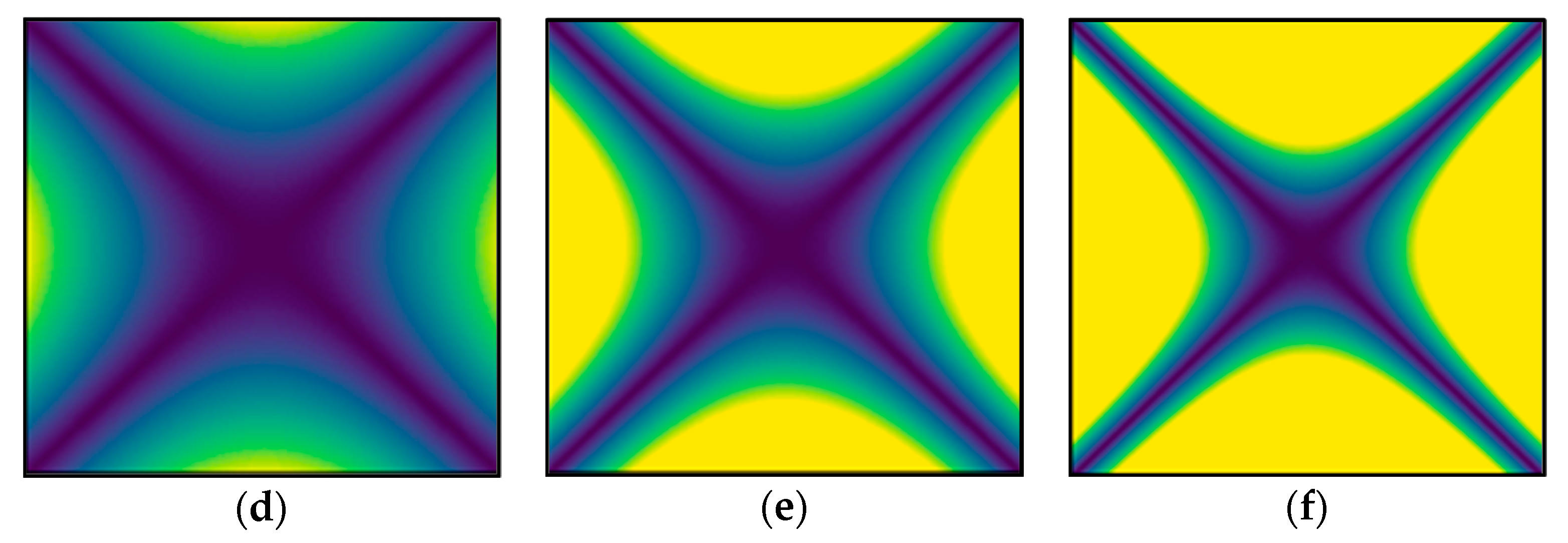
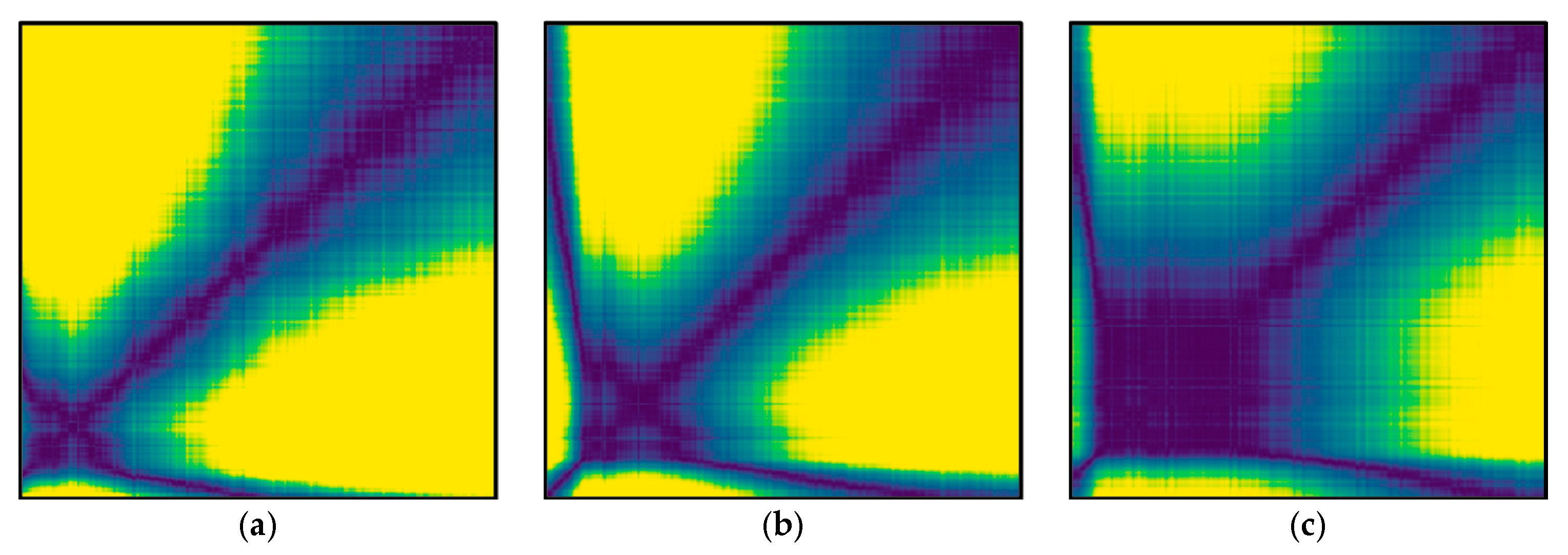
2.1. Waveform Imaging Using a Modified Recurrence Plot
2.2. Unsupervised Feature Extraction by CNN
2.3. Health Indicator with Mahalanobis Distance
3. Case Study
3.1. Experimental Setup
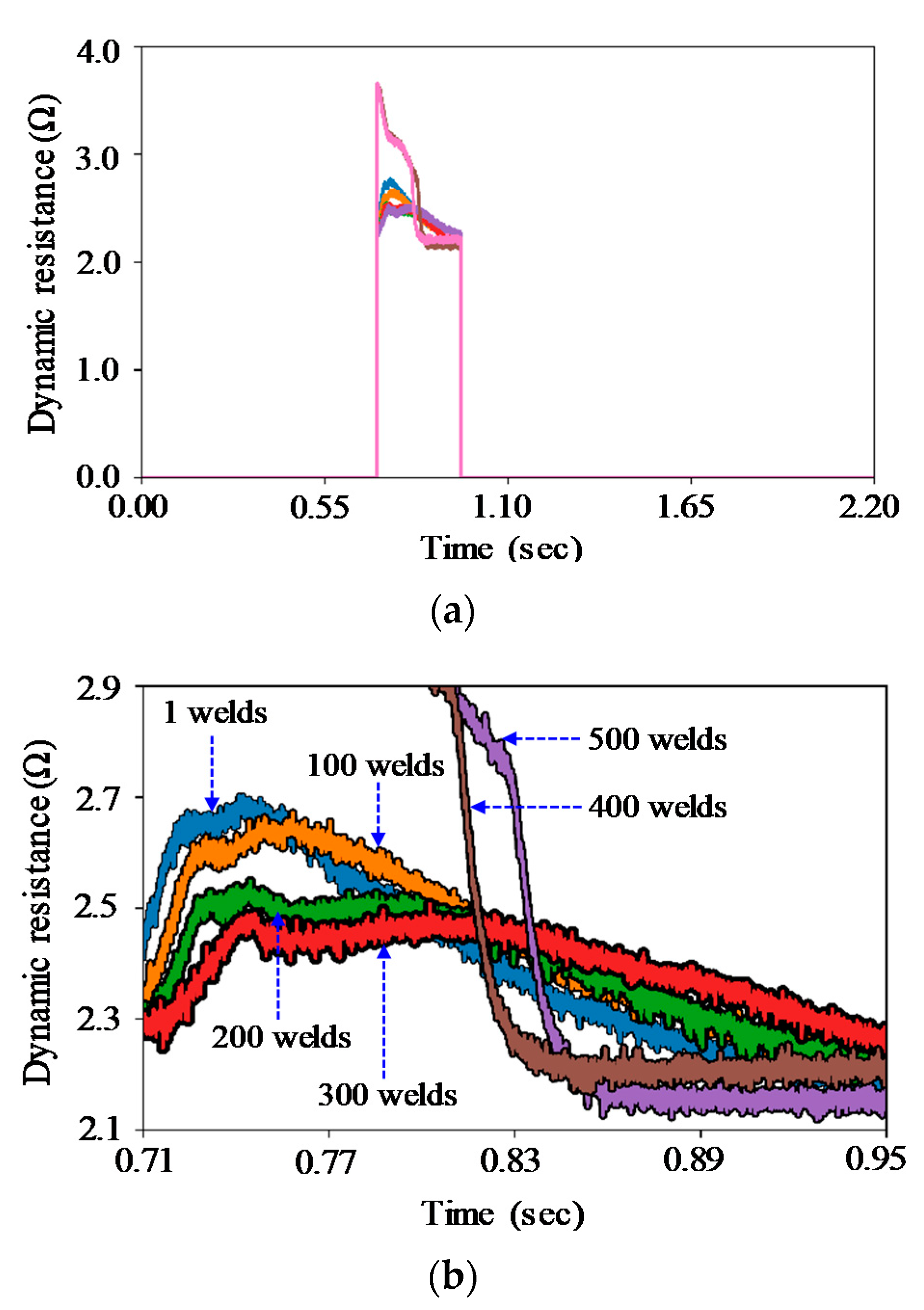
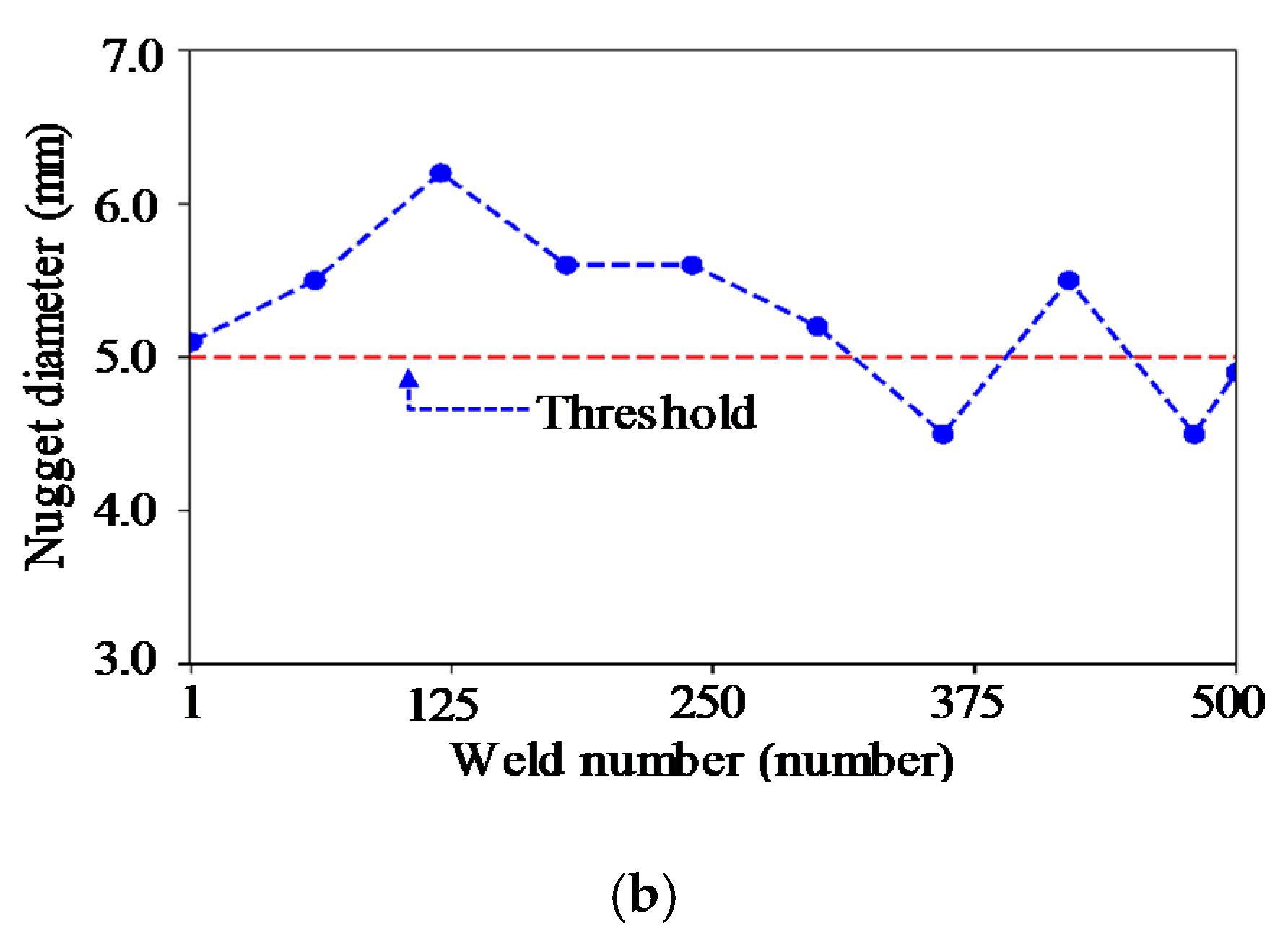
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, W. Monitoring and Diagnosis of Resistance Spot Welding Process. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1999. [Google Scholar]
- Ma, Y.; Wu, P.; Xuan, C.; Zhang, Y.; Su, H. Review on techniques for on-line monitoring of resistance spot welding process. Adv. Mater. Sci. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Zapata, J.; Vilar, R.; Ruiz, R. Performance evaluation of an automatic inspection system of weld defects in radiographic images based on neuro-classifiers. Expert Syst. Appl. 2011, 38, 8812–8824. [Google Scholar] [CrossRef]
- Peng, J.; Fukumoto, S.; Brown, L.; Zhou, N. Image analysis of electrode degradation in resistance spot welding of aluminum. Sci. Technol. Weld. Join. 2004, 9, 331–336. [Google Scholar] [CrossRef]
- Simoncic, S.; Podrzaj, P. Image-based electrode tip displacement in resistance spot welding. Meas. Sci. Technol. 2012, 23, 065401. [Google Scholar] [CrossRef]
- You, D.; Gao, X.; Katayama, S. WPD-PCA-based laser welding process monitoring and defects diagnosis by using FNN and SVM. IEEE Trans. Ind. Electron. 2015, 62, 628–636. [Google Scholar] [CrossRef]
- Martín, Ó.; Pereda, M.; Santos, J.I.; Galán, J.M. Assessment of resistance spot welding quality based on ultrasonic testing and tree-based techniques. J. Mater. Process. Technol. 2014, 214, 2478–2487. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Rui, W.; Xie, X.; Zhu, Y. Study on the nugget growth in single-phase AC resistance spot welding based on the calculation of dynamic resistance. J. Mater. Process. Technol. 2016, 229, 492–500. [Google Scholar] [CrossRef]
- Tseng, K.H.; Chuang, K.J. Monitoring nugget size of micro resistance spot welding (Micro RSW) using electrode displacement-time curve. Adv. Mater. Res. 2012, 463–464, 107–111. [Google Scholar] [CrossRef]
- Ji, C.T.; Zhou, Y. Dynamic electrode force and displacement in resistance spot welding of aluminum. J. Manuf. Sci. Eng. 2004, 126, 605–610. [Google Scholar] [CrossRef]
- Dickinson, D.W.; Franklin, J.E.; Stanya, A. Characterization of spot welding behavior by dynamic electrical parameter monitoring. Weld. J. 1980, 59, 170–176. [Google Scholar]
- Hao, M.; Osman, K.A.; Boomer, D.R.; Newton, C.J. Developments in characterization of resistance spot welding of aluminum. Weld. J. 1996, 75, 1–8. [Google Scholar]
- Xing, B.; Xiao, Y.; Qin, Q.H.; Cui, H. Quality assessment of resistance spot welding process based on dynamic resistance signal and random forest based. Int. J. Adv. Manuf. Technol. 2018, 94, 327–339. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Y.; Zhao, D.; Huang, Y.; Yin, Z. Weld quality monitoring research in small scale resistance spot welding by dynamic resistance and neural network. Measurement 2017, 99, 120–127. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Y.; Zhao, D. Quality monitoring based on dynamic resistance and principal component analysis in small scale resistance spot welding process. Int. J. Adv. Manuf. Technol. 2016, 86, 3443–3451. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Y.; Zhao, D.; Huang, Y. A comparison of two types of neural network for weld quality prediction in small scale resistance spot welding. Mech. Syst. Signal Process. 2017, 93, 634–644. [Google Scholar] [CrossRef]
- Randall, R.B. Vibration-Based Condition Monitoring, 1st ed.; Wiley: New Delhi, India, 2011. [Google Scholar]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef] [Green Version]
- Nichols, J.M.; Trickey, S.T.; Seaver, M. Damage detection using multivariate recurrence quantification analysis. Mech. Syst. Signal Process. 2006, 20, 421–437. [Google Scholar] [CrossRef]
- Manetti, C.; Giuliani, A.; Ceruso, M.-A.; Webber Charles, L.; Zbilut, J.P. Recurrence analysis of hydration effects on nonlinear protein dynamics: Multiplicative scaling and additive processes. Phys. Lett. A 2001, 281, 317–323. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Guerin, J.; Gibaru, O.; Thiery, S.; Nyiri, E. CNN features are also great at unsupervised classification. In Proceedings of the 4th International Conference on Artificial Intelligence and Applications, Melbourne, Australia, 17–18 February 2018. [Google Scholar]
- Girish, D.; Singh, V.; Ralescu, A. Unsupervised clustering based understanding of CNN. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019; pp. 9–11. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Mahalanobis, P.C. On the generalized distance in statistics. Proc. Natl. Inst. Sci. India 1936, 2, 49–55. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]


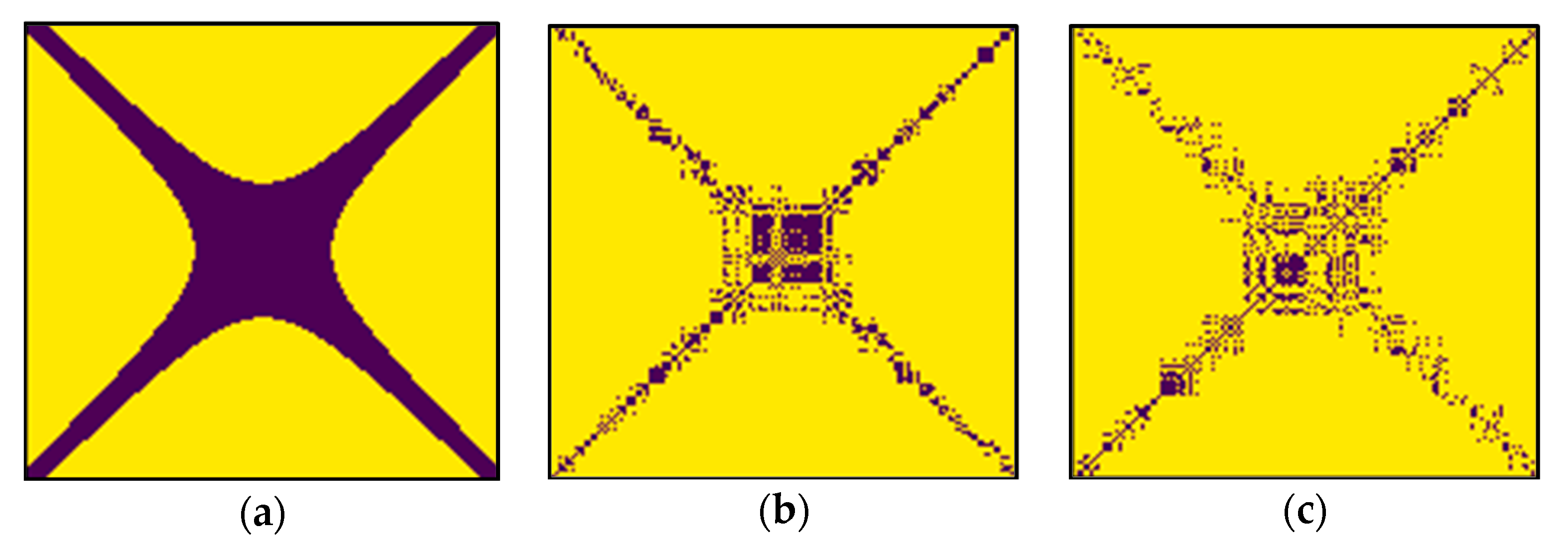
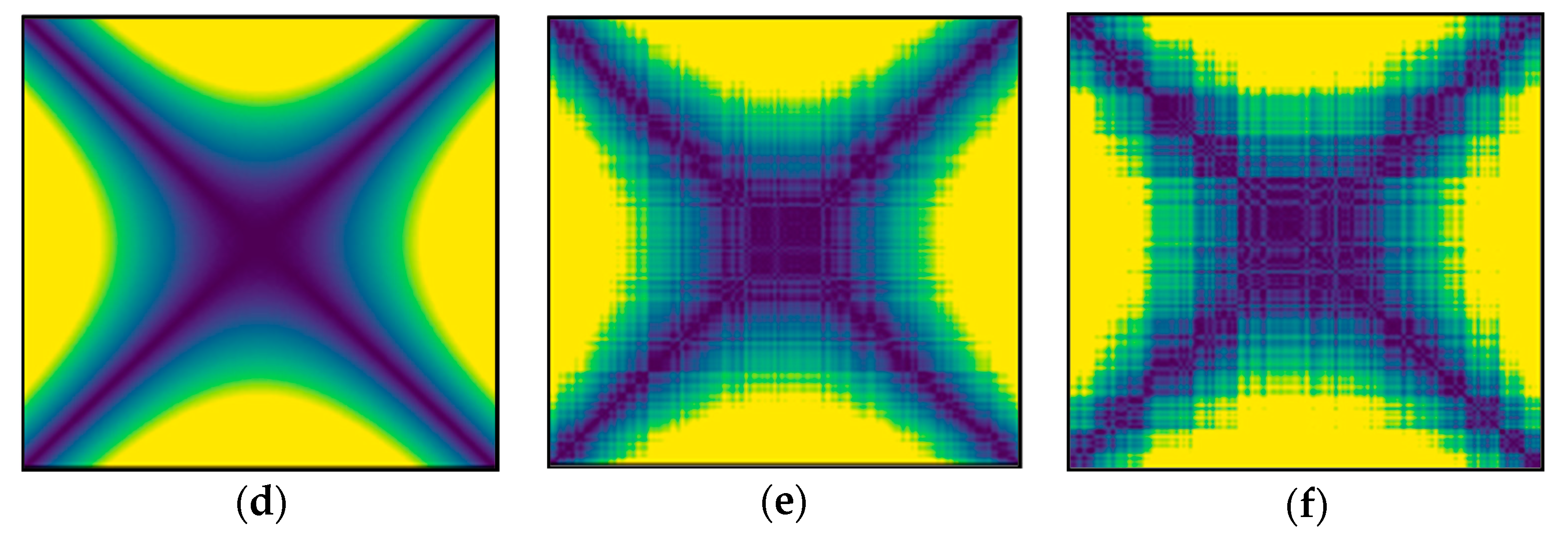


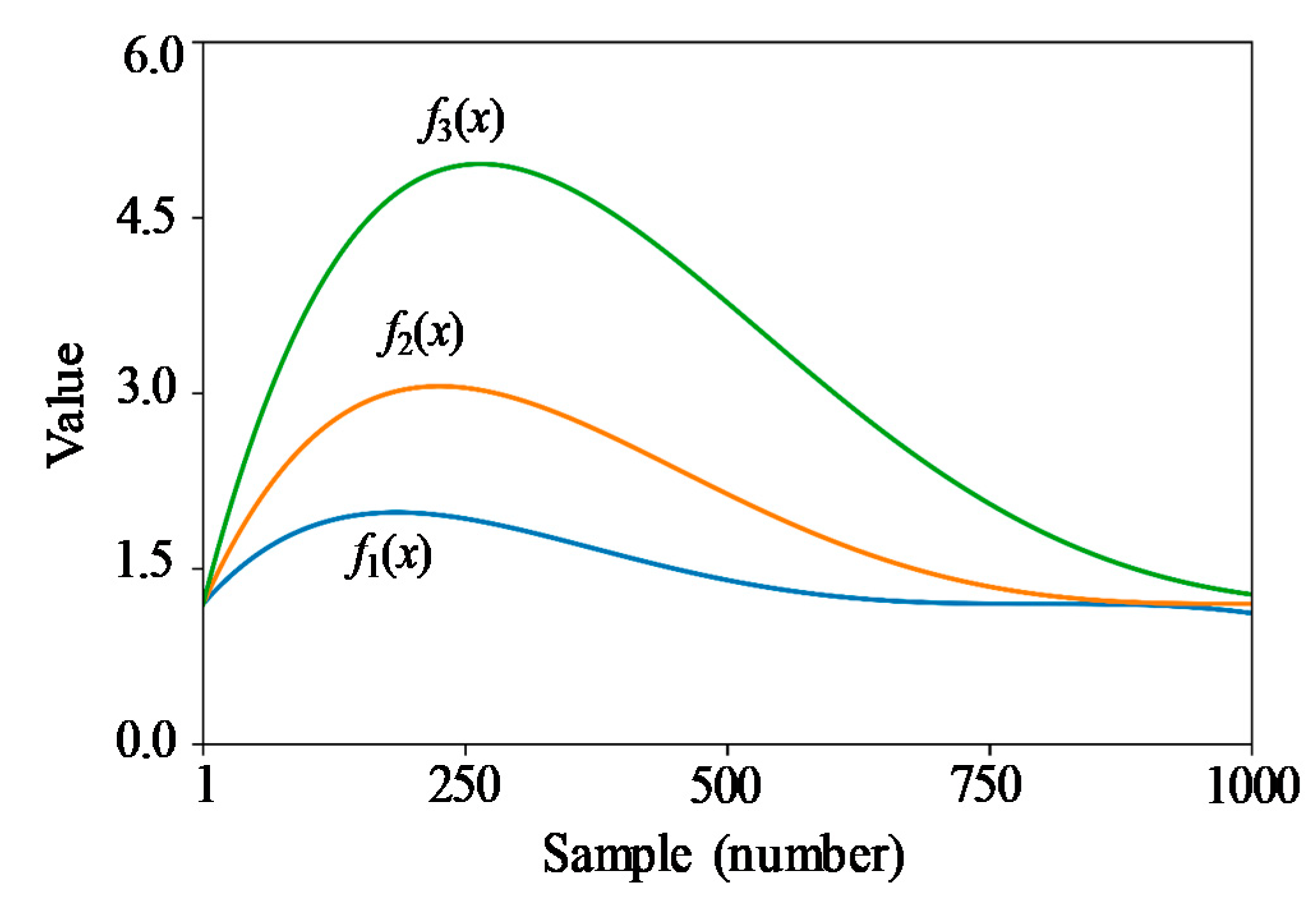

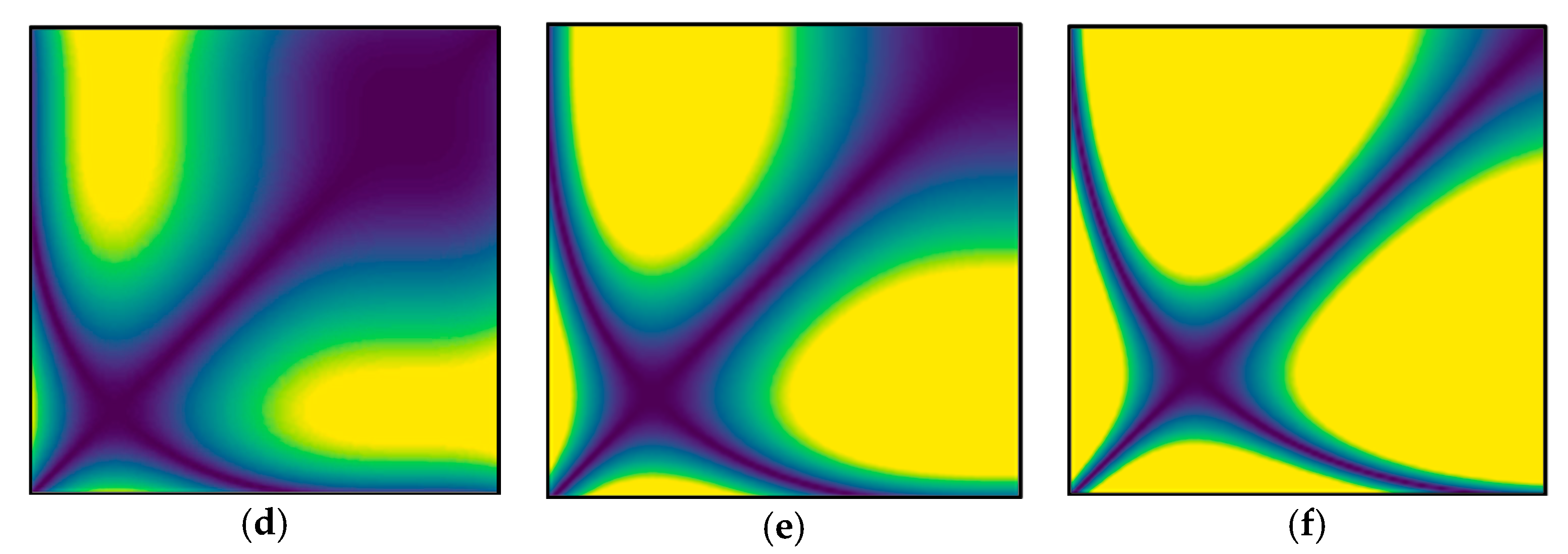
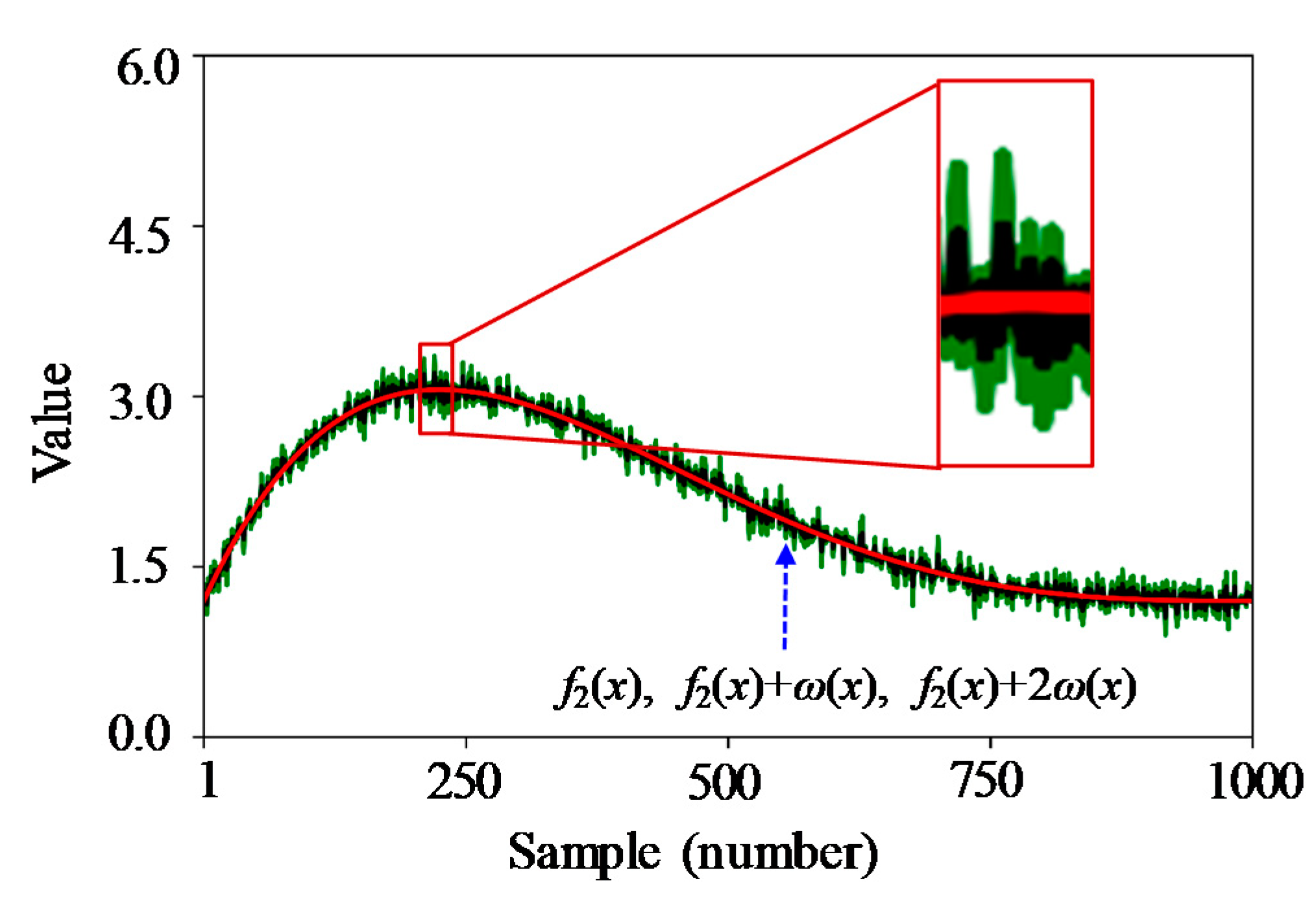

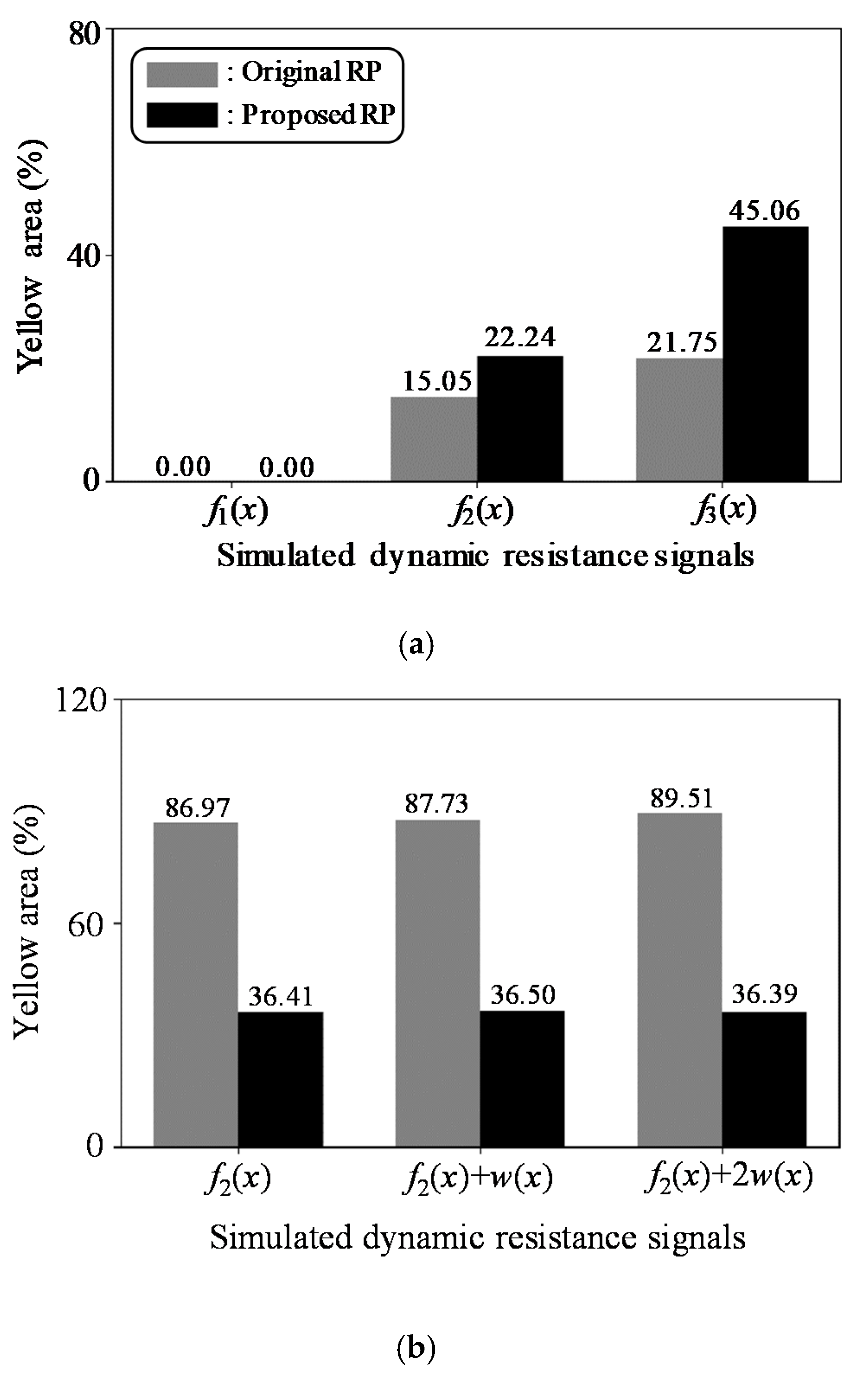


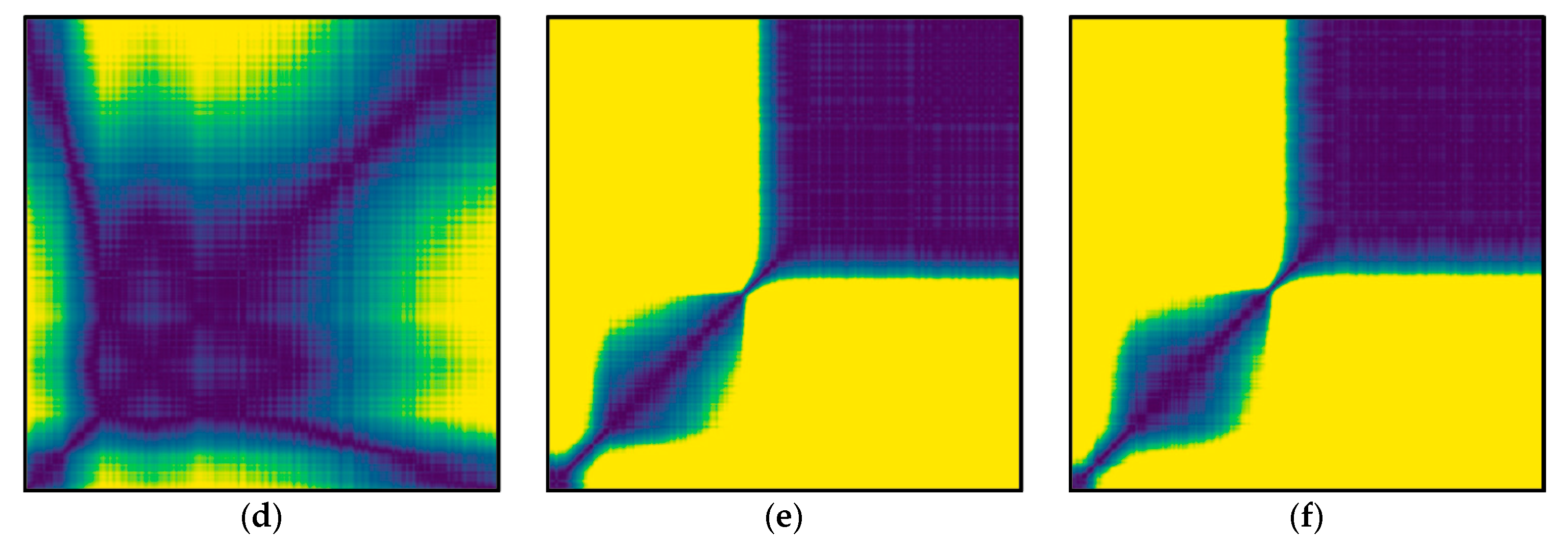



| Method | f(x) | 2f(x) | 4f(x) | 2f(x) + ω(x) | 2f(x) + 2ω(x) |
|---|---|---|---|---|---|
| Original RP | 62.79% | 78.39% | 87.74% | 93.95% | 94.64% |
| Proposed RP | 0.22% | 29.54% | 56.65% | 29.70% | 29.86% |
| Method | f1(x) | f2(x) | f3(x) | f2(x) + ω(x) | f2(x) + 2ω(x) |
|---|---|---|---|---|---|
| Original RP | 71.93% | 86.97% | 93.68% | 87.73% | 89.51% |
| Proposed RP | 14.17% | 36.41% | 59.23% | 36.50% | 36.39% |
| Pattern | Meaning |
|---|---|
| Homogeneity | The process is stationary. |
| Fading to the upper left and lower right corners | Nonstationary data; contains a trend or a drift. |
| Disruptions (White bands) | Nonstationary data; some states are rare or far from the normal. |
| Periodic/quasi-periodic patterns | Cyclicities in the process |
| Single isolated points | Strong fluctuation in the process |
| Diagonal lines (parallel to the LOI) | State evolution is similar at different epochs. |
| Diagonal lines (orthogonal to the LOI) | State evolution is similar at different times but with reverse time. |
| Vertical and horizontal lines/clusters | Some states do not change. |
| Long bowed line structures | State evolution is similar at different epochs but with different velocity. |
| Data Type | Signal | Set 1 | Set 2 | Set 3 | Set 4 | Set 5 | Set 6 |
|---|---|---|---|---|---|---|---|
| Waveform | Dynamic Resistance | 100 welds (sample /weld) | 100 welds (sample /weld) | 100 welds (sample /weld) | 100 welds (sample /weld) | 100 welds (sample /weld) | 500 welds (sample/ weld) |
| Pressure | |||||||
| Current | |||||||
| Image | Upper Electrode Lower Electrode | 500 welds(sample/ five welds) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, W.; Oh, H.; Yun, D.H.; Kim, Y.G.; Youn, J.P.; Park, J.H. Modified Recurrence Plot for Robust Condition Monitoring of Electrode Tips in a Resistance Spot Welding System. Appl. Sci. 2020, 10, 5860. https://doi.org/10.3390/app10175860
Jung W, Oh H, Yun DH, Kim YG, Youn JP, Park JH. Modified Recurrence Plot for Robust Condition Monitoring of Electrode Tips in a Resistance Spot Welding System. Applied Sciences. 2020; 10(17):5860. https://doi.org/10.3390/app10175860
Chicago/Turabian StyleJung, Wonho, Hyunseok Oh, Dong Ho Yun, Young Gon Kim, Jong Pil Youn, and Jae Hong Park. 2020. "Modified Recurrence Plot for Robust Condition Monitoring of Electrode Tips in a Resistance Spot Welding System" Applied Sciences 10, no. 17: 5860. https://doi.org/10.3390/app10175860
APA StyleJung, W., Oh, H., Yun, D. H., Kim, Y. G., Youn, J. P., & Park, J. H. (2020). Modified Recurrence Plot for Robust Condition Monitoring of Electrode Tips in a Resistance Spot Welding System. Applied Sciences, 10(17), 5860. https://doi.org/10.3390/app10175860







