An Experimentally Validated Numerical Model for the Near-Field Explosion of an Ammunition Storage Magazine
Abstract
:1. Introduction
2. Empirical Formulations
2.1. Chamber Pressure
- andfor; andfor
- : blast at the measuring point (kPa)
- : distance from the measuring point inside ammunition storage magazine to the portal (m)
- : portal diameter (m)
- : RDX charge weight (kg), where RDX is an organic compound with the formula (O2N2CH2)3.
- : distance from the explosion center point to the portal (m); is negative, meaning outside of the tunnel).
2.2. Exit Pressure
- DDESB [18]
- : blast pressure at the portal of the ammunition storage magazine (kPa)
- : C4 explosive weight (kg)
- : volume of the storage chamber (m3).
- b.
- Skjeltorp [19]
2.3. The Ratio of the Outside Pressure to the Exit Pressure
- (1)
- DDESB [18]
- : blast pressure outside the ammunition storage magazine (kPa)
- : distance from the measuring point to the portal (m)
- : portal diameter (m).
- (2)
- Helseth et al. [20]
- (3)
- Skjeltorp et al. [19]
3. Analytical Model
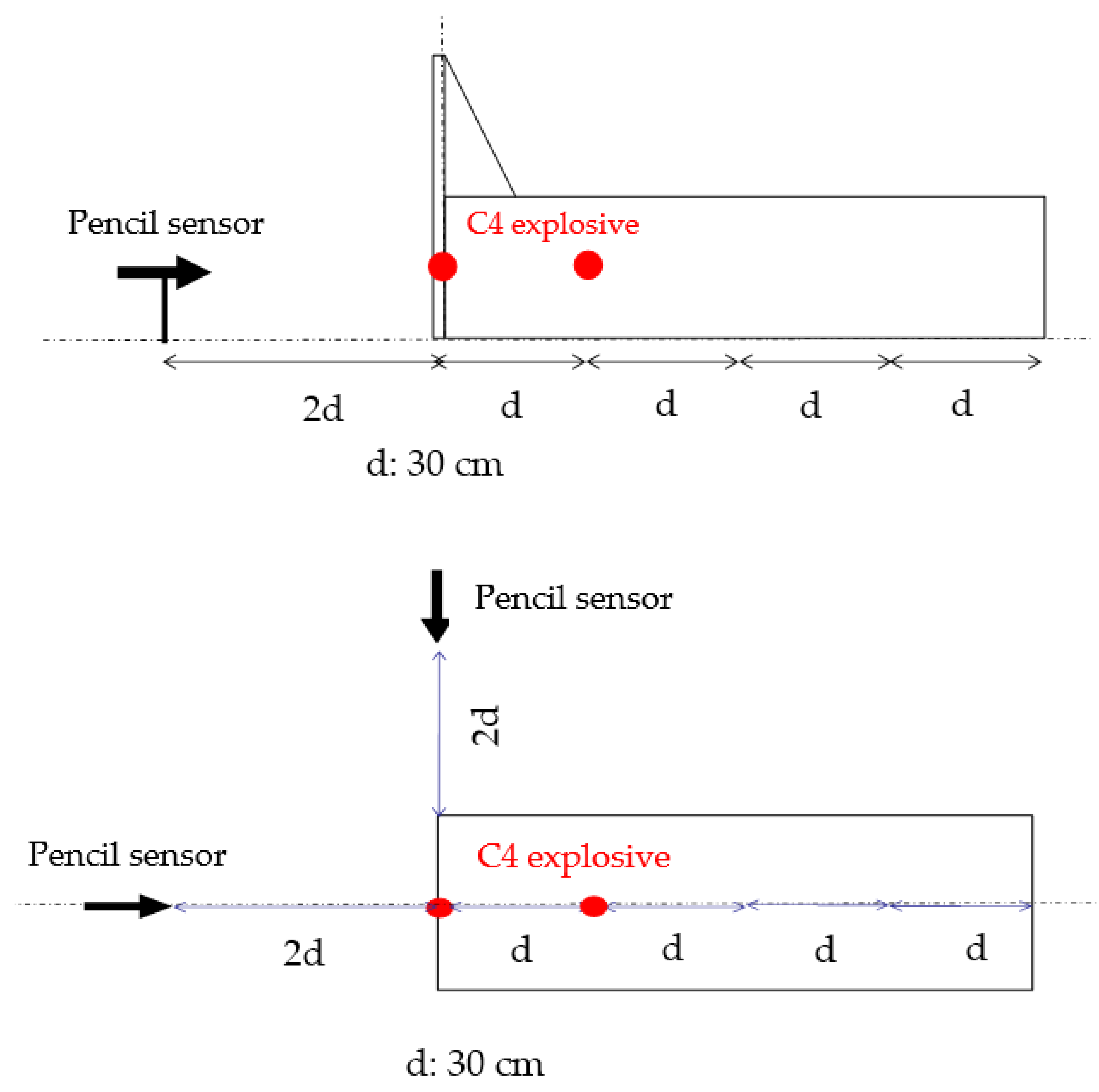
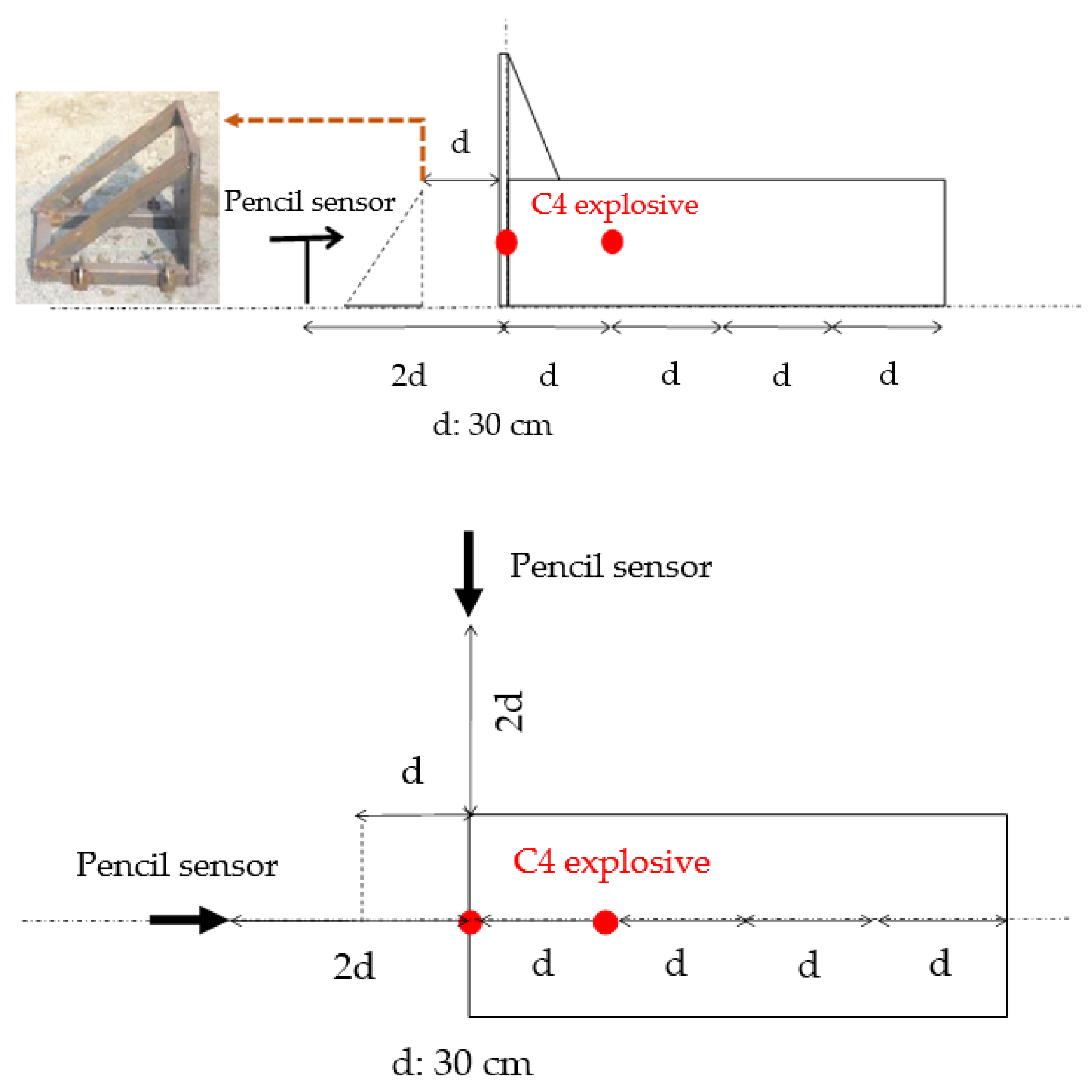
3.1. Explosion Experiment Inside the Ammunition Storage Magazine
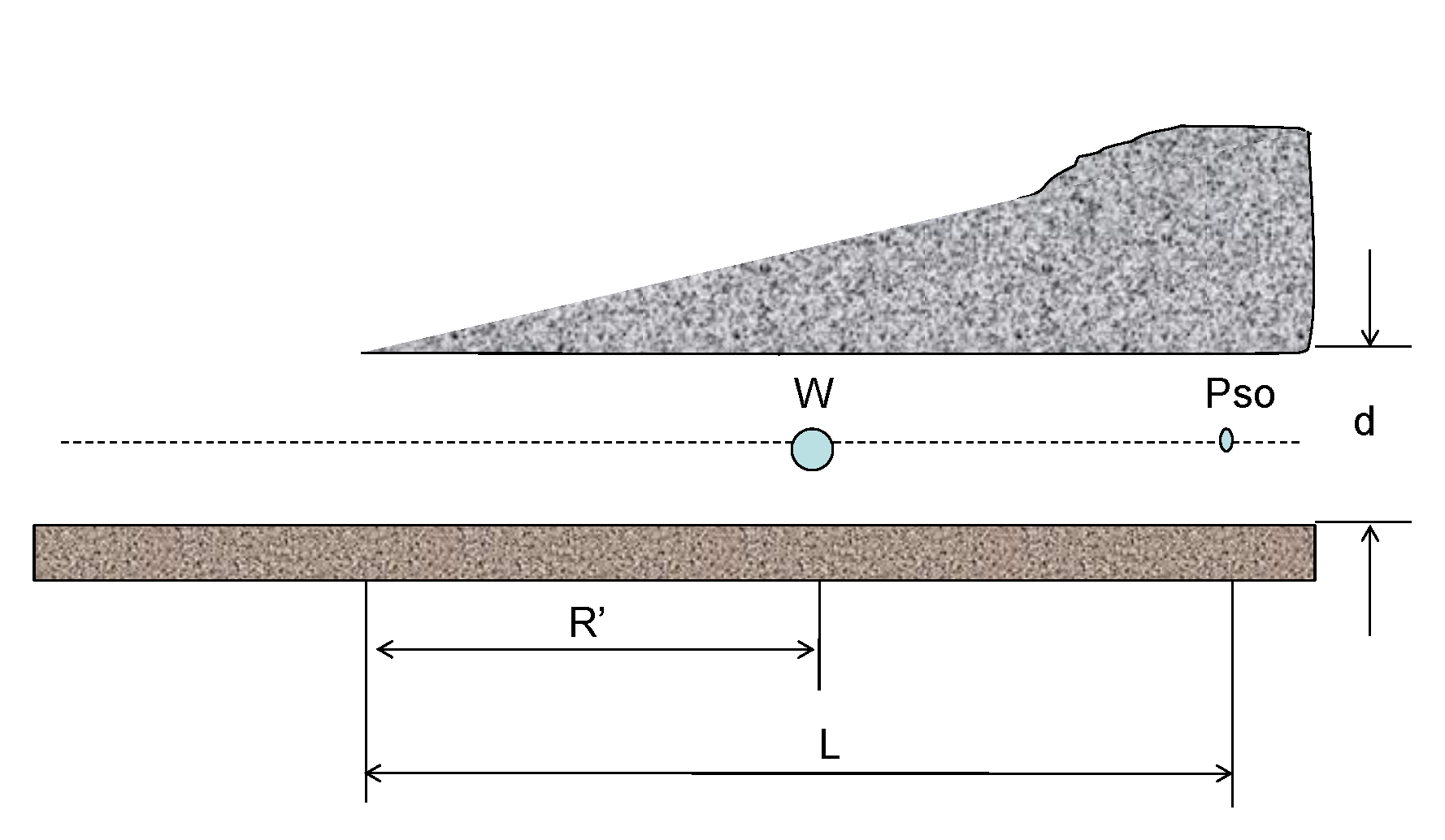
3.2. Experiment on the Retaining Wall Effect
- (1)
- Without a retaining wall
- (2)
- With a retaining wall
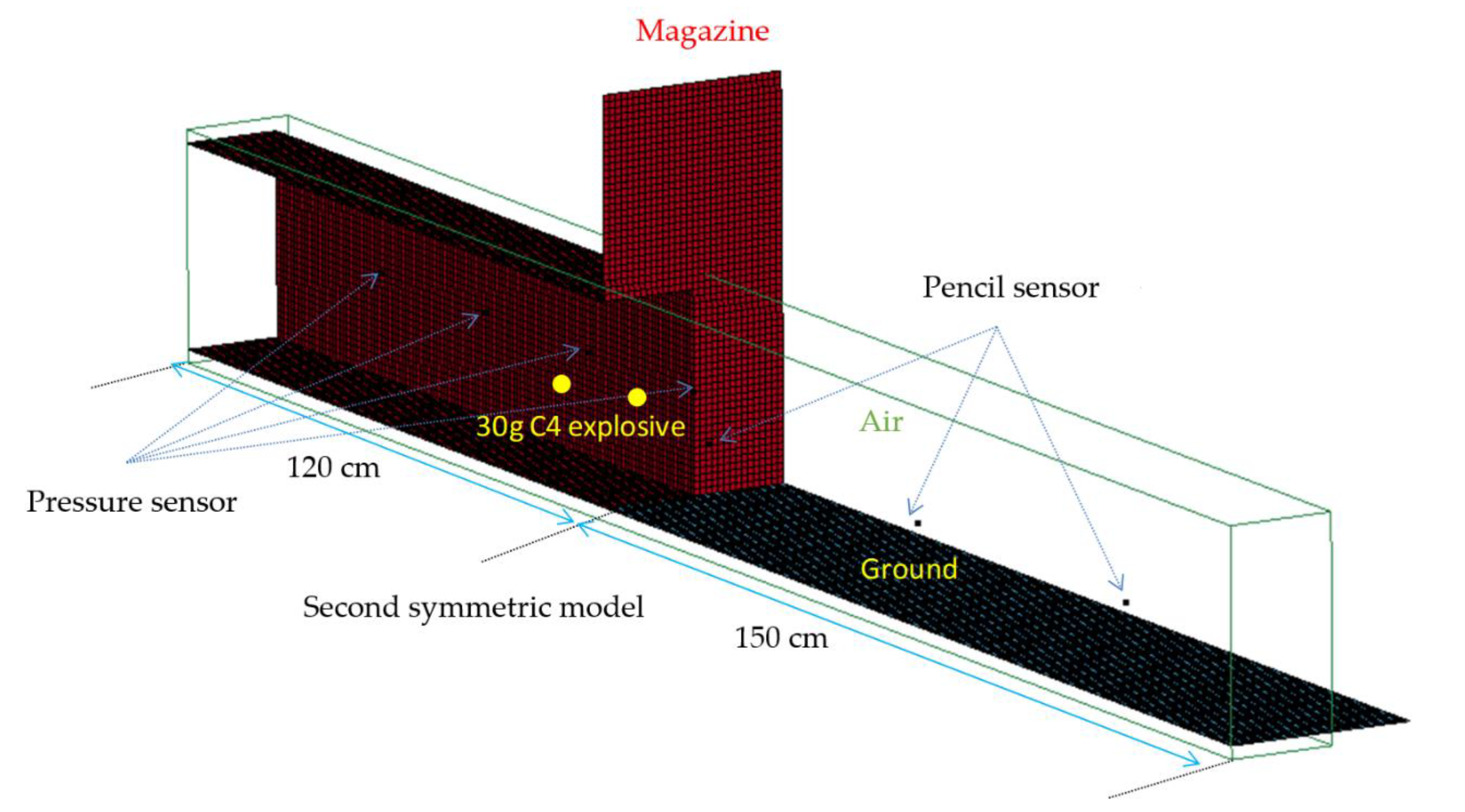
3.3. Numerical Simulations
4. Results
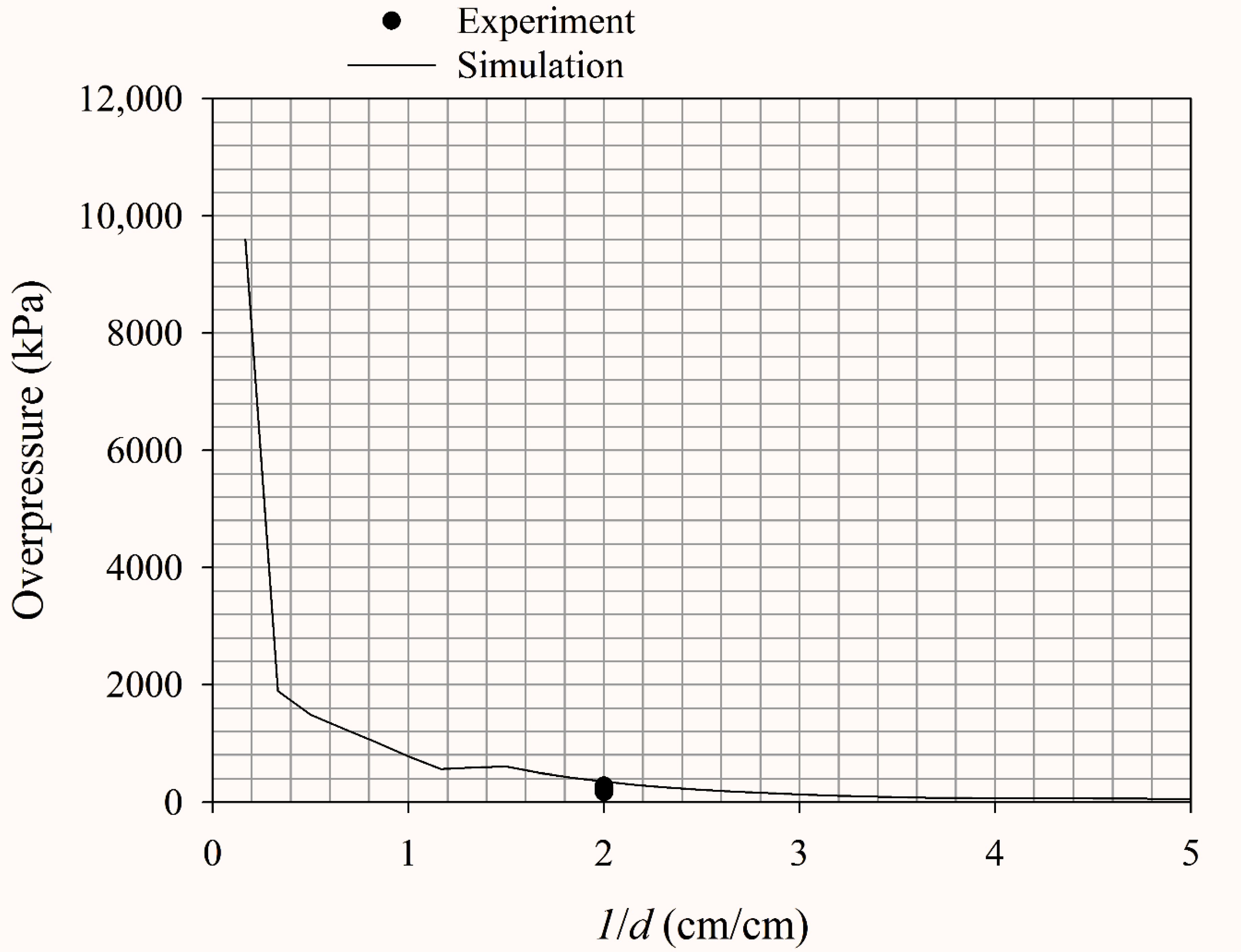
4.1. Blast inside the Ammunition Storage Magazine
- (1)
- Experimental results
- internal blast value of the ammunition storage magazine (kPa)
- ratio of the distance from the measuring point to the portal inside the ammunition storage magazine (l) to the portal diameter ().
- (2)
- Comparison of the empirical equations
- Explosion at the portal
- b
- Explosion at 1× the portal diameter inside the ammunition storage magazine
- (3)
- Numerical simulation results
- Explosion at the portal
- b
- Explosion at 1× the portal diameter inside the ammunition storage magazine
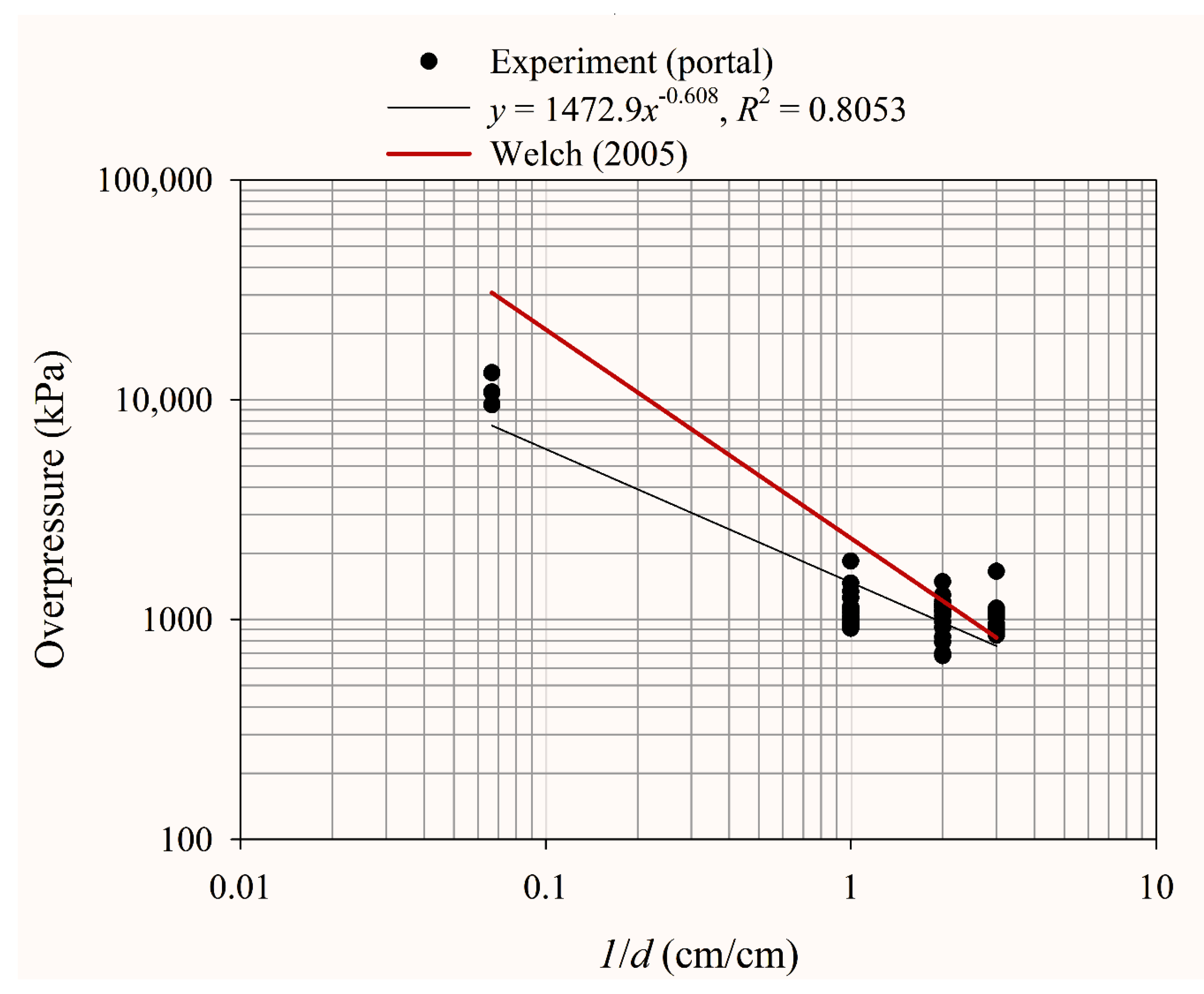
4.2. Blast at the Portal of the Ammunition Storage Magazine
- (1)
- Experimental results
- (2)
- Comparison of empirical equations
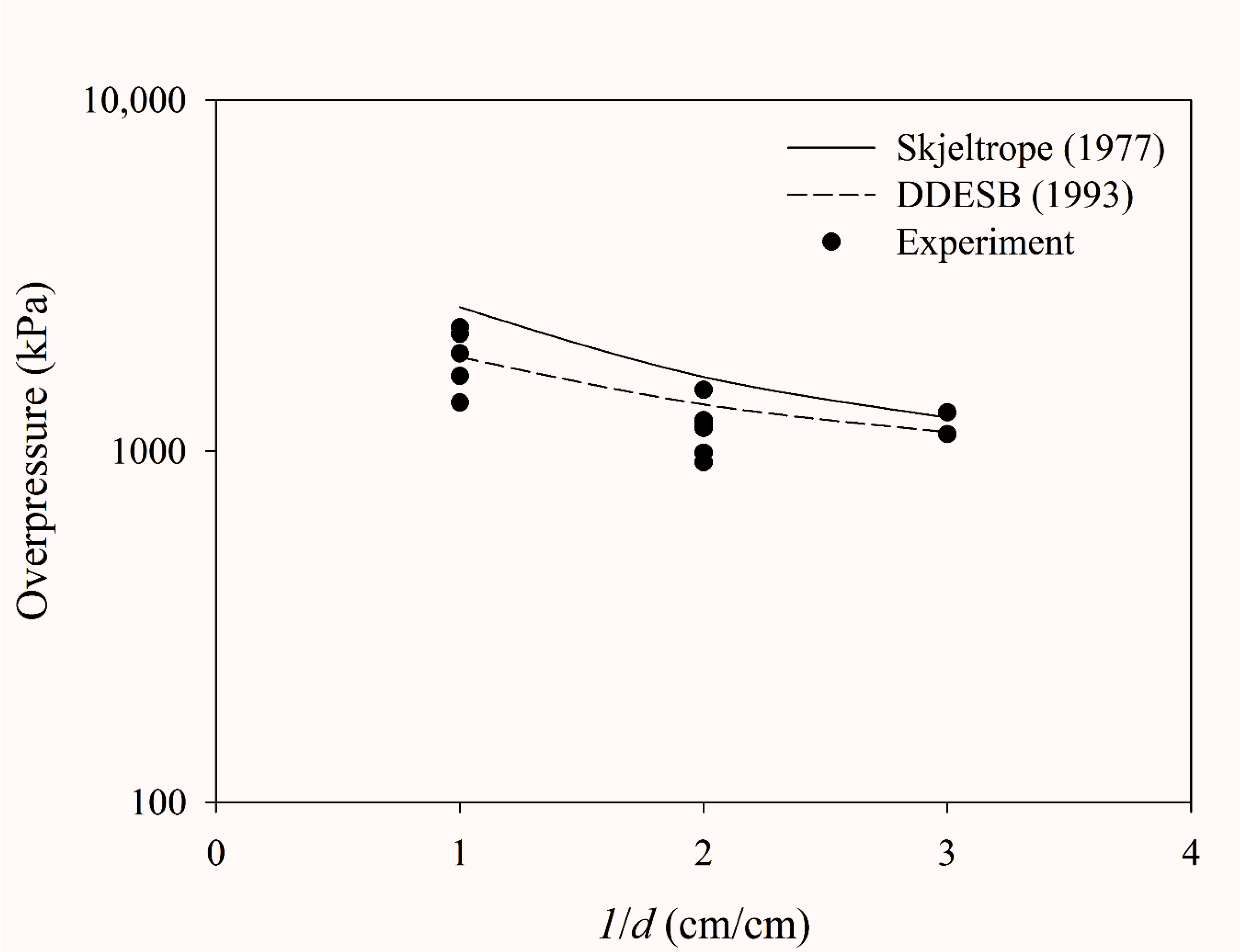
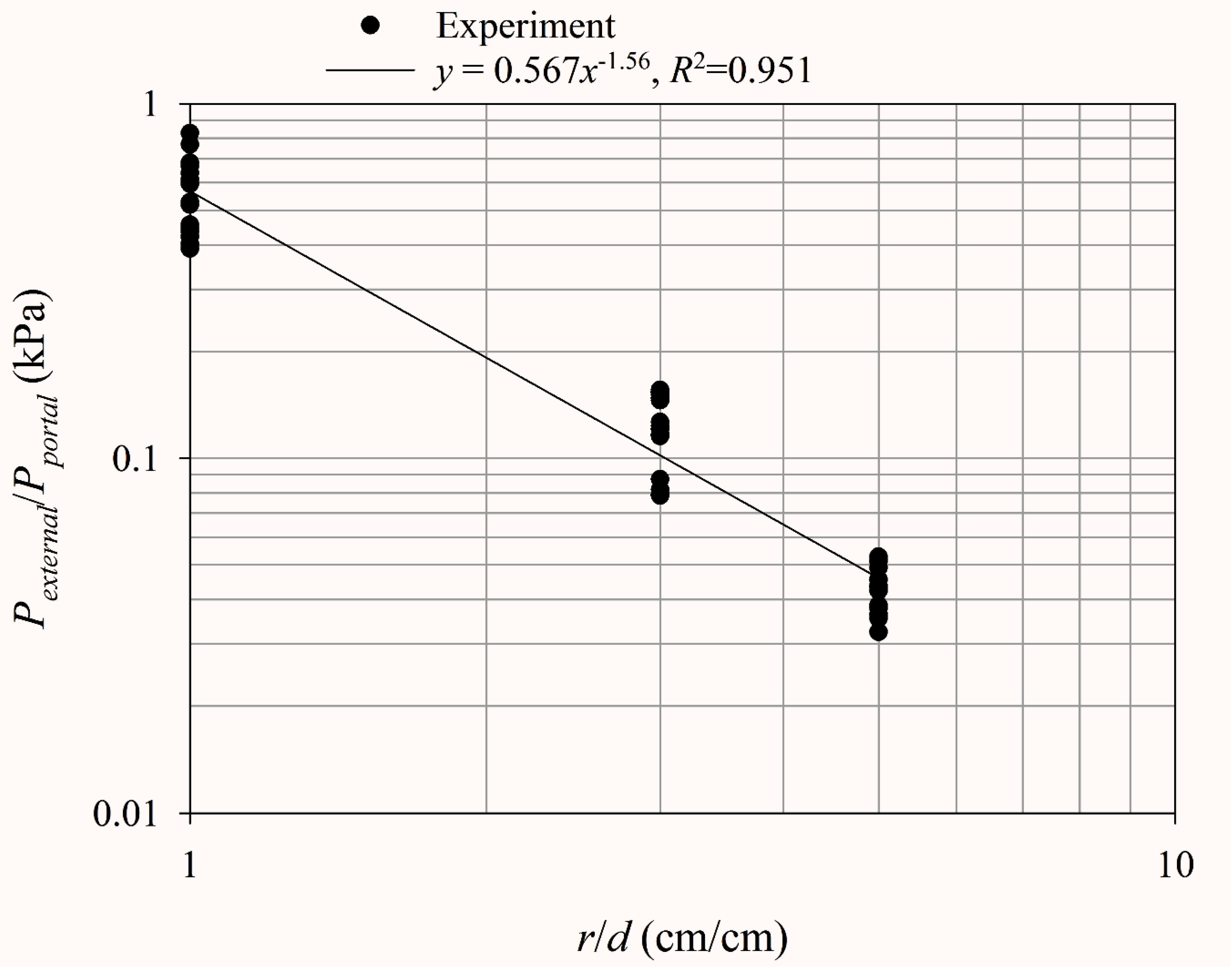
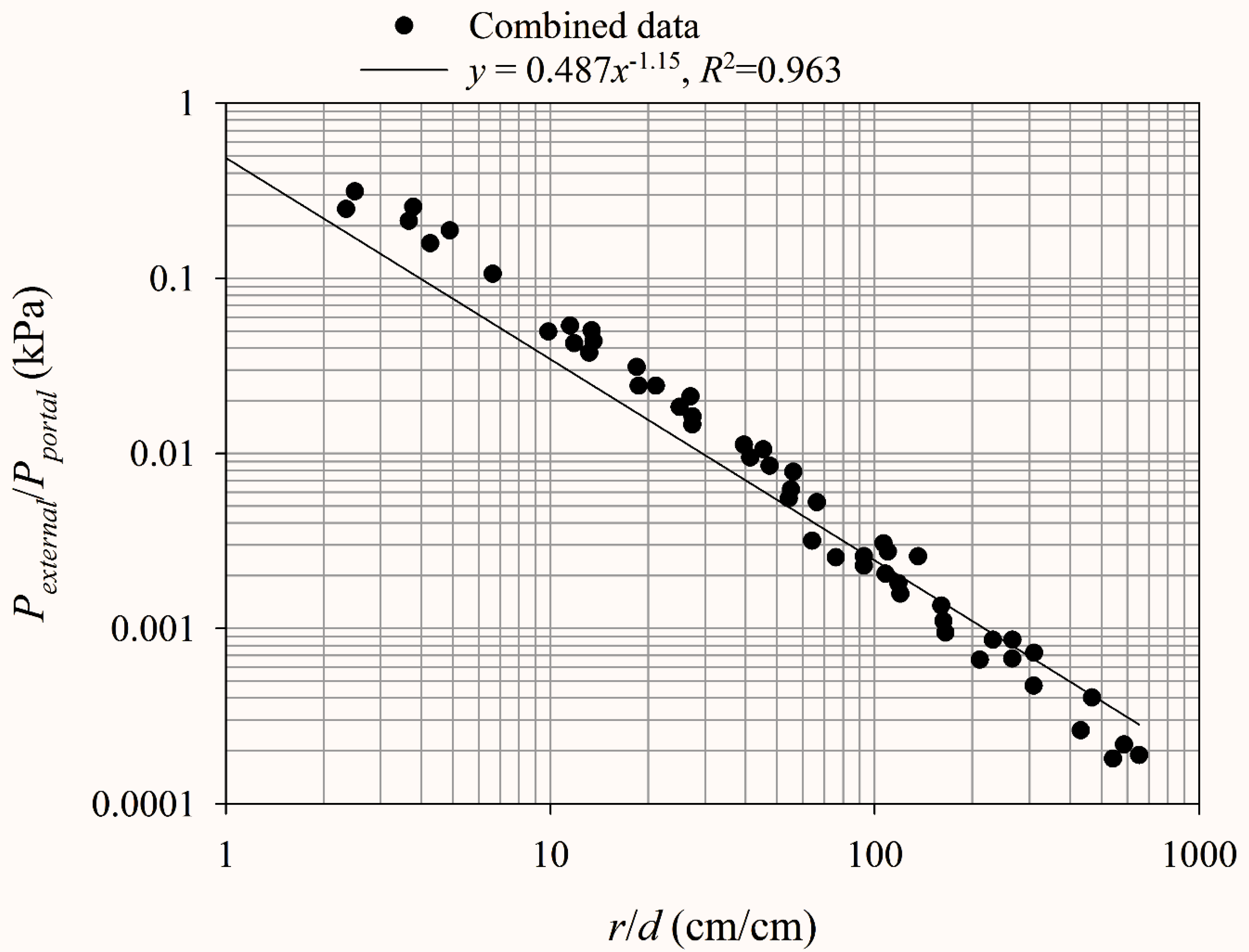
4.3. Ratio of the Blast outside the Ammunition Storage Magazine to the Blast at the Portal of Ammunition Storage Magazine
- (1)
- Experimental results
- (2)
- Comparison of the empirical equations
- (3)
- Empirical comparison with references
- (4)
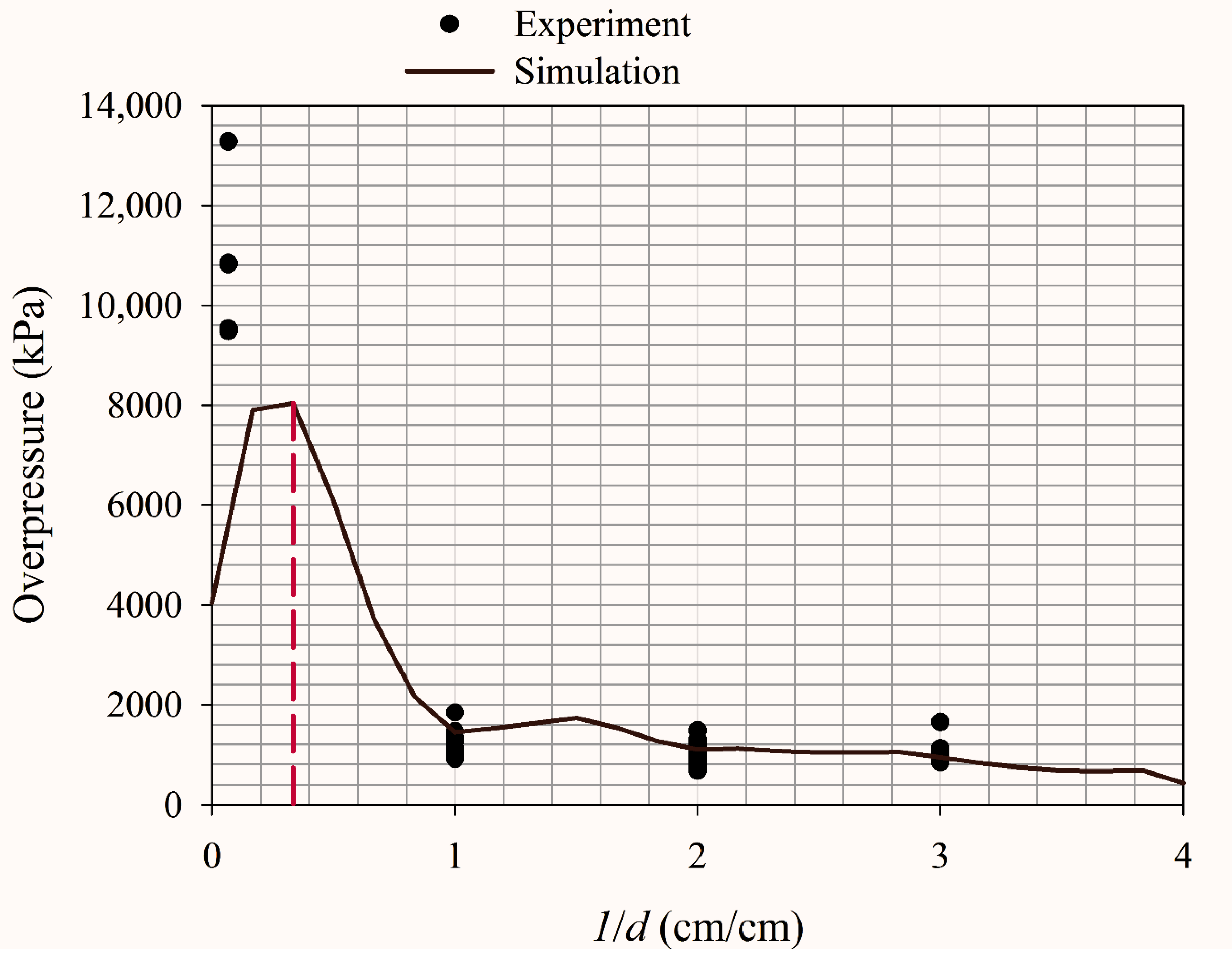
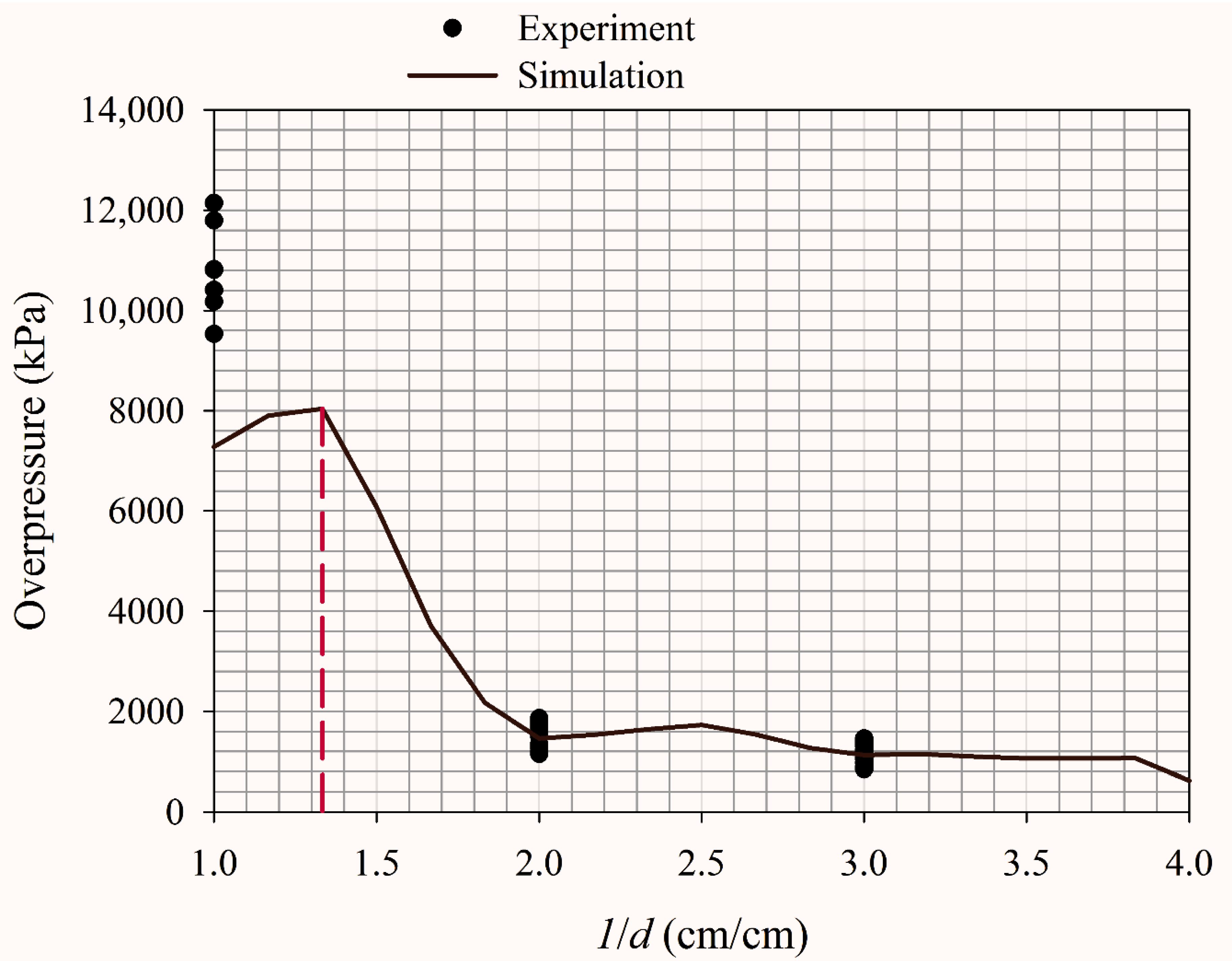
- Numerical simulation
- Portal explosion
- b
- Explosion at 1× the portal diameter inside the ammunition storage magazine
4.4. Effect of the Retaining Wall on the Near-Field Blast
- (1)
- Explosive detonating at the portal
- (2)
- Comparison with the explosion at 1× the portal diameter inside the ammunition storage magazine
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Swisdak, M.M. A Reexamination of the Airblast and Debris Produced by Expiosions Inside Earth–Covered Igloos; NAVSWC Report; TR 91–102; Paperback; USA, 1991; pp. 557–573. [Google Scholar]
- Weals, F.H. ESKIMO I Magazine Separation Test; NWC Report, TP 5430; USA, 1973; pp. 1–92. [Google Scholar]
- Weals, F.H. ESKIMO II Magazine Separation Test; NWC Report, TP 5557; USA, 1974; pp. 1–93. [Google Scholar]
- Weals, F.H. ESKIMO III Magazine Separation Test; NWC Report, TP 5771; USA, 1976; pp. 1–70. [Google Scholar]
- Weals, F.H.; Wilson, C.H. ESKIMO IV Magazine Separation Test; NWC Report; TP 5873; USA, 1977; pp. 1–54. [Google Scholar]
- Weals, F.H.; Finder, B. ESKIMO V Magazine Separation Test; NWC Report; TP 6076; USA, 1979; pp. 1–78. [Google Scholar]
- Kingery, C.N.; Coulter, G.A. Effect of Low Loading Density on Blast Propagation from Earth Covered Magazines; BRL Report; ARBRL–TR–02453; Maryland, USA, 1982; pp. 1–111. [Google Scholar]
- Kingery, C.N. Survey of Airblast Data Releated to Underground Munition Storage Sites; BRL Report; BRL–TR–3012; USA, 1989; pp. 1–34. [Google Scholar]
- Welch, B.; McMahon, W.; Davis, K. Transportation Tunnels and Ter–Rorist Attacks; ERDC: Vicksburg, MS, USA; pp. 1–77.
- Brill, A.; Me–Bar, Y.; Genussov, R.; Sadwin, L. Experimental Small–Scale Study of Blast Loads on Ammunition Magazines. In Proceedings of the 19th International Symposium on Military Aspects of Blast and Shock Conference, Calgary, AB, Canada, 2–6 October 2006; pp. 1–8. [Google Scholar]
- Hager, K.; Tancreto, J. AUTODYN 2D Predictions for Small Scale HP Magazine Cell Wall Tests. In Proceedings of the 25th Explosives Safety Seminar, Anaheim, CA, USA, 18–20 August 1992; pp. 373–420. [Google Scholar]
- Chen, H.C.; Hung, C.W.; Yu, W.F.; Cheng, D.S. Validation of Fluid Structure Interaction Models of Magazines Subjected to Internal Explosion. In Proceedings of the 8th International Conference on Shock & Impact Loads on Structures, Adelaide, Australia, 2–4 December 2009; pp. 1–9. [Google Scholar]
- Yu, W.F.; Hung, C.W.; Cheng, D.S. Effect of Subdividing Stacks on Blast Overpressure fromExplosion inside Ammunition Storage Magazine. J. Explos. Propellants 2009, 24, 25–40. [Google Scholar]
- Yu, W.F.; Hung, C.W.; Cheng, D.S. Effect of Blast wall on Safety Distance and Blast Overpressure for Ammunition Storage Magazine Subjected to Internal Explosion. J. Chung Cheng Inst. Technol. 2010, 39, 131–145. [Google Scholar]
- Cheng, H.L.; Wang, K.Y. A Study of the Effect of a Blast Wall on Pressure Attenuation. J. Chung Cheng Inst. Technol. 2011, 40, 85–96. [Google Scholar]
- Tancreto, J.E.; Conway, R.; Malvar, L.J. Response of Tilt–Up Reinforced Concrete and Unreinforced Masonry to Blast Loads. In Proceedings of the 12th International Symposium on Internation of the Effects of Munitions with Structures, Orlando, FL, USA, 18–21 September 2007; pp. 1–32. [Google Scholar]
- Ishikawa, N.; Beppu, M. Lessons From Past Explosive Tests on Protective Structures in Japan. Int. J. Impact Eng. 2007, 34, 1535–1545. [Google Scholar] [CrossRef]
- Swisdak, M.M.; Ward, J.M. The DDESB Blast Effects Computer. Available online: https://edms.energy.gov/EM/HASC%20Shared%20Documents/BlastEffectsComputer4.0Description.pdf (accessed on 11 April 2012).
- Skjeltorp, A.T. Underground Ammunition Storage: Blast Propagation in the Tunnel System. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a027066.pdf (accessed on 28 May 2015).
- Helseth, E.S. Blast Effects From Accidental Explosions; Report NR 174/85; Norwegian Defence Construction Service: Oslo, Noway, 1985. [Google Scholar]
- Hung, C.W.; Lai, H.H.; Shen, B.C.; Wu, P.W.; Chen, T.A. Development and Validation of Overpressure Response Model in Steel Tunnels Subjected to External Explosion. Appl. Sci. 2020, 10, 6166. [Google Scholar] [CrossRef]





| MAT_NULL, EOS_LINEAR_POLYNOMINAL | |||||
|---|---|---|---|---|---|
| Air | ρ (g/cm3) | C0 | C1 | C2 | C3 |
| 1.29 × 10−3 | 0 | 0 | 0 | 0 | |
| C4 | C5 | C6 | E0 (Mbar) | ||
| 0.4 | 0.4 | 0 | 2.5 × 10−6 | ||
| MAT_HIGH_EXPLOSIVE, EOS_JWL | |||||
| Explosive | ρ (g/cm3) | D (cm/μs) | PCJ (Mbar) | A (Mbar) | B (Mbar) |
| 1.601 | 0.819 | 0.28 | 6.097 | 0.1295 | |
| R1 | R2 | OMEG | E0 (Mbar) | V0 | |
| 4.5 | 1.4 | 0.25 | 0.09 | 1.0 | |
| MAT_PLASTIC_KINEMATIC | |||||
| Tunnel | ρ (g/cm3) | E (Mbar) | PR | SIGY (Mbar) | |
| 8.0 | 2.03 | 0.3 | 2.2 × 10−3 | ||
| MAT_RIGID | |||||
| Soil Ground | ρ (g/cm3) | E (Mbar) | PR | ||
| 1.8 | 2.0 × 10−3 | 0.498 | |||
| Item | Portal Section | 1d | 3d | 5d |
|---|---|---|---|---|
| Blast value from the numerical simulation (kPa) | 995.00 | 1040.00 | 153.00 | 61.30 |
| Blast value from the experiment (kPa) | 1864.59 | 1019.77 | 151.21 | 67.50 |
| Relative error (%) | −46.64 | 1.98 | 1.18 | −9.19 |
| Longitudinal Blast with a Retaining Wall (kPa) | Longitudinal Blast without a Retaining Wall (kPa) | Error (%) |
| 124.03 | 213.29 | −41.85 |
| Transverse Blast with a Retaining Wall (kPa) | Transverse Blast without a Retaining Wall (kPa) | Error (%) |
| 143.75 | 119.61 | 20.18 |
| Longitudinal Blast with a Retaining Wall (kPa) | Longitudinal Blast without a Retaining Wall (kPa) | Error (%) |
| 113.20 | 178.56 | −36.60 |
| Transverse Blast with a Retaining Wall (kPa) | Transverse Blast without a Retaining Wall (kPa) | Error (%) |
| 79.38 | 73.66 | 7.77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-W.; Tsai, Y.-K.; Chen, T.-A.; Wu, P.-W. An Experimentally Validated Numerical Model for the Near-Field Explosion of an Ammunition Storage Magazine. Appl. Sci. 2020, 10, 6849. https://doi.org/10.3390/app10196849
Hung C-W, Tsai Y-K, Chen T-A, Wu P-W. An Experimentally Validated Numerical Model for the Near-Field Explosion of an Ammunition Storage Magazine. Applied Sciences. 2020; 10(19):6849. https://doi.org/10.3390/app10196849
Chicago/Turabian StyleHung, Cheng-Wei, Ying-Kuan Tsai, Tai-An Chen, and Pin-Wen Wu. 2020. "An Experimentally Validated Numerical Model for the Near-Field Explosion of an Ammunition Storage Magazine" Applied Sciences 10, no. 19: 6849. https://doi.org/10.3390/app10196849
APA StyleHung, C.-W., Tsai, Y.-K., Chen, T.-A., & Wu, P.-W. (2020). An Experimentally Validated Numerical Model for the Near-Field Explosion of an Ammunition Storage Magazine. Applied Sciences, 10(19), 6849. https://doi.org/10.3390/app10196849





